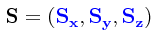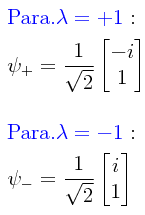Los operadores de desplazamiento espacial y temporal poseen la característica de que una función de onda Ψ, una vez desplazada mediante la aplicación de un operador de desplazamiento, ya no vuelve a quedar en su lugar original, ya sea en el espacio o en el tiempo. Puesto de otra manera, la aplicacion de un operador de desplazamiento sobre una función de onda Ψ(x,t) convirtiéndola en una función de onda Ψ’(x,t) nos dá la plena garantía de que:
Sin embargo, hay un tipo muy especial de desplazamientos en los cuales, tras la aplicación de un operador de desplazamiento, el cual no necesariamente es un operador identidad, la función de onda puede quedar exactamente en la misma posición en la que se encontraba antes de la aplicación de dicho operador.
Antes de emprender el camino que vamos a emprender, vale la pena formularnos una pregunta importante: ¿Cuál podría ser nuestro interés en desarrollar operadores de rotación de carácter general? ¿Qué puede tener esto que ver con las mediciones que llevamos a cabo en el laboratorio? La respuesta en parte ya fue dada previamente en la entrada titulada “Rotaciones de las matrices de Pauli”. Haremos aquí un breve repaso dada la importancia del tema, recurriendo al experimento clásico de Stern-Gerlach ya que representa el experimento más sencillo posible para el desarrollo y el entendimiento del aparato matemático que está siendo construído como base de la Mecánica Cuántica.
Supóngase que tenemos un aparato Stern-Gerlach que recibe a las partículas acabando de salir del horno, orientado de modo tal (paralelo al eje-z, el eje vertical en el laboratorio) que separe las partículas en aquellas partículas que tienen su spin apuntando “hacia arriba” y aquellas partículas que tienen su spin orientado “hacia abajo”. En términos matemáticos, lo que estamos midiendo es Sz. Los dos eigenvalores de la matriz Sz son precisamente lo que representa a las partículas cuyo spin está apuntando “hacia arriba” (en el sentido positivo del eje-z) con un valor igual a +ħ/2, y las partículas cuyo spín está apuntando “hacia abajo” (en el sentido negativo del eje-z) con un valor igual a -ħ/2. Efectuemos ahora una operación matemática de rotación sobre la matriz Sz convirtiéndola en una matriz Sx. Esto equivale a girar el aparato Stern-Gerlach en un ángulo de 90 grados. Viendo directamente hacia el haz de partículas que están saliendo del horno (encaminadas directamente hacia nuestros ojos), la rotación de que le hemos dado al aparato Stern-Gerlach ya no distingue a las partículas cuyo spin está apuntando “hacia arriba” de las partículas cuyo spin está apuntando “hacia abajo”. Al estar alineado el aparato Stern-Gerlach paralelamente al eje-x, lo que ahora distinguirá serán las partículas cuyo spin está apuntando “hacia la derecha” de las partículas cuyo spin está apuntando “hacia la izquierda”. Los dos eigenvalores de la matriz Sx son precisamente lo que representa a las partículas cuyo spin está apuntando “hacia la derecha” (en el sentido positivo del eje-x) con un valor igual a +ħ/2, y las partículas cuyo spín está apuntando “hacia la izquierda” (en el sentido negativo del eje-z) con un valor igual a -ħ/2. Si de un primer aparato Stern-Gerlach obtenemos un haz de partículas cuyo spin spin está apuntando “hacia la abajo”, y pasamos este haz por un segundo aparato orientado 90 grados con respecto al primer aparato de modo tal que obtengamos partículas cuyo spin spin esté apuntando “hacia la derecha”, entonces aparentemente tendríamos ya un haz de partículas cuyas dos componentes agrupadas como un par (Sx,Sy) serían iguales a (+ħ/2,-ħ/2). Sin embargo, al buscar obtener una confirmación (con la ayuda de un tercer aparato Stern-Gerlach) del valor del spin sobre el eje-z de las partículas, encontraríamos con mucha sorpresa que nuevamente volvemos a tener sobre el eje-z un haz de partículas con su spin apuntando “hacia arriba” y otro haz de partículas con su spin apuntando “hacia abajo” en cantidades iguales, confirmando de esta manera que el segundo aparato Stern-Gerlach destruye por completo la información que habíamos obtenido con el primer aparato.
En lo que respecta al caso muy peculiar en el cual recurrimos a una rotación matemática de 90° para representar los eigenvalores de Sy, en tal caso y pese a que la matriz S_y tiene como entradas números imaginarios, los eigenvalores de la matriz siguen siendo +ħ/2 y -ħ/2. Pero aquí ocurre una cosa muy curiosa. Por la forma en la cual se acostumbra montar el ejes de coordenadas rectangulares Cartesianas en un experimento Stern-Gerlach, una medición del haz de partículas sobre el eje-y implica que estaríamos midiendo el momento angular de las partículas no “hacia arriba” ni “hacia abajo”, ni tampoco “hacia la derecha” o “hacia la izquierda”, sino a lo largo de la misma dirección en la cual las partículas salen del horno, o sea (suponiendo que estamos mirando directamente hacia el orificio desde el cual salen las partículas encaminadas directamente hasta nuestros ojos), estaríamos midiendo el spin de las partículas que están apuntando “hacia adelante” o “hacia atrás”. Este pequeño detalle es la razón principal por la cual las matrices de Pauli son asignadas en la forma en la que son asignadas, dejando la matriz de Pauli con entradas imaginarias para la medición de Sy, aunque desde el punto de vista meramente matemático no hay razón para dar una preferencia en la asignación de las coordenadas Cartesianas a las matrices de Pauli.
El experimento hipotético que hemos llevado a cabo resulta algo simple porque la rotación que le hemos dado al aparato Stern-Gerlach es una rotación precisa de 90°. ¿Pero qué pasaría si en vez de darle al aparato una rotación de 90° le damos una rotación arbitraria de unos 50° ó de unos 73°? Intuitivamente, y armados con lo que ya sabemos, esperamos que en su nueva posición angular el aparato Stern-Gerlach subdivida el haz de partículas entrante en dos haces de partículas, con cada partícula del haz teniendo un valor igual +ħ/2 ó a-ħ/2 (podemos abandonar aquí, por necesidad imperiosa, la designación que estábamos usando previamente describiendo al spin de las partículas como “apuntando hacia arriba”, “apuntando hacia abajo”, “apuntando hacia la derecha”, “apuntando hacia la izquierda”, “apuntando hacia adelante” y “apuntando hacia atrás”, porque al hablar de un giro angular completamente arbitrario estas descripciones sencillas ya no resultan satisfactorias, y en lugar de ello podemos trataremos al haz de partículas como partículas cuyo spin puede apuntar en un sentido, en el sentido positivo, o en el sentido opuesto, en el sentido negativo). Esto es justo lo que esperamos, que una rotación arbitraria del aparato Stern-Gerlach nos siga sub-dividiendo al haz de partículas que salen del horno en dos haces. ¿Pero podemos ampliar nuestro aparato matemático para cubrir esta nueva situación, de rotaciones arbitrarias dadas al instrumento Stern-Gerlach? Si no podemos hacer tal cosa, el aparato matemático no nos serviría de mucho excepto para casos muy especiales. La búsqueda de operadores de rotación general para describir rotaciones del momento angular de spin se convertirá en nuestra primera prioridad, y posteriormente intentaremos ampliar la estructura matemática que desarrollemos para cubrir rotaciones que tengan que ver con la medición del momento angular orbital, lo cual requerirá pasar de las matrices de Pauli 2×2 a matrices 3×3 o inclusive de mayor dimensión.
Así pues, si podemos girar en el laboratorio un aparato Stern-Gerlach en ángulos múltiples de 90°, también podemos girarlo en cualquier ángulo arbitrario o inclusive en cualquier dirección en el espacio tridimensional. Esto implica que para la descripción matemática de una rotación arbitraria del aparato Stern-Gerlach tendremos que llevar a cabo una combinación de las tres matrices de Pauli asociadas con las tres coordenadas rectangulares Cartesianas que sea capaz de producirnos un operador de rotación general.
Si el generador de desplazamientos espaciales es el operador del momentum p, y si el generador de desplazamientos temporales es el operador de energía Hamiltoniano H, ¿que podría ser entonces el generador de las rotaciones? La única respuesta posible: un operador del momento angular. En realidad, esta conclusión en cierta forma ya se había obtenido previamente en la entrada “La matriz generadora de rotación”. Sin embargo, es importante destacar el hecho de que dicha entrada forma parte del área de estudio conocida como la Mecánica Matricial en donde no existen las funciones de onda sobre las cuales actúe un operador de rotación (en la Mecánica Matricial lo que cambia son las componentes de la matriz que tiene incrustadas como componentes matriciales a las observables, fuera de la matriz todo permanece igual), y esta es una diferencia importante. Sin embargo, en virtud de la plena equivalencia que hay entre la Mecánica Matricial y la Mecánica Ondulatoria, es de esperarse que muchas de las conclusiones obtenidas bajo la Mecánica Matricial puedan ser transplantadas, con cambios menores, a la Mecánica Ondulatoria.
Pero habiendo dos tipos de momento angular, el momento angular intrínseco asociado al spin de una partícula y el momento angular orbital, ¿cuál de los dos habremos de utilizar? La respuesta obvia: los dos. Todo depende de lo que esté siendo “girado”.
Como ya se asentó arriba, al entrar en el estudio de las rotaciones bajo la óptica de la Mecánica Ondulatoria, nos fijaremos un objetivo importante. A diferencia de lo que se vió en la entrada titulada “Rotaciones de las matrices de Pauli”, en donde las rotaciones estaban limitadas a aquellas rotaciones finitas en múltiplos enteros de 90° ó 180° en las cuales los ejes coordenados rectangulares una vez girados caían coincidiendo sobre los ejes coordenados rectangulares previos, intentaremos llevar a cabo algo más ambicioso: rotaciones no necesariamente limitadas a múltiplos enteros de 90° ó 180° sino susceptibles de ser llevadas a cabo a lo largo de cualquier ángulo arbitrario φ. Y lo haremos poniendo énfasis en este tópico recurriendo a la notación bra-ket de Dirac, con la cual se le dará al asunto el enfoque moderno que se acostumbra darle en textos actualizados. Con este propósito, se definirán primero los siguientes kets de base con los cuales se dará una representación matricial a una partícula cuando tiene su spin apuntando “hacia arriba” (↑) asociado a un valor +1/2, y cuando tiene su spin apuntando “hacia abajo” (↓) asociado a un valor -1/2:
De acuerdo a la notación que es utilizada para obtener la contraparte de los kets en el espacio dual, los bras que corresponden a los kets de arriba serán:
Si tomamos los productos internos de estos kets y estos bras, obtenemos lo siguiente que confirma la ortonormalidad de las representaciones matriciales (vector renglón y vector columna) definidas arriba:
Los kets que han sido definidos arriba son conocidos formalmente en la literatura especializada como espinores (en inglés, spinors) y representados con la letra griega χ:
de forma tal que un espinor general está representado mediante una combinación lineal de los espinores de base:
Definidos los kets de base o espinores de base, podemos usarlos para definir algo más general, un ket de estado, también como un vector columna, recurriendo para ello al operador identidad apropiado (véase la entrada titulada “La notación bra-ket de Dirac”) e injertándolo de la manera que se muestra a continuación:
Del mismo modo, podemos definir al bra de estado como un vector renglón que vendría siendo el dual del ket de estado:
Estaremos trabajando aquí con las tres matrices de Pauli 2×2:
Con estas tres matrices, se puede definir un vector de matrices de Pauli de la siguiente manera:
Obsérvese que las tres componentes del vector σ son matrices 2×2. Sin embargo, obsérvese otra circunstancia curiosa: σ no puede ser considerado como una matriz, sino como un vector, por la manera en la cual ha sido definido; esta es precisamente la razón por la cual no se le ha destacado en color azul. Es un vector de matrices 2×2.
PROBLEMA: Dados los siguientes vectores:
demuéstrese la siguiente relación:
Podemos demostrar esta relación recurriendo a las relaciones de conmutación y anticonmutación:
Las matrices de Pauli son a su vez utilizadas para definir las tres componentes del spin para una partícula cuyo spin es igual a 1/2 (como el electrón y el protón):
Definimos el vector de spin S de la siguiente manera:
De nueva cuenta, obsérvese que las tres componentes del vector S son matrices 2×2. S no puede ser considerado como una matriz, sino como un vector, por la manera en la cual ha sido definido, esta es precisamente la razón por la cual no se le ha destacado en color azul. Es un vector de matrices 2×2.
PROBLEMA: Obténganse las representaciones para las componentes Sx, Sy y Sz del vector de spin S en función de productos externos de los kets y bras que han sido definidos arriba.
Empezaremos con la descomposición de Sz para obtenerlo en función de los productos externos de los kets y bras especificados arriba:
Procediendo del mismo modo, se obtiene:
La esperanza matemática de cualquiera de estos tres componentes del vector de spin para un estado cualquiera puede ser definida con la ayuda de los kets y bras de estado dados arriba:
Con la finalidad de poder asignar una dirección arbitraria en cualquier dirección en un sistema de ejes coordenados rectangulares Cartesianos, definiremos un vector unitario n en función de los vectores unitarios usuales de base {i,j,k}de la siguiente manera:
La otra simbolización alterna del vector unitario n es mediante el triplete usual ordenado de los elementos que lo especifican en función de sus componentes Cartesianos:
A continuación tenemos dos vectores unitarios, el primero apuntando sobre el plano x-y, y el tercero apuntando en una dirección en la que forma ángulos iguales con los tres ejes coordenados rectangulares:
Una representación equivalente que nos resultará más útil para discusiones posteriores es aquella en la cual este mismo vector unitario n está especificado en relación a dos ángulos, un ángulo polar β que representa el ángulo que forma el vector n con el eje-z, y un ángulo azimutal α que indica un giro en torno al eje-z:
La relación apropiada para expresar al vector unitario n en función de los ángulos α y β es la siguiente:
PROBLEMA: Compruébese que el vector n especificado arriba es realmente un vector unitario sin importar la dirección en la cual esté apuntando.
Esto resulta fácil de verificar usando en la expresión anterior combinaciones de ángulos para las cuales el vector n debe estar apuntando en la misma dirección del eje-z (tanto α como β iguales a cero), debe estar apuntando en la dirección del eje-x (α igual a cero y β igual 90°), y debe estar apuntando en la dirección del eje-y (α igual a 90° y β igual a cero ):
Al ser girado el vector n para ser puesto apuntando a lo largo de cualquiera de los tres ejes coordenados, toma la longitud unitaria que corresponde al vector de base para el eje coordenado en cuestión. Entonces la especificación dada para el vector n es tal que mantiene su longitud unitaria sin variación al ser desplazado de un eje a otro. Otra forma un poco más elegante y general de comprobar que este vector es unitario consiste en obtener la longitud |n| del mismo mediante la aplicación del teorema Pitagórico en tres dimensiones.
Si tomamos el producto punto del vector de spin S con el vector unitario n, o sea S·n, se tiene:
Substituyendo aquí aquello que representan las matrices Sx, Sy y Sz:
Sumando las tres matrices para ponerlo todo dentro de una sola:
Esto que tenemos aquí es un operador matricial. Definiremos ahora para el spin de la partícula un ket de estado de la siguiente manera a través de una eigenecuación en la cual el operador que actuará sobre dicho ket de estado será precisamente el operador S·n, regresándonos como resultado el eigenvalor de +ħ/2:
Este “ket de estado” debe ser capaz de poder ser obtenido a través de una combinación lineal de los kets de base:
en donde a y b son cantidades a ser determinadas. Tomando el ket de estado como acaba de ser definido en función de los kets de base, su dual correspondiente dual será entonces el siguiente bra:
Para que el ket de estado que se ha definido pueda estar normalizado, se requiere que el producto del ket de estado con su bra sea igual a la unidad, para lo cual se tiene entonces (sin intención alguna de confundir usaremos la simbología de flechas en la segunda línea con la finalidad de evitar que el signo “+” que simboliza un spin apuntando “hacia arriba” pueda ser confundido con el mismo signo “+” que representa una adición aritmética):
Usando las relaciones de ortonormalidad obtenidas arriba para los productos internos que aparecen en la última expresión, se obtiene la siguiente condición de normalidad:
Tomando por un lado a S·n como la matriz que se obtuvo arriba en funcion de los ángulos α y β, e igualándola a la matriz S·n que se obtiene cuando para el vector de matrices S se usan las representaciones para las componentes Sx, Sy y Sz del vector de spin S en función de productos externos de kets y bras, llegamos estas dos relaciones:
Trabajaremos sobre la primera relación:
Usaremos aquí las siguientes relaciones trigonométricas:
Con estas relaciones trigonometricas, se obtiene de la primera de las dos relaciones de arriba:
Procediendo del mismo modo y recurriendo nuevamente a las identidades trigonométricas dadas arriba, se obtiene de la segunda relación:
que es en realidad el mismo resultado que el anterior. Comparando lo que se tiene en ambos lados de esta última igualdad, esto nos sugiere que, usando como ayuda intermedia los ángulos θa (asociado con el parámetro a) y θb (asociado con el parámetro b) a ser determinados posteriormente según lo indiquen los desarrollos, intentemos usar dos relaciones como las siguientes:
Estas dos relaciones tentativas cumplen cabalmente con la condición de normalidad obtenida arriba para a y b, como podemos verificarlo de inmediato:
De las dos relaciones propuestas, se tiene:
Ahora bien, y por otro lado, de la primera relación se tiene:
Si usamos la siguiente identidad trigonométrica:
entonces:
Comparando esto con lo anterior, resulta evidente que la relación entre los ángulos θa y θb debe ser tal que:
Escogiendo el valor θa.=.0 con lo cual necesariamente θb.=.α, podemos ver que la definición precisa del ket de estado que estábamos buscando debe ser entonces (ignorando a estas alturas el factor de fase eiα tomando en cuenta el hecho de que los ángulos de fase en muchas funciones de onda no llevan peso alguno):
Vale la pena llevar a cabo una verificación del resultado que se acaba de obtener. Para los casos en los cuales el ángulo β es igual a cero, o sea con el vector unitario n apuntando “hacia arriba” a lo largo del eje-z, y cuando el ángulo β es igual a 180°, o sea con el vector n girado “hacia abajo”, se tiene como consecuencia:
Estos resultados son justo lo que esperaríamos, ya que con un ángulo β igual a cero el ket de estado que se ha definido debe regresarnos un spin apuntando “hacia arriba”, y es precisamente lo que ocurre; mientras que dando un giro de 180° al vector n el ket de estado debe darnos un spin apuntando “hacia abajo”, lo cual también ocurre. ¿Y qué sucede si demos un giro de 90° al vector n? En tal caso, se tiene:
Si tomamos el producto interno de esto considerando la condición de normalidad, el resultado nos dice que habrá una probabilidad de 1/2 de que las partículas en una lectura que se tome en el laboratorio bajo estas condiciones tendrán su spin apuntando “hacia arriba”, mientras que 1/2 de las partículas tendrán su spin apuntando “hacia abajo”.
En última instancia, el problema central de la Mecánica Cuántica es lo que se puede obtener en el laboratorio a través de los procesos de medición, un tema que no resulta fácil de asimilar para muchos principiantes. El físico Paul Adrien Maurice Dirac definió el proceso de medición con las siguientes palabras publicadas en 1958: “Una medición siempre ocasiona que el sistema salte a un eigenestado de la variable dinámica que está siendo medida (observada)”. Este es precisamente el proceso del colapso de la función de onda del cual se habló en la entrada “El acto de medición”, y significa que, antes de llevarse a cabo una medición, se supone que el sistema simbolizado como un eigenket de estado puede ser representado como una combinación lineal de eigenkets de base:
Recurriendo al “truco de Fourier”, nosotros podemos entresacar de esta serie (que puede ser infinita) cualquiera de los eigenkets así como el eigenvalor que está asociado al eigenket seleccionado con el simple expediente de tomar el producto interno del ket de estado con el bra que servirá para entresacar un componente de entre todos los demás de la serie (supondremos que los kets de base son ortonormales, de modo tal que el producto interno de dos kets de base será igual a cero si son diferentes y será igual a la unidad si son iguales):
Esto mismo que nosotros hacemos matemáticamente en un pizarrón es lo que la Naturaleza hace por nosotros al llevarse a cabo el acto de medicion, excepto que la Naturaleza lo hace de una manera completamente aleatoria. Para fines prácticos, dentro de la Mecánica Cuántica el llevar a cabo una medición equivale a tomar parte de un juego de dados. Cuando se lleva a cabo una medición, el sistema “salta” hacia uno de los eigenestados de la observable, lo cual se puede representar de la siguiente manera:
En el experimento de Stern-Gerlach, el ket de estado representa un átomo de plata orientado al azar saliendo del horno, con un spin arbitrario que podemos imaginar como una superposición de dos estados, el estado en el cual el spin está apuntanto “hacia arriba” (+ħ/2) y el estado en el cual el spin está apuntando “hacia abajo” (-ħ/2). Es el acto de medición (el acto de observación) lo que cambia el estado. Si se lleva a cabo una segunda medición con otro aparato Stern-Gerlach sobre la misma partícula con el aparato orientado en la misma dirección que el aparato Stern-Gerlach previo, el resultado de la medición será la certeza absoluta, ya que habiendo medido +ħ/2 una nueva medición sobre la misma partícula arrojará el mismo resultado +ħ/2, y si se midió -ħ/2 entonces una nueva medición sobre la misma partícula arrojará el resultado -ħ/2. Sin embargo, si el segundo aparato Stern-Gerlach está orientado en una dirección diferente al primer aparato Stern-Gerlach, entonces la certeza que se tenía de la medición anterior se destruye al llevarse a cabo la nueva medición. Cada medicion sucesiva que se lleve a cabo sobre la misma partícula pero usando aparatos Stern-Gerlach orientados en direcciones diferentes irá destruyendo la información previa que se tenía produciendo una nueva conclusión experimental:
La formulación, en notación bra-ket de Dirac, de la interpretación probabilista de Born, dando la probabilidad de que un sistema representado por un ket de estado “salte” hacia uno de los eigenvalores del sistema, es la siguiente:
Esto último amerita ser ilustrado de alguna manera.
PROBLEMA: Se tiene un sistema el cual se encuentra en un eigenestado S·n con un eigenvalor igual a +ħ/2, estando el vector unitario n situado en el plano xz haciendo un ángulo θ con el eje-z positivo. Suponiendo que se mide Sx, encuéntrese la probabilidad de obtener el valor +ħ/2.
La eigenecuación general del sistema es:
estando dado el eigenket del sistema por:
Si se mide Sx, entonces esto significa que en la medición el vector unitario n estará apuntando en la dirección del eje-x sobre la cual se efectúa dicha medición del momento angular de spin, no habiendo componentes de medición sobre los otros dos ejes coordenados, con lo cual:
Con el vector unitario n apuntando no a lo largo del eje-z sino en la dirección del eje-x sobre el cual se lleva a cabo la medición del momento angular de spin Sx, situación descrita por la eigenecuación:
no resulta difícil ver que el ángulo θ deberá ser igual a 90°, de modo tal que el eigenket de Sx al cual le corresponde el eigenvalor +ħ/2 será:
de modo tal que la eigenecuación del sistema toma el siguiente aspecto:
El eigenbra (vector renglón) que corresponde al eigenket (vector columna) que resulta de la medición será:
Entonces, de acuerdo a la definición de Born que se ha dado arriba en notación bra-ket de Dirac para la probabilidad de encontrar a una partícula con el valor especificado de +ħ/2 al hacerse una medición de Sx será:
o bien:
Usando la identidad trigonométrica sen(2a).=.2sen(a)cos(a), la probabilidad será entonces:
Para θ.=.π/2, la probabilidad de obtener +ħ/2 como resultado de la medición de Sx será igual a la unidad, como era de esperarse. Podemos visualizar esto como una situación en la cual después de haber salido un haz de partículas de un aparato Stern-Gerlach con el haz apuntando “hacia la derecha” (con las partículas que apuntan “hacia la izquierda”, con un valor de -ħ/2, desechadas como resultado de la medición), si se repite la medición con otro aparato Stern-Gerlach alineado sobre esa misma dirección el resultado será indudablemente igual a la certeza. Sin embargo, si el vector n está apuntando ya sea en el sentido positivo o en el sentido negativo del eje-z, o sea si θ.=.0 ó θ.=.π, la probabilidad de obtener como resultado de la medición de Sx el valor de +ħ/2 (apuntando “hacia la derecha”) será igual a 1/2, habiendo una probabilidad igual también a 1/2 de obtener como resultado de la medición de Sx el valor de -ħ/2 (apuntando “hacia la izquierda”). La situación para la cual el vector n está apuntando ya sea en el sentido positivo o en el sentido negativo del eje-z pero la medición que se lleva a cabo es la de Sx corresponde a una medición sobre otra coordenada Cartesiana (perpendicular) que destruye la información previa que se tenía del haz.
Si en el enunciado de este problema lo que se hubiera buscado es la probabilidad de obtener el valor de -ħ/2 (en lugar del valor +ħ/2) al llevar a cabo la medición de Sx, entonces la eigenecuación a ser utilizada es la siguiente:
PROBLEMA: En el problema anterior, calcúlese la dispersión en Sx, tal y como se define para propósitos de aplicación del principio de incertidumbre de Heisenberg, y verifíquese la integridad del resultado obtenido para algunos casos especiales.
La definición estadística de la dispersión, si se estuviese trabajando con variables continuas, sería:
Pero en este caso no estamos trabajando con variables continuas, sino con matrices, específicamente, con la matriz Sx, razón por la cual tenemos que modificar en forma apropiada la definición de dispersión (la matriz I representa la matriz identidad):
Para la evaluación de esto, por un lado tenemos:
mientras que por el otro lado partiendo de la definición de la esperanza matemática para Sx:
se tiene:
Entonces la dispersión estadística de los valores del momento angular de spin será:
Tenemos ya suficiente material arriba para poder intentar describir matemáticamente lo que sucede en un experimento en el cual se cuente con dos o más aparatos Stern-Gerlach y en el cual se lleve a cabo la rotación física de uno de los aparatos con respecto al otro.
PROBLEMA: Supóngase que se lleva a cabo un experimento Stern-Gerlach efectuando mediciones con tres aparatos idénticos sobre un haz entrante de partículas cuyo spin es 1/2. En la primera medición, con el aparato orientado verticalmente para medir Sz, se dejan pasar las partículas cuyo spin es Sz.=.+ħ/2, rechazándose las partículas cuyo spin sea Sz.=.-ħ/2. En la segunda medición, con el aparato orientado en forma tal que Sn sea el eigenvalor del operador S·n con el vector unitario n haciendo un ángulo β en el plano-xz con respecto al eje vertical, se dejan pasar las partículas cuyo spin es Sn.=.+ħ/2, rechazándose las partículas cuyo spin sea Sn.=.-ħ/2. Finalmente, en la medición llevada a cabo con el tercer aparato, la medición acepta las partículas Sz.=.-ħ/2 rechazando las partículas Sz.=.+ħ/2. Obténgase una expresión para el haz resultante de partículas obtenidas de la medición triple llevada a cabo en el experimento Stern-Gerlach secuencial.
La naturaleza del experimento es tal que dos de los aparatos, el primero y el tercero, se encuentran en una posición fija, y el único aparato que puede ser cambiado de posición es el segundo aparato, girándolo en un ángulo polar β con respecto al eje-z vertical sobre un plano xz que es perpendicular a la dirección del haz de partículas:
Partiendo sobre la base de que se tiene al primer aparato orientado verticalmente en forma tal que el haz entrante de partículas será separado en dos haces, un haz de partículas con el spin apuntando “hacia arriba” con un valor igual a +ħ/2, y otro haz de partículas con el spin apuntando “hacia abajo” con un valor igual a -ħ/2, el resultado de esto se puede representar mediante una matriz en la cual estos valores sean puestos como eigenvalores de la matriz en su diagonal principal, lo cual a su vez se puede descomponer en la forma que se muestra a continuación:
La matriz puesta al principio, por ser una representación diagonal de los eigenvalores que están siendo medidos sobre el eje-z, frecuentemente es conocida como base Sz diagonal. El producto ket-bra (en color azul) que aparece multiplicando al primer eigenvalor es lo que representa al haz de partículas cuyo spin apunta “hacia arriba”, mientras que el producto ket-bra (en color magenta) que aparece multiplicando al segundo eigenvalor es lo que representa al haz de partículas cuyo spin apunta “hacia abajo”. Podemos darle a cada uno de estos productos ket-bra la siguiente simbolización que mete el concepto de la medición que se está llevando a cabo:
Como resultado de la primera medición con el aparato orientado verticalmente para medir Sz, dejándose pasar las partículas cuyo spin es Sz.=.+ħ/2 y rechazándose las partículas cuyo spin es Sz.=.-ħ/2, la simbolización correcta de la primera medición es la siguiente:
Como resultado de la segunda medición, con el aparato orientado en forma tal que Sn es el eigenvalor del operador S·n con el vector unitario n haciendo un ángulo β en el plano-xz con respecto al eje vertical, dejándose pasar las partículas cuyo spin es Sn.=.+ħ/2, y rechazándose las partículas cuyo spin es Sn.=.+ħ/2, usando lo que se desarrolló arriba previamente y tomando:
la simbolización correcta de la segunda medición debe ser la siguiente:
Y en lo que respecta al tercer aparato, con la medición orientada en forma tal que se acepta a las partículas Sz.=.-ħ/2 y se rechaza las partículas Sz.=.+ħ/2, la simbolización correcta de la tercera medición es la siguiente:
El resultado de la medición total es igual al producto operacional de las tres mediciones que se llevan a cabo. El orden de los factores en el producto operacional es importante, porque generalmente hablando, las rotaciones a menos de que siempre se lleven a cabo en la misma dirección y sentido en torno a un mismo eje no son conmutativas. En este caso, el orden debe ser el siguiente sobre el supuesto de que el producto operacional de las mediciones actúa sobre una función de onda espinor puesta a la derecha del producto operacional múltiple:
Substituyendo en esto último las tres expresiones que tenemos arriba, se obtiene:
Llevando a cabo en forma directa la multiplicación de los productos bra-ket y eliminando todo aquello que se pueda eliminar de acuerdo a las condiciones de ortonormalidad, se encuentra rápidamente que sólo sobrevive un término, quedando como resultado final:
Por la forma en la que se conduce el experimento, el primer aparato se encuentra fijo al igual que el tercer aparato. El único aparato que se puede girar es el segundo aparato, en un ángulo β. Esto implica que la intensidad final del haz dependerá directamente del factor multiplicativo:
En la intensidad final del haz, la contribución de este factor multiplicativo será:
Para un ángulo β igual a cero grados, el factor multiplicativo hará que la intensidad final del haz de partículas sea igual a cero. Lo mismo ocurrirá para un ángulo igual a 180°. Si se desea obtener la mayor intensidad posible del haz resultante de la medición total (la mayor cantidad de partículas), el segundo aparato deberá ser posicionado a un ángulo β igual a 90°. Esta intensidad, en el mejor de los casos, no será superior a la cuarta parte del haz de partículas que entró al primer aparato.
Aunque hemos estado manejando el concepto de probabilidad bajo la interpretación estadística de Born mediante la cual se le asigna un valor probabilista de 1 a la certeza (la probabilidad de que algo ocurra o que pueda darse) y un valor de cero a la incertidumbre total, igual podríamos haber manejado una probabilidad del 0% para la incertidumbre total y del 100% para la certeza total (como se acostumbra hacerlo en el caso de los sondeos pre-electorales que predicen de antemano los resultados de una votación dentro de cierto margen de incertidumbre). Hay, sin embargo, otra manera de medir la probabilidad que aunque no es utilizada mucho en la Mecánica Cuántica resulta conveniente tener en mente para aquellos casos esporádicos en los cuales se le utilice, y esto es mediante la probabilidad absoluta, en la cual manejamos números que miden en cantidades reales aquello de lo que estamos hablando. Es así como decimos, por ejemplo, que la probabilidad de que un boxeador gane una pelea según las apuestas es de 7 a 4, o que la probabilidad anual de que ocurran cierto número de accidentes en cierta carretera es igual a 125 accidentes, o que la temperatura más probable a cierta hora del día será igual a 20.°C. Del mismo modo puede plantearse este tipo de situación con el problema típico en el cual se debe calcular la probabilidad de obtener algún resultado en la medición de algo. Supóngase que, dado el siguiente estado de spin:
y trabajando con la siguiente matriz de Pauli:
se desea calcular la probabilidad de obtener el resultado +ħ/2 si se mide en el laboratorio Sy. En este caso, la ecuación matricial que debe satisfacer la eigenfunción ψ viene siendo:
que a su vez se traduce en la siguiente ecuación secular:
Llevando a cabo los cálculos como se ha hecho en las entradas previas para la determinación de los eigenvalores, se encuentra que las raíces de la ecuación secular son ±1. Por lo tanto, usando nuevamente:
esto nos conduce a las siguientes soluciones:
Si usamos ahora la condición de normalización, de acuerdo a la cual:
obtenemos como soluciones las siguientes eigenfunciones normalizadas:
Ahora bien, sabemos que:
y sabemos también que:
Estando la situación general representada por un electrón en el estado de spin:
la probabilidad de que un electrón con tal estado de spin se encuentre en ψ+ a lo cual a su vez le corresponde el eigenvalor +ħ/2 cuando se mide Sy, será:
Para la evaluación de esto último, usamos:
obteniendo:
Obsérvese que en la respuesta obtenida aparece el factor ħ2, el cual es un factor numérico experimental. Por lo tanto, la probabilidad que se ha obtenido es la probabilidad absoluta de que se obtenga el resultado ħ/2 al medir en el laboratorio Sy.
Con el vector unitario n, una vez comprendida la acción de una operación de rotación en un experimento en el que se esté midiendo la intensidad de un haz emergente de partículas que haya pasado por un aparato Stern-Gerlach, estamos ya en condiciones de poder iniciar la búsqueda de un operador de rotación para el momento angular (intrínseco) del spin de la partícula, el cual debe ser extensible con cambios mínimos para poder describir las rotaciones que tienen que ver con las mediciones que se lleven a cabo sobre el momento angular orbital. En esto nos servirá como guía y ayuda el material que ya vimos con anterioridad en las entradas tituladas “El operador de traslación” y “El operador de evolución del tiempo” en donde se dedujo la naturaleza de ambos operadores:
Nota Bene: La columna izquierda en ésta página Web solo muestra los primeros 93 capitulos de ésta obra. La lista completa de enlaces hacia todos los capítulos de los que consta la obra se encuentra disponible por orden numérico en la primera entrada titulada "Indice"
Seguidores
Archivo del blog
-
▼
2009
(152)
-
▼
agosto
(152)
- Indice
- Prólogo
- El modelo atómico planetario de Bohr I
- El modelo atómico planetario de Bohr II
- La espectroscopía de rayos-X
- La extraña ecuación de Max Born
- Vectores y matrices I
- Vectores y matrices II
- El análisis de Fourier
- La regla de multiplicación de Heisenberg
- Observables compatibles e incompatibles
- Oscilador armónico simple: solución matricial
- Matrices y probabilidad
- El principio de incertidumbre I
- El principio de incertidumbre II
- El experimento Stern-Gerlach
- El spin del electron
- Momento angular: tratamiento matricial I
- Momento angular: tratamiento matricial II
- Momento angular: tratamiento matricial III
- La energía rotacional
- Matrices y sub-matrices
- Solución matricial del átomo de hidrógeno
- Funciones matriciales
- De la mecánica clásica a la mecánica matricial
- La matriz momentum como generadora de traslación
- La matriz generadora de rotación
- Rotaciones de las matrices de Pauli
- El aspecto estadístico de la Mecánica Matricial
- Evolución temporal de los sistemas físicos
- Matrices continuas
- Ondas de materia
- La ecuación de Schrödinger
- Solución matemática de la ecuación de onda
- Solución numérica de la ecuacion de Schrödinger
- Interpretación probabilista de ψ I
- Interpretación probabilista de ψ II
- Interpretación probabilista de Ψ III
- Operadores y esperanzas matemáticas I
- Operadores y esperanzas matemáticas II
- Oscilador armónico simple: solución ondulatoria
- La función delta de Dirac
- Transmisión y reflexión de partículas I
- Transmisión y reflexión de partículas II
- Transmisión y reflexión de partículas III
- Transmisión y reflexión de partículas IV
- El potencial delta de Dirac
- Ondas de simetría circular y esférica
- La notación bra-ket de Dirac
- El espacio de Hilbert I
- El espacio de Hilbert II
- Operadores Hermitianos
- Los operadores escalera I
- Los operadores escalera II
- El principio de incertidumbre, revisitado
- El acto de medición
- Momento angular orbital: análisis ondulatorio I
- Momento angular orbital: análisis ondulatorio II
- Momento angular orbital: funciones de onda I
- Momento angular orbital: funciones de onda II
- Polinomios de Legendre: aspectos matemáticos
- La función de onda radial
- La función de onda del momento angular del spin
- El principio de exclusión de Pauli
- El proceso de construcción Aufbau
- El acoplamiento LS
- La suma de momentos angulares
- Las reglas de selección
- Técnicas de aproximación I
- Técnicas de aproximación II
- Técnicas de aproximación III
- Técnicas de aproximación IV
- Perturbacion y estados degenerados I
- Perturbacion y estados degenerados II
- Modelos perturbativos para átomos hidrogenoides
- El efecto Stark I
- El efecto Stark II
- Corrección perturbativa relativista
- La estructura fina del hidrógeno
- Perturbaciones dependientes del tiempo I
- Perturbaciones dependientes del tiempo II
- Perturbaciones dependientes del tiempo III
- Interacción con un campo electro-magnético I
- Interacción con un campo electro-magnético II
- Interacción con un campo electro-magnético III
- El método de aproximación WKB I
- El método de aproximación WKB II
- El método de aproximación WKB III
- El método de aproximación WKB IV
- El enlace molecular I
- El enlace molecular II
- La hibridación de los orbitales atómicos
- La teoría de los orbitales moleculares
- Teoría del campo cristalino
- Operadores clase T
- El espacio-posición y el espacio-momentum I
- El espacio-posición y el espacio-momentum II
- El espacio-posición y el espacio-momentum III
- El espacio-posición y el espacio-momentum IV
- La partícula libre I
-
▼
agosto
(152)