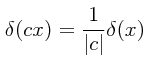La función delta de Dirac

Para ciertas situaciones tales como una partícula que no está confinada en un pozo potencial y que se está desplazando libremente de un lado a otro, necesitamos algo que nos permita describir al menos la posición de esa partícula libre, algo que nos permita situarla como una partícula puntual en cierto sistema de coordenadas como (x,y,z). Para hacer frente a esta necesidad, el físico-matemático inglés Paul Adrien Maurice Dirac propuso un nuevo tipo de función conocida en nuestros días como la función delta de Dirac. Esta función, extremadamente impropia (matemáticamente hablando, es casi una imposibilidad, que sin embargo puede ser manipulada matemáticamente), está inspirada directamente en el delta de Kronecker, definido de la manera usual:

δ_ij = 1___para i = j

δ_ij = 0___para i ≠ j

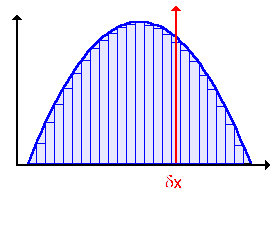
en donde i y  j son números discretos (enteros). Lo que se quiere es tomar el concepto del delta de Kronecker haciéndolo extensivo para sub-índices que representan cantidades continuas que en principio pueden tomar cualquier valor que forme parte del conjunto de los números reales. Con esto en mente, definiremos a la función delta de Dirac como una función límite. Considérese la siguiente figura:

El área de esta figura, colocada de modo tal que está centrada en la coordenada x.=.x’, es obviamente igual a la unidad, o sea que A = (a)(1/a) = 1.

A continuación, iremos recortando el ancho de la figura y ampliando al mismo tiempo su altura, de modo tal que el área siga siendo la misma, igual a la unidad:

Obsérvese que en (d) hemos llevado al extremo el proceso iniciado en (a) y continuado en (b) y en (c). En efecto, le hemos dado a la figura una altura infinitamente grande, y una anchura infinitamente pequeña. Esto de primera vista puede parecer absurdo, pero si lo consideramos como un proceso límite, no hay nada errado en lo que hemos hecho. Hemos mantenido todo el tiempo el “área bajo la curva” igual a la unidad.

En base al proceso extremo que hemos llevado a cabo, se antoja tentador definir a esta función de la manera siguiente situando el “pico” en una posición x.=.a en donde a puede ser igual a cero (situando el “pico” en el centro del sistema de coordenadas) :

δ(x - a) = ∞___para x = a

δ(x - a) = 0___para x ≠ a

La desventaja de esta definición por sí sola es que involucra un infinito que no se presta a la manipulación matemática. Tenemos que ampliarla (o confinarla) de alguna manera.

Una forma de ampliar la definición de nuestra función extrema sería basarnos en el hecho de que el “área bajo la curva” es igual a la unidad, y en el cálculo infinitesimal ya hay una forma de definir el “área bajo la curva” para cualquier función dentro de un rango a.≤.x.≤.b para la variable independiente:

Esta definición del “área bajo la curva” es una definición precisa, exacta, que se presta a la manipulación matemática; es el resultado de ir subdividiendo el área bajo la curva que hay debajo de una función cualesquiera:

y sumar el área de los rectángulos entre x₁.=.a y x₂.=.b para obtener de este modo una buena aproximación al área. A cada uno de estos rectángulos le damos la misma anchura Δx, y cada rectángulo tendrá una altura diferente en cada punto x_n de la función. Esta manera de definir a la integral es conocida más formalmente como una integración mediante sumas de Riemann, y la noción intuitiva de llevar a cabo una sub-división del área bajo la curva en rectángulos cada vez más pequeños para aproximar el área real es conocida como la regla del rectángulo. En el proceso extremo, llevamos a cabo la subdivisión hasta el infinito, haciendo la anchura de cada rectángulo lo más cercano a cero que podamos (Δx→0) y sumando las contribuciones de una cantidad prácticamente infinita de rectángulos, lo cual en el proceso límite de la definición de la integral puede ser simbolizado de la siguiente manera:

con lo cual queda definida el área bajo la curva como el resultado de un proceso de integración o suma de áreas infinitesimales:

Puesto que en el proceso de construcción de nuestra función extrema se utilizó precisamente el área bajo la curva manteniéndose todo el tiempo igual a la unidad, y puesto que a los rectángulos, o mejor dicho, al rectángulo límite, se le fué disminuyendo su anchura Δx hasta hacerla igual a cero para fines prácticos, podemos definir a la función no por sí sola sino dentro de una integral, una integral que podemos especificar que sea llevada a cabo desde -∞ hasta +∞ a sabiendas de que el “pico” tiene que estar situado necesariamente entre los dos extremos del infinito para la coordenada que representa a la variable independiente, entre el infinito negativo y el infinito positivo. Esto nos dá la clave para tratar de darle una definición matemática completa a la función delta de Dirac δ(x) con la siguiente condición:

Sin embargo, hay muchos teóricos que consideran que, siendo la función delta de Dirac una función extraordinariamente impropia, se le debe definir por el efecto que tiene sobre otra función cuando multiplica a dicha función bajo el signo de la integral. Si la función a la que multiplica es una función cualquiera f.(x), entonces la definición de la función delta de Dirac (que es la que se usa en cálculos mecánico-cuánticos) vendría siendo la siguiente:

PROBLEMA: Demuéstrese, a partir de la definición formal de la función delta de Dirac que se ha dado, que el “área bajo la curva” de una función delta de Dirac es igual a la unidad.

Considérese primero la figura de una función delta de Dirac centrada en el origen:

Obsérvese que al “área bajo la curva” se le ha dado un color verde claro. Haciendo a.=.0 en la definición formal, se tiene entonces la siguiente relación para una función delta de Dirac centrada en el origen:

Esta expresión es válida matemáticamente para cualquier función f.(x). Selecciónese una función f.(x) tal que dicha función sea igual a la unidad en todo el espacio unidimensional. Entonces f.(0) ciertamente debe ser igual a la unidad, ya que f.(0) es uno de los valores posibles de f.(x). Siendo así, podemos efectuar entonces la siguiente operación:

Entonces el “área bajo la curva” de una función delta de Dirac que está ubicada en el origen es igual a la unidad.

Para el caso en el cual la función delta de Dirac no está posicionada en el origen del sistema de coordenadas, como en el siguiente caso en el cual ha sido desplazada a unidades hacia la derecha:

De nueva cuenta, selecciónese una función f.(x) tal que dicha función sea igual a la unidad en todo el espacio unidimensional. Entonces f.(a) ciertamente debe ser igual a la unidad, ya que f.(a) es uno de los valores posibles de f.(x). Siendo así, podemos efectuar entonces la siguiente operación:

Entonces el “área bajo la curva” de una función delta de Dirac es igual a la unidad, ya sea que la función δ esté posicionada en el origen o que esté posicionada en cualquier otro lugar del eje coordenado. Resaltaremos la importancia de la última relación del modo siguiente:

PROBLEMA: Demuéstrese que δ(x) = δ(-x).

La demostracion es trivial, ya que por la esencia misma de su definición δ(x) es una función par de su variable. Si no lo fuera, si fuese una función impar, se tendría entonces que:

δ(-x) = -δ(x)

Pero esto implicaría a la vez que:

El resultado final contraviene el supuesto de que el “área bajo la curva” de una función delta de Dirac es una cantidad positiva igual a la unidad.

Si hemos de hablar en estricto apego a la verdad, se debe resaltar el hecho de que la función delta de Dirac en realidad sólo tiene sentido cuando se utiliza bajo el signo integral. Y este es el punto central que nunca hay que perder de vista:

La función δ de Dirac por sí sola carece de sentido matemático y físico; dicha función solo tiene sentido cuando es usada bajo el signo de integración.

Resulta desafortunado (así como fuente de muchas confusiones entre los principiantes) el hecho de que en muchos textos al discutir relaciones que tienen que ver con la función delta de Dirac se omiten las integrales, causando la falsa impresión de que una función delta de Dirac es algo que puede ser manejado algebraicamente. A nosotros nos corresponde suplir esta deficiencia tipográfica en donde sea necesario. Considérense por ejemplo las siguientes dos relaciones tal y como aparecen en varios libros de texto:

La simbolización correcta (completa) de las dos relaciones anteriores es la siguiente:

Así como definimos una función delta de Dirac a lo largo de un solo eje coordenado, también podemos extender la definición hacia una función delta de Dirac en tres dimensiones, la cual no es más que el producto de tres funciones δ. La definición de este triple producto depende del sistema de ejes coordenados que se utilicen. En el caso más sencillo, el de ejes coordenados rectangulares Cartesianos, esperamos que la relación definitoria de una función delta de Dirac en tres dimensiones cumpla el siguiente requisito:

siendo dv el elemento infinitesimal de volumen. Puesto que el punto en el cual está ubicada la “discontinuidad δ” (en el espacio tridimensional) se puede simbolizar como un vector (a,b,c) medido con respecto al origen O del centro del sistema de coordenadas, y puesto que cualquier otro punto arbitrario en el espacio tridimensional se puede simbolizar como un vector (x,y,z), si simbolizamos a dichos vectores con tipo de letra “negrita” como se acostumbra hacerlo en muchos textos:

y tomando en cuenta que el vector que proporciona la distancia entre las puntas de dos vectores x y x’ está dada por la diferencia vectorial entre los mismos:

podemos entonces emplear la siguiente simbología para definir vectorialmente una función delta de Dirac en el espacio tridimensional:

en donde el super-índice 3 significa que se trata de una función delta construida con el producto de tres funciones delta especificadas sobre cada eje coordenado respectivo. Con la finalidad de que dicho super-índice no se preste a malinterpretaciones confundiéndolo con un exponente (cúbico) es común ver en algunos textos que se le ponga entre paréntesis:

Se debe aclarar que, en rigor de verdad, la función delta de Dirac no es una función en el sentido usual que se le dá a dicha palabra en las matemáticas, ya que cualquier función que sea igual a cero excepto en un solo punto debería de tener un valor de integración igual a cero, y aunque para fines formales se le puede definir como una distribución, la costumbre ha hecho que se le siga identificando como una función. Tal vez la mejor manera de visualizar a la función delta de Dirac sea como lo que realmente es, como un proceso límite en el cual se tiene, por ejemplo, un rectángulo (que supondremos centrado en el origen x.=.0) cuya área es igual a la unidad con su lado izquierdo situado en x.=.-ε y con su lado derecho situado en x.=.+ε (en la figura puesta a continuación, en virtud de que el rectángulo tiene una anchura igual a 2ε, la altura del rectángulo debe ser igual a 1/2ε para que el producto de la anchura por la altura sea igual a la unidad):

De este modo, al llevar a cabo una integración desde -∞ hasta +∞, en realidad se está llevando a cabo una integración sobre tres regiones: la región que está a la izquierda de la función delta de Dirac (a la izquierda de -ε), la región en la cual está situado el rectángulo hipotético que estamos utilizando como función delta (entre -ε y +ε), y la región que está situada a la derecha de la función delta (a la derecha de +ε). De este modo, al llevar a cabo la integración desde -∞ hasta +∞ sobre una función δ(x), el proceso matemático viene siendo:

Obsérvese que a la segunda integral se le ha escrito como un proceso límite en el cual ε.→.0, simbolizando con ello al rectángulo cuya anchura se va haciendo infinitamente pequeña. Puesto que fuera de la región situada entre -ε y +ε la función δ(x) es igual a cero, la primera integral y la tercera integral se nulifican quedando únicamente la integral intermedia, de modo que:

De este modo, llegamos a la raíz esencial de la definición ampliada de la función δ(x) de Dirac:

La notación intermedia dando como límites inferior y superior a -ε y +ε resulta particularmente útil para la resolución de problemas al momento de llevar a cabo una integración que involucre a la función δ(x). Específicamente, estamos hablando de una situación en la cual se lleva a cabo una integración de una función ψ(x) cualesquiera tomando el producto de la misma con la función delta de Dirac. ¿Cuál será el resultado de la integración? De acuerdo con el procedimiento que se acaba de delinear, debemos tener lo siguiente:

Nuevamente, puesto que fuera de la región cubierta por la función δ(x) de Dirac, el valor de δ(x) se toma como cero, esto nulifica la primera integral y la tercera integral dejándonos únicamente la integral intermedia. Al tomarse el límite ε.→.0, podemos dar por hecho de que justo en el punto x.=.0 la función ψ(x) toma el valor ψ(0), un valor fijo y constante, por lo que se tiene entonces:

Lo que se ha bosquejado arriba supone una función δ(x) centrada en el origen. Pero esto no tiene por qué ser necesariamente así, ya que como lo vimos arriba podemos ubicar a la función δ(x) en cualquier otro punto que no sea el origen, por ejemplo en el punto x.=.a. Si multiplicamos a la función delta de Dirac por una función ordinaria ψ(x) cualesquiera, esto es equivalente a multiplicar a la función delta de Dirac por ψ(a) siendo x.=.a el punto en donde está centrado el “pico”, ya que el producto de ambas es igual a cero en cualquier lado excepto en el punto a. Esto es lo que nos lleva a suponer que, informalmente, se debe obtener lo siguiente:

ψ(x) δ(x - a) = ψ(a)

Sin embargo, lo que acabamos de escribir no está justificado de una manera adecuada, en virtud de que como ya se ha señalado arriba la función delta de Dirac debe ser definida bajo el signo de la integral, por lo cual una manera un poco más formal de definir el producto de ambas funciones obteniendo lo que se acaba de escribir viene siendo:

Esta es quizá la propiedad más importante de la función delta de Dirac. Bajo un signo de integración, sirve para “entresacar” el valor de ψ(x) en el punto x.=.a, regresándonos ψ(a). Si tenemos alguna dificultad para visualizar lo que se acaba de definir, podemos considerar la siguiente integral que es el producto de dos funciones f(x) y g(x) bajo un mismo signo de la integral:

como la evaluación de las áreas conjuntas de ambas funciones, una evaluación que en el caso de las funciones f(t) = 3t³ y g(t) = 4t nos daría el siguiente resultado al llevarse a cabo la integración dentro del rango 0.≤.t.≤.2:

En nuestro caso, si una de las dos funciones es la función delta de Dirac, la integración de las áreas conjuntas resulta más fácil porque el “área bajo la curva” de la función delta de Dirac es igual a 1 en el lugar x.=.a en donde está posicionado el “pico”, y en ese punto específico la otra función f(x) adquiere un valor preciso f(a). No importan los límites de la integración, siempre y cuando el rango de los límites incluya el punto en donde está situado el “pico” de la función delta de Dirac que entresaca el valor de la función f(x) en dicho punto:

PROBLEMA: Evaluar la siguiente integral:

El único punto en el cual la integral no es igual a cero es en el punto x.=.-2 en donde la evaluación depende únicamente del valor que tenga la función f(x.=.-2):

(-2)³ - 3(-2)² + 2(-2) + 1 = -23

PROBLEMA: Evaluar la siguiente integral:

En este caso la integral es igual a cero, puesto que el punto en el cual la función delta de Dirac aplica su efectividad, x = -5, está fuera de los límites de la integración (-2 y +4).

Una pregunta interesante surge cuando multiplicamos a la función δ(x) por una constante y llevamos a cabo la integración. Específicamente, ¿qué interpretación puede dársele al resultado que se obtenga después de que se ha efectuado la integración? Puesto que la evaluación de una integral equivale a evaluar el “área bajo la curva”, el resultado que se obtenga equivale a multiplicar por una constante el área del rectángulo que estamos utilizando para definir mediante un proceso límite a la función delta de Dirac. En pocas palabras, se le aumenta su “área interna” a la función δ(x), como lo indica el siguiente procedimiento:

Si la constante α es igual a 5 unidades, entonces el área de la función delta será cinco veces mayor que el área unitaria del rectángulo de base. Podemos intentar visualizar esto con la siguiente figura de una función δ(x) centrada en el origen que ha sido multiplicada por una constante α, infinitamente estrecha en su anchura e infinitamente alta en el origen x.=.0, a cuya “área interna” se le ha dado un color marrón claro:

PROBLEMA: Demuéstrese que

Tómese cualquier función continua de la variable independiente, tal como f.(x). Entonces, puesto que:

se tiene que haciendo f(x).=.x:

ya que f.(0) ocurre en el punto x = 0, lo cual nulifica la contribución dada por δ(x) en dicho punto. (Estrictamente hablando, puesto que la función delta de Dirac se extiende un poco hacia ambos lados del punto central en donde toma su altura máxima, fuera del punto x.=.0 las contribuciones conjuntas de x y δ(x) harán que la integral no sea igual a cero. Para poder tomar lo anterior como cierto, se supone que se tiene una función delta de Dirac en la cual hacia los lados del punto x.=.0 la función delta cae tan rápidamente que podemos tomar lo anterior como una buena aproximación.)

PROBLEMA: Si c es una constante que puede ser positiva o negativa, demostrar que:

Dése asimismo una interpretación a esta relación.

Para llevar a cabo la demostración, nuestro punto de partida será la definición de la función delta δ(x) de Dirac bajo el signo de la integral conjuntamente con otra función cualesquiera f(x):

La comilla que se le ha puesto aquí a la variable no tiene nada que ver con diferenciación alguna, y su propósito es simplemente simbolizar a la variable independiente multiplicada por una constante, esto es:

x' = cx

Tomando diferenciales:

dx' = c dx

Con esto tenemos entonces:

Podemos sacar fuera de la integral la constante que está a un lado de la diferencial dx y pasarla del otro lado para así escribir:

Concentrémonos en el lado derecho de la igualdad ignorando por un momento el lado izquierdo. De la misma definición del delta de Dirac bajo el signo de la integral, tenemos lo siguiente:

Entonces podemos escribir lo siguiente:

Metiendo 1/c dentro del signo de integración tenemos entonces:

Comparando ambos lados, llegamos entonces a la siguiente conclusión:

Repitiendo los pasos considerando para la constante un valor negativo obtenemos el mismo resultado. Podemos entonces generalizar el resultado tanto para valores positivos como para valores negativos de la constante usando las barras con las cuales tomamos el valor absoluto:

Al igual que todo lo que tiene que ver con la función δ, la interpretación a cualquier resultado que se obtenga tiene que ser llevado a cabo situándola bajo el signo de una integral en la cual los dos extremos de la integral son un proceso límite que va cerrando a la función δ hacia una anchura cero. De este modo, si tomamos la relación obtenida se puede escribir lo siguiente:

Lo que se tiene en el lado izquierdo de la igualdad es el área de una función puesta sobre un sistema de ejes rectangulares Cartesianos en donde el eje horizontal (el eje-x) ha sido redimensionado por un factor de escala que viene siendo la constante c. Si el área de la función δ(x) bajo el signo de la integral es igual a la unidad, entonces el área de δ(cx) representará un valor diferente, y como el área de la función δ(x) en sí debe seguir siendo la misma, la ampliación (o reducción) del eje horizontal por un factor de escala tiene que ser balanceada por el recíproco de ese factor escala (1/|c|) que multiplique a la función δ(x). En términos llanos, un estiramiento (o encogimiento) de la “anchura” del rectángulo con el que definimos a la función delta de Dirac tiene que ser compensado con un encogimiento (o estiramiento) que mantenga siempre igual al área del rectángulo.

PROBLEMA: Demostrar que para la función de paso unitario, también conocida como la función de Heaviside H(x):

la derivada de dicha función es igual a la función delta de Dirac.

En este caso, a diferencia del problema anterior, sí utilizaremos la comilla para denotar la diferenciación de una función.

La resolución de este problema se efectuará de dos maneras, una de ellas más intuitiva de modo tal que permita la visualización de lo que está ocurriendo, y la otra un poco más formal. Empezaremos con la resolución intuitiva.

La definición de la derivada para cualquier función incluyendo la función de paso unitario H(x) está basada en el siguiente concepto esencial del límite:

En la gráfica que será dada a continuación se superimpondrán a la función de paso unitario los extremos para los cuales se considerará la diferencia Δx, uno en:

y el otro en:

Esquemáticamente, esto equivale a lo siguiente:

Gráficamente, para las regiones en las que x es menor que x.=.0 y mayor que x.=.0, la derivada dH/dx es muy clara: H(x) debe ser una línea plana en esas regiones y la pendiente (derivada) de una línea plana es igual a cero. En términos de la definición de derivada, puesto que H no cambia entonces ΔH.=.0 y consecuentemente dH/dx.=.0 en dichas regiones. Pero si tomamos dos puntos igualmente espaciados con respecto a x.=.0, uno de ellos en:

y el otro en:

entonces ΔH = 1 y Δx = a. No importa qué tan pequeño sea a, ΔH se mantendrá igual. Entonces la derivada de H(x) para x.=.0 será:

Gráficamente, esto es también bastante claro. H(x) salta de H(x).=.0 a H(x).=.1 en el punto x.=.0, de modo tal que la pendiente es esencialmente vertical, esto es, infinita. Juntando los resultados para dH/dx en uno solo tenemos lo siguiente:

Pero esto es esencialmente la definición de la función delta de Dirac. Se concluye que la derivada de la función de paso unitario es igual a la función delta de Dirac.

Aunque no hay nada erróneo en la derivación que se acaba de llevar a cabo, para quienes buscan un resultado más formal se presentará una demostración un poco más elaborada. Empezaremos por demostrar la siguiente igualdad matemática:

El punto de partida para la demostración será la expresión izquierda de la igualdad:

Si llevamos a cabo una integración por partes sobre esto, obtenemos lo siguiente:

Puesto que requerimos que el primer término se desvanezca en los límites infinitos (de lo contrario lo que tenemos no es integrable), el primer término debe ser igual a cero, quedándonos entonces:

A continuación, igualaremos la función f(x) a la función de paso unitario, f(x) = H(x), con lo cual la anterior expresión se convierte en:

En este último paso hemos cambiado el límite inferior de integración en el lado derecho en virtud de que para la función de paso unitario H(x) es igual a cero para valores de x inferiores a cero, y hemos utilizado también el hecho de que para valores de x mayores que cero la función de paso unitario tiene un valor igual a la unidad. Podemos llevar a cabo ahora la integración simbólica en el lado derecho obteniendo:

De nueva cuenta, se debe tener que φ(∞) = 0, porque de lo contrario la función no es integrable. Entonces:

En el lado derecho podemos substituír a φ(0) por su equivalente en la definición del delta de Dirac bajo el signo de la integral:

Comparando ambos lados de la igualdad, llegamos a la conclusión de que H’(x) = dH(x)/dx debe ser igual al delta de Dirac, o sea:

En palabras, la derivada de la función de paso unitario es igual a la función delta de Dirac.

La función delta de Dirac nos puede describir una partícula móvil que se está desplazando a lo largo de un eje coordenado temporal de la siguiente manera:

En una situación más realista, con la ayuda de la función delta de Dirac debe ser posible localizar una partícula no sólo a lo largo de un eje coordenado sino en un espacio tri-dimensional, ya que toda partícula real existe en un espacio tri-dimensional. Como ya se mencionó arriba, para una situación así, podemos definir tres funciones delta de Dirac, una para cada eje, y conjuntarlas todas por medio de un producto en una definición como la siguiente suponiendo que la partícula está ubicada en la posición (x,y,z) = (a,b,c):

δ(x - a) δ(y - b) δ (z - c) = ∞___para x = a y y = b y z = c

δ(x - a) δ(y - b) δ (z - c) = 0___para x ≠ a ó y ≠ b ó z ≠ c

De este modo, si ubicamos a una partícula en un sistema de coordenadas rectangulares Cartesianas mediante un vector r, de modo tal que, a modo de ejemplo, la partícula esté situada en el punto (x,y,z) = (3,1,5), entonces podemos dar la siguiente definición al delta de Dirac en tres dimensiones bajo el sistema de coordenadas Cartesianas:

En el sistema de coordenadas Cartesianas, un elemento infinitesimal de volumen dV está dado por un cubito de dimensiones laterales dx, dy y dz, por lo cual el volumen infinitesimal viene siendo dxdydz. Se tiene entonces que:

Aquí puede surgir nuevamente la duda del por qué es necesario recurrir a una función impropia tal como el delta de Dirac para ubicar a una partícula en un punto en el espacio si tal punto (a,b,c) podría especificarse mediante deltas de Kronecker como:

El problema es que, por convención, los sub-índices en los deltas de Kronecker son enteros, y no variables continuas. Pero aún si quisiéramos levantar la restricción, el otro problema es que el delta de Kronecker no puede ser integrado, porque se trata de algo cuyo valor (o cuya altura, recurriendo a la visualización geométrica) es igual a la unidad. La integral de un delta de Kronecker es exactamente igual a cero, porque se trata de una función cuya anchura es cero y cuya altura es finita (igual a la unidad), no habiendo por lo tanto ninguna “área bajo la curva” susceptible de ser integrada. Aplicado al mundo de las partículas puntuales, todas sus propiedades terminarían siendo iguales a cero al tratar de llevar a cabo cualquier tipo de integración. Esto fue lo que llevó a Dirac a “estirar” el concepto del delta de Kronecker dándole a los sub-índices de la función delta la capacidad de poder tomar valores continuos y no simplemente discretos, y requiriendo además que dicha función sea tal que al ser integrada la integral ésta no dé un valor igual a cero sino un valor finito (igual a la unidad), representando de este modo y en forma más realista una partícula en el espacio que en rigor de verdad no puede ser puntual ni siquiera en teoría porque en tal caso existiría al ser ubicable bajo ciertas coordenadas pero sin poder existir al ser su volumen (el producto de tres deltas de Kronecker) igual a cero.

Hemos trabajado hasta este punto con funciones delta de Dirac definidas mediante coordenadas rectangulares Cartesianas. Pero puesto que la especificación de algún punto en el espacio tridimensional debe ser algo independiente del sistema de coordenadas utilizado para ubicar dicho punto, debe ser posible definir una función delta de Dirac en cualquier otro sistema de coordenadas ortogonales, por ejemplo, en un sistema de coordenadas cilíndricas (r,θ,z). ¿Y cómo habremos de encontrar la forma de un delta de Dirac tridimensional en un sistema de coordenadas diferente del sistema usual de coordenadas rectangulares Cartesianas? La clave está en el elemento infinitesimal de volumen utilizado en el sistema de coordenadas en cuestión. En un sistema de coordenadas cilíndricas, por ejemplo, el elemento infinitesimal de volumen está dado por:

dV = r dr dθ dz

Llevando a cabo la triple integral sobre todo el espacio tridimensional (en el caso de las coordenadas cilíndricas, la integración de r se lleva a cabo desde 0 hasta ∞, la integración de θ se lleva a cabo desde 0 hasta 2π, y la integración de z se lleva a cabo desde “menos ∞” hasta “más ∞”), el equivalente al “área bajo la curva” debe ser igual a la unidad. Si no se produce tal resultado, entonces hay que meter los factores necesarios dentro de la definición delta que se construye para que la triple integral pueda ser igual a la unidad.

PROBLEMA: Expresar el delta de Dirac tridimensional δ(r-r’) en coordenadas esféricas polares.

En un sistema de coordenadas esféricas, la ubicación de cierto punto en el espacio se lleva a cabo mediante la especificación de una distancia radial r al origen y mediante la especificación de dos ángulos θ y φ tomados con respecto a ejes ortogonales, o sea como (r,θ,φ). Teniendo en mente que en un sistema de coordenadas esféricas el elemento infinitesimal de volumen dV está dado por r²dr·sen(θ)dθ·dφ, entonces usando los siguientes dos vectores:

la especificación más adecuada posible al delta de Dirac tridimensional debe ser la siguiente:

A continuación se tiene la verificación de que efectivamente esta es la definición correcta (obsérvese que en la verificación se recurre a un cambio de variables hacia la variable u):

Como ya se ha señalado en todo lo que tiene que ver con esta entrada, no se debe olvidar por un solo momento que todas estas definiciones se dan considerando a las funciones delta como procesos límite, y que su correcto significado y manipulación se debe realizar siempre bajo un signo integral.

Antes de continuar, vale la pena hacer una advertencia. El uso de dV para simbolizar un elemento infinitesimal de volumen tiene la desventaja de que la letra V puede ser malinterpretada (principalmente por quienes inician sus estudios en la Mecánica Cuántica) no como algo representando el volumen sino algo representando el potencial. Desafortunadamente, hay una práctica muy arraigada en el uso de dV para simbolizar un elemento infinitesimal de volumen, y con la finalidad de acostumbrar al lector al uso de tal símbolo también ha sido incorporado aquí en varias partes de esta obra, aunque se ha tratado de darle algo de variedad al asunto incorporando otros símbolos usados para representar al elemento infinitesimal de volumen, tales como dτ, d³τ, etc. El lector irá encontrando estos símbolos diversos conforme vaya avanzando en su lectura de esta obra.

Es posible darle a la función delta de Dirac varias definiciones considerándola como una aproximación tomada en el límite extremo de ciertas funciones matemáticas que se presten a ello. El ejemplo introductorio basado en un rectángulo cuya anchura se va reduciendo a cero y cuya altura se eleva hacia el infinito es una de tales funciones. Sin embargo, esta función “rectangular” puede dejarle un mal sabor de boca a quienes están acostumbrados a funciones continuas “suaves”, funciones con forma de curva. A continuación tenemos cuatro ejemplos de distintas funciones, todas las cuales en el límite ε.→.0 se van acercando más y más a las propiedades características de una función delta de Dirac:

Las gráficas respectivas de tales funciones son las siguientes (el color rojo en las curvas representa una aproximación de ε más cercana a cero que el valor de ε que corresponde a las curvas de color azul):

Sin embargo, aunque pueden ser buenas aproximaciones, ninguna de estar curvas puede ser una verdadera función delta de Dirac, porque en cada caso el valor de δ(x) para ε.=.0 y x.=.0 no está definido.

Otra función que también tiene un gran parecido con la función delta de Dirac pero en la cual el límite se toma acercando el parámetro de aproximación n no a cero sino al infinito, o sea  n.→.∞, es la siguiente:

Esta función tampoco puede ser ser una verdadera función delta de Dirac, porque el valor de δ(x) para n.=.0 y x.=.0 no está definido.

Se había mencionado previamente que para fines formales a la función delta de Dirac se le puede tomar como una distribución. No resulta difícil ver el origen de tal idea. Lo podemos ver en la tercera aproximación dada arriba. Resulta evidente que se trata de una función que define una curva Gaussiana o curva normal usualmente encontrada en textos de Estadística con la fórmula:

La curva Gaussiana, tal y como es usada con fines de análisis estadísticos, es una función normalizada a la unidad, esto es, el área bajo la curva (y aquí sí podemos hablar del área bajo la curva con plena justificación de la expresión) es igual a 1, con lo cual se dá a entender que la probabilidad de encontrar cualquier espécimen de una población bajo cualquier parte de la curva Gaussiana (la cual se extiende desde menos infinito hasta más infinito) es igual a la certeza. Y resulta que “el área bajo la curva” de la función δ de Dirac también es igual a la unidad, definida también entre los límites de menos infinito y más infinito. La distribución Gaussiana, al igual que la función delta de Dirac, también tiene su “pico máximo”, aunque el “pico” de la distribución Gaussiana tiene una altura finita mientras que el “pico” de la función δ tiene una altura infinita. Por otro lado, como cualquier estudiante de Estadística puede atestiguarlo, disminuyendo la cantidad que se conoce como la desviación estándard o dispersión estadística de los valores, simbolizada como σ (o bien, la varianza σ²), la anchura de la curva disminuye haciéndose a la vez más y más pronunciado el “pico máximo” de la curva Gaussiana de modo tal que el área bajo la curva Gaussiana siga manteniendo un valor igual a al unidad. En la siguiente figura se tienen superpuestas tres curvas Gaussianas para distintos valores de σ, y puede apreciarse que conforme σ se va haciendo más y más pequeña la anchura de la curva (medida, por ejemplo, a la mitad del pico de altura máxima de la curva) va disminuyendo a la vez que el pico de la curva se va haciendo más y más pronunciado, acercándose tanto como queramos a una verdadera función delta de Dirac:

Llevando hacia el extremo el procedimiento de ir disminuyendo el valor de σ, haciéndolo casi igual a cero (aunque nunca a cero exactamente, ya que ello conduce a una indefinición matemática) se obtiene gráficamente lo que para cualquiera parecerá ser una función δ de Dirac, aunque no pueda serlo.

Puesto que la función delta de Dirac en dos dimensiones (en un plano) está dada por:

entonces, si cada función delta que corresponde a cada eje coordenado es aproximada mediante una curva Gaussiana cuya anchura tiende a cero, podemos visualizar la aproximación Gaussiana a la función delta de Dirac en dos dimensiones de la manera siguiente (obviamente, este tipo de visualizacion no puede ser extendido hacia tres dimensiones, aunque el concepto en tal caso es intuitivamente fácil de asimilar):

Todo lo anterior nos dá la pista para tratar de darle una justificación un poco más formal a la función delta de Dirac como el resultado de una aproximación llevada a cabo sobre una función matemática que posea algún significado físico. Para ello, recurrimos a la simbolización de una onda plana como una función exponencial periódica (el carácter oscilatorio de la misma está garantizado por la fórmula de Euler):

Recurriremos también a la herramienta matemática conocida como la transformada de Fourier, usada para tomar una función f(x) convirtiéndola del espacio-x al espacio-k, multiplicándola por la función e^-ikx e integrando dicho producto desde menos infinito hasta más infinito obteniendo así la función F(k) (la constante que multiplica a la integral no es una constante de normalización, pero resulta conveniente para obtener compatibilidad en el proceso opuesto conocido como la transformada inversa de Fourier usado para tomar una función F(k) especificada en el espacio-k convirtiéndola a una función f(x) especificada en el espacio-x):

Desafortunadamente, no es posible obtener la transformada de Fourier de una onda plana que es representada como una función oscilatoria que se extiende indefinidamente hacia adelante y hacia atrás. Sin embargo, aunque una onda plana no tiene una verdadera transformada de Fourier, es posible definir una función impropia delta de Dirac para que desempeñe el papel de tal transformada. Para poder lograr tal cosa, escribimos a la función periódica exponencial de la manera siguiente:

Para cualquier valor finito, real y positivo de α, la integral de esto último existe. Esto nos permite llevar a cabo el cálculo de la transformada de Fourier como se muestra a continuación:

El límite resultante se desvanece para k.≠.k₀ y diverge para k.=.k₀., dando como forma de la función impropia F(k) lo siguiente:

Esto se parece ya mucho a la substancia con la que hemos estado trabajando. Pese a que esta función F(k) es una función singular en k₀, aún es posible definir la integral sobre todos los valores de k mediante el recurso de llevar a cabo la integración antes de tomar el límite:

Esto nos sugiere la propuesta de una función singular que llamaremos precisamente la función delta de Dirac δ(k) definida del siguiente modo:

Se entiende que la integral aquí está definida de acuerdo con el procedimiento límite asentado antes. Definida de este modo, la función δ(k) tiene las siguientes propiedades:

que son precisamente lo que define a la función delta de Dirac.

Llevando a cabo una simple diferenciación bajo el signo de la integral con respecto a k de δ(k), podemos dar la siguiente definición formal a la derivada de la función δ(k):

De nueva cuenta, esto tiene significado únicamente en el sentido de un límite.

Pese a tratarse de una función sumamente impropia, hay una literatura extensa acerca de la función delta de Dirac y propiedades de la misma que muchos ignoran y cuyo conocimiento pudiera ser de utilidad en desarrollos nuevos. A manera de ejemplo, se tiene la siguiente relación considerada por varios autores como la ecuación fundamental que sirve para definir las derivadas de orden n de una función delta de Dirac (el super-índice n puesto entre paréntesis sobre la función δ simboliza la n-ava derivada de la función δ con respecto a la variable independiente):

Para el caso n.=.1, la anterior ecuación nos produce el siguiente resultado (obsérvese que al pasar de la segunda línea a la tercera línea se recurre al efecto fundamental de la función delta de Dirac, dándose por hecho de que la derivada df/dx es continua en x.=.0):

Otra relación interesante, válida para relaciones que involucran no una sola sino varias funciones delta de Dirac, es la siguiente:

en donde la comilla puesta sobre la función g(x) simboliza la derivada de g con respecto a x, y en donde las x_i son las raíces de la función g. Para una aplicación de esta fórmula, considérese lo siguiente:

Entonces:

con lo cual:

para obtener:

¿Y para qué podrían sernos útiles relaciones de este tipo que involucran no una sino varias funciones delta de Dirac? Una aplicación posible puede ser en el caso en el que se tiene no una sino varias discontinuidades en el espacio tridimensional, como en el caso de un dipolo eléctrico formado por dos cargas puntuales, cada una de ellas ubicada en el espacio mediante su propia función delta de Dirac.