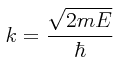Ya vimos que esta ecuación diferencial -de primer orden en el tiempo y de segundo orden en el espacio- tiene las siguientes dos soluciones:
Estas dos soluciones las podemos escribir de la siguiente manera:
Es muy importante darse cuenta de que ambas soluciones son complejas. Esto a su vez implica necesariamente que las funciones de onda para las ondas de materia son cantidades no observables. No representan en sí algo que podamos medir con un aparato en el laboratorio. ¿Significa esto entonces que no les podemos dar interpretación física alguna, así sea modificándolas de alguna manera? Esto nos lleva a cuestionar la naturaleza de la esencia básica de aquello que estamos manejando.
La lógica cuántica probabilista es tan contraria a nuestra forma de pensar porque no tenemos un contacto directo a través de nuestros limitados sentidos con lo que realmente está ocurriendo en el mundo sub-microscópíco, lo cual se debe gracias a que (afortunadamente) la constante de Planck h tiene un valor extremadamente pequeño, y de hecho si esta constante fuese cero entonces los resultados de la física clásica serían extensibles hasta el mundo sub-microscópico. Pero, ¿qué sucedería si la constante de Planck no tuviese un valor tan pequeño? Podemos darnos una idea de ello suponiendo precisamente tal cosa, suponiendo que en vez de tener el pequeñísimo valor de:
h = 6.625×10-34 joule·segundo
la constante de Planck tuviera un valor igual a:
h = 6.625×10-3 joule·segundo
y llevando a cabo el experimento de “doble rendija” arrojando esferas sólidas hacia el interior de una casa a través de dos ventanas altas, paralelas, y angostas, ambas abiertas, las cuales actuarían como una “doble rendija”:
Supondremos en nuestro hipotético experimento gedanken que las dos ventanas paralelas y angostas están separadas una distancia d igual a medio metro, que hay una pared situada a una distancia L igual a 10 metros detrás de las ventanas que actuará como “pantalla receptora”, y que estaremos lanzando hacia las dos ventanas esferas de 66.25 gramos a una velocidad de 5 metros/segundo. El patrón de interferencia que se observa en la pared después de haber arrojado un gran número de pelotas, el cual haría su aparición aunque sólo se arrojase una esfera sólida a la vez hacia el interior de la casa a través de las dos ventanas, se puede analizar como un fenómeno ondulatorio para el cual los parámetros de interés en los lugares en donde hay interferencia constructiva (los lugares en donde la intensidad es más alta, en contraposición a los lugares en donde hay interferencia constructiva distinguidos por ser las zonas obscuras) son los siguientes:
La longitud de onda de De Broglie para las esferas que estaremos arrojando está dada por la relación:
y evaluada numéricamente nos arroja el siguiente resultado en el sistema de unidades MKS-SI:
λ = (6.625×10-3 joule·segundo)/[(6.625×10-3 Kg)(5 metros/segundo)]
λ = 0.02 metro
De acuerdo a la teoría ondulatoria que extendemos ahora para ondas de materia, en un modelo de interferencia de doble rendija los ángulos θn a las líneas de intensidad cero que se obtienen en los lugares en donde las ondas provenientes de cada ventana llegan desfasadas en media longitud de onda están dadas por:
La distancia y mostrada en la gráfica se obtiene, para ángulos θ lo suficientemente pequeños, de la siguiente manera:
La distancia entre dos franjas adyacentes será por lo tanto:
Metiendo los valores numéricos dados arriba, tenemos entonces para la distancia entre dos franjas adyacentes el siguiente valor:
Δ.y = [(10 metros)(0.02 metro)]/(0.5 metro)
Δ.y = 0.4 metro
Tras haber arrojado muchas esferas hacia las dos ventanas, encontraríamos como algo sumamente curioso que hay zonas en la pared en donde prácticamente las esferas nunca llegan, mientras que hay zonas en donde la intensidad del golpeteo es mucho mayor, con una distribución indudable de franjas de alta intensidad y baja intensidad. Y algo que tal vez intrigaría aún más al que estuviera llevando a cabo este experimento hipotético, suponiendo que esté arrojando las esferas hacia las ventanas en una dirección perfectamente perpendicular al plano de las ventanas, lo sería el hecho de que la zona de mayor intensidad de impactos en la pared que está detrás de las ventanas es precisamente la que está detrás del borde sólido que separa a ambas ventanas, ¡una zona en la pared en donde no debería de haber absolutamente ningún impacto! Si las esferas se comportasen como partículas sólidas, esto sería imposible de explicar. Sólo suponiendo que las esferas no son tan “sólidas” como creíamos podemos empezar a ver alguna lógica en lo que está sucediendo. La interpretación probabilista nos dice que cada esfera golpeará en algún lugar aunque este lugar no sea determinable de antemano. Pero aunque no sea posible predecir el lugar de impacto de cada una de las esferas antes de arrojarla, cada esfera tiene una alta probabilidad de llegar a un máximo y una probabilidad muy baja de llegar a un mínimo. El modelo de interferencia se obtiene contando el número de esferas que impactan en cada parte de la pared. Al empezar el experimento, las esferas golpearán la pared en forma esporádica sin que haya un patrón evidente, y solamente después de haber lanzado un gran número de esferas a través de las ventanas se hará detectable el patrón de interferencia, puesto que el número de choques aumentará gradualmente en cada sitio correspondiente a un máximo, mientras que el número de choques en un mínimo será muy bajo o igual a cero.
Hemos visto que mediante la ecuación de onda de Schrödinger podemos obtener los valores de energía que puede tomar un sistema físico cuya energía total H pueda ser enunciada matemáticamente. ¿Es ésta toda la información que podemos extraer con dicha ecuación? Esta interrogante nos lleva a enfocar nuestra atención sobre la función de onda ψ en un intento por darle una interpretación física a la misma. La lógica nos dice que en un lugar cerrado en donde la función de onda ψ sea igual a cero no debe de existir partícula alguna, mientras que en un lugar cerrado en donde ψ pueda tomar un valor diferente de cero en cualquier instante de tiempo debe de haber algo de masa, y que entre mayor sea la magnitud de ψ podamos ver la posibilidad de asociar a la magnitud de ψ con la cantidad que haya presente de “masa”. Pero el primer tropiezo que enfrentamos es que se trataría de una masa que está “ondulando”. De cualquier manera, aún admitiendo esta posibilidad, no es el único problema que enfrentamos en nuestro intento por darle una interpretación física a la función de onda ψ.
Resulta conveniente retomar el problema de una partícula confinada a un movimiento unidimensional, la cual está restringida a moverse a lo largo de un segmento de recta de longitud L en una caja. La solución obtenida para la función de onda resultó ser la siguiente función de tipo senoidal:
en la cual el argumento de la función senoidal es tal que en los extremos de la caja x.=.0 y x.=.L el valor de ψ es igual a cero. La gráfica de esta función para varios valores enteros del número cuántico que nos dá los valores posibles de la energía es la siguiente:
Para n =1 tenemos una cresta que adquiere un valor máximo en el centro de la distancia L entre ambas paredes de la caja. Para n = 2 además de dos crestas tenemos un nodo en el centro de la distancia L que hay entre ambas paredes de la caja. Y para n = 3 tenemos dos nodos, mientras que para n = 4 tenemos tres nodos. Puesto que en una cuerda vibrante no hay movimiento alguno en los nodos, si la amplitud de ψ está relacionada de algún modo con la probabilidad de encontrar a la partícula a cierta distancia x de la pared izquierda (el origen del eje coordenado-x en este problema) entonces la probabilidad de encontrar a la partícula en un segmento pequeño de recta Δx que incluya a un nodo debe tener un valor cercano a cero. Del mismo modo, en los puntos cercanos a las crestas de la onda senoidal, la probabilidad de encontrar a la partícula en segmentos pequeños de recta Δx que incluyan dichos puntos debe ser máxima. Esto significaría que para n = 2 la probabilidad de encontrar a la partícula debe ser mayor en segmentos pequeños de recta Δx que incluyan los puntos x = L/4 y x = 3L/4 de la recta. Del mismo modo, para n = 3 la probabilidad de encontrar a la partícula debe ser mayor en en segmentos pequeños de recta Δx que incluyan los puntos x = L/6, x = L/2 y x = 5L/6 de la recta. Esto que hemos expresado desde un punto de vista cualitativo desearíamos expresarlo desde un punto de vista cuantitativo, metiéndole números. Pero aquí nos topamos con un problema. Con excepción de la onda que corresponde al número cuántico n = 1, todas las demás tienen por lo menos una cresta que dá a ψ un valor negativo. Y los números negativos no tienen cabida en los enunciados matemáticos relacionados con la probabilidad.
Antes de desechar a la magnitud de ψ como una medida de la probabilidad de encontrar a la partícula en un segmento pequeño de recta Δx, podemos recurrir a un expediente matemático fácil que consiste simplemente en elevar al cuadrado la magnitud de ψ. De este modo, tendremos únicamente valores positivos, los valores proporcionados por ψ² cuando ψ(x) es un número real para cualquier valor de x (esto es, ni complejo ni imaginario). ¿Y cómo manejamos una situación en la cual ψ(x) sea una función compleja, esto es, formada por una parte real y una parte imaginaria? Pues simplemente tomamos el conjugado complejo ψ(x)* de la función ψ(x) y lo multiplicamos por dicha función (obsérvese cómo se está agregando un asterisco para simbolizar que la conversión hacia el conjugado complejo se ha llevado a cabo). Así como un número x multiplicado por su conjugado complejo x* siempre dá una cantidad positiva:
x* x = (a - ib)(a + ib) = a2 + b2
del mismo modo una función compleja (al menos las funciones matemáticas de interés en la física teórica) multiplicada por su conjugado también producirá una cantidad que siempre será positiva, o expresado de modo un poco más elegante, definitivamente positiva (del inglés positive definite). Haciendo uso de este recurso, para las dos funciones de onda ψ+ y ψ- dadas al principio de esta entrada tenemos lo siguiente:
Una vez que hemos eliminado el inconveniente de los números complejos e imaginarios, los cuales no tienen cabida en las mediciones estadísticas usuales de eso que llamamos probabilidad, podemos intentar adjudicarle al cuadrado de la función de onda |ψ(x)|² = ψ*ψ el significado de que representa la probabilidad de encontrar a una partícula en cierta región del espacio. Puesto de un modo un poco más formal, la expresión |ψ(x)|² vendría representando por sí sola la densidad de probabilidad, y en el caso unidimensional al multiplicarla por un segmento infinitesimal de longitud dx en cierto punto nos vendría dando una medida de la probabilidad de encontrar a la partícula en ese segmento de longitud. Esta interpretación dada a la función de onda de una onda de materia se la debemos a Max Born, el mismo al cual le debemos la “extraña ecuación” que asentó a la Mecánica Matricial de Heisenberg sobre una base sólida, y por esto mismo es conocida como la interpretación probabilista de Born (la acepción interpretación probabilística de Born es usada también, ambas son lingüisticamente correctas). Pero es conveniente que tengamos más argumentos válidos para poder justificar esta interpretación que le estamos dando a la función de onda, o mejor dicho al cuadrado de la misma. Hay una justificación para darle una interpretación más a ψ² que a ψ y que veremos a continuación, la cual proviene de la teoría del electromagnetismo. Recuérdese cómo en la “derivación” de la ecuación de Schrödinger el punto de partida para la obtención de una ecuación de onda para las ondas de materia fueron las ecuaciones del electromagnetismo que siguen siendo válidas para esas ondas electromagnéticas discretas que llamamos fotones. La ecuación de onda que gobierna a la radiación electromagnética, en lo que respecta a la componente eléctrica de dicha radiación (hay además una componente magnética para la cual la ecuación de onda es la misma) es la siguiente:
Se puede demostrar clásicamente dentro de la teoría del electromagnetismo de Maxwell que la energía por unidad de volumen en una onda luminosa es proporcional no a ε sino a ε2. Sin embargo, sabemos que esta energía no es continua sino que está discretizada en unidades de hf por cada fotón que forma parte del “chorro” electromagnético. Podemos esperar entonces que el número de fotones por unidad de volumen sea proporcional a ε2. Consideremos a continuación un patrón de interferencia obtenido en un experimento de doble rendija como el que vimos arriba pero utilizando fotones en vez de partículas materiales. De acuerdo con la descripción ondulatoria del electromagnetismo, la intensidad I (energía por unidad de área en unidad de tiempo) en cualquier punto de la pantalla está dada por:
en donde ε es el valor del campo eléctrico en un punto dado de la pantalla, ε0 es la permitividad eléctrica del espacio vacío, y c es la velocidad de la luz. Por otro lado, bajo el modelo de fotones discreto, la intensidad en un punto de la pantalla está dada por la relación:
en donde hf es la energía de cada fotón y N es el flujo de fotones (número de fotones por unidad de área en la unidad de tiempo) que golpea un punto de la pantalla.
No existe método alguno con el que se pueda predecir el punto de impacto de un fotón individual en la pantalla, para producir un destello único o una impresión individual sobre una placa fotográfica. De cualquier modo, al producirse un patrón final sobre la pantalla formado alternadamente por bandas brillantes y obscuras, un fotón tiene una alta probabilidad de llegar a una banda brillante, siendo la probabilidad de impacto tanto mayor cuanto mayor sea la brillantez de la parte de la banda en la cual incide, y pocas probabilidades de llegar a una banda obscura, siendo cero la probabilidad de impacto en la parte más obscura de cada banda. El flujo N de fotones es, por lo tanto, una medida de la probabilidad de encontrar un fotón cerca de ese punto. Puesto que:
se concluye entonces que el flujo de fotones N es proporcional a ε2, o sea:
Consecuentemente, de acuerdo con la interpretación cuántica de la radiación electromagnética, la cantidad que oscila, en este caso el campo eléctrico ε, es aquella función cuyo cuadrado dá la probabilidad de encontrar un fotón en un lugar dado. Una vez asentado esto, el siguiente paso consiste en extender este modelo para ondas de materia en lugar de ondas de luz. En este caso, la interpretación probabilista basada en la dualidad onda-partícula de la luz se transporta directamente a la dualidad onda-partícula de la materia. De este modo, con ondas de electrones, la cantidad que oscila con una longitud de onda λ = h/mv es aquella función de onda cuyo cuadrado dá la probabilidad de encontrar al electrón en un lugar dado. Para poder reconciliar las descripciones ondulatoria y de partícula de la materia, debemos abandonar definitivamente la noción de que una partícula material puede ser localizada con exactitud. Al no poder hablar ya con certeza, podemos en cambio hablar de la probabilidad de poder encontrar una partícula en un lugar y en un tiempo dados. Y esta probabilidad es aquella función de onda ψ cuyo cuadrado dá la probabilidad de encontrar a la partícula en un lugar dado.
PROBLEMA: Calcúlese el flujo de fotones que está asociado con un haz de luz monocromática con una longitud de onda de 3,500 Angstroms y con una intensidad de 2.5×10-14 watt/metro2.
La energía de cada fotón será:
Poniendo números en el sistema de unidades MKS-SI:
E = [(6.63×10-34 joule·seg)(3×108 metros/seg)] / (3.5×10-7 metro)
E = 5.68×10-19 joule/fotón
El flujo de fotones será entonces:
N = I/hf
N = (2.5×10-14 joule/seg·metro²)/(5.68×10-19 joule/fotón)
N = 4.4×104 fotones/seg·metro²
N = 4.4 fotones/seg·cm²
En promedio, 4.4 fotones incidirán sobre cada centímetro cuadrado de la pantalla durante cada segundo. Naturalmente, al no existir los fotones fraccionarios, sólo un número entero de ellos incidirá sobre cada centímetro cuadrado de la pantalla durante cada segundo, digamos 2, 3, 4, 5 ó 6 fotones, pero nunca 4.4 fotones. Unicamente cuando se toma un promedio sobre muchos intervalos de tiempo el número de fotones se aproximará a 4.4 por segundo por centímetro cuadrado. Y únicamente cuando ha transcurrido una cantidad apreciable de tiempo empezará a manifestarse el patrón de difracción con sus típicas franjas blancas y obscuras sobre toda la pantalla, confirmando la naturaleza estadística de lo que está sucediendo a nivel sub-microscópico.
Como se indicó arriba, si vamos a utilizar ψ² en lugar de ψ como una medida cuantitativa de la probabilidad, no tenemos por qué limitarnos a funciones de onda ψ que sean números reales, podemos utilizar también funciones de onda cuyos valores numéricos sean imaginarios o complejos.
Para el problema de la partícula confinada a moverse dentro de una caja entre dos paredes, el gráficado de |ψ(x)|² resulta ser el siguiente:
De este modo, la probabilidad (infinitesimal) dp(x) de encontrar a la partícula en un segmento infinitesimal dx de la recta será igual a:
|ψ(x)|²dx = ψ*ψdx
Esta es la definición de probabilidad que utilizamos para un problema unidimensional como el de una partícula dentro de una caja. Pero en una situación más realista, el problema será un problema tridimensional, especificado en tres coordenadas tales como las coordenadas Cartesianas rectangulares, y la región de interés será no elemento infinitesimal de recta sino un elemento infinitesimal de volumen dV:
en cuyo caso la probabilidad de encontrar a la partícula en ese elemento infinitesimal de volumen estará dada por:
|ψ(x)|²dV = ψ*ψdV
Si aceptamos la idea de que:
|ψ(x)|²Δx
nos dá la probabilidad de que podamos encontrar a la partícula dentro de un segmento pequeño de recta Δx, entonces para n =1 la probabilidad de encontrar a la partícula justo a la mitad de la región es mayor que para cualquier lugar a lo largo de la coordenada-x. Una forma de explicarlo sería diciendo que la partícula se la pasa la mayor parte del tiempo más cerca del centro que en cualquier otro lugar. Por otro lado, la probabilidad de encontrar a la partícula en los extremos de la región es cero, en virtud de que al rebotar no permanece tiempo alguno durante la acción del rebote. Sin embargo, este comportamiento no es el mismo que el comportamiento que el comportamiento que podemos observar para n = 2. En este caso, la probabilidad de encontrar a la partícula dentro de un segmento pequeño de recta Δx justo en el centro de la región es prácticamente cero, mientras que hay dos lugares dentro de la región en los cuales la probabilidad de encontrar a la partícula es un máximo dentro de un segmento pequeño de recta Δx. Una duda que frecuentemente aflora en este punto es la siguiente: si para n = 2 la probabilidad de encontrar a la partícula justo en el centro, ¿entonces cómo pasa la partícula de una mitad de la región a la otra? Esta duda tiene que ver directamente con el hecho de que no se ha entendido bien la probabilidad de la que estamos hablando. Por sí solo |ψ(x)|² no nos dá la probabilidad de encontrar a la partícula en algún lugar específico, es |ψ(x)|²Δx lo que nos dá la probabilidad de encontrar a la partícula dentro de un segmento pequeño de recta Δx. Decir que para n = 2 la probabilidad de encontrar a la partícula justo en el centro de la región es igual a cero implicaría suponer que Δx debe ser igual a cero puesto que ya no estaríamos hablando de un rango infinitesimalmente pequeño de recta Δx sino de un valor exacto. Y en el caso Δx = 0 se pierde la interpretación probabilista, no tiene sentido hablar acerca de probabilidad alguna para un valor exacto de la variable independiente.
En el experimento de interferencia de Young con haces luminosos al igual que en el experimento de la doble rendija con ondas de materia que vimos arriba al principio, la onda que llega a la pantalla no es una onda plana sino una onda compleja. Sin embargo, tal onda compleja puede ser descompuesta en ondas planas, esto es, puede ser considerada como la superposición linear de ondas planas. Es importante por lo tanto considerar al estado de una partícula descrito por una función de onda compleja como una superposición de dos o más ondas planas. En base a esto, y usando dos ondas planas para nuestra representación, la función de onda de una partícula puede ser escrita del modo siguiente:
siendo r el vector posición expresado en coordenadas rectangulares Cartesianas:
r = (x, y, z)
y siendo k el vector número de onda para cada onda plana tridimensional:
k = (kx, ky, kz)
De acuerdo con la interpretación fundamental probabilista de la función de onda, |ψ(x)|² se debe interpretar aquí como una medida de la probabilidad por unidad de volumen de encontrar a una partícula en el punto r. Aplicando la definición a la función de onda compuesta que tenemos arriba tenemos lo siguiente:
Removiendo los paréntesis tras llevar a cabo la multiplicación se tiene entonces:
Simplificando un poco y reacomodando:
De acuerdo con la misma definición que hemos venido manejando para el cuadrado de una función de onda compleja, los dos primeros términos los podemos escribir de la siguiente:
Con esta simplificación notacional y factorizando a r en los exponentes, se tiene lo siguiente:
Dada la simetría del problema, podemos dar por hecho que el tercer término y el cuarto término en esto último contribuyen por partes iguales:
Aplicando sobre esto la relación de Euler y el hecho de que el seno de un ángulo negativo es igual al negativo del seno del ángulo del mismo modo que el coseno de un ángulo negativo es igual al positivo del coseno del ángulo:
la expresión de la igualdad entre el tercer término y el cuarto término se transforma primero en lo siguiente:
y tras esto en:
Las partes imaginarias en ambos lados de la igualdad no pueden válidas en virtud de que un número positivo no es lo mismo que el mismo número negativo. Esto nos deja simplemente la parte real:
Para que esto sea cierto, se requiere forzosamente que:
De este modo, la probabilidad por unidad de volumen para encontrar a la partícula en un punto r está dada por::
Como puede verse, la probabilidad relativa no es igual a la simple suma de cada una de las contribuciones de las dos ondas planas, ya que tenemos un a contribución adicional, dada por el tercer término destacado entre corchetes, un término de interferencia. Para este caso en particular, la densidad de probabilidad en cada posición r está en cierto modo localizada, ya que no está distribuída uniformemente sobre todo el espacio. Sin embargo, si |ψ|² es promediada sobre todo el espacio, el término entre corchetes se promedia a cero en virtud del carácter oscilatorio del término de interferencia. Promediada sobre todo el espacio, |ψ|² puede ser interpretada como una medida de la probabilidad de encontrar a la partícula en algún lado sin darse importancia a la localización. Y esta probabilidad debe ser la certeza, debe ser igual a la unidad. Siendo así, |A1|² y |A2|² pueden ser interpretadas como medidas de la probabilidad de encontrar a la partícula en algún lugar (sin consideración a la localización) con los momentums p1 y p2 respectivamente. Bajo esta interpretación, la probabilidad de que la partícula tenga un momentum p1 es:
y de este modo tanto la posición exacta como el momentum exacto de la partícula son inciertos cuando están caracterizados por la función de onda compleja compuesta por la suma de dos ondas planas como la que hemos considerado en este desarrollo. Se debe enfatizar el hecho de que las probabilidades asociadas con una partícula descrita por esta función de onda compleja se refieren a una situación prevaleciente antes de que se lleve a cabo una observación, antes de que se lleve a cabo un acto de medición. Si se observa que la partícula está confinada a cierta región limitada del espacio, se debe suponer que un acto de medición ha perturbado a la partícula y a su función de onda. Alternativamente, si se observa el momentum de la partícula, este momentum deberá ser p1 ó p2 y nunca cualquier otro valor, y de nueva cuenta se debe suponer que un acto de medición ha perturbado el estado del sistema. Después de la observación, en lugar de la función compleja la función de onda observada será la que corresponda al momentum específico observado.
En la caja unidimensional que vimos arriba, al hablar sobre probabilidad lo hacemos a sabiendas de que la probabilidad de encontrar a la partícula entre los dos extremos de la caja (en lugar de un pequeño segmento de recta Δx para un valor dado del número cuántico n) debe ser igual a la certeza, la cual podemos definir alternativamente como un 100 por ciento o como igual a la unidad, prefiriéndose el segundo concepto (no se acostumbra manejar porcentajes al hablar sobre probabilidad en la Mecánica Ondulatoria, ya que es más práctico para fines de cálculo utilizar medidas fraccionarias teniendo a una probabilidad del cien por ciento representada como la unidad). Esto significa que el “área bajo la curva” de |ψ(x)|² evaluada (en este caso) desde x.=.0 hasta x.=.L debe ser igual a la unidad:
∫ |ψ(x)|² dx = 1
Pero en la función senoidal ψ(x) que tenemos arriba como solución al problema de una partícula en una caja, no está garantizado que esta última condición se cumpla, y de hecho no se cumple porque no está normalizada. Tenemos que normalizar la función de onda para que se cumpla la condición, lo cual en nuestro caso requiere que apliquemos la condición para determinar el valor de la constante A para dar cumplimiento a la condición.
PROBLEMA: Dada la función de onda:
encontrar la constante de normalización A para la misma entre los límites x = 0 y x = L.
Usando la condición de normalización en este caso en el cual por no haber números imaginarios o complejos el conjugado de la función de onda ψ* resulta ser igual a la función de onda ψ, o sea:
ψ* = ψ
tenemos lo siguiente efectuando la integración desde x = 0 hasta x = L:
Efectuamos aquí un ligero cambio de variable haciendo α = πx/L para facilitar la integración:
Puesto que la integral definida tiene el siguiente valor para cualquier valor de n:
lo anterior se nos reduce a:
dándonos la siguiente constante de normalización:
La función de onda, ya normalizada, es la siguiente (se ha agregado un sub-índice al símbolo de la función de onda para relacionar cada función de onda respectiva a un número cuántico diferente):
Podemos comprobar fácilmente que estas funciones de onda que acabamos de obtener no sólo están normalizadas a la unidad, también son ortogonales, en virtud de que:
Esta situación ya la habíamos encontrado antes en la Mecánica Matricial, excepto que lo que tenemos aquí son funciones ortogonales mientras que lo que teníamos en la Mecánica Matricial eran vectores ortogonales. Y puesto que las funciones no sólo son ortogonales sino que han sido normalizadas mediante la constante de normalización que acabamos de obtener, las funciones de onda son ortonormales, algo que también habíamos encontrado en la Mecánica Matricial excepto que en ese caso se trataba de vectores ortonormales. De este modo, aunque las técnicas matemáticas son diferentes, poco a poco nos vamos encontrando más similitudes entre la Mecánica Matricial y la Mecánica Ondulatoria basada en la ecuación de Schrödinger.
La función que se acaba de normalizar en el problema de arriba es la que corresponde al problema de una partícula confinada en una caja moviéndose unidimensionalmente, resuelto en una entrada anterior (en la entrada “La ecuación de Schrödinger”). Puesto que en el caso tridimensional la función de onda es igual al producto de las tres funciones de onda para cada uno de los ejes coordenados, la función de onda ya normalizada para el problema ondulatorio de una partícula en una caja moviéndose en tres dimensiones será la siguiente:
Una vez que tenemos normalizada una función de onda, podemos recurrir a la definición probabilista para determinar la probabilidad Pab encontrar a la partícula entre dos puntos a y b cualesquiera de la siguiente manera:
La condición de normalización se puede extender fácilmente de un espacio unidimensional a un espacio tridimensional para una función de onda especificada en tres dimensiones, por ejemplo ψ(x,y,z) en un espacion rectangular Cartesiano, habido el hecho de que la probabilidad de encontrar una partícula en cualquier volumen lo suficientemente amplio debe ser igual a la certeza, a la unidad, o sea:
∫∫∫ |ψ(x,y,z)|² dV = 1
∫∫∫ |ψ(x,y,z)|² dx dy dz = 1
∫∫∫ |ψ(x,y,z)|² dx dy dz = 1
PROBLEMA: Demuéstrese que en las soluciones obtenidas a la ecuación de Schrödinger dependiente del tiempo, la constante de seperación E que aparece en el exponencial de la parte temporal debe ser real.
En una dimensión, la solución general Ψ(x,t) de la ecuación de Schrödinger dependiente del tiempo consta de una función de onda ψ(x) que representa a la parte espacial multiplicada por un exponente que representa la parte temporal:
Supondremos que E es un número complejo con una parte real E0 sumada a una parte imaginaria:
E = E0 + iΓ
Substituyendo esto en la solución general obtenemos entonces:
Tomaremos ahora el conjugado complejo de Ψ(x,t), lo cual requiere reemplazar todas las instancias en las que aparezca el número imaginario i por su negativo -i:
Si la función de onda es normalizable, entonces se debe cumplir con la condición esencial de normalización en la cual podemos reemplazar tanto Ψ(x,t) como Ψ*(x,t):
Simplificando un poco cancelando los exponenciales que tienen signos opuestos y sacando el resto fuera de la integral:
En el lado izquierdo de la igualdad tenemos una expresión cuyo valor es única y exclusivamente una función de la coordenada espacial, mientras que en el lado derecho tenemos una expresión que es una función exponencial decreciente en función del tiempo, lo cual es una contradicción. La única manera de evitar esta contradicción es haciendo Γ igual a cero. Se concluye que para soluciones normalizables, la constante de separación E necesariamente debe ser un valor real.
Un problema interesante es aquél en el cual consideramos una cuenta de masa m ensartada en un alambre circular de circunferencia L que se desliza libremente sin fricción alrededor del alambre. Se trata de determinar los niveles permitidos de energía E de la partícula. El punto de partida es la ecuación de Schrödinger independiente del tiempo:
Para simplificar un poco las cosas, podemos escribir la ecuación diferencial anterior de la siguiente manera:
siendo:
La solución más general a la ecuación de Schrödinger para un problema de este tipo es una función de onda ψ como la siguiente:
siendo A y B dos constantes a ser determinadas. Después de haber recorrido una distancia L a lo largo del alambre circular, la función de onda ψ será entonces:
Pero puesto que la trayectoria de la partícula es una trayectoria circular, después de haber recorrido una distancia L la partícula se volverá a encontrar necesariamente en la misma posición, lo cual impone la condición:
En base a lo anterior, esto implica que:
Para x.=.0, esta relación se reduce a:
Pero por otro lado, para x.=.π/2k, la relación se convierte en:
Podemos simplificar esto último recurriendo a la fórmula de Euler:
con lo cual se obtiene:
Así pues, de la relación original derivamos dos relaciones:
Sumando ambas relaciones, obtenemos de inmediato la siguiente identidad:
Esta igualdad matemática solo puede ser cierta de dos maneras distintas. La primera es cuando A.=.0, y la segunda es cuando eikl.=.1. El segundo caso requiere que:
kl = 2nπ (n = 0, 1, 2, 3, ...)
Pero en el primer caso cuando A.=.0, se requiere entonces que Beikl.=.B, llegándose a la misma conclusión. Se deduce entonces que para cada valor positivo de n hay dos soluciones
siendo dos soluciones independientes para cada eigenenergía En, una correspondiendo a la partícula moviéndose a lo largo del alambre circular en una dirección (por ejemplo, en el sentido de las manecillas del reloj) y la otra correspondiendo a la partícula moviéndose a lo largo del alambre circular en la dirección opuesta (en un sentido contrario al sentido de las manecillas del reloj). La única excepción ocurre para n.=.0, en cuyo caso la solución es única.
Podemos determinar las constantes A y B usando el criterio de Born. En el caso de la constante A, la condición de normalización se determina de la siguiente manera:
La determinación de la constante B procede de la misma manera obteniéndose el mismo resultado:
Las eigenfunciones de onda ψn(x), tanto para la partícula cuando se mueve en el sentido de las manecillas del reloj como para la partícula cuando se mueve en un sentido contrario a las manecillas del reloj a lo largo del alambre circular, son:
De todo esto se concluye que la energía de la partícula moviéndose a lo largo del alambre circular está discretizada, y podemos determinar los niveles de energía de la siguiente manera recurriendo a la ecuación de Schrödinger:
El caso de la partícula de masa m deslizándose libremente sin fricción a lo largo de un alambre circular nos recuerda otro caso, el de un electrón moviéndose en una órbita circular en torno al núcleo del átomo de hidrógeno:
A primera vista, resulta tentador concluír que el resultado que hemos obtenido en la solución de este problema que acabamos de ver es aplicable directamente al caso del átomo de hidrógeno. Ciertamente, el hecho de que los niveles de energía estén discretizados a lo largo de una órbita circular es una consecuencia directa del hecho de que en una órbita circular sólo caben múltiplos enteros de las longitudes de onda de De Broglie que le podamos asignar a la partícula en función de su energía como se concibe en la siguiente figura:
siendo inadmisibles aquellas longitudes de onda que no “quepan” en múltiplos enteros en la circunferencia como la siguiente que se anularía de inmediato por el efecto de la interferencia destructiva:
Concebiblemente, extendiendo los resultados obtenidos arriba para una partícula moviéndose en una trayectoria circular fija, la absorción de un fotón haría “saltar” al átomo de hidrógeno de un estado energético a otro estado más energético aumentando el número de longitudes de onda a lo largo de la misma trayectoria circular. Todos los estados energéticos posibles ocurrirían a lo largo de una misma órbita radial con el simple remedio de ir aumentando el número de longitudes de onda asignadas a la partícula en dicha trayectoria circular de radio fijo. Sin embargo, este modelo excesivamente simplista entra en conflicto directo con el modelo atómico planetario de Bohr, el cual asigna los distintos valores energéticos no a una misma capa sino a distintas capas en torno al núcleo atómico; en el modelo de Bohr el átomo de hidrógeno es excitado haciendo brincar su electrón circundante de una capa situada a cierta distancia radial del núcleo atómico a otra distancia radial mayor, y el átomo emite un fotón cuando el electrón cae de una capa de cierto radio a una capa interna de radio menor. En rigor de verdad, Bohr no tuvo ninguna otra opción disponible para la construcción de su modelo atómico planetario en virtud de que las fórmulas para el mismo son obtenidas mediante una aplicación de las reglas de la electrodinámica clásica concernientes a la atracción entre dos cargas eléctricas de signos opuestos. En pocas palabras, en el modelo atómico planetario de Bohr hay un potencial radial V(r) de naturaleza Coulómbica, mientras que en el problema que acabamos de resolver aquí hemos recurrido a la ecuación de Schrödinger sin especificar potencial alguno considerándolo constante e igual a cero. Pero eventualmente llega un momento en el cual el mismo modelo de Bohr, pese a su incuestionable triunfo en explicar las líneas espectrales del átomo de hidrógeno, nos dejará insatisfechos, esto debido a que en el caso del átomo de hidrógeno (por ejemplo) el electrón gira todo el tiempo en torno al núcleo atómico a lo largo de un plano:
Sin embargo, podemos concebir una cantidad infinitamente grande de planos distintos, todos los cuales pasan también a través del núcleo atómico, en los cuales también son posibles órbitas circulares del electrón en torno al núcleo. ¿Por qué razón habría de darle la Naturaleza una preferencia a cierto plano sobre todos los demás infinitamente posibles? La asignación de una órbita circular llevándose a cabo sobre cierto plano fijo y único sería un desafío directo al principio de incertidumbre, ya que permitiría ubicar con precisión teóricamente ilimitada al electrón en cierto plano por encima de todos los demás planos concebiblemente posibles, y la descripción de los fenómenos del mundo sub-microscópico adquiriría no un carácter probabilista sino un carácter determinista, tal y como ocurre con la mecánica Newtoniana. No estaríamos hablando ya de probabilidades e incertidumbres sino de certeza y seguridad plenas. A menos de que la misma base estructural de la Mecánica Cuántica esté equivocada, la interpretación probabilista de ψ nos requiere que haya tantas probabilidades de poder encontrar al electrón en cierto plano como en todos los demás planos posibles, en algo que bajo el criterio de Born puede ser visualizado como una nube de probabilidad difusa y borrosa. Puesto de otra manera, la función de onda ψ para un electrón ligado a un átomo de hidrógeno tendrá que ser necesariamente tridimensional, y de antemano se anticipa que el sistema ideal de coordenadas para la resolución de este problema tridimensional será el sistema de coordenadas esféricas. Especificándose un potencial V(r) y escribiéndose la ecuación de onda de Schrödinger en coordenadas esféricas, el problema está prácticamente resuelto. La interpretación probabilista de ψ complementa entonces a la ecuación de Schrödinger dándonos las formas de las nubes de probabilidad que nos servirán para poder explicar, entre otras cosas, las propiedades de los enlaces químicos de la materia.