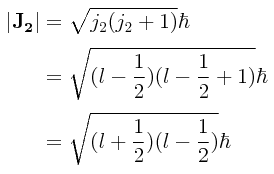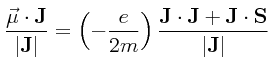Un tratamiento cuántico formal que dé un estimativo cuantitativo a la modificación de las energías del átomo de hidrógeno ocasionadas por el efecto del acoplamiento LS requiere familiarizarse con las técnicas matemáticas de aproximación tales como la teoría de las perturbaciones, lo cual tendrá que esperar a ser tratado en una entrada posterior en esta obra. Mientras tanto, podemos efectuar un análisis cualitativo que explique muchas cosas con los resultados que ya se han acumulado hasta este punto de todas las entradas previas.
Empezaremos considerando a un electrón girando sobre sí mismo como si fuese un trompo, una imagen que representa una buena simbolización del momento angular de spin de dicha partícula. El mismo electrón además de poseer este momento angular intrínseco posee también otro tipo de momento angular al estar atrapado orbitalmente como parte de un átomo:
Aunque ambos momentos angulares son cosa aparte, aceptemos que poseen la característica de poder acoplarse para dar origen a nuevas líneas en el espectro, las cuales no pueden ser explicadas sin la presunción de ese acoplamiento. Por acoplamiento entendemos la suma de los momentos angulares, orbital y de spin, y dándoles a estas cantidades una cualidad pseudo-vectorial al igual que como se acostumbra a hacerlo en la mecánica clásica, el momento angular total J se define como la suma “vectorial” del momento angular de spin S y el momento angular orbital L:
J = L + S
No se debe confundir este vector momento angular total J con ninguna de las matrices J tratadas en la entrada titulada “Momento angular: tratamiento matricial II” las cuales fueron utilizadas a la manera de las matrices de Pauli para representar única y exclusivamente al momento angular orbital sin acarrear la constante reducida de Planck ħ (como en el caso Lx = ħJx).
El concepto del momento angular total J como suma vectorial no debe ser tomado literalmente al pie de la letra. Más bien, la interpretación que debemos darle es como una suma de operadores, del mismo modo que el enunciado “un electrón tiene un momento angular orbital L” significa que la función de onda del electrón es una eigenfunción del operador Lop2 con el eigenvalor:
√ l( l+1) ħ
De este modo, una definición más adecuada del momento angular total J vendría siendo, operacionalmente hablando, la siguiente:
Puesto que J es un momento angular, esperamos que obedezca las mismas reglas cuánticas que las que se aplican en el caso de los momentos angulares orbital L y de spin S; esto es, esperamos que los eigenvalores de Jop2 puedan ser escritos como:
√ j( j+1) ħ
y que los eigenvalores de Jz sean mjħ en donde mj pueda tomar un total de 2j+1 valores enteros cuyo rango vaya de -j a +j en pasos integrales, lo cual resulta ser efectivamente el caso. Podemos encontrar los valores que puede tomar el número cuántico .j considerando la componente-z de la ecuación operacional que se acaba de dar arriba:
Jz,op = Lz,op + Sz,op
En términos de los eigenvalores, la ecuación correspondiente a esta ecuación operacional es la siguiente:
mj = ml + ms
Para el spin del electrón, sólo hay dos valores posibles de ms, -1/2 y +1/2. Y para el momento angular orbital, hay un total de 2l+1 valores posibles de ml. Esto significa que, para el caso especial en el cual l = 2, habrá un gran total de diez valores posibles considerando todas las combinaciones posibles de valores de ml y ms.
Si hemos de formarnos una imagen de la suma vectorial de los vectores L y S para dar origen al vector J, podemos tener en mente algo como lo siguiente:
Aunque es costumbre enraizada llamar a un diagrama de este tipo “suma vectorial”, en realidad no estamos sumando “vectores” en el sentido clásico, sino en el sentido cuántico. Si estuviésemos sumando vectorialmente en el sentido clásico el momento angular orbital L y el momento angular de spin S, además de tener que utilizar las magnitudes |L| y |S| para el cálculo de la magnitud del vector resultante J necesitaríamos el ángulo hipotético entre los vectores L y S para aplicar la ley de los cosenos. Pero esto no es lo que ocurre en la Mecánica Cuántica. ¡Ni siquiera tenemos que andar calculando ángulos entre vectores para obtener el vector resultante J!
Sabiendo de antemano que tanto el momento de angular orbital L como el momento angular de spin S están cuantizados de acuerdo a las siguientes reglas:
|L|2 = l(l+1)ħ2____|S|2 = s(s+1)ħ2
por esto mismo podemos y debemos esperar que también la suma vectorial de ambos momentos angulares esté cuantizada de acuerdo a una regla como la siguiente:
|J|2 = j( j+1)ħ2
Cuánticamente, en virtud de que la magnitud de cualquiera de los vectores de momento angular no coincide con su propio eje-z de medición experimental en torno al cual el vector que dá la magnitud total está girando, podemos imaginarnos a grosso modo una representación como la siguiente que aunque algo inexacta ilustra lo que está ocurriendo desde el punto de vista cuántico:
Ahora bien, el spin del electrón sólo puede tomar dos valores, - ħ/2 y +ħ/2. Esto significa que al ser sumado “vectorialmente” al vector momento angular orbital, sólo puede producir un desdoblamiento en dos componentes, el primero cuando el vector momento angular de spin S está apuntando en la misma dirección que el vector momento angular orbital L, y el segundo cuando el vector momento angular de spin S está apuntando en dirección contraria al momento angular orbital L. En el primer caso decimos que ambos vectores son “paralelos”, mientras que en el segundo caso decimos que ambos vectores son “antiparalelos”. Pero la condición de cuantización impuesta arriba sobre el vector J precluye la posibilidad de que los vectores “paralelos” L y S puedan estar apuntando en la misma dirección. De cualquier modo, podemos retener la terminología de vectores “paralelos” considerando a ambos vectores L y S lo más “paralelos” posible, y podemos retener la terminología de vectores “antiparalelos” considerando a ambos vectores L y S lo más “antiparalelos” posible.
En cuanto a la suma de los números cuánticos ml y ms (¡no las magnitudes!) que corresponden al momento angular orbital l y al momento angular de spin s se refiere, puesto que ms puede tomar únicamente dos valores entonces sólo hay dos posibilidades para el valor que puede tomar el número cuántico j. La primera es cuando ambos están apuntando “en la misma dirección” con ms = +1/2:
Y la segunda posibilidad es cuando ambos están apuntando “en direcciones opuestas”:
De este modo, podemos obtener una fórmula para la magnitud del momento angular total |J| con la cual, dado un valor de l, calculamos la magnitud del momento angular total J cuando los momentos angulares orbital y de spin son “paralelos”:
Tomando en cuenta que la magnitud del momento angular de spin S que debe ser igual a:
|S|2 = s(s+1)ħ2 = (1/2)(1/2 + 1)ħ2 = 3ħ2/4
|S| = (√3/2)ħ
la imagen que corresponde a esta posibilidad es la siguiente:
Y de la misma manera, podemos obtener una fórmula para la magnitud del momento angular total |J| con la cual, dado un valor de l, calculamos la magnitud del momento angular total J cuando los momentos angulares orbital y de spin son “anti-paralelos”:
La imagen que corresponde a esta segunda posibilidad es la siguiente:
PROBLEMA: Obténganse todas las combinaciones posibles del número cuántico mj para el caso en el cual l = 2.
Para el caso en el cual l = 2, el valor máximo de mj será l+s, o sea 5/2. Si .j = 5/2, entonces deberá haber un total de 2.j+1 = 6 valores posibles de mj. Además de estos valores, debe de haber otras cuatro combinaciones posibles que corresponden a .j = 3/2. Estos valores aparecen enumerados en la siguiente tabla en la cual se muestran los seis valores posibles de mj para .j = 5/2 de color rosa claro, y en la cual se muestran los cuatro valores posibles de mj para .j = 3/2 de color ciano claro:
La forma en la cual se construye una tabla como ésta es la siguiente: para l = 2, el número ml que corresponde al momento angular orbital puede tomar todos los valores enteros posibles entre +2 y -2, que son las “coordenadas” horizontales que aparecen en la parte superior de la tabla. Y el número ms que corresponde al momento angular de spin sólo puede tomar los valores +1/2 y -1/2, que son las “coordenadas” verticales que aparecen en la parte superior de la tabla. Para ml = 1 y ms = -1/2 (por ejemplo), el valor del número mj que corresponde al momento angular total tomará el valor de:
mj = ml + ms = 1 + (-1/2) = 1/2
que es el valor que aparece dentro de la tabla en el área de color ciano claro. Generalizando lo que tenemos en la tabla de arriba, no cuesta mucho trabajo verificar que el número cuántico j puede tomar todos los valores fijados entre los límites marcados por la siguiente desigualdad:
(l + s) ≥ .j ≥ |.l - s.|
De este modo, designando a l como los posibles valores enteros que puede tomar el número cuántico que corresponde al momento angular orbital (múltiplos enteros de la constante ħ) y a s como los dos posibles valores fraccionarios que puede tomar el número cuántico que corresponde al momento angular de spin (+1/2 y -1/2), los posibles valores que puede tomar el número cuántico .j que representa al momento angular total son, enumerados a manera de un “conteo descensivo” hacia abajo empezando desde el valor máximo l+s y disminuyendo de uno en uno hasta llegar al valor mínimo |.l-s.|:
_____________j = l + s,
_________________l + s - 1
_____________________l + s - 2_...
__________________________|.l - s.|
siendo además los valores que puede tomar la magnitud del momento angular total los siguientes:
|J| = √ j( j+1) ħ
tal y como en el caso de los momentums orbital y de spin. Más aún, la componente de J en la dirección del eje-z, o sea Jz, se encuentra cuantizada separadamente, siendo:
Jz = mj ħ
y aplicándose para los valores de mj un conteo igualmente “descensivo” hasta abarcar todos los valores posibles entre +j y -j:
_____________mJ = j
___________________j - 1
_____________________j - 2_...
________________________- j
PROBLEMA: Calcúlense los valores posibles de j para l = 1 y s = 1/2.
De acuerdo con lo anterior, los valores posibles de j son:
j = l + s = 1 + 1/2 = 3/2
j = l + s - 1 = 1 + 1/2 - 1 = 1/2
Puesto que |.l - s.| = |.1 - 1/2.| = 1/2, no hay valores más bajos para j, y los dos valores de j dados arriba son los únicos posibles.
PROBLEMA: Calcúlense los valores posibles de j para l = 3 y s = 1/2.
En este caso:
j = l + s = 3 + 1/2 = 7/2
j = l + s - 1 = 3 + 1/2 - 1 = 5/2
Puesto que |. j - s.| = |.3 - 1/2.| = 5/2, no hay valores más bajos para .j, y los dos valores de .j dados arriba son los únicos posibles.
PROBLEMA: Obténgase los valores posibles para la magnitud del momento angular total de un átomo que se encuentra en el estado l = 1.
Hay dos valores posibles para la magnitud |J|, uno de ellos ocurrirá cuando los “vectores” L y S sean “paralelos”, y el otro de ellos ocurrirá cuando los “vectores” L y S sean “antiparalelos”. Evaluando las dos posibles magnitudes de J ya sea con las fórmulas obtenidas arriba o con los valores obtenidos también arriba de j1.=.1/2 y j2.=.3/2 usando la relación |J|2 = j(.j+1)ħ2 para el caso l = 1, obtenemos:
PROBLEMA: Obténgase los valores posibles para la magnitud del momento angular total de un átomo que se encuentra en el estado l = 2.
Al igual que en el problema anterior, también aquí habrá dos valores posibles para la magnitud |J|, uno de ellos ocurrirá cuando los “vectores” L y S sean “paralelos”, y el otro de ellos ocurrirá cuando los “vectores” L y S sean “antiparalelos”. Evaluando las dos posibles magnitudes de J para el caso l = 2 con las fórmulas obtenidas arriba, obtenemos:
Tal vez aún no resulte del todo claro el por qué tienen que aparecer nuevas líneas espectrales como resultado de una combinación del momento angular orbital L y del momento angular de spin S del electrón. ¿Acaso no deberían ser independientes el uno del otro? La respuesta es definitivamente negativa, al considerar que en la evaluación del vector J.2 que los combina aparece claramente un término que antes no se tenía, un término que combina en forma multiplicativa ambos momentos angulares orbital y de spin:
J 2 = J · J = (L + S)·(L + S)
J 2 = L·L + L·S + S·L + S·S
Lo que tenemos en la segunda línea es una expresión puramente operacional, en la cual tanto L como S pueden representar los operadores diferenciales propios de la Mecánica Ondulatoria. Puesto que el momento angular orbital y de spin L y S son observables compatibles, el producto de ambos es conmutativo, o sea que L·S = S·L, con lo cual podemos reducir la expresión a lo siguiente:
J 2 = L·L + 2L·S + S·S
El término L·S, destacado en color magenta, es conocido como el acoplamiento LS. De no ser por este término, no habría esas líneas espectrales adicionales.
PROBLEMA: Obténgase la magnitud del acoplamiento L·S en función de j, l y s, esto es, en función de los eigen-valores de J, L y S.
Puesto que J.·.J = J.2, entonces tomando j = l + s se tiene lo siguiente:
J 2 = (L + S)·(L + S)
J 2 = L·L + 2L·S + S·S
L·S = (1/2)(J 2 - L2 - S2)
|L·S| = (1/2)( |J|2 - |L|2 - |S|2)
|L·S| = (1/2)( |J|2 - |L|2 - |S|2)
Puesto que |J|2 = j(.j+1)ħ2, |L|2 = l(l+1)ħ² y |S|2 = s(s+1)ħ2, se obtiene entonces lo siguiente para la magnitud del acoplamiento LS:
|L·S| = (1/2)[.j(.j+1) - l(l+1) - s(s+1)]ħ2
PROBLEMA: Calcúlense los valores posibles del acoplamiento L·S para l = 1 y s = 1/2.
En un problema anterior encontramos que para l = 1 y s = 1/2 hay dos valores posibles para .j, los cuales son 3/2 y 1/2. Entonces, para .j = 3/2:
|L·S| = (1/2)[(3/2)(3/2 + 1) - 1(1 + 1) - (1/2)(1/2 + 1)]ħ2
|L·S| = ħ2/2
Y para .j = 1/2:
|L·S| = (1/2)[(1/2)(1/2 + 1) - 1(1 + 1) - (1/2)(1/2 + 1)]ħ2
|L·S| = - ħ2
PROBLEMA: Calcúlense los valores posibles del acoplamiento L·S para l = 3 y s = 1/2.
En un problema anterior encontramos que para l = 3 y s = 1/2 hay dos valores posibles para .j, los cuales son 7/2 y 5/2. Entonces, para .j = 7/2:
|L·S| = (1/2)[(7/2)(7/2 + 1) - 3(3 + 1) - (1/2)(1/2 + 1)]ħ2
|L·S| = 3ħ2/2
Y para .j = 5/2:
|L·S| = (1/2)[(5/2)(5/2 + 1) - 3(3 + 1) - (1/2)(1/2 + 1)]ħ2
|L·S| = - 2ħ2
Una manera de darle una explicación algo mecanística al origen de la interacción L·S se tiene al considerar a un solo electrón que se mueve en torno a un núcleo N con carga Ze. Si se adopta un sistema de ejes coordenados en el que el electrón esté en reposo (y no moviéndose en torno al núcleo), el núcleo aparentemente se moverá en torno al electrón, y debido a este movimiento producirá un campo magnético en donde se encuentra el electrón, perpendicular al plano de la órbita (ya que toda carga eléctrica en movimiento relativo como un protón con su carga eléctrica positiva es equivalente a una corriente eléctrica que produce un campo magnético de acuerdo a las leyes de la electrodinámica clásica de Maxwell). Este campo magnético interno interaccionará con el momento magnético del electrón (usualmente simbolizado como μ) produciendo un efecto físico semejante al de dos pequeños imanes interactuando entre sí, y la energía dependerá del ángulo entre el momento magnético del electrón y el campo magnético producido por el protón en su movimiento aparente en torno al electrón, y por lo tanto de la dirección del spin del electrón y de la normal a la órbita. Podemos visualizar esto por medio de las siguientes figuras:
En la figura (a), se tiene al electrón e orbitando en torno al núclo N, mientras que en la figura (b) el electrón considerándose a sí mismo en reposo ve al núcleo N con su carga eléctrica positiva orbitando en torno a él, produciendo un campo magnético sobre el electrón. Es importante tener presente que se trata de un campo magnético que es interno al mismo átomo, no se trata de un campo magnético exterior que le sea aplicado a la muestra. Por lo tanto, aún en ausencia total de un campo magnético externo, el efecto del acoplamiento L·S se dá por sí solo, aunque por lo general se requiere de un espectógrafo con la suficiente potencia para poder distinguir las líneas de la estructura fina que se forman.
El vector momento angular orbital L del electrón produce un vector momento magnético μL del mismo modo que el vector momento angular del spin S del electrón produce un vector momento magnético μS. No es difícil demostrar, recurriendo para ello a simples argumentos de la geometría básica, que el vector del momento angular total J que resulta de la suma vectorial de L y S y el vector del momento magnético μ que corresponde a J no son paralelos. En efecto, sabiendo que, en función de los momentos angulares (vectoriales), los momentos magnéticos están dados por las relaciones:
y tomando en cuenta las relaciones vectoriales:
entonces con un simple trazado de los triángulos de las sumas vectoriales que representan dichas relaciones se puede apreciar que μ y J no son paralelos:
lo cual es obvio en virtud de que:
y los triángulos no son congruentes (semejantes), y por lo tanto μ y J no son paralelos. (Recuérdese que en la geometría Euclideana, para que dos tríangulos ΔABC y ΔA’B’C’ sean congruentes, esto es, que si uno de ellos es ampliado o el otro reducido ambos coincidirán en sus tres lados y en sus tres ángulos, basta con que la razón de dos lados cualesquiera de uno de los triángulos sea igual a la razón de los dos lados correspondientes del otro triángulo, o sea a/b.=.a’/b’.)
PROBLEMA: Calcúlese la proyección del vector momento magnético total μ sobre el vector J.
De lo que acabamos de ver, se tiene que:
La proyección de μ sobre J es:
Ahora bien, hablando vectorialmente:
o lo que es lo mismo:
De este modo:
Tomando en cuenta que el valor de J.2 es .j(.j+1)ħ2 del mismo modo que el valor de L2 es l(l+1)ħ2 y que el valor de S2 es s(s+1)ħ2, se concluye por lo tanto que:
en donde:
es una cantidad que fué definida por vez primera por Alfred Landé, usualmente conocida como el factor g de Landé, el cual es necesario para poder calcular el desdoblamiento relativo de diferentes niveles de energía en campos magnéticos débiles.
PROBLEMA: Calcúlense los factores g de Landé para los niveles energéticos definidos en notación espectroscópica como 2S1/2, 2P1/2, y 2P3/2.
Al nivel espectroscópico 2S1/2 le corresponden los números cuánticos l.=.0, s.=.1/2 y .j.=.1/2. Por lo tanto:
Al nivel espectroscópico 2P1/2 le corresponden los números cuánticos l.=.1, s.=.1/2 y .j.=.1/2. Por lo tanto:
Y al nivel espectroscópico 2P3/2 le corresponden los números cuánticos l.=.1, s.=.1/2 y .j.=.3/2. Por lo tanto:
PROBLEMA: Calcúlese la energía de desdoblamiento de un átomo en un campo magnético B, suponiendo que el desdoblamiento dependa solamente del componente del momento magnético total μ a lo largo de J.
De lo anterior, la componente del vector momento magnético μ a lo largo de J es (usando me para simbolizar a la masa del electrón con el fin de evitar confusiones, ya que estaremos usando al símbolo mj para el número cuántico relacionado con J):
Empleando notación vectorial:
La energía de desdoblamiento, dada por el producto escalar punto entre el momento magnético μJ a lo largo de J y el campo magnético B, viene siendo entonces:
PROBLEMA: Usando el sistema de unidades MKS-SI, calcúlese el desdoblamiento anómalo de Zeeman ocasionado por un campo magnético externo de 0.5 Teslas para los estados más bajos en el hidrógeno (2S1/2, 2P1/2 y 2P3/2) a causa de la interacción L·S, suponiendo para ello que esta interacción es mucho más fuerte que la interacción con el campo magnético externo.
Usando los resultados del problema anterior y metiendo los valores apropiados de las constantes físicas, se tiene:
Usando los factores g de Landé calculados en el penúltimo problema anterior, podemos resumir los cálculos en la tabla siguiente:
Quizá el ejemplo más sobresaliente y citado del acoplamiento L·S es el que dá origen a las líneas D del sodio. La sal común, por ser cloruro de sodio, al ser puesta en la flama de un mechero de Bunsen como los que se utilizan en los laboratorios de química, dá un color amarillo a la llama, el cual si es observado a través de un espectroscopio óptico calibrado a una resolución baja proporciona una línea distintiva con una longitud de onda de unos 590 nanometros:
Sin embargo, si se aumenta el poder de resolución del espectroscopio y se observa la línea más de cerca, se descubre que la línea en realidad consta de dos líneas distintivas, características de un doblete. Este doblete es debido precisamente al acoplamiento L·S. Para el átomo de sodio, su configuración electrónica es:
1s22s22p63s
Los 10 electrones interiores se pueden visualizar como formando una nube electrónica simétricamente esférica. En lo que estamos interesados aquí es en la excitación del onceavo electrón solitario que se encuentra en el nivel 3s. La posibilidad más cercana de excitación es hacia el nivel 3p. En virtud de que por la presencia de los 10 electrones interiores que ejercen un efecto de pantalla el potencial central ya no es un potencial Coulómbico puro, los niveles 3s y 3p se encontrarán desdoblados. La estructura fina introducida por el potencial de interacción VLS es un desdoblamiento más fino aún que se lleva a cabo en el nivel 3p, entre 3p1/2 y 3p3/2, en donde el sub-índice es el número cuántico .j. Experimentalmente, se observan las dos líneas D del sodio separadas a corta distancia la una de la otra, una de ellas con una longitud de onda de 5896 Angstroms, y la otra con una longitud de onda de 5890 Angstroms:
En rigor de verdad, el modelo físico usado arriba, suponiendo al electrón estático y al protón circulando en torno suyo creando un campo magnético interno al átomo, para explicar el origen del acoplamiento L·S, es demasiado mecanístico como para ser tomado muy en serio, y se vuelve necesario recurrir directamente a la ecuación de Schrödinger y resolverla introduciendo en ella el término de interacción para poder justificar matemáticamente la aparición de las líneas espectrales adicionales debidas al acoplamiento L·S. La forma de introducir el término de interacción es mediante un Hamiltoniano de interacción HLS que es agregado al Hamiltoniano ordinario H que se utiliza en la resolución mecanico-cuántica del átomo de hidrógeno:
Aquí se vuelve necesario especificar alguna función radial .f(r) a la cual se le pueda ser hacer concordar con los datos experimentales. El término de interacción más frecuentemente utilizado para explicar el acoplamiento L·S es el siguiente (usando el sistema de unidades cgs-Gaussiano):
en donde Vc es el potencial central (Coulómbico, de naturaleza eléctrica, cuyo origen está en el centro del átomo, aunque alterado por los electrones que se interponen entre el núcleo atómico y el electrón de valencia localizado en la capa más exterior del átomo) que actúa sobre el electrón que gira en torno al núcleo (más abajo veremos la derivación de este Hamiltoniano de interacción L·S). Desafortunadamente, al agregarle este término de interacción a la ecuación de Schrödinger para el átomo de hidrógeno, aunque la solución (usando la técnica matemática de separación de variables) sigue teniendo una parte radial y una parte angular, la ecuación en sí se vuelve irresoluble por técnicas matemáticas exactas, y se vuelve necesario recurrir a aproximaciones. Afortunadamente, gracias a que el efecto del acoplamiento L·S es relativamente pequeño (hablando en términos absolutos en relación a las magnitudes de las energías involucradas), se vuelve posible introducir la teoría de las perturbaciones para obtener aproximaciones que dán una aproximación teórica razonablemente buena con los resultados que se obtienen experimentalmente en el laboratorio. Estas técnicas se verán en mayor detalle en las entradas tituladas “Técnicas de aproximación”, aunque más abajo se dará un anticipo de las mismas.
El acoplamiento L·S debido al campo magnético interno al átomo introduce pues un término de interacción a la ecuación de Schrödinger, esto sin que se le haya aplicado en lo absoluto ningún campo magnético externo a la muestra. ¿Y qué ocurrirá si le aplicamos un campo magnético externo B al espécimen bajo observación? En ausencia del acoplamiento L·S, esperaríamos observar un efecto Zeeman normal con el desdoblamiento de líneas que esperamos ver aumentando la separación entre las líneas conforme se va aumentando la intensidad del campo magnético externo. Pero habiendo un acoplamiento L·S, entonces la ecuación de Schrödinger para describir lo que ocurra deberá de incorporar un total de cuatro términos:
en donde HB es el Hamiltoniano que se tiene que agregar para poder explicar lo que sucede al aplicársele un campo magnético externo B a la muestra. Tomando en cuenta los parámetros involucrados, la ecuación de Schrödinger ampliada resulta ser (en el sistema de unidades cgs-Gaussiano):
¿Qué es lo que ocurre entonces cuando a un átomo en el cual hay un desdoblamiento en los niveles energéticos a causa del acoplamiento L·S producido por el campo magnético interno al átomo se le va aplicando un campo magnético externo B? Todo dependerá de la magnitud del campo magnético externo que le sea aplicado a la muestra. Para fines de análisis simplificado, podemos considerar dos casos especiales, el primero en el cual el campo magnético externo que se le aplica a la muestra es un campo magnético relativamente débil, de forma tal que ambos efectos puedan interactuar mostrando sus efectos combinados en el espectógrafo; y el segundo caso siendo aquél en el cual el campo magnético que se le aplica a la muestra es tan intenso que el campo magnético interno resulta muy pequeño (relativamente hablando). Cuando se le aplica a la muestra un campo magnético relativamente pequeño, a los desdoblamientos energéticos debidos al efecto Zeeman normal hay que sumarles los desdoblamientos ocasionados por el acoplamiento L·S (produciéndose así un efecto Zeeman anómalo con una cantidad de líneas mayor a la predicha). La siguiente figura nos muestra en mayor detalle lo que ocurre:
Cuando el campo magnético externo que se le aplica a la muestra es muy intenso, imponiéndose sobre el efecto del campo magnético interno que dá origen al acoplamiento LS, los niveles energéticos aparecen desdoblados en cinco niveles igualmente separados tal y como ocurre en el efecto Zeeman normal, y hay únicamente tres energías diferentes de transición. Este comportamiento que se observa mediante la aplicación de campos magnéticos intensos es conocido como el efecto Paschen-Back, así nombrado en honor a sus descubridores Friedrich Paschen y Ernst Back. Podemos apreciar mejor el efecto Paschen-Back en el extremo izquierdo de la siguiente gráfica cuando el campo magnético exterior aplicado tiene una intensidad de aproximadamente 100 Teslas:
Elaborando sobre las mismas gráficas de arriba, los cinco niveles energéticos observados (al llevarse a cabo el traslape de niveles) así como las tres lineas espectrales observadas que corresponden a las transiciones permisibles en dichos niveles energéticos se muestran en la siguiente figura:
El tratamiento formal del acoplamiento LS requiere de la postulación de una función de onda que incorpore los números cuánticos n (el número cuántico principal relacionado con la función de onda radial que fija los niveles de energía en el modelo atómico planetario de Bohr), el número cuántico l asociado al momento angular orbital y el número cuántico .j asociado al momento angular total:
Anticipándonos un poco a lo que veremos en la serie de entradas tituladas “Técnicas de aproximación”, y designando como ΔEnlj a la energía debida al término de interacción LS que debe ser agregada como Hamiltoniano a la ecuación de Schrödinger para tomar en cuenta el efecto de dicho término, entonces se puede demostrar que para un desplazamiento de energía de primer orden (ignorando efectos cuadráticos y de orden mayor) el valor aproximado de ΔEnlj se puede obtener tomando el valor esperado (la esperanza matemática) del Hamiltoniano de acoplamiento HLS con respecto a la función de onda utilizada para llevar a cabo el análisis:
Usando el término dado arriba para el acoplamiento y sacando fuera del producto interno bra-ket las cantidades físicas constantes, se tiene entonces:
En la solución matemática del átomo hidrogenoide, se ha visto ya en entradas previas que es posible introducir la técnica conocida como separación de variables para “romper” la función de onda en el producto de dos funciones de onda, una de las cuales es una función de onda radial, y la otra una función de onda que corresponde a la parte angular, usualmente especificada en su forma infinitesimal por un ángulo sólido dΩ. Podemos hacer lo mismo para la función de onda utilizada en la evaluación del efecto de la interacción, postulando lo siguiente:
De este modo, haciendo la conversión del formalismo bra-ket de Dirac al formalismo propio de la Mecánica Ondulatoria, y separando la expresión en el producto de dos integrales, una de las cuales corresponde a la parte radial y la otra correspondiendo a la parte angular, se tiene lo siguiente a ser evaluado (el factor r2 que aparece en la integral que corresponde a la parte radial proviene del uso de las coordenadas esféricas en lugar de las coordenadas Cartesianas para llevar a cabo la evaluación de las integrales en coordenadas esféricas):
Compactando la parte radial a su simbolización simplificada como esperanza matemática, y recurriendo a la relación dada arriba para la expansión del término L·S en función de J.2, L2 y S2, se tiene:
Usando los eigenvalores que corresponden a los operadores, y sacando las constantes fuera de la integral que corresponde a la parte angular, vemos que:
Por la ortonormalidad que se supone con la cual están definidas las funciones de onda, puesto que (aquí la integral llevada a cabo sobre un ángulo sólido dΩ es en realidad una doble integral llevada a cabo sobre los ángulos dθ y dφ):
la relación se reduce entonces a:
Puesto que el número cuántico asociado al momento angular de spin sólo puede tomar dos valores posibles, +1/2 y -1/2, en tal caso para cierto valor del número cuántico l asociado al momento angular orbital el número cuántico .j sólo puede tomar dos valores:
Substituyendo estos dos valores en la expresión de arriba, se obtienen así las siguientes dos relaciones:
El par de relaciones es mejor conocido como la regla del intervalo de Landé.
Había quedado pendiente arriba la explicación del origen del Hamiltoniano de interacción HLS, lo cual se procederá a hacer a continuación.
De acuerdo a la electrodinámica clásica, un electrón que se traslada en línea recta a una velocidad v en ausencia de cualquier influencia externa experimentará de pronto una desviación en su trayectoria si penetra en una región del espacio en donde hay un campo magnético B, actuando sobre el electrón una fuerza conocida como fuerza de Lorentz dada por la siguiente relación vectorial (la letra en tipo negrita será usada para representar vectores):
siendo q la carga eléctrica de la partícula. El producto vectorial cruz v×B siendo los vectores v y B perpendiculares es el que nos proporciona la dirección en la cual actúa la fuerza F que modifica la trayectoria de la partícula, de acuerdo con la regla de la mano derecha en donde se extiende el dedo índice de la mano derecha apuntando hacia una dirección A y el dedo medio apuntando hacia una dirección B perpendicular a la dirección A en la que apunta el dedo índice, con el dedo pulgar puesto perpendicular al plano en el que se encuentran ambos vectores A y B apuntando en la dirección C que resulta del producto vectorial cruz A y B (obsérvese que de acuerdo a la regla de la mano derecha el producto vectorial cruz B×A apunta en una dirección opuesta a la dirección en la que apunta el producto vectorial cruz y A×B y por lo tanto A×B y B×A son de signos contrarios):
Clásicamente, la fuerza de Lorentz es precisamente lo que retiene al electrón en su órbita circular alrededor del núcleo del átomo ¿Pero de dónde sale el campo magnético B que proporciona el ingrediente necesario para que pueda actuar la fuerza centrípeta F que retiene en órbita en órbita? Ya se vió arriba que el electrón, si se considera a sí mismo como una partícula en reposo, “verá” al núcleo atómico de carga positiva girando en derredor suyo creando el equivalente de una corriente eléctrica y por lo tanto un campo magnético B de acuerdo a la ley de Biot-Savart. Con tal corriente eléctrica ocasionada por el movimiento del protón (núcleo) en torno al electrón se crea pues un campo magnético efectivo que en ocasiones es designado como Bef.
Si en la relación de la fuerza de Lorentz, pasamos la carga eléctrica q del otro lado de la ecuación haciendo que divida a la fuerza F:
lo que tenemos entonces del lado izquierdo es precisamente la definición de lo que es un campo eléctrico E:
Si queremos “despejar” para B en la relación anterior, no se puede hacer algebraicamente como acostumbramos hacerlo con las cantidades escalares debido a que se trata de vectores que tienen magnitud y sentido y no simples cantidades escalares como la temperatura o la humedad que no tienen dirección alguna. Hacer tal “despeje” requiere recurrir nuevamente a la regla de la mano derecha y la definición del producto cruz vectorial preparando un diagrama como el siguiente:
Obviamente, de acuerdo a este diagrama de vectores, la relación vectorial para el vector B en función de los vectores v y E debe ser:
Antes de continuar, tenemos que hacer una pausa para meditar que, si bien el sistema MKS de unidades es lo más común en la física del mundo macroscópico en donde las masas se gradúan en kilos (o inclusive en toneladas) y las distancias se miden en metros (o inclusive en kilómetros), no tiene mucho sentido aferrarse a tal sistema de unidades cuando en el mundo submicroscópico tenemos partículas como el electrón y el protón cuyas masas ciertamente no se miden en kilos, interactuando entre sí a distancias que ciertamente no se miden en metros. Es precisamente por tal razón que en la Mecánica Cuántica se prefiere prescindir del uso del sistema MKS de unidades optando mejor por el sistema de unidades cgs-Gaussianas en donde además de medirse todo en centímetros, gramos y segundos se utiliza como factor de escala la velocidad de la luz c que es una constante física universal (posiblemente la constante física más absoluta de todas, de acuerdo a la Teoría de la Relatividad). De este modo, por convención la relación anterior es modificada para que tome la siguiente forma (y se repite que ésto es una mera cuestión de conveniencia para manejos numéricos relacionados con cantidades muy pequeñas):
Se repite que en todo momento se debe tener presente el uso de la regla de la mano derecha para el manejo de estas cantidades vectoriales:
Ahora bien, y razonando de manera independiente, se supone que además de orbitar en torno al núcleo atómico el electrón está girando sobre sí mismo. Una partícula como el electrón con carga eléctrica que está girando sobre su propio eje constituye lo que se conoce como un dipolo magnético simbolizado como μ (obsérvese que es una cantidad vectorial, con dirección y sentido). Si el electrón no estuviese girando sobre su propio eje no habría dipolo magnético alguno, y la presencia de un campo magnético de origen submicroscópico se toma como evidencia directa de que el electrón gira sobre su propio eje creando un campo magnético. El momento de dipolo magnético μ es directamente proporcional al momento angular de spin del electrón S:
μ = γS
en donde el factor de proporcionalidad γ es conocido como la relación giromagnética. Cuando un dipolo magnético (como lo es el caso del electrón girando sobre su propio eje) es inmerso dentro de un campo magnético B, el dipolo magnético experimenta un torque μ×B que a su vez produce una precesión al igual que la que vemos en un trompo inclinado que tiende a alinear a la partícula en una dirección paralela a la del campo magnético B tal y como ocurre con la aguja de un compás. La energía asociada con éste torque está dada por la relación:
Podemos substituír aquí la relación que se obtuvo arriba, resultando en lo siguiente (en unidades del sistema CGS-Gaussiano):
El producto vectorial cruz que tenemos dentro de los paréntesis lo podemos invertir, advertidos de que al hacer tal cosa se necesario cambiar el signo en virtud de que el producto vectorial cruz no es conmutativo en el sentido algebraico usual:
Para mayor simplicidad, sacaremos fuera el factor de proporcionalidad dado por la velocidad de la luz c. Se tiene entonces:
A continuación meteremos en ésta relación dentro de los paréntesis como factor multiplicativo la masa me del electrón de la manera en que se muestra:
Esta última manipulación tuvo un propósito muy definido, meter el momentum del electrón p en el lado derecho. ¿Y por qué habríamos de hacer tal cosa? Porque en la Mecánica Cuántica lo que se utiliza es el momentum de una partícula en la solución de la ecuación de Schrödinger, y carece de sentido hablar de la velocidad v de la partícula que no aparece para nada en la ecuación. Es así como tenemos ahora lo siguiente:
Antes de proseguir, vamos a tomar una ligera desviación para recordar otra definición clásica de lo que es el vector campo eléctrico E. Un campo eléctrico E es igual a:
en donde Φ es la función escalar del potencial electrostático asociada con el campo eléctrico, cuyo gradiente negativo radial produce el campo E. Precaución: no se confunda jamás por ningún motivo el potencial electroestático Φ, una cantidad medida en volts, con la función de energía potencial V que se acostumbra usar en la Mecánica Cuántica, medida en joules o ergs). Para asignar también dirección en el lado derecho de la relación vectorial y hacer más correcta y consistente la expresión, hay autores que incorporan del lado derecho el factor r (una magnitud vectorial radial que puede tomar cualquier valor) dividido entre la magnitud escalar r cuya magnitud toma el mismo valor que r, de modo tal que el cociente r/r viene constituyendo un vector unitario que no cambia en nada la magnitud de E pero que le asigna dirección al lado derecho de la expresión. Usaremos aquí también dicha convención por ser efectivamente el ejemplo de una notación más correcta y consistente:
De éste modo, la energía de interacción H toma el siguiente aspecto:
Los dos signos negativos se cancelan y llegamos así a lo siguiente:
Si nos fijamos bien, veremos que el producto vectorial cruz r×p que tenemos del lado derecho es precisamente la definición de lo que es el momento angular clásico L, lo que permite hacer la siguiente simplificación:
Obsérvese que no tenemos ya ningún producto vectorial cruz del lado derecho de la relación, únicamente un producto escalar de los vectores μ y L.
Metiendo ésto en la expresión para la energía de interacción, se tiene entonces:
Clásicamente hablando, hasta este punto la expresión obtenida es correcta. Sin embargo, fue obtenida recurriendo a argumentos de la mecánica Newtoniana. Si en vez de recurrir a la mecánica Newtoniana utilizamos la Teoría Especial de la Relatividad, encontramos que ocurre otro movimiento de precesión (independiente del movimiento de precesión del electrón sobre su propio eje causado por el torque que ejerce el campo magnético B producido por el núcleo del átomo desde la perspectiva de un electrón en reposo), conocido como la precesión de Thomas. La precesión de Thomas, descubierta por Llewellyn Thomas y aplicada al análisis del electrón en el átomo con el trabajo “The Motion of the Spinning Electron” publicado en la revista Nature en 1926, es de naturaleza general y se aplica también a los fenómenos del mundo macroscópico, inclusive a escala de movimientos astronómicos, en donde tal precesión es conocida como la precesión de Sitter y también como el efecto geodético en homenaje al físico holandés Willem de Sitter que predijo tal efecto.
Lo increíble es que para toda la complejidad teórica requerida para incorporar las consideraciones de la Teoría Especial de la Relatividad en el estudio del movimiento del electrón en torno al núcleo atómico, se llega a una conclusión ridículamente sencilla (esto suele ocurrir dentro de la física), la conclusión de que la expresión que hemos obtenido clásicamente arriba tiene que ser modificada anexándole un factor multiplicativo de 1/2 conocido como el factor de Thomas, de modo tal que una expresión más correcta para H tiene que ser la siguiente (el factor de Thomas es resaltado en color azul):
Es importante agregar que la realidad de éste factor multiplicativo ha sido confirmada experimentalmente, lo cual proporciona en cierto modo una confirmación experimental de la Teoría Especial de la Relatividad de Einstein.
El factor de Thomas no es el único factor que entra en el panorama. No es difícil derivar una expresión clásica para la relación giromagnética γ citada arriba que relaciona al momento magnético μ con el momento angular de spin S del electrón. Y resulta que el resultado clásico que se obtiene así también es incorrecto en el sentido de que hay que agregarle un factor multiplicativo de 2 de acuerdo a una de las conclusiones que se obtienen de la ecuación relativista de Dirac. El resultado de ésto es que podemos substituír la relación giromagnética γ para obtener lo siguiente que incorpora el factor multiplicativo, también de 2, predicho por la ecuación de Dirac:
Es así como llegamos a la siguente expresión final:
Aquí podemos incorporar de inmediato la relación obtenida arriba para el producto L·S:
J 2 = L·L + 2L·S + S·S
y podemos producir argumentaciones adicionales sobre las implicaciones del desdoblamiento en los niveles de energía ocasionados por la interacción entre el momento angular L del electrón y el momento angular del spin S también del electrón. Se trata, en efecto, de dos características distintas que producen consecuencias a causa de algo que tiene que ver única y exclusivamente con el mismo electrón.
La relación obtenida es esencialmente lo que se había dado anteriormente como el operador Hamiltoniano que representa a la energía de interacción spin-órbita. Es una de las cosas que producen el desdoblamiento de líneas espectrales en los espectros de emisión y en los espectros de absorción en los átomos. No se ha dicho nada sobre el cálculo de las energías desdobladas, el cual debe empezar a partir del término de interacción spin-órbita que se ha obtenido, en virtud de que hasta este punto no se han desarrollado las herramientas matemáticas para ello. El punto de entrada en éste análisis lo proporciona el método de las perturbaciones, dándonos específicamente lo que se conoce como la corrección perturbativa de primer orden, con lo cual es posible predecir teóricamente la separación energética entre las líneas espectrales desdobladas. Esto necesariamente tiene que esperar para ser tratado en una entrada posterior.
Viendo más adelante, siendo tanto el momento angular orbital L como el momento angular de spin S momentos angulares, esto es precisamente lo que nos lleva a preguntarnos sobre la posibilidad de que el acoplamiento de estos dos momentos angulares (spin y orbital) no sea más que un caso especial de un problema más general, el problema del acoplamiento de dos momentos angulares en el cual los momentos angulares pueden ser, por ejemplo, los momentos angulares de spin S1 y S2 de dos partículas del mismo tipo (por ejemplo, dos electrones) o dos partículas distintas (por ejemplo, un protón y un neutrón) confinadas en un espacio reducido en proximidad cercana la una a la otra. Y de hecho es posible llevar a cabo el análisis matemático del acoplamiento de dos momentos angulares de cualquier tipo y de cualquier magnitud, obteniéndose al final algunas reglas sencillas que permiten predecir las intensidades relativas de las líneas espectrales que se puedan obtener en experimentos de laboratorio en donde se busque este tipo de acoplamientos. Pero introducirnos más a fondo en este tópico requerirá primero obtener una familiarización con otras herramientas matemáticas y conceptuales que se irán introduciendo en entradas posteriores. El tema en sí de la suma de dos momentos angulares, estudiado desde una panorámica más amplia que la que hemos visto hasta ahora, se logrará cuando hayamos llegado a las entradas tituladas “Los coeficientes Clebsch-Gordan”, en donde veremos nuevamente el acoplamiento L·S desde una perspectiva más formal y rigurosa. De cualquier modo, analizaremos en la siguiente entrada algunos resultados accesibles que se pueden obtener utilizando las reglas que son consecuencia del análisis formal y riguroso.