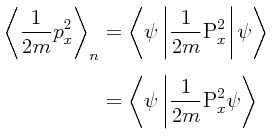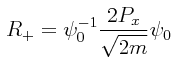L+ = Lx + iLy
L- = Lx - iLy
L- = Lx - iLy
Se acostumbra representar ambas expresiones en una sola:
L± = Lx ± iLy
PROBLEMA: Defínase a partir de los operadores diferenciales Px y Py para el momentum de una partícula al siguiente operador:
P+ = Px + iPy
Demuéstrese que:
[P+,(x + iy)] = 0
Aunque no es absolutamente indispensable, para mayor claridad y transparencia en la resolución de este problema se aplicará la expresión sobre una función de onda ψ cualesquiera que no sea igual a cero:
[P+,(x + iy)]ψ
Expandiendo el conmutador:
{P+(x + iy) - (x + iy)P+}ψ
Substituyendo el operador escalera por su definición operacional:
{(Px + iPy)(x + iy) - (x + iy)(Px + iPy)}ψ
Expandiendo:
{Px(x) + iPx(y) + iPy(x) + i²Py(y) - xPx - ixPy - iyPx + yPy}ψ
Aplicando cada término operacional sobre la función de onda:
Px(xψ) + iPx(yψ)
+ iPy(xψ) - Py(yψ)
- xPx(ψ)
- ixPy(ψ)
- iyPx(ψ)
+ yPy(ψ)
+ iPy(xψ) - Py(yψ)
- xPx(ψ)
- ixPy(ψ)
- iyPx(ψ)
+ yPy(ψ)
Puesto que los operadores diferenciales para Px y Py son:
la expansión nos produce entonces lo siguiente (hay que tomar precaución al tomar la diferencial de productos como xψ):
- iħx(∂ψ/∂x) - iħψ(∂x/∂x) + ħy(∂ψ/∂x) + ħψ(∂y/∂x)
+ ħx(∂ψ/∂y) + ħψ(∂x/∂y) + iħy(∂ψ/∂y) + iħψ(∂y/∂y)
+ iħx(∂ψ/∂x)
- ħx(∂ψ/∂y)
- ħy(∂ψ/∂x)
- ħy(∂ψ/∂y)
+ ħx(∂ψ/∂y) + ħψ(∂x/∂y) + iħy(∂ψ/∂y) + iħψ(∂y/∂y)
+ iħx(∂ψ/∂x)
- ħx(∂ψ/∂y)
- ħy(∂ψ/∂x)
- ħy(∂ψ/∂y)
Tras haber cancelado los términos obvios por la independencia de las coordenadas, lo que queda se va eliminando en pares:
- iħx(∂ψ/∂x) - iħψ + ħy(∂ψ/∂x)
+ ħx(∂ψ/∂y) + iħy(∂ψ/∂y) + iħψ
+ iħx(∂ψ/∂x)
- ħx(∂ψ/∂y)
- ħy(∂ψ/∂x)
- iħy(∂ψ/∂y)
= 0
+ ħx(∂ψ/∂y) + iħy(∂ψ/∂y) + iħψ
+ iħx(∂ψ/∂x)
- ħx(∂ψ/∂y)
- ħy(∂ψ/∂x)
- iħy(∂ψ/∂y)
= 0
y puesto que la función de onda ψ no es igual a cero, se concluye que:
[P+,(x + iy)] = 0
PROBLEMA: Demostrar que el operador:
Q+ = a + ib
en donde a y b son constantes no es un operador Hermitiano.
La demostración es trivial, obtenida evaluando por separado ambas integrales usadas para la definición de un operador Hermitiano:
∫ψa*(Q+ψb) dV = ∫ψa*(a+ib)ψb dV = a∫ψa*ψbdV + ib∫ψa*ψbdV
= (a + ib)∫ψa*ψbdV
∫(Q+ψa)*ψbdV = ∫Q+*ψa*ψbdV = ∫(a-ib)ψa*ψbdV
= a∫ψa*ψbdV - ib∫ψa*ψbdV
= (a - ib)∫ψa*ψbdV
= (a + ib)∫ψa*ψbdV
∫(Q+ψa)*ψbdV = ∫Q+*ψa*ψbdV = ∫(a-ib)ψa*ψbdV
= a∫ψa*ψbdV - ib∫ψa*ψbdV
= (a - ib)∫ψa*ψbdV
Los resultados obtenidos en cada caso son diferentes. Entonces ambos lados en la definición de Hermiticidad son diferentes, o sea:
∫ψa*(Q+ψb) dV ≠ ∫(Q+ψa)*ψbdV
y se concluye que el operador Q+ no es Hermitiano. Lo mismo podemos demostrar para el operador Q-. Ultimadamente, la razón sencilla por la que en este caso Q+ no es Hermitiano es porque el conjugado de un número complejo (o de una función de variables complejas) no es igual al número complejo original.
Si los operadores escalera que acabamos de ver no son operadores Hermitianos, podríamos cuestionarnos qué aplicación práctica podrían tener dentro de la Mecánica Cuántica. La utilidad de los mismos radica en el hecho de que pueden ser utilizados ventajosamente para obtener las autofunciones eigen de un sistema cuando el problema ha sido resuelto para cierto número cuántico. Y comparten además una característica que los hace sumamente interesantes: si bien un operador escalera Q+ no es Hermitiano como tampoco lo es su contraparte Q-, cada uno de ellos es el adjunto Hermitiano del otro:
∫ψa*(Q+ψb) dV = ∫(Q-ψa)*ψbdV
Los operadores Hermitianos surgen en forma casi natural cuando tenemos cantidades tales como el operador de energía H que corresponde al oscilador harmónico simple que consta de la suma de los cuadrados de dos términos que también son operadores (el operador momentum Px y el operador posición X):
Esto por sí solo sugiere una factorización del tipo:
A² + B² = (A + iB)(A - iB)
Si bien es cierto que esto nos mete números imaginarios y complejos dentro del panorama, no debemos dejarnos intimidar por tal hecho en virtud de que como ya lo hemos visto, en la Mecánica Cuántica las matemáticas tienen la característica curiosa de que siempre terminan produciéndonos números reales que podemos medir con algún aparato de laboratorio. En todo caso, lo que más nos podría preocupar sobre una factorización de este tipo es que al tratar de aplicarla en sentido inverso no podemos llegar a la expresión original cuando se trata del caso de operadores no-conmutativos:
(A + iB)(A - iB) = A² - iAB + iBA + B² = A² + B² + i(BA - AB)
Sin embargo, este obstáculo aparente tampoco tiene por qué serlo en virtud de que el término imaginario contiene una cantidad que podemos compactar con la ayuda del conmutador, y si los operadores A y B son observables compatibles entonces dicha cantidad se vuelve cero, pero si se trata de observables incompatibles entonces podemos meter aquí la ecuación de Born. Lo importante en todo caso es tratar de llegar hasta donde las matemáticas nos permitan llegar.
Con lo anterior en mente, en el caso del oscilador armónico simple se vuelve casi irresistible el proponer y considerar para su uso el siguiente par de operadores escalera:
A continuación formaremos el producto R+R- en ese orden:
Desarrollando el producto y simplificando mediante el uso del conmutador:
Los primeros dos términos son simplemente el operador H. En el tercer término, reconocemos la ecuación de Born como:
[P, X] = - iħ
Simplificando con esto y haciendo uso de la relación ω = √k/m para el oscilador harmónico simple llegamos al resultado deseado:
Trabajando de igual manera, obtenemos la siguiente relación:
PROBLEMA: Trabajando con los operadores dados arriba, obténgase una relación para el siguiente conmutador:
[H, R+]
simplificando lo más que se pueda.
Con el fin de hacer la derivación más fácil, utilizaremos la siguiente notación:
haciendo a = 1/√2m y b = √k/2, con lo cual:
R+ = aPx + ibX
Desarrollando el conmutador proporcionado tenemos entonces:
[H, R+] = HR+ - R+H
[H, R+] = (a²Px² + b²X²)(aPx + ibX) - (aPx + ibX)(a²Px² + b²X²)
[H, R+] = (a²Px² + b²X²)(aPx + ibX) - (aPx + ibX)(a²Px² + b²X²)
Desarrollando los productos la expresión al lado derecho de la igualdad toma la siguiente forma:
a3Px3 + ia²bPx²X + ab²X²Px + ib3X3
- a3Px3 - ab²PxX² - ia²bXPx² - ib3X3
- a3Px3 - ab²PxX² - ia²bXPx² - ib3X3
Tras las cancelaciones por pares, podemos hacer los siguientes agrupamientos:
ab²(X²Px - PxX²) + ia²b(Px²X - XPx²)
Simplificando con el conmutador:
ab²[X², Px] + ia²b[Px², X]
A continuación podemos reemplazar los conmutadores por las siguientes relaciones fácilmente demostrables a partir de la ecuación de Born:
[x², Px] = 2iħX___[Px², X] = -2iħPx
Tenemos entonces:
ab²(2iħX) + ia²b(-2iħPx) = 2ħab(aPx + ibX) = 2ħabR+ = 2ħ(ω/2)R+
Entonces:
[H, R+] = ħωR+
Procediendo de la misma manera, podemos demostrar que:
[H, R -] = - ħωR -
Podemos resumir ambos resultados en una sola expresión:
[H, R±] = ħωR±
Debe ser obvio que, en base a argumentaciones físicas, cualquier teoría razonable acerca del oscilador armónico simple debe producir valores de energía para el oscilador que sean positivos, habido el hecho (de acuerdo al operador Hamiltoniano de energía H) la energía total del oscilador es igual a la suma de factores positivos que multiplican los cuadrados de la posición y el momentum. Resulta interesante ver que esta conclusión también es obtenida a partir de consideraciones muy elementales del álgebra de operadores. Considérese el término del operador Hamiltioniano de energía que involucra a la posición. El operador posición es un operador Hermitiano que por tal hecho sólo puede tener valores reales. En consecuencia, el cuadrado del operador posición solo puede tener eigenvalores reales positivos. Del mismo modo, el cuadrado del operador del momentum Px solo puede tener eigenvalores reales positivos. Por lo tanto, el valor esperado tanto de la energía cinética como de la energía potencial y por ende el Hamiltoniano solo pueden ser positivos. Si el valor esperado del Hamiltoniano solo puede ser positivo, la energía del oscilador armónico simple solo puede ser positiva (o posiblemente cero). Esto implica que no puede haber estados de energía negativa para el oscilador armónico simple.
Puesto que el oscilador armónico simple tiene solo estados de energía positivos, posiblemente incluyendo a cero, resulta evidente que debe de haber una cota mínima en la energía del oscilador armónico simple. Supóngase que E0 representa el estado más bajo de energía que puede tener el oscilador armónico simple, y que la función de onda correspondiente es ψ0. Entonces estas cantidades satisfacen la ecuación de eigenvalores:
No sabemos por el momento si esta función de onda es única; esto es, no se ha determinado aún si el nivel de energía de E0 es un nivel degenerado. Aplicando el operador R.- a la ecuación anterior nos produce lo siguiente (sin que ello implique pérdida de claridad, escribiremos de aquí en adelante a los operadores R+ y R.- en itálicas como R+ y R.- sobreentendiéndose el carácter operacional de ambos, aunque por disciplina seguiremos escribiendo al operador Hamiltoniano H en su forma no-itálica así como al operador del momentum Px):
Haciendo uso de la relación de conmutación obtenida previamente para R -, tenemos entonces:
que podemos continuar reagrupando como:
Esto está en la forma de la eigenecuación:
con un nuevo eigenvalor E0-ħω y para el cual la nueva eigenfunción es R.-ψ0. Por otro lado, la suposición de que E0 es el eigenvalor más bajo indica que esta solo puede ser una solución trivial a la ecuación de eigenvalores; esto es, que la función de onda se debe desvanecer incondicionalmente. Por lo tanto:
Si a esto le aplicamos el operador R+, obtenemos con la ayuda de las relaciones que tenemos arriba:
Esto último está en la forma de una ecuación de eigenvalores para la cual el eigenvalor más bajo de energía debe ser:
De modo similar, si en vez de haber utilizado el operador R.- hubiéramos utilizado el operador R+, junto con las relaciones de conmutación obtenidas arriba, tendríamos entonces lo siguiente:
Este procedimiento puede ser repetido una y otra vez en forma iterativa con R+, produciendo el siguiente resultado general:
Esta es una ecuación de eigenvalores, dando un conjunto de eigenvalores y eigenfunciones del operador H definido como:
en donde la constante de normalización cn es escogida de modo tal que la función ψn resulte normalizada. Como ya se dijo, los operadores R+ y R.- son operadores escalera sobre la base de que pueden convertir una eigenfunción del operador Hamiltoniano en otra eigenfunción que corresponda a eigenvalores mayores o menores. Si escribimos la ecuación:
en forma explícita, se obtiene la siguiente ecuación diferencial de primer orden:
Esta es una ecuación diferencial elemental, cuya solución es la siguiente:
El factor constante ha sido seleccionado de modo tal que la función de onda ψ0 quede normalizada. Consecuentemente, existe una eigenfunción única que corresponde al eigenvalor de la ecuación:
siendo este eigenvalor un eigenvalor no-degenerado. De modo semejante, todos los eigenvalores dados por:
también son no-degenerados, y las eigenfunciones correspondientes son generadas de manera unívoca por R+. Si esto no fuese así, uno podría, mediante aplicaciones sucesivas de R.-, generar una eigenfunción asociada con E0 que sería independiente de ψ0, lo cual contradeciría el resultado anterior de que ψ0 es única. Además, el conjunto de eigenvalores En dados por la relación de arriba constituye la totalidad de los eigenvalores, porque si hubiera algún otro eigenvalor que no fuese miembro de este conjunto, aplicaciones sucesivas del operador escalera R.- a la eigenfunción correspondiente nos llevarían a una cota inferior al conjunto de eigenvalores que sería diferente de la cota dada por E0.=.(1/2)ħω que se ha demostrado ya que es única.
Obsérvese que el operador R+ es un operador impar que cambia de signo tras la reflexión de la variable x en el origen al pasar la variable del lado positivo de las x al lado negativo de las x, y dado que la función ψ0 que se acaba de obtener arriba como solución a la ecuación diferencial elemental es una función par (no dá cambio de signo), las eigenfunciones son todas pares o impares dependiendo de que n sea par o impar.
De este modo, para obtener las funciones de onda de los estados excitados podemos aplicar el operador escalera de subida al estado fundamental. Esto es reminiscente de la técnica de inducción matemática utilizada para la demostración de teoremas, en la cual después de demostrar que cierta proposición matemática es válida para cierto valor k si podemos demostrar que al ser válida para tal valor k es válida también para el valor k+1 que le sigue entonces será válida para todos los valores posibles de k, excepto que en nuestro caso usamos el operador de subida para ir obteniendo dichos valores de uno en uno. La siguiente figura puede clarificar la acción de los operadores escalera de subida R+ tanto en el aumento de los eigenvalores de energía a partir de cierto valor de energía E (la cual puede ser el nivel de energía fundamental E0) como en las funciones de onda que se van generando y que corresponden a los eigenvalores de energía del peldaño asociado (para mayor claridad, en la figura prescindiremos de las constantes de normalización cn que van normalizando cada función de onda):
Del mismo modo, para ir descendiendo de cualquier peldaño de la escalera pudiendo llegar incluso hasta el estado fundamental debajo del cual ya no es posible descender aún más, podemos aplicar el operador escalera de bajada. La siguiente figura puede clarificar la acción de los operadores escalera de bajada R- tanto en la disminución de los eigenvalores de energía a partir de cierto valor de energía E como en las funciones de onda que se van generando y que corresponden a los eigenvalores de energía del peldaño asociado (nuevamente, para mayor claridad, en la figura prescindiremos de las constantes de normalización cn que van normalizando cada función de onda):
Puesto que la constante cn debe ser seleccionada de modo tal que las funciones de onda queden normalizadas a la unidad:
entonces tomando en cuenta la propiedad de que los operadores escalera R+ y R.- son la adjunta Hermitiana el uno del otro:
y usando también los resultados intermedios de arriba:
podemos recurrir a técnicas puramente algebraicas para el cálculo de las constantes de normalización sin necesidad de tener que recurrir a procedimientos de integración. Empezaremos con la misma definición de normalidad para cada uno de los estados estacionarios n del oscilador armónico simple:
Puesto que:
de lo cual, despejando para ψn y aplicando el operador escalera R+ inverso (obsérvese cómo se obtiene un operador identidad con este proceso):
se puede escribir entonces lo que se muestra a continuación en la relación definitoria de normalidad:
lo cual se simplifica del modo siguiente:
Por otro lado:
Por lo tanto:
De este modo, se tiene:
Despejando:
A continuación, vamos a determinar algunos cuantos de estos coeficientes de normalización partiendo de la cota mínima que es c0.=.1, empezando con c1:
Ahora evaluaremos c2:
Procediendo de la misma manera, tenemos además los siguientes coeficientes de normalización:
Por simple inspección de lo que tenemos evaluado, podemos deducir la siguiente prescripción iterativa para generar todos los coeficientes de normalización que queramos generar:
Podemos hacer uso también de las técnicas del álgebra de operadores para evaluar algunas esperanzas matemáticas de valores relacionados con el oscilador armónico simple. Para calcular, por ejemplo, la esperanza de la energía cinética del oscilador, hacemos uso del operador:
Cuando la función de onda es ψn correspondiendo a un estado estacionario n del oscilador armónico simple, la esperanza matemática de este operador se puede escribir del modo siguiente:
El primer término puede ser evaluado en la forma en que se muestra a continuación escribiéndolo como un producto interno (par) bra-ket:
La expresión resultó ser igual a cero debido a la ortogonalidad de las funciones de onda ψn y ψn+2. Para llegar a este resultado, se hacen las siguientes operaciones:
tras lo cual se hace el despeje:
Procediendo de modo semejante con el segundo término, se puede demostrar que también es igual a cero. En consecuencia, la ecuación con la que habíamos comenzado se reduce a:
De este modo, el valor promedio de la energía cinética del oscilador armónico simple lineal es igual a la mitad de la energía total del oscilador cuando éste está en un estado bien definido de energía. Esto se corresponde con el resultado que se obtiene en la mecánica clásica de que la energía cinética promedio del oscilador armónico simple lineal (en el caso clásico, estamos hablando de un promedio tomado sobre la variable del tiempo) es igual a la mitad de la energía total.
Puede ser deseable calcular el valor esperado de la energía cinética cuando el oscilador está en un estado que no es un estado de energía bien definida, esto es, cuando está en un estado de superposición de energías. En este caso, la esperanza matemática se puede escribir del modo siguiente:
en donde:
Por cálculo directo, de estas ecuaciones se obtiene lo siguiente:
Si se toma el promedio sobre la variable del tiempo, las funciones oscilatorias se desvanecerán todas para n.≠.n’, dando para el promedio temporal de la esperanza matemática del operador de la energía cinética (se ha puesto encima una barra horizontal azul que denota promediación con respecto al tiempo, lo cual nos dá una instancia curiosa de una promediación temporal llevada a cabo sobre una promediación cuántica, una doble promediación pero bajo conceptos diferentes):
Haciendo uso del resultado previo:
podemos escribir entonces lo siguiente:
Nuevamente, este resultado es idéntico al resultado clásico de que el promedio temporal de la energía cinética es igual a la mitad de la energía total del oscilador.
De modo semejante, el valor esperado del momentum de un oscilador armónico simple lineal para un estado de energía definida puede ser evaluado si para ello recurriemos a la siguiente relación:
Esto nos conduce al siguiente resultado para la esperanza matemática del momentum del oscilador armónico simple:
Se debe enfatizar el hecho de que las técnicas involucradas en esta entrada para los cálculos de las funciones de onda y de los valores esperados del oscilador armónico simple han sido esencialmente de carácter algebraico, involucrando el álgebra de operadores. La única ecuación diferencial que tuvo que ser resuelta es la ecuación diferencial indicada arriba, la cual resultó ser relativamente elemental. Todas las demás soluciones fueron derivadas de la solución de esta ecuación usándose para ello técnicas de operadores de escalera, y la evaluación de los valores esperados también se llevó a cabo algebraicamente, lo cual nos muestra la importancia de las técnicas algebraicas en la Mecánica Cuántica. Desafortunadamente, no son muchos los problemas que pueden ser resueltos de una manera tan elegante, plenamente algebraica.
PROBLEMA: Demuéstrese que el operador escalera como se ha definido arriba se puede escribir de la siguiente manera:
siendo ψ0 (la función de onda que corresponde al estado de energía más bajo, el estado basal) del oscilador armónico simple.
Para el oscilador armónico simple, la función de onda que corresponde al estado basal se puede escribir de la siguiente manera:
Entonces, después de un poco de álgebra:
y usando ω = √k/m:
Entonces:
Finalmente, suponiendo que la acción del operador escalera cumple con la propiedad asociativa
PROBLEMA: Demuéstrese que la siguiente relación:
es una relación válida para el estado fundamental del oscilador armónico simple.
Procederemos en una forma parecida a como lo hicimos en el problema anterior. En este caso, se tiene:
Aplicando el operador diferencial del momentum:
Por otro lado:
Con esto y lo obtenido previamente llegamos a la relación pedida en el encabezado del problema.