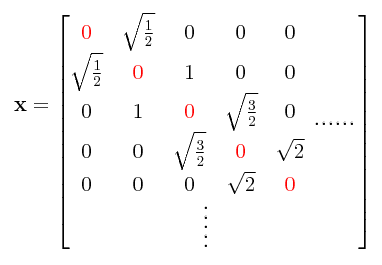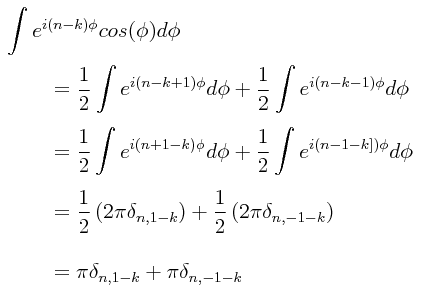En lo que veremos a continuación, partiremos del supuesto de que para la ecuación diferencial que queremos resolver ya se tiene desarrollada la solución para otra ecuación diferencial semejante pero más sencilla (esto es, con menos términos), de modo tal que se supone que contamos ya con un punto de partida sólido.
Considérese la siguiente ecuación diferencial de segundo orden, la cual obviamente es una ecuación no-linear cuya solución casi nunca se estudia en los cursos ordinarios de ecuaciones diferenciales:
en donde K es una constante numérica, y u(x) es una función sobre la variable independiente x.
Frecuentemente, en la resolución de ecuaciones diferenciales, resulta útil darle preferencia a la búsqueda de soluciones que tengan sentido desde considerandos propios de la física en lo que tiene que ver con que cualquier solución que pueda haber deberá ser una solución que no se dispare hacia el infinito al darle todos los valores posibles a la variable independiente. En la solución de una ecuación diferencial como la que se ha dado arriba, solución obtenida ya sea analíticamente o por métodos numéricos o mediante consideraciones intuitivas, suele suceder que para encontrar una solución que tenga sentido desde el punto de vista físico algo como la constante numérica K no puede tomar cualquier valor numérico arbitrario. Específicamente, no vamos a considerar como una solución aceptable una función u(x) que para grandes valores de la variable independiente x entonces también u(x) vaya creciendo disparándose eventualmente hasta el infinito. Con esta imposición, dictada por consideraciones físicas pero que también tiene sentido desde el punto de vista puramente matemático, para la ecuación diferencial que estamos considerando, K está limitada a tomar valores enteros de acuerdo a la siguiente relación:
K = 2n + 1
que podemos escribir, más apropiadamente, como:
Kn = 2n+1
De este modo, la ecuación diferencial bajo estudio se puede escribir del siguiente modo:
Pero se encuentra también que no solo K está restringida a tomar valores enteros. Resulta que la función u(x) tampoco puede ser una solución general para cualquier valor de n. Para cada valor de K habrá una función diferente u(x) diferente de todas las demás, de modo tal que nos vemos obligados a expresar de una manera un poco más apropiada la ecuación aparejando cada valor de Kn con cada función un(x) que le corresponda:
De este modo, de la ecuación diferencial original saldrá una cantidad infinita de ecuaciones diferenciales, cada una de ellas válida para cada valor de n:
De que cada una de las funciones un(x) es diferente no nos debe caber la menor duda. como lo muestran las primeras soluciones a cada una de las ecuaciones diferenciales dadas arriba (cada una de las funciones Hn(x) es una función diferente de las demás, del tipo conocido como polinomios de Hermite):
Podemos volver a expresar la ecuación diferencial original simplificando nuevamente la notación hacia Kn teniendo de este modo:
Así pues, como punto de partida suponemos que se tiene una ecuación diferencial de segundo orden como la anterior completamente resuelta, cuyas funciones un(x) ya han sido obtenidas para cada valor de Kn.
Es común ver que muchos estudiantes en su Licenciatura de Matemáticas con unos cuantos cursos introductorios de Ecuaciones Diferenciales se queden perplejos al enterarse de que dada una ecuación diferencial como la que tenemos arriba, la variable independiente x que es una variable continua pueda ser reformulada como una matriz con elementos discretos xmn. Aquí es cuando un físico puede iluminarlos haciéndoles ver que, si se tiene ya resuelta la ecuación diferencial, lo cual implica que se tienen ya definidas las funciones un(x) para varios valores de n, entonces se pueden obtener los elementos matriciales xmn de la siguiente manera:
aclarándole al matemático que lo que está puesto en color rojo es el conjugado complejo de la función que está representada en color azul, por si acaso hay números imaginarios o complejos en las funciones solución. Resulta obvio, como consecuencia de la integración que es llevada a cabo, que todos los elementos matriciales xmn que van acomodados dentro de una matriz x son números reales. Y así como podemos construír una matriz x, podemos extraer de dicha matriz cada uno de sus elementos xmn empleando los números enteros m y n para entresacar simbólicamente el elemento matricial que va puesto dentro de la matriz x en el renglón m y la columna n, esto es:
En la notación bra-ket de Dirac, esto se puede llevar a cabo formalmente especificando el bra que corresponde a m como un vector renglón que contiene ceros en todas sus entradas excepto el 1 que tiene en su posición m, y especificando al ket que contiene a n como un vector columna que contiene ceros en todas sus entradas excepto el 1 que tiene en su posición n, lo cual permite llevar a cabo las operaciones de multiplicación matricial directamente para cálculos evaluatorios, como en los siguientes ejemplos:
Para la ecuación diferencial que hemos estudiado hasta este punto, si llevamos a cabo la evaluación de cada elemento matricial xmn usando la definición dada arriba encontramos que se tiene una matriz x de dimensiones infinitas en la cual la diagonal principal que va desde la esquina superior izquierda hasta la esquina inferior derecha consta únicamente de ceros, mientras que las diagonales que van arriba y abajo de la diagonal principal son las que constan de elementos diferentes de ceros.
Aquellos estudiantes de matemáticas que tengan nociones elementales de vectores y matrices a partir del álgebra linear podrán comprobar por sí mismos que esta matriz x es una matriz que no puede ser diagonalizada, esto es, convertida a una matriz equivalente (con los mismos eigenvalores) en la cual los elementos que van puestos a lo largo de la diagonal principal sean elementos diferentes de cero.
En la especificación matricial de la ecuación diferencial cuya solución se conoce, se encuentra que la variable continua x que se convierte en una matriz x sus elementos xmn están dados por cualquiera de las siguientes tres fórmulas:
siendo δ es el delta de Kronecker.
PROBLEMA: Demostrar que las tres fórmulas que se acaban de dar para obtener los valores de los elementos matriciales de la ecuación diferencial bajo consideración son iguales.
La demostración se puede llevar a cabo en forma constructiva para varios valores de m y n generalizando los resultados mediante una matriz infinita cuya diagonal principal consta de ceros y que resulta ser la misma que la que se obtiene con cualquiera de las tres relaciones:
Obsérvese que las tres fórmulas usadas para obtener los valores de los elementos matriciales xmn generan exactamente la misma matriz aunque parezcan ser matemáticamente diferentes. Se hace aquí la advertencia de que en la literatura técnica se pueden encontrar estas tres variedades de fórmulas e inclusive otras, aunque hay que tener presente que todas generan los mismos valores para cada m y cada n, una matriz simétrica con ceros en su diagonal principal, con elementos diferentes de cero tanto en la subdiagonal superior como en la subdiagonal inferior a la diagonal principal, y ceros en todas las demás posiciones.
Con las soluciones un(x) de la ecuación diferencial podemos formar un vector columna u del siguiente modo:
Si se tiene una matriz x como la que vemos arriba, y se aplica dicha matriz sobre el vector columna u, entonces por multiplicación matricial directa con el operador matricial x actuando sobre el operando u obtenemos entonces el siguiente vector columna x·u:
Operacionalmente hablando, ésto tiene un símil en la ecuación diferencial. Resulta obvio inspeccionando los elementos del producto matricial x·u y llevando a cabo la generalización correspondiente que el n-avo elemento del vector columna tiene su símil en la siguiente relación general que corresponde al término xun(x):
A esto lo llamaremos nuestra “primera relación de recursión”. Del mismo modo, repitiendo la aplicación del operador matricial x al vector columna u se nos producirá el equivalente de x2·u produciéndonos el siguiente vector columna:
Operacionalmente hablando, ésto también tiene su símil en la ecuación diferencial. Resulta obvio inspeccionando los elementos del producto matricial x2·u y llevando a cabo la generalización correspondiente, que el n-avo elemento del vector columna obtenido tiene su símil en la siguiente relación general que corresponde al término x2un(x):
A esto lo llamaremos nuestra “segunda relación de recursión”. Tanto la relación xun(x) como la relación x2un(x) se pueden utilizar para calcular los términos de corrección, definidos con mayor formalidad como términos de perturbación, de una nueva ecuación diferencial ampliada a partir de la ecuación diferencial original cuyas propiedades y soluciones hemos estado estudiando arriba.
Suponiendo que tenemos ya como punto de partida una ecuación diferencial como la anterior resuelta en detalle, con los valores de Kn determinados por la fórmula dada arriba (Kn.=.2n+1) y algunas de las funciones solución un(x) especificadas, a continuación queremos ir en pos de las solucies de otra ecuación diferencial v(x) un poco más elaborada, una ecuación diferencial como la siguiente (el término que se ha agregado se ha destacado con color azul):
siendo α una constante numérica que suponemos relativamente pequeña (esto es, no mayor de la unidad) a la cual le podemos dar inicialmente algún valor pequeño como 0.25 antes de aventurarnos a darle otro valor cualesquiera.
Resulta lógico anticipar que si la ecuación diferencial original estaba restringida a tomar únicamente ciertas soluciones cuantizadas o cuantificadas con un entero n, entonces la nueva ecuación diferencial también estará restringida, hecho resaltado al escribirla de la siguiente manera:
Ahora viene la parte interesante. ¿Cómo podemos encontrar el símil, si es que existe, de ésta última ecuación diferencial, en su forma matricial? El primer paso en nuestro análisis consiste en tratar de expresar la ecuación diferencial original (con la que empezamos al principio, cuyas soluciones nos son conocidas) en forma operacional del siguiente modo:
siendo el operador diferencial O:
Esto lo podemos reconocer como una eigenecuación como las que ya hemos estado estudiando, en donde un operador diferencial aplicado sobre cierta función nos produce la misma función multiplicada por un eigenvalor o valor propio.
El operador diferencial O que se acaba de definir podemos de hecho considerarlo como formado por dos sub-operadores, el primero correspondiente a la derivada de segundo orden d2/dx2 y el segundo correspondiente al término x2. Esto se volverá importante al llevar a cabo la transfiguración de la ecuación diferencial a su símil matricial.
Muchas veces es posible (no siempre), dada alguna ecuación diferencial, encontrar un símil de dicha ecuación en su formulación matricial correspondiente. Esta es precisamente la razón del por qué la Mecánica Ondulatoria, basada en la ecuación diferencial de Schrödinger, es completamente equivalente a la Mecánica Matricial de Heisenberg basada en la “extraña” ecuación matricial de Max Born, y fue precisamente Erwin Schrödinger el que demostró dicha equivalencia entre ambos modos de desarrollar la Mecánica Cuántica. El hecho de que una amplia variedad de ecuaciones diferenciales podían ser reformuladas empleando matrices era un hecho ya conocido incluso desde antes del advenimiento de la Mecánica Cuántica. Reformular una ecuación diferencial en su símil matricial no significa necesariamente que será más fácil resolver la ecuación diferencial original tras ser reformulada en su ropaje de matrices, y de hecho el problema original puede complicarse enormemente. Hay ocasiones en las cuales resulta mucho más fácil buscar la ecuación diferencial que corresponde a cierto sistema matricial y resolverla de éste modo, y hay otras ocasiones en las cuales resulta conveniente expresar una ecuación diferencial en su ropaje matricial.
Habiendo llegado a este punto, el símil matricial de la ecuación diferencial cuyas soluciones nos son conocidas casi nos salta a la vista:
en donde M es la matriz que actúa como un operador sobre el vector función u, siendo el vector función el mismo que ya se dió arriba:
Regresando a la ecuación diferencial ampliada cuyas soluciones buscamos:
podemos repetir el mismo procedimiento de recurrir a notación operacional:
y si definimos dos operadores O0 y O1 de modo tal que:
entonces operacionalmente tenemos una eigenecuación diferencial con un operador O que por ser igual a la suma de dos operadores O0 y O1 nos conduce a lo siguiente:
El símil matricial de lo anterior debe ser obviamente:
en donde M0 y M1 son respectivamente los símiles matriciales de los operadores diferenciales O0 y O1.
Una expresión un poco más general de lo anterior es la siguiente en donde multiplicamos a la matriz M1 por un factor numérico α teniendo entonces:
M0v + αM1v = K'v
En la ecuación diferencial, esto equivale a factorizar fuera de M1 el factor α que es a fin de cuentas una constante. Para α→0, la anterior ecuación matricial se reduce a:
M0v = K'v
Pero ya sabemos cuál es la solución de ésta eigenecuación matricial, usando para ello el vector de funciones u, con lo cual necesariamente K'→K:
M0u = Ku
En otras palabras, para α→0 entonces v→u, en cuyo caso K' se convierte en el vector K que corresponde a la ecuación diferencial original.
No podemos suponer a priori que en el símil matricial de la ecuación diferencial aumentada su vector K' sea el mismo K que el que corresponde a la ecuación diferencial original, se debe suponer que ambos son diferentes, esto es, K'.≠.K. Esto nos permite afirmar de modo más general en la ecuación matricial que:
M0v + αM1v = K v + K'v
Ha llegado el momento de intentar resolver la ecuación diferencial ampliada mediante la Teoría de las Perturbaciones, tratando de mantener el enfoque puramente matemático sin hacer referencia alguna a cuestiones propias de la física.
Un matemático que no esté familiarizado con cuestiones físicas puede desarrollar por cuenta propia sus propios métodos de aproximación para resolver una ecuación diferencial cuando tiene a la mano otra ecuación diferencial más sencilla (que se puede considerar como un caso especial de la ecuación diferencial ampliada) cuyas soluciones se conocen. Y llegará a los mismos resultados que los obtenidos por el físico. Específicamente, los valores propios o eigenvalores K'n que buscamos para la ecuación diferencial ampliada cuando se conocen los valores propios Kn de la ecuación diferencial más sencilla estarán dados por una serie como la siguiente:
siendo Kn(1) el término de corrección de primer orden, Kn(2) el término de corrección de segundo orden, y así sucesivamente. Para una mayor generalidad en la notación, en algunos textos suele hacerse:
sobreentendiéndose que este término no corresponde a algo a ser evaluado como una perturbación sino que se trata de algo que corresponde a aquello a lo cual se le irán agregando las perturbaciones sucesivas en orden creciente. De este modo:
En el desarrollo de la teoría de las perturbaciones, el matemático encontrará que la perturbación de primer orden para el estado n está dada por una relación como la siguiente:
aunque es posible que no usará notación bra-ket de Dirac como la que estamos utilizando aquí. Por otro lado, la perturbación se segundo orden para el estado n estará dada por una sumatoria:
llevada a cabo sobre el subíndice m, quedando fuera de evaluación el término que correspondería al caso m.=.n (en cuyo caso se tendría una división entre cero).
Las correciones de orden mayor son, como es de esperarse, evaluadas por expresiones aún más complejas. Así pues, evaluar la serie de pertubación en forma explícita requiere de lo siguiente:
Enfocándonos en la perturbación de primer orden, el hecho más relevante es que, si nos fijamos bien, no tardaremos en caer en la cuenta de que la perturbación de primer orden es de hecho la esperanza matemática o el promedio estadístico de la observable O1 no al igual que como se ve en esta obra en las entradas tituladas “Operadores y esperanzas matemáticas” en donde, para una variable continua Q que corresponde a cierto estado n se le define su esperanza matemática como:
Para un físico, esto implica la posibilidad de poder darle una interpretación física inmediata a lo que se obtenga en la evaluación de la corrección de primer orden.
En el caso de la corrección de segundo orden, para un cierto n (por ejemplo, n.=.3) la evaluación de la sumatoria involucra la evaluación de todos los términos de la sumatoria tanto para cuando n es mayor que m (en cuyo caso se genera una cantidad finita de términos) como para cuando m es mayor que n (en cuyo caso y hablando en términos generales se genera una cantidad infinita de términos).
Antes de continuar, introduciremos un requerimiento de carácter netamente físico en la evaluación de las integrales usadas para evaluar sobre todo los términos de perturbación de segundo orden en adelante. Desde el punto de vista estrictamente matemático, se requiere únicamente que las funciones un(x) de la ecuación diferencial original sean todas ortogonales, esto es, que se cumpla una relación como la siguiente:
en donde W es una constante numérica que en principio puede tener cualquier valor y en donde como siempre δ es el delta de Kronecker. Lo relevante es que cuando m.=.n, entonces la evaluación de la integral anterior puede producir en principio un número cualesquiera. Esto no es de importancia alguna para el matemático que considera su labor terminada en cuanto ha resuelto el problema desde una perspectiva matemática pura. Sin embargo, el físico requiere además, por consideraciones de carácter utilitario (específicamente, el cumplimiento del criterio de Born que asume que se les debe dar a las funciones un(x) una naturaleza tal que conduzca a probabilidades estadísticas de ocurrencia), que la constante W sea igual a la unidad. En pocas palabras, se requiere que las funciones no solo sean orgotonales, se requiere también que sean ortonormales por necesidades no de carácter matemático sino de carácter puramente físico para poder darle a los resultados una aplicación práctica. Esto implica que todas las funciones un(x) tienen que acarrear consigo una constante numérica (la constante de normalización) para poder darle a los resultados una interpretación física; se requiere que:
Supondremos por lo pronto que las funciones un(x) de la ecuación diferencial original cumplen con este criterio, aunque seguiremos suponiendo que todas las demás constantes físicas como la constante de Planck h y la velocidad angular ω tienen un valor igual a la unidad, lo cual hará feliz al matemático puro.
Usando los resultados que se obtienen mediante el desarrollo de las técnicas de perturbación, y recurriendo a la ayuda de la “primera relación de recursión” obtenida arriba, la corrección de primer orden o término de perturbación de primer orden cuando el operador O1 es αx se obtiene de la siguiente manera:
Puesto que la función un(x) es real (no contiene factores imaginarios o complejos), su conjugado complejo un*(x) también será real, y por lo tanto se le remueve aquí por superfluo el asterisco con el que se denota aquí el proceso de conjugación compleja, además de eliminar las tonalidades de color rojo así como la de color azul.
Para un físico (no así para el matemático) el resultado obtenido tiene una interpretación inmediata, siendo la interpretación de que la partícula, en promedio, se encuentra en el origen del sistema de coordenadas, con tantas excursiones en el sentido positivo como en el sentido negativo de su posición.
Proseguiremos con la evaluación de algunos términos que corresponden a la corrección de segundo orden. La evaluación de los términos de perturbación de segundo orden requiere la evaluación de todos los términos que se puedan obtener (en principio, una cantidad infinitamente grande de ellos), para la siguiente sumatoria:
Aunque esta sumatoria nos parezca algo intimidante, para el ejemplo que estamos considerando no lo es si usamos las propiedades de ortogonalidad y normalidad de las funciones de base En general, para obtener una corrección de segundo orden, la perturbación de segundo orden estará dada por una sumatoria que requiere la evaluación de los siguientes términos:
Se ha resaltado en la última línea el hecho de que la gran sumatoria consta de sumas de términos para dos situaciones ligeramente diferentes:
- Cuando m es menor que n
- Cuando m es mayor que n
PROBLEMA: Obtener para el ejemplo bajo estudio los siguientes términos:
Para el cálculo de estos dos términos requeridos en la evaluación de la perturbación de segundo orden según lo requiere la evaluación de la sumatoria indicada, usaremos primero lo siguiente:
Es satisfactorio confirmar el hecho de que no tendremos aquí en los denominadores una división entre cero. Obsérvese, por lo que tenemos en los denominadores, que el signo de todos los términos con valores m inferiores a n tendrán un signo matemático opuesto al signo de todos los términos con valores de m superiores a n.
Podemos ahorrarnos una cantidad considerable de trabajo posterior si nos damos cuenta de que el segundo de los dos términos a ser evaluados cuando el operador O1 es αx, lo cual requiere evaluar la combinación:
es apenas un caso especial que forma parte de muchas otras combinaciones posibles del mismo tipo, por ejemplo:
para las cuales la expresión general es:
o lo que es lo mismo (con la aclaración previa de que solo será válida para valores de n iguales o mayores que 1):
Podemos ahorrarnos una cantidad considerable de trabajo obteniendo primero esta expresión general en vez de hacerlo para solo unas cuantas de las posibles combinaciones particulares. Para el segundo término, recurrimos a la “primera relación de recursión” obtenida arriba:
de la cual obtenemos de inmediato:
Así pues, se tiene que:
Del mismo modo, recurriendo de nueva cuenta a la “primera relación de recursión”, se obtiene el otro término:
Con los resultados obtenidos, podemos afirmar para cualquier n que:
Usando estar fórmulas recién obtenidas, se logran de inmediato los siguientes dos resultados particulares:
Es importante darse cuenta de que los dos términos particulares:
no corresponden a la misma sumatoria de una serie de perturbación sino a dos series de perturbación diferentes, el primero es un término que forma parte de la serie de perturbación para n.=.1, mientras que el segundo término forma parte de la serie de perturbación para n.=.0.
No cuesta mucho trabajo verificar que, para un cierto n, términos generales como los siguientes:
se desvanecen. Por ejemplo, tomando la “primera relación de recursión” y modificándola ligeramente para escribir lo siguiente:
obtenemos de inmediato:
Entonces, juntándolo todo para un n fijo, podemos deducir que la corrección de segundo orden será:
Esta es tan solo la corrección de segundo orden. Nos faltaría agregar la corrección de tercer orden en la que anticipamos un factor de α3, la corrección de cuarto orden con un factor de α4, y así sucesivamente. Desafortunadamente, la evaluación de los términos de corrección de orden cuatro en adelante para una serie de perturbación se va complicando considerablemente. Sin embargo, si se requieren términos de correcciones de sexto orden o más porque la convergencia de la serie de perturbación es lenta, entonces la técnica de la serie de perturbaciones pierde su valor y es mejor recurrir a otro método de análisis, tal como una aproximación numérica con el auxilio de una computadora.
Los valores eigen K.'n para la ecuación diferencial:
en donde el operador O1 involucrado es αx serán por lo tanto (aproximadamente):
El primer ejemplo que acabamos de ver de hecho tiene una solución analítica exacta. Y de hecho, es en esencia el mismo problema del oscilador armónico simple cuántico que ya vimos en entrada previa, tal vez el lector ya se haya dado cuenta de ello.
Aclarado ya el hecho de que la ecuación diferencial que hemos estado resolviendo arriba con una perturbación añadida es la del oscilador armónico simple complicado un poco con la presencia de la perturbación que se le ha agregado, entonces habiendo visto una entrada previa que trata el tema de los “Operadores escalera II” (véase) se puede dar por hecho que usando operadores escalera se podrían haber obtenido las mismas dos “relaciones de recursión” a las que hemos llegado arriba pero de una manera más elegante y más directa, más formal por así decirlo, o sea de un modo axiomático y deductivo (yendo de lo general a lo particular) en vez de hacerlo como lo hemos hecho aquí siguiendo una metodología no deductiva sino inductiva yendo de lo particular hacia lo general. Sin embargo, esto pasa por alto el hecho de que antes de ir en pos de la solución de una ecuación diferencial la mayoría de los matemáticos no tendrán una pista sobre la existencia de operadores escalera que pueden ser usados como atajos en la obtención de soluciones, ese tipo de pista la tienen los físicos. La metodología que se ha usado aquí prescindiendo del uso de los operadores escalera es algo que usaría un matemático que está buscando soluciones a una ecuación diferencial.
Veremos a continuación un segundo ejemplo que también parte de la misma ecuación diferencial original que se ha estado considerando. Tomando como referencia nuvamente a dicha ecuación diferencial:
trabajaremos ahora sobre la siguiente ecuación diferencial ampliada:
en donde el término que le ha sido agregado a la ecuación diferencial original ha sido resaltado en color azul. En lugar de la constante numérica α usaremos la constante numérica λ sin ninguna otra razón para ello excepto resaltar el hecho de que se trata de otro problema ligeramente diferente.
Repitiendo los mismos pasos y razonamientos que los que se usaron para obtener la solución de la primera ecuación diferencial aumentada, para la nueva ecuación diferencial aumentada en donde el término de perturbación no es αx sino λx2, el término de corrección de primer orden será:
Esto lo podemos expresar de la siguiente manera:
Obsérvese en el último desarrollo que en la evaluación de las tres integrales tanto la primera integral como la tercera integral son iguales a cero al haberse aplicado el requerimiento (matemático) de ortogonalidad. Obsérvese también que la segunda integral es igual a la unidad al haberse aplicado el requerimiento (físico) de ortonormalidad.
De nueva cuenta, la evaluación de los términos de perturbación de segundo orden requiere la evaluación de todos los términos que se puedan obtener para la siguiente sumatoria:
En esta ocasión evaluaremos unos términos particulares para n y m fijos, recurriendo para la evaluación a las propiedades de ortogonalidad y normalidad de las funciones de base.
PROBLEMA: Obtener para el ejemplo bajo estudio los siguientes términos:
Para el cálculo de estos dos términos requeridos en la evaluación de la perturbación de segundo orden según lo requiere la evaluación de la sumatoria indicada, usaremos primero lo siguiente:
Es satisfactorio el hecho de que no tendremos aquí en los denominadores una división entre cero.
Usando la “segunda relación de recursión” obtenida arriba:
Del mismo modo, haciendo n.=.1 en la misma relación se tiene:
De este modo, para el primer caso se tiene:
a causa de la ortogonalidad entre las funciones u0 y u1 así como la ortogonalidad entre las funciones u0 y u3. Por lo tanto:
Procediendo de modo semejante para el segundo caso, vemos que:
con lo cual:
Así pues, estas dos contribuciones a la gran sumatoria se desvanecen al resultar los numeradores en ambos casos iguales a cero a causa de la condición de ortogonalidad. Sin embargo, no todos los términos en la gran sumatoria serán iguales a cero, como pronto lo habremos de comprobar.
Obsérvese algo importante. Los dos términos en el problema que se acaba de resolver pertenecen a dos series de perturbación diferentes, una para n.=.0 y la otra para n.=.1. Podemos dar mayor claridad a ésto inventando una matriz sin mayor propósito útil para la misma que el poder agrupar y visualizar dentro de ella todos los términos que corresponden a cada sumatoria usada en la evaluación de cada corrección de segundo orden. En cada renglón n de la matriz podemos escribir explícitamente cada uno de los términos de la sumatoria que corresponden a la evaluación de la corrección perturbativa de segundo orden para el susodicho n, un renglón diferente para cada número cuántico n diferente (se destacan los tres renglones que corresponden a la evaluación de la serie de perturbación respectiva para los casos n.=.3, n.=.6 y n.=.8). La siguiente ilustración aclarará mejor ésto (las líneas de color café resaltan la “distancia” creciente entre los dos niveles de energía que corresponden a la evaluación del denominador de cada término de una sumatoria):
En ésta matriz Mnk en donde n es el renglón y k la columna de la matriz en la que hemos tratado de representar algunos de los términos requeridos para evaluar las sumatorias de perturbación de segundo orden, se ha resaltado la serie de pertubación para n.=.3. La sumatoria requerida de términos para el cálculo de la serie de perturbación n corre de izquierda a derecha, habiendo solo dos términos a la izquierda de k.=.3 (representando los casos en los que k es menor que 3), y los primeros cinco términos (de lo que se supone que es una serie infinta de términos) puestos en orden creciente de k a la derecha de k.=.3 para el caso en el que k es mayor que 3. Los bloques en color negro no dan ninguna contribución a ninguna de las sumatorias de la corrección perturbativa de segundo orden para ningún n porque representan la situación en la cual n.=.k implicaría una división por cero en el cálculo de las sumatorias. Los dos bloquecitos horizontales en n.=.3 con coloración azul más intensa corresponden a los dos términos con k más cercanos a k.=.3 (que a su vez es de color negro y está excluído en el cálculo de la corrección de segundo orden para n.=.3). En los demás bloquecitos horizontales de n.=.3 la coloración azul va disminuyendo de tonalidad al aumentar la “distancia” hacia k.=.3 reflejando el hecho de que la contribución de tales términos a la serie de perturbación para dicho n también va disminuyendo como lo esperaríamos en una serie que sea convergente hacia un valor finito. La siguiente figura que extiende la anterior aclara un poco más la figura anterior sobre lo que se está tratando de representar en la matriz en forma de “distancias” de cada término de la sumatoria a k.=.3 para la evaluación del tercer término de la corrección de segundo orden para n.=.3:
El segundo de los dos términos de la gran sumatoria que fueron evaluados arriba en detalle para un operador O1 que es λx2, lo cual requirió evaluar la combinación:
es apenas un caso especial que forma parte de muchas otras combinaciones posibles del mismo tipo, por ejemplo:
para las cuales la expresión general es:
o lo que es lo mismo (con la aclaración previa de que solo será válida para valores de n iguales o mayores que 1):
Podemos ahorrarnos una cantidad considerable de trabajo recurriendo directamente a la obtención de la expresión general en vez de hacerlo para cada una de las combinaciones particulares. Para el segundo término, recurriendo a la “segunda relación de recursión” obtenida arriba, podemos llegar al siguiente resultado general:
Esto nos permite afirmar que para todas las combinaciones de este tipo las contribuciones de términos a la gran sumatoria serán iguales a cero. Procediendo igual que como acabamos de hacerlo, podemos llegar a la misma conclusión en relación a todas las combinaciones del tipo general:
o lo que es lo mismo:
Obsérvese que la segunda de estas dos últimas expresiones generales es la que mejor se presta de manera inmediata al uso de la “segunda relación de recursión”.
Vayamos ahora en pos de otras combinaciones que sabemos que pueden contribuír a la gran sumatoria con términos diferentes de cero.
Podemos evaluar otros dos términos de la gran sumatoria, empleando para ello combinaciones como las siguientes::
Sin embargo, en vez de estar evaluando individualmente combinaciones como las siguientes:
el sentido común nos dicta que resulta mucho más provechoso intentar una generalización llevando a cabo simplemente la evaluación de un término más general como el siguiente que incluye todos los casos especiales para valores de n menores que 2:
Del mismo modo, a ésta evaluación le corresponde la evaluación de otro término más general como el siguiente que incluye todos los casos especiales para valores de n mayores que 2:
que abarca combinaciones como las siguientes:
Así pues, en vez de estarle asignando valores específicos a n, nos referiremos en general a cualquier n, de modo tal que si usamos nuevamente la “segunda relación de recursión” para x2un así como la propiedad de ortogonalidad y ortonormalidad de las funciones, se tiene de un modo más general que:
Efectuando el mismo procedimiento, se puede demostrar también con relativa facilidad que:
No cuesta mucho trabajo verificar, teniendo las condiciones de ortogonalidad en mente, que todos los demás términos de la gran sumatoria como:
se desvanecerán al quedar iguales a cero en el cálculo de la perturbación de segundo orden.
De este modo, resumiendo todo lo anterior, y usando las siguientes generalizaciones:
se concluye que el término general de perturbación de segundo orden evaluado bajo la gran sumatoria será:
Así pues, la serie de perturbación para la ecuación diferencial aumentada será:
Podemos continuar evaluando más términos para la serie de perturbación, aunque cada contribución posterior será más y más pequeña hasta volverse insignificantes las contribuciones posteriores. Al llegar a este punto, el físico considera que tiene su problema esencialmente resuelto, puesto que el físico está interesado principalmente en obtener los eigenvalores que correspondan a observables que se puedan medir con algún instrumento en un laboratorio, no así el matemático que está interesado en obtener las funciones un(x) que resuelven la ecuación diferencial modificada que se ha estado considerando.
Como cualquier matemático proficiente nos diría, éste segundo ejemplo que acabamos de ver considerando a λx2 como una perturbación de hecho tiene solución analítica (expresable mediante una fórmula cerrada), la cual no es difícil de obtener efectuando un simple cambio de variables. La solución exacta, que en realidad no es tan exacta por tener que recurrir a una serie de aproximación que consta de la suma de una cantidad infinitamente grande de términos, utiliza la siguiente expansión en serie de Taylor:
De este modo, el matemático le proporcionaría al físico la siguiente solución analítica:
La interpretación física para la ecuación diferencial modificada es que todos los nuevos eigenvalores que pueden representar alguna observable como la energía son desplazados por igual en la misma magnitud determinada por el factor constante que incorpora la influencia del parámetro λ.
PROBLEMA: Usando los primeros cuatro términos de la serie de pertubación obtenida, evaluar los efectos de una pertubación en el ejemplo que se acaba de ver suponiendo que λ.=.3/4, estimando así mismo el error que se comete al usar los primeros cuatro términos de la serie de perturbación en lugar de la expresión analítica obtenida mediante una serie de Taylor.
Usando la expresión analítica obtenida mediante una serie de Taylor, para λ.=.3/4 la solución exacta de la ecuación diferencial ampliada indica que los nuevos valores tendrán que ser corregidos mediante el siguiente factor:
Sin embargo, si usamos para la misma evaluación los primeros cuatro términos obtenidos en la serie de perturbación, el resultado obtenido será:
De este modo, pese a usar únicamente los primeros cuatro términos de la serie de perturbación, el resultado numérico obtenido no difiere mucho del resultado que se obtiene usando la expresión analítica exacta.
PROBLEMA: Extendiendo lo anterior, y suponiendo que cada término obtenido para la serie de pertubación infinita sea lo mismo que lo que le corresponde al que se obtiene mediante la expansión en serie de Taylor, obténganse relaciones recursivas para poder obtener cualquier término de la serie de perturbación.
Tomando como base los primeros cuatro términos en la serie de Taylor mostrada arriba, las relaciones recursivas deseadas para poder llegar a cualquier término en la serie de perturbación infinita serán:
Estas relaciones recursivas se pueden verificar fácilmente en los primeros términos:
Para la ecuación diferencial que usamos como punto de partida:
en donde K es una constante numérica, y u(x) es una función sobre la variable independiente x, el matemático ya sabe de antemano que las soluciones un(x) que se dieron arriba al principio seguirán siendo soluciones válidas si son multiplicadas por una constante numérica cualesquiera. Aunque en los desarrollos efectuados arriba hemos hecho una apelación a la condición de normalización, el lector observador habrá notado que las funciones un(x) que hemos estado manejando de hecho no están normalizadas, esto es, no cumplen con el criterio puramente físico:
Pero de cualquier modo, se recuerda que éste es un requerimiento impuesto única y exclusivamente por consideraciones de la física. Desde el punto de vista del matemático, la ecuación diferencial se encuentra en cierta forma resuelta. Si queremos que además se cumpla el criterio físico, las funciones de la ecuación original tienen que ser especificadas ya normalizadas de la siguiente manera:
No hemos tomado en cuenta todavía que, además de estas cuestiones relacionadas con asuntos de normalización que nos llevan a meter en la ecuación diferencial constantes de normalización, se le tienen que meter adicionalmente otras constantes relacionadas con las mediciones que se lleven a cabo bajo algún sistema de unidades, como la constante de Planck ħ así como otras constantes. En los cálculos mostrados arriba no se ha metido ninguna unidad de mensuración física y las constantes físicas han estado ausentes, casi todo ha tenido un enfoque estrictamente matemático.
En la teoría de las perturbaciones, para obtener la solución de una ecuación diferencial que es una modificación de una ecuación diferencial más sencilla cuyas soluciones un(x) se conocen, el matemático no se dará por satisfecho hasta en tanto no haya llegado a las funciones vn(x) que son las funciones solución para la ecuación diferencial modificada. Al físico experimentalista también le interesan estas funciones porque además de los eigenvalores que representan las cosas que se pueden medir en el laboratorio, cosas a las cuales se les pueden dar valores numéricos, se requieren dichas funciones para poder calcular las probabilidades de transición de un cierto estado de energía a otro estado de energía, lo cual requiere evaluar el “traslape” de dos funciones de onda distintas pero provenientes de la misma ecuación diferencial, en el entendido de que cuando no hay traslape alguno las probabilidades de pasar de un estado a otro son nulas al no existir un terreno común entre ambas funciones de onda en donde la partícula pueda cohabitar y pueda moverse de un lado a otro.
Es posible, desde luego, obtener las funciones solución vn(x) que son lo que realmente busca desde un principio el matemático puro y que a la postre también necesita el físico experimentalista. La misma teoría de las perturbaciones nos proporciona la receta para poder obtener tales funciones partiendo de las funciones es un(x) que nos son conocidas. Haciendo a un lado cuestiones tales como la normalización de las funciones vn(x), ya se ha visto previamente en otras entradas que la teoría de las perturbaciones proporciona el siguiente resultado a un primer orden para obtener la nueva función v en presencia de una perturbación:
La nueva función de onda del sistema perturbado evaluada de acuerdo a la relación anterior tiene su propio número cuántico que llamaremos m para evitar confusiones, y suponemos que el sistema perturbado seguirá siendo un sistema cuantizado y que a cada número cuántico n del sistema no-perturbado le corresponde un estado cuántico en el sistema perturbado con su propio número cuántico m, aunque aquí no se le ha puesto m como subíndice a la función de onda del sistema perturbado precisamente porque se trata de números cuánticos que reflejan situaciones diferentes (por ejemplo, al número cuántico n.=.2 del sistema no-perturbado que vendría siendo el primer estado excitado le correspondería el número cuántico m.=.2 que vendría siendo también el primer estado excitado del sistema ya perturbado, aunque se espera que los valores de las eigenenergías de ambos sistemas para un mismo m y n sean diferentes). La situación se complica cuando intentamos meter el efecto de una corrección de segundo orden, en cuyo caso la nueva función de onda será:
Como puede verse, el efecto de la perturbación es “mezclar” todas las eigenfunciones de onda originales. A estas alturas debe resultar obvio que las series de perturbaciones se complican sobremanera cuando tratamos de obtener los términos de corrección de tercer grado en adelante para el cálculo de las eigenfunciones de un sistema perturbado.
En casi todo el tratamiento que se ha considerado arriba, se ha intentado desligar la cuestión física de la cuestión matemática, enfocándolo todo a una manera distinta de resolver ecuaciones diferenciales cuya solución por métodos analíticos posiblemente no sea fácil e inclusive tal vez no exista. Y lo más importante es el hecho de tomar consciencia de que hay una equivalencia que nos permite reformular un problema de ecuaciones diferenciales resolviéndolo mediante la ayuda de su equivalente matricial. Arriba la equivalencia nos sirvió para obtener una “primera relación de recursión” y una a “segunda relación de recursión” que nos permitieron seguir adelante. Es posible, desde luego, resolver un problema de física cuántica en la Mecánica Matricial recurriendo desde el principio hasta el final únicamente al empleo de matrices, aunque no hay que perder de vista que tales matrices no salen de la nada, al final de cuentas hay que construírlas a partir de consideraciones de carácter cuántico que se deducen de ecuaciones diferenciales previas. Lo importante en todo caso es la plena equivalencia entre la Mecánica Ondulatoria y la Mecánica Matricial. Entender ésto nos permite el acceso a nuevas ideas que iluminan el camino hacia la solución de ciertos problemas que de otro modo parecerían imposibles de resolver.
Veremos a continuación otro problema en el que se aplica la teoría de las perturbaciones sin hacer mención a matriz alguna, y en esta ocasión lo veremos desde el punto de vista del físico, incluyendo unidades físicas de medición.
Manteniéndonos dentro del tema de la aplicación de las series de perturbación a la solución de ecuaciones diferenciales, lo veremos no bajo la perpectiva del matemático sino desde la perspectiva del físico, para lo cual tenemos que modificar la notación empleada arriba de una manera que nos sea más familiar aunque en esencia solo se trata de un cambio de notación que deja intacto lo verdaderamente básico. La ecuación diferencial con la que empezamos arriba como nuestro punto de partida:
es de hecho la del oscilador armónico simple. Ello nos permite reconocer a la constante K como lo que nos proporciona cada eigenvalor de la energía E del oscilador para cada número cuántico n, Con ello en mente, reescribimos la serie de perturbación y los términos que denotan la corrección de primer orden y la corrección de segundo orden de la siguiente manera:
Obsérvese que en vez de usar al operador O1 empleamos al operador Hamiltoniano de perturbación H1 que denota aquello que agregamos como perturbación a una ecuación más sencilla cuyas soluciones se conocen.
Un problema de interés teórico que demuestra la prevalencia de todo tipo de ecuaciones diferenciales cuya resolución puede aclarar muchas dudas en la Mecánica Cuántica cuando se recurre a la teoría de las perturbaciones en la estimación de las contribuciones de otros efectos físicos que tomamos como perturbaciones es el del péndulo cuántico. Podemos encontrar referencias de este problema yendo tan atrás como 1928 en el trabajo The Physical Pendulum in Quantum Mechanics de Edward Condon cuando la Mecánica Cuántica aún estaba en su infancia, esos eran los tiempos en los cuales los matemáticos ya habían desarrollado muchos conocimientos sobre las funciones de Mathieu descubriéndose el hecho de que fueron las funciones de Mathieu las que resultaron ser las funciones características que corresponden a la solución analítica del péndulo cuántico. (Las funciones de Mathieu son un caso especial de las funciones de Lamé; las soluciones admisibles a la ecuación de Schrödinger para el péndulo cuántico son la cosenoidal elíptica de Mathieu, y la senoidal elíptica, de orden impar.) El problema del péndulo cuántico es interesante porque une dos límites distintos: para oscilaciones de amplitud pequeña (ángulos pequeños φ de oscilación) se reduce al problema del oscilador armónico simple (cuántico), mientras que para energías grandes los estados del oscilador se acercan a los del rotor cuántico. Debe destacarse el hecho de que una partícula cargada en presencia de un campo eléctrico uniforme y constante ℇ constreñida a moverse sin fricción sobre una circunferencia en el plano del campo eléctrico es, a causa de la ecuación diferencial que describe su movimiento, un péndulo cuántico.
Clásicamente, un péndulo actuando bajo la acción de la gravedad puede ser ilustrado de la siguiente manera:
en donde la energía potencial U por convención se toma como más positiva al ir “de abajo hacia arriba”.
El Hamiltoniano H del péndulo clásico de longitud l es, para un sistema conservativo en el que no hay disipación de energía, igual a la suma directa de la energía cinética T y la energía potencial U del péndulo clásico, lo cual nos permite obtener para el péndulo cuántico la ecuación diferencial a resolver de la siguiente manera considerando a la coordinada generalizada q (en este caso, un arco de círculo) como aquella en la cual se hace el recorrido:
siendo la energía potencial U, en concordancia con la figura mostrada arriba:
habiéndose recurrido al artificio matemático:
La variable q es el arco de círculo s, o sea la distancia recorrida por la partícula, y puesto que por definición el ángulo φ (medido en radianes) es igual al arco entre el radio que estamos simbolizando aquí como la longitud l, se tiene entonces que s.=.lφ como lo hemos usado arriba. Para el caso del campo eléctrico ℇ, se debe hacer el siguiente cambio de notación::
mg → - eℇ
Con el siguiente cambio de variable:
en donde se ha hecho:
Un matemático “puro” reconocerá la ecuación diferencial obtenida como la ecuación diferencial de Mathieu, en memoria del matemático francés Émile Léonard Mathieu quien fue el primero en obtener soluciones para éste tipo de ecuaciones diferenciales en sus investigaciones sobre la vibración de membranas elípticas.
La solución analítica de la ecuación de Mathieu general no es un asunto sencillo, de hecho la solución general resulta ser un asunto algo complicado, todo ocasionado por el hecho de que tenemos una ecuación diferencial en la que aparece un término cosenoidal, cos(2η). En la célebre referencia matemática Handbook of Mathematical Functions de Abramowitz y Stegun aparecen listadas varias funciones de Mathieu que dan soluciones a la ecuación diferencial de Mathieu.
Para la solución exacta, el caso Ω.=.0 que corresponde a g.=.0 existe solución inmediata en términos de las funciones sen(2η) y cos(2η) cuya necesaria invariancia frente al cambio angular (en π radianes) que representa una vuelta completa de círculo regresando al péndulo a su posición original:
η → η + π (que corresponde a φ → 2π)
requiere que se cumpla:
Λ = 4n2 (n = 0, 1, 2, ...)
y en este caso especial las funciones propias o eigenfunciones serán:
ψ = asen[(2n+2)η]
ψ = bcos(2nη)
Lo anterior fue para un caso especial. La situación Ω.≠.0 entendiblemente complica el problema, y se vuelve necesario recurrir a las funciones de Mathieu para una solución exacta:
se2n+2(Ω,η) y ce2n(Ω,η) (n = 0, 1, 2, ...)
las cuales tienen a sen(2n+2η) y cos(2nη) como límites cuando Ω.→.0 respectivamente. Al mismo tiempo, los correspondientes valores propios eigen se convierten en funciones de Ω. No existen funciones físicamente permitidas para E.<.0 ni para funciones de Mathieu de orden impar puesto que no satisfacen la condición de periodicidad en η.
De la ecuación de Mathieu:
se deduce que en el límite Ω.→.0 el sistema se comporta como un rotor plano, mientras que en el límite contrario Ω.→.∞ se comporta como un oscilador no-lineal en el que para amplitudes pequeñas de oscilación puede aproximarse como un oscilador lineal según lo que se obtiene mediante un desarrollo en potencias de φ de la función coseno.
Para la ecuación diferencial de Mathieu hay dos tipos de soluciones posibles: periódicas y aperiódicas. Por lo general, las funciones de Mathieu son aperiódicas. Las soluciones aperiódicas para el problema de péndulo cuántico que es esencialmente un fenómeno periódico carecen de utilidad, lo cual nos restringe a recurrir a las funciones periódicas que son (simbolizando a θ como el ángulo de recorrido del péndulo): las funciones senoidales de Mathieu sen(θ,q) identificadas también como MathieuS(b,q,z) y las funciones cosenoidales de Mathieu cen(θ,q) identificadas también como MathieuC(a,q,z).
La solución general para la ecuación diferencial de Mathieu para ciertos valores de a (ó b) y de q es un conjunto de senos y cosenos de Mathieu linealmente independientes que son soluciones pares e impares respectivamente de la ecuación diferencial de Mathieu. Aunque las funciones de Mathieu son generalmente aperiódicas, para ciertos valores característicos an(q) y bn(q) tanto el seno de Mathieu como el coseno de Mathieu se vuelven funciones periódicas con un período igual a 2π. Es importante agregar que las funciones de Mathieu no están normalizadas en el sentido en el que lo requiere el físico, tal reajuste dimensional se tiene que llevar a cabo para que el cuadrado de la función represente la densidad de probabilidad que estamos acostumbrados a manejar en la Mecánica Cuántica.
A continuación se muestran las gráficas de algunas de las primeras funciones periódicas cosenoidales de Mathieu para q.=.1:
Obsérvese que la gráfica en color verde se asemeja a la gráfica de una función cosenoidal, excepto que las crestas y los valles resultan estar algo aplanados.
De la referencia Handbook of Mathematical Functions arriba citada de Abramowitz y Stegun, se reproduce a continuación la gráfica de las seis primeras funciones periódicas pares (simétricas con respecto al eje vertical) de Mathieu para q.=.1:
De la misma referencia, se reproduce a continuación la gráfica de las seis primeras funciones periódicas impares (antisimétricas con respecto al eje vertical) de Mathieu, también para q.=.1:
Queda claro que las funciones cosenoidales y senoidales de Mathieu son simétricas y antisimétricas, respectivamente. Podemos invocar el argumento físico de que enuncia que los eigenestados del problema tienen que ser simétricos o antisimétricos, en virtud de que el operador Hamiltoniano H tiene que ser simétrico. Las funciones de Mathieu nos indican que el estado basal del péndulo cuántico tiene que ser simétrico. A continuación se presenta una gráfica tanto de la solución simétrica como la solución antisimétrica para el estado fundamental o estado basal del péndulo cuántico:
Claramente, la solución antisimétrica a la ecuación de Mathieu no sería aceptable para el físico porque no es periódica. Esto hace que el estado basal sea único, producido por una función simétrica.
A continuación se presenta la gráfica de la densidad de probabilidad Ψ2(φ) para el estado basal (la curva de color verde) sobre la cual se ha superpuesto la gráfica (en color rojo) del potencial V(φ) del péndulo cuántico:
Ahora se presentarán las dos soluciones posibles que pueden corresponder a la función de onda del primer estado excitado del péndulo cuántico:
Obviamente, aquí la solución simétrica (la curva en color rojo) no es aceptable puesto que no es periódica. Solo hay un primer estado excitado, producido por una eigenfunción antisimétrica.
La siguiente gráfica nos muestra una superimposición tanto de la gráfica de la densidad de probabilidad Ψ2(φ) para el estado basal (la curva de color verde) como la de la densidad de probabilidad para el primer estado excitado (la curva de color magenta) sobre las cuales se ha superpuesto la gráfica (en color rojo) del potencial V(φ) del péndulo cuántico:
Obsérvese la similitud entre ésta gráfica con las gráficas de éste tipo usualmente presentadas en los libros de texto para las densidades de probabilidad del oscilador armónico simple tanto en su estado basal y en su primer estado excitado, lo cual nos confirma que para valores bajos de eigenenergía el comportamiento del péndulo cuántico es parecido al del oscilador armónico simple.
Resumiendo varios ejemplos, podemos graficar la densidad de probabilidad polar Ψ2(θ) para cada estado eigen del péndulo cuántico tomando como línea de base de referencia Ψ2(θ).=.0 la ruta alrededor de una circunferencia del círculo de radio l (la longitud l del péndulo) por donde la masa m hace su recorrido, siendo algunos resultados típicos arrojados por las funciones de Mathieu los siguientes:
En el primer caso ilustrado en la figura que aparece en la esquina superior izquierda, obsérvese que θ.=.0 es el lugar en donde hay mayores probabilidades de encontrar a la partícula sujeta al péndulo, mientras que en la segunda figura de izquierda a derecha dicha probabilidad decrece a la vez que aparecen a cada lado de la vertical dos lugares simétricos en donde hay mayores probabilidades de encontrar a la partícula, exhibiéndose un comportamiento parecido al que vemos en el oscilador armónico simple. Y en la tercera figura de izquierda a derecha hay mayores probabilidades de poder encontrar a la partícula por encima de la horizontal marcada por un ángulo θ.=.π a cada lado de la vertical. Observaciones parecidas se pueden hacer en las seis figuras restantes. Obsérvese tanto en ce8(θ,q) como en se8(θ,q) que la distribución de densidad de probabilidad se va aproximando a la de un rotor plano.
Habiendo visto la solución exacta del problema del péndulo cuántico recurriendo a las funciones de Mathieu, adoptaremos el punto de vista del físico práctico que prefiere buscar una aproximación poco penosa al problema en cuestión sin tener que gastar previamente para ello tiempo en la obtención de un Doctorado en Matemáticas, aceptando las aproximaciones que se pueden lograr con la ayuda de la teoría de las perturbaciones.
En lo que se discutió arriba, podríamos haber obtenido un atajo en el desarrollo del problema tan solo recordando que la energía potencial no es medida en términos absolutos sino relativos, y en el diagrama anterior podemos hacer un ligero cambio que representa la misma diferencia de energía potencial entre las alturas consideradas respetando la misma convención de que la altura potencial vaya aumentando en el sentido positivo con cualquier ascenso “hacia arriba”:
De este modo, el Hamiltoniano para el péndulo tomaría el siguiente aspecto:
lo cual ciertamente parece menos laborioso que lo que teníamos anteriormente, ya que con esto tenemos entonces simplemente:
en donde haciendo:
la ecuación diferencial se reduce a:
que de nueva cuenta es esencialmente la ecuación de Mathieu.
Tomando para fines de discusión en esto último un parámetro λ tan pequeño que para fines prácticos puede considerarse igual a cero, la ecuación diferencial se reduce a:
Esta ecuación diferencial tiene una solución analítica exacta. Se trata ni más ni menos que la ecuación del rotor plano (o rotor rígido) cuyas soluciones eigen de energía cuantizada son:
Las funciones de onda respectivas, ya normalizadas, son:
Esto sugiere que podemos utilizar el Hamiltoniano H del rotor plano como punto de partida para la aplicación de la teoría de las perturbaciones, considerado al Hamiltoniano perturbado como la suma del Hamiltoniano no perturbado H0 al cual se le ha agregado una perturbación H1:
H = H0 + H1
En el análisis anterior se hizo el cambio de variable φ.=.2η para estar en mayor concordancia con la notación convencional usada en la solución exacta de la función de Mathieu, y se usó la versión de la energía potencial definida en la primera figura. Como en la aproximación que se llevará a cabo aquí no se hará mención alguna a la ecuación de Mathieu, no se hará tal cambio notacional, y usaremos la definición de la energía potencial como se dá en la segunda figura en lugar de la definición que se dá en la primera figura. Puesto que podemos identificar a cos(φ) como la perturbación H1, esto nos permite escribir lo siguiente para obtener la corrección de primer orden:
habiéndose tomado φ1.=.φ2.=.φ. Podemos interpretar el resultado obtenido de la siguiente manera: Puesto que φ1.=.φ2.=.φ (a partir de la vertical, el péndulo se desplaza hacia la derecha hasta recorrer un ángulo φ1 que es igual en magnitud al ángulo φ2 que recorre cuando se desplaza en dirección contraria hacia la izquierda), el resultado final termina siendo igual a cero en virtud de que la corrección de primer orden es un simple promedio estadístico, el resultado obtenido de cero simplemente es consecuencia directa del hecho de que el péndulo pasa tanto tiempo moviéndose hacia la derecha (en sentido contrario a las manecillas de un reloj mecánico) como hacia la izquierda (en el sentido usual de las manecillas del reloj). No habiendo correcciones de primer orden, el siguiente paso consiste en obtener la corrección de segundo orden:
Para no confundir el subíndice m con el símbolo que representa a la masa m de la partícula, cambiaremos aquí el subíndice a k procediendo de inmediato a efectuar el cálculo:
Por lo que tenemos en el denominador, una confirmación importante es que el valor que puede tomar el entero k no puede ser igual al número cuántico n porque ello implicaría una división por cero :
k ≠ n
Haciendo momentáneamente:
p = n - k
tenemos entonces la siguiente integral a evaluar:
Para poder llevar a cabo la integración, recurriremos a la fórmula de Euler:
de la cual se obtiene:
De este modo, la integral se toma el siguiente aspecto:
Es bien sabido que la integral de algunas funciones exponenciales complejas puede generar tanto funciones delta de Dirac como funciones delta de Kronecker, un hecho que es ampliamente usado en el estudio de las transformadas de Fourier. Recordando que para el cálculo nos estamos basando en el rotor plano que tiene un período de recorrido T que va desde un ángulo de cero hasta 2π radianes tras lo cual el movimiento se repite periódicamente, sin mayores preámbulos, se presenta el siguiente resultado que se obtiene al llevar a cabo la integración sobre un período:
PROBLEMA: Demuéstrese la veracidad de la relación anterior.
Tomaremos como punto de partida una integral de contorno (cerrada) sobre una trayectoria que recorre un período completo de un ángulo que va desde θ.=.0 hasta θ.=.2π (un período circular completo) recurriendo de inmediato a la fórmula de Euler para simplificar la integral:
El resultado producido por las dos integrales dependerá del valor que tome k que supondremos un entero positivo. En el caso en el que k posea un valor diferente de cero, entonces ambos sinusoides darán un valor igual a cero al tomar los límites de la integración:
¿Pero qué es lo que ocurre cuando k toma un valor igual a cero? La integral senoidal se volverá desde luego cero inclusive antes de llevarse a cabo la integración, pero en virtud de que cos(0) es igual a 1 la integral cosenoidal no será igual a cero y de hecho al tomar los límites la evaluación terminará produciendo un valor exactamente igual a 2π:
La situación para ambos casos de k las podemos resumir mediante el uso de un delta de Kronecker:
Haciendo k.=.a-b obtenemos finalmente aquello que se deseaba demostrar:
Regresando al péndulo cuántico, puesto que se tiene que:
entonces, adaptando esta fórmula a las dos integrales del problema del péndulo cuántico poniendo especial atención en los signos, se obtiene:
Por lo tanto:
Obsérvese que sobreviven únicamente dos términos de la sumatoria a causa de los deltas de Kronecker que en este caso son mutuamente excluyentes, y los únicos términos de la sumatoria que no se desvanecen son aquellos para los cuales:
k = 1 - n
k = -1 - n
Juntándolo todo, tenemos nuestro resultado final mediante la siguiente serie de perturbación:
En los análisis que se han llevado a cabo aquí se ha enfocado el punto de vista matemático de la teoría de perturbaciones aplicada a la obtención de soluciones a ecuaciones diferenciales como suele suceder en la Mecánica Ondulatoria, y hemos visto las ventajas de pensar en la equivalencia que hay entre la Mecánica Ondulatoria y la Mecánica Matricial para poder obtener atajos que nos pueden ayudar a resolver problemas. Usamos esta equivalencia arriba para obtener tanto una “primera relación de recursión” como una “segunda relación de recursión”. Sin embargo, hay problemas en los cuales el objetivo no es resolver alguna ecuación diferencial sino trabajar única y exclusivamente dentro del ámbito de la Mecánica Matricial usando vectores y matrices. En tal caso, la notación empleada en las fórmulas de la teoría de perturbaciones tiene que ser modificada para que refleje el hecho de que estamos empleando operadores matriciales como H1 en donde H es una matriz en toda la extensión de la palabra en vez de ser un operador no-matricial como O1 en el caso del péndulo cuántico en donde el operador usado fue cos(φ). La modificación de la notación no presenta mayores problemas, pero hay que tener presente de que en vez de trabajar con eigenfunciones tales como ψn o como un(x) estaremos trabajando con vectores Ψ que pueden ser usados como vector renglón o vector columna al unísono con un operador matricial como H1. Pero en el fondo, aunque los desarrollos matemáticos parezcan ser diferentes, en realidad estamos hablando de dos caras diferentes de una misma moneda.