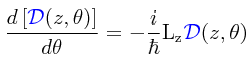Concebimos un operador de rotación como algo que al aplicársele a un eigenket definido por su posición angular nos regresará al eigenket girado de alguna manera (aquí estaremos usando como símbolo del operador de rotación a la letra Ð, tomada de la palabra en alemán Drehung que significa “rotación”).:
Naturalmente, no es necesario que un operador de rotación restringa su acción a un vector unitario n. En principio, el operador de rotación debe ser capaz de actuar sobre cualquier otro vector que no sea unitario, por ejemplo:
El operador de rotación, el cual para una mayor claridad representaremos de la siguiente manera simbolizando como θ al ángulo de giro en torno a cierto eje de simetría (por ejemplo, el eje-z o el eje-x):
debe ser tal que su aplicación operacionalmente multiplicativa sobre la parte angular de una función de onda Φ(φ) produzca una nueva función de onda Φ’(φ+θ):
Sin embargo, esta notación no es la ideal porque sugiere que los ángulos φ y θ siempre se estarán midiendo en la misma dirección (por ejemplo, un ángulo φ medido en 10° en un sentido de Norte a Sur, al cual se le añade un desplazamiento angular θ de 5° medido también en un sentido de Norte a Sur), cuando los sentidos de los desplazamientos angulares pueden ser, a fin de cuentas, diferentes (por ejemplo, un ángulo φ medido en 10° en un sentido de Norte a Sur, al cual se le añade un desplazamiento angular θ de 5° medido en un sentido de Este a Oeste). Y el sentido de los desplazamientos angulares es importante porque la posición final de la “punta de la flecha” de un vector que está siendo girado dependerá no solo de la magnitud sino también de la dirección de cada giro dado. Obviamente, se vuelve necesario ejercitar precaución, ya que no es posible extender a un operador de rotación las propiedades que vimos anteriormente para el operador de traslación.
¿Cuáles son las propiedades que exigimos que pueda cumplir el operador de rotación que estamos buscando?
Una propiedad esencial que debe cumplir el operador de rotación, la más esencial, la más básica, es que cuando el desplazamiento angular θ se aproxima a cero su efecto sobre la función de onda en la cual actúa debe ser tal que la función de onda venga quedando en la misma posición angular. En efecto, estamos requiriendo que para un desplazamiento angular igual a cero el operador de rotación se convierta en un operador identidad:
En este caso, al operador identidad lo podemos tomar simplemente como el número 1. Sin embargo, dejamos abierta la posibilidad de que el operador de rotación pueda ser un operador matricial, como de hecho lo es en muchos los casos de interés, en cuyo caso la condición anterior estipula que al reducirse θ a cero el operador de rotación se debe convertir en la matriz identidad:
Si llevamos a cabo operaciones de rotación en la misma dirección angular, debe ser posible aplicar dos o más operadores de rotación en sucesión (uno tras otro) sobre una función de onda, y el efecto resultante es semejante al que se obtiene con la aplicación sucesiva de dos operadores de traslación. En este caso y sólo en este caso las dos operaciones de rotación se pueden combinar en una sola operación de rotación:
¿Y qué del caso en el cual se lleven a cabo dos rotaciones en direcciones distintas? En una situación así, un giro en cierta dirección (por ejemplo, de 20° de Norte a Sur) seguido de un segundo giro en otra dirección diferente (por ejemplo, un 35° de Este a Oeste) es de tal Naturaleza que la suma numérica directa de los dos ángulos de giro (55°) carece por completo de significado. Sin embargo, sigue siendo cierto que una rotación combinada debe poder ser agrupada bajo un solo operador de rotación que una al punto inicial de partida con el punto final de recorrido. Si suponemos que dos operadores de rotación son matrices 3×3, por ejemplo, siempre es posible multiplicar las dos matrices para obtener una sola matriz que puede ser representada como un solo operador de rotacíon:
Obsérvese que el ángulo ω no es igual a la simple suma de los ángulos θ y φ, y de hecho, los tres operadores de rotación pueden ser diferentes. Como notación alterna, podemos simbolizar a un operador de rotación que resulta de la aplicación de dos giros distintos en direcciones angulares distintas como un par ordenado:
Esto mismo lo podemos extender a tres operaciones de rotación sucesivas, las cuales tras llevar a cabo el producto de las matrices que representan a cada operador nos resulta en una sola matriz definida como una función de los tres ángulos α, β y γ:
La notación que tenemos aquí es todavía insuficiente porque no hace resaltar la naturaleza diferente de tres operadores de rotación (los ángulos α, β y γ no revelan por sí solos si los giros se llevan a cabo en la misma dirección o en direcciones diferentes). Recurriendo a un sistema de coordenadas rectangulares Cartesianas, podemos ser un poco más explícitos agregando sub-índices para representar los ejes en torno a los cuales se lleva cada rotación de la manera siguiente:
Esto nos dice (leyendo la secuencia de las rotaciones de derecha a izquierda, por ser esta la manera en la que va actuando cada uno de los operadores de rotación sobre una función de onda situada a la derecha del grupo de operadores) que el operador combinado representa primero una operación de rotación de una magnitud angular γ en torno al eje-z, seguida de una segunda operación de rotación de una magnitud angular β en torno al eje-y, seguida de una tercera operación de rotación de una magnitud angular α en torno al eje-x. ¿Y por qué no especificar la tercera operación de rotación como una rotación en torno al eje-x? Porque a la hora de entrar en los detalles finos, se descubre que esto no es necesario, encontrándose que en realidad bastan las rotaciones en torno a dos ejes rectangulares Cartesianos para poder especificar una rotación que cubra todas las relocalizaciones angulares posibles en el espacio tridimensional. Y se descubre también que las rotaciones, especificadas en un orden así sobre dos ejes Cartesianos en lugar de tres, conducen a notaciones más sencillas en los resultados finales. Los ángulos usados en esta convención de rotaciones que se ha dado (la cual no es universal y puede variar de texto a texto) son mejor conocidos como los ángulos de Euler (en la siguiente figura, las rotaciones se llevan a cabo en el orden α, β y γ):
Al llevar a cabo rotaciones en el espacio tridimensional usando un marco rígido de coordenadas rectangulares Cartesianas, no cuesta mucho trabajo descubrir que una rotación en torno a uno de los ejes siempre cambia la posición de los otros dos ejes a la vez que deja inalterada la posición del eje de simetria. Por ejemplo, una primera rotación en torno al eje-z cambia las coordenadas de un punto (x,y,z) a las nuevas coordenadas (x’,y’,z). Si esta rotación es seguida de una segunda rotación en torno al eje-y’, las coordenadas del punto (x’,y’,z) cambian hacia una nueva posición (x’’,y’,z’). Y si tras esto aplicamos una tercera operación de rotación en torno al eje-x’’, las coordenadas del punto (x’’,y’,z’) cambian hacia una nueva posición (x’’,y’’,z’’):
La sucesión de rotaciones del “ladrillo” mostrado en la figura, el cual está anclado al sistema de coordenadas rectangulares Cartesianas que podemos imaginar que está pegado a su cuerpo, nos empieza a sugerir una diferencia importante entre los operadores de traslación espacial y los operadores de rotación: a menos de que todas las rotaciones se lleven a cabo siempre en una misma dirección y sentido, los operadores de rotación no son conmutativos:
Sin embargo, una propiedad que aunque en estos momentos no sea muy obvia pero que esperamos que se cumpla para los operadores de rotación es que las operaciones de rotación deben ser asociativas:
Si suponemos que cada uno de los tres operadores de rotación dados arriba son matrices, no resulta difícil ver el por qué las operaciones de rotación deben ser asociativas, ya que en el caso de las matrices la operación de multiplicación también es asociativa.
Otra propiedad que aquí puede parecer trivial pero que no lo será tanto al momento de resolver problemas que involucren otros tipos de operadores es que debe ser posible invertir cualquier operación de rotación aplicando una rotación de la misma magnitud pero en la dirección contraria. Puesto de otra manera, para cada operador de rotación debe de haber un operador inverso de rotación. A continuación se muestra del lado izquierdo de la igualdad la representación simbólica del operador de rotación inverso utilizando el exponente -1 que se acostumbra utilizar (sin que ello implique ni remotamente hablando una operación aritmética de división como ocurre cuando se trabaja con números), mostrándose del lado derecho de la igualdad que esta operación de inversión de rotación se debe poder llevar a cabo con un operador de inversión en el cual se le ha invertido el signo a la magnitud del desplazamiento (si se considera a un desplazamiento angular en el sentido contrario a las manecillas del reloj como positivo, entonces el desplazamiento angular en el sentido de las manecillas del reloj es tomado como negativo):
PROBLEMA: Dado el siguiente operador de rotación:
obténgase el operador de rotación inverso que le corresponde a este operador.
Puesto que el operador de rotación es una matriz, el operador de rotación inverso:
se puede obtener resolviendo el sistema de ecuaciones que resulta de la ecuación matricial:
con lo cual se pueden determinar las cantidades a, b, c y d tras la resolución del sistema lineal de cuatro ecuaciones con cuatro incógnitas. Sin embargo, hay una manera mucho más sencilla y rápida de obtener el operador de rotación inverso, la cual consiste en usar la relación:
Esto nos permite escribir de inmediato al operador de rotación inverso como:
o bien:
Habiendo visto las propiedades que debe satisfacer un operador de rotación general, el siguiente paso lógico consiste en construírlo. En la construcción de un operador de rotación, vale la pena repasar el trabajo previo que nos permitió obtener operadores de desplazamiento espacial y temporal. En el caso del desplazamiento espacial, ya se vió bajo el contexto de la Mecánica Ondulatoria que el generador de desplazamientos espaciales es el operador del momentum (.px para un desplazamiento unidimensional a a lo largo del eje-x). Y se vió también que el generador de desplazamientos temporales es el operador de energía Hamiltoniano H. Una pista en la búsqueda de un operador de rotación que esté relacionado con las rotaciones para cierto momento angular (intrínseco, en el caso del spin del electrón) lo es el hecho de que en la mecánica clásica el generador de rotaciones es precisamente el momento angular. Esto nos lleva a considerar la siguiente posibilidad (dimensionalmente correcta) mediante el simple recurso de establecer comparaciones:
Este operador de rotación que estamos considerando como candidato para llevar a cabo una rotación angular de φ en torno al eje-z tiene una diferencia marcada con respecto al operador de desplazamientos espaciales. El operador es una función matricial (el lector tal vez quiera hacer un repaso de la entrada titulada “Funciones matriciales”). Pero hay otro hecho importante que es necesario destacar. En el formalismo que estamos desarrollando, el operador del momento angular ya no está siendo definido como el producto cruz clásico de la posición y el momentum, o sea como x×p. El momento angular del spin no tiene nada que ver con los vectores posicion x y momentum p, ni tiene contraparte alguna en la mecánica clásica.
En conformidad con el símbolo Đ introducido arriba para simbolizar operadores de rotación en Mecánica Cuántica, estaremos trabajando con simbología como la siguiente:
habiéndose seleccionado la letra Đ por su origen de la palabra en alemán Drehung que significa “rotación”. Si este operador de rotación es una función matricial, esto nos lleva de nuevo a lo que se discutió en una entrada previa titulada “La matriz de rotación” cuando llevamos a cabo nuestro estudio de la Mecánica Matricial. Y si bien, dentro de la Mecánica Ondulatoria las funciones de onda que manejamos son los espinores, la estructura matemática es aquí cien por ciento matricial. De este modo, la línea divisoria que se había marcado previamente entre la Mecánica Matricial y la Mecánica Ondulatoria se empieza a difuminar, volvíendose algo borrosa. Siguen siendo dos maneras distintas de ver las cosas y en muchas situaciones siguen siendo técnicas matemáticas distintas para el análisis de una gran variedad de situaciones, pero eventualmente la Mecánica Matricial y la Mecánica Ondulatoria se van integrando en un solo cimiento que es el que conocemos como Mecánica Cuántica.
Antes de continuar desarrollando al operador de rotación para el momento angular (intrínseco) del spin de una partícula como el electrón, es necesario repasar el hecho de que hay dos tipos de momento angular, el momento angular de spin que tiene la partícula por sí sola cuando está en una posición fija en el espacio, y el momento angular orbital que tiene la partícula cuando está llevando a cabo un movimiento rotacional periódico en torno a un centro de atracción como ocurre con el caso del electrón en el átomo de hidrógeno. Aquí resulta fructífero intentar obtener primero de modo formal un operador de rotación para el momento angular orbital, para después tratar de proyectar los resultados obtenidos al caso del momento angular de spin. Empezaremos por considerar primero las fórmulas usuales para llevar a cabo la conversión de las coordenadas polares (r,θ) que especifican la posición de un punto cualquiera a coordenadas rectangulares Cartesianas (x,y,z):
Considérese ahora que se lleva a cabo un desplazamiento angular dθ muy pequeño, infinitesimal, manteniendo al radio vector r con la misma longitud. Las nuevas coordenadas Cartesianas serán:
Llevando a cabo una expansión por series de Taylor, lo anterior puede escribirse con un muy buen grado de aproximación como:
Sobre un espacio tri-dimensional Cartesiano (x,y,z), la rotación que se está llevando a cabo arriba en un desplazamiento angular dθ en el plano xy es una rotación en torno al eje-z. Simbolizando al operador de rotación como Đ(z,dθ), el cual actuará sobre un ket de posición (representado en color magenta a continuación), podemos ver que la acción del operador de rotación en esta situación es de tal índole que se puede descomponer como el producto de dos operaciones de traslación:
Esto es válido para un desplazamiento angular infinitesimal dθ. Como puede deducirse de la última línea, el operador de rotación angular ha sido reducido al producto de dos operadores de traslación espacial:
Ya vimos previamente en la entrada titulada “Operadores de desplazamiento espacial y temporal” que, en su forma exponencial para cada coordenada-k, un operador de traslación está dado en lo general por la siguiente relación:
Esto nos permite escribir de la siguiente manera al operador de rotación en función de las formas exponenciales de los operadores de traslación que se tienen arriba:
Poniendo atención cuidadosa en lo que tenemos en la última línea dentro de los paréntesis ordinarios, podemos reconocer a lo que se tiene allí esencialmente como el momento angular definido para el eje-z:
Por lo tanto:
Pero esta relación es válida para un desplazamiento angular infinitesimal dθ, cuando en realidad lo que estamos buscando es una relación valida para un desplazamiento angular finito θ (no podemos medir cantidades infinitesimalmente pequeñas con ningún instrumento de laboratorio). Llevando a cabo una expansión en series del exponencial, lo anterior es igual a:
Obviamente, cuando el desplazamiento angular es exactamente igual a cero, este operador de rotación se reduce a la rotación identidad (al no haber desplazamiento angular alguno):
Por la propiedad de que dos rotaciones sucesivas en la misma dirección θ y dθ deben ser equivalentes a una sola rotación θ+dθ, esto mismo reflejado en operadores de rotación debe ser:
De ambos lados de esta igualdad podemos llevar a cabo la siguiente substracción:
Factorizando y substituyendo el resultado obtenido arriba para el operador de rotación infinitesimal, se tiene entonces:
Lo anterior lo podemos escribir de la siguiente manera:
¿Y por qué ponerlo todo de esta manera? Porque esencialmente vamos a reproducir el mismo procedimiento efectuado en la entrada “Operadores de desplazamiento espacial y temporal” para obtener la forma exponencial del operador de traslación. Obsérvese que lo que se tiene en el lado izquierdo de la igualdad es básicamente, por lo que es la definición de la derivada infinitesimal, la derivada del operador de rotación con respecto al ángulo de rotación, que puesto en notación diferencial convencional nos produce:
Esto lo podemos expresar también de la siguiente forma:
Pero esto es ya una ecuación diferencial elemental cuya solución es bien conocida, llevándonos directamente a una expresión para el operador de rotación en torno al eje-z del momento angular orbital:
Este resultado es válido no sólo para ángulos infinitesimalmente pequeños, sino para cualquier ángulo finito. Y nos está dejando muy en claro algo de importancia fundamental: el momento angular es el generador de rotaciones.
Obviamente, por la definición exponencial obtenida, el inverso de un operador de rotación para llevar a cabo un giro en una dirección igual y opuesta a la que se produce con el operador de rotación en torno a cierto ángulo θ será igual al conjugado complejo del operador de rotación:
Es común en la literatura darle la simbolización de transconjugado al operador de rotación inverso anexándole al operador de rotación una daga puesta como super-índice:
Habiendo obtenido el operador de rotación para el momento angular orbital, podemos buscar ahora la manera de obtener formalmente el operador de rotación para el momento angular de spin (intrínseco), por ejemplo para el momento angular Sz. Pero ni siquiera es necesario llevar a cabo cálculo alguno, porque las expresiones para ambos momentos angulares deben ser prácticamente las mismas, ya que ambas cantidades Lz y Sz están medidas (en el mismo sistema de unidades) en unidades de momento angular, las mismas unidades en las que está especificada la constante reducida de Planck ħ (lo cual se encarga de hacer que el exponente sea adimensional, carente de dimensiones físicas, lo cual se requiere para que el exponencial sea matemáticamente válido). Lo único que cambiará en las expresiones para los operadores de rotación será el tipo de momento angular a ser utilizado:
Así como se ha propuesto arriba un operador de rotación Đz para el spin en torno al eje-z, también debe de haber operadores de rotación Đx y Đy para los otros ejes. Ahora bien, la introducción más elemental al tema de las rotaciones está basada en la especificación del eje de rotación y el ángulo de rotación. Es obvio que se requieren tres números para poder caracterizar una rotación general. De acuerdo al problema que fue resuelto arriba, estos números son los ángulos de rotación polar y azimutal del vector unitario n tomados en la dirección del eje de rotación, así como el mismo ángulo de rotación φ. De hecho, puesto que el efecto de una combinación de rotaciones sucesivas (por ejemplo, una rotación angular con un giro de 30° en el sentido en que corren las manecillas del reloj en torno al eje-z, seguida de otra rotación de 75° en el sentido contrario al que corren las manecillas del reloj en torno al eje-x, seguida de otra rotación de 48° en el sentido en que corren las manecillas del reloj en torno al eje-y) debe poder ser obtenida de un operador de rotación más general que combine las tres rotaciones sucesivas, para ello resulta conveniente introducir el mismo vector unitario n que se ha definido arriba. A reserva de dar una justificación más formal a la definición que se está dando para operadores de rotación de spin, podemos simbolizar una rotación de carácter general como:
Frecuentemente, y como una simplificación para propósitos didácticos, puesto que Si es lo mismo que (ħ/2)σi, no es inusual encontrar lo anterior definido en función del vector de spin (a su vez definido sobre las matrices de Pauli) como:
Con la ayuda de la siguiente identidad matricial (fácilmente verificable para una matriz 2×2 mediante expansiones de Taylor):
que nos permite escribir:
se tiene entonces, evaluando primero σ·n:
el siguiente resultado:
Esta es la matriz de rotación (o mejor dicho, el operador de rotación) que aplicamos sobre un eigenespinor σ·n cualquiera para darle un giro especificado al eigenespinor.
La naturaleza de lo anterior es tal que, para obtener una rotación en torno a cada eje coordenado Cartesiano considerado fijo (el cual consideramos como eje de rotación) se tiene que usar la matriz de Pauli asociada con dicho eje. De este modo:
____Para una rotación alrededor del eje-x: Usar σ1 (σx)
____Para una rotación alrededor del eje-y: Usar σ2 (σy)
____Para una rotación alrededor del eje-z: Usar σ3 (σz)
Ahora veremos nuevamente un problema que fue resuelto en la entrada anterior como una eigenecuación, pero trabajando en esta ocasión con operadores de rotación que serán aplicados en sucesión (uno tras otro) a un espinor χ+ que representa el eigenestado de spin apuntando “hacia arriba”, al cual se le aplicará primero una rotación igual a un ángulo polar β, seguida de una rotación igual a un ángulo azimutal α, en la forma ilustrada por la siguiente secuencia animada:
Después de las dos rotaciones, el espinor rotado χ’ estará relacionado al espinor χ+ inicial de la siguiente manera:
La secuencia de operaciones mostrada es tal que el operador de rotación que será el primero en actuar sobre el espinor que está situado inmediatamente a su derecha es el que llevará a cabo un giro en un ángulo β, tras lo cual el segundo operador de rotación que será aplicado a lo que resulte de la primera rotación será el que lleve a cabo un giro en un ángulo α.
Puesto que la primera rotación se lleva a cabo en torno al eje-y, el vector direccional n a ser utilizado en la relación de arriba debe ser:
Entonces la relación de arriba nos produce el siguiente primer operador de rotación:
En lo que respecta al segundo operador de rotación, puesto que la rotación se llevará a cabo en torno al eje-z, el vector direccional n a ser utilizado en la relación de arriba debe ser:
Entonces la relación de arriba nos produce el siguiente segundo operador de rotación:
La primera acción de rotación sobre el espinor arroja el siguiente resultado:
Si aplicamos el segundo operador de rotación sobre esto, se tiene entonces:
habiéndose aplicado arriba la simplificación:
Lo que está resaltado en color azul en la respuesta al problema es simplemente un factor de fase que es común a la componente superior y a la componente inferior del espinor que ha sido girado. Si aceptamos el hecho de que una fase que es común a ambos componentes del espinor carece de significado físico (al igual que el ángulo de fase en una onda senoidal cuando es observada en el laboratorio), tenemos entonces el mismo resultado que el que se obtuvo en la entrada anterior (“Operadores de rotación I”), excepto que anteriormente se llegó a esto como consecuencia de la resolución de una eigenecuación, mientras que aquí el mismo problema se ha resuelto usando operadores de rotación. Esto nos comprueba que la definición que se ha dado arriba al operador de rotación para el caso de espinores bi-dimensionales es correcta.
Si enfocamos nuestra atención sobre el hecho de que los operadores de rotación usados para girar espinores son matrices, podemos obtener de inmediato una conclusión importante.
PROBLEMA: Demuéstrese, sin recurrir a argumentos geométricos, que las aplicaciones sucesivas de operadores de rotación a funciones del momento angular de spin (espinores) no son conmutativas.
La respuesta a este problema está implícita en la operación combinada de rotaciones que se acaba de llevar a cabo arriba, en donde los operadores de rotación han resultado ser matrices 2×2. Puesto que el producto de dos matrices A y B no es conmutativo, o sea que A·B.≠.B·A, si dichas matrices representan operadores de rotación entonces la operación A·Bχ engeneral dará un resultado diferente a la operación B·Aχ. Se concluye que las operaciones de rotación no son conmutativas para el caso del momento angular de spin.
A estas alturas, tenemos en nuestras manos para los movimientos espaciales de una función de onda (o de un ket) tanto operadores de traslación como operadores de rotación. Podemos juntar ambos tipos de operadores para aplicarlos sobre una función de onda Ψ. Sin embargo, la acción de cada uno de estos operadores debe estar restringida necesariamente al tipo de variable sobre la cual se esté actuando. Para llevar a cabo la traslación de una función de onda, no aplicamos un operador de traslación sobre su parte angular, lo aplicamos sobre la variable estipulada por una (o varias, en el caso tridimensional) de las componentes especificadas en el sistema de coordenadas rectangulares Cartesianas. Suponiendo que, mediante la técnica matemática de separación de variables, podemos tomar una función de onda Ψ(r,θ) descomponiéndola en el producto de dos funciones de onda, siendo una la parte “radial” ψ(r) y siendo la otra la parte angular ψ(θ), entonces la acción sucesiva de un operador de traslación y un operador de rotación sobre la función de onda descompuesta debe ser acorde con la variable sobre la cual se debe de actuar:
En la entrada titulada “El operador de traslación” ya se vió que el operador de traslación puede ser utilizado de dos maneras distintas, una de ellas para llevar a cabo el desplazamiento espacial de una función de onda situada inmediatamente a la derecha del operador de traslación, y la otra para llevar a cabo el desplazamiento espacial de un operador. Lo mismo debe ser cierto tratándose de operadores de rotación. Habiendo visto arriba la manera de hacer actuar un operador de rotación sobre una función de onda espinor, para comprobar que también es posible llevar a cabo una rotación de operadores considérese el siguiente ket general de estado que representa a un sistema de spin 1/2, el cual será girado alrededor del eje-z en un ángulo finito θ:
El operador de rotación que necesitamos para llevar a cabo una rotación alrededor del eje-z en un ángulo finito θ es el siguiente:
Aplicando este operador sobre el ket general de estado nos debe producir un ket rotado (girado):
En el espacio dual, el bra rotado (girado) que se corresponde con el ket rotado es el siguiente (recuérdese que, en este caso, el operador de rotación transconjugado actúa sobre el bra que está a su izquierda):
Ahora bien, la esperanza matemática del operador Sz es la siguiente:
Para obtener la esperanza matemática del operador rotado (girado), en lugar del ket y el bra que tenemos en esta relación debemos utilizar tanto el ket rotado como el bra rotado que obtuvimos arriba bajo la acción del operador de rotación:
Obviamente, para obtener esta esperanza matemática, tenemos que evaluar:
o lo que es lo mismo:
Aquí resultará ventajoso recurrir a la representación que se dió a Sz (en la entrada anterior) en función de productos externos ket-bra:
Sacando fuera al factor ħ/2 y convirtiendo la expresión a dos términos:
Para llevar a cabo los cálculos matriciales, recurriremos a las siguientes expresiones:
La expansión en series del término exponencial que está al lado derecho en ambos términos es como se muestra a continuación:
Con esto, y en el caso del primer término, la evaluación matricial llevada a cabo de derecha a izquierda (el orden aquí es inmaterial, igual podemos llevar a cabo la evaluación matricial de derecha a izquierda) empieza del modo siguiente:
Substituyendo a σ3 por la matriz que representa y llevando a cabo los productos matriciales, se tiene:
Después de una serie de pasos, esto nos lleva sucesivamente, para el primer término, a:
Llevando a cabo una serie de pasos similares para el segundo término, se llega a lo siguiente:
Por lo tanto, la evaluación del operador Sx ya rotado, lo cual era nuestro objetivo, viene siendo:
Tomando la esperanza matemática de ambos lados de la igualdad, la esperanza matemática del operador Sx ya rotado es entonces:
Reconocemos esta expresión como correcta, ya que para una rotación nula (con un ángulo θ igual a cero) esta expresión se reduce a una igualdad, mientras que para una rotación igual a 90° la esperanza matemática para Sx se nulifica,habiéndose llevado a cabo una giración completa hacia la esperanza matemática de Sx.
Repitiendo los pasos anteriores, llevando a cabo una rotación (nuevamente) en torno al eje-z en un ángulo θ no de Sx sino de Sy, se puede comprobar que la esperanza matemática de Sy tras la rotación está dada por:
¿Y si tratamos de obtener la esperanza matemática de Sz repitiendo los mismos procedimientos? En tal caso la esperanza matemática de Sz permanecerá inalterada, en virtud de que Sz conmuta con el operador de rotación para Sz.
Acomodando de la siguiente manera las tres relaciones para las esperanzas matemáticas de los momentos angulares de spin cuando se lleva a cabo una rotación en torno al eje-z en un ángulo θ:
resulta evidente que el sistema de ecuaciones puede ser puesto en forma matricial del siguiente modo:
Esto resalta el hecho de que la esperanza matemática del vector momento angular de spin se comporta como un vector clásico bajo operaciones de rotación. En efecto, si tomamos el siguiente vector clásico tridimensional:
y le aplicamos la siguiente matriz ortogonal de rotación (recuérdese que, por definición, una matriz ortogonal es aquella que deja la longitud del vector original intacta):
se obtiene un vector girado:
cuyas componentes nuevas se obtienen de la siguiente igualdad matricial:
Todo esto se traduce en que, para el caso de las esperanzas matemáticas de las componentes del vector momento angular de spin, cada esperanza matemática del momento angular girado se obtiene de la siguiente relación:
en donde los Rmn son los elementos de una matriz ortogonal clásica de rotación 3×3. Esta propiedad no está restringida a sistemas físicos de operador de spin para los cuales el spin es igual a 1/2. Es también válida para sistemas físicos de operador de spin 1, 3/2, etc. Y extendiendo los argumentos que se han utilizado aquí, la propiedad debe de ser válida también no sólo para las rotaciones del momento angular de spin sino para las rotaciones del momento angular orbital L:
Obsérvese que aquí la sumatoria se ha dejado abierta para permitir la existencia de matrices ortogonales en espacios que van más allá del espacio tridimensional Euclideano, las cuales son requeridas para poder llevar a cabo rotaciones en los casos en los cuales el momento angular está especificado por más de tres componentes. Aunque no sea todavía evidente (con lo que hemos visto) la manera en la cual se pueden construír matrices ortogonales de tamaño n×n que sean capaces de producir rotaciones en un espacio n-dimensional, y menos obvio aún considerando que nuestros cerebros no están equipados para visualizar lo que pueda ocurrir en espacios multidimensionales, matemáticamente ello no presenta obstáculo alguno aún sin la ayuda de la intuición geométrica.
Considerando que, en base al modelo vectorial mediante el cual simbolizamos la suma mecánico-cuántica del momento angular de spin S y el momento angular orbital L para producir un momento angular total J que explica la aparición de lineas espectrales adicionales en virtud del acoplamiento L·S:
podemos intentar ir aún más lejos presionando las estructuras matemáticas para que nos permitan llevar a cabo rotaciones del momento angular total J, en cuyo caso anticipamos que las esperanzas matemáticas (que es a fin de cuentas lo que se viene midiendo en el laboratorio) de las componentes posibles del momento angular total de un sistema en el cual hay acoplamiento L·S, cuando se ha llevado a cabo una rotación, estén dadas por:
Este objetivo que nos estamos fijando aquí tal vez parezca algo ambicioso, pudiendo anticipar de antemano que el manejo de este tipo de situaciones puede resultar irremediablemente en un aumento en la complejidad notacional. Sin embargo, mientras las estructuras matemáticas que iremos desarrollando puedan manejar estas situaciones, y mientras que lo que predice la teoría pueda ser confirmado mediante el experimento, no hay razón alguna para detenerse en el camino que hemos emprendido. Afortunadamente, los resultados experimentales han confirmado y siguen confirmando sólidamente que la pirámide que se ha estado construyendo está levantada sobre pilares sólidos.
PROBLEMA: Dado el vector:
demuéstrese que el determinante de la matriz 2x2 σ·v en donde σ es el vector de spin en función de matrices de Pauli permanecerá invariante bajo la siguiente operación de rotación:
Asimismo, suponiendo que el vector unitario n está apuntando en la dirección positiva del eje-z, dése una interpretación al resultado obtenido.
Tomando el producto interno σ·v del vector de matrices σ y el vector v:
el determinante de esto será:
La operación de rotación, para el caso en el cual el vector unitario está apuntando a lo largo del eje-z, será:
Definiendo K de la siguiente manera con la finalidad de abreviar el simbolismo de los cálculos:
lo cual implica:
se tiene entonces:
Por lo tanto:
En base a este resultado, se concluye que el determinante de σ·v permanece invariante bajo la operación de rotación especificada.
El producto σ·v’ usándose el vector girado v’ está dado por la siguiente matriz:
Reemplazando las componentes primas del vector v’ ya girado en función de lo que eran las componentes del vector v antes de la rotación en base a las componentes indicadas por la matriz de arriba:
Se deduce que:
Esto último representa una rotación en torno al eje-z en sentido contrario al giro de las manecillas del reloj, a través de un ángulo φ, llevada a cabo sobre el plano x-y. Es más de lo mismo que ya habíamos visto arriba.
De la misma manera en la que el operador exp(-iS·nθ/ħ) actúa sobre un ket de estado, la matriz 2×2 exp(-iσ·nθ/2) actúa sobre un espinor χ de dos componentes:
Si hemos de hablar en términos más formales y rigurosos, se debe destacar el hecho de que los σk (las tres matrices de Pauli) permanecen sin cambio alguno al llevarse a cabo las rotaciones. En rigor de verdad, y pese a su apariencia por la manera en la cual se le ha definido, σ no es lo que pudiera ser considerado como un vector. Más bien, lo que obedece las propiedades de transformación de un vector es:
La transformación de este vector bajo una operación de rotación se puede expresar en su forma más explícita para cada σk como:
Como ya se ha estado señalando, el spin del electrón, imaginado mecanísticamente (aunque incorrectamente, desde el punto de vista formal de la Mecánica Cuántica) como el resultado del electrón girando sobre sí mismo, no es lo único que puede ser asociado a un momento angular. Se tiene también el momento angular orbital, simbolizado frecuentemente como L. Manteniendo las analogías, esperamos que el operador de rotación para el momento angular orbital sea una expresión como la siguiente:
Obsérvese que no se está resaltando el operador L con el color azul utilizado para simbolizar matrices. Ello se debe a que estaremos trabajando tanto bajo el contexto de la Mecánica Matricial como bajo el contexto de la Mecánica Ondulatoria en donde en esta última los operadores pueden ser operadores diferenciales en lugar de matrices. Con la finalidad de no confundir al operador de rotación asociado al momento angular de spin con el operador de rotación asociado al momento angular orbital, sobre todo cuando estamos aplicando ambos tipos de rotaciones a cierta función de onda, podemos empezar a establecer una diferencia entre ambos a través de notación en super-índices, a reserva de refinar posteriormente la notación:
Si bien es cierto que en un espacio tridimensional se puede girar un vector con respecto a tres ejes coordenados rectangulares Cartesianos manteniendo a los ejes en una posición rígida, igualmente es posible sostener al vector en una posición rígida y girar a los ejes coordenados rectangulares Cartesianos de una manera como la siguiente:
Ambas acciones producen el mismo efecto. En un caso, se gira el vector hacia una nueva posición manteniendo la base (los kets de base) fija, mientras que en el otro caso lo que se gira es la base (en el sentido opuesto) manteniendo al vector fijo. Estas dos posibilidades tienen una analogía directa en la Mecánica Cuántica: La rotación del vector de estado es lo que se lleva a cabo en la representación de Schrödinger, mientras que la rotación de la base manteniendo al vector de estado fijo es lo que se lleva a cabo en la representación de Heisenberg.
Los operadores de rotación necesariamente sólo pueden actuar sobre la parte angular de una función de onda, no sobre su parte radial. Aparte de las funciones de onda del spin (espinores) usadas en el estudio del momento angular intrínseco de las partículas, ¿hay alguna otra función de onda en especial en la cual estemos interesados? La respuesta es definitivamente positiva. Y estas funciones de onda son las mismas que se obtuvieron previamente en el estudio de la función de onda Ψ(r,θ,φ) del átomo de hidrógeno, la cual para su análisis se separó en el producto de una función de onda ψ(r) para la parte radial y otra función de onda Y(θ,φ) para la parte angular. Y las funciones de onda que resultaron de la solución de onda de la ecuación de Schrödinger para la parte angular resultaron las armónicas esféricas:
Se trata de las mismas funciones de onda angulares que fueron introducidas y graficadas en la entrada titulada “Momento angular orbital: funciones de onda I”. Podemos postular un operador de rotación general para estas funciones de onda que sea capaz de actuar sobre las mismas produciendo una rotación llevando a la función de onda hacia una nueva posición:
Hemos visto ya que, para cierto valor del número cuántico entero positivo l que representa al momento angular, hay una serie de valores posibles m que pueden tomar todos los valores enteros posibles desde -l hasta +l. Y resulta que, desde el punto de vista estrictamente matemático, para cierto valor de l este conjunto de valores de m puede ser considerado como un vector en toda la extensión de la palabra. Y este vector de armónicas esféricas, para un valor de l.=.1 (en cuyo caso m puede tomar los valores +1, 0 y -1), puede ser sometido a una rotación que lleve al vector inicial de armónicas esféricas desde:
hasta un nuevo vector rotado:
mediante la acción de un operador matricial de rotación:
La operación de rotacion matricial, en su forma más explícita, es la siguiente:
En analogía con las fórmulas para conversión de un vector de una base de vectores unitarios a otra base distinta, cada componente del vector de armónicas esféricas rotado estará dado por la siguiente expresión:
Todo esto último que acabamos de ver nos sugiere que, al igual que los vectores unitarios de base usados para especificar dirección y sentido en un sistema de coordenadas rectangulares Cartesianas y los vectores unitarios de base usados para especificar dirección y sentido en un sistema de coordenadas esféricas:
también debe ser posible llevar a cabo la expansión de la parte angular de una función de onda usando armónicas esféricas como funciones de base, lo cual debe ser posible porque una característica que distingue a las armónicas esféricas es que (al igual que los vectores unitarios de base empleados en un sistema de coordenadas rectangulares Cartesianas) las armónicas esféricas son irreducibles, no se pueden obtener como una combinación lineal de algo más sencillo. Aunque para quien no haya tomado un buen curso de Álgebra Lineal pueda parecer extraño usar funciones de base en lugar de vectores de base, en realidad y visto desde el punto de vista abstracto (general) del Álgebra Lineal es tan válido usar funciones que dependan de algún parámetro independiente como el ángulo θ que usar vectores unitarios de base como el conjunto de vectores {i,j,k} que se acostumbra utilizar en el Análisis Vectorial. Para el caso l.=.1, puesto que los valores permisibles de m son -1, 0 y +1, el conjunto de armónicas esféricas que podemos utilizar como funciones de base es el siguiente:
Para el caso l.=.2, puesto que los valores permisibles de m son -2, -1, 0, 1 y +1, el conjunto de armónicas esféricas que podemos utilizar como funciones de base es el siguiente:
En el ejemplo dado arriba, el lector tal vez tenga alguna curiosidad acerca del aspecto de los nueve elementos del operador matricial de rotación para el caso l.=.1. No entraremos aquí en detalles explícitos, los cuales serán tratados a partir de la entrada titulada “Los grupos de rotación II”, pero para satisfacer de antemano esta curiosidad a continuación se enlistarán los nueve elementos de este operador matricial de rotación en función de los ángulos de Euler dados arriba, obtenidos con la ayuda de una fórmula conocida como fórmula de Wigner:
Cuando este tipo de operadores de rotación basados en los ángulos de Euler son estudiados en mayor detalle, se aprecia que la parte media en todos los elementos matriciales que se acaban de enlistar es la parte más importante por ser la que mezcla los distintos valores del número cuántico magnético m, los demás factores (los factores exponenciales) vienen siendo factores de fase sin mayor trascendencia física. Es por ello que resulta conveniente definir una nueva matriz más sencilla que prescinde de los factores de fase, conocida comúnmente como la matriz matriz reducida de rotación. Para el ejemplo con l.=.1 dado arriba, la matriz reducida de rotación será:
En la obtención de todos los operadores de rotación que se ha llevado a cabo aquí, se ha supuesto implícitamente como cierto algo que debe parecer obvio a primera vista: la isotropía del espacio, lo cual equivale a suponer que el espacio tiene la misma estructura en todas las direcciones, lo cual significa que el espacio tiene la misma estructura en el sentido Norte-Sur que en el sentido Este-Oeste (esto es algo parecido a la suposición de que el espacio es homogéneo en el desarrollo del operador de traslación, excepto que al hablar acerca de rotaciones en lugar de traslaciones hablamos de isotropía en lugar de hablar de homogeneidad). Aceptar como cierta la suposición de la isotropía del espacio es aceptar también que la solución a cierto problema físico es invariante bajo las rotaciones que se lleven a cabo. En otras palabras, si giramos un aparato Stern-Gerlach para que todo el aparato (horno, imanes, pantalla de recolección de partículas desviadas, etc., todo) apunte hacia otra dirección, los resultados que se obtendrán serán exactamente los mismos que los que se estaban obteniendo antes, algo que ha sido confirmado numerosas veces en el laboratorio. Pero de nueva cuenta, si dejamos que entre en acción la Teoría de la Relatividad, la suposición de la isotropía del espacio ya no puede tomarse como válida al pie de la letra porque no sólo el espacio deja de ser absoluto como lo marca la Teoría Especial de la Relatividad, lo que llamamos espacio-tiempo (en la unificación de ambos conceptos bajo un 4-vector) deja de ser Lorentziano (plano) para adquirir una curvatura. De nueva cuenta, y al igual que como ocurre en el caso del operador de traslación y el operador de evolución del tiempo los efectos gravitacionales en los fenómenos del mundo sub-microscópico solo adquieren relevancia bajo la acción de campos gravitacionales intensos como los que hay en la cercanía de los agujeros negros o los que hay en estrellas con una gran cantidad de masa, y se puede seguir trabajando en el planeta Tierra con lo que ya se tiene.
