Al chocar bruscamente con el ánodo, los electrones emitidos por el cátodo poseen la energía suficiente para vencer la repulsión eléctrica de las capas exteriores de electrones de los átomos del elemento que está siendo utilizado como recubrimiento del ánodo, “perforando” de alguna manera el blindaje exterior de los átomos, pudiendo llegar hasta el interior del mismo átomo para sacar uno de los electrones que están en las capas más cercanas al núcleo del átomo, y al hacer tal cosa alguno de los electrones que está en las capas superiores desciende para llenar el hueco, emitiendo de paso un fotón de energía tan elevada que a diferencia de la luz visible posee la capacidad de poder penetrar materiales sólidos y líquidos. Esta radiación de alta energía, bautizada desde su descubrimiento en 1895 por Wilhelm Roentgen como rayos-X, no debe ser confundida con otro tipo de radiación intensa conocida como radiación de frenado o bremsstrahlung, predicha por la electrodinámica clásica cuando una carga eléctrica es acelerada, entendiéndose por aceleración no sólo el cambio en la velocidad de una partícula cuando se está moviendo siempre de frente en la misma dirección sino también cuando está cambiando el sentido de su movimiento experimentando con ello una aceleración de tipo vectorial. De este modo, un electrón de alta energía que impacta el interior de un átomo puede generar fotones de rayos-X no sólo a través del proceso de expulsión de uno de los electrones más cercanos al núcleo del átomo sino también por el solo hecho de que su trayectoria sea desviada por el núcleo atómico sin que altere en su recorrido la estructura electrónica del átomo que está atravesando:
En un átomo polielectrónico tridimensional, podemos imaginar en el proceso de generación del fotón de rayos-X bremsstrahlung una situación un poco más interesante como la siguiente:
Sin embargo, para nuestros fines, en lo que estamos interesados realmente no es la radiación bremsstrahlung que a fin de cuentas lo que produce es una radiación de fondo, en lo que estamos interesados es en la radiación provocada por la expulsión de uno de los electrones interiores del átomo, porque este proceso es precisamente el que acarrea información importante acerca de la estructura interna del átomo.
PROBLEMA: Antes del advenimiento de los televisores LED de pantalla plana, se utilizaban tubos de rayos catódicos (CRT) al vacío, los cuales solían utilizar fuentes de alto voltaje proporcionando potenciales típicos de 25 kilovolts, y los electrones emitidos por el cátodo al impactar contra la pantalla emitían rayos-X que en un tiempo se consideró que podrían resultar nocivos por el alto tiempo de exposición de las personas a estas pantallas de televisión. ¿Cuál es la longitud de onda de los rayos-X correspondientes a este tipo de televisores?
Considerando que cada uno de los electrones emitidos por el cátodo adquieren una energía de 25 keV, la longitud de onda correspondiente será:
λ = c/f = hc/hf = (12.4 keV·Å)/(25 keV)
λ = 0.496 Å
La espectroscopía de rayos-X se basa en recubrir el ánodo del tubo generador de rayos-X con el elemento que será analizado. De este modo, los fotones de rayos-X al salir fuera del tubo llevarán información importante concerniente al elemento.
A diferencia de la espectroscopía óptica en la cual podemos simplemente enviar los fotones de la luz a un prisma de vidrio o, mejor aún, a una rejilla de difracción, en la espectroscopía de rayos-X no tenemos esa comodidad. Afortunadamente, se cuenta con las técnicas desarrolladas en 1913 por los hermanos William Lawrence Bragg y William Henry Bragg quienes descubrieron que los sólidos cristalinos son capaces de producir patrones sorprendentes de rayos-X reflejados de los sólidos cristalinos, patrones que no se dan en los líquidos, encontrando que estos patrones, a ciertas longitudes de onda y ángulos de incidencia de los rayos-X sobre la superficie cristalina, producían picos intensos de radiación reflejada, lo cual fue explicado como el resultado de un proceso de difracción que se produce al ser reflejados los haces incidentes de rayos-X por varias capas de planos discretos de átomos del cristal separadas por una distancia fija, proceso conocido hoy como la difracción de Bragg.
El funcionamiento del espectógrafo de rayos-X se basa en obtener de la fuente de rayos-X un haz fino con la ayuda de un colimador de plomo que envía el haz directamente hacia la superficie de un cristal que forma cierto ángulo con el haz incidente de rayos-X, enviando el haz reflejado hacia un detector que puede ser un simple galvanómetro o algo más sofisticado con la electrónica con la que contamos hoy en día. El aparato se puede girar hasta obtener los ángulos en los cuales se miden los “picos” de mayor intensidad:
Los patrones de intensidad que se observan dependen del hecho de que el ángulo de dos haces cualesquiera reflejados de los planos discretos de los átomos de cristal salgan reflejados en fase, dando lugar a una interferencia constructiva que aumenta la intensidad de la señal, o que salgan reflejados fuera de fase, dando lugar a una interferencia destructiva de la señal:
Para poder obtener un máximo en los fotones reflejados por el cristal mediante el proceso de interferencia constructiva, se debe cumplir la condición estipulada por la ley de Bragg:
nλ = 2d sen(θ)
PROBLEMA: Supóngase que en un espectógrafo de rayos-X el cristal que se utiliza como patrón de referencia es el NaCl (cloruro de sodio), para el cual la distancia entre los planos de la estructura cristalina (conocidos como planos de Bragg) es de 2.81 Angstroms. Si al girar el aparato la primera reflexión que se detecta (la reflexión de primer orden) ocurre a un ángulo de 15.8°, ¿cuál será la longitud de onda de los fotones que están siendo reflejados?
La aplicación de la ley de Bragg es directa en este caso:
nλ = 2d sen(θ)
(1)λ = 2(2.81 Å) sen(15.8°)
λ =1.53 Å
Esta es la manera en la cual se mide la frecuencia de los fotones de rayos-X que están siendo generados por el tubo de rayos-X.
A los pocos meses y en el mismo año de haberse dado a conocer al mundo el modelo atómico planetario de Bohr, el químico inglés Henry Moseley aprovechándose de las recién descubiertas leyes de difracción para los rayos-X descubiertas por los hermanos Bragg (sus coterráneos) llevó a cabo un estudio sobre el espectro de rayos-X de una amplia variedad de elementos, un esfuerzo que culminó con un importante triunfo de la ciencia moderna cuando Moseley dió a conocer en 1913 su ya famosa ley de Moseley hoy enunciada de la siguiente manera:
en donde Z es el número atómico del material del blanco, y tanto A como b son constantes que dependen de la transición que se esté observando, mientras que en el lado izquierdo tenemos a la raíz cuadrada de la frecuencia de los rayos-X producidos.
Previo a los trabajos de Moseley, la extensión de la teoría de Bohr hacia átomos más complicados que el átomo de hidrógeno había demostrado ser un verdadero reto. Y aunque no era posible llevar a cabo cálculos cuantitativos para determinar los niveles energéticos de átomos distintos al hidrógeno, el descubrimiento experimental de Moseley fue fundamental para apoyar la imagen del modelo atómico planetario Rutherford-Bohr del átomo como un núcleo con carga eléctrica positiva circundado por electrones situados a una distancia relativamente grande del núcleo.
De acuerdo a la teoría de Bohr, la energía de un electrón en el estado fundamental, la capa energética más cercana al núcleo, es proporcional al cuadrado de la carga eléctrica del núcleo, o lo que es lo mismo, al número atómico Z del elemento. Moseley, quien ya estaba al tanto dell modelo atómico planetario de Bohr, razonó que la energía, y por lo tanto la frecuencia, de un fotón característico de rayos-X emitido por una muestra bombardeada con electrones de alta energía generados en un tubo de rayos-X, debería variar en razón directa a la raíz cuadrada del número atómico del elemento blanco que estaba siendo bombardeado. Es así como se le ocurrió graficar la raíz cuadrada de la frecuencia de una línea particular de rayos-X en contra del número atómico del elemento utilizado como blanco, una gráfica hoy conocida como gráfica Moseley. Y encontró que las líneas obtenidas en la gráfica podían ser acomodadas dentro de la fórmula que se ha enunciado arriba.
En la espectroscopía óptica, las líneas características de absorción y emisión que se observan provienen de los saltos energéticos en que incurren los electrones más exteriores al núcleo del átomo, los llamados electrones de valencia. Pero en la espectroscopía de rayos-X, a diferencia de lo que ocurre en la espectroscopía óptica, los electrones utilizados para llevar a cabo el bombardeo poseen la energía suficiente para “perforar” a través de varias capas llegando hasta la capa más interior del átomo, la capa que corresponde al estado fundamental identificada con el número cuántico n = 1 en el modelo atómico planetario de Bohr y con la letra K en la espectroscopía de rayos-X, echando fuera a uno de los electrones situados en dicha capa. Al ocurrir esto, el átomo se encuentra en un estado altamente inestable, con un “hueco” en su capa más próxima al núcleo y con las capas superiores repletas de electrones listos para descender para llenar el hueco, liberando energía en el proceso mediante la emisión de fotones de rayos-X que son los fotones cuya frecuencia es registrada diligentemente. La línea con la frecuencia más baja corresponderá a la transición de energía más baja, de n = 2 a n = 1, con un átomo de la segunda capa -identificada con la letra L en la espectroscopía de rayos-X- descendiendo a la primera capa para llenar el hueco. Esta línea es la línea designada como Kα. La siguiente línea para llenar el hueco en el estado corresponderá a la de un electrón que se encuentra en la siguiente capa más exterior, identificada con la letra M en la espectroscopía de rayos-X (la cual corresponde al número cuántico n = 3 en el modelo de Bohr). Esta línea es la línea designada como Kβ. Podemos describir lo que ocurre en varios pasos de la manera siguiente:
En el tubo de rayos-X, un electrón después de salir disparado del filamento-cátodo llega al ánodo con la suficiente energía para vencer la repulsión eléctrica de los electrones más exteriores al átomo, “perforando” en cierto modo las capas superiores logrando llegar hasta la capa más cercana al núcleo del átomo (1). Al impactar con uno de los dos electrones en la primera capa (que en el modelo atómico planetario de Bohr corresponde a la capa del estado basal o estado fundamental n = 1), lo saca fuera del átomo dejando con ello un “hueco” (2). Este es un estado inestable, y el hueco tiene que ser llenado a la menor brevedad posible, lo cual puede llevarse a cabo en una primera instancia con un electrón de la capa n = 2 descendiendo a la capa n = 1 para llenar el hueco (3). Y en el proceso de descender de la capa n = 2 a n = 1, el átomo libera un fotón de alta energía, un fotón de rayos-X (4).
Ahora bien, al descender un electrón de la capa L a la capa K para llenar el hueco que allí había, dejará su propio hueco que también tiene que ser llenado por algún electrón situado en una capa superior, preferentemente el de la capa superior inmediata que viene siendo la capa M. Esta transición de la capa M a la capa L produce su propia línea característica en el espectro de rayos-X, la línea designada como Lα. Y si el electrón que llenará el hueco en la capa L procede no de la capa M sino de la capa N (la cual corresponde al número cuántico n = 4 en el modelo de Bohr), entonces se producirá la línea característica designada como Lβ. De este modo, se van generando las líneas características del espectro de rayos-X que corresponde al descenso de un electrón de una capa superior a la capa del átomo que corresponde a su estado basal:
Cuando se observa el espectro de rayos-X de un átomo polielectrónico (un átomo que consta de varios electrones, a diferencia del átomo de hidrógeno en base al cual fue elaborado el modelo atómico planetario de Bohr para explicar las líneas características de absorción y emisión en el espectro visible) producido por el bombardeo de los electrones en la superficie del cátodo del tubo de rayos-X y desmenuzado en el espectógrafo de Bragg, se observa una suave radiación de frenado de fondo (la radiación bremsstrahlung) con una interrupción en la longitud de onda mínima correspondiente al máximo voltaje de aceleración (a unos 19 keV en el lado izquierdo de la gráfica que sigue) junto con líneas agudas producidas por las transiciones Kα, Kβ, etc.:
Cada elemento tiene su propio espectro característico de rayos-X. A continuación tenemos en un mismo sitio los espectros de rayos-X del molibdeno (Mo) y del cobre (Cu):
Si recurrimos al modelo atómico planetario de Bohr para establecer comparaciones, podemos empezar por la relación para la frecuencia de un átomo que contenga un solo electrón (el átomo de hidrógeno):
Para un salto en el cual uno de los niveles energéticos corresponde a n = 1 (la capa K), poniendo Z-1 en lugar de Z tenemos entonces para la serie de líneas K:
Esto lo podemos simplificar un poco de la siguiente manera:
en donde fR es la frecuencia de Rydberg que a su vez está relacionada con la constante de Rydberg R (simbolizada frecuentemente como R∞) de la siguiente manera:
Comparando esta expresión del modelo atómico planetario de Bohr con la ley de Moseley enunciada arriba, encontramos que la constante A en la ley de Moseley está dada por:
Si aplicamos esta relación para la determinación de la longitud de onda λ de la línea Kα del molibdeno cuyo número atómico es Z = 42, tenemos entonces que:
Metiendo valores, encontramos que la longitud de onda λ de la línea Kα del molibdeno es λ = 0.725 Å, un valor que compara favorablemente con el resultado experimental obtenido por Moseley.
El hecho de que la frecuencia f sea proporcional a (Z-1)² en lugar de ser proporcional a Z² como ocurre para el átomo de hidrógeno en el modelo atómico planetario de Bohr es explicado por la presencia del “blindaje” de la carga nuclear producido por el otro electrón que aún permanece en la capa n = 1 (capa K) del átomo. En efecto, podemos considerar a (Z-1)e como la carga neta positiva que actúa sobre el electrón. Usando esta línea de razonamiento, Moseley concluyó que, en virtud de que la constante b = 7.4 para la serie de líneas características L, estas línas involucraban electrones alejados aún más del núcleo, el cual está blindado por una cantidad aún mayor de electrones.
A continuación tenemos una composición que nos permite apreciar mejor la correlación que hay entre el espectro característico de rayos-X de un elemento y los saltos de una capa superior a una capa inferior que producen las líneas características que corresponden al elemento:
De este modo, aunque la teoría de Bohr fue desarrollada para átomos en estado gaseoso (los cuales al estar distanciados el uno del otro no interactúan entre sí), se ve que también proporciona una explicación de las propiedades de los átomos de un material sólido, los cuales interactúan muy frecuentemente unos con otros.
Lo que sigue a continuación son citas tomadas del segundo papel del trabajo original de Moseley:
1. Cada elemento del aluminio al oro está caracterizado por un entero Z que determina su espectro de rayos-X. Cada detalle en el espectro de un elemento puede por lo tanto ser predicho de los espectros de sus vecinos.Antes del trabajo pionero de Moseley, el número atómico Z era simplemente el número del lugar de cada elemento en la tabla periódica de Mendeleiev acomodados según su masa. Ya desde antes se sabía que el número atómico Z de cada elemento era aproximadamente igual a la mitad de la masa atómica (relativa) del elemento. Los experimentos llevados a cabo por Geiger y Marsden demostraron que la carga nuclear era aproximadamente igual a la mitad de la masa atómica relativa, mientras que los experimentos de esparcimiento del científico inglés Charles Barkla demostraron que el número de los electrones en un átomo era también igual a la mitad de la masa atómica relativa del elemento. Sin embargo, había discrepancias en la tabla periódica de los elementos al estar acomodados según su masa, y varios de los elementos parecían estar fuera de lugar. Un ejemplo es el del dieciochavo elemento según la masa (después del cloro), el potasio, con masa atómica relativa igual a 39.102, y el diecinonavo elemento, el gas argón, con masa atómica relativa igual a 39.948. El acomodo según la masa pone al potasio en la columna que corresponde a los gases nobles o inertes, y pone a la vez al gas argón con los metales activos, algo contrario a sus propiedades químicas conocidas. Moseley demostró que para que estos elementos pudieran ser acomodados dentro de la línea recta que corresponde a la raíz cuadrada de la frecuencia, √ f graficada contra el número Z, el número Z para el argón tenía que ser 18 y para el potasio tenía que ser 19. Acomodando a los elementos de acuerdo al número Z obtenido de la gráfica de la ley de Moseley y no de acuerdo a su masa produjo una tabla periódica en completo acuerdo con las propiedades físicas y químicas conocidas de los elementos. Por otro lado, antes del trabajo de Moseley, el níquel, cuyo masa atómica es de 58.69, se había anotado en la tabla periódica antes que el cobalto, cuya masa atómica es 58.94, y se creía que los números atómicos del níquel y del cobalto eran 27 y 28, respectivamente. Utilizando sus datos experimentales, Moseley demostró que tanto el ordenamiento como los correspondientes números atómicos deberían invertirse.
2. Este entero Z, el número atómico del elemento, es identificado con el número de unidades positivas de electricidad contenidas en el núcleo atómico.
3. Los números atómicos de todos los elementos del Al al Au han sido tabulados sobre la suposición de que Z para el Al es 13.
4. El orden de los números atómicos es el mismo que el de los pesos atómicos, excepto en donde el último esté en desacuerdo con el orden de las propiedades químicas.
5. Elementos conocidos corresponden con todos los números entre 13 y 79 exceptuando tres. Hay posiblemente tres elementos que aún no han sido descubiertos.
6. La frecuencia de cualquier línea en el espectro de rayos-X es aproximadamente proporcional a A(Z-b)², en donde A y b son constantes.
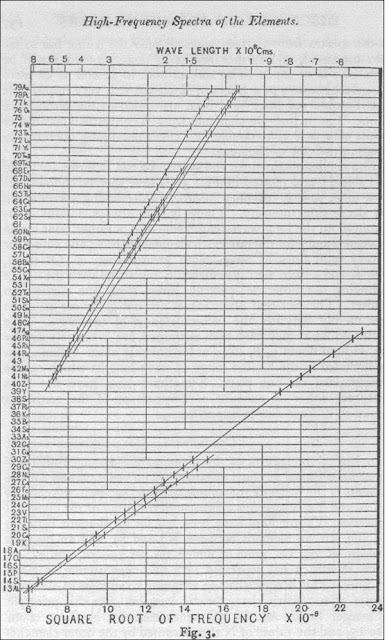
La siguiente imagen es una fotografía del documento original elaborado por el mismo Moseley (la cual puede apreciada mejor ampliándola):
La columna puesta en el lado izquierdo de la gráfica nos muestra, en orden ascendente de abajo hacia arriba de acuerdo con el número atómico Z, cada uno de los elementos con los cuales trabajó Moseley, mientras que la escala horizontal nos muestra la raíz cuadrada de la frecuencia. El conjunto de líneas superiores en la gráfica de Moseley corresponde a la serie de líneas L, mientras que el conjunto de líneas inferiores en la misma gráfica corresponde a la serie de líneas K. Hay dos líneas en el conjunto de líneas inferiores, una de ellas corresponde a Kα mientras que la otra corresponde a Kβ. Obsérvese que mientras que en la línea horizontal inferior de la gráfica (identificada como SQUARE ROOT OF FREQUENCY) leemos la raíz cuadrada de la frecuencia (la cual tenemos que multiplicar por 108 para tener el valor dimensionalmente correcto para cálculos numéricos), en la línea horizontal superior de la gráfica (identificada como WAVE LENGTH) podemos leer la longitud de onda en Angstroms.
PROBLEMA: Obténgase directamente de la gráfica elaborada por Moseley la longitud de onda de la línea Kα del molibdeno cuyo número atómico es Z = 42, y compárse dicho valor con el valor obtenido teóricamente de acuerdo con el modelo de Bohr.
En la gráfica de Moseley, para la línea Kα tenemos que consultar el conjunto de líneas inferiores. Buscando el elemento molibdeno con número atómico Z = 42 en la columna izquierda de la gráfica, y yéndonos hasta toparnos con la línea recta descendemos hacia abajo para leer lo siguiente:
√ f = 20.4×108 √Hertz
La frecuencia de los rayos-X será entonces:
f = 4.161×1018 Hertz
Entonces la longitud de onda para la línea Kα del molibdeno será:
λ = c/f = (3×1018 metros/segundo)/(4.161×1018 Hertz)
λ = 0.721 Å
Este valor compara favorablemente con el valor λ = 0.725 Å obtenido arriba con la ayuda del modelo de Bohr.
PROBLEMA: Obténganse con la ayuda del modelo de Bohr los valores de la constante A en la ley de Moseley para la serie de líneas Kα y la serie de líneas Lα.
De lo que vimos con anterioridad:
siendo nsup y ninf los números cuánticos principales de los estados superior e inferior, y siendo Z* lo que pudiéramos llamar el “número atómico neto” tras haber considerado a (Z-1)e como la “carga neta positiva” que actúa sobre el electrón.
Para las transiciones Kα tenemos nsup = 2 y ninf = 1, con lo cual:
Por otro lado, para las transiciones Lα tenemos nsup = 3 y ninf = 2, con lo cual:
Entonces de esto obtenemos directamente:
AKα = 4.97×107 √Hertz
ALα = 2.14×107 √Hertz
Estos son los valores para la constante A en la ley de Moseley predichos por el modelo de Bohr. En la práctica, los valores de A variarán de un elemento a otro, aunque de cualquier modo la concordancia entre los resultados experimentales y lo que predice el modelo de Bohr es buena.
PROBLEMA: Obténgase el valor experimental de la constante A de la ecuación de Moseley para el calcio para una línea Lα si la línea tiene un valor característico de longitud de onda λ = 30.1 Å.
Despejando para la constante A en la ley de Moseley, obtenemos:
A = √ f /(Z - b)
y puesto que se trata de una línea Lα, el valor que tenemos que usar para la constante b es 7.4
Siendo la longitud de onda λ = 30.1 Å, la raíz cuadrada de la frecuencia será:
√ f = √c/λ = 3.57×108 √Hertz
Entonces, tomando en cuenta que para el calcio su número atómico es Z = 20:
A = (3.57×108 √Hertz)/(20 - 7.4)
A = 2.51×107 √Hertz
PROBLEMA: Obténgase el valor experimental de la constante A de la ecuación de Moseley para el zinc para una línea Lα si la línea tiene un valor característico de longitud de onda λ = 11.2 Å.
El problema procede en forma idéntica al problema anterior, usando la relación:
A = √ f /(Z - b)
y de nueva cuenta, puesto que se trata de una línea Lα, el valor que tenemos que usar para la constante b es 7.4
Siendo la longitud de onda λ = 11.2 Å, la raíz cuadrada de la frecuencia será:
√ f = √c/λ = 5.175×108 √Hertz
Entonces, tomando en cuenta que para el zinc su número atómico es Z = 30:
A = (5.175×108 √Hertz)/(30 - 7.4)
A = 2.29×107 √Hertz
PROBLEMA: Después de llevarse a cabo un experimento en el cual se midieron las líneas Kα, se encontró que para el Cu se obtenía una longitud de onda igual a 1.54 Å, para el Ni se obtenía una longitud de onda igual a 1.66 Å, y para el Fe se obtenía una longitud de onda igual a 1.94 Å. ¿Cuáles serán los números atómicos de estos elementos, suponiendo válida la ley de Moseley?
Para las líneas Kα, la relación de Moseley obtenida arriba es:
√ f = (4.97×107 √Hertz)(Z - 1)
de donde:
Z = 1 + √ f /(4.97×107 √Hertz)
y puesto que f = c/λ se tiene entonces:
Z = 1 + √ c/λ /(4.97×107 √Hertz)
Entonces, de acuerdo a esta relación:
Para el Cu: Z ≈ 29.08 = 29
Para el Ni: Z ≈ 28.04 = 28
Para el Fe: Z ≈ 26.02 = 26
Se mencionará aquí de paso otro tipo de espectroscopía de rayos-X basada en el hecho de que cuando un haz de rayos-X pasa a través de un material, parte de los fotones puede interactuar con los átomos del material ocasionando la absorción de los fotones del haz, siendo la reducción en la intensidad de los rayos-X provocada primordialmente por el efecto fotoeléctrico y por la dispersión de Compton. La intensidad de un haz monocromático (con fotones que constan de una sola longitud de onda) de rayos-X después de que ha penetrado una distancia x en un blanco de cierto material está dada por la siguiente relación:
siendo I0 la intensidad del haz incidente y siendo μ el coeficiente de absorción del material. El coeficiente μ depende tanto de los átomos del blanco como de la energía de los fotones de rayos-X. Supóngase que para un blanco de material dado μ es una función de los rayos-X incidentes. Entonces a medida que la energía crece el coeficiente de absorción μ por el contrario decrece en virtud de que los fotones altamente energéticos son menos aptos para producir fotoelectrones o para sufrir una dispersión de Compton. Este decrecimiento continúa hasta que la energía de los rayos-X es exactamente igual a la energía de uno de los electrones en el blindaje. En ese punto, un mayor número de electrones se vuelve de repente en electrones disponibles para producir emisión fotoeléctrica ocasionando una disminución importante en la intensidad de los rayos-X transmitidos, o lo que es lo mismo, un aumento repentino en el coeficiente de absorción. Este crecimiento brusco en el coeficiente de absorción μ ocurre en las energías de enlace propias de cada uno de los electrones del blindaje, dando como resultado picos de absorción, y la medida de los picos de absorción sirve para determinar las energías de enlace que corresponde a los electrones internos del material bajo estudio.
En la siguiente figura tenemos una gráfica que nos muestra el aumento en el coeficiente de absorción μ para tres valores de energía de los fotones de rayos-X utilizados:
Como es de esperarse, el pico de absorción K que corresponde a la capa K del átomo está a la derecha del pico de absorción L que corresponde a la capa L en virtud de que un fotón de rayos-X requiere de más energía para interactuar con los electrones de la capa K que es la más cercana al núcleo que para llegar hasta la capa L para interactuar con los electrones de dicha capa.
Observando más de cerca un espectro de rayos-X con la ayuda de un espectógrafo de buena resolución, se descubre que con excepción del pico de absorción K cada pico de absorción consta en realidad de un número de picos muy unidos que corresponden a lo que llamamos la estructura fina de los niveles de energía, como se muestra en la siguiente gráfica que nos muestra los “sub-picos” que corresponden a un pico de absorción L típico:
En la siguiente figura tenemos un ejemplo de la aplicación de la espectroscopía por absorción de rayos-X (XAS, por sus siglas en inglés) en donde un material que consta de tres capas de metales (cobre en la superficie exterior, hierro en la parte media, y níquel en la capa interior) es impactado por fotones de rayos-X, los cuales atraviesan cada uno de los metales dejando su rastro en los picos de absorción propios de cada metal:
La espectrocopía de rayos-X ha sido ampliamente refinada, contándose el día de hoy con técnicas sofisticadas tales como la espectroscopía XANES (X-ray Absorption Near Edge Structure) también conocida como NEXAFS (Near Edge X-ray Absorption Fine Structure).
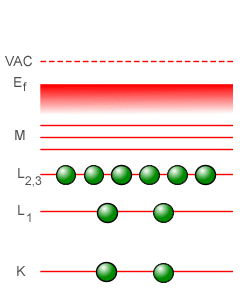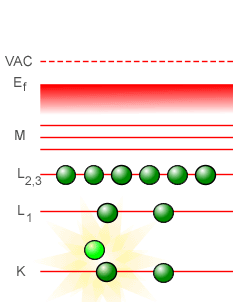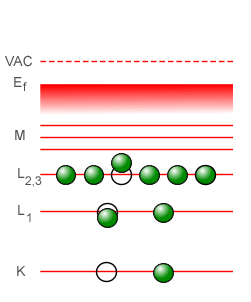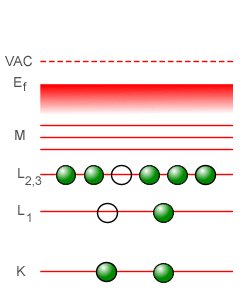
Un efecto interesante que suele encontrarse en la espectroscopía de rayos-X es el efecto Auger, así llamado en memoria del físico francés Pierre Victor Auger, aunque la física Lise Meitner descubrió en forma independiente el mismo efecto unos años antes que Auger, en 1922. El efecto Auger se basa en que es posible que un fotón de rayos-X emitido por una transición interna dentro de un átomo sea absorbido por un electrón del mismo átomo, produciendo la expulsión del electrón. De este modo, los átomos excitados en su interior en vez de producir fotones de rayos-X echados hacia el exterior lo que producen son electrones. Los fotoelectrones producidos por estas conversiones internas de rayos-X son denominados electrones Auger. A continuación tenemos un gráfico animado que nos muestra los pasos sucesivos que tienen lugar para la producción de un electrón Auger, en donde podemos ver que (1) un electrón de alta energía que proviene del vacío exterior al átomo (VAC) impacta a un electrón en la capa K, expulsándolo por completo fuera del átomo, (2) un electrón de la capa L1 desciende para llenar el hueco que hay en la capa K, (3) al caer el electrón de la capa L1 a la capa K se genera un fotón de rayos-X que sólo llega hasta otra capa superior en donde le dá a un electrón de dicha capa la energía suficiente para ser expulsado fuera del átomo. El fotón de rayos-X interno nunca se llega a ver, porque es creado y destruído dentro del mismo átomo. Lo que se detecta es el electrón Auger expulsado del átomo.
El fenómeno de los electrones Auger tiene su propia aplicación importante, que es la espectroscopía de electrones Auger, una técnica analítica común utilizada en el estudio de las superficies, en el área de la ciencia de los materiales.
PROBLEMA: Se encuentra en un experimento que la energía cinética de un electrón Auger emitido por una línea Kα de rayos-X de la capa L es de 10 keV, teniendo el material un pico de absorción K con una longitud de onda igual a 0.84 Å. Encuéntrese la energía de la línea Kα de rayos-X, así como la longitud de onda del pico de absorción L que corresponde al material utilizado.
El fotón interno de rayos-X debe tener la energía suficiente no sólo para llevar al electrón Auger desde el nivel energético EL -correspondiente a la capa L- hasta el nivel energético E = 0 sino además proporcionarle una energía cinética de 10 keV.
Si el pico de absorción K tiene una longitud de onda λK = 0.84 Å, entonces el nivel energético de la capa K debe ser:
EK = - hc/λK
EK = - (12.4 keV·Å)/(0.84 Å)
EK = - 14.76 keV
Desde el punto de vista de un diagrama de niveles, la situación que tenemos es la siguiente:
La energía Ee con la que sale fuera del átomo el electrón Auger desde la capa L debe ser igual a la diferencia de energías entre las capas L y K, que es a su vez la energía del fotón interno de rayos-X que provoca la expulsión del electrón. Entonces, usando como guía el diagrama de niveles (es importante aquí tomar en cuenta los signos de las energías), podemos asentar lo siguiente:
Ee - EL = EL - EK
EL = (Ee + EK)/2
EL = (10 keV - 14.76 keV)/2
EL = - 2.38 keV
Entonces la energía de la línea Kα de rayos-X que es igual a la diferencia de energía entre las capas K y L deberá ser:
ΔE = EL - EK
ΔE = - 2.38 keV- (- 14.76 keV)
ΔE = 12.38 keV
Y la longitud de onda del pico de absorción L deberá ser:
λL = hc/|EK|
λL = (12.4 keV·Å)/(2.38 keV)
λL = 5.21 Å
De este modo, como lo hemos visto arriba, el modelo atómico planetario de Bohr, un modelo semi-clásico basado en una combinación heurística de reglas clásicas y reglas cuánticas, sirvió para dar también una explicación teórica a la tabla periódica de los elementos con la ayuda de la espectroscopía de rayos-X. Pero esto ultimadamente no fue suficiente, y se requería con urgencia un modelo nuevo que pudiera solventar por lo menos algunas de las deficiencias y las omisiones del modelo atómico planetario de Bohr, algo que pudiera explicar entre otras cosas esas líneas de estructura fina observadas no sólo en los espectros de rayos-X sino inclusive en los espectros ópticos. Y tal modelo no tardaría mucho tiempo en llegar.