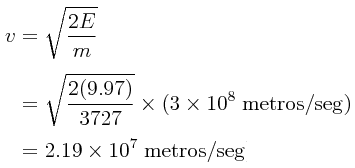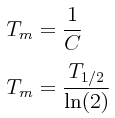Un ejemplo relativamente elemental que ilustra el uso del método de aproximación WKB consiste en tomar el caso de una partícula rebotando elásticamente dentro de una caja de paredes rígidas (o lo que es lo mismo, una partícula atrapada en un pozo de potencial con paredes infinitamente altas). Supondremos que dentro del pozo de potencial de anchura a, en lugar de ser el potencial V un potencial constante supondremos que se trata de un potencial V(x) que varía de alguna manera indeterminada con la posición:
Dentro del pozo de potencial, suponiendo que la energía E de la partícula es mayor que el potencial V(x), entonces de acuerdo a lo que hemos visto previamente la función de onda ψ(x) al ser aproximada mediante una aproximación WKB puede constar de dos soluciones, pudiendo ser representada de la siguiente manera:
Otra manera convencional de escribir la función de onda anterior es la siguiente:
Como lo vimos previamente, la aproximación WKB puede ser escrita más convenientemente en términos reales como:
en donde, en conformidad con lo obtenido previamente bajo el método WKB y usando la libertad que tenemos para asignar un límite inferior a la integral indefinida le podemos asignar el cero que corresponde al origen del sistema de coordenadas mostrado en la figura:
Una cosa de la que podemos estar absolutamente seguros es que la función de onda ψ(x) debe ser igual a cero justo en el borde de la pared en donde está el origen del sistema de coordenadas, la cual suponemos que corresponde a un potencial infinitamente grande, y puesto que φ(0).=.0 entonces se debe tener entonces que c1.=.0. Del mismo modo, la función de onda ψ(x) debe ser igual a cero justo en el borde de la pared contraria, o sea en x.=.a, de modo tal que:
Se concluye entonces que:
Esta condición de cuantización es nuestro principal resultado. Aunque resulta tentador confundirla con la condición de cuantización Bohr-Sommerfeld, hay que recordar que aquella condición de cuantización corresponde a la Mecánica Cuántica “vieja”, y en ella la integral es una integral que se lleva a cabo sobre una trayectoria cerrada (a diferencia del resultado que hemos obtenido en el que la integral se lleva a cabo sobre una trayectoria abierta). Lo que hemos obtenido aquí es lo más importante de carácter general que se puede obtener de la aproximación WKB para una partícula atrapada en un pozo de potencial con paredes infinitamente altas. No podemos continuar a menos de que se especifique alguna función potencial V(x) entre las paredes del pozo. La función más sencilla posible es la de una partícula atrapada en un pozo de potencial constante. En tal caso, el fondo del pozo de potencial es un “piso plano” correspondiendo un potencial constante V(x).=.0, y entonces p(x).=.√2mE (el momentum de la partícula es constante), con lo que de lo anterior se deduce de inmediato:
Estos son precisamente los niveles de energía discretos que ya hemos obtenido previamente para una partícula atrapada en un pozo de potencial con paredes infinitamente altas. En este caso, la aproximación WKB proporciona una conclusión exacta.
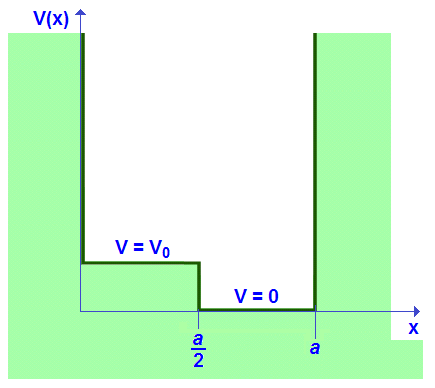
Un problema un poco más interesante que justifique el recurrir al método de aproximación WKB es aquél en el cual tenemos un pozo de potencial con un peldaño escalonado como lo muestra la siguiente figura:
Para efectuar la solución de este problema con un potencial escalonado en el interior, usaremos los potenciales mostrados en la figura de arriba. La aplicación de la aproximación WKB obtenida arriba es métodica y directa, empezando con los siguientes pasos;
Elevando al cuadrado ambos lados de la última igualdad, se tiene:
Obsérvese que hemos usado la simbolización En(0) para compactar un poco lo que tenemos en el lado derecho de la igualdad, siendo:
los niveles discretos de energía que corresponden a un pozo de potencial con el piso “plano. De este modo, se tiene algo que puede ser manejado recurriendo nuevamente a una elevación al cuadrado:
Finalmente, simplificando un poco más llegamos a la expresión final para los niveles discretos de energía que puede tener una partícula dentro de un pozo de potencial de esta índole:
Un problema de un pozo de potencial con paredes infinitamente grandes que puede ser un poco más interesante es aquél en el cual el potencial en el interior del pozo realmente exhibe una variación continua, que es a fin de cuentas para el tipo de situaciones para las cuales fue concebida la aproximación WKB. La aproximación general WKB obtenida arriba para un pozo de potencial con potencial variable V(x) puede ser usada para un pozo de potencial como el siguiente que exhibe una variación linear dentro del mismo:
En el pozo de potencial mostrado arriba, el potencial V(x) aumenta linearmente, pudiendo ser modelado con una fórmula como:
siendo w la pendiente de la recta y C una constante. Si colocamos el sistema de coordenadas de modo tal que el origen del sistema de coordenadas coincida con el vértice inferior del pozo de potencial (como se muestra la figura) de forma tal que la línea recta V(x) pasa por el origen del sistema de coordenadas, entonces la constante C es igual a cero, o sea:
Entonces la descripción matemática del momentum p(x) dentro del pozo de potencial es:
Usando nuevamente, para este caso, la condición de cuantización para un pozo de potencial obtenida arriba con la aproximación WKB, se tiene entonces lo siguiente:
La integral se puede resolver fácilmente mediante una substitución de variables:
De este modo:
Por lo tanto:
La simplificación de esto último procede en forma casi idéntica a la simplificación llevada a cabo arriba, recurriendo al recurso de elevar al cuadrado, despejar y elevar nuevamente al cuadrado, para poder deshacernos de los exponentes fraccionarios. Podemos meter aquí también en el desarrollo la simbolización:
que usamos arriba. Los destalles restantes son semejantes aunque no idénticos a lo que ya resolvimos arriba.
Habiendo visto la manera en la cual se utiliza la aproximación WKB para el análisis de pozos de potencial con paredes infinitamente altas, el siguiente paso natural consiste en explorar el uso de la técnica en otras situaciones algo diferentes. Lo primero que se nos puede venir a la mente es buscar una aproximación WKB para probarla en el caso del oscilador armónico simple, modificando tras esto el potencial del oscilador de modo tal que ya no sea algo tan simple. Pero es aquí en donde enfrentamos una situación que se antoja complicada. En efecto, repasando la estructura general de la aproximación WKB, podemos ver que todos los procedimientos de aproximación WKB tienen en el denominador la cantidad √p(x), lo cual no representa ningún obstáculo mientras el potencial tenga un valor real. Para una partícula atrapada dentro de una caja rebotando elásticamente, el momentum jamás tiene un valor igual a cero ya que la partícula está moviéndose siempre hacia la derecha (la mitad del tiempo) o hacia la izquierda (la otra mitad del tiempo). ¿Pero qué sucede si por la naturaleza del potencial V(x) se permite que la partícula se vaya desacelerando paulatinamente hasta tener un valor igual a cero? Pues lo que se tiene entonces en la aproximación WKB es una división por cero al tomar el denominador el valor de cero. Esta es precisamente una de las razones por las cuales muchos textos y tratados que hablan de la aproximación WKB representan la integral con el límite inferior ausente, lo cual sirve de recordatorio de que en uno de los límites de la integración podemos tener una situación que amenaza con salirse fuera de control. Esto no significa que una situación así no sea manejable, se le puede dar la vuelta al asunto usando funciones ψ(x) de “unión” que permitan “pegar” dos segmentos diferentes de la función de onda que corresponden a regiones distintas, quizá una función ψ(x) linear. Esto implica que además de requerirse dos funciones de onda ψ(x) distintas para poder describir el comportamiento en regiones contiguas, se requiere una tercera función de onda en la zona de transición para poder “pegarlas”. Al hablar de tres funciones de onda matemáticamente distintas que supuestamente representan a la misma función de onda ψ(x), esto quizá no sea algo tan agradable como el tener una sola expresión matemática que representa una sola función de onda en todo el espacio. Sin embargo, nos vemos forzados a llevar a cabo tales fracturas en la función de onda porque en muchas situaciones no hay una solución analítica exacta (en forma cerrada) para una partícula que pasa de una región a otra; tenemos que conformarnos con aproximaciones, y ello implica muchas veces el tener que fracturar a la función de onda definiéndola de distinta manera para regiones distintas.
Veamos nuevamente el caso del oscilador armónico simple, cuyo potencial es parabólico, desde la perspectiva de la aproximación WKB, suponiendo que la energía de la partícula es E:
Tanto en -a como en +a, la partícula se desacelera y el momentum p(x) toma el valor de cero al invertir el sentido de su movimiento al tocar esos puntos de volteo (en literatura técnica inglesa, se les conoce como turning points). La aproximación WKB en este caso tiene que ser manejada de modo tal que la presencia de una división por cero en el denominador pueda ser esquivada de alguna manera.
Irónicamente, resulta menos problemático manejar una situación en la cual el momentum p(x) pueda tomar un valor imaginario. Hasta este punto, hemos supuesto que la energía E de la partícula es mayor que el potencial V, con lo cual p(x) es real. Pero igualmente podemos escribir la aproximación WKB para una región no-clásica en la cual la energía de la partícula es menor que el potencial, en cuyo caso p(x) se vuelve imaginario, en cuyo caso la fórmula general WKB corregida toma la siguiente forma:
Una situación en la cual esto tiene una aplicación inmediata es aquella en la cual se tiene una barrera de potencial con una altura finita pero variable entre los extremos de la barrera de acuerdo a una función aún no especificada V(x). Ya hemos visto algo de este tipo de problema en la serie de entradas “Transmisión y reflexión de partículas”. En estos problemas el espacio se puede seguir subdividir en tres regiones como se muestra a continuación, con una región situada hacia la izquierda de la barrera en donde el potencial se mantiene constante, otra región a la derecha de la barrera en donde el potencial también se mantiene constante, y una región intermedia en la cual el potencial varía de acuerdo a alguna función V(x):
Puesto que la energía E del haz de partículas (mostrada en color magenta) es inferior en todo momento al potencial (indeterminado) V(x) mostrado en la figura, la región 2 es una región no-clásica, y lo que ocurre en la región 2, en efecto, no puede ser otra cosa más que un tunelaje a través de la barrera de potencial que clásicamente no sería posible, porque clásicamente ninguna partícula con cierta energía E puede subir encima de un potencial V(x) cuya energía sea mayor que E. Obsérvese que el potencial de carácter general que se ha dibujado en la región 2 no se supone ya como un potencial constante y “plano” como lo habíamos supuesto al llevar a cabo nuestro estudio de transmisión y reflexión de partículas. Para la región 1, podemos escribir la función de onda de la siguiente manera:
En lo que toca a la región 3, la función de onda se puede expresar del siguiente modo:
En el análisis de la transmisión y reflexión de partículas, se definió de la siguiente manera un coeficiente de transmisión T que nos proporciona la probabilidad de que una cierta cantidad de partículas que incide desde la izquierda (región 1) puedan atravesar la barrera saliendo hacia la derecha (región 3):
Falta por ver la forma en la cual manejaremos la región intermedia, la región 2. Es aquí en donde entra la aproximación WKB inicialmente por partida doble, para especificar las partículas dentro de la barrera de potencial que se están moviendo hacia la izquierda, y para especificar las partículas que se están moviendo hacia la derecha. La aproximación WKB para la región 2 la escribimos inicialmente por lo tanto como una combinación de dos términos:
Si la barrera de potencial es muy alta o muy ancha, la probabilidad de tunelaje es muy pequeña, y en tal caso el coeficiente C del término exponencialmente creciente puede tomarse como cero. Y la función de onda en la región intermedia debe tener un aspecto como el que se muestra a continuación, con una caída exponencial (se ha sobrepuesto a la función de onda un potencial como el que puede producir el tipo de barrera que se muestra en la figura, y es de hecho un potencial Coulómbico):
De este modo, las amplitudes relativas de las ondas incidente y transmitida están determinadas básicamente por la caída total del exponencial sobre la región no-clásica:
De este modo:
en donde:
Una aplicación inmediata al resultado obtenido con la aproximación WKB se tiene especificando el potencial V(x) en la parte superior de la barrera como un potencial plano de magnitud V0:
En esta situación, la aproximación WKB especifica que dentro de la barrera de potencial:
De este modo, el exponente γ está dado por:
Con esto, el coeficiente de transmisión T que nos dá la probabilidad de que una partícula pueda atravesar la barrera de potencial viene siendo aproximadamente:
La solución exacta para este tipo de problema, en base a la metodología de desarrollo dada en la serie de entradas “Transmisión y reflexión de partículas”, y sin recurrir a ningún tipo de aproximación, es la siguiente:
Por la derivación dada previamente, la aproximación WKB supone que la probabilidad de tunelaje a través de la barrera es pequeña, lo cual solo se cumple si el exponente γ es grande. Siendo así, podemos dar las siguientes simplificaciones al seno hiperbólico que aparece en la solución exacta:
De este modo, el resultado exacto se reduce a:
El coeficiente entre los paréntesis cuadrados está en el orden de la unidad, la preponderancia dominante de E se encuentra por lo tanto en el factor exponencial. En tal caso, el resultado exacto se reduce a la misma expresión obtenida mediante la aproximación WKB.
Lo que hemos visto arriba nos permite darle una justificación desde el punto de vista de la Mecánica Ondulatoria a un fenómeno importante, el fenómeno de la radioactividad natural, cuya explicación teórica era un misterio hasta el advenimiento de la Mecánica Cuántica. Fue en 1928 cuando a George Gamow (e independientemente Edward Condon y Ronald Wilfred Gurney en su trabajo “Quantum Mechanics and Radioactive Disintegration” publicado en el volumen 122 de la revista Nature en 1928) se le ocurrió darle una explicación al fenómeno apoyado en el efecto del tunelaje cuántico. El decaimiento alfa, la emisión espontánea de una partícula alfa (α) de ciertos núcleos radioactivos, puede ser analizado considerando que la partícula-α formada por dos protones y dos neutrones es portadora de una carga eléctrica positiva 2e, la cual es repelida por el núcleo atómico residual con carga Ze en cuanto la partícula-α se pueda alejar lo suficiente como para escapar de la fuerza nuclear que la liga al núcleo. Gamow imaginó a la curva de energía potencial para la partícula-α como un pozo de potencial rectangular finito (representando a la fuerza atractiva nuclear) extendiéndose hacia el radio del núcleo que simbolizaremos aquí como r1, unido a la cola de un potencial Coulómbico repulsivo. Esquemáticamente, para el polonio-212 con número atómico 84, la gráfica energética de los potenciales (hacia ambos lados del núcleo atómico) mostrando el decaimiento radioactivo es la siguiente (obsérvese la similitud de la función de onda con la función de onda dibujada arriba; tómese en cuenta que en realidad este es un problema tridimensional que estamos simplificando aquí considerándolo unidimensional):
Clásicamente, no es posible que una partícula cuya energía es E pueda pasar a través de una barrera de potencial V(r) cuyo pico es mayor que la energía de la partícula. Sin embargo, la Mecánica Ondulatoria se encarga de hacer posible lo imposible, y siempre hay una posibilidad pequeña de que la partícula “perfore” la barrera de potencial. Resulta evidente que hay tres regiones al igual que como en el caso general que acabamos de describir arriba en la derivación de la aproximación WKB para esta situación, una región 1 de color verde (clásica) que va de cero a r1, otra región 2 intermedia de color dorado (no-clásica) que va de r1 a r2, y una región 3 de color verde (clásica) que va desde r2 hasta el infinito.
Si la energía de la partícula-α emitida es E, el punto de volteo exterior en r2 fija la energía potencial de la partícula como (en el sistema de unidades MKS-SI):
El exponente γ obtenido en la relación WKB de arriba puede ser evaluado de la manera siguiente (para llevar a cabo la integración es necesario recurrir a una substitución de variables; obsérvese además en la figura que en este caso el potencial no cae a cero en ambos lados de la barrera tanto en r1 como en r2, aunque esto no altera las conclusiones finales):
En virtud de que el núcleo atómico es muy pequeño, podemos tomar la aproximación de índole física r1.«.r2 con lo cual podemos despreciar el segundo término. Por otro lado, el argumento del coseno inverso es algo cercano a cero, de modo tal que el ángulo que le sirve de argumento tiene un valor cercano a π/2. Si llamamos a este ángulo θ, podemos entonces hacer lo siguiente:
Se tiene entonces que:
Por lo tanto:
Se deduce entonces que el valor del exponente γ está dado por la relación:
siendo las constantes C1 y C2:
Yéndonos de nueva cuenta al aspecto físico del asunto, podemos imaginarnos a la partícula-α agitándose sin cesar dentro del núcleo con una velocidad promedio v, siendo el tiempo promedio t de las colisiones internas con la pared del núcleo igual a 2r1/v, con lo cual la frecuencia de las colisiones es igual a v/2r1, (el recíproco). La probabilidad de escape en cada colisión es:
de modo tal que la probabilidad de emisión de una partícula-α desde el núcleo atómico por unidad de tiempo debe ser:
Por lo tanto, la vida media τ del núcleo radioactivo progenitor debe ser:
En el dibujo dado arriba para esquematizar la función de onda ψ(r) en las tres regiones requeridas para poder dar una explicación al fenómeno del decaimiento radioactivo, se tomó como ejemplo el isótopo 212 del polonio. Resulta instructivo llevar a cabo algunas evaluaciones numéricas para estimar lo cerca que está o lo lejos que está el modelo en predecir las vidas medias de los elementos radioactivos. De acuerdo con los datos experimentales más recientes que se tienen, el isótopo 212 del polonio tiene una vida media τ de:
τ ≈ 0.5 microsegundos
En los cálculos que llevaremos a cabo usaremos el hecho de que la densidad nuclear es más o menos constante de elemento a elemento, dependiendo por lo tanto el radio del núcleo atómico del número total de nucleones (protones y neutrones) que a su vez se ve reflejado en la masa atómica A de cada elemento, y supondremos también que el núcleo atómico tiene una forma aproximadamente esférica. Siendo el volumen de la esfera:
entonces nuestras suposiciones equivalen a afirmar que el cubo del radio del núcleo es proporcional a la masa atómica A del elemento:
De las anteriores consideraciones deriva la siguiente fórmula para el radio del núcleo atómico de un elemento de masa A (tomaremos el radio del núcleo como r1 para hacerlo concordar con la figura de arriba):
siendo R0 una constante que tiene que ser determinada experimentalmente a partir de la densidad medida para la materia nuclear, y la cual resulta ser:
De este modo, se tiene la fórmula:
Si se comparan los datos experimentales y los datos teóricos para el radio calculado de un núcleo atómico, se llega a la conclusión de que hay una zona alrededor de la orilla del núcleo en donde la densidad nuclear ρn cae a cero aunque no ocurriendo de un modo brusco (con una caída vertical), aunque de cualquier modo la parte interior de la esfera nuclear parece tener una densidad constante. En pocas palabras, no podemos pensar en la superficie del núcleo atómico como si fuese una capa sólida bien definida, y es probable que se tenga algo como lo siguiente:
Al llevarse a cabo la desintegración radioactiva del polonio 84Po212 por decaimiento-α, el elemento residual es el plomo 82Pb208, de modo tal que la reacción de decaimiento es la siguiente (en un decaimiento-α el núcleo progenitor pierde dos protones y dos neutrones, y por lo tanto su número atómico Z disminuye en dos unidades y su número de masa A disminuye en cuatro unidades):
84Po212 → 82Pb208 + 2He4
Con la fórmula dada arriba, podemos estimar el radio nuclear del átomo de polonio 84Po212:
En el balance energético de un decaimiento α, tenemos que tomar en cuenta los efectos de índole relativista. La energía de desintegración ΔE con la cual sale expulsada la partícula α del núcleo está dada por el balance energético de acuerdo a la fórmula de Einstein para la conversión de una masa a su equivalente en energía:
en donde el primer término tiene en mp a la masa del núcleo progenitor, el segundo término tiene en mh a la masa del núcleo hijo residual después del decaimiento, y el tercer término tiene la masa de la partícula α, ecuación que para el caso presente viene quedando como:
La masa atómica de la partícula α así como las masas atómicas del polonio y del torio son, respectivamente (en unidades de masa atómica u.m.a.):
mα = 4.001506179125 u.m.a.
mPo = 211.9888680 u.m.a.
mPb = 207.9766521 u.m.a.
Entonces la energía de una partícula α expulsada por el decaimiento del isótopo 212 del polonio será (en la figura de arriba se ha dibujado una partícula con una energía de 8.95 MeV):
ΔE = (211.9888680 - 207.9766521 - 4.001506179125) (931 MeV)
ΔE = 9.97 MeV
De este modo, y aunque la idea no parezca tener mucho sentido, podemos estimar una velocidad promedio para una partícula α al estar rebotando dentro del núcleo atómico:
Así, estamos en condiciones de poder estimar primero el factor γ que obtuvimos arriba para el tiempo de vida media τ del núcleo radioactivo progenitor con la fórmula:
Usando valores:
De este modo, la vida media τ para la desintegración radioactiva del polonio-212 viene siendo:
Si constrastamos el resultado obtenido con la vida media del isótopo 212 del polonio dada arriba de 0.5 microsegundos, el cálculo teórico ciertamente deja mucho que desear al estar fuera en dos órdenes de magnitud, lo cual es indicativo de que el modelo empleado es algo simplista y tiene que ser refinado. En el caso importante de la desintegración espontánea por decaimiento-α del uranio 92U238 que tras la expulsión de una partícula alfa termina convertido en torio:
92U238 → 90Th234 + 2He4
las masas atómicas son:
mα = 4.001506179125 u.m.a.
mU = 238.0507882 u.m.a.
mTh = 234.04360 u.m.a.
Entonces la energía de desintegración ΔE que será llevada por una partícula α al expulsada del isótopo 238 del uranio será:
ΔE = (238.0507882 - 234.04360 - 4.001506179125) (931 MeV)
ΔE = 5.2899 MeV
Por otro lado, podemos estimar el radio nuclear del átomo de uranio 92U238 como sigue:
Una estimación de la velocidad promedio para una partícula α al estar rebotando dentro del núcleo atómico es entonces:
En este caso, la estimación del factor γ produce el siguiente resultado:
De este modo, la vida media τ para la desintegración radioactiva del uranio-238 viene siendo:
Nuevamente, encontramos que para el decaimiento radioactivo del uranio 92U238 el resultado predicho teóricamente también deja mucho que desear en comparación con el resultado obtenido experimentalmente de 6.×.109 años, aunque de cualquier modo hay una concordancia importante entre los cálculos teóricos y los resultados experimentales: la aproximación WKB arroja una amplia distancia de separación temporal en las vidas medias del 84Po212 y del 92U238, situando al 84Po212 en el lado bajo y al 92U238 en el lado alto, confirmando además la extraordinaria sensibilidad de la vida media τ a las masas nucleares, ya que un cambio pequeño en la energía de desintegración ΔE provocará cambios enormes en el tiempo de vida media τ que pueden ir desde los microsegundos incluso hasta los millones de años.
Ya que el uso de la aproximación WKB para entender el fenómeno de la radioactividad natural nos ha llevado a una revisión de los procesos de decaimiento, esta es una oportunidad excelente para darle un repaso rápido al tema del decaimiento de núcleos inestables.
En un decaimiento radioactivo, un núcleo inicialmente inestable denominado padre emite una partícula y decae en un núcleo denominado hijo; el nacimiento del hijo se ocasiona por la muerte del padre. El hijo puede ser el mismo núcleo en un estado de energía más bajo, como en el caso del decaimiento γ, o un núcleo completamente nuevo, como ocurre en los decaimientos α y β. Todos los núcleos siguen la misma ley de decaimiento radioactivo, sin importar qué tipo de partículas sean emitidas. Si inicialmente hay N0 núcleos padres inestables, el número N de padres que quedan después de un tiempo t es:
La constante C se denomina constante de decaimiento o constante de desintegración y depende del proceso particular de decaimiento. Esta ecuación es una ley estadística (como todo lo que tiene que ver con la Mecánica Cuántica basado en conceptos probabilistas) y no determinista que da el número esperado de padres que sobreviven después de un tiempo t. Sin embargo, si N0 no es muy grande (como ocurre en la práctica), el número presente de supervivientes y el número esperado casi siempre difieren en una fracción muy insignificativa de N0.
PROBLEMA: Deducir la ley de decaimiento radioactivo.
Partimos del supuesto estadístico de carácter general de que el número de núcleos dN que decaen en un intervalo de tiempo dt será proporcional a ese intervalo de tiempo y al número de núcleos presentes, lo cual expresado simbólicamente:
donde el signo menos se introduce debido a que N decrece. Podemos expresar la proporcionalidad como una igualdad metiendo una constante de proporcionalidad C, la constante de decaimiento:
Integrando:
La rapidez de decaimiento de una muestra radioactiva se mide generalmente por la vida media T1/2, definida como el intervalo en el cual el número de núcleos padres N se reduce a la mitad. La vida media se obtiene de lo anterior en términos de la constante de decaimiento C haciendo N igual a N0/2:
Así, con N0 núcleos inicialmente, a cabo de un tiempo T1/2 quedarían N0 /2 núcleos, después de un tiempo 2T1/2 quedarían N0 /4 núcleos, y así sucesivamente.
PROBLEMA: ¿A qué distancia en el espacio libre se reduce a la mitad la intensidad de un haz de neutrones de 5 eV? Tómese la vida media de los neutrones libres igual a 12.8 minutos.
La velocidad de los neutrones en el haz se encuentra a partir de:
Usando valores numéricos y trabajando dentro del sistema MKS-SI:
Durante un tiempo T1/2.=.12.8 minutos, la mitad de los neutrones del haz habrá decaido. La distancia recorrida por los neutrones que no han decaído durante este tiempo es:
Este valor corresponde aproximadamente a dos diámetros terrestres.
Otra cantidad que mide la rapidez con que una muestra decae es el promedio o tiempo de vida medio de un núcleo, dado por:
PROBLEMA: Obténgase la expresión para el tiempo de vida promedio de un núcleo radioactivo.
Si inicialmente la muestra tiene N0 núcleos, el tiempo de vida promedio Tm para obtener cero núcleos está dado por:
A partir de la ley de decaimiento exponencial:
se obtiene:
y los límites N0 y 0 varían con t entre 0 y ∞. Así:
Una aplicación práctica del estudio del fenómeno de la radioactividad consiste en la determinación de las edades de fósiles o restos de organismos vivientes que perecieron hace ya algún tiempo, en lo que es conocido como el método del carbono-14 para datación por radiocarbono. La determinación de la vida media del carbono radioactivo 6C14 sugiere que este tiene un valor de 5.57.×.103 años. El 6C14 se produce constantemente en la atmósfera superior debido a la interacción de los rayos cósmicos con el aire. Este carbono radioactivo se mezcla con el carbono no radioactivo que en forma de anídrido carbónico (CO2) se encuentra en el aire. La velocidad de producción del 6C14 a partir de rayos cósmicos es igual a su velocidad de desintegración; consecuentemente, se mantiene en el aire una determinada concentración de 6C14. El carbono del aire (como anhídrido carbónico) se disuelve en el agua que hay en la tierra y también es utilizado por los seres vegetales y, subsecuentemente, por los seres animales. Por esta razón, todos los seres vivientes tienen el mismo contenido de 6C14 que el aire en el cual viven. A partir del momento en que un ser viviente perece, deja de tomar del medio ambiente este carbono radioactivo, empezando a disminuír la concentración de 6C14 en el cuerpo muerto a causa del fenómeno de la radioactividad natural. Esta disminución proporciona la clave para poder llevar a cabo la datación por radiocarbono.
PROBLEMA: El carbono extraído del marco de la puerta de una casa construida en la época de Hammurabi de Babilonia tiene una actividad de 9.3 desintegraciones por minuto y por gramo de carbono. Si la casa se construyó inmediatamente después de haberse cortado (matado) el árbol del cual se obtuvo la madera para el marco de la puerta, ¿podríamos determinar cuándo vivió Hammurabi?
Primero que nada, sabiendo que la vida media T1/2 del carbono radioactivo 6C14 tiene un valor de 5.57.×.103 años, tenemos que determinar la constante de desintegración o constante de decaimiento del 6C14, lo cual se lleva a cabo de la siguiente manera:
Recurriendo a la ley estadística del decaimiento radioactivo, se tiene entonces que:
Usamos el valor de la constante de desintegración C obtenida arriba para el 6C14:
Situados en el año 2010, todo parece indicar que Hammurabi vivió y murió aproximadamente en 2,000 A. de C.
Otra definición ampliamente usada es la que se conoce como la actividad de una muestra radioactiva, definida de la siguiente manera:
La unidad de medida de la rapidez de desintegración o actividad es el curie, en memoria de la investigadora Marie Curie que fue pionera en la investigación de fenómenos, definido como:
1 curie = 3.700 × 1010 desintegraciones/segundo
PROBLEMA: ¿Cuál es la actividad de un gramo de 88Ra226, cuya vida media es de 1,622 años?
El número de átomos en un gramo de radio es:
N = (1 gr)(1 gramo-mol/226 gramos)(6.02×1023 átomos-gramo/gramo-mol)
N = 2.666×1021 átomos
La constante de decaimiento se relaciona con la vida media así:
C = 0.693/T1/2
C = (0.693/1,622 años)(1 año/365 días)(1 día/8.64×104 segundos)
C = 1.355×10-11/segundo
La actividad se encuentra a partir de:
actividad = CN
actividad = (1.355×10-11/segundo)(2.666×1021 átomos)
actividad = 3.612×1010 desintegraciones/segundo
El resultado obtenido es aproximadamente igual a 1 curie, lo cual no es ninguna coincidencia, ya que precisamente de este modo se obtuvo la definición del curie.
Una pregunta central es, desde luego, ¿qué relación hay entre la vida media τ obtenida con la aproximación WKB para un decaimiento-α, predicha teóricamente en base a las masas y las energías, y el tiempo de vida media T1/2 de naturaleza estadística general con la constante C de decaimiento determinada experimentalmente? ¿Son lo mismo?
El análisis que se ha llevado a cabo arriba del fenómeno del tunelaje cuántico para explicar el decaimiento alfa de núcleos radioactivos se enfocó exclusivamente en el uso de la aproximación WKB en la región intermedia comprendida entre r1 y r2, sin hacerse esfuerzo alguno por definir una función de onda que abarque las tres regiones, esto es, definiendo con la ayuda de la aproximación WKB la forma de la función de onda ψ(r) en las regiones 1 y 3, definiendo además las tres funciones de onda de tal manera que el paso de la función de onda ψ(r) de una región a otra sea suave y continua, lo cual requiere “pegar” las tres regiones. Hay claramente dos junturas (la capa entre la región 1 y la región 2, así como la capa entre la región 2 y la región 3) que requiere en los dos casos el tener que “pegar” una región clásica a una región no-clásica. Muchos problemas analizables mediante la aproximación WKB son problemas de esta índole. Volveremos a analizar posteriormente en la siguiente entrada de una manera un poco más sofisticada con el método de aproximación WKB el problema del decaimiento de partículas-α por expulsión de un núcleo radioactivo en cuanto tengamos una mayor familiaridad con el asunto de tener que estar “pegando” regiones clásicas con regiones no-clásicas, definiendo la función de onda ψ(r) en las tres regiones. Y nos encontraremos con que, aún en los casos más sencillos, se requerirá del uso de funciones matemáticas tales como las funciones de Bessel y las funciones de Airy. Este es el precio que se tiene que pagar para poder seguir adelante, ¡y recuérdese que ni siquiera estamos procurando obtener soluciones analíticas exactas en forma cerrada, tenemos que conformarnos con lo que podamos extraer mediante aproximaciones tales como la aproximación WKB!
PROBLEMA: Supóngase que una partícula libre moviéndose en una dimensión está sujeta a una fuerza constante derivable de un potencial que está dado por la siguiente expresión:
siendo α una constante positiva mayor que cero. Determínese si el espectro energético de la partícula es discreto o continuo, y hágase asimismo un bosquejo de la eigenfunción de energía para esta situación.
El potencial dado divide al espacio en dos regiones distintas, la región clásicamente permitida para la cual la energía E de la partícula es mayor que el potencial V(x), y la región clásicamente prohibida para la cual la energía de la partícula es menor que el potencial V(x), lo cual podemos bosquejar de la siguiente manera:
De acuerdo con el procedimiento WKB, hay una solución para cada región. Para la región #.1, en donde la energía E es mayor que el potencial V(x), la solución es de tipo oscilatorio y tiene la siguiente forma:
mientras que para la región #.2 en donde la energía E es menor que el potencial V(x), la solución es de tipo exponencial y tiene la siguiente forma:
Suponiendo que la energía E de la partícula se mantiene constante al cruzar de una región a otra, la eigenfunción de energía producirá una función de onda que en las dos regiones manifestará una continuidad como la que se muestra a continuación:
A estas alturas debe ser claro que el espectro energético de la partícula debe ser continuo, puesto que no hay absolutamente nada en ambas regiones que le impida a la partícula tomar cualquier valor posible de E. Obsérvese que entre ambas regiones hay una región de color rosado en la cual no se llevó a cabo la “conexión” de ambos segmentos de la función de onda, el oscilatorio y el exponencial, en virtud de que justo en el punto x0 las dos soluciones WKB explotan hacia el infinito en virtud de que V.=.E, lo cual nos produce un cero en el denominador. El punto en donde cruzamos de una región a otra, o sea de una región en la cual la energía E es mayor que el potencial V a otra región en la cual la energía E es menor que el potencial V, es lo que hemos llamado el punto de volteo clásico y que hemos designado aquí como x0.
Habiendo obtenido, pues, las soluciones que propone el método WKB desde el punto de vista puramente matemático, el problema que tenemos ahora ocurre justo en el punto de volteo E.=.V en donde la constante de propagación se desvanece y la longitud de onda se vuelve infinita. Aunque ambas soluciones fallan en la proximidad del punto de volteo, se puede determinar una solución adecuada aproximando la variación actual del potencial V(x) en la cercanía del punto de volteo con una variación lineal:
V(x) = A(x - x0) + E
Esquemáticamente, la labor de “conectar”o “pegar” las soluciones dadas por el método WKB reemplazando la zona en la cual ambas soluciones se vuelven indeterminadas por una aproximación lineal de la función de onda en dicho punto toma el siguiente aspecto:
en donde la curva de color azul representa la solución WKB en una región y la curva de color café representa la solución WKB en la otra región, siendo la línea recta de color magenta una aproximación al potencial actual que es válido cerca del punto de volteo. Se supone que esta aproximación lineal al potencial V(x) es válida sobre una región pequeña situada a ambos lados del punto de volteo. Con esta aproximación lineal, la ecuación de Schrödinger se puede resolver de manera exacta para esta región pequeña, y las soluciones que se obtengan de la misma se pueden utilizar para “pegar” adecuadamente las dos soluciones WKB que son válidas fuera de la zona pequeña en donde está situado el punto de volteo (la solución oscilatoria y la solución exponencial, esto es). La linearización en la “zona prohibida” para el métodoWKB en donde está el punto de volteo se traduce en una ecuación diferencial como la siguiente en donde la función de onda que describe la zona del punto de volteo se simboliza como uE(x) en lugar de ψ(x):
Esto ya es algo adicional a lo que es el método WKB en sí. Suponiendo que la región clásicamente prohibida (para la cual la energía E es menor que el potencial V) está hacia el lado positivo de la abcisa (x), entonces las soluciones matemáticas para la ecuación diferencial de Schrödinger cerca del punto de volteo x0 requieren del uso de funciones de Bessel de orden fraccionario, tomando la forma:
en donde lo que está resaltado de color azul es conocido como la función de Bessel de orden ±1/3, y la forma:
en donde lo que está resaltado de color azul es conocido como la función de Bessel de argumento imaginario, en donde las constantes C deben ser seleccionadas para poder “pegar” suavemente las dos soluciones justo en el punto de volteo x0. Queda pendiente, desde luego, la tarea de “pegar” estas dos soluciones a las soluciones WKB que se habían obtenido previamente. Para ello, se requiere hacer uso del comportamiento asintótico de las soluciones WKB en la cercanía del punto de volteo:
Así como están dadas, estas fórmulas asintóticas no pueden ser utilizadas en virtud de que incluyen tanto exponenciales crecientes como decrecientes para x.→.+∞. Sin embargo, esto se puede corregir tomando combinaciones lineales apropiadas mediantes las cuales las “relaciones de conexión” pueden ser encontradas:
Aquí ξ puede tener cualquier valor tal que sen(ξ) no sea aproximadamente cero. Las flechas de color azul indican que la conexión debe ser llevada a cabo en la dirección del exponencial creciente. Si las conexiones son llevadas a cabo en el sentido opuesto, en el caso de la primera fórmula el pequeño error de fase introducido por la aproximación metería en el panorama al exponencial (dominante) que aumenta fuera del punto del volteo, mientras que en el caso de la segunda fórmula el desprecio del exponencial que aumenta hacia el punto de volteo introduce un error considerable de fase en la solución oscilatoria.
PROBLEMA: Supóngase que una partícula en una dimensión está sujeta a una fuerza constante derivable de un potencial dado por la siguiente expresión:
siendo α una constante positiva mayor que cero. Determínese si el espectro energético de la partícula es discreto o continuo, y hágase asimismo un bosquejo de la eigenfunción de energía para esta situación.
Este problema es muy parecido al anterior que habíamos visto, excepto que el potencial no puede tomar un valor negativo. Esto hace que la función potencial divida al espacio no en dos regiones sino en tres regiones como se muestra a continuación:
En la región #.1, en donde la energía E es menor que el potencial V, se tiene una solución exponencial creciente en el sentido positivo del eje-x, dada por:
Por su parte, en la región #.2, en donde la energía E es mayor que el potencial V, se tiene una solución oscilatoria dada por:
Y en lo que respecta a la región #.3, en donde la energía E es nuevamente menor que el potencial V, se tiene una solución exponencial decreciente en el sentido positivo del eje-x, dada por:
Aunque no parezca obvio a primera vista, el espectro energético de la partícula será discreto, en virtud de que una partícula con cierta energía E estará confinada en la región # 2 entre dos paredes, las cuales aunque no sean verticales de cualquier modo siguen siendo paredes, y entre estas dos paredes sólo puede haber un número entero de medias longitudes de onda a lo largo de un eje horizontal imaginario que atraviese las paredes. Podemos visualizar esto mejor recordando el pozo de potencial parabólico característico del oscilador armónico simple, en donde también sólo son posibles niveles de energía discretos. Con un poco de imaginación, podemos deformar el peculiar pozo de potencial especificado en este problema para hacerlo tomar la forma del pozo de potencial parabólico característico del oscilador armónico simple, notando que en ambos casos las paredes son infinitamente altas. Y de hecho, el pozo de potencial que hemos estudiado en este problema es conocido frecuentemente como un pozo de potencial triangular.
Para cada una de las eigen-energías permisibles, la función de onda ψ(x) de la partícula quedará conectada de región a región de una manera como se muestra en la siguiente figura:
Obsérvese en la figura que no se ha llevado a cabo la conexión completa justo en las líneas azules divisorias que representan al potencial, esto en virtud de que justo en los puntos que corresponden a las líneas azules divisorias se tiene E.=.V y con ello el denominador en las soluciones WKB se hace infinitamente grande. En este último problema, al igual que en el problema anterior, tenemos el problema de las indeterminaciones que ocurren al cruzar de una región a otra cuando los denominadores se hacen iguales a cero. Aquí para cierta eigen-función ψ(x) habrá dos puntos de volteo en lugar de dos, el punto de volteo que le corresponde a ψ(x) al cruzar de la región #.1 a la región #.2, y el punto de volteo que le corresponde al cruzar de la región #.2 a la región #.3. Afortunadamente, dada la simetría del potencial, la resolución matemática de cualquiera de los dos puntos de volteo automáticamente nos produce la solución matemática del otro punto de volteo, comprobando así las ventajas de recurrir a la simetría para la solución de este tipo de problemas.