Si la Mecánica Ondulatoria realmente es equivalente a la Mecánica Matricial, debe ser posible entonces obtener las mismas conclusiones de ambas, y una de tales conclusiones debe serlo sin lugar a dudas el principio de incertidumbre, de forma tal que si dicho principio no hubiese sido descubierto primero dentro de la Mecánica Matricial habría sido descubierto tarde o temprano con las herramientas matemáticas de la Mecánica Ondulatoria, y esto es precisamente lo que queremos llevar a cabo aquí con el fin de verificar la consistencia interna y la unidad de la Mecánica Cuántica en sus dos vertientes.
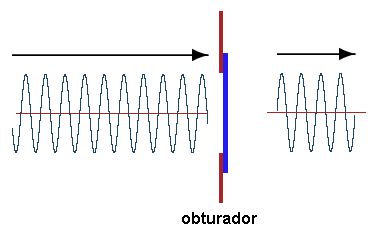
Desde la perspectiva de la Mecánica Ondulatoria, si imaginamos a una partícula representada por una función de onda unidimensional ψ(x) de tipo senoidal infinitamente larga (de modo tal que su posición exacta nos es desconocida pero cuyo momentum nos será conocido mediante la relación de Louis de Broglie p = h/λ), podemos concebir el siguiente experimento hipotético con el cual formamos un paquete de onda abriendo y cerrando rápidamente un obturador como el de las cámaras fotográficas antigüas, dejando pasar un segmento de la onda electromagnética:
En rigor de verdad, el paquete de onda supuestamente obtenido no es muy realista porque se trata de un pulso rectangular de onda. Un paquete de onda más realista obtenido mediante un obturador como el arriba mostrado podría ser uno de tipo normal Gaussiano como el que se muestra a continuación en donde en lugar de graficar a ψ(x) graficamos a |ψ(x)|² por ser esta función la que mejor nos representa a la onda de materia que está actuando casi como si fuera una partícula:
Trataremos de determinar ahora la localización del fotón luminoso dentro del paquete de onda y su momentum. Si la dirección de propagación de la onda es en el sentido positivo del eje-x, y la longitud del “pulso de onda” es Δx, resulta obvio que la posición exacta del fotón dentro del paquete de onda será incierta en el orden de Δx. Al mismo tiempo, puesto que un paquete de onda de esta naturaleza requiere para su representación una superposición de ondas planas de longitudes de onda distintas, el momentum del fotón no puede ser predicho con certeza. Sería necesario hacer una medición del momentum para determinar su valor exacto. Para obtener un paquete de onda que tenga una longitud Δx, es necesario incluír un rango Δk de constantes de propagación (números de onda k) del orden:
Δk ≈ 1/Δx
en la superposición de ondas planas. Usando la relación de Louis de Broglie que nos dá la conexión entre entre la constante de propagación (número de onda) k y el momentum p de la partícula, tenemos que esto implica un rango de momentums tales que:
Δk = Δpx/ħ ≈ 1/Δx
Esto último podemos escribirlo de la siguiente manera:
Δx·Δpx ≈ ħ
Tenemos entonces que el producto de la incertidumbre en la posición del fotón sobre el eje-x y la incertidumbre en el momentum sobre esta dirección en particular es del orden ħ. El hecho de que hayamos podido llegar a esta conclusión recurriendo a argumentos puramente ondulatorios nos confirma que podemos llegar al principio de incertidumbre por medio de la Mecánica Ondulatoria además de haber podido llegar a lo mismo previamente mediante la Mecánica Matricial.
Pudiera objetarse que la “demostración” llevada a cabo sería aplicable para fotones luminosos pero que el resultado no necesariamente sería válido para otro tipo de partículas. Para resolver esta duda, el mismo Werner Heisenberg propuso un experimento idealizado conocido como el microscopio de Heisenberg, en el cual tratamos de determinar simultáneamente con precisión ilimitada la posición y el momentum de un electrón. Podemos bosquejar un detector como el microscopio de Heisenberg de la siguiente manera:
Para poder “ver” al electrón que suponemos inicalmente en reposo, tenemos que enviarle un fotón luminoso que “rebote” sobre dicho electrón. Al recibir al fotón rebotado en un detector, posiblemente en la lente de un microscopio, sabiendo de dónde vino el fotón podemos determinar la posición inicial del electrón. Pero aquí nos topamos con un problema. Al enviarle al electrón un fotón que posee un momentum p = h/λ, al rebotar el fotón necesariamente habrá una transferencia de momentum que pondrá en movimiento al electrón que estaba en reposo, y ahora su posición se vuelve incierta. Haciendo un cálculo aproximado, obtendremos nuevamente la misma relación de incertidumbre. Se han concebido muchos experimentos idealizados para darle la vuelta al principio de incertidumbre, pero al final de cuentas siempre terminamos con lo mismo: no es posible ubicar la posición de cualquier tipo de partícula con precisión ilimitada manteniendo al mismo tiempo una conocimiento ilimitado sobre su momentum. Y esto no tiene absolutamente nada que ver con la precisión de los instrumentos utilizados, se trata de una característica muy propia de la naturaleza ondulatoria de la materia.
Supóngase que el detector (óptico) es la lente del microscopio de Heisenberg como lo muestra la siguiente figura:
Podemos considerar a la apertura del microscopio esencialmente como una rejilla de difracción de ranura sencilla capaz de producir el típico patrón de difracción de la luz como lo muestra la parte superior del dibujo. Para poder ser detectado, el fotón debe poder viajar en cualquier parte dentro del cono de iluminación del objetivo (en la figura es el cono cuyo ángulo interno con respecto a la vertical viene siendo el ángulo θ). De la ciencia de la óptica ondulatoria, se sabe que el poder de resolución del microscopio estará dado por la siguiente relación:
Δx ≈ λ/[2 sen(θ)]
en donde λ representa la longitud de onda de la luz empleada (la longitud de onda del fotón luminoso), siendo θ el medio ángulo subtendido por el objetivo del microscopio. Δx representa entonces la precisión con la cual se puede determinar la posición del electrón usando luz monocromática con esta longitud de onda. Por otro lado, para ser recogido por la lente, el fotón debe estar dentro de un rango angular entre -θ y θ. Esto significa que el momentum del fotón podrá tener un valor que está entre p1x y p2x, o sea, entre (de la figura antepenúltima):
p1x = p1 sen(θ) = (h/λ1) sen(θ) = (h/λ) sen(θ)
y:
p2x = p2 sen(θ) = (h/λ2) sen(θ) = (h/λ) sen(θ)
Entonces la incertidumbre en el momentum provocada por la transferencia de momentum del fotón al electrón será igual a:
Δpx ≈ 2 (h/λ) sen(θ)
Si tomamos conjuntamente el producto de ambas relaciones para Δx y Δpx, entonces la relación entre la incertidumbre en la posición y la incertidumbre en el momentum estará dada por:
Δx·Δpx ≈ (λ/[2 sen(θ)]) · [2 (h/λ) sen(θ)]
Δx·Δpx ≈ h
Δx·Δpx ≈ h
Nuevamente, considerando a esta relación aproximadamente correcta en orden de magnitud, tenemos que el producto de la incertidumbre en la posición del electrón a lo largo del eje-x y la incertidumbre en el conocimiento de su momentum en la dirección del mismo eje es del orden de magnitud de la constante de Planck. Y si movemos el experimento hacia un espacio tridimensional descrito mediante coordenadas Cartesianas rectangulares, tenemos un resultado interesante: podemos medir con precisión casi ilimitada la posición del electrón a lo largo de cualquiera de los tres ejes, y podemos medir simultáneamente el momentum del electrón a lo largo de cualquiera de los otros dos ejes, y en tal caso tenemos lo mismo que anteriormente habíamos definido dentro de la Mecánica Matricial como observables compatibles. En forma simbólica:
Δx·Δpy = 0___Δx·Δpz = 0
Δy·Δpx = 0___Δy·Δpz = 0
Δz·Δpx = 0___Δz·Δpy = 0
Δy·Δpx = 0___Δy·Δpz = 0
Δz·Δpx = 0___Δz·Δpy = 0
Esto es lo mismo que lo que habíamos obtenido previamente, excepto que en esta ocasión hemos llegado a nuestras conclusiones sin usar una sola matriz, manejando todo desde el punto de vista puramente ondulatorio.
El microscopio de Heisenberg es un experimento gedanken, hipotético, que no resulta fácil de llevar a cabo por las dificultades técnicas que entraña. Pero hay otro tipo de experimento mediante el cual podemos deducir, dentro de la Mecánica Ondulatoria, la existencia de un límite teórico a nuestra capacidad de conocimiento sobre lo que está ocurriendo en el mundo sub-microscópico, un límite en el que la constante de Planck interviene de manera fundamental. El experimento es esencialmente nuestro viejo experimento de difracción en el cual se envían ya no fotones de luz sino partículas como electrones a una doble rendija, aunque podemos simplificar un poco las cosas haciéndolo un experimento de difracción con una sola rendija que sea lo suficientemente pequeña para que se manifieste el fenómeno. Una difracción de este tipo es conocida como difracción de Fraunhofer.Al enviar un haz de electrones a través de una rendija lo suficientemente pequeña hacia una pantalla receptora, observaremos la formación de un patrón de difracción con sus característicos máximos y mínimos:
El patrón de difracción que se observa en la pantalla es explicable únicamente dándole un caracter ondulatorio a las partículas que están llegando a la rendija, con las partículas comportándose como ondas de materia. El primer máximo de intensidad observado en la pantalla, Imax, el más intenso, obviamente estará en el centro de la pantalla. Tras esto, a ambos lados habrá otros máximos (como I1, I2, etc.) así como otros mínimos entre dichos máximos, correspondiendo a los patrones ondulatorios de interferencia constructiva y destructiva. Si en vez de utilizar una rendija en forma de ranura lineal utilizamos una rendija circular extremadamente pequeña, entonces el patrón de difracción que podemos esperar observar se obtiene haciendo girar el patrón de difracción que tenemos en la figura de arriba alrededor del eje de simetría:
Como podemos verlo en la siguiente figura que nos muestra a las partículas pasando a través de una rendija de anchura (o diámetro) igual a d:
la posición del primer punto de intensidad cero en la pantalla se obtendrá a partir de la teoría de difracción (que se estudia en los cursos elementales de óptica) cuando:
sen(θ) = λ/d
siendo λ la longitud del frente de onda que está pasando a través de la rendija. De este modo, en virtud de que cada una de las partículas tiene una onda de De Broglie dada por la relación λ = h/p, la partícula sufrirá una difracción a su paso por la ranura y en consecuencia adquirirá un momentum desconocido en la dirección vertical (ya sea hacia abajo o hacia arriba) designada como coordenada-x. Aunque no conozcamos el lugar exacto en el cual la partícula incidirá sobre la pantalla, el lugar más probable para que esto ocurra será dentro de la región central del modelo de difracción, la de mayor intensidad. Por lo tanto, es lógico pensar que la componente Δpx en la coordenada-x del momentum tendrá un valor entre 0 y psen(θ), lo cual nos lleva a lo siguiente para el máximo valor posible que pueda tener Δpx dentro del primer máximo de intensidad:
Esta relación nos indica que la incertidumbre Δpx en el momentum se puede hacer tan pequeña como se quiera aumentando el ancho de la ranura. Pero al aumentar el ancho de la ranura, aumentará la incertidumbre Δx sobre el lugar exacto a lo largo de la coordenada-x por donde haya pasado la partícula. Y esto es en esencia la naturaleza básica del principio de incertidumbre. De hecho, la misma relación nos lleva a una buena aproximación al principio de incertidumbre:
A continuación, le daremos a la incertidumbre dentro de la Mecánica Ondulatoria un significado matemático exacto recurriendo para ello a la estadística. Definiremos al cuadrado de la incertidumbre de cierta cantidad en particular como la desviación media cuadrática con respecto a la media aritmética. La desviación con respecto a la media aritmética está dada por:
La variable en este caso que representa a la posición medida sobre la coordenada-x es una variable continua.
Habiendo formulado la definición anterior, el valor de la esperanza matemática del cuadrado de la desviación, o desviación media cuadrática, estará dada operacionalmente por la siguiente expresión:
Obsérvese que en esta definición se ha considerado a Δx como un operador Hermitiano.
De modo semejante, podemos definir también a la incertidumbre en el momentum como la desviación media cuadrática con respecto a la media aritmética del momentum:
El producto Π de ambas cantidades que es en lo que estamos realmente interesados será simplemente:
Recurriremos ahora a la bien conocida desigualdad de Schwarz aplicada a funciones de variables continuas:
en donde f* es el conjugado complejo de la función f. (Recuérdese que al obtenerse el principio de incertidumbre dentro de la Mecánica Matricial también se tuvo que recurrir a la desigualdad de Schwarz aplicada a un número complejo a.+.ib considerado como un “vector”, aunque aquí está siendo aplicado a dos funciones continuas. En realidad, todas las demostraciones del principio de incertidumbre recurren de un modo u otro a la desigualdad de Schwarz.)
Al aplicar la desigualdad de Schwartz al producto Π de las dos incertidumbres haciendo:
f = Δxψ___g = ΔPxψ
tenemos entonces:
El operador ΔxΔPx que aparece en la desigualdad bajo el signo de la integral puede ser escrito de otra manera más conveniente para nuestros propósitos:
En la última línea hemos recurrido a la ecuación de Born. Como puede verse, tenemos ahora una expresión que consta de dos términos, un término imaginario y un término real:
Puesto que:
podemos afirmar entonces que la desigualdad puede ser escrita de la manera siguiente:
El segundo término ΔxΔpx+ ΔpxΔx en esta expresión es obviamente un operador Hermitiano, y más aún se trata de un operador Hermitiano con valores propios eigen reales, teniendo por lo tanto una esperanza matemática que debe ser real y además positiva. Puesto que el menor valor posible que esta esperanza matemática pueda tomar es cero, entonces de la desigualdad de Schwartz aplicada a este problema obtenemos la siguiente relación:
Esta última expresión nos dice que el producto de la desviación media cuadrática en la coordenada-x y la desviación media cuadrática en el momentum debe ser igual o mayor que (ħ/2)². Este es precisamente el enunciado del principio de incertidumbre de Heisenberg, sin haber tenido que recurrir para la derivación del mismo a matriz alguna. Sin embargo, podemos establecer paralelos entre la obtención del principio de incertidumbre en la Mecánica Matricial y la obtención del mismo principio en la Mecánica Ondulatoria, y podemos ver que las líneas de pensamiento son esencialmente las mismas.
El principio de incertidumbre, enunciado por primera vez como consecuencia directa de la “extraña ecuación” de Born que relacionaba como observables incompatibles a la posición y al momentum, elevándolos de las simples variables que eran a la calidad de operadores (matrices), puede ser extendido a cualquier par de variables que sean observables incompatibles, y en este respecto hay una versión más amplia del principio de incertidumbre que podríamos bautizar como el principio de incertidumbre generalizado bajo el cual dadas dos observables físicas incomptabibles A y B cuyos operadores respectivos sean A y B, el producto de las incertidumbres está dado por la siguiente igualdad-desigualdad:
en el cual se utiliza el conmutador de Born que resalta el hecho de que solo en el caso en el cual las observables sean observables compatibles el producto de las incertidumbres será igual a cero al ser el conmutador de Born igual a cero debido a la conmutatividad de los operadores asociados con operadores compatibles.
A continuación llevaremos a cabo la derivación del principio de incertidumbre generalizado recurriendo para ello a la notación bra-ket de Dirac. Usaremos itálicas para representar a la observable física Q y tipografía románica para representar al operador Q asociado con la observable. Es importante tener presente que todas las derivaciones del principio de incertidumbre eventualmente recurren a la desigualdad de Schwarz.
Primero que nada, para un estado determinado de una observable Q en el cual es posible obtener con precisión teórica ilimitada el valor de dicha observable (como la energía de una partícula encerrada en una caja), la incertidumbre o desviación estándard estadística σQ de dicha observable debe ser igual a cero:
En términos de las esperanzas matemáticas, lo anterior es lo mismo que:
Puesto que todo lo que está al lado izquierdo de la igualdad es una esperanza matemática, se puede expresar como tal bajo el contexto de la Mecánica Ondulatoria mediante la notación bra-ket de Dirac suponiendo para ello una función de onda Ψ que caracteriza al estado del sistema:
En la segunda línea se ha hecho actuar al “operador dispersión” sobre el ket que está a su derecha.
Supondremos que el “operador dispersión” es un operador Hermitiano, lo cual nos permitirá hacer el siguiente desarrollo:
Lo último nos dice que la norma del “vector” que está al lado izquierdo de la igualdad es igual a cero. Puesto que el único vector con una norma igual a cero es el vector nulo, se deduce que:
Lo que tenemos al final es una eigenecuación, con un operador Q actuando sobre un ket de estado, regresándonos un eigenvalor de Q en el lado derecho. Esto nos confirma que los estado determinados con valores bien definidos son eigenvectores del operador Q. Y nos confirma también que la notación y los conceptos que estamos utilizando son consistentes.
De este modo, y en base a lo anterior, para cualquier observable física A se tiene:
en donde se ha hecho:
Del mismo modo, para otra observable física B, se tiene:
en donde se ha hecho:
Haciendo uso de la desigualdad de Schwarz, podemos entonces escribir lo siguiente:
Por otro lado, sabemos que para cualquier número complejo:
dándose por hecho obvio que:
Obsérvese también que:
Por lo tanto, haciendo:
se tiene:
Pero:
Del mismo modo:
Y así:
De este modo, juntando lo que tenemos, queda demostrado el principio de incertidumbre generalizado.
Haciendo A.=.x y B.=.p (los operadores de la posición y del momentum), podemos obtener del principio de incertidumbre generalizado la relación de incertidumbre “clásica” de Heisenberg. Para ello, todo lo que tenemos que hacer es recurrir a la ecuación fundamental de Born que relaciona a la posición y al momentum a lo largo de una misma coordenada como observables incompatibles:
Haciendo uso de este conmutador, se tiene entonces:
Obsérvese que esta relación es igualmente válida ya sea que los operadores posición y momentum sean matrices (Mecánica Matricial) o que sean operadores diferenciales (Mecánica Ondulatoria). Y de hecho, el principio de incertidumbre generalizado es completamente válido tanto dentro de la Mecánica Matricial como la Mecánica Ondulatoria, de allí su utilidad.
Como un ejemplo de la aplicación del principio de incertidumbre generalizado, obtendremos la expresión del principio de incertidumbre que corresponde a la posición y a la energía de una partícula cuyo operador es el operador de energía Hamiltoniano H. En este caso, el conmutador de Born que corresponde a estas dos observables físicas es el siguiente:
en donde hemos utilizado las propiedades algebraicas del conmutador para llegar a la expresión en la cuarta línea. Para poder continuar, se requiere evaluar los dos conmutadores que tenemos en la cuarta línea. Para la evaluación del primer conmutador, podemos hacer lo siguiente recurriendo a la “extraña ecuación” de Born (al pasar de la tercera línea a la cuarta línea):
Puesto que el potencial lo suponemos como una función de la posición, ambas observables (y sus operadores correspondientes) deben conmutar, lo cual significa que el segundo conmutador debe ser igual a cero:
Por lo tanto:
De este modo, el principio de incertidumbre generalizado:
nos produce lo siguiente:
Tomando la raíz cuadrada en ambos lados se tiene finalmente:
Obsérvese que para estados estacionarios (como en el caso de una partícula atrapada en una caja o un oscilador armónico simple), esta relación no nos dice nada porque en el lado izquierdo de la desigualdad la dispersión que corresponde a la medición de la energía de la partícula es igual a cero en virtud de que para un estado estacionario la energía se conoce con precisión ilimitada, no hay incertidumbre alguna de índole teórica en su medición, o sea que σH.=.0. Y en el lado derecho, puesto que para un estado estacionario como la partícula encerrada en una caja, el valor esperado (la esperanza matemática) del momentum es igual a cero en virtud de que esperamos encontrar a la partícula moviéndose tantas veces hacia la izquierda como hacia la derecha. De este modo, para estados estacionarios la relación nos dice que 0.≥.0, lo cual no dice nada. Sin embargo, para algo como una partícula libre, la relación nos puede revelar cosas útiles.
Suponiendo que los efectos relativistas propios de la Teoría Especial de la Relatividad (variación de la masa con la velocidad) sean comparativamente insignificantes, en tal caso recurriendo a la definición clásica de lo que es el momentum la relación anterior puede ser desarrollada como:
Como una medida de la rapidez con la cual pueda estar variando un sistema, supóngase que se tiene una observable física Q(x,.p,.t) a la cual le corresponda un operador cuántico Q. Entonces, si se toma la variable con respecto al tiempo del valor esperado (esperanza matemática) de dicha observable física, se tiene:
Ahora bien, de la relación fundamental de Schrödinger se tiene que:
siendo H el operador Hamiltoniano de energía:
Con esto se tiene, por lo tanto:
Pero el operador Hamiltoniano H es un operador Hermitiano, o sea que:
Por lo tanto, haciendo uso de la relación del conmutador de Born, en este caso el conmutador entre el operador Hamiltoniano de energía H y el operador Q, se tiene:
Este resultado es particularmente útil e interesante. En el caso usual en el que el operador Q no depende explícitamente en la variable tiempo, la relación obtenida nos dice que la razón de cambio del valor esperado para la observable física Q está determinada por el conmutador del operador Hamiltoniano H de energía con el operador Q que corresponde a la observable física en cuestión. Y en el caso especial en el cual los operadores Q y H conmutan, entonces el valor esperado de la observable física Q se mantiene constante con el transcurso del tiempo, y en este sentido Q es una cantidad conservada. Vale la pena analizar algunas de las conclusiones que se pueden obtener para casos especiales con lo que se acaba de obtener. Tomemos el caso especial para el cual Q.=.1. Puesto que el número 1 conmuta con todo, se tiene entonces que la relación se reduce a:
Esto no es más que un enunciado de la conservación de la normalización. Tomemos ahora el caso especial para el cual Q.=.H. Puesto que todo conmuta consigo mismo, se tiene entonces que [H,H].=.0, de modo tal que, si H no tiene una dependencia en el tiempo, se tiene entonces que la relación se reduce a:
Esto no es más que el enunciado del principio de la conservación de energía. Tomemos ahora el caso especial para el cual Q.=.x. En una situación así, usando el resultado intermedio obtenido arriba:
la relación nos dá lo siguiente:
o bien:
Este es el equivalente mecánico-cuántico de la segunda ley de Newton, dándole una naturaleza estadística a lo que en la mecánica clásica es una relación cien por ciento determinista.
Supóngase ahora que tomamos el principio de incertidumbre generalizado obtenido más arriba y hacemos A.=.H y B.=.Q, suponiendo además que Q no depende explícitamente en la variable temporal. En tal caso:
o bien, usando la relación que acabamos de obtener (en recuadro azul):
que podemos simplificar a lo siguiente:
Extrayendo la raíz cuadrada en ambos lados, se tiene:
De este modo, obtenemos la siguiente expresión:
Esta relación es una de varias variantes de la relación mejor conocida como la formulación Mandelstam-Tamm del principio de incertidumbre, en memoria de los científicos soviéticos Leonid Mandelstam y Ígor Tamm que la enunciaron por vez primera. Se trata de una reformulación del principio de incertidumbre energía-tiempo, y en esta versión nos proporciona la cantidad de tiempo Δt que le toma al valor esperado de Q en cambiar por una desviación estándard. Δt depende por completo en la observable física Q que estemos mirando, y el cambio puede ser rápido para una observable física y lento para otra, pero si ΔE es pequeño entonces la razón de cambio de todas las observables físicas debe ser muy gradual. Visto de otro modo, si cualquier observable física cambia con mucha rapidez, entonces la incertidumbre en la energía debe ser grande.
En la Mecánica Ondulatoria, al igual que como ocurrió en la Mecánica Matricial, el principio de incertidumbre sigue siendo una relación que nos fija un límite absoluto mínimo al producto de dos incertidumbres, constituyendo generalmente una relación de desigualdad. Obviamente, nos interesa mucho indagar la situación para la cual se cumple la relación de igualdad en el principio de incertidumbre. ¿Qué tipo de funciones de onda serán capaces de resultarnos en una relación de igualdad?
De acuerdo al principio de incertidumbre, una mayor precisión en la determinación de la posición de una partícula tendrá que llegar a expensas de una mayor ignorancia sobre el momentum de la misma, y viceversa. Si aceptamos una menor precisión en el conocimiento sobre la posición de la partícula, lo cual equivaldría a ir ampliando cada vez más y más la anchura de la curva estadística, a medida que vaya aumentando nuestra incertidumbre σx.=.Δx en este parámetro irá disminuyendo a la par la anchura de la curva estadística de la cual se infiere la incertidumbre σp.=.Δp en el momentum de la partícula, hasta que llegará un punto en el cual la incertidumbre conjunta de ambas cantidades, σxσp, tomará un valor mínimo:
En el punto mínimo, ambas curvas deberán tener la misma forma (o estructura), y la disminución de la anchura σ de una de ellas resultará en el aumento de la anchura σ de la otra resultando en un producto de incertidumbres mayor que el producto mínimo.
Las condiciones bajo las cuales el producto de ambas incertidumbres sea tal que la desigualdad se convierte en una igualdad son que la desigualdad de Schwartz utilizada arriba sea también una igualdad, y que la cantidad:
o bien:
sea igual a cero.
La condición para que la desigualdad de Schwartz se convierta en una igualdad está fijada por el requerimiento de que:
f = αg
en donde α puede ser un número complejo. En términos de incertidumbres, esta relación actuando operacionalmente sobre una función de onda ψ se nos convierte en:
Δxψ = αΔpxψ
La condición de que la cantidad que requiere desvanecerse para que la desigualdad se nos convierta en igualdad puede ser reformulada en términos de la esperanza matemática de dicha cantidad:
∫ψ*(ΔxΔpx + ΔpxΔx) ψ dx = 0
Combinando las últimas dos expresiones obtenemos lo siguiente:
(α* + α) ∫ψ*(Δpx)² ψ dx = 0
Puesto que se presume que la integral no es igual a cero, el factor multiplicativo fuera de la misma debe serlo. Y en virtud de que la integral debe ser definitivamente positiva (positive definite), α debe ser puramente imaginario y no un número complejo, o sea, i veces una constante C que debe ser determinada. Si α.=.i, entonces por la definición de un número complejo tendríamos:
α + α* = i - i = 0
Esto último no sería posible si α fuese un número complejo como a+ib ya que en tal caso:
α + α* = a + ib + (a - ib) = 2a
y no habría forma en que la expresión dada arriba podría ser igual a cero.
A continuación determinaremos la constante C relacionada con la hipótesis α.=.iC. De la expresión:
Δxψ = αΔpxψ
tenemos:
Δxψ = iCΔpxψ
Entonces:
El producto mínimo de incertidumbres se logra cuando en el principio de incertidumbre obtenido arriba la desigualdad se convierte en igualdad, o sea:
Con esto podemos continuar adelante con el proceso de integración que había quedado pendiente:
Llevando a cabo la integración:
En esta solución la condición de frontera de que la función de onda ψ se desvanezca para valores grandes de la coordenada-x (ψ→0 para x→±∞) impone al signo negativo en el primer término dentro de los corchetes como la única alternativa posible de solución. Escogiendo a la constante de integración K como:
e introduciendo una constante de normalización A tenemos entonces:
La constante de normalización la podemos obtener de la condición usual:
y puesto que:
obtenemos fácilmente lo siguiente:
La función de onda que nos dá el mínimo producto de incertidumbres cumpliéndose así la condición de igualdad en el principio de incertidumbre es entonces la siguiente:
Esta curva la podemos reconocer de inmediato como la curva normal o curva Gaussiana que tanto se utiliza en estadística:
De este modo, la función de onda para la cual existe un mínimo en el producto de la incertidumbre en la posición y el momentum es un paquete de onda cuyo “envoltorio” (o cubierta) corresponde al de una curva normal o Gaussiana:
Si suponemos que esta función de onda representa a una partícula en movimiento, en rigor de verdad una función de onda así no sólo existe a lo largo de la coordenada sobre la cual se está moviendo, también podemos visualizarla distribuída sobre de un plano x-y con el movimiento de la misma efectuándose a lo largo de uno de los ejes coordenados:
Y si hemos de ser realistas, la partícula es una partícula que existe no en un plano sino en un espacio tridimensional, estando especificada por un triplete (x,y,z). Desafortunadamente, no es posible representar una función Gaussiana tridimensional en la forma que lo hemos hecho con las figuras de arriba. En cualquier caso, lo importante es que para que se cumpla la condición de igualdad en el principio de incertidumbre se requiere que la función de onda sea una función de tipo Gaussiano; en caso contrario el producto de las incertidumbres deberá ser forzosamente mayor que ħ/2.
El principio de incertidumbre ha sido puesto a pruebas rigurosas tanto en una gran variedad de situaciones gedanken, puramente teóricas, como en una amplia variedad de situaciones experimentales, y no ha sido posible encontrar hasta la fecha un solo caso en el cual se viole dicho principio. Para ilustrar el amplio campo de acción y aplicabilidad del principio de incertidumbre, consideraremos el caso de una partícula encerrada dentro de un pozo de potencial esférico. Dentro de una esfera de radio a, tomaremos el potencial como idénticamente igual a cero, o sea V.=.0, mientras que fuera de la esfera tomaremos el potencial infinitamente alto, o sea V.=.∞. Se trata, en efecto, de una partícula-onda encerrada dentro de una esfera hueca por dentro y sólidamente rígida por fuera. En realidad, cualquier esfera con un interior vacío y con una capa exterior de grosor lo suficientemente dura para impedir que la partícula pueda escapar servirá para nuestro propósito, una esfera como la que se muestra a continuación:
Un problema de este tipo se puede resolver con mayor facilidad mediante el uso de coordenadas esféricas, lo cual supone que la función de onda de la partícula se puede expresar como ψ(r,θ,φ). En entradas posteriores en donde se tratará el tema del momento angular, se verá que una función de onda tal se puede descomponer -en muchas ocasiones- como el producto de dos funciones de onda, siendo una de ellas la función de onda que depende de la parte radial r, y siendo la otra función de onda aquella que depende de los parámetros angulares θ y φ, pudiéndose representar la descomposición de la siguiente manera:
La parte en color azul es la parte radial, mientras que la parte en color magenta es la parte angular. Los sub-índices iguales a cero en la función de onda de color magenta Y que es una armónica esférica indican que estaremos considerando una partícula carente de momento angular orbital (varios de los conceptos y términos que estamos usando aquí se volverán más claros al entrar en mayor detalle sobre lo que es el momento angular orbital estudiado dentro de la Mecánica Ondulatoria). En el estudio posterior de las armónicas esféricas, se verá con mayor detalle que cuando la partícula carece de momento angular orbital la armónica esférica es simplemente igual a una constante numérica:
Del mismo modo, se verá que para un problema de este tipo (partícula aprisionada dentro de una esfera) la parte radial se puede expresar de la siguiente manera:
en donde la función χ(r) es una función que satisface la ecuación de onda de Schrödinger de la siguiente manera:
De este modo, la función de onda para una partícula aprisionada dentro de una esfera viene siendo:
La solución más general para χ(r) viene siendo:
en donde:
En el centro geométrico de la esfera en donde r.=.0, la condición de que la función radial posea un valor finito (y no un valor infinitamente grande) impone el requerimiento de que B.=.0. El primer término puede tener un valor diferente de cero en virtud de una bien conocida propiedad matemática que nos dice que:
Por otro lado, puesto que la partícula no puede escapar al exterior por ser la pared esférica impenetrable, se impone también la condición de frontera χ(a).=.0. Esto a su vez impone el requerimiento de que αa.=.π con lo cual:
La constante de normalización de acuerdo al criterio de Born queda prefijada por el requerimiento:
siendo dτ un elemento infinitesimal de volumen (podríamos haber usado dV, pero se puede prestar a confusiones con el símbolo utilizado para representar el potencial). Intruduciendo en forma explícita el elemento infinitesimal de volumen expresado en coordenadas esféricas, lo anterior se convierte en:
Agregaremos a lo anterior los límites de integración que lleva implícito el uso de las coordenadas esféricas:
Llevando a cabo las integraciones sobre la parte angular, se tiene:
Usando la parte que habíamos acordado utilizar para χ(r), entonces:
Llevando a cabo la integración, se tiene lo siguiente para la constante de normalización:
Por lo tanto:
o bien:
La dispersión estadística de valores para la posición de la partícula, suponiendo que el mismo experimento se repita muchas veces, es:
La evaluación de la esperanza media cuadrática de los valores obtenidos para la posición se lleva a cabo de una manera directa sin mayores preámbulos:
La evaluación de la esperanza matemática de la posición no requiere tanto esfuerzo, si recordamos lo que ocurre en la integración de funciones impares:
De este modo, el cuadrado de la esperanza matemática de la posición es igual a cero.
Si lo que queremos obtener es el principio de incertidumbre aplicado a las observables físicas de la posición y el momentum, entonces tenemos que evaluar:
Para ello, se tiene que;
con lo cual:
Efectuando las integraciones que corresponden a las variables angulares, se tiene;
Simplificando todo esto previo a la integración que corresponde a la parte radial, para después llevar a cabo dicha integración, se tiene:
De nueva cuenta, la parte que corresponde a la evaluación de la esperanza matemática del momentum es aún mucho más fácil de obtener, habido el hecho de que la integración de las funciones impares siempre es igual a cero:
Esto nos permite evaluar la dispersión estadística en los valores del momentum:
Así pues, juntándolo todo:
Llevando a cabo la evaluación numérica de esto último, se tiene:
De nueva cuenta, hemos verificado, para este caso en particular, que el principio de incertidumbre se cumple, en este caso aplicándose la relación de desigualdad.
A continuación, veremos un problema conocido postulado en muchos textos de Mecánica Cuántica.
PROBLEMA: Usando como única limitación las incertidumbres impuestas por el principio de incertidumbre, obténgase una estimación del orden de magnitud para el tiempo expresado en segundos que un picahielos puede permanecer balanceado sobre su punta suponiendo que la punta es filosa y que tanto la punta como la superficie en la cual está apoyada son duras.
Este problema resultará familiar a quienes han estudiado alguna vez el caso conocido como el péndulo invertido dado el gran parecido entre ambos. Podemos considerar al picahielos:
como una masa situada a una distancia fija L de su punta, fija al punto de giración en la mesa que le impide al picahielos resbalar obligándolo a caer a una aceleración angular constante, lo cual podemos considerar válido para valores pequeños del ángulo θ con respecto a la vertical:
Para el torque producido por la acción de la gravedad, la ecuación de movimiento está dada por:
La solución general de esta ecuación diferencial de segundo orden es relativamente sencilla:
Para un tiempo de inicio muy cercano a t = 0, la expresión anterior se nos convierte en:
θ(0) = A + B
En su caída, el extremo del picahielos describe un arco de círculo Δs, y ese arco de círculo dividido entre el radio L es igual al ángulo θ expresado en radianes, o sea θ.=.Δs/L. Para un recorrido muy pequeño como podemos esperar que ocurra al inicio, dicho arco de círculo puede ser aproximado razonablemente bien como un segmento de línea recta Δx, con lo cual podemos escribir Δx.≈.θL.≈.(A+B)L. Por otra parte, la velocidad angular ω del extremo del picahielos es igual a la velocidad tangencial entre el radio, o sea ω = dθ/dt.=.v/L, con lo cual el momentum al inicio de la caída será igual p.=.mv y la incertidumbre correspondiente será Δp.=.mΔv.=.mLdθ/dt. De la relación dada arriba como solución a la ecuación diferencial de segundo orden tenemos:
con lo cual:
Tomaremos la relación de incertidumbre ΔxΔp.≥.ħ/2 y supondremos el caso óptimo en el cual aplica la igualdad debajo de la cual el principio de incertidumbre no se cumple:
ΔxΔp = ħ/2
Metiendo los resultados que hemos obtenido tenemos entonces:
Despejando para A²:
En la solución a la ecuación diferencial de segundo orden del sistema, la constante de integración A está asociada a una exponencial positiva que crecerá rápidamente conforme la variable tiempo vaya aumentando, mientras que la constante de integración B está asociada a una exponencial negativa que irá cayendo exponencialmente también conforme la variable tiempo vaya aumentando. En base a esto, es la constante A la constante en la cual estamos interesados, razón por la cual tomaremos B.=.0 para obtener así:
De este modo, regresando a la solución a la ecuación diferencial y metiendo estos resultados así como despejando para el tiempo de caída tcaída del picahielos:
Nótese que de las dos raíces obtenidas arriba para la constante A, la positiva y la negativa, se ha descartado la raíz negativa como posible solución al problema, esto con el fin de garantizar que el resultado final sea definitivamente positivo (positive definite) como se ve a continuación:
Podemos meter en ésta fórmula los valores de masa y longitud típicos para un picahielos obteniendo de este modo un tiempo aproximado de unos cuantos segundos.