En la gráfica anterior el trío de estados degenerados se desdobla en un triplete en forma tal que mientras que uno de los niveles energéticos mantiene el mismo valor original que mantenía el conjunto en ausencia de perturbación alguna, los otros dos estados degenerados se van separando del nivel central. No hay desde luego ningún requerimiento de que el nivel energético central en un triplete mantenga su valor igual que el valor original que tenía el trío de estados, y es bien posible que los tres niveles energéticos se vayan desplazando al aumentar la intensidad de la perturbación como lo ilustra la siguiente gráfica que muestra cómo el estado energético E1 se va desdoblando en tres niveles energéticos distintos E1a, E1b y E1c conforme va aumentando la intensidad de la pertubación λ que aquí identificamos como un potencial V creciente :
PROBLEMA: Suponiendo que en la gráfica anterior el nivel energético E0 del estado basal permanece constante, describir la manera en la cual se detectaría en un espectrómetro de laboratorio el rompimiento de la degeneración al ir aumentando la intensidad del efecto perturbador usado para romper la degeneración.
Para mayor simplicidad, supondremos que los efectos ocurrirán no en la porción ultravioleta del espectro ni en la porción del infrarrojo sino en la porción visible del espectro electromagnético. Entonces, a medida que se va rompiendo la degeneración, veríamos algo como lo que muestra el siguiente gráfico animado sobre un espectro de absorción:
Puesto que el nivel energético de los tres estados degenerados va aumentando conforme aumenta la intensidad de la perturbación, las bandas visibles de absorción se irán desplazando juntas desde la porción menos energética del espectro electromagnético (el infrarrojo) hacia la porción más energética del espectro (la zona ultravioleta), o sea de derecha a izquierda en el espectro continuo que tenemos arriba, y la separación entre las bandas irá aumentando. Es importante tener presente que las bandas negras de absorción se deben a la absorción de los fotones luminosos del espectro luminoso desapareciendo dichos fotones para hacer saltar a los electrones desde el estado fundamental hacia uno de los tres estados degenerados como se muestra a continuación en donde suponemos que las bandas visibles ocurren cuando la perturbación ha tomado un valor fijo V0:
¿Y cómo habremos de manejar los problemas de pertubación con degeneración de tres pliegues, así como degeneración con más de tres pliegues? Exactamente de la misma manera en que se hace con la degeneración de dos pliegues. Se construye primero una “matriz de trabajo” W. Hecho ésto, se trabaja sobre la ecuación característica de dicha matriz para obtener sus valores propios eigen, lo cual nos permite obtener las correcciones de primer orden para las energías de los estados degenerados conforme aumenta la intensidad de la perturbación y los niveles energéticos se van separando. Logrado ésto, podemos buscar las combinaciones lineales apropiadas para poder obtener las eigenfunciones que corresponden a los estados degenerados, con lo cual el problema de varios estados degenerados se puede considerar resuelto a un primer orden.
En una degeneración de tres pliegues, la “matriz de trabajo” W es construída de la siguiente manera:
Si una vez construída la matriz W resulta ser una matriz diagonal, estamos de suerte y el problema se puede considerar resuelto. Sin embargo, si no es una matriz diagonal, entonces la matriz tiene que ser diagonalizada usando para ello las herramientas proporcionadas por el Algebra Linear; esto es, a partir de la matriz W montamos el determinante que nos proporcione el polinomio característico con el propósito de poder obtener los eigenvalores de la matriz W. Sin olvidar que lo que nos proporciona la matriz W son las correcciones perturbativas de primer orden del sistema, para poder obtener los niveles de energía del sistema perturbado tenemos que sumar las correcciones obtenidas con la matriz W que corresponden al Hamiltoniano de perturbación H1 a los valores característicos de la matriz (diagonal) que corresponde al sistema no-perturbado H0.
El siguiente problema clarificará un poco más lo anterior en lo que concierne a una degenaración de tres pliegues.
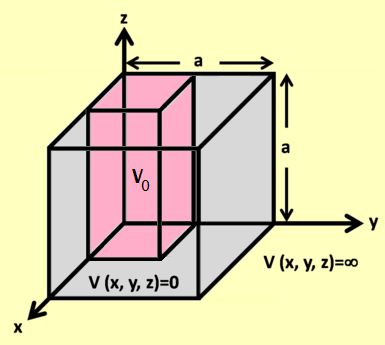
PROBLEMA: Considérese el problema de una partícula atrapada en una caja herméticamente sellada como un problema en tres dimensiones a ser manejado usando un sistema de coordenadas Cartesianas. Supóngase que dentro de la caja hay una región (destacada en color rosa) con un potencial V0 de la manera en que se muestra a continuación:
Usando el método de las perturbaciones, encuéntrese la corrección de primer orden para la energía fundamental del sistema. Hecho ésto, llevar a cabo un análisis sobre lo que sucede en el primer estado excitado del sistema perturbado.
Por hipótesis, el sistema sin la perturbación presente puede ser descrito de la siguiente manera:
El problema es la extensión hacia tres dimensiones de una partícula encerrada en una caja. En un sistema así, la función de onda completa para describir los estados estacionarios sin perturbación alguna es la siguiente (estaremos haciendo referencia aquí a lo que se discutió previamente en la entrada en ésta obra titulada La ecuación de Schrödinger):
o bien:
Las energías que puede tener una partícula encerrada en la caja tridimensional, en ausencia de perturbación alguna, son:
El estado basal es necesariamente degenerado puesto que cada uno de los tres números cuánticos solo puede tomar el valor de 1, siendo la energía:
Introduciremos ahora en el sistema la perturbación arriba citada, cuyo efecto es aumentar el potencial en un cuarto del volumen del interior de la caja. La corrección de primer orden para la energía del estado basal será por lo tanto:
habiéndose usado para la evaluación de cada una de las tres integrales anteriores la siguiente integral general tomada de las tablas de integrales:
Sin embargo, cuando el sistema se encuentra en su primer estado excitado, lo cual ocurre cuando uno de los números cuánticos nx ó ny ó nz (¡y sólo uno de ellos) es igual a 2, entonces tenemos tres estados degenerados, y se vuelve necesario recurrir a la teoría de perturbaciones para estados degenerados. Empezaremos por construír la matriz W que combina las nueve posibilidades en una matriz 3×3 en donde se hará el acomodo asignando los estados degenerados (2,1,1), (1,2,1) y (11,2) como renglones y como columnas identificadas como a, b y c en ese orden:
Podemos empezar con la evaluación de los elementos diagonales de la matriz. Para el elemento matricial Waa se tiene:
Para el elemento matricial Wbb se tiene:
mientras que para el elemento matricial Wcc se tiene:
No es cosa del otro mundo verificar que para los tres casos se obtiene el mismo resultado:
Ahora evaluaremos uno de los elementos que está fuera de la diagonal principal, el elementoWab:
Simplificando y reagrupando:
A la integral general tomada de las tablas sumaremos otra integral general tomada también de las tablas de integrales:
En Wab la integral sobre z termina siendo evaluada a cero, y la transpuesta Wba por lo tanto también debe ser cero. Del mismo modo, se encuentra que Wac y su transpuesta Wca son ambas cero. Todo parecería indicar a estas alturas que la matriz W contendrá puros ceros. Sin embargo, se encuentra que Wbc (al igual que su transpuesta Wcb) tienen un valor diferente de cero:
Colocando los resultados dentro de la matriz W tenemos lo siguiente:
en donde se ha hecho A.=.(8/3π)2.
A continuación, usamos la matriz W para obtener su ecuación característica tal y como se acostumbra hacer tal cosa en el Algebra Lineal, trabajando por cuestiones de simplicidad sobre lo siguiente:
con lo cual se tiene entonces:
dándonos el polinomio característico a resolver:
El polinomio característico tiene tres raíces que son:
De éste modo, las energías de los estados degenerados agregando las correcciones de primer orden a la energía del primer estado no-perturbado con degeneración de tres, estado que llamaremos aquí E1(0), se pueden especificar de la siguiente manera:
Conforme aumenta V0, se puede apreciar que los aumentos en la energía de cada uno de los estados degenerados son aumentos lineales. Sin embargo, los tres tienen pendientes diferentes, y por lo tanto los estados anteriormente degenerados se irán separando más y más conforme aumenta la magnitud de la peturbación. Aunque a primera vista éste comportamiento parece corresponder al gráfico animado que se vió arriba al tratar el primer problema de ésta entrada, en realidad no lo es, porque en el gráfico animado de arriba se supuso que el estado fundamental permanecía constante mientras que los tres niveles degenerados que corresponden al primer estado excitado iban aumentando todos ellos. Sin embargo, en este problema el estado fundamental no permanece constante, y de hecho también va aumentando según va aumentando la magnitud de la perturbación V, siendo la energía del estado fundamental perturbado:
De este modo, la gráfica del problema presente mostrando la variación en los niveles de energía tanto del estado fundamental como del primer estado excitado una vez que se ha roto la degeneración del estado excitado (posiblemente mediante la aplicación de un campo magnético o un campo eléctrico o algún otro método ingenioso) es como se muestra a continuación:
Obsérvese que, en virtud de tener la misma magnitud de incremento al ir aumentando la perturbación V0, tanto el estado excitado E1(0) como del estado fundamental E0(0), irán manteniendo la misma separación entre ambos como lo confirman las líneas rojas verticales que van marcando la distancia entre los dos niveles energéticos, lo cual implica que en un espectro de absorción la banda central permanecerá en el mismo sitio al ir aumentando la separación, mientras que las bandas laterales se irán separando de la banda central. El siguiente gráfico animado nos dá una mejor idea de lo que irá ocurriendo:
Pero ocurre además algo que al principio puede parecer sorprendente. Conforme aumenta la perturbación, el nivel energético degenerado E1c se encamina directamente hacia un encuentro con el nivel energético no-degenerado E’0, y de hecho ambas líneas se van a cruzar en algún lugar al haber continuado su trayectoria más allá de la cajita resaltada de color magenta en la figura de arriba. En principio, justo al momento en que se cruzan ambas líneas, no debe haber intercambio energético alguno porque no hay diferencia alguna en la energía entre ambos niveles capaz de absorber ningún fotón. Lo sorprendente es que, a causa de una perturbación, un nivel energético que corresponde a un número cuántico superior (como n.=.4) pueda terminar siendo inferior a un nivel energético que normalmente corresponde a un número cuántico inferior (n.=.3). Este tipo de encuentros no es inusual, y de hecho ocurre una y otra vez en simulaciones llevadas a cabo modeladas sobre fenómenos del mundo real. Como prueba de ello, se tiene la siguiente gráfica tomada de la página Wikipedia que versa sobre el efecto Stark (de lo cual se tratará más a fondo posteriormente en ésta obra) en donde podemos ver cómo con una perturbación suficientemente grande se van a producir varios “cruces”:
Nos falta calcular las eigenfunciones “buenas” que corresponden a cada uno de los estados degenerados. Estas deben ser combinaciones lineales del tipo:
Aquí los coeficientes α, β y γ son los elementos con los cuales se forman los eigenvectores de la matriz W:
Usando cada uno de los tres valores de w obtenidos arriba, obtenemos tres sistemas de ecuaciones lineales. Por ejemplo, con w1.=.1, se obtiene α.=.1, β.=.0 y γ.=.0. Resolviendo los tres conjuntos de ecuaciones lineales y normalizando cada eigenvector, llegamos al siguiente trío de eigenfunciones normalizadas:
En el caso de la degeneración de dos pliegues, ya vimos mediante la construcción de la matriz W que existe una fórmula (la que vimos en la entrada anterior) que nos puede proporcionar las dos raíces que corresponden a las correcciones perturbativas de primer orden para obtener las energías de los estados degenerados del sistema. Desearíamos también que hubiera alguna fórmula con la cual para una degeneración de tres pliegues pudiéramos llegar a una ecuación cúbica mediante la cual podamos obtener también en forma analítica exacta las tres correcciones de primer orden para poder obtener con dichas tres correcciones los valores eigen de energia para los tres estados degenerados del sistema. El dilema aquí al dar el salto de dos estados degenerados a tres estados degenerados es que para poder resolver el sistema tratando de emplear una ecuación cúbica tenemos que recurrir a un aparato matemático algo laborioso como lo es la fórmula de Tartaglia-Cardano. Y para casos en donde hay una degeneración de cinco o más pliegues, nos podemos ir olvidando de poder resolver analíticamente tales sistemas con fórmulas exactas en virtud de que está formalmente demostrado (lo demostró Evariste Galois al fundar la Teoría de Grupos) de que no es posible, ni siquiera en principio, poder obtener fórmulas generales exactas como la fórmula cuadrática para resolver ecuaciones de quinto grado en adelante mediante radicales (raíces cuadradas, raíces cúbicas, etcétera). Podemos, eso sí, resolver casos especiales, como aquellos casos en los cuales una factorización sencilla puede reducir una ecuación de tercer grado al producto de una ecuación cuadrática y una ecuación lineal, ambas con soluciones exactas. Y para casos generales, hay una variedad de métodos numéricos con los cuales con la ayuda de la computadora podemos obtener buenas aproximaciones. A fin de cuentas, la posibilidad de poder resolver un problema de degeneración de varios pliegues así sea en forma aproximada dependerá del grado de ingenio y de las herramientas teóricas disponibles para aplicar una técnica cuando otras técnicas han fracasado. En última instancia, siempre podemos recurrir a aproximaciones numéricas auxiliados por computadoras. No en vano en el siglo pasado se consideró imperativo y urgente el desarrollo de máquinas de cómputo capaces de realizar en horas o minutos el trabajo aritmético que requería de grupos combinados de matemáticos trabajando arduamente por varios meses con calculadoras hoy obsoletas.
En algunos textos de Mecánica Cuántica circula un teorema que afirma lo siguiente: “en problemas que involucran una sola dimensión, no hay estados ligados degenerados”. Dicho teorema se puede demostrar suponiendo que para una situación unidimensional hay dos soluciones distintas ψ1 y ψ2 con la misma energía, multiplicando por ψ2 la ecuación de Schrödinger para ψ1, multiplicando por ψ1 la ecuación de Schrödinger para ψ2, y restando ambas expresiones, que es lo que haremos a continuación:
Restando una expresión de la otra se tiene:
Pero por otro lado:
Pero se acaba de demostrar arriba que lo que está entre los paréntesis cuadrados es igual a cero. Si tal cosa es cierta, entonces el resultado de la derivación implica que:
Pero para que cualquier función de onda ψ pueda ser normalizable, se debe ir a cero en el infinito, y por lo tanto la constante debe ser igual a cero. Por lo tanto:
Se concluye entonces que ψ1 es un submúltiplo de ψ1 (o viceversa) y por lo tanto las dos soluciones no son distintas.
El teorema que se acaba de demostrar no es de aplicación universal, y para comprobarlo aplicaremos lo que acabamos de ver al análisis de una partícula de masa m que está libre para moverse unidimensionalmente en una región de longitud L, como en el caso de una cuenta que se desliza recorriendo el trayecto de un alambre circular:
Para un partícula así, no habiendo potencial alguno V a tomar en cuenta, el desarrollo de la ecuación de Schrödinger será como se muestra a continuación:
en donde x lo podemos tomar como la distancia recorrida a lo largo de la circunferencia de longitud L:
Puesto que un recorrido de x.+.L nos regresa al mismo punto de partida, o sea x, entonces:
Tomando lo anterior como las condiciones de frontera y usando las mismas técnicas y procedimientos detallados en las entradas tituladas "Transmisión y reflexión de partículas", podemos enunciar la validez de lo siguiente:
Esto es válido para cualquier valor de x, como x.=.0, en cuyo caso se produce lo siguiente:
Por otro lado, la expresión también es válida para x.=.π/2k, en cuyo caso se produce lo siguiente:
Sumando las dos relaciones obtenidas, se tiene:
Para que ésto último sea cierto, se requiere que A.=.0 o bien eikL.=.1, en cuyo caso:
Para A.=.0, entonces se tendría Be-ikL.=.B, lo cual nos lleva a la misma conclusión. De este modo, se deduce que para cada n positivo hay dos soluciones (para el caso n.=.0 hay una sola solución):
La normalización de la función de onda general, para cada signo:
nos conduce a lo siguiente:
agregándose que cualquier otro tipo de solución para la misma energía eigen será una combinación linear de estas dos soluciones. De éste modo, se obtienen la siguiente función de onda general y expresión para las energías discretas permisibles:
Este ejemplo parece contradecir un teorema generalmente aceptado que nos dice que “en problemas que involucran una sola dimensión, no hay estados ligados degenerados”. Sin embargo, tal teorema no se aplica en una situación como ésta en virtud de que la función de onda ψ no se va a cero cuando la variable independiente x se va hasta el infinito.
en donde el segmento de longitud a es mucho más breve que la longitud total de la circunferencia del “aro”. Nuestro propósito será tratar de encontrar las correcciones perturbativas de primer orden para los estados degenerados.
Habiendo establecido ya la técnica de la construcción de una matriz de trabajo W, el objetivo será evaluar los elementos matriciales que corresponden a dicha matriz para el problema en cuestión. En virtud de que los números cuánticos n pueden tomar tanto valores positivos como valores negativos (además del valor cero), haremos primero las equiparaciones:
y usando para los estados estacionarios la función de onda:
entonces el cálculo de los elementos diagonales empezando con Waa procede de la siguiente manera (precaución: no confundir la letra “a” minúscula usada para representar elementos matriciales de la matriz de trabajo W con la letra “a” minúscula usada para representar la pequeña longitud del hoyuelo en el aro):
Para llevar a cabo la integración, podemos explotar el hecho de que fuera de los límites del pequeño segmento de longitud a la perturbación es esencialmente cero, y por lo tanto podemos tomar (comparativamente hablando) los límites superior e inferior como infinitos:
El mismo resultado se obtiene para Wbb. En cuanto a los elementos no-diagonales, el procedimiento de integración requiere el mismo truco matemático de “completar el cuadrado” en la parte exponencial del integrando que ya se vió previamente en la entrada “La partícula libre II” que forma parte de ésta obra:
Puesto que Wab resultó ser un número real, el mismo resultado se obtiene para Wba. Recurriendo a los resultados intermedios obtenidos arriba, encontramos entonces que las correcciones perturbativas de primer orden son:
Veamos ahora si podemos determinar las funciones de onda “buenas” para éste ejemplo. De los resultados intermedios usados en la definición de la matriz W, se tiene:
De éste modo, las funciones de onda “buenas” son obtenidas mediante las siguientes combinaciones lineares con la ayuda de la fórmula de Euler:
Podemos comprobar que con estas funciones de onda “buenas” obtenemos exactamente las mismas correcciones de primer orden que se obtuvieron arriba con la ayuda de la matriz de trabajo W:
Recurriendo a las identidades trigonométricas:
se puede comprobar que se obtienen las mismas correcciones perturbativas de primer orden que las que se obtuvieron arriba:
En todos los problemas que se han manejado, ha estado notoriamente ausente el factor tiempo. Ello no significa que no se puedan analizar correcciones perturbativas que tengan alguna variación con respecto al tiempo. Pero dar ese salto representa un salto enorme que tiene que ser postpuesto para entradas posteriores dada la amplitud del tema.