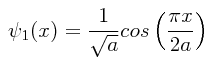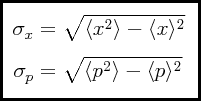En la ecuación de Schrödinger tenemos ya nuestro primer operador, un operador H que representa a la energía de la partícula, el cual a diferencia de lo que teníamos en la Mecánica Matricial resulta ser un operador diferencial en lugar de ser una matriz. La solución de la ecuación diferencial:
Hψ = Eψ
es la que nos proporciona los eigen-valores E que puede tomar la energía del sistema. En forma similar a como ocurrió en la Mecánica Matricial, esta ecuación debe ser vista como una ecuación para la cual sus soluciones eigen van aparejadas con funciones eigen ψ o eigenfunciones (compárese con la situación en la Mecánica Matricial en la cual en vez de funciones de onda continuas ψ lo que manejamos son vectores).
PROBLEMA: Para el siguiente operador diferencial:
demuéstrese que la función ψ = 8e5x es una eigenfunción del operador Dx. ¿Cuál es el valor propio eigen?
Aplicando el operador diferencial Dx sobre la función ψ obtenemos lo siguiente:
En la última línea podemos ver que la aplicación del operador diferencial Dx sobre la función ψ nos regresa a la misma función multiplicada por una constante. Entonces ψ es una eigenfunción. En este caso, el valor propio eigen es 5.
Si en la Mecánica Matricial teníamos un operador matricial P para representar al momentum, esto nos permite suponer que también dentro de la Mecánica Ondulatoria debe ser posible definir un operador momentum, el cual esperamos que sea también un operador diferencial. En nuestro intento por descubrir o definir dicho operador, podemos tomar la ecuación de Schrödinger independiente del tiempo restringiendo el movimiento a una sola dimensión y haciendo el potencial V(x) igual a cero. Lo que nos queda es esencialmente un operador diferencial que representa a la energía cinética de la partícula, la cual sabemos que está relacionada clásicamente con el momentum a través de la relación E.=.P²/2m. Usando la relación clásica como guía, esto nos permite establecer las siguientes comparaciones:
Puesto de otra manera, si clásicamente la energía E puede ser obtenida del momentum P mediante la relación E.=.P²/2m, ¿cómo podemos obtener el operador diferencial que corresponde a la energía del sistema, de la aplicación repetida de un operador diferencial momentum P que dividido entre 2m nos produzca el término diferencial que ya tenemos identificado como el operador energía? Nos puede ayudar en nuestra búsqueda el reescribir el operador energía de la siguiente manera haciéndolo que se parezca un poco más a la relación clásica:
Tenemos una constante ħ² que puede ser obtenida simplemente multiplicando a ħ consigo misma. Y tenemos una derivada de segundo orden que, operacionalmente hablando, puede ser considerada como la doble aplicación sucesiva del operador diferencial d/dx, o sea d²/dx² = (d/dx)(d/dx). Esto nos sugiere que podemos hacer la siguiente “factorización”:
Nos queda el problema del signo negativo. ¿Cómo podemos hacer que un operador diferencial P aplicado sucesivamente (simbolizado como P²) nos dé un signo negativo? Es aquí en donde tenemos que recurrir al número i, la base de los números imaginarios. Una forma de meterlo en lo que estamos tratando de definir es la siguiente:
Si removemos los paréntesis obtendremos el operador diferencial para la energía con el que habíamos empezado. Pero más importante aún es que podemos establecer la siguiente correspondencia:
Hemos llegado al punto en el que la definición del operador diferencial para el momentum prácticamente nos está saltando a nuestros ojos. Definiendo a la cantidad entre los paréntesis como Px en atención al hecho de que la definición se ha hecho para un movimiento unidimensional a lo largo de un solo eje coordenado, podemos entonces escribir lo siguiente:
Si queremos extender nuestra definición hacia un espacio tridimensional, lo podemos hacer sin problema alguno recurriendo a las derivadas parciales, con lo cual podemos asentar las siguientes relaciones:
Estos son los operadores en la Mecánica Ondulatoria para el momentum lineal. Y del mismo modo en el que los operadores matriciales actuaban sobre vectores de estado en la Mecánica Matricial, los operadores diferenciales que acabamos de obtener actuarán sobre una función de onda ψ.
La disponibilidad de un operador diferencial para el momentum lineal nos permite llegar a un resultado extraordinariamente importante.
PROBLEMA: Repasando la definición matemática del conmutador:
[A,B] = AB - BA
evalúese el conmutador para el caso en el cual A representa el operador posición y B el operador momentum en el entorno de la Mecánica Ondulatoria.
Al operador posición le daremos aquí una definición trivial en la cual seguirá siendo lo mismo, en tanto que al operador momentum le daremos la interpretación obtenida arriba como un operador diferencial. Siendo así, entonces [A,B] será también un operador al estar construído a base de operadores, y podrá actuar también sobre una función de onda:
[x, Px] ψ
A continuación, respetando la convención usual de que un operador diferencial actúa siempre sobre el término o los términos que tiene a su derecha, y cuando actúa sobre un producto se debe aplicar la regla usual para la diferencial del producto de dos variables, desarrollamos esta expresión siguiendo las reglas usuales de las matemáticas:
Si prescindimos de la función de onda ψ concentrándonos únicamente en el aspecto operacional del operador combinado que fué definido con la ayuda del conmutador, lo que tenemos (operacionalmente hablando) es lo siguiente:
El resultado que hemos logrado nos debe resultar familar de nuestro tratamiento introductorio a la Mecánica Matricial en donde teníamos lo siguiente bajo otro disfraz:
QP - PQ = iħI
Hemos obtenido la ecuación de Born. Y lo hemos logrado sin haber recurrido a matriz alguna, trabajando exclusivamente dentro del ámbito de la Mecánica Ondulatoria. Lo único que cambia es la naturaleza de los operadores matemáticos, ya que si en la Mecánica Matricial se define todo a base de matrices en la Mecánica Ondulatoria todo se define a base de operadores diferenciales. Pero si vemos más allá de la notación y establecemos las siguientes correspondencias:
x → Q
Px → P
Px → P
entonces es indudable que lo que tenemos es esencialmente lo mismo, y debe ser una de las cosas más fundamentales que pueda haber en la Naturaleza. Si la Mecánica Ondulatoria de Schrödinger puede explicar exitosamente lo que ocurre en el mundo sub-microscópico es porque entre sus pilares se encuentra la roca sólida de la ecuación de Born. Si la Mecánica Matricial de Heisenberg pese a ser de naturaleza matemática diferente puede también explicar exitosamente lo que ocurre en el mundo sub-microscópico es porque entre sus pilares también se encuentra la roca sólida de la ecuación de Born. Y si el modelo atómico planetario de Bohr pudo funcionar pese a ser un modelo demasiado mecanístico ello se debe a que sus postulados son una consecuencia directa de la cuantización del momento angular que a su vez es una consecuencia directa de la ecuación de Born. Podemos dar por hecho que cualquier sistema descriptivo del mundo sub-microscópico que cumpla con la ecuación de Born producirá resultados que concordarán con lo que se obtenga experimentalmente en el laboratorio, mientras que cualquier cosa que no concuerde con la ecuación de Born seguramente no tardará en colapsarse tarde o temprano bajo su propio peso. No en vano por este descubrimiento Max Born se hizo merecedor del Premio Nóbel.
Puesto que el principio de incertidumbre de Heisenberg es una consecuencia directa de ecuación de Born, la Mecánica Ondulatoria nos vuelve a confirmar a través del conmutador la existencia de observables incompatibles, cantidades que no pueden ser medidas simultáneamente con un grado ilimitado de precisión a lo largo de una misma coordenada al no ser el conmutador igual a cero. Con esto, cualquier esperanza que pudiéramos haber tenido de sobreponernos en la Mecánica Ondulatoria a los límites teóricos dictados por el principio de incertidumbre se desvanecen hasta perderse en forma definitiva. Esto es algo en lo que la misma Naturaleza nos tiene atados de manos.
Así como lo hicimos para el caso de una sola coordenada, en un espacio tridimensional Cartesiano tenemos otras dos coordenadas para las cuales, dentro de la Mecánica Ondulatoria, también podemos postular las siguientes ecuaciones de Born:
No podemos medir con precisión ilimitada la posición y el momentum de una partícula a lo largo de un mismo eje coordenado. Sin embargo, esto no significa que no podamos medir con precisión ilimitada la posición de una partícula a lo largo de cierta coordenada, y medir también con precisión ilimitada el momentum de la misma partícula a lo largo de otra coordenada.
PROBLEMA: Demostrar que, cuando se utilizan coordenadas distintas, es posible medir simultáneamente con un grado ilimitado de precisión la posición y el momentum de una partícula, siendo en tal caso observables compatibles.
A continuación tenemos a la posición medida a lo largo de la coordenada-x,y al momentum lineal medido a lo largo de la coordenada-y, combinados en un conmutador como un operador que actúa sobre una función de onda ψ:
[x,Py] ψ
Desarrollando esta expresión operacionalmente sin mostrar ya el operador diferencial en su forma explícita (lo cual es una ventaja porque simplifica la tipografía) tenemos lo siguiente:
En la tercera línea hemos aplicado el hecho de que por tratarse de coordenadas rectangulares (ortogonales):
Py(x) = - iħ (∂x/∂y) = - iħ (0) = 0
mientras que la última línea nos confirma que la posición de la partícula se puede medir a lo largo de la coordenada-x simultáneamente con el momentum de la partícula medido a lo largo de la coordenada-y, siendo por lo tanto ambas observables compatibles sobre las cuales no aplica el principio de incertidumbre.
Tenemos entonces un total de seis combinaciones posibles de observables compatibles:
Si bien en la Mecánica Matricial manejábamos conjuntos de valores discretos que nos permitían definir estadísticamente la esperanza matemática de una cantidad mediante simples sumas y divisiones, en la Mecánica Ondulatoria no tenemos tal beneficio, porque ahora al estar manejando funciones de onda estamos manejando funciones continuas que varían suavemente trazando una curva sobre una gráfica. Tenemos que ampliar nuestras definiciones estadísticas para cubrir esta nueva eventualidad con la finalidad de poder seguir definiendo esperanzas matemáticas (valores esperados) para una o varias cantidades. Para poder hacer esta extensión vamos a repasar primero lo que ya sabemos.
Dado un conjunto de valores discretos xi, como las calificaciones de 50 estudiantes de un salón de clases, podemos obtener el promedio xprom de las calificaciones simplemente sumando todas las calificaciones obtenidas y dividiendo dicha cantidad entre el número N de alumnos, o sea mediante una aplicación de la definición:
Cuando algunos de los valores sobre los cuales se va a tomar el promedio aritmético aparecen repetidos, la fórmula dada arriba para un conjunto de valores discretos tomando en cuenta la frecuencia ni con la cual aparece cada valor es modificada quedando de la siguiente forma:
PROBLEMA: En cierta tienda, las ventas del día de unos pantalones en cuatro tallas distintas medidas en pulgadas registran las siguientes salidas:
De acuerdo con estos datos, ¿cuál es, en promedio, la talla de pantalón que más se vendería, si tal talla estuviera disponible?
El cálculo, llevado a cabo de acuerdo con la definición estadística del promedio que se acaba de dar, es el siguiente (empezaremos a utilizar aquí paréntesis angulados para denotar el promedio aritmético o esperanza matemática que se está evaluando):
Existe otra manera de definir el promedio aritmético que consiste en ponerlo en una forma probabilista. El resultado final será exactamente el mismo, pero la interpretación filosófica posterior que habremos de darle a la definición probabilista será de enorme importancia para nuestros propósitos. Obtenemos la forma probabilista de la media aritmética de la manera siguiente:
PROBLEMA: Repetir el problema anterior usando la definición probabilista de la media aritmética.
En este caso tenemos:
Obsérvese que p1 puede y debe ser considerada como la probabilidad de que sea vendido un pantalón de talla 34", p2 puede y debe ser considerada como la probabilidad de que sea vendido un pantalón de talla 36", p3 puede y debe ser considerada como la probabilidad de que sea vendido un pantalón de talla 38", y p4 puede y debe ser considerada como la probabilidad de que sea vendido un pantalón de talla 40", La suma de las probabilidades debe ser igual a la unidad:
p1 + p2 + p3 + p4 = 1.0
De este modo, la media aritmética evaluada de acuerdo a la fórmula probabilista es:
Este es, estadísticamente hablando, el valor esperado para la cantidad que está esparcida sobre una gama de valores distintos; es un valor representativo que con un solo número nos describe brevemente a toda la población de valores que estamos considerando.
La misma estructura simbólica puede ser empleada para definir otras esperanzas matemáticas, por ejemplo, la media cuadrática:
que interpretamos como el valor esperado de x² medido a través de un solo número.
Las definiciones que hemos visto son válidas para conjuntos discretos de valores. Sin embargo, no son muy útiles para obtener las esperanzas matemáticas (o los valores esperados) de cantidades que varían de acuerdo a una función continua que no está discretizada. En una situación en la cual tenemos un fenómeno natural en el cual para cada valor xi tomado de un conjunto finito de valores hay una función f(xi) que adquiere cierto valor, la definición del promedio aritmético sigue siendo válida si obtenemos el “promedio” de dicha función de la siguiente manera:
Pero si tomamos a la función f(x) como lo que es, como una función continua que varía suavemente entre cierto rango de valores de la variable independiente, tenemos entonces lo que equivale a un conjunto infinito de puntos que ya no puede ser promediado estadísticamente mediantes simples sumatorias. Obviamente, tenemos que reemplazar la sumatoria por una integral. Si la variable independiente define a la función f(x) entre dos extremos a y b:
a ≤ x ≤ b
entonces una definición que resulta útil para el valor promedio de una función continua es la siguiente:
PROBLEMA: Dada la función:
f(x) = 1 - 2x
obténgase el promedio de la función entre los límites a = 0 y b = 3.
Aplicando la definición dada arriba:
El valor promedio de la función es igual a -2.
En algunos casos podemos visualizar al tanteo cuál será el valor promedio aproximado de una función entre cierto rango de valores, como en la siguiente figura:
Sin embargo, en la ciencia no existe margen para las visualizaciones al tanteo en donde distintas personas obtendrán distintas conclusiones. Se requiere trabajar con números.
PROBLEMA: Al ir variando el tiempo, una temperatura ambiental registrada en grados Centígrados en un lapso de 24 horas ha sido ajustada a la siguiente curva empírica:
T = 0.001 t4 - 0.280 t2 + 25
en el rango:
- 12 ≤ t ≤ 12
¿Cuál podría decirse que es la temperatura promedio entre este rango?
Una gráfica de la función nos produce el siguiente resultado:
Repasando la gráfica, podemos ver que posiblemente la temperatura promedio tendrá un valor entre unos 14 y 16 grados Centígrados. Aplicando la definición para la resolución de este problema:
Metiendo números:
Los ejemplos que se acaban de dar para la obtención de promedios de funciones continuas están basados en la definición estadística convencional del promedio extendida a funciones continuas, no en una definición probabilista del promedio para funciones continuas. Si vamos a trabajar dentro de una filosofía probabilista, en vez de trabajar con una distribución discreta de probabilidades pi para cierto conjunto de datos discretos, tenemos que cambiar a una distribución continua de probabilidades π(x):
Para que la distribución continua pueda ser de utilidad como una distribución probabilista, el “área bajo la curva” de dicha función evaluada a lo largo de toda su extensión tiene que ser igual a la unidad, por ejemplo:
Un ejemplo entre muchos que se pueden dar es la siguiente función:
cuya gráfica es la siguiente:
Llevando a cabo la integración entre los límites a = 0 y b = +∞ podemos verificar que el área bajo la curva a lo largo de toda su extensión es igual a la unidad:
Definida la distribución continua de probabilidad o densidad de probabilidad que usaremos para cierto problema, estamos en condiciones de poder obtener un valor esperado (una esperanza matemática) del modo siguiente:
Del mismo modo y procediendo de manera análoga a como lo hicimos para el caso de un conjunto de datos discretos, podemos definir una esperanza media cuadrática del modo siguiente:
Más importante, podemos definir la esperanza matemática de una función continua f(x), evaluada entre ciertos límites, de la manera siguiente:
De acuerdo a esta definición, si queremos obtener la esperanza matemática de la función f(x) = x² entre los límites x = 0.48 y x = 0.50 bajo la distribución continua de probabilidades π(x) dada arriba, tenemos que evaluar entonces la siguiente integral:
Sin embargo, si queremos obtener la esperanza matemática de la función f(x) = x² bajo esta distribución de probabilidades a lo largo de todo el rango posible de interés, o sea lo que vendría siendo el verdadero “promedio aritmético” de la función bajo dicha distribución de probabilidades, tenemos que llevar a cabo la integración desde cero hasta +∞ (en este caso).
Habiendo dejado en claro lo que representa el valor medio o el valor esperado (o la esperanza matemática) de una función continua, evaluado entre cierto rango de valores, estamos preparados para extender el concepto hacia la definición de las esperanzas matemáticas dentro de la Mecánica Ondulatoria.
Hemos visto ya que el cuadrado absoluto de una función de onda normalizada es lo que debemos tomar como una medida de la densidad de la probabilidad de encontrar a la partícula en cierto lugar del espacio. Es necesario estar de acuerdo en lo que queremos decir por “probabilidad” bajo este contexto. Al hablar de la probabilidad, uno tiene en mente la siguiente situación: imagínese un gran ensamble de sistemas preparados de modo semejante, y al decir “preparados de modo semejante” lo que se quiere decir es que, en lo que concierne a cualquier medición física, los sistemas son idénticos, esto es, están descritos por funciones de onda idénticas. Ahora bien, si se lleva a cabo una medición en uno de estos sistemas para determinar si la partícula se encuentra dentro de cierto elemento de volumen, el resultado será definitivo: la partícula estará allí o no estará. Cuando la misma medición se lleva a cabo sobre una gran cantidad de sistemas preparados de modo semejante, el número relativo de veces que la partícula sea encontrada dentro de cierto elemento particular de volumen será tomado como una medida de la probabilidad de que la partícula sea encontrada en ese elemento de volumen. De este modo, si llevamos a cabo las mediciones sobre cierto elemento de volumen repitiendo el experimento en mil sistemas preparados de modo semejante, y encontramos a la partícula en ese elemento de volumen un total de 45 veces, entonces la probabilidad de encontrar a la partícula en ese elemento de volumen será igual a 45/1000 = 0.045.
Si el cuadrado de la función de onda |ψ(x)|² es lo que nos dá la distribución de probabilidades π(x) que estaremos utilizando, entonces con el simple expediente de hacer:
en la definición general dada arriba para el valor esperado de una función continua tendremos la definición de todas las esperanzas matemáticas que estaremos buscando.
PROBLEMA: Una partícula encerrada en una caja unidimensional de anchura igual a 2a se encuentra en el estado fundamental del pozo infinito de potencial. Suponiendo que el origen de las coordenadas está situado justo a la mitad del pozo, obténgase la probabilidad de encontrar a la partícula en un intervalo de anchura igual a 0.01a en el punto: (1) x.=.0, (2) x.=.a/2, (3) x.=.2a/3.
Si el origen de las coordenadas x.=.0 está situado justo a la mitad del pozo de potencial, entonces la función de onda que describe adecuadamente a la partícula cuando ésta está en un estado con n impar es:
Siendo la anchura de la caja L.=.2a, y siendo n.=.1 para una partícula en el estado fundamental, la función de onda que debemos utilizar es entonces:
La densidad de probabilidad de acuerdo al criterio de Born es entonces:
Como una aproximación a la integral que normalmente se requeriría, la probabilidad de encontrar a la partícula en el estado fundamental dentro de un intervalo de anchura:
Δx = x2 - x1
cuando el intervalo de anchura Δx es relativamente pequeño viene siendo:
o bien:
Para x.=.0 la probabilidad será:
Para x.=.a/2 la probabilidad será:
Y finalmente, para x.=.2a/3, la probabilidad será:
Obsérvese que, en base a los resultados obtenidos, la probabilidad de encontrar a la partícula en el centro de la caja dentro de un intervalo Δx.=.0.01a es mayor que para los otros dos puntos en un intervalo Δx similar.
En el problema anterior, ¿qué diferencia habríamos obtenido si en vez de fijar el centro de las coordenadas justo a la mitad de la caja unidimensional lo hubiésemos fijado en el borde de la pared izquierda como lo hemos hecho antes? Ninguna, porque en tal caso si bien la eigen-ecuación de la función de onda para el estado basal de una partícula atrapada en una caja de longitud L.=.2a habría sido:
y en todo caso esto también habría cambiado la especificación de los tres puntos usados en la solución del problema, los cuales serían entonces a, 3a/2 y 5a/3, dando los mismos resultados como es de esperarse. Sin embargo, en ciertas situaciones resulta ventajoso explotar la simetría de los problemas con la finalidad de simplificar y acotar los procedimientos de resolución.
En lo que sigue, se supondrá que la función de onda ψ con la que estaremos trabajando en cada caso es normalizable y que en el caso tridimensional está normalizada a la unidad sobre todo el espacio volumétrico V de interés:
Este requerimiento no presenta realmente limitación alguna, puesto que para cualquier sistema físicamente realizable siempre es posible imaginar que el sistema está encerrado en una caja muy grande para la cual siempre es posible definir funciones de onda normalizables. En ciertas ocasiones resultará conveniente usar funciones de onda que no han sido normalizadas (como los casos en los que el procedimiento de normalización parece que resultará bastante laborioso), aunque esto no es esencial. Con funciones de onda normalizadas, si el cuadrado absoluto de la función de onda representa la densidad de probabilidad por unidad de volumen de encontrar a la partícula en cierto lugar del espacio, entonces la esperanza matemática de cierta coordenada de la partícula (representada entre paréntesis angulados), que viene siendo lo mismo que el valor promedio de la coordenada para cierta función de onda, estará dada por:
Lo que acabamos de hacer lo podemos ver como un proceso límite en el cual vamos tomando segmentos infinitesimales de recta dx, multiplicando cada segmento infinitesimal de la recta por la probabilidad que le corresponde a cada segmento, y sumando, o mejor dicho, integrando, el total de los sub-productos para obtener el “gran promedio”. Substituyendo arriba la medida de la densidad de la probabilidad por el cuadrado absoluto de la función de onda que la genera a lo largo de la coordenada, tenemos la siguiente expresión:
Esto se suele escribir de la siguiente manera usada más convencionalmente en los textos de Mecánica Cuántica que destaca el hecho de que el cuadrado absoluto de una función de onda se obtiene del producto de la función de onda y su conjugado complejo:
Antes de continuar adelante, el lector atento podrá objetar al hecho de que la función de onda que estamos utilizando es una función de onda en la cual el tiempo no interviene en lo absoluto como variable independiente. ¿Acaso la ecuación de onda de Schrödinger no admite funciones de onda del tipo Ψ(x,t)?, podría preguntarse. En realidad, estamos utilizando aquí una simplificación, la simplificación de que la densidad de la probabilidad para una partícula con cierta energía es independiente del tiempo (más no así para una mezcla de varios estados, como lo veremos posteriormente cuando tratemos el tema de la evolución temporal de las ondas de materia para estados mezclados).
PROBLEMA: Demostrar que la densidad de la probabilidad para una función de onda para una partícula con cierta energía es independiente del tiempo.
Ya hemos visto que las soluciones para la ecuación de Schrödinger dependiente del tiempo cuando la partícula está en cierto estado de energía En pueden ser escritas del modo siguiente tras una separación de variables:
Entonces la densidad de probabilidad estará dada de acuerdo a la definición que hemos estado utilizando de la siguiente manera:
Se concluye entonces que la densidad de la probabilidad para una partícula que se encuentra en cierto estado de energía definido es independiente del tiempo y depende únicamente de la posición.
Por razones que pronto serán obvias, el valor esperado de la posición (o bien, la esperanza matemática de la posición) se suele escribir de la siguiente manera:
Esta prescripción que tenemos para obtener el “valor promedio” de la posición de una partícula a lo largo de un cierto eje coordenado para cierta función de onda se puede generalizar para permitir el cálculo de los valores promedios de varias potencias de la posición, y esto se puede extender al caso más realista en el cual consideramos la posición no sólo a lo largo de un solo eje coordenado sino en un espacio tridimensional integrando sobre elementos infinitesimales de volumen dV. Las definiciones a ser utilizadas para la obtención de estos promedios de potencias de la posición son las siguientes en el caso unidimensional:
Si podemos obtener un valor promedio para la posición, o sea la ubicación de la partícula, o inclusive para una potencia de la posición, debería ser posible definir también una esperanza matemática para el momentum lineal de la partícula. Ello sería posible si pudiéramos definir al momentum en función de la posición, p(x), lo cual nos permitiría calcular la esperanza matemática del momentum del siguiente modo:
Sin embargo, aquí nos topamos con un problema insalvable, ya que de acuerdo con el principio de incertidumbre, es imposible en principio definir al momentum en función de la posición, ya que la posición y el momentum son observables incompatibles que no pueden ser medidas simultáneamente con un grado ilimitado de precisión. Además, aquí aparentemente nos topamos con otra dificultad porque en la Mecánica Ondulatoria el operador utilizado para definir la cantidad que representa al momentum lineal de una partícula es un operador diferencial que tiene anexado un número imaginario de lo cual no se antoja factible el poder extraer un valor promedio:
Sin embargo, si recurrimos a la prescripción dada para obtener la esperanza matemática de la posición de la partícula a lo largo de un eje coordenado, en el mismo orden en el que fue dada, descubriremos que tenemos la receta justa para poder obtener el valor promedio del momentum lineal de la partícula, el cual debe ser un valor real. De este modo, llegamos a las siguientes definiciones:
En virtud de que el operador del momentum es un operador diferencial que actúa sobre lo que tiene inmediatamente a su derecha, al aplicar estas definiciones es importante obedecer en todo momento el orden en el cual se deben llevar a cabo las operaciones, ya que para un operador diferencial D no es lo mismo evaluar Df(x) que tratar de hacer algo con f(x)D, o sea que primero se aplica el operador diferencial del momentum a la función de onda ψ que tiene a su derecha, tras lo cual se toma el producto de lo que resulte con el conjugado complejo ψ* de la función de onda (la necesidad de llevar a cabo las operaciones en este orden se puede justificar de un modo formal, pero por razones pedagógicas es preferible postponer la discusión sobre la derivación de este tipo de definiciones hasta que se cubra el tema del espacio-momentum). Obsérvese aquí que estamos hablando de una no-conmutatividad en las operaciones, al igual que encontramos una no-conmutatividad en la Mecánica Matricial en virtud de que el producto de dos matrices no es conmutativo. En realidad, lo que está actuando aquí son los efectos de la no-conmutatividad de la “extraña ecuación” de Born, la cual es el pilar fundamental tanto de la Mecánica Ondulatoria como de la Mecánica Matricial.
Así como ψ* es el conjugado complejo de la función de onda ψ, del mismo modo podemos considerar a ψ como el conjugado complejo ψ* de dicha función de onda ψ. Esto nos lleva a preguntarnos si no habrá una manera en la cual podamos obtener el valor esperado del momentum (su esperanza matemática) en forma tal que, dentro del signo de la integral, el operador diferencial del momentum sea aplicado sobre ψ* en lugar de ser aplicado sobre ψ, lo cual a primera vista parece resultar truculento en virtud de que el orden de las operaciones ha adquirido ya una enorme importancia. Y podemos asentar una definición para ello con el operador diferencial del momentum actuando sobre ψ* y no sobre ψ. Esta definición de la esperanza matemática del momentum viene siendo dada por la siguiente expresión:
en donde el conjugado complejo del operador diferencial del momentum, P ha sido tomado de la siguiente manera:
Puesto que el conjugado complejo del producto de dos cantidades es igual al producto de los conjugados complejos de dichas cantidades, la definición que acabamos de dar puede ser escrita de la siguiente manera:
Y puesto que la esperanza matemática del momentum observable, lo que vamos a medir, es siempre una cantidad real que debe ser la misma sin importar la manera en la cual sea evaluada, lo que estamos afirmando aquí es que se debe cumplir en todo momento la siguiente condición:
Esto es precisamente lo que declaramos como la condición de Hermicidad (o Hermiticidad) del operador del momentum, y lo podemos tomar como el enunciado matemático preciso que define dicha condición. Más aún, esta definición se puede extender a cualquier otro operador de la Mecánica Cuántica sobre el cual vayamos a obtener una esperanza matemática que nos produzca el observable que corresponde a dicho operador.
El poder definir valores esperados tanto para la posición como para el momentum (o bien, sus esperanzas matemáticas, conocidas en la lengua inglesa como expectation values) nos permite obtener de inmediato el cuadrado de los valores promedios de ambos. Por otro lado, el poder definir la experanza matemática del cuadrado de la posición y el momentum nos permite restar los primeros de los segundos. La extracción de la raíz cuadrada de estas diferencias nos produce lo que se conoce como la desviación estandard σ, lo cual es una medida de la incertidumbre de una variable dentro de la Mecánica Ondulatoria. Y el producto de la incertidumbre en la posición con la incertidumbre en el momentum nos resulta en algo que también cumple con el principio de incertidumbre. Anteriormente esto lo habíamos obtenido por el camino de la Mecánica Matricial. Ahora llegamos a lo mismo por el camino de la Mecánica Ondulatoria.
Usando la interpretación estadística, las definiciones para las incertidumbres en la posición y el momentum, desde la perspectiva de la Mecánica Ondulatoria, vienen siendo exactamente las mismas que las que fueron definidas en la Mecánica Matricial, excepto que las esperanzas matemáticas usadas en la evaluación de dichas incertidumbres son obtenidas en la Mecánica Ondulatoria por la vía de la función de onda en lugar de utilizarse matrices para ello:
Usando la interpretación estadística, el principio de incertidumbre tal y como fue definido y utilizado en la Mecánica Matricial viene siendo también el mismo dentro de la Mecánica Ondulatoria:
Por lo que hemos visto arriba, las esperanzas matemáticas de los operadores asociados con cantidades físicas están relacionados a una función de onda ψ mediante la siguiente relación de carácter general:
La consistencia de este orden preciso de cosas (integral, conjugado complejo de función de onda, operador, función de onda, diferencial) nos puede meter eventualmente en la cabeza la idea de una posible simplificación simbólica en la cual podríamos intentar llevar a cabo una “compartimentalización” de símbolos que nos podría conducir hacia algo como lo siguiente:
En realidad, a partir del primer paso de “compartimentalización” estaríamos trabajando sobre algo esencialmente erróneo, porque el símbolo de la integral por sí solo o adjuntado a una función carece de sentido si no lleva aparejado el signo diferencial. Sin embargo, si eliminamos los pasos intermedios (los cuales pueden ser útiles únicamente como una ayuda mnemotécnica) y tomamos lo último como una representación de manera compacta de lo primero:
entonces estaríamos hablando ya de algo más cuerdo. Dejaremos una discusión acerca de este tipo de compactación simbólica pendiente para una entrada posterior, ya que no es indispensable para lo que estaremos estudiando, y a estas alturas en vez de darnos mayor claridad nos puede introducir algunas confusiones innecesarias.
Aunque pueda parecer un poco desconcertante al principio, podemos extender esta definición de esperanza matemática de un operador al operador diferencial H relacionado con la energía del sistema que quedaría definido de la siguiente manera tanto unidimensionalmente como en tres dimensiones:
Podemos esperar razonablemente que el valor esperado del operador diferencial Hamiltoniano de energía H (su esperanza matemática) una vez evaluado nos dé el promedio de la energía del sistema para cierto eigenestado del sistema.
PROBLEMA: Demostrar que la esperanza matemática de una suma de operadores es igual a la suma de las esperanzas matemáticas de cada operador tomadas por separado.
La solución de este problema es trivial, como podemos verlo a continuación:
PROBLEMA: Obténgase el valor esperado (su esperanza matemática) del operador H para el caso de una partícula confinada a moverse unidimensionalmente dentro de una caja de longitud L, con la partícula rebotando entre dos paredes impenetrables.
La ecuación de Schrödinger independiente del tiempo, expresada operacionalmente en su forma más compacta posible:
Hψ = Eψ
requiere que para el problema de una partícula encerrada en una caja el potencial V(x) fuera de la misma sea infinitamente grande, no habiendo por lo tanto solución posible fuera de la caja, y que el potencial V(x) sea igual a cero dentro de la caja, en cuyo caso la ecuación de Schrödinger expresada en forma más explícita para este problema adquiere el siguiente aspecto:
En la segunda línea se ha resaltado en color azul lo que vendría siendo esencialmente el operador energía H para este problema:
Para una partícula encerrada en una caja moviéndose unidimensionalmente, la función de onda ψ (ya normalizada) con el origen de las coordenadas situado en el extremo (en donde está situada la pared izquierda de la caja) es la siguiente
El conjugado complejo de esta función de onda es:
La esperanza matemática del operador H está dada entonces por:
Metiendo las funciones de onda y tras tomar la segunda derivada como lo pide esta última relación, obtenemos entonces:
Simplificando un poco:
Con un cambio de variables para poder llevar a cabo la integral definida obtenemos finalmente lo siguiente:
El valor esperado del operador Hamiltoniano H de energía es igual al autovalor eigen obtenido de la solución a la ecuación de onda de Schrödinger, lo cual era de esperarse ya que esta es precisamente la energía promedio del sistema para un valor dado del número cuántico. Este es el mismo resultado que ya habíamos obtenido previamente al estudiar la Mecánica Matricial de Heisenberg, pero lo hemos obtenido ahora a través de la esperanza matemática del un operador diferencial H que simboliza operacionalmente a la energía del sistema dentro de la Mecánica Cuántica. Puesto de otra manera:
Esto que se acaba de asentar arriba parece decepcionantemente simple, y hasta podría caerse en el grave error de tomarlo como algo trivial, pero lo que tenemos a la izquierda es la esperanza matemática de un operador matricial, mientras que lo que tenemos a la derecha es la esperanza matemática de un operador diferencial. Tenemos aquí un “punto de conexión” entre la Mecánica Matricial y la Mecánica Ondulatoria que merece ser resaltado:
Posteriormente iremos encontrando otros “puntos de conexión”, y eventualmente se demostrará que no se trata de meras coincidencias sino de la consecuencia directa de que ambas ramas de la Mecánica Cuántica en realidad están hablando de una misma cosa pero desde puntos de vista diferentes, tanto filosóficos como matemáticos.
Hemos llegado al punto apropiado para dejar asentada una precaución que le puede evitar al lector caer en muchas confusiones que suelen darse al estar consultando textos diversos que utilizan cierta terminología cuyo uso ha sido dictado por la práctica más que por la formalidad y cuyo contexto es perfectamente claro para quienes ya han sido prevenidos por sus maestros o sus tutores pero que no necesariamente es igualmente claro para quienes están estudiando la materia por vez primera sin la ayuda de alquien familiarizado con la terminología:
Integrales del tipo:
usualmente son llamadas elementos matriciales aún cuando no se estén utilizando métodos matriciales para nada.
Los conceptos que se han dado aquí para la definición de la esperanza matemática de un operador que representa los valores que pueda tomar cierta cantidad física como observable no pueden ser aplicados, sin embargo, para definir un operador de velocidad de una partícula, ya que para medir la con exactitud la velocidad de una partícula es necesario determinar primero su posición exacta en un instante dado, y después de cierto tiempo su nueva posición se debe poder determinar también con exactitud. Pero la medición de la posición en el instante de tiempo inicial perturba el momentum de la partícula, haciendo que una determinación de la velocidad basada en dos mediciones sucesivas de la posición carezca de sentido, todo lo cual en realidad viene siendo una consecuencia del principio de incertidumbre. Es por esto que, generalmente hablando, no hay operadores para la velocidad dentro de la Mecánica Ondulatoria. No había operador alguno relacionado directamente con la velocidad de una partícula en la Mecánica Matricial, y tampoco lo hay dentro de la Mecánica Ondulatoria. Se puede, sin embargo, definir la esperanza matemática de la velocidad de una partícula recurriendo de la siguiente manera a la definición misma del momentum de la partícula: