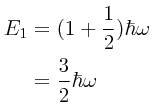Oscilador armónico simple: solución ondulatoria

Resolveremos aquí el problema del oscilador armónico simple mediante la ecuación de Schrödinger. El punto de partida será la ecuación diferencial eigen:

en donde H es un operador diferencial que representa la energía total del sistema con las variables clásicas reformuladas como operadores diferenciales, y E son los valores eigen que resultarán de la solución a la ecuación diferencial. Para este caso, la ecuación de onda de Schrödinger independiente del tiempo para un cuerpo de masa m moviéndose dentro de un campo potencial V será:

El movimiento del cuerpo en el oscilador armónico simple es unidimensional, a lo largo de una coordenada que aquí identificaremos como el eje-x, el eje de las abcisas. En una dimensión, el operador ∇² se reduce simplemente a ∂²/∂x², o lo que es lo mismo, d²/dx². Por otra parte, la energía potencial en el oscilador armónico simple es V = kx²/2; esta es una parábola que podemos graficar de la siguiente manera:

En la gráfica se ha colocado una esfera dentro de la parábola que nos puede describir a la perfección el comportamiento del oscilador armónico simple. Clásicamente, si la esfera se encuentra en reposo en el fondo del recipiente parabólico, allí permanecerá por siempre sin ir jamás a ningún lado. Sin embargo, si la esfera se encuentra inicialmente en reposo en un punto como el mostrado en la figura que corresponde a una energía potencial V(x).=.5 estando sujeta a un campo gravitacional, la esfera empezará a perder energía potencial y a ganar energía de movimiento (cinética) al caer al fondo de la parábola. Suponiendo que no hay fricción alguna entre la esfera y la parábola (y por lo tanto no hay pérdidas de energía por rozamientos), al llegar al fondo de la parábola toda la energía potencial de la esfera se habrá convertido en energía cinética. Pero la cosa no para allí. La esfera continúa su movimiento, pero esta vez en ascenso, perdiendo energía cinética al ir ganando energía potencial hasta llegar a una altura igual a la que tenía inicialmente en el lado opuesto de la parábola, tras lo cual el ciclo volverá a repetirse indefinidamente.

Con una energía potencial V(x) = kx²/2, la ecuación de Schrödinger se nos convierte en lo siguiente:

Removiendo los paréntesis para que los términos del operador combinado puedan actuar directamente sobre el operando ψ:

Podemos hacer la siguiente substitución de variables:

en donde λ = 2E/ħω.

Para un oscilador armónico simple se sabe que ω.=.√k/m, o bien k.=.mω². Por otra parte, podemos hacer el siguiente cambio de variable:

con lo cual podemos escribir lo siguiente:

de lo cual obtenemos:

Obsérvese que esta substitución “limpia” el coeficiente de la derivada de segundo orden. Además:

De este modo, la ecuación diferencial es ahora, puesta en función de la variable y:

o bien:

En la búsqueda de soluciones para esta ecuación diferencial, vemos que cuando y→∞ entonces λ se vuelve despreciable en comparación con y², y la ecuación se reduce asintóticamente a:

La solución de esta ecuación diferencial de segundo orden es simplemente (indicaremos aquí proporcionalidad en lugar de igualdad a espera de completar posteriormente la solución agregándole el factor que le falte ):

lo cual podemos comprobar de inmediato de la siguiente manera:

La dependencia asintótica es válida únicamente para un signo negativo en el exponencial, porque con un signo positivo la función de onda adquiere valores infinitamente grandes y no puede ser normalizada.

Por otra parte, la función ψ(y) mantendrá la caída asintótica (debido a la caída rápida producida por el exponencial) si es multiplicada por un polinomio finito H(y). La solución tentativa será entonces:

Substituyendo esta solución tentativa en la ecuación diferencial de arriba, obtenemos lo siguiente:

Supóngase ahora una solución polinómica, en la forma de un polinomio finito:

H(y) = a₀ + a₁y + a₂y² + ... + a_py^p

H(y) = Σ_i=0 a_iyⁱ

en donde el sub-índice en la sumatoria especifica que la sumación corre desde i.=.0 hasta un entero i.=.p. Si substituímos este polinomio en la ecuación diferencial después de haber tomado la primera y segunda derivadas, e igualamos la sumas de los coeficientes con exponentes iguales a cero, obtenemos la siguiente relación recursiva:

Para que no tengamos un polinomio infinito, se requiere ponerle un “tope”, lo cual se logra cuando el numerador de la relación recursiva se hace cero para un entero s.=.n, o sea:

2n + 1 - λ = 0

λ = 2n + 1

Pero ya habíamos hecho previamente λ = 2E/ħω. Revirtiendo a la notación original tenemos entonces:

2E/ħω = 2n + 1

Despejando para E tenemos entonces el siguiente resultado que nos indica que los valores de la energía E que puede tomar un oscilador armónico simple no pueden tomar cualquier valor dentro de un rango continuo, están cuantizados:

A continuación se muestran estos niveles de energía superimpuestos en el diagrama de la energía potencial del oscilador armónico simple:

Este es exactamente el mismo resultado que el que obtuvimos mediante la Mecánica Matricial de Heisenberg. Sin embargo, en la Mecánica Matricial no se tuvo que recurrir a ecuaciones diferenciales ni a ninguno de los elementos del cálculo infinitesimal, todo se llevó a cabo manejando matrices en combinación con la “extraña ecuación” de Max Born. El haber obtenido el mismo resultado puede y debe despertar sospechas de que no se trata de una simple coincidencia, y de que hay un mar de fondo que conecta ambas formas de hacer la Mecánica Cuántica. Si bien en la resolución del problema del oscilador armónico simple mediante la Mecánica Ondulatoria no se ha recurrido a la ecuación de Born, ello no implica que dentro de toda la estructura matemática de la Mecánica Ondulatoria no esté operando en forma oculta dicha ecuación a grado tal que sin ella todo lo que hemos logrado aquí se nos vendría abajo. Lo menos que podríamos esperar en este momento es que la ecuación de Schrödinger nos conduzca tarde o temprano a la conclusión de que el momento angular está cuantizado de la misma manera en la que lo está bajo el modelo atómico planetario de Bohr y bajo la Mecánica Matricial de Heisenberg. Investigaremos posteriormente este asunto que no es un asunto superficial sino un asunto de fondo.

En el caso de los polinomios finitos que nos resultan arriba como parte de la solución del problema, los primeros polinomios resultan ser:

H₀ = 1

H₁ = 2y

H₂ = 4y² - 2

H₃ = 8y³ - 12y

H₄ =16y⁴ - 48y² + 12

H₅ =32y⁵ - 160y³ + 120y

Estos polinomios son ampliamente conocidos en las matemáticas como los polinomios de Hermite (en honor al matemático francés Charles Hermite, el mismo que contribuyó a la Mecánica Cuántica con el concepto de los operadores Hermitianos y las matrices Hermitianas), siendo las gráficas de los mismos las siguientes:

Y los polinomios de Hermite son polinomios ortogonales, en el sentido de que si tomamos cualquier par de dichos polinomios e integramos el producto de los mismos desde un rango que vaya desde -1 hasta +1 el resultado será igual a cero. Esto se parece mucho a los vectores ortogonales que encontramos al empezar con el estudio de la Mecánica Matricial, y de hecho si a cada una de estas funciones polinómicas Hermitianas las llamamos “vectores”, en cierta forma (aunque no aplique aquí la geometría vectorial ordinaria) están a “ángulos rectos” cada una de ellas con respecto a las demás. Sin embargo, si tomamos el producto de cualquiera de los polinomios de Hermite consigo mismo e integramos el producto nuevamente desde un rango que vaya desde -1 hasta +1, el resultado no será cero. Los polinomios de Hermite como están dados arriba no están normalizados, pero los podemos normalizar sin problema alguno, con lo cual son capaces de generar un conjunto de funciones ortonormales, justo el tipo de funciones que resultan útiles para introducir el concepto de la probabilidad en los problemas de la Mecánica Ondulatorial.

Una fórmula ampliamente utilizada para generar los polinomios de Hermite es la fórmula de Rodrigues descubierta por el matemático francés Benjamín Olinde Rodrígues (nos volveremos a encontrar esta misma fórmula, aplicada al caso de los polinomios de Legendre en la entrada titulada “Polinomios de Legendre: aspectos matemáticos”):

PROBLEMA: Obténganse los primeros cuatro polinomios de Hermite con la fórmula de Rodrígues.

La aplicación de la fórmula de Rodrígues es directa y no tiene mayor ciencia:

Las funciones de onda ψ(x) correspondientes a cada uno de los números cuánticos del oscilador armónico simple serán iguales al producto de cada uno de los polinomios de Hermite dados arriba multiplicados por la función exponencial decreciente que se sobrepone rápidamente a los exponentes de los polinomios logrando que ψ(x).→.0 cuando x.→.∞ tanto para los valores positivos como los valores negativos de x, multiplicadas por una constante de normalización dada por la siguiente expresión para cada uno de los números cuánticos principales n:

Las gráficas de cada una de las funciones de onda que corresponden al oscilador armónico simple se dan a continuación.

Para n = 1:

Para n = 2:

Para n = 3:

Para n = 4:

Para n = 5:

Para n = 6:

Se debe recordar que es el cuadrado de la función de onda, o sea |ψ(x)|², el que nos dá la probabilidad de encontrar a la partícula en una región Δx de la gráfica.

En la siguiente figura tenemos una gráfica tridimensional en la cual tenemos en un plano el diagrama de los niveles de energía del oscilador armónico simple y en el cual aparecen superimpuestos en tercera dimensión las amplitudes de probabilidad para las funciones de onda de los estados del oscilador armónico simple:

En la siguiente figura tenemos graficadas 25 funciones de onda para 25 estados del oscilador armónico simple:

PROBLEMA: El siguiente diagrama dá la curva que corresponde a la probabilidad |Ψ1² = ψ*ψ para el estado n = 10 del oscilador armónico simple, y asímismo dá la curva (en líneas punteadas) que corresponde al comportamiento de una partícula clásica. ¿Cómo ilustra este diagrama el principio de correspondencia de Bohr?

De acuerdo al principio de correspondencia, para números cuánticos grandes el oscilador se aproximará en comportamiento al de un oscilador clásico macroscópico, tal como un péndulo. En la figura podemos ver que la distribución de probabilidades aumenta en los extremos en donde tenemos los “puntos de viraje” (conocidos en inglés como turning points) donde la energía del sistema es únicamente energía potencial. Esto nos describe el comportamiento de un péndulo real el cual gasta más tiempo en disminuír su velocidad e invertir la dirección de su movimiento en los extremos de su desplazamiento que en el centro del movimiento en donde adquiere su máxima velocidad permaneciendo un tiempo menor que en los extremos. Entre mayor sea el número cuántico, tanto mejor será la aproximación al modelo clásico, como lo muestra la siguiente figura:

PROBLEMA: Clásicamente, la función de probabilidad para el oscilador harmónico simple está dada por la siguiente expresión:

en donde el origen de la coordenada-x está situado a la mitad de la trayectoria recorrida por el cuerpo conforme se traslada de un extremo a otro, en lo que vendría siendo el punto de reposo si el cuerpo no estuviese en movimiento. Evalúese a partir de dicha expresión la probabilidad de que el cuerpo se encuentre entre x.=.0 y x.=.+√2E/k.

Conforme el cuerpo se mueve de un extremo a otro, viaja desde el extremo izquierdo situado en x.=.-√2E/k y después de pasar por x.=.0 llega hasta x.=.+√2E/k invirtiendo el sentido de su movimiento para volver hacia el punto de inicio. En la teoría clásica, la probabilidad de encontrar al cuerpo en algún punto específico de la trayectoria es inversamente proporcional a su velocidad en dicho punto, volviéndose infinitamente grande en los “puntos de volteo” (turning points) del movimiento en donde la velocidad del cuerpo es instantáneamente igual a cero.

Identificaremos como A la máxima excursión del cuerpo desde su punto central, de modo tal que el cuerpo se mueve repetidamente entre -A y +A. Al hablar acerca de la probabilidad de encontrar al cuerpo en algún punto de la trayectoria, en realidad estamos hablando acerca de la probabilidad de encontrarlo dentro de cierto segmento de longitud, ya que lo que nos mide la probabilidad en realidad es el área bajo la curva, cualquier punto de la distribución de probabilidades P(x) por sí solo no nos dá información alguna. De este modo, la probabilidad (infinitesimal) de encontrar al cuerpo en un segmento infinitesimal de longitud será igual al área infinitesimal de interés obtenida multiplicando al segmento infinitesimal de longitud por la altura dada por la distribución de probabilidades:

La probabilidad de encontrar al cuerpo entre x.=.0 y x.=.+√2E/k se obtiene llevando a cabo la integración para obtener el área bajo la curva entre dichos puntos:

La evaluación de la integral entre los límites especificados nos dá lo siguiente:

Este resultado nos dice que el cuerpo se la pasará la mitad de su tiempo entre los puntos x.=.0 y x.=.+√2E/k, ya que la probabilidad de encontrarlo entre dichos puntos es igual a 1/2 al tomarle una “instantánea” al cuerpo con una cámara fotográfica. El resto del tiempo se la pasará entre los puntos x.=.0 y x.=.-√2E/k.

PROBLEMA: Obténgase la distribución de probabilidad dada en el enunciado del problema anterior para el oscilador armónico simple clásico.

Puesto que la función de probabilidad para el oscilador armónico simple clásico igual a la probabilidad de que encontremos a la partícula dentro de cierto intervalo infinitesimal de longitud en su desplazamiento al tomar una fotografía “instantánea”, podemos definir también a la distribución de probabilidad para el oscilador armónico simple clásico como la probabilidad de que en cierto intervalo infinitesimal de tiempo encontraremos a la partícula dentro de cierto intervalo infinitesimal de longitud, lo cual dependerá de la velocidad de la partícula en el punto bajo consideración, siendo dicha probabilidad máxima en un segmento de longitud en donde la partícula se esté moviendo más rápidamente (permaneciendo menor tiempo en dicho punto) y siendo mínima en un segmento de longitud en el cual la partícula pierde toda su velocidad (los puntos extremos de su desplazamiento o puntos de volteo). Desde el punto de vista puramente energético, la energía total E de la partícula es igual a la suma de su energía cinética (que es mv²/2) y su energía potencial (que para el oscilador armónico simple clásico es kx²/2), de lo cual se obtiene lo siguiente:

Pero para el oscilador armónico simple la frecuencia angular ω.=.√k/m, estando a su vez relacionada con el período τ del movimiento mediante la expresión ω.=.2π/τ. Si usamos únicamente el semi-período de tiempo τ/2, que es igual al tiempo que la partícula tarda en ir de un extremo a otro, vemos entonces que:

con lo cual el problema queda esencialmente resuelto.

No nos debe preocupar mucho el hecho de que la distribución de probabilidades se vuelva infinitamente grande en los “puntos de volteo”, ya que lo único que cuenta es el área bajo la curva, y como lo hemos verificado en la resolución de este problema, el área bajo la curva no es infinitamente grande, de hecho es igual a la unidad entre los dos extremos del movimiento. Obsérvese cómo el modelo cuántico se va aproximando al modelo clásico al irse sumando todas las áreas que contribuyen a la probabilidad total.

Para aquellos que hayan estudiado ya desde el punto de vista clásico el comportamiento del oscilador armónico simple, algo que será bastante obvio aquí es la ausencia de la variable del tiempo en la descripción del movimiento oscilatorio. En la mecánica clásica, la variable del tiempo es fundamental en las ecuaciones diferenciales del movimiento, y la solución de tales ecuaciones diferenciales frecuentemente conduce a soluciones de tipo senoidal o cosenoidal en las cuales el tiempo está presente describiendo el cambio oscilatorio en la posición de la partícula dada como una función de la variable del tiempo, que en el caso unidimensional viene siendo x(t). La solución clásica al problema dinámico del oscilador armónico simple empieza con la formulación vectorial segunda ley de Newton aplicada a la ecuación de la fuerza restauradora de un resorte de constante k:

con una solución relativamente sencilla para lo que viene siendo una ecuación diferencial lineal de segundo orden:

La solución clásica nos dá la posición de la partícula directamente en función de la variable del tiempo. Pero en la Mecánica Cuántica no es posible dar una descripción así porque si fuese posible conocer la posición exacta de la partícula en cada instante de tiempo sería posible entonces definir el momentum de la partícula en cada instante de tiempo con sólo conocer la masa de la partícula, y ya hemos visto que el principio de incertidumbre impide que se puedan conocer con precisión ilimitada tanto la posición como el momentum de la partícula al ser variables incompatibles en la “extraña ecuación” de Born. Simple y sencillamente no es posible tener una expresión como x(t) en la Mecánica Cuántica. Podemos, eso sí, procurar una expresión para la esperanza matemática de la posición de la partícula en función del tiempo, y aún así encontraremos que la respuesta usual será un resultado que no incluye a la variable del tiempo. ¿Significa entonces que la variable del tiempo está proscrita en los casos que hemos estado analizando? No necesariamente. Recuérdese que la ecuación general de Schrödinger incluye tanto una parte espacial como una parte temporal. Sin embargo, para hacer que la parte temporal salga a relucir, ello requiere por lo general de un sistema físico que conste por lo menos de dos estados mezclados (la discusión de esto será vista posteriormente una vez que el lector haya adquirido una mayor familiaridad con los conceptos que aquí se están discutiendo). Pero si un sistema como el oscilador armónico simple se encuentra en un estado definido de energía, por ejemplo el estado fundamental de más baja energía (E₀) o el primer estado excitado (E₁), la función de onda Ψ no puede describir un movimiento oscilatorio, todo lo que tenemos es una visión estática y no dinámica.

A continuación tenemos un resumen de las eigenfunciones de onda y los eigenvalores que corresponden al oscilador armónico simple, usando como una medida simplificadora la constante adimensional ξ.=.√mω/ħ·x que nos permite simplificar un poco la notación permitiéndonos concentrar nuestros esfuerzos sobre “el gran panorama”:

PROBLEMA: Haciendo a.=.mω/ħ para fines de mayor simplicidad, verifíquese que la eigenfunción ψ₃ en las relaciones dadas arriba está normalizada.

Si ψ₃(x) está normalizada, se debe cumplir entonces lo siguiente:

De acuerdo con lo que tenemos arriba y haciendo a.=.mω/ħ, la eigenfunción normalizada ψ₃(x) está dada por:

A continuación evaluaremos |ψ₃(x)|².=.ψ₃(x)*ψ₃(x) llevando a cabo la integración sobre todo el espacio:

Esto viene siendo lo mismo que:

Elevando el binomio al cuadrado y rompiendo la integral en tres integrales:

Para evaluar cada una de las tres integrales podemos utilizar la siguiente receta tomada directamente de las tablas de integrales convencionales:

Por lo tanto:

Simplificando:

que termina siendo:

Se concluye entonces que ψ₃(x), escrita de conformidad con las convenciones dadas arriba, está normalizada.

PROBLEMA: Obténgase la esperanza matemática de la posición para una partícula sometida a un potencial de oscilador armónico simple suponiendo que la partícula se encuentra en el estado basal.

Para un oscilador armónico simple en el estado fundamental, n.=.0. Tomando ψ₀ en las relaciones dadas arriba y haciendo a.=.mω/ħ para fines de simplicidad, el valor esperado de la posición de la partícula es evaluado entonces de la manera siguiente:

El valor de la integral es cero debido a que el integrando es una función impar. Entonces el valor esperado de la posición resulta ser:

que es el centro de la parábola. De este modo, el estado n.=.0 puede interpretarse como una oscilación simétrica alrededor de la posición de equilibrio; o bien, puede decirse que en promedio a la partícula la podemos esperar encontrar tanto tiempo a la izquierda (-x) como a la derecha (+x) de la posición de equilibrio x.=.0.

PROBLEMA: Obténgase la esperanza matemática del momentum para una partícula sometida a un potencial de oscilador armónico simple suponiendo que la partícula se encuentra en el estado basal.

Simbolizando como P_x al operador diferencial cuántico que representa al momentum de la partícula, la esperanza matemática del momentum estará dada por la relación:

En la Mecánica Ondulatoria, el operador del momentum es:

Substituyendo este operador en la expresión de arriba así como la eigenfunción de onda que corresponde al estado basal del oscilador armónico simple, se tiene:

Este resultado de un promedio estadístico igual a cero para el momentum de la partícula en un potencial de oscilador armónico simple podemos justificarlo argumentando que, en promedio, la partícula se mueve tantas veces hacia la derecha como hacia la izquierda, cancelando las contribuciones positivas al momentum en igual monto a las contribuciones negativas al momentum.

PROBLEMA: Usando la siguiente integral definida que se puede encontrar en cualquier referencia decente de tablas de integrales:

obténgase la esperanza matemática del cuadrado de la posición para una partícula sometida a un potencial de oscilador armónico simple suponiendo que la partícula se encuentra en el estado basal.

Procediendo de modo semejante a como se hizo en los problemas anteriores, la esperanza matemática del cuadrado de la posición se puede definir cuánticamente de la manera siguiente:

Substituyendo en esta expresión la eigenfunción de onda ψ₀ que corresponde al estado basal del oscilador armónico simple, se tiene:

Entonces, usando la integral definida dada arriba tal y como la proporcionan las tablas, la esperanza matemática del cuadrado de la posición será:

PROBLEMA: Usando la información suministrada en el problema anterior y usando la siguiente integral definida que se puede encontrar en cualquier referencia decente de tablas de integrales:

obténgase la esperanza matemática del cuadrado de la posición para una partícula sometida a un potencial de oscilador armónico simple suponiendo que la partícula se encuentra en el estado basal.

Simbolizando como P_x² al operador diferencial cuántico que representa operacionalmente al cuadrado del momentum de la partícula, la esperanza matemática del cuadrado del momentum (la observable) estará dada por la siguiente relación:

Puesto que, operacionalmente hablando, se tiene:

entonces:

Integrando desde cero hasta +∞ en lugar de integrar desde -∞ hasta +∞ (lo cual logramos metiendo un factor de 2) y separando lo que tenemos entre los paréntesis cuadrados en dos integrales:

Recurriendo a las integrales definidas dadas en este problema y en el problema anterior, llegamos entonces al resultado deseado:

PROBLEMA: Obténgase la esperanza matemática del operador Hamiltoniano de energía para una partícula sometida a un potencial de oscilador armónico simple suponiendo que la partícula se encuentra en el estado basal.

Como se vió al principio, el operador Hamiltioniano de energía H para el oscilador armónico simple es igual a la suma de los términos de energía cinética y energía potencial del oscilador:

Tomando las esperanzas estadísticas de ambos miembros de la igualdad y usando los resultados obtenidos previamente para la esperanza matemática del cuadrado del momentum y la esperanza matemática del cuadrado de la posición, obtenemos el valor esperado de la energía para el oscilador armónico simple en su estado basal:

Obsérvese que este eigenvalor de energía es justo lo que obtenemos empleando la fórmula obtenida arriba para el caso de un oscilador armónico simple en el estado basal n.=.0.

PROBLEMA: Verifíquese que para el estado basal (n.=.0) del oscilador armónico simple la energía cinética promedio es igual a la energía potencial, o lo que es lo mismo, la esperanza matemática de la energía cinética es igual a la esperanza matemática de la energía potencial.

La esperanza matemática de la energía potencial del oscilador armónico simple en su estado basal se puede obtener de la siguiente manera:

Por otro lado, la esperanza matemática de la energía cinética del oscilador armónico simple en su estado basal se puede obtener de la siguiente manera:

Obviamente, la energía potencial promedio y la energía cinética promedio del oscilador armónico simple en su estado basal son iguales, esto es:

La conclusión que se obtuvo en este problema se puede generalizar para todos los demás estados estacionarios del oscilador armónico simple.

PROBLEMA: Clásicamente, un oscilador armónico simple tiene su movimiento estrictamente acotado. Si imaginamos una masa conectada a un resorte, entonces la masa oscilante tendrá una excursión máxima con respecto a su punto de reposo cuando el resorte esté estirado al máximo, en cuyo punto toda la energía cinética de la partícula habrá sido transferida y almacenada como energía potencial en el resorte. Y en la excursión contraria, cuando el resorte esté comprimido al máximo, la partícula dejará de moverse momentáneamente de modo tal que de nueva cuenta toda la energía cinética de la partícula habrá sido transferida y almacenada como energía potencial en el resorte. La partícula no puede ir más allá de sus puntos de viraje al haberse transferido toda su energía al resorte. Sin embargo, desde la perspectiva de la Mecánica Ondulatoria, algo de la función de onda de la partícula alcanza a filtrarse fuera de la región clásica para penetrar en una región clásicamente prohibida. Usando el oscilador armónico simple como modelo cuántico, calcúlense las distancias que fijan las barreras clásicas para las funciones de onda ψ₀(x), ψ₁(x) y ψ₂(x) del oscilador armónico simple fuera de las cuales “algo” de la partícula es capaz de penetrar en una región clásicamente prohibida. Hecho esto, hágase una gráfica del cuadrado de la función de onda ψ₂(x) indicando claramente los límites de cada región clásicamente prohibida.

Para el estado fundamental del oscilador armónico simple, con n.=.0 la eigen-energía E₀ será:

La distancia crítica x₀ ocurre justo cuando la energía potencial V(x) se ha igualado a este valor de la eigen-energía E₀, con lo cual:

Para el primer estado excitado del oscilador armónico simple, con n.=.1 la eigen-energía E₁ será:

La distancia crítica x₁ ocurre justo cuando la energía potencial V(x) se ha igualado a este valor de la eigen-energía E₁, con lo cual:

Por último, para el segundo estado excitado del oscilador armónico simple, con n.=.2 la eigen-energía E₂ será:

La distancia crítica x₂ ocurre justo cuando la energía potencial V(x) se ha igualado a este valor de la eigen-energía E₂, con lo cual:

De acuerdo con lo que se ha visto previamente, la eigenfunción ψ₂(x) estará dada por la expresión:

El cuadrado de esta función de onda ψ₂(x) es:

La gráfica de esto último con los límites de acotamiento superimpuestos en la gráfica es la siguiente:

Las regiones clásicamente prohibidas han sido destacadas con fondo gris. Como puede verse, “algo” de la partícula se puede filtrar hacia afuera en ambos lados. O mejor dicho, si preparamos muchos experimento con muchas partículas, algunas de ellas podrán terminar encontrándose en regiones clásicamente prohibidas. Aunque esto nos parezca un absurdo, se trata de uno de los hechos de la vida a los que tenemos que irnos acostumbrando en el extraño mundo de la Mecánica Cuántica, anticipando aún más sorpresas en camino.

PROBLEMA: Obténgase con una precisión de cuatro cifras significativas la probabilidad de encontrar en una región clásicamente prohibida a una partícula que se encuentra en un estado basal que corresponde a un oscilador armónico simple .

La probabilidad de encontrar en todo el espacio (desde -∞ hasta +∞) a una partícula que se encuentra en el estado basal que corresponda a un oscilador armónico simple ciertamente debe ser igual a la unidad, lo cual expresamos formalmente con la interpretación de Born:

Para una partícula en el estado basal de un oscilador armónico simple, la gráfica del cuadrado de la función de onda correspondiente, |ψ₀(x)|², resulta ser el de una distribución normal o distribución Gaussiana. De acuerdo a lo que obtuvimos en el problema anterior, “algo” de la función de onda se filtrará fuera de la región clásica hacia cualquiera de dos regiones clásicamente prohibidas (destacadas con color gris obscuro):

Lo que tenemos en la gráfica nos indica que la integración que se lleva a cabo arriba desde desde -∞ hasta +∞ se puede “romper” en la suma de tres integrales: una integral que corresponde a la región clásicamente prohibida que va desde -∞ hasta -x₀ (de color gris obscuro), otra integral  que corresponde a la región clásicamente permisible que va desde -x₀ hasta +x₀ (de color ciano), y una una integral que corresponde a la región clásicamente prohibida que va desde +x₀ hasta +∞ (de color gris obscuro), siendo la suma total de las “áreas bajo las curvas” igual a la unidad:

La simetría de la función |ψ₀(x)|², una función de onda par, nos permite afirmar que las dos regiones a cada lado de la curva normal tienen áreas iguales:

Entonces podemos juntar ambas regiones “prohibidas” en una sola:

Lo anterior es lo mismo que:

Lo que tenemos en ambos lados de la igualdad de esto último es precisamente lo que estamos buscando, la probabilidad de que la partícula se encuentre en una región clásicamente prohibida. Trabajaremos sobre la expresión derecha y apelando nuevamente a la simetría de la curva normal haremos otra simplificación:

Haciendo uso de la simplificación a.=.mω/ħ, recurriremos ahora a la expresión explícita para la función de onda del estado basal del oscilador armónico simple ψ₀(x) en conformidad con lo estipulado arriba, con lo cual lo anterior se puede escribir como:

Elevando al cuadrado y sacando las constantes fuera de la integral:

Lo anterior no está aún en una forma que pueda ser consultada en las tablas numéricas para la curva normal. Con tal cosa en mente, ahora efectuaremos el siguiente cambio de variables:

Con este cambio de variables, la expresión se convierte en:

o lo que es lo mismo:

Nos falta redefinir el límite superior x₀ en función de la nueva variable, para lo cual usando:

se tiene entonces:

Por lo tanto:

Lo que está entre los paréntesis cuadrados está ya en conformidad con la forma especificada en muchas tablas comunes para la curva normal. Recurriremos a las tablas del libro Biometrica Tables for Statisticians de E. S. Pearson y H. O. Hartley (publicado por Cambridge University Press) para obtener:

Por lo tanto:

En promedio, habrá una probabilidad del 15.86% de encontrar a la partícula en una región clásicamente prohibida.

Los desarrollos llevados a cabo aquí bajo la filosofía de la Mecánica Ondulatoria con la ayuda de la ecuación de onda de Schrödinger deben ser contrastados con los procedimientos de solución utilizados bajo la filosofía de la Mecánica Matricial en la entrada titulada “Oscilador armónico simple: solución matricial”. Téngase en cuenta que las funciones de onda no aparecen para nada en la Mecánica Matricial, como tampoco se utiliza allí el concepto de las ondas de materia. Y sin embargo, ambas técnicas y filosofías nos conducen a las mismas soluciones para todo lo que tiene que ver con las cantidades observables en el laboratorio. Esto se debe al hecho de que, como se verá en una entrada posterior titulada “Mecánicas Matricial y Ondulatoria: equivalencia”, desde el punto de vista estrictamente matemático ambas técnicas son esencialmente la misma cosa, aunque cueste trabajo creerlo.

Nos queda por aclarar un punto importante. Hemos estado trabajando arriba con la ecuación de onda de Schrödinger independiente del tiempo, lo cual implica que hemos estando dejando fuera el factor:

Tómese por ejemplo la eigenfunción de onda ψ₀(x) para el caso n.=.1 en el oscilador armónico simple (simbolizada también como ψ₁(x) como lo hemos hecho arriba, aunque la interpretación del sub-índice se vuelve obvia dentro del contexto que esté siendo analizado). ¿Realmente está oscilando esta función de onda? Porque de ser así, esta función estaría moviéndose de arriba hacia abajo y de abajo hacia arriba como lo hace una cuerda tensada, lo cual parecería razonable. Sin embargo, si metemos dentro del panorama el criterio de Born, esto parecería algo totalmente absurdo, porque al estar dada la densidad de probabilidad del sistema por |.ψ₀(x).|², esto implicaría que al estar la onda completamente plana (al cruzar el punto arriba del cual la onda tiene su cúspide apuntando hacia arriba pasando a donde la cúspide de la onda está apuntando hacia abajo) en ese preciso instante de tiempo  |.ψ₀(x).|² tendría un valor exactamente igual a cero a lo largo de toda la coordenada de abcisa x; en pocas palabras, la partícula desparecería por completo dejando de existir en ese preciso instante de tiempo. Sin embargo, esta interpretación es errónea, porque la función de onda completa (dependiente del tiempo) consta de una parte real y de una parte imaginaria. Y en la evaluación matemática de la densidad de probabilidad tenemos que tomar en cuenta tanto la parte real como la parte imaginaria. Si graficamos tanto la parte real como la parte imaginaria de la función de onda en un archivo dinámico haciendo que ambas oscilen al mismo ritmo (lo cual supone que ambas partes tienen el mismo factor temporal exponencial), podemos entender que la suma cuadrática de ambas se mantendrá constante. Esto lo podemos apreciar con mayor claridad en el siguiente gráfico animado que nos muestra las primeras dos funciones de onda ψ₀(x,t) y ψ₁(x,t)  para el oscilador armónico simple recurriendo para ello a la fórmula de Euler (se muestra una tercera función de onda ψ_N(x) que será explicada más abajo):

En conformidad con la convención que hemos estado adoptando a lo largo de esta obra, las curvas azules representan la parte real de cada función de onda, mientras que las curvas rojas representan el conjugado complejo de cada función de onda. Como puede apreciarse en las primeras dos gráficas de la derecha para ψ₀(x,t) y ψ₁(x,t), al tomar el valor absoluto del producto de la función de onda y su conjugado complejo el factor temporal se elimina y todo lo que nos queda es una densidad de probabilidad estática. ¿Y qué de la tercera función de onda, para la cual la densidad de probabilidad parece mostrar una oscilación? Resulta que esta función de onda ψ_N(x,t) es una combinación de las funciones de onda que corresponden a los dos primeros estados del oscilador armónico simple pero con un factor temporal diferente anclado a cada estado. Lo que tenemos en la tercera gráfica viene siendo, en efecto, lo que se conoce como una mezcla de estados o estados mezclados. Tendremos algo más que decir sobre este tema en las entradas tituladas “Evolución temporal de las ondas de materia”.