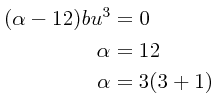Supóngase que tenemos una partícula que está especificada por un número cuántico l.=.2, el número cuántico relacionado con el momento angular orbital. Por lo que hemos visto en las entradas previas, la función de onda de una partícula en el estado l.=.2 puede estar de hecho “desdoblada” en cinco sub-estados distintos (m.=.-2, m.=.-1, m.=.0, m.=.1 y m.=.2). Para que estos estados puedan ser vistos como grupos de líneas espectrales adicionales en la muestra que está siendo estudiada, es necesario someter a la muestra a un campo magnético, el cual producirá el “desdoblamiento” de la línea espectral solitaria en las cinco líneas. Así, de un ensamble de partículas cierta cantidad de ellas estará en un estado m, otra cantidad estará en otro estado m, y así sucesivamente. Resta decir que la intensidad relativa de cierta línea espectral con respecto a las demás estará directamente relacionada con la probabilidad de encontrar a una partícula cualquiera en dicho estado con respecto a las probabilidades de encontrar a las otras partículas con l.=.2 en sus estados respectivos. Si una línea espectral tiene una intensidad tres veces mayor que otra, se sobreentiende que habrá una probabilidad tres veces mayor de encontrar a la partícula en un estado que en el otro.
Para una partícula que está especificada por el número cuántico l.=.2, la parte angular de la función de onda total que llamaremos Θ será igual a la combinación lineal de las armónicas esféricas que especifican a cada estado, lo cual expresado matemáticamente se puede escribir del modo siguiente:
Tomemos a modo de ejemplo el estado Y2,1. La magnitud relativa de la “intensidad” de dicho estado la podemos especificar como:
La suma de las intensidades de todos los estados debe ser igual al gran total que sirve como referencia para evaluar las intensidades relativas. De este modo, la intensidad relativa que corresponde al estado m.=.1 debe ser:
que debe ser a su vez igual a la probabilidad de encontrar a la partícula en el estado m.=.1. De la misma manera, la intensidad relativa que corresponde al estado m.=.0 debe ser:
En la entrada anterior se llevó a cabo el análisis del momento angular orbital partiendo de la ecuación de onda de Schrödinger aplicada a un problema de simetría esférica sin poner mucho énfasis al principio en la acción de los operadores del momento angular orbital sobre la parte angular de la función de onda. Para dar una perspectiva más amplia sobre lo que está sucediendo, en esta entrada se volverá a llevar a cabo el mismo tipo de análisis excepto que en esta ocasión se irá dando énfasis desde un principio a los operadores del momento angular; y se verá también en mayor detalle el aspecto matemático de los polinomios de Legendre llegando a los mismos de una manera más intuitiva.
Nuevamente, partiendo de la definición clásica del vector momento angular L:
L = r × p
y empezando a trabajar en coordenadas rectangulares Cartesianas, si empleamos la definición operacional mecánico-cuántica del momentum podemos obtener las tres componentes mecánico-cuánticas del momentum Lx, Ly y Lz expresadas en coordenadas rectangulares Cartesianas en la forma en que las obtuvimos en la entrada “Momento angular orbital: tratamiento ondulatorio I”. Pero para un problema de simetría esférica, las coordenadas que mejor se prestan para llevar a cabo cualquier tipo de análisis no son las coordenadas rectangulares Cartesianas (x,y,z) sino las coordenadas esféricas (r,θ,φ). Haciendo la conversión a coordenadas esféricas, los operadores Lx, Ly y Lz vienen siendo:
pudiéndose obtener con los operadores Lx y Ly los operadores escalera L+ y L.-:
Usando estas relaciones, el operador que nos dá el cuadrado de la magnitud del momento angular orbital, L2, y que semi-clásicamente está dado como:
viene siendo, tras un poco de álgebra poco interesante:
Si comparamos esto último con la ecuación de onda de Schrödinger que expresada en coordenadas esféricas es:
se tiene entonces que la ecuación de Schrödinger puede ser escrita de la siguiente manera:
Nuevamente, aquí podríamos tratar de recurrir al método de la separación de variables haciendo:
Sin embargo, en este punto, puesto que el operador L2 involucra únicamente a las variables θ y φ, lo prudente es mantener juntas a las variables angulares haciendo:
De este modo, se tiene:
Dividiendo ambos miembros de la igualdad entre R(r)Y(θ,φ) y reagrupando, se obtiene:
Lo que está a la izquierda del signo de la igualdad depende únicamente de las variables angulares θ y φ, mientras que lo que está del lado derecho del signo de la igualdad depende únicamente de la variable radial r. Para que esto pueda ser cierto, se requiere forzosamente que cada lado de la ecuación sea igual a una constante. Llamemos a esta constante α. Entonces de lo anterior se puede deducir la siguiente ecuación de eigenvalores:
En base a lo que vimos en las entradas anteriores, sabemos ya que:
Y de hecho, sabemos también con mayor detalle que la función de onda Y(θ,φ) depende de dos números cuánticos l y m pudiéndose por lo tanto representar lo anterior de la siguiente manera:
Sin embargo, puesto que esta información viene de conocimiento previo obtenido por otras vías y no como resultado de lo que hemos estado desarrollando aquí, seguiremos suponiendo que no sabemos todavía absolutamente nada acerca de esto último, seguiremos suponiendo que no sabemos que la constante α es igual a l(l+1).
Para la determinación de α, tenemos que substituír en la ecuación de eigenvalores el operador diferencial L2 que obtuvimos arriba:
De todo lo anterior, podemos obtener lo siguiente para la parte angular (por conveniencia matemática posterior en el desarrollo, haremos a la constante -α en lugar de +α, lo cual no cambia en lo absoluto la validez de lo que estamos llevando a cabo):
Puesto que el operador diferencial L2 involucra derivadas tomadas con respecto a las variables angulares θ y φ, resulta necesario recurrir nuevamente aquí a la separación de variables, lo cual haremos de la siguiente manera:
Con esta separación de variables, la ecuación anterior toma la siguiente configuración:
que tomando en cuenta la naturaleza de la diferenciación parcial (con la cual Φ se comporta ante el operador diferencial ∂/∂θ como si fuese una constante, e igualmente Θ también se comporta ante el operador diferencial ∂/∂φ como si fuese una constante) podemos reacomodar como:
Dividiendo ambos lados entre ΘΦ y multiplicando ambos lados por sen2(θ):
Esto último lo podemos reacomodar de la siguiente manera:
Lo que tenemos del lado derecho es una función únicamente de θ mientras que lo que tenemos del lado izquierdo es una función únicamente de φ. Entonces ambas cantidades deben ser iguales a una constante. Llamaremos a esta constante -m2. Entonces trabajando sobre la relación que involucra a θ, se tiene:
Esta expresión, tal y como está dada, no resulta nada fácil de resolver. Es aquí en donde podemos recurrir al truco que se le ocurrió por vez primera al matemático francés Adrien-Marie Legendre, haciendo el siguiente cambio de variable:
de lo cual, naturalmente:
y usando la regla de la cadena:
con lo cual:
Haremos otra abreviatura que tiene que ver únicamente con simplificación notacional:
Todo esto nos lleva a lo siguiente:
Esto que tenemos aquí es una ecuación de Legendre. Esta ecuación se puede atacar mediante un desarrollo en una serie infinita de potencias al estilo de las series de Taylor. Como puede verse en la indeterminación que ocurre en el denominador del tercer término, en los extremos ±1 de la variable u que a su vez corresponden a θ.=.0° y θ.=.180° la serie infinita de potencias que satisfaga la ecuación diferencial se vuelve infinitamente grande, conduciendo a una función de onda que no puede ser normalizada. Sin embargo, para ciertos valores de α, la serie termina, quedando como un polinomio. Haciendo algunas pruebas tentativas como las que a continuación se llevarán a cabo, eventualmente se descubre que los valores de α para los cuales existen soluciones “bien-comportadas” son α.=.l(l+1) en donde l.=.0,1,2,3,... y l≥|m|. Si hacemos m.=.0, entonces podemos empezar a trabajar de inmediato con la siguiente ecuación diferencial:
para empezar a obtener soluciones “bien-comportadas” que resultan ser precisamente polinomios de Legendre. En este caso, los polinomios obtenidos contienen únicamente potencias pares o potencias impares de u. Empezaremos a probar suerte con el que debe ser el polinomio más sencillo de todos, f0.=.1, para el cual:
En este caso, la ecuación diferencial nos dá una solución trivial:
Ahora probaremos suerte con el polinomio f0.=.u para el cual:
En este caso, la ecuación diferencial nos dá lo siguiente:
Ahora probaremos suerte con el polinomio f0.=.1 + au2 para el cual:
Con esto, la ecuación diferencial nos resulta en lo siguiente:
Del primer término de esto último que debe ser igual a cero, se deduce que:
mientras que del segundo término que también debe ser igual a cero se deduce que:
Entonces el polinomio debe ser:
PROBLEMA: Para la ecuación de Legendre que vimos arriba en la cual m.=.0, obténgase tanto el valor de α como la constante que corresponde al siguiente polinomio:
Para este polinomio, se tiene:
Con esto, la ecuación diferencial nos resulta en lo siguiente:
que reagrupando en potencias de u podemos reescribir como:
Del primer término que debe ser igual a cero se obtiene el valor deseado de α:
mientras que del segundo término que también debe ser igual a cero se deduce que:
Entonces el polinomio correspondiente debe ser:
PROBLEMA: Para la ecuación de Legendre que vimos arriba en la cual m.=.0, obténgase tanto el valor de α como la constante que corresponde al siguiente polinomio:
Para este polinomio, se tiene:
Con esto, la ecuación diferencial nos resulta en lo siguiente:
que reagrupando en potencias de u podemos reescribir como:
Del primer término que debe ser igual a cero se obtiene el valor deseado de α:
mientras que del tercer término que también debe ser igual a cero se deduce que:
Usando esto último en el segundo término, se obtiene:
Por lo tanto, el polinomio debe ser:
Lo que hemos estado haciendo aquí es generar, uno por uno, varios polinomios de Legendre. Esta es una manera de generarlos que quizá no sea muy elegante o eficiente pero que de cualquier manera funciona, y más que nada, nos revela cómo conforme va aumentando la potencia del polinomio el valor de α también va aumentando como l(l+1) en donde l es un número entero positivo. Algo que no resulta obvio a estas alturas es que los polinomios de Legendre que se van generando resultan ser polinomios ortogonales. Pero lo que sí debe resultar obvio es que estos polinomios que hemos ido obteniendo no están normalizados; esta es una condición adicional impuesta como consecuencia de la aplicación de los polinomios de Legendre en la Mecánica Cuántica.
PROBLEMA: Los polinomios de Legendre Pn(u) son proporcionales a las soluciones que hemos estado obteniendo en los problemas anteriores, y el enunciado matemático para describir esto es el siguiente:
Usando el hecho de que:
obténganse las constantes Cn para f0, f1, f2, f3, y f4. Hecho esto, escríbanse los polinomios explícitamente.
Para n.=.0:
Para n.=.1:
Para n.=.2:
Para n.=.3:
Y finalmente, para n.=.4:
Entonces, haciendo el cambio notacional x.=.u, los polinomios pedidos son:
Estos polinomios, así como están dados, son conocidos entre los matemáticos como los polinomios especiales de Legendre. Si revertimos hacia la variable cosenoidal original haciendo x.=.cos(θ) obtenemos entonces los primeros cinco polinomios asociados de Legendre para m.=.0, los cuales estableciendo un paralelo entre la notación Ylm y la notación Plm podemos escribir como:
Estas son las mismas funciones asociadas de Legendre, para m.=.0, que ya vimos con anterioridad.
El hecho de que en la obtención de relaciones fundamentales para los operadores del momento angular orbital la parte angular del problema sea independiente de la parte radial implica que con un poco de cautela podemos aplicar nuestros conocimientos recién adquiridos en una amplia variedad de problemas (como el problema de la partícula libre a la cual le podemos tratar de asignar un valor de momento angular) trasladando hacia dichos problemas sin cambio alguno lo que ya sabemos acerca de las ecuaciones de eigenvalores del momento angular, el concepto del eigenket simultáneo bajo L2 y Lz, el concepto de los números cuánticos l y m, el concepto de las armónicas esféricas, en fin todo lo que hemos aprendido en estas últimas entradas. Considérese por ejemplo la siguiente función de onda ψ que está expresada en coordenadas rectangulares Cartesianas:
Un problema clásico elaborado sobre esta función de onda le pide al estudiante determinar la probabilidad de obtener para una medición de L2 y Lz los resultados 2ħ2 y 0 respectivamente. Así como está postulado, el problema en realidad tiene el propósito de poner a prueba el ingenio del estudiante que tarde o temprano debe darse cuenta de que para la resolución del problema es necesario hacer primero el cambio de la función de onda de coordenadas rectangulares Cartesianas (x,y,x) a coordenadas esféricas con la prescripción de rigor:
Si se lleva a cabo la conversión:
entonces la función de onda resulta ser:
que podemos simplificar como:
en donde como puede verse la función de onda está expresada en función del producto de una parte angular y de una parte radial. De este modo, si lo que queremos es resolver el problema de determinar la probabilidad de obtener para una medición de L2 y Lz los resultados 2ħ2 y 0 respectivamente, lo primero de lo cual echaremos mano es de la ecuación de eigenvalores para L2:
De esta ecuación, puede verse de inmediato que la única manera posible de obtener un eigenvalor de 2ħ2 para una medición de L2 es haciendo l.=.1:
Esto nos fija el valor de l a la unidad (como se ha destacado en el sub-índice de la función de onda). Sin embargo, falta por determinar el valor o los valores posibles de m. Recordemos que para cierto valor de l, los valores posibles de m son todos los enteros (positivos y negativos) que sean menores o iguales al valor absoluto de l. Esto se traduce aquí en tres valores posibles de m, que son -1, 0 y +1:
A estas alturas, se requiere echar mano de las tres armónicas esféricas que corresponden a las tres funciones de onda que tenemos en las eigenecuaciones de arriba, las cuales son:
Haciendo por lo pronto caso omiso de las constantes de proporcionalidad numéricas utilizadas para la normalización de las armónicas esféricas, podemos ver de las siguientes equivalencias:
que las tres armónicas esféricas serán soluciones a la eigenecuación de L2 para la función de onda ψ con la cual habíamos empezado.
PROBLEMA: Una partícula que está sometida a un potencial esféricamente simétrico V(r) tiene una función de onda que está dada por la siguiente expresión:
Determínense las probabilidades de que la partícula sea encontrada en uno de los estados diversos m que le son permitidos.
El primer paso para la solución del problema consiste en llevar a cabo la conversión de la función de onda de coordenadas rectangulares Cartesianas a coordenadas esféricas, lo cual nos produce lo siguiente:
En esta expresión se ha destacado de color azul la parte angular y se ha destacado de color magenta la parte radial. Puesto que:
mientras que de la fórmula de Euler:
resulta evidente que la función de onda ψ es una eigenfunción de L2 con l.=.1. Esto a su vez implica que hay tres valores posibles para el número cuántico m que son -1, 0 y +1. Para poder encontrar la probabilidad de que la partícula se encuentre en cada uno de dichos estados, primero tenemos que poner a ψ en función de las armónicas esféricas que corresponden a las tres posibilidades, esto es, en función de Y1,-1, Y1,1 e Y1,0. Esto lo podemos lograr si tomamos la fórmula de Euler obteniendo de la misma las siguientes relaciones trigonométricas:
Por un lado tenemos que:
de lo cual se obtiene:
Procediendo de modo semejante, por otro lado tenemos que:
De lo cual se obtiene:
Y por último, se tiene:
Sumando los tres términos trigonométricos, se tiene por lo tanto:
Reacomodando, obtenemos las contribuciones de cada armónica esférica a la parte angular de la función de onda ψ:
Puesto que las probabilidades de las que estamos hablando son probabilidades relativas, siendo suficiente que la suma de todas las probabilidades relativas sea igual a la unidad, en el cálculo de las probabilidades el factor √4π/3 se cancelará (al aparecer tanto en el numerador como en el denominador de los cálculos), razón por la cual podemos ignorar dicho factor, concentrándonos mejor en las magnitudes de los factores que multiplican a cada una de las armónicas esféricas que han sido destacadas de color azul en esta última expresión. El cálculo de dichas magnitudes nos dá en cada caso lo siguiente:
Entonces las probabilidades de que la partícula sea encontrada en cualquiera de los tres estados que corresponden al número cuántico m que identificamos como -1, 0 y +1 son:
Desde la perspectiva de un laboratorista, la línea espectral cuya intensidad sea cuatro veces mayor que la intensidad de las otras dos líneas será la que corresponderá al estado m.=.0 de la partícula.
PROBLEMA: ¿Cómo podría determinarse el potencial V(r) para una partícula cuya función de onda ψ que nos es conocida es una eigenfunción de energía con un eigenvalor E y de la cual se sabe que está en un estado con un momento angular orbital especificado por l.=.1?
El primer paso consiste en substituír la función de onda ψ que nos es conocida en la ecuación de Schrödinger y utilizar el hecho de que la función de onda es una eigenfunción de L2. Siendo la ecuación de onda:
entonces, recurriendo al método de separación de variables, suponemos que esta función de onda ψ es una función compuesta formada por el producto de una parte radial R(r) y una parte angular que llamaremos Ω:
Sabiendo que el operador Laplaciano en coordenadas esféricas aplicado a la función de onda ψ nos produce la siguiente expresión:
y sabiendo además que el operador L2 aplicado a una armónica esférica nos produce un eigenvalor l(l+1):
entonces, tomando en cuenta que el operador L2 expresado en coordenadas esféricas es:
podemos escribir lo siguiente:
Usando el hecho de que l.=.1 se tiene entonces que la ecuación de onda es:
Por lo tanto, de esto último deducimos que el potencial V(r) tiene que estar dado por:
Una cosa que había quedado pendiente era el investigar la posibilidad de que el momento angular orbital además de poder tener valores enteros de l pudiera tener también valores fraccionales de l, específicamente, medias fracciones (1/2, 3/2, 5/2, etc.) Esta posibilidad había quedado abierta en las conclusiones obtenidas con la ayuda de los operadores escalera aplicados al estudio del momento angular orbital. Sin embargo, esto no es posible, y se pueden esgrimir varios argumentos en contra de tal posibilidad. Supóngase una función de onda Yl,m(θ,φ) con un valor mitad-fraccionario de l. Para mayor especificidad, considérese el caso:
Entonces la posibilidad fraccionaria que estamos considerando es:
Recurriremos ahora a la relación general:
Si son posibles los valores medio-fraccionales de l, entonces debe ser posible escribir:
Con la ayuda del operador escalera L.- expresado en coordenadas esféricas, si lo anterior fuese cierto entonces debemos esperar algo como lo siguiente:
evaluado como se muestra a continuación:
Pero esta expresión no es permisible porque se vuelve indeterminada en θ.=.0 y θ.=.π.
Al igual que la aplicación del operador escalera L+ nos debe resultar en lo siguiente:
del mismo modo una segunda aplicación del operador escalera sobre lo que obtuvimos arriba nos debe de dar:
La resolución de esta última ecuación diferencial debe producir una solución tentativa como la que se muestra a continuación:
La solución:
contradice sin embargo el resultado previo que habíamos obtenido para la función de onda Y1/2,-1/2(θ,φ) en donde la función senoidal no está invertida además de que aquí nos aparece un factor trigonométrico extra (cotangente). Esta contradicción nos lleva a postular la imposibilidad de que haya valores fraccionarios de l. Por otro lado, desde el punto de vista puramente matemático, de acuerdo a la teoría Sturm-Liouville de ecuaciones diferenciales las soluciones a la ecuación diferencial de Schrödinger cuando se suponen valores enteros para l forman un conjunto completo, lo cual significa que cualquier función arbitraria de θ y de φ puede ser expandida en términos de las armónicas esféricas Yl,m suponiendo únicamente valores enteros para l y para m, lo cual vuelve supefluo el considerar valores de media-fracción para l. Es por razones como estas que se vuelve futil el considerar para el momento angular orbital valores de l que no sean enteros. El único momento angular que hemos visto anteriormente con un valor fraccionario igual a 1/2 es el que corresponde al momento angular del spin del electrón, el cual es un momento angular intrínseco que no tiene nada que ver con el momento angular orbital, razón por la cual el electrón puede conservar esta propiedad cuántica aún cuando el electrón no esté ligado a ningún potencial.