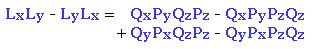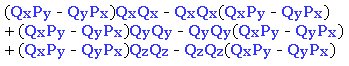Momento angular: tratamiento matricial I

El caso especial del momento angular, visto desde la perspectiva de la Mecánica Cuántica, adquiere una importancia central en todo lo que nos ocupa en virtud de que fue precisamente la cuantización del momento angular propuesta por Niels Bohr en su modelo planetario del átomo:

L = nħ

lo que dió una explicación matemática extraordinariamente exitosa, por vez primera, a las líneas de los espectros de emisión y absorción de los elementos. Antes de Bohr, se suponía que el momento angular de una partícula podía tomar cualquier valor posible en el universo del mundo sub-microscópico. Pero la cuantización del momento angular de inmediato impuso una restricción severa en el modelo del átomo de hidrógeno, en el sentido de que a un electrón ligado al átomo de hidrógeno sólo le era posible tomar alguno de una cantidad posible de valores discretos de energía, estando vedados los valores intermedios.

El momento angular cuantizado, tal y como fue definido por Bohr para su modelo atómico planetario, era una cantidad medible, observable, pero ciertamente no era una cantidad a la cual le correspondiera un operador matemático como las matrices que serían utilizadas posteriormente por Heisenberg para representar a la posición y al momentum. A Bohr no se le había ocurrido que tal cosa se pudiera llevar a cabgo, y no tenía base alguna para suponer lo contrario, especialmente dado el éxito que tuvo su modelo del átomo. Pero si la posición y el momentum de una partícula podían ser representados mediante matrices, no tardó en surgir la sospecha de que el momento angular, definido precisamente en base a la posición y al momentum, también pudiera ser representado mediante una matriz.

A diferencia del spin del electrón, idealizado hipotéticamente como una carga eléctrica negativa girando sobre su propio eje dando lugar a un momento angular de spin, ciertamente existe otro tipo de momento angular que puede tomar una variedad mucho más amplia de valores que los dos valores relacionados con el spin. Recurriendo nuevamente a la imagen del modelo atómico planetario de Bohr, se trata del momento angular L debido al electrón girando en torno al núcleo a una distancia r del núcleo con un momento lineal p. Clásicamente, este momento angular está definido como el producto cruz de los dos vectores r y p:

L = r× p

En un sistema de coordenadas Cartesianas (x, y, z), esta definición nos produce tres componentes ortogonales de L: (L_x, L_y, L_z), los cuales se obtienen de las proyecciones de los vectores r = (x, y, z) y p = (p_x, p_y, p_z):

L = (L_x, L_y, L_z) = (x, y, z)× (p_x, p_y, p_z)

usando un sistema de vectores unitarios de base {i, j, k} a través de un determinante:

de donde se puede leer directamente:

En estas fórmulas lo que tenemos son variables continuas, las cuales pueden tomar los valores que medimos experimentalmente en un laboratorio. Pero ya vimos que en la Mecánica Matricial lo que representa a las variables físicas son matrices, no variables reales. Si queremos incorporar al momento angular orbital bajo el concepto matricial, tenemos que hacer algún cambio que nos dé las matrices que serán utilizadas. Es en situaciones como ésta cuando echamos recurso de una de las técnicas más potentes que hay en el arsenal de la Mecánica Cuántica: en las relaciones clásicas reemplazamos a las observables por matrices. Este es un recurso directo que no requiere mayor explicación. Sobre esto, el notable físico Arno Bohm una vez dijo: “La representación de observables físicas por operadores es uno de los más grandes logros de la ciencia”. Y en la Mecánica Matricial, los operadores son matrices.

En la Mecánica Cuántica, las proyecciones de las coordenadas de posición y el momentum están representadas por las matrices Q_x, Q_y, Q_z, y P_x, P_y, P_z, con lo cual obtenemos las siguientes relaciones matriciales para la especificación matricial del momento angular como una cantidad vectorial cuyas proyecciones son:

Por otro lado, tenemos las siguientes relaciones dadas por la ecuación de Born:

PROBLEMA: Demostrar que:

A continuación empezamos con la derivación de la relación pedida:

Ahora bien, las matrices Q_x, Q_y y Q_z conmutan entre sí al igual que las matrices P_x, P_y y P_z, del mismo modo que Q_x conmuta con P_y, Q_y conmuta con P_z, y así sucesivamente, lo cual podemos utilizar aquí para mover dentro de los productos matriciales las matrices individuales ya sea corriéndolas hacia la izquierda o corriéndolas hacia la derecha según convenga. En este caso:

con lo cual Q_xP_zQ_yP_z cancela a Q_yP_zQ_xP_z, y Q_zP_xQ_zP_y cancela a Q_zP_yQ_zP_x:

dejándonos con:

Reacomodando nuevamente los factores matriciales dentro de cada término tomando ventaja de las matrices que son conmutativas, y reacomodando los términos:

Factorizando hacia la izquierda:

Aquí podemos echar mano de la ecuación de Born para los factores que tenemos entre paréntesis, obteniendo:

L_xL_y - L_yL_x = Q_xP_y(iħI) + Q_yP_x(iħI)

Factorizando nuevamente:

L_xL_y - L_yL_x = [Q_xP_y + Q_yP_x] iħI

Pero lo que tenemos entre los paréntesis cuadrados es L_z. Se concluye que:

L_xL_y - L_yL_x = iħL_z

Del mismo modo, podemos obtener las siguientes relaciones:

L_yL_z - L_zL_y = iħL_x

L_zL_x - L_xL_z = iħL_y

PROBLEMA: Demostrar la siguiente relación matricial:

[L_z, Q_x] = iħQ_y

Tomaremos la relación:

L_z = Q_xP_y - Q_yP_x

y obtendremos dos relaciones pre-multiplicando y post-multiplicando esta relación por la matriz Q_x:

Restando la primera expresión de la segunda:

Pero de las relaciones de conmutación de Born, [Q_x, P_y] es igual a la matriz cero. Por lo tanto:

Puesto que las matrices Q_x y Q_y representan observables compatibles, estas matrices conmutan, con lo cual Q_xQ_y = Q_yQ_x, lo cual nos lleva a:

habiéndose utilizado en el último paso la relación de conmutación básica de Born.

PROBLEMA: Demostrar la siguiente relación matricial:

[L_z, P_x] = iħP_y




PROBLEMA: Evalúense y simplifíquense las siguientes tres relaciones:

Empezaremos con la primera relación haciendo la substitución de la componente matricial L_z en función de las componentes matriciales de la posición y el momentum, y simplificando lo que resulte aprovechando las conmutatividades que podamos encontrar entre los matrices posición y matrices momentum que se puedan conmutar:

Continuamos con la evaluación de la segunda relación haciendo nuevamente la substitución de las componentes matriciales del momento angular y simplificando lo que resulte aprovechando las conmutatividades que podamos encontrar entre los matrices posición y matrices momentum que se puedan conmutar:

Concluímos con la evaluación de la tercera relación cuyo resultado posiblemente podríamos haber anticipado:

PROBLEMA: Evalúense y simplifíquense las siguientes tres relaciones:

Empezaremos con la primera relación haciendo la substitución de la componente matricial L_z en función de las componentes matriciales de la posición y el momentum, y simplificando lo que resulte aprovechando las conmutatividades que podamos encontrar entre los matrices posición y matrices momentum que se puedan conmutar:

Continuamos con la evaluación de la segunda relación haciendo nuevamente la substitución de las componentes matriciales del momento angular y simplificando lo que resulte aprovechando las conmutatividades que podamos encontrar entre los matrices posición y matrices momentum que se puedan conmutar:

Concluímos con la evaluación de la tercera relación cuyo resultado posiblemente podríamos haber anticipado:

PROBLEMA: Evalúese:

L_zQ² - Q²L_z

Recurriendo a la definición de Q² = Q_x² + Q_y² + Q_z² y de L_z, tenemos lo siguiente:

Ahora recurrimos a la definición de L_z para obtener:

Lo cual se convierte en:

Como se ha destacado a través de los colores, todos los términos se cancelan en pares para darnos como resultado la matriz cero:

L_zQ² - Q²L_z = O

Si vemos a la matriz Q² como una especie de equivalente de la “longitud Pitagórica”:

x² + y² + z²

la cual en el análisis vectorial clásico es una cantidad escalar que conmuta con los tres componentes del vector posición (x,y,z), podemos ver que aquí también tenemos una propiedad parecida en Q², aplicable en la componente-z del momento angular matricial L.

PROBLEMA: Si definimos matricialmente un momento angular “total” P² de la siguiente manera:

P² = P_x² + P_y² + P_z²

obténgase entonces lo siguiente:

L_zP² - P²L_z

La evaluación matricial pedida resulta directa en este problema haciendo uso de las conmutatividades en donde las haya, cancelándose de este modo todos los términos en pares:

Una cantidad que resulta extremadamente útil para poder medir lo que podríamos llamar el “momento angular total” de una partícula es la siguiente, la cual tiene la propiedad de poder conmutar con todas las componentes matriciales L_x, L_y y L_z del momento angular:

L² = L_x² + L_y² + L_z²

PROBLEMA: Demostrar que el operador matricial L² conmuta con las tres componentes matriciales L_x, L_y y L_z del momento angular.

La resolución de problemas de este tipo puede avanzar con mucha mayor rapidez si recurrimos al uso intensivo del conmutador en lo que podríamos tomar como una especie de álgebra de conmutadores que no viene siendo más que una especie de “taquigrafía” matemática para abreviar pasos. Empezaremos por demostrar la conmutatividad de L² con L_x:

A continuación reduciremos el primer término de esto último recurriendo a una pre-multiplicación y una post-multiplicación con L_y actuando sobre [L_y,L_x]:

Sumando (1) y (2):

Del mismo modo, expandiendo y simplificando [L_z,L_x] para llegar a [L_z²,L_x]:

Podemos ver de inmediato que:

[L_y²,L_x] + [L_z²,L_x] = O

Entonces:

[L²,L_x] = O

Procediendo de igual manera, podemos demostrar que

[L²,L_y] = O

[L²,L_z] = O

concluyéndose que la matriz L² conmuta con todas las componentes matriciales del momento angular.






Las conclusiones obtenidas del tratamiento mecánico cuántico del momento angular orbital tienen un impacto importante y directo en el entendimiento de los espectros rotacionales de las moléculas diatómicas tales como la molécula de hidrógeno (H₂), e inclusive en los espectros rotacionales de moléculas diatómicas formadas por elementos distintos tales como la molécula del monóxido de carbono (CO):

Clásicamente, antes del advenimiento de la Mecánica Cuántica, se creía que una molécula diatómica podía girar en torno a su centro de masa a cualquier velocidad angular ω, no había razón lógica alguna para esperar lo contrario. Sin embargo, la “extraña ecuación” de Max Born que condujo a la cuantización de las vibraciones que puede tener una molécula a lo largo de su eje internuclear también conduce inevitablemente a la cuantización de las rotaciones que puede tener la molécula en torno a su eje de rotación. Esto resultó ser una sorpresa mayúscula que nadie esperaba. Y posiblemente la nueva teoría habría sido rechazada de no ser por el hecho de que fue confirmada experimentalmente en el laboratorio miles y miles de veces.

Si la velocidad angular ω a la cual puede girar una molécula diatómica en torno a un eje propio de rotación está cuantizada, ello implica que los niveles de energía de energía que son posibles debido a dicha rotación también estarán cuantizados, lo cual significa que las moléculas diatómicas exhibirán necesariamente espectros rotacionales, los cuales se manifestarán con la aparición de nuevas líneas espectrales que no pueden ser explicadas de otra manera.




a