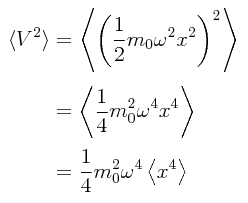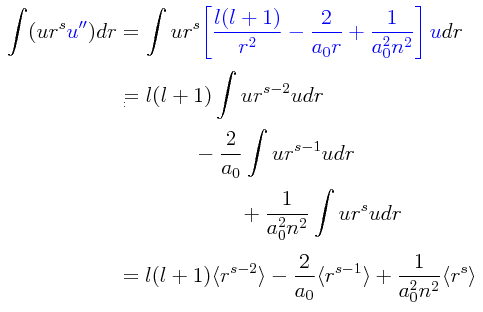En el trabajo citado, el Hamiltoniano principal H0 es producido por el campo central generado por la atracción que el núcleo atómico positivo ejerce sobre los electrones, y el trabajo citado hace referencia a la situación que corresponde a átomos multielectrónicos en donde se puede presumir que los momentos angulares orbitales de los electrones individuales se suman para formar un momento angular orbital resultante L; del mismo modo que los momentos angulares de spin individuales se acoplan para producir un momento angular de spin resultante S tras lo cual L y S se combinan sumándose vectorialmente para formar el momentum angular total J del átomo (o mejor dicho, del electrón de valencia) bajo el modelo de acoplamiento conocido como el acoplamiento LS o acoplamiento de Russell-Saunders.
¿Y cómo habremos de manejar con la teoría de las perturbaciones el caso en el cual haya no solo una sino varias pertubaciones originadas por causas distintas, cada una de las cuales puede producir a su vez su propio enjambre de desdoblamientos? Lo primero que viene a la mente es considerar cada perturbación posible por separado como si las demás perturbaciones debidas a causas distintas no existieran, y una vez obtenido el efecto independiente de cada perturbación sumar todas las correcciones perturbativas para así poder obtener el efecto total en el sistema no-perturbado. Lo cual sugiere prestar atención a la mayor cantidad posible de mecanismos de perturbación que se puedan presentar en cada caso. Y hay un tipo de perturbación que hasta ahora no se había considerado pero que ahora se estudiará más a fondo.
Además del término de energía producido por el acoplamiento spin-órbita (o acoplamiento LS, como quiera llamársele) cuyo efecto puede ser evaluado considerándolo como una perturbación al Hamiltoniano no-perturbado del átomo de hidrógeno, hay otros términos perturbatorios producidos por otras causas cuyos efectos también deben ser incorporados para obtener un modelo más realista del electrón de valencia en el átomo de hidrógeno. Es en este punto en donde tenemos que incorporar consideraciones propias de la Teoría Especial de la Relatividad (hay mayores detalles sobre éste tema en mi obra La Teoría de la Relatividad disponible también en Internet a través de Blogger).
En el modelo cuántico fundamental del átomo de hidrógeno, se considera que el electrón de valencia posee una energía total que es igual a la suma de sus energías cinética K y potencial V. Para la especificación del operador Hamiltoniano H0 del átomo de hidrógeno, se uso el modelo clásico de energías en el cual la energía cinética clásica está dada por:
La segunda versión usando el momentum en lugar de la velocidad es la que usamos en la Mecánica Cuántica. Estas son las expresiones correctas clásicas de la energía cinética. Sin embargo, al tomar en cuenta los efectos propios de la Teoría Especial de la Relatividad que se suponen válidos para cualquier escala de dimensiones ya sea para el mundo macroscópico como para el mundo microscópico y submicroscópico, la expresión correcta (relativísticamente hablando) para la energía cinética tiene que ser la siguiente:
en donde m0 es la masa en reposo de la partícula en movimiento. El primer término en el lado derecho de la igualdad representa la energía relativista total sin tomar en cuenta a la energía potencial que por el momento no nos concierne. El segundo término, m0c2 representa la energía en reposo de la partícula. La diferencia entre ambos términos es la energía que podemos atribuír al movimiento de la partícula.
El problema con la última relación es que está en función de la velocidad de la partícula, y ello no nos sirve en la Mecánica Cuántica. Queremos por lo tanto reformular la relación en términos del momentum p de la partícula, el cual tiene que ser no el momentum clásico sino el momentum relativista que está dado por la relación:
Para ello, podemos hacer las siguientes manipulaciones algebraicas:
De este modo, obtenemos la siguiente expresión para la energía cinética relativista de la partícula en función del momentum relativista:
Esto mismo lo podemos expresar de una manera un poco diferente para poder llevar a cabo una expansión en serie de potencias:
Llevando a cabo la expansión, vemos que:
Podemos reconocer de inmediato al primer término de la serie como la expresión clásica de la energía cinética con la que hemos estado trabajando en las entradas previas. El segundo término lo podemos tomar como la corrección de primer orden a nuestros cálculos previos. Por lo tanto, la corrección relativista de orden más bajo viene siendo:
Podemos hacer ahora lo que antes no podíamos hacer. Podemos usar la teoría de las perturbaciones para obtener la corrección perturbativa de primer orden a la energía En(0), corrección que hemos visto ya previamente que viene siendo la esperanza matemática o promedio estadístico del Hamiltoniano de perturbación que en este caso es H’r, siendo esta corrección:
En el caso que nos ocupa, la corrección de energía de primer orden a ser agregada por efectos relativistas a la energía no-perturbada será:
El paso que se tomó en la última línea debe ser tomado con precaución, porque supone como hecho la Hermiticidad de p2 (véase la entrada Operadores Hermitianos puesta dentro de esta obra). Al dar esto por hecho, estamos suponiendo que para dos funciones f y g cualesquiera se cumple lo siguiente:
Sin embargo, y estrictamente hablando, lo que nos puede poner a pensar es que el operador p4 no es Hermitiano para el caso en el que el número cuántico l.=.0, y se puede poner en tela de duda la aplicabilidad de la teoría de las perturbaciones para el caso l.=.0. Específicamente, se puede demostrar que para las siguientes dos funciones de prueba f y g:
se obtiene lo siguiente:
lo cual comprueba que p4 no es Hermitiano.
Sin embargo, aquí nos ayuda el hecho de que existe una solución exacta para dilucidar esta interrogante, la cual se puede obtener recurriendo a la ecuación relativista de Dirac en vez de usar la ecuación de Schrödinger independiente del tiempo, y el resultado exacto que se obtiene con la ecuación de Dirac confirma lo que se ha obtenido aquí por medios menos rigurosos.
De la ecuación de Schrödinger independiente del tiempo en su forma más general sabemos que:
Por lo tanto:
Esta expresión es de naturaleza general, aplicable a cualquier situación mecánico-cuántica y válida hasta el primer orden de corrección perturbativa relativista. A continuación queremos aplicar dicha relación al caso del átomo de hidrógeno cuya energía potencial está dada dentro del sistema de unidades CGS (Gaussianas) como:
haciéndose la aclaración de que si queremos obtener resultados válidos en el sistema SI (MKS) de unidades entonces la expresión a usar para la energía potencial debe ser:
Trabajaremos dentro del sistema CGS, con lo cual obtenemos lo siguiente para el átomo de hidrógeno:
Para poder continuar necesitamos evaluar las siguientes esperanzas matemáticas para el átomo de hidrógeno:
para su estado general no-perturbado ψnlm. En el caso de la primera relación se tiene lo siguiente:
siendo a0 el radio de Bohr.
PROBLEMA: (a) Demostar con la ayuda del Teorema Virial aplicado al caso del hidrógeno que:
(b) Hecho lo anterior, demuéstrese que para el átomo de hidrógeno la esperanza matemática (promedio) del inverso del radio del radio está dada por la relación:
(a) Para el átomo de hidrógeno, sabemos ya que la función de potencial V(r) está dada en unidades CGS (Gaussianas) por la expresión:
Aplicando el operador diferencial nabla ∇ en ambos lados de la relación y usando vectores radiales, lo anterior se va transformando en (obsérvese el uso del operador radial unitario r̂ de magnitud unitaria usado únicamente para asignar dirección radial así como el vector radial r que puede tener cualquier magnitud):
Tomando el promedio (esperanza matemética) en ambos lados de la última línea y recurriendo a un resultado que se obtiene del Teorema Virial para el átomo de hidrógeno, se tiene entonces que:
Obsérvese que para pasar de la segunda línea a la tercera línea en el lado izquierdo de la igualdad se ha utilizado una extensión del siguiente resultado que se puede obtener con la ayuda del Teorema Virial (véase la demostración de ello en la entrada titulada El teorema virial que forma parte de ésta obra):
Apelamos ahora a lo que es la esencia del Teorema Virial, que nos dice que la energía cinética total T de un sistema promediada en el transcurso del tiempo es igual al total de la energía potencial V del sistema también promediada con respecto al transcurso del tiempo, lo cual a su vez estaremos equiparando a la energía del átomo de hidrógeno para un estado cuántico n del mismo:
Pero aquí podemos usar también otro resultado del Teorema Virial:
Con esto último queda probada la relación que se quería demostrar.
(b) Ya se sabe que la energía del átomo de hidrógeno (o mejor dicho, la energía de su electrón de valencia) cuando se encuentra en un estado n está dada por la siguiente relación:
Tomando el promedio matemático de ambos lados de la igualdad y apelando al resultado que se obtuvo en el inciso (a) se llega así a la resultado deseado:
Por otro lado, obtener:
resulta ser una cosa más complicada. Podemos simplificar las cosas si recurrimos a una fórmula conocida como la relación de Kramer (también se le conoce como la relación Pasternak):
en donde tres esperanzas matemáticas de funciones radiales r son relacionadas entre sí mediante varias potencias especificadas por el entero s que haya sido seleccionado.
PROBLEMA: Usando la relación de Kramer, obténganse las siguientes esperanzas matemáticas para el átomo de hidrógeno:
Por razones que pronto serán obvias, tomaremos un orden diferente en el cómputo de las anteriores esperanzas matemáticas. Comenzaremos primero con la cuarta esperanza matemática que se pide haciendo s.=.0 en la relación de Kramer:
Ahora procederemos a evaluar la primera esperanza matemática haciendo s.=.1 en la relación de Kramer y utilizando el resultado que acabamos de obtener arriba:
Continuamos con la evaluación de la segunda esperanza matemática haciendo s.=.2 en la relación de Kramer y utilizando el resultado que acabamos de obtener arriba:
obteniendo tras un breve desarrollo:
Por último, haciendo s.=.3 en la relación de Kramer y utilizando dos de los resultados que hemos obtenido arriba:
llegamos tras un breve desarrollo a la cuarta esperanza matemética que se quería obtener:
Resulta evidente que la relación de Kramer es una relación recursiva; a veces para obtener un cierto resultado es necesario evaluar antes otras esperanzas matemáticas con la misma relación. En estos casos, hemos estado usando potencias positivas en orden ascendente. Pero si usamos una potencia negativa, podemos toparnos con un obstáculo. Supóngase que queremos obtener la esperanza matemática para la inversa radial haciendo s igual a menos 1. Al hacer tal cosa, todo lo que se obtiene es una relación entre dos esperanzas matemáticas que no nos lleva a ningún lado al igual que como ocurre con otras potencias negatias en orden descendente:
Este tipo de dificultad se puede solventar si obtenemos la esperanza matemática de la inversa del cuadrado de la función radial recurriendo a otras técnicas distintas. Si hacemos tal cosa recurriendo, por ejemplo, al Teorema de Hellmann-Feynman con el cual podemos obtener:
y ya con esto logramos iniciar la obtención de una nueva cadena de esperanzas matemáticas en forma recursiva mediante potencias negativas de s:
Pero nos hemos alejado de nuestro objetivo principal al cual regresamos ahora, que es la obtención de la corrección perturbativa relativista de primer orden para el átomo de hidrógeno. Retomando lo que había quedado inconcluso arriba, y usando las dos esperanzas matemáticas radiales inversas que se necesitan para completar el trabajo, se puede llegar así de este modo a la relación buscada:
Podemos simplificar esta relación un poco si eliminamos a0 de lo anterior expresando todo en términos de En:
Podemos ponerle números a ésto de inmediato. Haciendo tal cosa, encontramos que la corrección perturbativa relativista es menor que En en un factor aproximado de:
La principal objección que se le puede poner a los cálculos que se han efectuado es que no se ha utilizado para nada la teoría de perturbación para estados degenerados pese al hecho de que el átomo de hidrógeno está repleto en la gran mayoría de sus niveles (capas) de estados degenerados. Aquí se responderá diciendo que la perturbación es esféricamente simétrica (la única dependencia es radial, no hay dependencia angular alguna) y por lo tanto conmuta con los operadores cuánticos L2 y Lz que son los que entran en acción cuando hay alguna dependencia angular. Más aún, para un cierto estado cuántico En las eigenfunciones de estos dos operadores tomadas juntas tienen distintos valores propios eigen para los n2 estados diferentes que son asociados con cada estado cuántico En. Las funciones de onda ψnlm son los estados “buenos” para este problema, o lo que es lo mismo, n, l y m son los “números cuánticos buenos”, de forma tal que el uso de la teoría de las perturbaciones para estados no-degenerados está justificada en ésta situación.
El Hamiltoniano relativista obtenido al principio para el cálculo de las correcciones relativistas perturbativas de primer orden:
es de aplicación general, y se puede usar para una gran variedad de casos además del caso del átomo de hidrógeno que hemos visto aquí, como por ejemplo el oscilador armónico simple.
PROBLEMA: Obténgase la corrección relativista de primer orden para el oscilador armónico simple.
Empezaremos usando la expresión de carácter general que se había obtenido arriba:
Puesto que para el oscilador armónico simple se tiene:
entonces el desarrollo de la evaluación de la corrección perturbativa relativista de primer orden para el oscilador armónico simple viene siendo:
habiéndose usado:
Se requiere obtener las siguientes esperanzas matemáticas:
para poder proceder con el resto del problema, lo cual se puede lograr mediante el uso de los operadores escalera (operadores de aniquilación y destrucción) para el oscilador armónico simple. Sin embargo, podemos usar provechosamente los resultados obtenidos previamente en la entrada “Técnicas de aproximación IV”, en donde habiendo prescindido de todas las constantes físicas con fines de mayor simplicidad se obtuvieron ciertas relaciones llamadas “primera relación de recursión” y “segunda relación de recursión” para una ecuación diferencial que en esencia es la misma que se utiliza para resolver el oscilador armónico simple.
La “primera relación de recursión” resultó ser la siguiente:
con el operador posición x2 actuando sobre la función de onda ψ que corresponde al estado cuántico n.
Usando las propiedades de ortonormalidad para las funciones de onda del oscilador armónico simple, podemos obtener la esperanza matemática de x2 de la siguiente manera:
Pero tenemos que restablecer el factor ausente que incorpora las constantes físicas de las cuales se había prescindido con fines de mayor simplicidad. Para el caso de la esperanza matemática de x2 el factor ausente es el siguiente:
La expresión completa para la esperanza matemática a ser usada es entonces:
en donde se destaca que m0 es la masa en reposo del oscilador armónico simple. Esto nos permite llevar a cabo el siguiente paso intermedio en el que se eliminan dos términos en lo que se tiene arriba para la corrección perturbativa relativista Er(1):
Queda pendiente obtener algo similar para la esperanza matemática del operador posición x4, lo cual no fue calculado en la entrada “Técnicas de aproximación IV”. Sin embargo, lo podemos calcular a partir de la expresión que corresponde a la esperanza matemática del operador posición x2 recurriendo al siguiente truco: descomponiendo a x4 en el producto de los dos operadores posición x2 y x2, con uno de ellos actuando sobre el bra a la izquierda (como lo resalta la flecha roja) y el otro actuando sobre el ket a la derecha (como lo resalta la flecha azul):
El paso que se ha tomado arriba supone que hay una Hermiticidad plena del operador posición x2 actuando por igual sobre la función de onda que corresponde al bra a la izquierda que actuando sobre la función de onda que corresponde al ket a la derecha, produciendo presumiblemente el mismo resultado en ambos cálculos. Aunque no hay una razón a priori para suponer Hermiticidad, se puede investigar ésto mediante el mismo procedimiento usado para demostrar en la entrada “Operadores Hermitianos” que forma parte de esta obra que la Hermiticidad no es siempre algo que se deba suponer garantizado. Daremos por hecho que aquí sí hay Hermiticidad por tratarse de una potencia del operador posición y no de una potencia del operador del momentum, y por lo tanto seguiremos adelante dando como hecho la Hermiticidad.
Después de haber llevado a cabo las operaciones para obtener todos los productos posibles en la relación de arriba, se encuentra que se tienen tres integrales a ser evaluadas:
En virtud de la ortogonalidad de las funciones de onda para el oscilador armónico simple, la primera integral y la tercera integral necesariamente se desvanecen, y nos queda únicamente la segunda integral, cuyo valor es la unidad por tratarse de funciones que suponemos normalizadas. Por lo tanto:
Nos falta restablecer en esto el factor ausente que incorpora las constantes físicas de las que habíamos prescindido para mayor simplicidad. El factor en este caso debe ser:
La expresión completa para la esperanza matemática a ser usada es entonces:
Con esto tenemos todo lo que necesitamos para llegar al final deseado de la resolución del problema:
Así pues, la energía total del oscilador armónico simple perturbado a causa de la corrección de primer orden relativista vendrá siendo:
Esto puede dejar una sensación de incomodidad en virtud de que mientras que el efecto principal va creciendo linealmente en razón de n, la corrección perturbativa relativista va creciendo cuadráticamente al ir creciendo el número cuántico n, y eventualmente el efecto de la perturbación tiene que superar al efecto principal. Sin embargo, es aquí que se tiene que tener presente que toda la teoría de la perturbación descansa sobre el supuesto de que la magnitud de la perturbación es inferior a la magnitud del efecto principal, además de que al ir aumentando n se debe suponer que deben entrar en acción las perturbaciones de segundo orden, de tercer orden, y así sucesivamente, Términos que no tomamos en cuenta aquí por considerar que el efecto de perturbación era lo suficientemente pequeño como para ignorar términos de orden mayor en la corrección perturbativa relativista. Como puede verse, la teoría de las perturbaciones tiene sus limitaciones que debemos tener presentes en cuanto los resultados experimentales dejen de coincidir con lo que predice la teoría.
Ahora veremos unas cosas que habían quedado pendientes arriba de justificar más a fondo la obtención de esperanzas matemáticas radiales para el átomo de hidrógeno.
PROBLEMA: Partiendo de la ecuación radial de Schrödinger independiente del tiempo para el átomo de hidrógeno, derívese la relación de Kramer.
Antes de emprender la demostración, se hará un repaso a lo más relevante que tiene que ver con la notación que será empleada en la demostración. Si consideramos una “función de prueba” como la siguiente:
entonces la esperanza matemática o promedio estadístico sobre dicha función de prueba se obtiene llevando a cabo la siguiente integración:
en donde la función de onda que está puesta de color rojo y resaltada con un asterisco, o sea u* tiene que ser lo que se obtiene mediante el proceso de conjugación compleja aplicado a la función de onda u resaltada en color azul. Sin embargo, en las funciones radiales que se utilizan en la Mecánica Cuántica, no hay funciones radiales que incorporen números imaginarios o complejos, todas las funciones radiales son esencialmente números reales. Entonces no hay proceso de conjugación compleja, y la esperanza matemática es simplemente:
De cualquier modo, el orden de operaciones tiene que ser respetado, porque no hay manera de saber la forma en la cual f(r) actuando como un operador sobre la función u produzca un resultado tal que permita suponer que f(r) y u puedan ser conmutativas. A estas alturas del juego, ya nos deberíamos de haber acostumbrado a que hay muchas cosas en la Mecánica Cuántica (sobre todo la Mecánica Matricial) que no son conmutativas.
En los desarrollos que se llevarán a cabo, se hará uso repetido del proceso de integración por partes:
resaltándose el hecho de que lo anterior tiene que ser tomado al pie de la letra, literalmente hablando, considerando que tanto u como v pueden ser cualquier cosa, incluso derivadas de primer orden. Aclarado todo ésto, podemos proceder adelante con la demostración.
La ecuación radial para el átomo de hidrógeno en unidades MKS es:
siendo u(r).=.rR(r). Despejando para la derivada de segundo orden:
Tomando la definición del radio de Bohr e inviritiendo:
De este modo, podemos efectuar la siguiente simplificación:
aEsto nos permite escribir la ecuación radial de Schrödinger de una manera más compacta con la finalidad de simplificar nuestro trabajo:
Podemos integrar esto de la siguiente manera para empezar a trabajar en la demostración:
Tomando lo anterior y rompiéndo el lado derecho en tres integrales separadas, apelando a la definición cuántica de lo que es la esperanza matemática en cada una de las tres integrales resultantes, se tiene:
Trabajando ahora por separado con otra expresión, llevaremos a cabo aquí una integración por partes:
Del mismo modo, trabajaremos ahora con otra expresión, llevando a cabo también una integración por partes:
De nueva cuenta, trabajaremos sobre una tercera expresión, sujetándola también a una integración por partes:
Estamos ahora en posición para juntar los resultados parciales que se han acumulado arriba para poder efectuar el siguiente desarrollo:
De este modo, juntando los anteriores resultados parciales, se tiene lo siguiente:
Pasando todo al lado izquierdo de la igualdad y factorizando usando las esperanzas matemáticas como factores, vemos que:
Multiplicando todo por s.+.1, podemos simplificar lo anterior llegando al siguiente resultado intermedio:
Podemos continuar simplificando, y así llegar al resultado final:
Esta es la relación de Kramer.
PROBLEMA: El teorema de Hellmann-Feynman que relaciona la derivada de la energía total de un sistema con respecto a un parámetro con el valor esperado de la derivada del hamiltoniano con respecto al mismo parámetro, frecuentemente se enuncia de la siguiente manera:
o equivalentemente, en caso de que las funciones de onda no estén normalizadas:
Demostrar el teorema de Hellmann-Feynman.
Considérese un Hamiltoniano H(λ0) no-perturbado para un valor fijo de λ0. Hágase variar λ a un valor nuevo λ0.+.dλ. El efecto de la perturbación en el Hamiltoniano perturbado será:
que podemos reformular del siguiente modo:
en donde la derivada es evaluada en λ0. De acuerdo con la teoría de las perturbaciones, el cambio de primer orden en la energía está dado por:
Para un cambio muy pequeño en la energía, tomado como infinitesimal, se puede considerar lo anterior como:
O bien:
Que podemos enunciar como:
Este es el teorema Hellmann-Feynman. Se hace hincapié en que pese a haber sido obtenido recurriendo a la teoría de las perturbaciones, el resultado es exacto al haber usado para la especificación de la derivada un cambio infinitesimal en la energía.
PROBLEMA: Usese el teorema Hellman-Feynman para obtener las siguientes esperanzas matemáticas para el átomo de hidrógeno:
Para el átomo de hidrógeno, las energías eigen que corresponden al átomo de Bohr en el sistema MKS de unidades son:
La expresión más completa de energías eigen que incorpora los números cuánticos l y j es:
Es sobre ésta última expresión sobre la cual queremos trabajar, tomando a la carga eléctrica e del electrón como la perturbación λ para fines de la aplicación del teorema Hellmann-Feynman, con lo cual se tiene:
Por otra parte, el operador Hamiltoniano de energía H para el átomo de hidrógeno también en el sistema de unidades MKS es:
Tomando la derivada parcial de H con respecto a e se tiene:
Tenemos ya todo lo que se requiere para aplicar el teorema Hellmann-Feynman:
A continuación haremos la siguiente simplificación reemplazando a En con la expresión que tenemos arriba:
Pero lo que tenemos como factor en el lado derecho es el inverso del radio de Bohr:
Se concluye entonces que, para el átomo de hidrógeno:
Tomaremos ahora nuevamente la expresión:
pero ahora tomaremos la derivada parcial con respecto al número cuántico l:
Ahora haremos lo mismo pero en lo que toca al operador Hamiltioniano H tomando la derivada parcial con respecto a l:
Tenemos ya todo lo que se requiere para aplicar el teorema Hellmann-Feynman:
Pero puesto que:
se tiene entonces finalmente:
El teorema Hellmann-Feynman tiene muchas aplicaciones, y una de las cosas más interesantes en la aplicación de dicho teorema es que lo que se use como perturbación λ al tomar la derivada con respecto a λ puede ser cualquier cosa, literalmente hablando. Puede ser el número cuántico n o el número cuántico l como se vió arriba, puede ser también la masa m o la frecuencia angular ω. Hasta puede ser algo como la constante de Planck ħ. Vale la pena ilustrar ésto más a fondo con algún ejemplo sencillo, y tal vez lo que más se presta para ello es el oscilador armónico simple. Las energías eigen del oscilador armónico simple están dadas por la relación:
Si tomamos la frecuencia angular ω como la perturbación λ, entonces al tomar la derivada con respecto a ω de lo anterior se tiene:
Por otro lado, el operador de energía Hamiltoniano H del oscilador armónico simple está dado por:
Tomando la derivada con respecto a ω de H se tiene:
Tenemos ya todo lo que se requiere para aplicar el teorema Hellmann-Feynman:
Por otro lado, sabemos que la energía potencial V del oscilador armónico simple está dada por:
La esperanza matemática de la energía potencial será, de acuerdo con ésto:
en donde en la tercera línea se hizo uso del resultado proporcionado por el teorema Hellmann-Feynman. Esta es la esperanza matemática de la energía potencial del oscilador armónico simple, ya cuantizada.
Ahora haremos algo que tal vez dejará sorprendido al lector. Consideraremos a la constante de Planck ħ como la perturbación, ignorando el hecho de que se trata de una constante absoluta universal. Tomando la derivada con respecto a ésta constante, se tiene:
Ahora tomaremos la derivada del operador Hamiltoniano con respecto a ħ:
Obsérvese que al final hemos substituído la expresión entre los paréntesis cuadrados por lo que realmente representa, la energía cinética T del oscilador armónico simple.
Tenemos ya todo lo que se requiere para aplicar el teorema Hellmann-Feynman:
Hemos obtenido así la esperanza matemática de la energía cinética del oscilador armónico simple, ya cuantizada.
Por último, consideraremos la masa m como variable, con lo cual:
Por otro lado, la derivada del operador Hamiltoniano de energía H con respecto a la masa viene siendo:
Tenemos ya todo lo que se requiere para aplicar el teorema Hellmann-Feynman:
Este es exactamente el mismo resultado que predice el teorema viria (véase la entrada El teorema virial puesta como parte de ésta obra). Obtener los mismos resultados pero por medios distintos nos dá otra confirmación que se suma a las muchas que ya hay sobre la consistencia y unidad de la Mecánica Cuántica. Dada la gran versatilidad y facilidad de uso con que se puede aplicar el teorema Hellmann-Feynman, se puede sospechar que se ha estado desaprovechando el uso de dicho teorema en la resolución de problemas de gran interés.