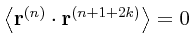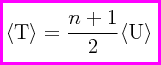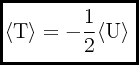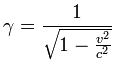El núcleo central de la demostración del teorema virial se fundamenta en un hecho matemático conceptualmente sencillo.
El promedio de la derivada de una función acotada es igual a cero o puede ser aproximado asintóticamente a cero cuanto se desee.Una manera intuitiva de comprender este hecho fundamental consiste en considerar un carro que manteniendo su velocidad de movimiento constante (de acuerdo con lo que indica el velocímetro en el tablero del carro) se la pasa dando vueltas en círculos alrededor de un estacionamiento buscando un espacio vacante. Después de un período considerable de tiempo, la velocidad promedio del vehículo (desde el punto de vista vectorial) se aproxima a cero, puesto que a medida que el tiempo transcurre yendo en aumento la distancia neta recorrida no aumenta al estar el movimiento del vehículo confinado (acotado) a estar dando vueltas en círculos. Esto no ocurriría si el vehículo estuviera trasladándose en línea recta (un desplazamiento no acotado) en una carretera a velocidad constante, en cuyo caso la velocidad promedio del vehículo sería la misma que la velocidad que marca el velocímetro en el tablero del carro.
Un ejemplo de una función acotada es el siguiente vector posición r(t) que describe el movimiento de una partícula en una órbita planetaria elíptica, expresado vectorialmente sobre la base ortogonal usual de vectores unitarios {i,j} (para el caso en el cual a.=.b la punta del vector posición describirá una órbita circular):
Obsérvese que si tomamos la derivada de este vector posición r(t) con respecto al tiempo, el resultado dr(t)/dt también será una función acotada. El desplazamiento de este vector posición se puede apreciar mejor en el siguiente gráfico animado:
Si convenimos en utilizar la notación del punto puesto encima de una variable para denotar la derivada de dicha variable con respecto al tiempo (y un doble punto para denotar la segunda derivada con respecto al tiempo), lo cual en caso de que la variable sea un vector posición r(t) que va cambiando con respecto al tiempo denota lo siguiente:
y que se puede conceptualizar esquemáticamente como:
entonces si la función está acotada (como ocurre con el caso de una partícula cuyo vector posición que la ubica se la pasa dando vueltas alrededor de un círculo o una elipse) tendremos como hecho inevitable que la magnitud del desplazamiento vectorial:
|r(t2) - r(t1)|
siempre será menor que alguna constante k, con lo cual:
La magnitud del numerador está acotada mientras que el intervalo de tiempo t2.–.t1 en el denominador puede aumentar sin límites, de modo tal que la derivada asintótica de dr/dt conforme el intervalo de tiempo aumenta se irá aproximando a cero tanto como se quiera, o sea:
Puesto que tanto r(t) como dr(t)/dt son funciones acotadas en el tiempo, se deduce que si tomamos la derivada temporal del producto escalar de ambas cantidades vectoriales, o sea si tomamos la derivada con respecto al tiempo de r(t)·dr(t)/dt, el promedio también deberá ser igual a cero:
Aplicando la regla del producto, lo anterior se puede escribir y simplificar paulatinamente como:
Multiplicando esto por la masa y reacomodando, se tiene entonces:
Viendo esto en mayor detalle, resulta claro que lo que tenemos entre los paréntesis curvos en el primer término es la masa por la aceleración (la aceleración siendo igual a la segunda derivada con respecto al tiempo del vector posición), lo cual en la segunda ley de Newton equivale a la fuerza total F que actúa sobre la partícula, mientras que lo que tenemos adentro de los paréntesis angulados en el segundo término es igual a la energía cinética T de la partícula, o sea:
Entonces podemos escribir la relación anterior como:
Consecuentemente, para un conjunto de N partículas con posiciones acotadas positions r1, r2, … rN, sujetas a las fuerzas F1, F2, …, FN, y con una energía cinética total T se tiene:
Esta relación, deceptivamente sencilla tanto en su enunciado como en su obtención, conocida como el teorema virial de Clausius, tiene enormes alcances y repercusiones en muchos campos de la física, tanto la física clásica como la física cuántica, y su importancia no puede ser soslayada. Despejando arriba para el promedio temporal de la energía cinética T, tenemos lo siguiente:
De este modo, el teorema virial puede enunciarse de la siguiente manera: “El promedio estadístico en el tiempo de la energía cinética de un sistema es igual a ...”. A Clausius se le ocurrió darle un nombre a la cantidad que aparece en el lado derecho de la anterior igualdad, bautizando de este modo a la cantidad:
con el nombre de virial, una palabra derivada del Latín vis que significa “fuerza” o “energía”. De este modo, el enunciado completo del teorema de Clausius dice así: “El promedio estadístico en el tiempo de la energía cinética de un sistema es igual al virial del sistema”.
En su quintaesencia, el teorema virial de Clausius es tan sólo una entre una cantidad infinitamente grande de proposiciones que son consecuencia del hecho de que el promedio (en el tiempo) de la derivada de una función acotada es igual a cero. El teorema de Clausius está basado sobre el producto escalar entre r(t) y dr(t)/dt, pero del mismo modo podríamos considerar otras funciones suponiendo que tanto r(t) como todas sus derivadas están también acotadas. Usando una convención de comillas para indicar derivadas sucesivas:
podemos postular los siguientes ejemplos (el primer ejemplo es el que corresponde al teorema virial):
Como puede apreciarse en la segunda identidad dada arriba, es fácil ver que el promedio temporal del producto punto dos derivadas de orden consecutivo será igual a cero. Hablando en términos más generales, se tiene (los superscriptos entre paréntesis no indican exponenciación sino el orden de al derivación con respecto al tiempo):
para dos enteros no-negativos cualesquiera n y k. En otras palabras, el promedio temporal del producto punto de dos derivadas cualesquiera cuyos órdenes difieran en un número impar será igual a cero. Esta es la razón del por qué las identidades “interesantes” (para el matemático) involucran productos punto de derivadas cuyos órdenes difieren en números pares. Podemos inferir también la siguiente generalización del teorema de Clausius:
o en forma aún más general:
Puesto que en la Mecánica Cuántica no se utiliza el concepto de la fuerza como lo define clásicamente la segunda ley de Newton, sino el concepto del momentum relacionado con la fuerza Newtoniana como el cambio en la cantidad del momentum con respecto al tiempo, una variante del teorema virial de Clausius obtenido arriba que es más adaptable a la Mecánica Cuántica es la siguiente:
El teorema virial de Clausius es un teorema de naturaleza esencialmente estadística, pero no porque sea utilizado frecuentemente para el análisis de sistemas con una gran cantidad de partículas (el teorema sigue siendo válido aún cuando está siendo aplicado al análisis del comportamiento dinámico de un sistema que conste de dos partículas) sino porque involucra promedios sobre la variable del tiempo.
La derivación que se llevó a cabo arriba del teorema virial de Clausis tuvo como principal objetivo reforzar el concepto de que la idea esencial radica en el comportamiento asintótico de las funciones acotadas al ir transcurriendo el tiempo. A continuación veremos la manera en la cual se obtiene el teorema virial en los textos usados para el estudio de la mecánica clásica pre-cuántica. Reteniendo la notación del punto puesto encima de una variable para indicar derivación con respecto al tiempo, y considerando un sistema de N masas puntuales con vectores posición ri ubicando a cada partícula sobre la cual actúa una fuerza Fi, empezaremos con el enunciado clásico Newtoniano que nos dice que el cambio en la cantidad del momentum de un cuerpo es igual a la fuerza que actúa sobre dicho cuerpo produciendo dicho cambio en el momentum:
Defínase ahora la siguiente cantidad G obtenida de la suma del producto punto del vector momentum de cada partícula del sistema por el vector posición que ubica a la partícula respectiva:
Utilizando la regla para la derivada de un producto, la derivada temporal (derivada con respecto al tiempo) de esta cantidad es entonces:
Inspeccionando el primer término, podemos ver que está relacionado directamente con la energía cinética total T del sistema de la siguiente manera:
Por otro lado, con segundo término se puede afirmar lo siguiente:
Entonces dG/dt puede escribirse de la siguiente manera:
En concordancia con la definición del promedio para una función continua, el promedio temporal de esto último sobre un intervalo de tiempo τ se obtiene llevando a cabo una integración con respecto al tiempo desde un tiempo igual a cero hasta un tiempo igual a τ y dividiendo entre el lapso de tiempo transcurrido que viene siendo τ:
De este modo, para la expresión promediada estadísticamente con respecto al tiempo:
se tiene:
Si el movimiento del sistema es un movimiento periódico, esto es, si todas las coordenadas se repetirán después de transcurrido cierto tiempo, entonces G(τ).=.G(0), y lo último se desvanece. Se llega a una conclusión similar aún si el movimiento no es un movimiento periódico siempre y cuando las coordenadas de posición y velocidad para las partículas permanezcan finitas y sobre todo siempre y cuando la función G sea una función acotada. Escogiendo un tiempo τ suficientemente grande, el promedio temporal de dG/dt se puede hacer tan pequeño como se quiera, llevándonos entonces al mismo resultado que se había obtenido arriba:
Este resultado es tan flexible que, por principio de cuentas, puede ser utilizado para derivar la ley del gas ideal, la ley de Boyle, tomando como punto de partida el teorema de la equipartición de la energía.
PROBLEMA: Tomando como base el teorema de la equipartición de la energía, de acuerdo al cual la energía cinética promedio de cada átomo que forma parte de un gas dentro de un recipiente de volumen V es igual a:
en donde T es la temperatura del gas (¡no confundir con el símbolo T que hemos estado usando arriba para denotar a la energía cinética!) y k la constante de Boltzmann, obténgase la ley del gas perfecto o gas ideal.
Si la expresión dada en el enunciado del problema es la que corresponde a la energía de un solo átomo, la energía de un total de N átomos será;
Repasando el teorema virial de Clausius, vemos que las fuerzas Fi incluyen a las fuerzas de interacción entre las partículas y las fuerzas de constricción sobre el sistema. Un gas perfecto es aquél en el cual las fuerzas de interacción tienen una contribución prácticamente nula en el virial, lo cual ocurre cuando el gas es tan poco denso que las colisiones entre las partículas ocurren muy rara vez en comparación con las colisiones contra las paredes del recipiente que contiene al gas. Las paredes del recipiente son las fuerzas de constricción sobre el sistema y se hacen presentes cada vez que un átomo choca contra una pared del recipiente, sobreentendiéndose que se trata de colisiones perfectamente elásticas como las que podemos visualizar en un juego de billar. De este modo, tomado en cuenta que el número de partículas es extremadamente grande, podemos reemplazar la sumatoria por una integral en el teorema virial. La fuerza de constricción representa la reacción de la pared (tercera ley de Newton) sobre las fuerzas de colisión ejercidas por los átomos del gas al chocar contra la pared, lo cual interpretamos como la presión del gas P. Siendo la presión del gas P igual a la fuerza F por unidad de área, o sea F/A, ejercida por los átomos que chocan contra la pared, o en este caso siendo la presión igual a un elemento infinitesimal de fuerza dF por elemento infinitesimal de área dA, o sea dF/dA, con lo cual podemos escribir vectorialmente lo siguiente:
en donde en la segunda línea se ha utilizado un vector unitario normal n para asignarle “dirección” al elemento infinitesimal de área dA, tenemos entonces que el virial estará dado por:
Para llevar a cabo la integración, resulta conveniente efectuar una conversión transformando esta integral de una integral de superficie a una integral de volumen recurriendo al teorema de Gauss (también conocido como el teorema de la divergencia):
La integral de volumen puede llevarse a cabo fácilmente dando como resultado:
Entonces la integral de área original es simplemente igual a:
De este modo, apelando al teorema virial, se tiene lo siguiente:
que es lo que comúnmente conocemos como la ley del gas ideal.
Otra aplicación importante del teorema virial tiene que ver con todo aquello que tenga relación con fuerzas que puedan ser obtenibles de algún potencial. Considérese el caso más sencillo en el cual se tienen únicamente dos partículas entre las cuales actúa una fuerza F. En tal caso, el teorema virial toma la siguiente forma:
Supóngase que la fuerza de interacción F entre las dos partículas es procurable de un potencial U como el negativo de la derivada del potencial (así es como se le define en la física clásica), o más generalmente, como el gradiente vectorial del potencial (esta última definición se presta al uso de cualquier sistema de coordenadas, ya sea rectangulares, esféricas, etc.):
De interés primario es aquél caso en el cual las dos partículas interactúan de acuerdo con una fuerza central (radial) que es función de alguna potencia de la distancia, o sea F.=.krn. En tal caso, el potencial U tiene la forma:
Por lo tanto:
De este modo, el teorema virial para dos partículas se convierte en:
Para partículas o masas entre las cuales hay una atracción que varía en razón inversa al cuadrado de la distancia, como ocurre con dos cuerpos que obedecen la ley de la atracción universal de Newton, o como ocurre con la ley de Coulomb que se aplica a dos cargas eléctricas, n.=.-2, y entonces:
Aunque estas conclusiones fueron obtenidas considerándose únicamente dos partículas, el teorema virial es aplicable a un sistema físico con varias partículas o inclusive un número muy grande de partículas, lo cual permite atacar problemas que de otra manera serían insolubles. Supóngase un sistema que conste de cuatro partículas. Supóngase además que las fuerzas actuando sobre las partículas se deben por completo a las fuerzas mutuas que cada partícula ejerce sobre las demás. En tal caso cada fuerza Fi es la suma vectorial de las fuerzas individuales ejercidas sobre la i-ésima partícula por todas las demás partículas. Simbolícese como fij la fuerza ejercida sobre la partícula-i por la partícula-j. Podemos escribir entonces el teorema virial de la siguiente manera:
En virtud de la tercera ley de Newton (acción y reacción), se tiene fij = -fji, de modo tal que los términos diagonalmente simétricos en la suma de 16 términos pueden ser apareados en pares, permitiéndonos escribir lo anterior de la siguiente manera:
Si estipulamos además que la fuerza ejercida sobre la partícula-i por la partícula-j apunta vectorialmente a lo largo de la línea que pasa a través de ambas partículas y que dicha fuerza varía en proporción a alguna potencia de la distancia radial, esto es, si la fuerza tiene la forma;
para algún entero n y una constante K, tomando en cuenta que se ha definido a fij como la fuerza que actúa sobre la partícula-i, y que el vector ri.-.rj apunta hacia la partícula-i, entonces la energía potencial Vij del enlace es:
Esto último que se ha afirmado puede ser verificado observando sobre la magnitud de la diferencia vectorial ri.-.rj que:
de modo tal que la derivada parcial de Vij con respecto a Δx es:
o bien:
La misma consideración se puede aplicar a ∂Vij/∂(Δy):
y a ∂Vij/∂(Δz):
con lo cual tenemos la fuerza:
Por lo tanto, puesto que la energía potencial del enlace entre la partícula-i y la partícula-j es igual a [-1/(n+2)](ri.-.rj)∙fij, la cantidad:
es -(n+2) veces el promedio de la energía potencial total V del sistema de partículas. Por lo tanto, la ecuación multipartículas con la que habíamos empezado puede ser expresada como:
en concordancia con lo obtenido previamente.
El descubrimiento de la existencia en el Universo de lo que hoy se conoce como materia oscura fue posible gracias a la ayuda del teorema virial en esta forma. Esta conclusión fue lograda en 1933 por el astrofísico Fritz Zwicky al estar analizando el cúmulo de galaxias Coma:
en sus intentos por obtener una estimación de la masa promedio del cúmulo Coma, obteniendo un cálculo de una masa que resultó ser unas 160 veces mayor que lo que se esperaba en base a la luminosidad de las galaxias, lo cual lo llevó a proponer que la mayor cantidad de la materia no detectable por medios convencionales tenía que ser materia oscura (a diferencia de las estrellas que están radiando energía constantemente con la cual nos hacen saber su presencia, los cuerpos “fríos” no radían energía propia). Los mismos cálculos llevados a cabo hoy en día mediante mediciones más precisas de la luminosidad y el desplazamiento Doppler arrojan un factor más pequeño, pero sigue siendo claro que la mayor canridad de materia contenida en las galaxias es materia oscura. Las observaciones astronómicas nos permiten contar en una galaxia el número aproximado de todas las estrellas que la integran, sus velocidades relativas, sus separaciones, y sus masas, y con esta información podemos estimar la energía cínetica promedio global T; asimismo podemos estimar el campo potencial gravitacional estático producido por las estrellas con lo cual podemos estimar también la energía potencial global V. Suponiendo que las estrellas están ligadas por una fuerza gravitatoria de naturaleza Newtoniana que varía en razón inversa al cuadrado de la distancia, en base a lo que nos dice el teorema virial esperaríamos confirmar la relación 2<T>.=.-<V> pero lo que se encuentra de hecho es que 2<T> es por lo menos un orden de magnitud mayor que -<V>. Lo mismo se encuentra tanto para cúmulos de galaxias como para galaxias individuales. Para tratar de reconciliar los datos, podemos manejar tres hipótesis. La primera consiste en suponer que la gravedad en la escala macrcósmica de las galaxias y cúmulos de galaxias no es una ley que varíe en razón inversa del cuadrado de la distancia. Sin embargo, puesto que el área superficial de una esfera aumenta en razón inversa al cuadrado de la distancia al centro de la esfera, cualquier desviación de la fuerza que varía en razón inversa del cuadrado de la distancia implicaría una desviación al teorema de la divergencia de Gauss que nos relaciona una integral sobre el volumen de la esfera con una integral sobre la superficie de la esfera, a menos de que queramos postular también que el espacio a esa escala macrocósmica es no-Euclideano. Si seguimos postulando la validez de una ley que varíe en razón inversa de una potencia de la distancia, no necesariamente cuadrática, nos veríamos obligados a postular una fuerza proprcional a la inversa de la doceava potencia de la distancia, lo cual es poco creíble. Como una segunda hipótesis, podemos postular otro tipo de fuerza de carácter no gravitatorio que se vuelve significativa a escalas macrocósmicas, pero esto es lo mismo que suponer una forma diferente para la fuerza gravitacional a esas distancias. La tercera hipótesis consiste en suponer que las galaxias contienen por lo menos diez veces más masa que la que se nos muestra en forma visible a través de nuestros sondeos astronómicos. Esta última es la posibilidad aceptada, porque no hay razón para suponer que la mayor parte de materia esté radiando con la suficiente brillantez para ser visible.
PROBLEMA: Demuéstrese la validez del teorema virial para el átomo de hidrógeno en el modelo atómico planetario de Bohr que corresponde a la Mecánica Cuántica “vieja”, suponiendo que el átomo se encuentra en el estado basal.
En el modelo atómico planetario de Bohr, nos imaginamos al electrón en el estado basal girando en una órbita circular en torno al núcleo de átomo. Llevaremos a cabo la solución empleando notación vectorial clásica como la que se encuentra en muchos textos, definiendo por principio de cuentas un vector posición radial unitario cuya magnitud es igual a la unidad:
Este vector posición unitario sirve para fijar la dirección instantánea de un vector radial r cuya magnitud será igual a r:
Dicho de otra manera:
Se supone que la fuerza de atracción eléctrica entre el electrón y el protón situado en el núcleo está balanceada con la fuerza Newtoniana centrípeta requerida para mantener al electrón en su órbita circular (llevaremos a cabo el desarrollo en el sistema de unidades MKS-SI):
En el modelo atómico planetario del átomo de hidrógeno, la órbita circular está confinada a llevarse a cabo en un plano. Representando las componentes vectoriales como un vector columna
La velocidad instantánea v del vector radial r es igual a la derivada de r con respecto al tiempo:
Del mismo modo, la aceleración instantánea a es igual a la derivada de la velocidad instantánea v con respecto al tiempo:
Entonces, igualando componentes en la ecuación vectorial para el átomo de hidrógeno:
Podemos limitarnos a trabajar con ambas magnitudes de esta ecuación vectorial al ser cantidades iguales:
Podemos reconocer de inmediato lo que aparece en el lado derecho de la igualdad como la energía cinética T del electrón, mientras que la energía potencial V viene siendo:
Por lo tanto:
Esto es precisamente lo que predice el teorema virial para dos partículas que se atraen con una fuerza que varía en razón inversa del cuadrado de la distancia que las separa, ya que con n.=.-2:
Puesto que de acuerdo al modelo atómico planetario de Bohr la energía del electrón en el átomo de hidrógeno no puede tomar cualquier valor posible sobre un espectro continuo de energías sino que está cuantizada, y puesto que dicha energía que designaremos como En es igual a la suma de la energía cinética T y la energía potencial V:
entonces, tomando el promedio en ambos miembros de esta relación se tiene lo siguiente:
Puesto que el valor de En no es “borroso” sino un valor bien definido para cada estado estacionario que no puede ser el resultado de ninguna promediación estadística, el lado izquierdo de lo anterior se debe escribir simplemente como:
Usando en esto el resultado obtenido arriba:
se tiene entonces:
y se tiene también:
PROBLEMA: Compruébese la validez del teorema virial para un oscilador armónico simple clásico.
Para un oscilador armónico simple clásico, que consta de una masa conectada a un resorte, la fuerza sobre la masa es directamente proporcional a la distancia hacia el origen, lo cual nos conduce a la ecuación diferencial del movimiento:
Esta ecuación diferencial tiene una muy conocida solución de carácter senoidal:
dándonos la posición de la partícula en función del tiempo, x(t). En el caso del oscilador armónico simple clásico, la energía potencial V es:
Puesto que la fuerza tiene la forma sea F.=.-kxn.=.-kx1, entonces con el exponente n.=.1 de acuerdo al teorema virial se debe tener:
Esto es, para el oscilador armónico simple clásico, el promedio de la energía cinética T debe ser igual al promedio de la energía potencial V, o sea que <T> debe ser igual a <V>. Esto puede ser confirmado obteniendo primero la energía potencial V del oscilador armónico simple clásico usando la expresión obtenida para x(t):
Por otro lado, la energía cinética T del oscilador armónico simple clásico es:
que viene siendo, substituyendo la derivada dx/dt:
Ahora bien, los promedios a largo plazo (sobre intervalos grandes de tiempo) de sen2(ωt) y cos2(ωt) son iguales. Esto podemos verificarlo de una manera inmediata y sencilla para la función sen2(t) que ciertamente es una función acotada recurriendo a algún paquete computacional de integración numérica que nos permita ir evaluando las siguientes integrales que representan promedios de la función sobre intervalos crecientes de tiempos, dándonos los resultados que se muestran:
Como puede apreciarse, el promedio de la función tomado a largo plazo converge hacia 1/2. Pero de hecho no es necesario considerar tiempos muy prolongados para que la integral se acerque a dicho valor. Inclusive con intervalos de tiempo moderados el acercamiento hacia la respuesta esperada se hace notorio, lo cual nos permite afirmar que:
Expresado de modo más general, los promedios a largo plazo (sobre intervalos grandes de tiempo) de sen2(ωt) y cos2(ωt) son iguales:
Esto hecho hace que, para un oscilador armónico simple clásico, la energía cinética promedio y la energía potencial promedio a largo plazo sean iguales, comparando los resultados que hemos obtenido arriba para la energía potencial instantánea V(t) y para la energía cinética instantánea T(t).
En lo que se ha visto previamente, no se han tomado en cuenta efectos relativistas sobre el teorema virial. Existe, desde luego, una versión relativista del teorema virial, la cual toma en cuenta los efectos propios de la Teoría Especial de la Relatividad (descartando marcos de referencia acelerados). Para el caso relativista para una sola partícula, podemos empezar con la definición de la misma cantidad G (el producto punto del vector momentum la partícula por el vector posición que ubica a la partícula) utilizada arriba como punto de arranque:
en donde para p utilizaremos la definición del momentum relativista en lugar del momentum clásico (para quienes no están familiarizados con la Teoría de la Relatividad se recomienda consultar la obra con dicho título de este mismo autor). Tomando la derivada de G con respecto al tiempo:
Al igual que como se hizo en el caso no-relativista, se puede argumentar que sobre un promedio temporal prolongado la derivada con respecto al tiempo del virial es igual a cero, con lo cual:
Podemos agregar la cantidad mc2/γ a ambos lados de la ecuación sin alterarla:
Podemos reacomodar esta ecuación y factorizar fuera a gamma para dos de los términos:
Podemos substituír la expresión para gamma para hacer esto último más explícito:
con lo cual se tiene:
o lo que es lo mismo:
Haremos uso ahora del teorema virial para el asunto que aquí nos interesa, el campo de aplicación de la Mecánica Cuántica.
PROBLEMA: Partiendo de la ecuación del movimiento de Heisenberg, demuéstrese que:
Una vez demostrado lo anterior, verifíquese que, para un estado estacionario:
La ecuación del movimiento de Heisenberg, en la cual distinguiremos a las observables físicas de los operadores que las representan poniéndole a estos últimos un acento circunflejo encima (en realidad, el término acento circumflejo es inapropiado aquí, razón por la cual se usa el término más descriptivo de “sombrero”), es la siguiente:
Haciendo Q.=.xp en esta ecuación, se tiene:
Obsérvese que en el lado derecho se ha manejado a xp como un solo operador combinado, poniendo un solo “sombrero” a x y a p. Sin embargo, esta sigue siendo una combinación de operadores individuales aplicada en cierto orden (el segundo operador es el primero en actuar sobre lo que se le ponga a la derecha al operador combinado). Esto nos permite romper al operador combinado en dos operadores:
De este modo, se tiene:
Para ver el efecto resultante de esto sobre algo (lo que sea), es válido aplicarlo sobre una función de prueba f(x):
Trabajando dentro del espacio-posición, para el operador del momentum hacemos:
Para el operador Hamiltoniano tenemos también:
Y puesto que estamos trabajando en el espacio-posición, podemos tomar al operador posición igual que a la variable de la posición:
Tenemos entonces:
Esto lo podemos ir simplificando sucesivamente del modo siguiente:
Podemos reconocer lo que está entre los paréntesis cuadrados:
como la parte que corresponde a la energía cinética T del operador Hamiltoniano de energía:
Por lo tanto:
Borrando la función de prueba f(x) al haber servido su propósito y concentrándonos en la parte operacional:
Por lo tanto, regresando a la ecuación del movimiento de Heisenberg con esto que acabamos de obtener:
Finalmente, podemos ver que el operador:
no tiene dependencia explícita alguna de la variable tiempo, con lo cual:
Entonces el desarrollo previo nos conduce a:
o lo que es lo mismo:
Ahora bien, para un cierto estado estacionario fijo de energía E, la evolución temporal de la función de onda está dada por:
De este modo, para un estado estacionario:
Esto último es completamente independiente del tiempo. Por lo tanto, para un estado estacionario, la esperanza matemática de una observable tomada con respecto a cierta eigenfunción de energía no cambia con el tiempo, y en tal caso si hacemos Q.=.xp se debe tener:
Cuando esto ocurre, entonces de acuerdo a lo que se ha obtenido previamente:
Esto último es la versión mecánico-cuántica para el teorema virial aplicado a una dimensión.
El desarrollo previo puede ser llevado hacia cuatro dimensiones, y nuevamente se requerirá de la ecuación del movimiento de Heisenberg para poder obtener un resultado concreto.
PROBLEMA: Considérese el caso de una partícula en tres dimensiones cuyo operador Hamiltoniano está especificado de la siguiente manera:
Haciendo uso de la ecuación del movimiento de Heisenberg y empezando con el cálculo del siguiente conmutador:
demuéstrese que:
Este problema es la generalización hacia tres dimensiones del problema anterior. Empezaremos el cálculo resaltando a x·p con color magenta como x·p para mayor claridad:
Teniendo presente que:
se tiene entonces:
Recurriremos ahora a un poco de álgebra de conmutadores echando mano de la siguiente identidad:
con la que haciendo A.=.xi, B.=.pi, y C.=.pjpj en el primer término; y haciendo A.=.xi, B.=.pi, y C.=.V(x) en el segundo término se tiene:
Tenemos ahora cuatro términos. Pero el primer término se hace cero:
al llevarse a cabo la expansión de la doble sumatoria sobre todos los tres índices numéricos que corresponde a un espacio tridimensional. Asimismo, puesto que V(x) es una función vectorial de los xi, conmuta con los xi con lo cual todos los términos de la sumatoria estipulados por el cuarto término se hacen cero:
quedando:
Nuevamente, podemos recurrir a álgebra de conmutadores aplicando la acción de la siguiente identidad:
con la que haciendo A.=.xi, B.=.pi, y C.=.pjpj en el primer término se puede reescribir como:
La razón para haber hecho este último reacomodo es para poder introducir aquí la “extraña ecuación” de Born en los conmutadores que relacionan a la posición xi con el momentum =.pj:
Obsérvese que en el segundo término también se ha hecho uso de una relación demostrada previamente. De este modo, tomando en cuenta las propiedades de la función δ de Dirac, lo anterior viene quedando como:
Tomando las esperanzas matemáticas de ambos miembros de esta igualdad, llegamos a:
Recurriendo a la ecuación del movimiento de Heisenberg, podemos tomar el lado derecho de la igualdad substituyendo la expresión entre paréntesis para que nos quede finalmente lo siguiente:
Cabe destacar que este resultado es válido bajo cualquier sistema de coordenadas tridimensional.
PROBLEMA: Utilizando las siguientes relaciones que nos proporcionan los elementos matriciales para el cuadrado de la posición y el cuadrado del momentum de un oscilador armónico simple cuántico:
compruébese la validez del teorema virial para un estado estacionario cualesquiera que corresponda a un oscilador armónico simple cuántico. (Las relaciones dadas en el encabezado de este problema fueron demostradas en uno de los problemas resueltos puestos en la entrada “Los operadores escalera II”)
En base a los resultados obtenidos con anterioridad, en el caso de un oscilador armónico simple unidimensional cuyo operador hamiltoniano de energía H es:
para un estado estacionario el teorema virial tridimensional estipula:
Este enunciado, reducido a una dimensión, dicta lo siguiente:
Si el oscilador armónico simple cuántico obedece el enunciado del teorema virial, entonces esta relación se debe de cumplir incondicionalmente.
Para un estado estacionario n, la relación que nos proporciona los elementos matriciales de la esperanza matemática del cuadrado de la posición se obtienen haciendo n’.=.n en la primera relación dada en el enunciado del problema:
Por las propiedades del delta de Kronecker, los deltas destacados en color rojo se vuelven cero, y el único delta que sobrevive es el de color azul, con lo cual:
Esto significa que, para un eigenestado n estacionario:
Por otro lado, también para un estado estacionario n, la relación que nos proporciona los elementos matriciales de la esperanza matemática del cuadrado del momentum se obtienen haciendo n’.=.n en la segunda relación dada en el enunciado del problema:
Al igual que arriba, por las propiedades del delta de Kronecker, los deltas destacados en color rojo se vuelven cero, y el único delta que sobrevive es el de color azul, con lo cual:
Esto significa que, para un eigenestado n estacionario:
Obviamente, el teorema virial sigue siendo válido para un estado estacionario cualesquiera que corresponda a un oscilador armónico simple cuántico.
PROBLEMA: Compruébese la validez del teorema virial para un estado estacionario cualesquiera que corresponda a un oscilador armónico cuántico tridimensional.
Trabajando en un sistema de coordenadas Cartesianas rectangulares, podemos descomponer al operador Hamiltoniano de energia H del oscilador armónico tridimensional (el cual ya no es simple) en tres operadores Hx, Hy, y Hz, los cuales conmutan por representar observables compatibles:
Puesto que Hx, Hy, y Hz conmutan, y cada uno opera sobre una variable distinta a los demás, se pueden escribir las eigenfunciones de la siguiente manera:
siendo q, r y s enteros positivos, y en donde, usando los resultados obtenidos para el oscilador armónico simple unidimensional::
Aquí los números cuánticos q, r y s están asociados con el movimiento-x, el moviento-y y el movimiento-z de la partícula. La eigenecuación para el sistema tridimensional es por lo tanto:
Siendo q, r y s números enteros, la suma de los mismos dará un número cuántico n para el oscilador armónico tridimensional. Entonces cada eigen-estado estacionario tendrá una energía igual a:
Usaremos ahora los resultados obtenidos arriba. El primer término que evaluaremos para verificar la validez del teorema virial en el caso del oscilador armónico tridimensional es el siguiente:
Ahora evaluaremos el siguiente término:
Puesto que ambos términos son iguales para un estado estacionario del oscilador armónico tridimensional, se concluye que el teorema virial mantiene su validez en este caso.
La esperanza matemática de la energía cinética T del oscilador armónico tridimensional en función de la energía En de un estado estacionario resulta ser la siguiente:
Puesto que la energía En de un estado estacionario del oscilador tridimensional es igual a la suma de la energía cinética T y la energía potencial V, esto nos permite obtener la esperanza matemática de la energía potencial V del oscilador armónico tridimensional en función de la energía En del estado estacionario:
Podemos resumir estas últimas dos conclusiones en una sola: