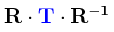En el núcleo central de la Teoría de Grupos, sobre todo en lo que concierne a varias operaciones básicas que se han estado llevando a cabo previamente dentro de la Mecánica Cuántica, algo que adquiere relevancia prominente es lo que se conoce como procesos conjugados (la definición dada a continuación será dada en forma tal que el orden de los procesos es leído de izquierda a derecha en lugar de derecha a izquierda, aunque esto en realidad no es de mayores consecuencias):
Lo anterior nos indica que primero se llevará a cabo un proceso R, seguido a continuación de otro proceso T, seguido por un tercer proceso R-1 que es el inverso del primer proceso. Un examen superficial de esta operación podría llevarnos a la conclusión errónea de que el resultado final de esta operación será T, ya que si el tercer proceso revierte lo que hizo el primer proceso entonces la única operación efectiva que se habrá llevado a cabo al final de cuentas es T. Sin embargo, las apariencias engañan, y para demostrarlo no hay nada mejor que recurrir a un ejemplo específico que nos demuestre la falsedad de tal conclusión. El ejemplo que tomaremos está basado en el cubo de Rubik 3×3, el paradigma más popular que existe para demostrar el efecto verdadero de los procesos conjugados. Tomaremos el siguiente cubo de Rubik en su posición prístina en la cual cada una de sus seis caras tiene a los cubos que forman las caras mostrando el mismo color:
A continuación, como una operación R, llevaremos a cabo una rotación en el mismo sentido en el que corren las manecillas de un reloj mecánico, en torno al eje que es perpendicular a la cara que muestra las nueve caritas de los “cubitos” de color rojo (R - right):
Como puede verse, la operación ha movido tres cubitos de color verde (F - front) hacia arriba, y ha movido también tres cubitos de color amarillo (D - down) que por estar abajo no eran visibles en la figura anterior hacia el frente.
A continuación, llevaremos a cabo una segunda operación de rotación, que llamaremos T, también en el sentido en el que corren las manecillas de un reloj mecánico, en torno al eje que es perpendicular a la cara superior, suponiendo para ello que en la parte trasera de un cubo en su condición inicial simétrica tiene los cubitos de la parte trasera (B - back) pintados de color azul:
La operación de rotación que es inversa a la primera operación de rotación, o sea R-1, consiste en llevar a cabo sobre esto último una operación en la cual se gire la cara lateral en cuyo centro hay un cubito de color rojo, dos cubitos azules, un cubito blanco y dos cubitos azules (además de los otros cinco cubitos de color rojo) en el sentido inverso al sentido en el que corren las manecillas del reloj. Y lo que nos queda definitivamente no es lo que quedaría si se hubiera efectuado una operación individual T (la segunda rotación intermedia) sobre el cubo en su configuración prístina original. De hecho, lo que queda es un cubo algo desarreglado que no le dá muchos indicios a un principiante sobre las otras dos operaciones R y R-1 que se llevaron a cabo. Este es precisamente el efecto de un proceso conjugado.
El siguiente gráfico animado nos muestra las primeras dos operaciones indicadas arriba:
PROBLEMA: Demuéstrese con un cubo de Rubik 3×3 que el proceso conjugado RTR-1 produce un resultado diferente al que produce la operación T efectuada por sí sola.
Usaremos para la demostración el mismo cubo de arriba en su configuración inicialmente simétrica (con el mismo color de cubitos en cada cara del cubo), suponiendo que en la cara trasera que es opuesta a la cara con cubitos de color rojo (identificados como R - right) hay cubitos de color naranja-café ( .) identificados como L - left, suponiendo además que en la cara trasera que es opuesta a la cara con cubitos de color verde (identificados como F - front) hay cubitos de color azul ( ) identificados como B - back, y suponiendo además que en la cara inferior que es opuesta a la cara con cubitos de color blanco (identificados como U - up) hay cubitos de color amarillo ( ) identificados como D - down. Una vez que se llevan a cabo las operaciones T y RTR-1 sobre dos cubos inicialmente simétricos, al comparar los resultados se ve que ambas operaciones producen resultados diferentes:
Si lo que se quiere es invertir una secuencia combinada de dos operaciones, o sea RT, para regresar a la configuración original que se tenía desde un principio, o sea el elemento identidad 1 (destaca el hecho de que al hablar aquí de un elemento identidad no estamos hablando del número 1, y de hecho lo que tenemos en manos es una matemática sin números), el inverso (RT)-1 se obtiene no sólo invirtiendo las operaciones usándose R-1 en lugar de R y usándose T-1 en lugar de T) sino invirtiendo también el orden de las operaciones. O sea (efectuando las operaciones de izquierda a derecha):
Este es un dogma central de la Teoría de Grupos que simple y sencillamente no se cuestiona, y como podemos apreciarlo con cualquier cubo de Rubik, no hay razón lógica alguna para cuestionarlo. Es consecuencia directa de la propiedad de asociatividad que debe caracterizar a todos los elementos de cualquier grupo, y su verificación usando dicha propiedad es elemental:
Así como para el cubo de Rubik se ha definido el proceso conjugado RTR-1, de igual manera se puede llevar a cabo el proceso conjugado:
con la única diferencia en en estos dos procesos conjugados del cubo siendo que si la primera rotación R es una operación que se lleva a cabo en el sentido de las manecillas del reloj, la misma primera operación especificada como R-1 es una operación que se llevará a cabo en un sentido contrario al giro de las manecillas del reloj.
Saliendo un poco fuera del tema de Rubik, y hablando de matrices, ya sabemos que para poder diagonalizar una matriz M mediante una relación de similitud esto se puede llevar a cabo obteniendo primero una matriz apropiada U, mediante la cual con la operación de similitud:
se obtiene la matriz diagonalizada. Esto se ve demasiado parecido a los procesos conjugados R-1TR llevados a cabo en un cubo de Rubik, si no fuera porque en la expresión que tenemos arriba estamos hablando de matrices y no de cubos de Rubik. Sin embargo, el enorme parecido que hay entre ambas expresiones nos sugiere que hay mucho mar de fondo en esto, y que los parecidos no son meras coincidencias. De hecho, y hablando en el sentido matemático general más estricto y puro, en realidad estamos hablando de dos caras diferentes de la misma cosa, estamos hablando aceca de la representación matricial de un grupo. Esta equiparación de grupos con matrices resulta ser una de las herramientas más potentes en la Mecánica Cuántica, y fue explotada hábilmente desde un principio por pioneros como Eugene Wigner. En relación a esto, se puede asentar aquí como teorema el siguiente enunciado que resulta ser de una utilidad extraordinaria:
Toda representación matricial de un grupo es equivalente a alguna representación del grupo llevada a cabo con matrices unitarias.Habiendo representaciones matriciales que no pueden ser reducidas o simplificadas aún más de modo alguno mediante operaciones de similitud o cualquier otro tipo de operaciones matemáticas, conocidas como representaciones irreducibles, esto trae como consecuencia una nueva formalización de las operaciones de simetría llevadas a cabo.
En lo que estaremos viendo a continuación, es importante tener bien clara la diferencia sobre lo que es un grupo discreto y lo que es un grupo continuo, así como lo que implica esta diferencia en las relaciones de simetría.
Considérese el siguiente cubo montado sobre un sistema de coordenadas rectangulares Cartesianas (x,y,z) cuyo origen coincide con el centro de masa (el centro geométrico) del cubo:
Como se ha destacado en la figura, si tomamos cualquiera de los ejes Cartesianos como referencia podemos girar al cubo en torno al eje seleccionado ya sea en 90°, 180° ó 270°, lo cual dejará a un cubo perfecto en una nueva posición que lo hace indistinguible de su posición previa (es decir, no nos será posible saber si permanece en su posición original o si fue girado hacia una nueva posición). Habiendo tres posibilidades de giro (90°, 180° ó 270°) en torno a un eje cualesquiera, y habiendo tres ejes coordenadas, se concluye que hay nueve maneras distintas de girar al cubo sin perderse la simetría original. Podemos decir entonces que tenemos un grupo de nueve elementos (diez en total, si se incluye la rotación identidad que deja al cubo en su misma posición original) al que podemos llamar el “grupo de rotaciones del cubo”. Se trata, pues, de un grupo discreto que contiene una cantidad finita de elementos discretos.
Considérese ahora el caso de una esfera sólida, el objeto geométrico “más perfecto posible”:
Si al igual que como lo hicimos con el cubo, colocamos al centro geométrico de la esfera de modo tal que coincida con el origen de un sistema de coordenadas rectangulares Cartesianas, comprobaremos que también podemos girar a la esfera en 90°, 180° ó 270°, sin que nos sea posible distinguir posteriormente (no habiendo visto la operación de rotación) que la esfera haya sido girada sobre uno de sus ejes. Pero el giro no tiene por qué estar limitado a 90°, 180° ó 270°, también podemos girar a la esfera en 30°, 45°, 75° ó 21° manteniendo la esfera sólida la misma apariencia, algo que no se puede hacer con el cubo de arriba. De hecho, el ángulo de giro puede ser cualquier ángulo, habiendo una cantidad infinitamente grande de ángulos de giro, en torno a cualquiera de los tres ejes. Si hablamos entonces del grupo de rotaciones de una esfera sólida, ese grupo necesariamente tiene que ser un grupo infinitamente grande, tiene que ser un grupo continuo.
Sin embargo, si deformamos la esfera sólida convirtiéndola en un elipsoide, encontraremos muy pronto que ya no es posible girar al cuerpo en cualquier ángulo como antes sin que se pierda la simetría original:
En la figura de arriba, el único eje en torno al cual se puede girar el cuerpo en cualquier ángulo manteniéndose la simetría original es el eje-x. Del grupo continuo que se tenía originalmente, la ruptura de la simetría ha traído como consecuencia que la descripción del cuerpo requiera tanto de un grupo continuo como de un grupo discreto. Se requiere de un grupo continuo para poder describir las operaciones de rotación del elipsoide en torno al eje-x, pero se requiere de otro grupo discreto para poder describir las operaciones de rotación del elipsoide en torno al eje-y así como en torno al eje-z (el eje vertical). Además de la rotación identidad, la que deja al elipsoide en su misma posición, hay dos operaciones de rotación que preservan la simetría: una rotación de π radianes en torno al eje-y que llamaremos ry(π), y otra rotación de π radianes en torno al eje-z que llamaremos rz(π). La “tabla de multiplicar” para el grupo discreto de las rotaciones del elipsoide contendrá por lo tanto tres elementos, el elemento identidad (I), ry(π) y rz(π). Identificaremos a este grupo de rotaciones simplemente como R. Pero tenemos también al grupo continuo de las rotaciones del elipsoide en torno al eje-x, el cual identificaremos como Φ. La “tabla de multiplicar” que describe al grupo de rotaciones del elipsoide estará entonces representada como el producto de estos dos grupos, el cual simbolizaremos como R×Φ. Este salto en complejidad no es algo que estemos inventando nosotros, es un hecho de la Naturaleza que solo podemos intentar describir mediante la notación que estamos desarrollando.
En la búsqueda de grupos, ya sea en las rotaciones de objetos geométricos o en los parámetros internos de alguna ecuación, es muy importante no dejarse llevar por las apariencias. Como ejemplo de ello, a continuación se citará al juguete conocido como la esfera de Rubik:
Cualquiera que haya intentado restablecer una esfera de Rubik a su posición original, además de haberse convertido intuitivamente en un experto en la Teoría de Grupos, podrá dar fé de que las posibilidades de combinaciones son tan grandes que no es posible esperar resolver un acertijo de este tipo recurriendo meramente a giros de azar, es necesario contar con algún tipo de teoría o algún conjunto de reglas que puedan servir como ayuda. Puesto que el objeto en cuestión es una esfera, aparentemente daría lugar a un grupo continuo, ¿no es así? La respuesta, desde luego, es un rotundo no. En un grupo continuo las combinaciones posibles son infinitamente grandes, y si la esfera de Rubik fuera descrita como un grupo continuo no habría entonces forma alguna de poder restablecerla a su configuración original (suponiendo que haya sido desacomodada), ni siquiera un buen adivino podría restablecer una esfera Rubik a su condición original si hubiera una cantidad infinitamente grande de combinaciones posibles. Sin embargo, la cantidad de combinaciones posibles en la esfera de Rubik no es infinitamente grande. El número de elementos (o, más elegantemente, el orden del grupo) de la esfera de Rubik ciertamente es grande, pero no es infinitamente grande, porque se trata de un grupo discreto. La esfera de Rubik es mecánicamente idéntica al cubo ordinario de Rubik 3×3, la única diferencia práctica es que es más latosa de manipular manualmente. Sin embargo, un experto en la resolución de un cubo de Rubik 3×3 desacomodado puede resolver también de inmediato y sin problema alguno una esfera de Rubik, porque ambos son en esencia la misma cosa, y ambos juguetes son descritos por el mismo grupo discreto de operaciones de rotación. Aquí no hay grupo continuo alguno. Si hemos de darle una explicación más formal, diríamos que la esfera de Rubik y el cubo de Rubik 3×3 son iguales topológicamente porque si uno de ellos estuviera hecho de plastilina moldeable, entonces con un poco de pericia podemos moldear una esfera de Rubik para que tome la forma de un cubo de Rubik 3×3, o viceversa.
Ya se ha bosquejado con anterioridad en otra entrada que el estudio de la simetría para el caso de los grupos continuos está basado en los trabajos llevados a cabo por el matemático noruego Sophus Lie, el cual fué el pionero en el estudio de las propiedades de simetría de estos grupos conocidos como los grupos de Lie (el apellido del matemático se pronuncia como “li”). Varias de las técnicas utilizadas previamente para dar el brinco de los grupos discretos a los grupos continuos son las mismas técnicas que las que fueron desarrolladas por vez primera por Sophus Lie.
Debe resultar obvio a estas alturas que los operadores mecánico-cuánticos que hemos estado estudiando con anterioridad, tales como el operador de traslación, el operador de evolución del tiempo y el operador de rotación:
tienen la misma estructura, la misma apariencia. Ello se debe a que los grupos a los cuales pertenecen estos operadores son todos ellos grupos continuos, esto es, son grupos de Lie. Resulta que para todos los grupos Lie, los operadores grupales (operador de traslación, operador de evolución del tiempo, operador de rotación, etc.) pueden ser escritos en esta forma exponencial de la siguiente manera:
en donde los operadores L1, L2, L3, etc. son lo que se conoce como los generadores del grupo Lie. En este sentido, el operador del momentum px es el generador del grupo de traslaciones, el operador Hamiltoniano de energía H es el generador del grupo de evoluciones temporales, y el operador Jz es el generador del grupo de rotaciones en torno al eje-z.
Los parámetros de un grupo Lie no deben ser confundidos en ningún momento con los generadores del grupo. Para el operador de traslación, el parámetro es obviamente la distancia a, mientras que para el operador de evolución del tiempo el parámetro es el tiempo t, en tanto que para el operador de rotación el parámetro es el ángulo θ de rotación. La característica más importante de un grupo Lie es que sus elementos tienen que ser funciones diferenciables de sus parámetros (o en términos más llanos, tienen que ser funciones continuas); esto es precisamente lo que convierte al grupo Lie en un grupo continuo. De este modo, el grupo Lie formado por los operadores de traslación tiene elementos que son funciones diferenciables del parámetro distancia a, mientras que el grupo Lie formado por operadores de evolución del tiempo tiene elementos que son funciones diferenciables del parámetro tiempo, en tanto que los grupos Lie de operadores de rotación tienen elementos que son funciones diferenciables de los ángulos de rotación. Nada de esto sería posible si el grupo Lie no fuese un grupo continuo.
En general, cualquier grupo de rotación continuo está compuesto de una cantidad infinitamente grande de operadores de rotación, para los cuales si bajo el contexto de la Mecánica Cuántica hacemos ħ.=.1 se tiene para cada uno de ellos empleando coordenadas generalizadas:
La sumatoria involucra el producto de dos cantidades que tienen el mismo sub-índice μ. Es costumbre ya, como medida de simplificación de la notación (aunque en ocasiones puede resultar confuso), recurrir a la convención de sumación de Einstein, que consiste simplemente en prescindir del símbolo Σ siempre y cuando dos o más sub-índices sean iguales:
La convención de sumación de Einstein permite escribir en forma más abreviada los elementos del grupo de rotación bajo análisis como:
Haciendo φ.=.(φ1,φ2,φ3) podemos recurrir también, desde luego, a la definición vectorial del producto escalar o producto punto, para representar lo anterior como:
Todas estas simbolizaciones son ampliamente utilizadas en la literatura, por lo que vale la pena estar al tanto de las variantes posibles.
Llevando a cabo una diferenciación, se puede demostrar que los operadores fundamentales Jk pueden ser obtenidos de los elementos continuos del grupo:
Obviamente, un requisito indispensable es la diferenciabilidad de los elementos del grupo de rotación con respecto a los parámetros φμ en la vecindad del operador identidad, resultando conveniente definir al operador identidad de cualquier grupo Lie (lo cual incluye a los grupos de rotación Lie) como:
para φ.=.0 (o sea, con φ1,φ2 y φ3 puestos todos a cero), de forma tal que se tiene lo siguiente:
de donde se concluye (despejando a -i y dejando únicamente a Jμ en el lado izquierdo de la igualdad) que es posible obtener a los operadores fundamentales Jμ de los elementos continuos del grupo.
Al obtener los operadores mecánico-cuánticos de traslación, de evolución del tiempo, y de rotación, es casi imposible el evitar establecer comparaciones y sospechar que todos estos operadores, en su esencia fundamental desprovista de cualquier significado físico, son casos particulares de una misma estructura matemática. Esto nos conduce a considerar un operador matemático general que abarque todos los casos posibles. En el camino hacia esa amplia generalización (abstracción), ya dimos el primer paso al tomar como ħ.=.1 a la constante reducida de Planck. Iremos aún más lejos considerando un operador unitario que puede ser función de varios parámetros α1, α2, α3, etc., los cuales en forma conjunta con los generadores del grupo continuo L1, L2, L3, etc. permiten definir al operador en su forma exponencial acostumbrada:
Es importante tener presente que el significado que le estamos dando aquí a los Lk es un significado matemático puro completamente general que no está necesariamente anclado al símbolo que se ha estado utilizando previamente para el momento angular total.
Refiriéndonos a lo que se obtuvo arriba, pero ahora interpretado en el sentido matemático puro, se tiene:
siendo los Lμ los generadores del grupo Lie.
En la vecindad cercana al elemento identidad del grupo, se debe tener la siguiente transformación para una variación δαμ muy pequeña de cada αμ:
en donde se ha definido como elemento infinitesimal:
en donde la manera más convencional y entendible de llegar a la definición de este infinitésimo es la siguiente:
siendo N un entero positivo (¡no un número continuo!).
Llevando a cabo N transformaciones infinitesimales sucesivas una tras otra para poder obtener la transformación finita, se obtiene:
Para esto hemos recurrido a la propiedad grupal que nos permite construír un operador nuevo finito mediante el producto sucesivo y en gran número de elementos infinitesimales. En virtud a esta propiedad grupal, los operadores del grupo Lie siempre deben ser representables en la forma:
En virtud de la diferenciabilidad suave y continua (el término matemático apropiado es analicidad) de los elementos del grupo Lie, y recurriendo a la expansión una serie de Taylor que corresponda al cálculo de varias variables, se debe tener para una variación pequeña δαμ:
El término resaltado en color rojo que es una expresión de segundo orden así como todos los términos subsecuentes se tomarán como iguales a cero. Independientemente, y al llegar a este punto, se debe tener presente que los generadores Lk de un grupo Lie deben ser linealmente independientes, o sea que:
puesto que el operador Lie tiene que ser igual al elemento identidad 1 para δα.=.{δαk}.=.0 (esto es, cuando todos los δαk son iguales a cero) en una forma única. La existencia de un δα.≠.0 con L·δα.=.0 implicaría la existencia de por lo menos dos operadores Lie distintos tales que U(δα).=.1, lo cual se descarta aquí.
Se requiere que el operador Lie sea unitario ya que por meras consideraciones físicas se requiere que haya también una conservación de la probabilidad. Esto significa que si el operador Lie con el cual estamos trabajando está definido como:
entonces el transconjugado del operador Lie (usamos la definición transconjugado cuando los Lk son matrices Lk que requiere tomar la transpuesta de la matriz tras convertir sus elementos a conjugados complejos, si no lo son entonces simplemente se refiere uno al conjugado complejo del operador Lie) que debe ser igual a su inverso queda definido de la siguiente manera:
Para que esto último sea cierto, se requiere que los αμ sean seleccionados como números reales (en física esto no presenta problema alguno, ya que los parámetros tales como la distancia de traslación, el tiempo de evolución y el ángulo de rotación necesariamente son números reales). Y del mismo modo, se impone la necesidad de que los Lk cumplan con la condición de Hermiticidad:
Si llevamos a cabo nuevamente una expansión en una serie de Taylor que corresponda al cálculo de varias variables, se debe tener para una variación pequeña δαμ, pero en esta ocasión para el operador inverso Lie, se tiene lo siguiente:
Obsérvese con atención en esto último que ya no consideraremos a los términos de segundo orden como despreciables, lo cual nos permitirá llegar a una conclusión de importancia extraordinaria.
A continuación, formaremos y desarrollaremos el siguiente producto cuádruple de cuatro operadores Lie, recurriendo como útil medida de simplificación a la convención de sumación de Einstein que nos autoriza a prescindir de los símbolos Σ en las sumatorias para productos en los cuales aparezcan sub-indices repetidos (si el lector lo desea, puede reinsertar los símbolos Σ en los productos de las sumatorias, pero posiblemente quedará convencido de la conveniencia de irse acostumbrando a la convención de sumación), y despreciando además términos de orden superior:
Puesto que todos los cuatro factores del producto cuádruple con el que comenzamos son elementos de un grupo Lie, tal producto cuádruple debe ser a su vez igual a un elemento grupal único.Y por la forma en la cual se formó el producto cuádruple de operadores tomado como punto de partida, este elemento grupal único debe estar situado en la vecindad de α.=.0. Podemos simbolizar y definir a este elemento grupal de la siguiente manera:
De este modo, se tiene la siguiente relación:
Comparando resultados, se debe tener entonces:
Podemos hacer:
en donde las Ckmj son constantes conocidas como las constantes de estructura. Pudimos hacer esto puesto que los δγj deben tender hacia cero ya sea que los δαk o los δβm tiendan a cero, y por consecuencia los δγj deben ser proporcionales a ambos. De este modo, podemos escribir lo siguiente:
Este es un resultado fundamental que nos dice que los generadores de un grupo Lie tienen que satisfacer relaciones de conmutación como la que se acaba de obtener arriba. Y este no es un resultado físico, es un resultado puramente matemático, pero que abarca todo lo que se ha desarrollado anteriormente. Esto significa que, partiendo de meras consideraciones matemáticas relacionadas con los aspectos más esenciales de la simetría, es posible obtener a partir de consideraciones matemáticas las relaciones propias de los fenómenos físicos. Puesto de modo más enérgico, las matemáticas dejan de ser simplemente una herramienta útil para los físicos para convertirse en el punto obligado de partida. Esta era precisamente la visión y la tesis principal del Albert Einstein, la hipótesis de que todo lo que tenga que ver con la física puede ser derivado de las matemáticas, relegando al laboratorio a un simple medio de confirmación de algo que ya se sabe y se anticipa por consideraciones puramente teóricas. Pero aunque esto último tenga algo de cierto, no es posible ignorar que fueron los resultados experimentales los que condujeron a la construcción del edificio de la Mecánica Cuántica.
Puesto que, por la misma definición de lo que es un conmutador:
entonces de la relación de conmutación que se ha obtenido para grupos Lie se puede verificar fácilmente que las constantes de estructura son antisimétricas en los dos primeros índices, o sea:
Para el resultado obtenido es igualmente fácil verificar que la identidad de Jacobi se mantiene válida:
Combinando los resultados anteriores, se puede obtener también la siguiente condición adicional para las constantes de estructura:
Más aún, al tenerse lo siguiente:
puesto que los generadores Ln son linealmente independientes, esto conduce al siguiente resultado:
Las relaciones encuadradas en marcos de color café forman las relaciones fundamentales de lo que se conoce como una álgebra Lie. Por otro lado, las constantes de estructura contienen toda la información relevante del grupo Lie en virtud de que estipulan la intercambiabilidad de las operaciones infinitesimales del grupo cuando son llevadas a cabo en diferente orden. Y como ha quedado establecido, todos los operadores finitos pueden ser construídos sucesivamente a partir de operadores infinitesimales.
Una característica importante de un grupo Lie es su rango (rank) definido como el máximo número de generadores de un grupo que conmutan el uno con el otro. En el caso del grupo abeliano (conmutativo) de traslación, este tiene tres generadores pν .=.-iħ∂/∂xν, todos los cuales conmutan el uno con el otro, y por lo tanto es un grupo Lie de rango 3. En este caso, el rango del grupo es en cierto modo trivial, ya que en virtud de la conmutatividad de los generadores pν se puede escribir:
alo cual significa que este grupo de rango 3 es de hecho el producto de tres grupos de rango 1. Un ejemplo más interesante es el que proporcionan los grupos de rotación tales como el grupo SO(3) en donde ninguno de los operadores conmuta con el otro siendo por lo tanto un grupo Lie de tres parámetros y rango 1.
Las relaciones de conmutación de un grupo Lie pueden ser comprendidas como una generalización directa del producto vectorial cruz entre dos vectores escribiéndolas de la siguiente manera:
y dándole el significado de que el producto vectorial cruz entre dos “vectores de base” Li y Lj es también un vector dentro del mismo espacio y por lo tanto igual a una combinación lineal de los vectores de base, lo cual equivale a la relación generalizada ei×ej.=.ek que es válida en un espacio tridimensional Euclideano para los vectores de base ei. El álgebra Lie de rango 2 es particularmente interesante con respecto a esta comparación, ya que contiene dos “vectores” cuyo producto vectorial cruz se desvanece, esto es:
aunque L1 y L2 sean linealmente independientes. Obviamente, la comparación con un producto vectorial cruz en un espacio de configuración tridimensional no debe ser llevada demasiado lejos.
En los procedimientos llevados a cabo, el punto de inicio ha sido un grupo Lie de carácter general que es determinado por sus generadores, calculándose con ello los conmutadores del grupo y definiendo con ello el álgebra Lie del grupo. Un teorema importante conocido como el teorema de Lie nos dice que este procedimiento puede ser invertido. Si el punto de partida es un conjunto de N operadores Hermitianos Ln, que esté cerrado bajo las operaciones de conmutación, entonces estos operadores especifican un grupo Lie. El teorema es evidente, puesto que dados los operadores Ln podemos escribir de inmediato los operadores infinitesimales del grupo:
La multiplicación sucesiva, una tras otra, de estos operadores infinitesimales en el límite M.→.∞ produce entonces los operadores del grupo Lie que corresponden a rotaciones finitas (no infinitesimales):
El procedimiento de análisis para grupos Lie dado arriba es completamente general. Los operadores pueden ser operadores diferenciales, pero también pueden ser operadores matriciales, como ocurre en el caso del grupo de rotaciones ortogonales O(3). Tómese de dicho grupo la matriz Rz(θ) para una rotación en torno al eje-z en un ángulo θ. Ya se vió anteriormente que en un sistema de coordenadas rectangulares Cartesianas dicha matriz viene siendo:
Cualquier cantidad de rotaciones en torno a un eje común como el eje-z se combinan como:
Puesto que la multiplicación de estas matrices es equivalente a la adición de sus argumentos, esto es precisamente lo que nos lleva a buscar una representación exponencial de las rotaciones. Tomando como punto de partida a la matriz Rz(θ) para una rotación finita (no-infinitesimal), y llevando a cabo una expansión en series de los términos seno y coseno, es posible obtener lo siguiente para ángulos δθ lo suficientemente pequeños para permitirnos despreciar términos de segundo orden en adelante:
Esto último ha sido puesto deliberadamente en la forma en que se le necesita para continuar llevando a cabo el análisis Lie. En base a esto, el generador del grupo de las rotaciones en torno al eje-z es:
Procediendo de modo semejante, se pueden obtener también los generadores de los grupos de rotaciones en torno al eje-x y en torno al eje-y:
Obsérvese que las trazas (o trazos) de las matrices Mx, My y Mz (las sumas de sus elementos a lo largo de la diagonal principal) son todas iguales a cero. Obsérvese también que, tomando las transpuestas de los conjugados complejos de las matrices Mx, My y Mz, se puede verificar fácilmente que todas ellas son Hermitianas El generador Mz puede ser obtenido también recurriendo a la diferenciabilidad (analicidad) de la matriz de rotación Rz(θ) si se interpreta a la derivada de una matriz como la matriz de las derivadas de sus elementos:
Habiendo obtenido el generador, se puede obtener una rotación finita θ mediante la composición (en producto sucesivo) de muchas rotaciones infinitesimales partiendo del primer producto:
y haciendo δθ.=.θ/N para llevar a cabo una cantidad enorme de productos con N.→.∞ que nos lleva al resultado deseado:
La expansión en series del exponencial es, desde luego:
lo cual puede ser simplificado aún más como se muestra a continuación:
habiéndose utilizado para esta última simplificación el hecho de que:
Se puede verificar de inmediato que los generadores satisfacen las relaciones de conmutación:
en donde εijk es el símbolo de permutación Levi-Civita que toma los valores de +1, -1 ó 0 para permutaciones pares e impares de los subíndices así como para el caso en el que hay dos subíndices iguales. El coeficiente iεijk de Mk es, naturalmente, la constante de estructura Cijk del grupo de rotaciones ortogonales, que dá a su vez el punto de partida para el desarrollo del álgebra Lie del grupo de rotaciones ortogonales O(3).
¿Es posible construír grupos continuos más complejos a partir de grupos continuos diversos? La respuesta es afirmativa, y un ejemplo de ello es el grupo traslación-rotación, construído con elementos que corresponden al operador de traslación (véase la entrada “El operador de traslación”) que tiene seis generadores p1, p2 y p3 (px, py y pz en caso de que se estén utilizando coordenadas rectangulares Cartesianas), y con elementos que corresponden al operador de rotación (véase la entrada “El operador de rotación”) que tiene seis generadores J1, J2 y J3 (Jx, Jy y Jz en caso de que se estén utilizando coordenadas rectangulares Cartesianas), siendo ambos grupos continuos. Para este grupo en particular, si simbolizamos una operación de rotación como R y una operación de traslación como T, intuitivamente puede comprobarse que una operación de rotación R-1, seguida de una operación de traslación T, seguida de una operación de rotación R, es equivalente a una traslación pura T':
como puede verificarse en la siguiente figura:
Esto significa que el grupo de traslaciones es un subgrupo conmutativo del grupo traslación-rotación. Obsérvese cómo a partir de dos (o más) grupos Lie es posible construír un super-grupo más complejo. Obsérvese también cómo dentro de un grupo puede haber un subgrupo abeliano de elementos (los cuales son conmutativos) aunque no todos los elementos del grupo principal satisfagan la propiedad de la conmutatividad.
Lo que hemos visto apenas toca la superficie de los grupos de Lie y de las álgebras Lie. Hay muchos otros grupos continuos Lie tales como el grupo E6, el grupo E7, el grupo E8, el grupo F4, y el grupo G2, siendo posible formar combinaciones grupales tales como el producto grupal G2×E6 en forma similar a como se construyó el grupo traslación-rotación de arriba. Hay especialistas que sospechan que el grupo E8 podría ser de importancia fundamental para la construcción de una Teoría del Todo. En realidad, con tantos grupos de dónde escoger, y con tantas combinaciones posibles que se pueden formar, el descubrimiento de aquellos grupos y combinaciones de grupos que pueden ser de importancia fundamental para la física ha resultado ser una ardua tarea que requiere de mucha paciencia, de mucha observación, algo de ingenio, y sin duda alguna, algo de suerte.
En la entrada anterior se habían visto algunos ejemplos del uso de la fórmula de Wigner para el cálculo de los elementos matriciales del operador de rotación en el caso j.=.1, sin darse explicación alguna sobre el origen de dicha fórmula. A continuación veremos la forma en la cual puede ser deducida la fórmula general usando un procedimiento de derivación muy parecido al que utilizó Eugene Wigner. La clave de la demostración radica en el establecimiento de una correspondencia entre las matrices 2×2 del grupo unitario unimodular SU(2) y las matrices ortogonales 3×3 del grupo de rotaciones ortogonales R. El establecimiento de estas correspondencias entre grupos aparentemente distintos, ya sea correspondencias biunívocas de uno-a-uno llamadas isomorfismos, o de dos-a-uno, tres-a-uno, cuatro-a-uno, etc. llamadas homomorfismos, es una herramienta de uso común dentro de la Teoría de Grupos para la obtención de muchos resultados útiles.
Al estudiar el grupo unitario unimodular SU(2), se vió que el elemento general del grupo, utilizando en la definición del mismo los parámetros Cayley-Klein, es:
Para establecer el homomorfismo (equivalencia) que existe entre el grupo unitario unimodular SU(2) y el grupo de rotaciones ortogonales O(3), podemos recurrir a la siguiente forma más elaborada del elemento general del grupo unitario unimodular SU(2) que está expresada en función de los números reales que aquí se simbolizarán como ξ, η y ζ:
Se puede verificar que esta forma alterna es unitaria tomándose el producto de U con su transconjugado U†, obteniéndose la matriz identidad I, como también puede verificarse que la matriz es unimodular (su determinante es igual a +1), satisfaciendo por lo tanto todos los requerimientos para poder ser clasificada como una matriz que es a su vez un elemento de un grupo SU(2).
Usuando como punto común los ángulos de Euler, para una rotación en un ángulo β en torno al eje-y se puede establecer la siguiente correspondencia:
Explícitamente, mostrando todos los componentes en ambos casos:
Por otro lado, para una rotación en un ángulo γ en torno al eje-x se puede establecer la siguiente correspondencia mostrada explícitamente:
Y por último, para una rotación en un ángulo α en torno al eje-z, la correspondencia es:
Sobre esto último, explícitamente:
Esta correspondencia no es una correspondencia sencilla de uno-a-uno, ya que conforme el parámetro de Rz que es α varía de 0 a 2π, el parámetro en Uz que es α/2 varía de 0 a π, teniéndose:
Entonces tanto Uz(α/2) como Uz(α/2 + π) que es igual a -Uz(α/2) se corresponden con Rz(α). Siendo la correspondencia de dos-a-uno, se asienta aquí que los grupos de rotación SU(2) y O(3) son homomórficos.
Para continuar adelante con la derivación de la fórmula de Wigner, apoyándonos inicialmente en las rotaciones llevadas a cabo usando matrices 2×2 para sistemas físicos con momento angular de spin igual a 1/2, las cuales caen dentro del grupo unitario unimodular SU(2); nos apoyaremos también en el hecho de que una operación general de rotación especificada en un espacio de tridimensional Euclideano definida en función de los ángulos de Euler:
se mantiene válida no sólo para j.=.1/2 sino también para j.=.1 y los demás valores medios enteros y enteros que pueda tomar el momento angular j.
Refiriéndonos nuevamente a la matriz unitaria 2×2 unimodular U describe la transformación de un vector columna de dos componentes χ conocido como espinor:
de acuerdo con esto, las operaciones matemáticas que llevan a cabo la transformación del espinor (u,v) están dadas por el siguiente par de ecuaciones:
Por el aspecto de esto, si nuestro punto de partida fuera un polinomio homogéneo de grado n en u y en v, al efectuar la transformación unitaria indicada seguiremos teniendo un polinomio homogéneo de grado n. Esto es relevante en el hecho de que los n+1 términos un, un-1v, un-2v2, y así sucesivamente, pertenecen a la representación-(n+1) dimensional de este grupo unitario.
Con el objeto de simplificar un poco la cantidad de texto algebraico involucrado y siguiendo los pasos de Wigner, haremos n.=.2.j y consideraremos la siguiente función (la cual es un monomio en lugar de un polinomio):
Se recalca que a estas alturas esto debe ser considerado como un artificio intermedio para simplificar un poco los pasos que se llevarán a cabo. La explicación sobre su utilidad y el por qué se le dió tal forma se debe apreciar dentro del mismo desarrollo. En la función dada, el índice m variará en pasos discretos desde -j hasta +j, cubriendo todos los términos que tengan la forma upvq de forma tal que p+q.=.2.j. El denominador de la función, por su parte, hace las veces de factor de normalización que permitirá que nuestra representación siga siendo unitaria (sin el denominador indicado, la representación deja de ser unitaria). Si se aplica el operador unitario unimodular U sobre la función que se acaba de definir, su acción llevará a cabo la siguiente transformación:
Por lo tanto:
A continuación, lo que se desea hacer es expresar lo que aparece en al lado derecho de la igualdad como una combinación lineal de términos de la forma fm(u,v). Sobre esto último, recuérdese cómo al llevarse a cabo una transformación lineal expresada por una matriz (en este caso, una matriz 2×2 actuando sobre un vector) cada componente del vector o de la función transformada viene siendo una combinación lineal de una suma de términos de la función o las funciones de base. Para ello, recurriremos al teorema del binomio:
Aplicando al pie de la letra el teorema del binomio, la primera expansión binomial sobre el primer factor que aparece en el numerador de la expresión sobre la que estamos trabajando viene dando:
Volviendo a aplicar el teorema del binomio, la segunda expansión binomial sobre el segundo factor que aparece en el numerador de la expresión sobre la que estamos trabajando viene dando:
De este modo, se obtiene lo siguiente:
Si se efectúa el siguiente cambio de variables:
con la finalidad de aparejar lo que tenemos con la función definida arriba:
se tiene entonces la forma deseada expresada como una combinación lineal de términos:
en donde los elementos matriciales Um,m’ están dados por la relación:
Como puede verse, en esto último el índice de sumación k empieza desde cero y llega hasta j+m, pero los factoriales de normalización en el denominador garantizan además que el coeficiente ligado al término que está siendo evaluado se desvanecerá si cualquiera de los exponentes toma un valor negativo, esto último en virtud de la siguiente propiedad de los factoriales:
Ahora bien, recurriendo a las rotaciones llevadas a cabo mediante los ángulos de Euler (α,β,γ), efectuando primero una rotación de α/2 en el eje-z, seguida de una segunda rotación de magnitud β/2 en el eje-y, seguida de una tercera rotación igual a γ/2 en el eje-z, la rotación general de Euler en el espacio 2×2 en base a lo que hemos visto previamente debe ser (el uso de medios ángulos de rotación conduce a una simplificación posterior en la derivación del resultado final):
Haremos uso del hecho de que esta expresión especificada en ángulos de Euler es válida no sólo para matrices 2×2 que representan sistemas físicos de spin j.=.1/2, también es válida para matrices 3×3 para matrices que representan sistemas físicos de spin j.=.1, e igualmente válida para matrices n×n que representen cualquier sistema físico con cualquier otro tipo de momento angular que se considere. Substituyendo cada uno de los operadores por las matrices que se llevan a cabo en el espacio SU(2):
Por multiplicación matricial directa se obtiene entonces:
Si se hace:
puede verse que lo obtenido es en realidad la forma alterna:
Estableciendo comparaciones, se pueden identificar los parámetros como:
De este modo, la representación SU(2) de los elementos matriciales Um,m’ viene siendo:
Se ha destacado de color azul la parte central que representa la rotación intermedia en torno al eje-y por ser la que mezcla los distintos valores del número cuántico magnético m. Obsérvese que las dos rotaciones en torno al eje-z (la primera y la tercera) producen ángulos de fase inconsecuentes por ser la fase algo inobservable en las mediciones físicas. En la Mecánica Cuántica se acostumbra tomar la adjunta de esto último definiendo al operador de rotación general como:
lo cual en realidad no hace más que invertir los signos de los exponentes imaginarios, resultando en la fórmula de Wigner:
Para el caso especial en el cual α.=.0 y γ.=.0, la matriz que representa a los elementos del operador general de rotación se convierte en la matriz reducida de rotación (de la cual ya se había hablado en una entrada previa) al desaparecer los factores de fase. Ahora bien, para el caso en el cual. j.=.0, el operador de rotación se convierte trivialmente en el número 1 (estrictamente hablando, se convierte en una matriz de un solo renglón y una sola columna conteniendo el número 1):
mientras que para el caso en el cual. j.=.1/2 la fórmula de Wigner reproduce el mismo resultado que ya se había obtenido previamente al iniciar el estudio de los operadores de rotación (con los ángulos de fase ahora incluídos):