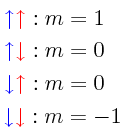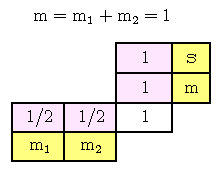PROBLEMA: Se llevan a cabo mediciones compatibles sobre un átomo que consta de un solo electrón, las cuales dan como resultado el que para tal átomo se obtengan l.=.3, j.=.7/2 y mj.=.1/2. (a) ¿Cuál es la probabilidad de que una medición posterior de Sx dará como resultado un valor igual a 1/2? (b) Si se lleva a cabo otra serie de mediciones obteniéndose l.=.1, ml..=.0 y ms.=.1/2, ¿cuál es la probabilidad de que una medición posterior dará como resultado un valor j.=.3/2?
Uno de los problemas más importantes en la Mecánica Cuántica es el de la suma de momentos angulares. Al hablar acerca de la suma de momentos angulares, el lector posiblemente está pensando en la suma del momento angular orbital L y la suma del momento angular del spin (intrínseco) S de una sola y misma partícula para dar un momento angular total J, algo como lo que vimos en la entrada “El acoplamiento LS”, aplicable a un electrón orbitando en cierto nivel de energía del átomo de hidrógeno:
Sin embargo, la adición de momentos angulares de que estaremos hablando será desde una perspectiva mucho más amplia y generalizada, ya que no estará limitada a la suma de los momentos angulares de una sola y misma partícula sino de dos partículas distintas. La duda que puede surgir aquí es que, si se trata de dos partículas distintas, por ejemplo dos átomos solitarios que están separados el uno del otro, ¿no es razonable suponer que los momentos angulares de cada átomo permanecerán separados? Si los átomos están separados, cada uno de ellos en efecto retendrá su propio espectro de emisión y su propio espectro de absorción, no hay razón alguna para que de alguna manera combinen sus líneas espectrales. Sin embargo, este razonamiento es válido para dos partículas separadas. El caso que estamos considerando aquí es el de dos partículas que están unidas para formar una unidad, por ejemplo, un átomo de cloro unido químicamente a un átomo de hidrógeno para formar una molécula de HCl (ácido clorhídrico, ácido muriático, etc.) En esta situación, debido a que una molécula es una unidad, energéticamente hablando, la interacción entre los momentos angulares de cada uno de los dos átomos que forman a la molécula es inevitable, y se debe esperar la aparición de nuevas líneas espectrales que los átomos individuales separados no producirían. Es aquí cuando necesitamos la postulación de nuevas reglas de adición para el momento angular de dos partículas.
Al ir aumentando el poder de resolución de los espectrometros, se fueron descubriendo nuevas líneas de emisión y de absorción que no podían ser explicadas sobre la simple base de líneas espectrales producidas (bajo la aplicación de un campo magnético externo) por los momentos angulares independientes (sin ningún tipo de interacción) de las partículas bajo análisis. La única manera de poder justificar la presencia de estas nuevas líneas espectrales era dar por hecho que los momentos angulares se acoplan de alguna manera que tenía que obedecer las reglas fundamentales enunciadas por la Mecánica Cuántica. Esto fue lo que motivó el modelo vectorial para la suma de los momentos angulares, el cual trabaja bien para la resolución de problemas de acoplamiento elementales de los momentos angulares de spin-spin, orbital-orbital y spin-orbital. Pero eventualmente se llega a un punto en el cual es necesario recurrir a nuevas técnicas matemáticas para poder formalizar y generalizar los casos sencillos hacia problemas más complejos. En una entrada previa titulada "La suma de momentos angulares", se trató desde una perspectiva introductoria el fenómeno de la suma de los momentos angulares, tanto la suma de un momento angular intrínseco (de spin) a otro momento angular de spin, como la suma de un momento angular orbital a otro momento angular orbital, así como la suma de un momento angular de spin a un momento angular orbital. Ha llegado el momento de extender el manejo de situaciones sencillas a problemas más complejos, pero para ello será necesario echar recurso de algo conocido como los coeficientes Clebsch-Gordan.
Los coeficientes Clebsch-Gordan tienen una historia interesante, porque fueron desarrollados por los matemáticos Alfred Clebsch (el cual murió en 1872) y su colega con el cual trabajó, Paul Gordan, mucho antes del advenimiento de la Mecánica Cuántica, sin que tuvieran jamás la más remota sospecha de que las estructuras matemáticas desarrolladas por ellos terminarían siendo empleadas para la formalización de algo que es una consecuencia directa de la discretización de la materia y la energía. De hecho, el problema original estudiado por ellos fue un problema en el área de la teoría de invariantes. En la física, los coeficientes Clebsch-Gordan hacen su aparición en el acoplamiento de los momentos angulares bajo las leyes de la Mecánica Cuántica. En terminología matemática, los coeficientes Clebsch-Gordan son utilizados en la teoría de las representaciones, especialmente en los grupos Lie compactos, para llevar a cabo la descomposición de la suma directa explícita del producto tensorial de dos representaciones irreducibles hacia representaciones también irreducibles, en casos en los cuales los números y los tipos de componentes irreducibles son conocidos ya de alguna manera abstracta (general). Pero esta definición puramente matemática posiblemente no arroje mucha luz, razón por la cual entraremos en el tema considerando ejemplos de la física atómica que no son ya conocidos.
Desafortunadamente, no hay una sola notación universal utilizada para representar a los coeficientes Clebsch-Gordan, y este es un caso en el que cada autor parece tentado a inventar su propia notación poniendo su granito de arena en una torre de Babel en donde lo que menos se necesita es de más variedades para representar una misma cosa, aumentando la confusión. A manera de ejemplo, a continuación tenemos un muestrario de las formas diversas que podemos encontrar en la literatura técnica para la representación de los coeficientes Clebsch-Gordan:
¡Todo esto está representando exactamente lo mismo!
A lo anterior, tenemos que sumarle agravantes tales como el hecho de que la ausencia de comas y semicolones separadores pueden causar en el neófito la impresión errónea de que ciertas cosas son productos multiplicativos cuando no lo son, cuando en realidad se trata de cosas diferentes que deben ser tomadas en cierta combinación. Esto significa que, arriba, al escribir m1m2 en realidad lo que se está tratando de dar a entender es m1,m2 y no el producto de m1 y m2. Del mismo modo, al escribir jm en realidad lo que se está tratando de dar a entender es j,m. Hay textos “amigables” que ciertamente hacen clara esta distinción recurriendo al uso de la coma y de la semicoma cuantas veces sea necesario, en los cuales se introducen las comas y semicomas para mayor claridad:
De cualquier modo, y aunque aquí de vez en cuando se hará clara la separación que debe de haber entre estas cosas puestas dentro de los kets (y los bras) de Dirac y que representan cosas distintas, también recurriremos a la notación más compacta que prescinde del uso de las comas y semicomas para ir acostumbrando al lector a estas simplificaciones que ciertamente economizan algo de tipografía (y espacio).
En el sentido más formal y estricto, el análisis matemático de la suma de dos momentos angulares está basado en la Teoría de Grupos, específicamente en los teoremas que nos hablan acerca de la descomposición del producto directo de dos representaciones matriciales del grupo de rotación en una suma directa de representaciones irreducibles, o sea (en la notación de la Teoría de Grupos):
Resulta útil visualizar la adición de dos momentos angulares j1 y j2 mediante la regla del triángulo basada en el hecho de que dos momentos angulares j1 y j2 pueden ser combinados (de varias maneras) para producir un momento angular total. j que sea compatible con el modelo de adición vectorial. Las siguientes figuras nos muestran tres casos distintos bosquejados mediante el llamado modelo vectorial de acoplamiento angular de dos momentos angulares:
En (a) tenemos el caso en el cual se obtiene el máximo acoplamiento posible jmax entre dos momentos angulares, el cual ocurre cuando los dos momentos angulares j1 y j2 orientados en la misma dirección. En (c) tenemos el caso en el cual se obtiene el mínimo acoplamiento posible jmin entre dos momentos angulares, el cual ocurre cuando los dos momentos angulares j1 y j2 están orientados en direcciones opuestas. Y en (b) el momento angular total está situado entre jmax y jmin.
En todo momento, puesto que las proyecciones m1 y m2 de dos momentos angulares están sobre el mismo eje-z, la proyección del momento angular total m sobre el eje-z debe ser igual a la suma de m1 y m2, lo cual nos dá la primera regla firme que debe ser obedecida en todo momento:
Posiblemente el caso más sencillo que podamos considerar de la suma de dos momentos angulares es el de la suma de dos momentos angulares intrínsecos, esto es, la suma de dos spins. Considérese el caso del spin de dos partículas diferentes, el del electrón y del protón del átomo de hidrógeno en su estado basal, por ejemplo (al poner a ambas partículas en un estado basal, no tenemos por que preocuparnos por tomar en cuenta los efectos del momento angular orbital). En ambos casos, el spin es de magnitud 1/2. Cada una de las partículas puede tener su spin apuntando “hacia arriba” o “hacia abajo”, de forma tal que tenemos cuatro combinaciones posibles (representaremos el spin de una partícula de color rojo y el spin de la otra partícula de color azul):
↑↑ , ↑↓ , ↓↑ , ↓↓
En todo momento, el estado del sistema, su momento angular total, está formado por la superposición de las funciones de onda de spin que corresponden a cada partícula. Habiendo cuatro combinaciones posibles de spins, debe de haber igualmente cuatro eigenestados posibles para el momento angular total. Cada eigenestado puede ser representado en notación bra-ket de Dirac mediante un eigenket que podemos simbolizar de varias maneras. A continuación se muestran algunas de las simbolizaciones de mayor uso en la literatura:
Los operadores así como los eigenvalores en la suma de dos spines son entonces los siguientes:
Podemos designar a la representación que hemos visto arriba basada en los eigenkets de los operadores S1z y S2z (para cada una de las dos partículas) como la representación {m1,m2}. Hay otro tipo de representación basada en los eigenkets de S2 y Sz (para el sistema combinado de partículas) a la cual podemos designar como la representación {s,m}, para la cual las posibilidades de eigenkets se escriben de la siguiente manera:
en donde el caso para el cual s.=.0 es conocido como singulete (o singlete) mientras que el conjunto de valores para los cuales s.=.1 es conocido como triplete.
Al hablar del vector de spin S para una sola partícula, en un sistema de coordenadas Cartesianas rectangulares estamos hablando en realidad de un vector de matrices, cada una de las cuales incorpora una de las matrices de Pauli:
siendo los operadores matriciales de spin para una sola partícula:
Al hablar de un sistema combinado de dos partículas, para cada una de las partículas (partícula 1 y partícula 2) continuamos dándole al vector de spin S de cada partícula su propia definición que es la misma para cada partícula considerada individualmente:
Es muy importante observar que, aún cuando dos partículas distintas sean puestas juntas en un sistema combinado de partículas, para cada una de las partículas seguimos hablando de observables compatibles y observables incompatibles. Tratándose de dos partículas distintas, los momentos angulares de spin de cada una de ellas se pueden medir simultáneamente con un grado ilimitado de precisión, son observables compatibles, lo cual podemos enunciar mediante las siguientes relaciones de conmutación:
Sin embargo, tratándose de una misma partícula, para cualquiera de las dos partículas sigue siendo cierto en todo momento que sus momentos angulares no pueden ser especificados simultáneamente en los tres ejes rectangulares Cartesianos con un grado ilimitado de precisión, siguen siendo observables incompatibles y el principio de incertidumbre sigue siendo válido como en los siguientes dos ejemplos:
Usando estos hechos, se puede verificar que para las componentes Cartesianas del momento angular total S de un sistema de dos partículas las relaciones de conmutación de Born siguen siendo válidas:
Aclarado lo anterior, ahora nos formularemos la siguiente pregunta: ¿Cuál será el momento angular total de un átomo formado con dos partículas cuyo spin es 1/2? Para este propósito, defínase operacionalmente al operador del momento angular S del sistema como la suma de los operadores del momento angular de spin S1 y S2 para cada partícula:
Cada uno de los cuatro eigen-estados posibles compuestos:
debe ser un eigen-estado de Sz, la proyección sobre el eje-z del momento angular total. Puesto que un eigenket puede ser substituído notacionalmente por la función de onda que representa, y puesto que para la función de onda del spin (conocida comúnmente como espinor) se acostumbra utilizar la letra griega χ, si representamos como χ1 a la función de onda de la primera partícula y como χ2 a la función de onda de la segunda partícula, entonces en virtud de que las proyecciones de los momentos angulares de spin de cada partícula sobre el eje-z simplemente se suman se tiene una eigenecuación que en un paso intermedio viene siendo reemplazada por dos eigenecuaciones (una para cada partícula):
Obsérvese que el operador S1z actúa únicamente sobre el espinor χ1, y que el operador S2z actúa únicamente sobre el espinor χ2. El último resultado nos dá la prescripción con la cual debe ir variando el número cuántico magnético m para el sistema combinado de partículas, siendo éste simplemente m1+m2. Considerando las cuatro posibilidades en donde cada spin puede tomar el valor ±1/2, se tiene entonces:
Esto a primera vista no parece concordar con lo que se ha visto previamente en el estudio del momento angular para una sola partícula en donde se ha demostrado que el momento angular va aumentando (o disminuyendo) en medias-fracciones o en unidades enteras. En este caso, designando como s al eigenvalor que corresponde al operador del momento angular del sistema S, éste parece avanzar de -s a +s con s.=.1, excepto que parece haber un estado extra adicional con m.=.0. La manera de resolver este aparente dilema consiste en definir un operador escalera S_ formado con la suma operacional de los operadores escalera para cada partícula:
Hemos visto arriba que hay dos representaciones posibles, la representación {m1,m2} y la representación {s,m}. En cada una de estas dos representaciones hay cuatro kets de base. La relación que hay entre los kets de base de ambas representaciones para el estado singulete es la siguiente:
mientras que la relación que hay entre los kets de base de ambas representaciones para el estado triplete es la siguiente:
Estas relaciones se obtienen utilizando precisamente las definiciones de los operadores escalera que se aplican al caso del momento angular. Aquí es usual recurrir al operador escalera de descenso (aunque se puede recurrir también al operador escalera de ascenso, todo es cuestión de gustos). Para un sistema descrito por los spins de dos partículas en la representación {s,m}, el operador mecánico-cuántico de escalera es:
Esto, evaluado para s.=.1 y m.=.1, dá:
Por otro lado, en la representación {m1,m2}, los operadores mecánico-cuánticos de escalera tanto para la primera partícula (partícula 1) como para la segunda partícula (partícula 2) son:
Para el caso de la primera partícula cuando los spins de ambas partículas están apuntando “hacia arriba”, la evaluación correspondiente dá:
mientras que para el caso de la segunda partícula cuando los spins de ambas partículas también están apuntando “hacia arriba”, la evaluación correspondiente dá:
Las evaluaciones que hemos llevado a cabo nos permiten establecer la “conexión” entre ambas representaciones recurriendo a la definición que se ha dado arriba para el operador escalera del sistema compuesto (formado por ambas partículas), escribiendo primero:
Removiendo los paréntesis en el lado derecho de la igualdad:
En este punto, podemos reemplazar tanto en el lado izquierdo de la igualdad como en el lado derecho de la misma las evaluaciones que llevamos a cabo previamente, teniendo así:
Despejando, obtenemos de este modo una de las relaciones dadas arriba que hay entre los kets de base de ambas representaciones:
Del mismo modo, podemos obtener las otras tres relaciones mediante la aplicación de los operadores escalera (esto resulta un ejercicio instructivo y se le recomienda al lector llevarlo a cabo).
Veamos ahora nuevamente la relación que hay entre los kets de base de la representación {s,m} y la representación {m1,m2}, destacando en color rojo los coeficientes de los kets que corresponden a la representación {m1,m2}:
Los coeficientes destacados en color rojo son el ejemplo más sencillo que pueda haber de los coeficientes Clebsch-Gordan. Como el lector puede percatarse de ello, son los elementos de una matriz de transformación que conecta a la base {m1,m2} con la base {s,m}.
En su formulación más general, por ejemplo para el caso en el cual los momentos angulares son .j1.=.2 y j2.=.1, la expansión dada arriba procede de una manera similar:
Podemos llevar a cabo también la transformación inversa, la cual tendrá un aspecto como el siguiente:
Una vez que se han evaluado todos los coeficientes Clebsch-Gordan para cierto par de momentos angulares .j1.y j2.(los cuales pueden ser números cuánticos del momento angular orbital, del momento angular de spin, o una combinación de ambos) y para cierto valor del número cuántico magnético m, los resultados obtenidos se suelen representar mediante un tipo de tablas conocidas genéricamente como tablas Clebsch-Gordan, como la siguiente (los coeficientes Clebsch-Gordan están puestos en los casilleros desprovistos de color) en la cual se ha utilizado .j1.=.l.=.2 como el valor para un momento angular orbital:
o como la siguiente:
Al dar lectura a estas tablas, se sobreentiende que para cada una de las entradas (o sea los coeficientes Clebsch-Gordan que están en los casilleros de color blanco) hay un radical, y el signo negativo (si lo hay) va fuera del radical. De este modo, en la última tabla los coeficientes Clebsch-Gordan se leen como √4/5, √1/5, √1/5 y -√4/5, mientras que los coeficientes Clebsch-Gordan en la primera tabla se leen como √2/5, √3/5, √3/5 y -√2/5.
Para el ejemplo detallado que vimos arriba sobre la evaluación de coeficientes Clebsch-Gordan cuando se tiene un momento angular total de un átomo formado con dos partículas cuyo spin es 1/2, hay tres tablas Clebsch-Gordan que son las siguientes (haremos aquí una excepción en la segunda tabla y pondremos a los coeficientes Clebsch-Gordan los radicales que casi siempre se dejan fuera):
Se pueden citar muchos otros ejemplos. A continuación se presentan las tablas de coeficientes Clebsch-Gordan en las cuales los momentos angulares son .j1.=.1 y j2.=.1/2:
En estas cuatro tablas, se sobreentiende que cada uno de los coeficientes Clebsch-Gordan (los números que están en los casilleros en blanco) van dentro de un radical, y el signo negativo (si lo hay) va fuera del radical.
Para el caso en el cual. j1.=.1 y j2.=.1/2 con m.=.-1/2, los cuatro coeficientes Clebsch-Gordan en su expresión simbólica son:
En ocasiones, y por cuestiones de limitaciones de espacio (pagando por ello un precio en legibilidad de los contenidos), las distintas tablas de coeficientes Clebsch-Gordan para una misma combinación de valores j1 y j2 son “pegadas” en una forma como la que se muestra a continuación (seguimos usando las tablas de coeficientes Clebsch-Gordan para las cuales los momentos angulares son j1.=.1 y j2.=.1/2:):
A continuación se presentan algunas de las tablas (no todas) de los coeficientes Clebsch-Gordan para el caso en el que los momentos angulares son .j1.=.2 y j2.=.1:
La expansión en términos de los coeficientes Clebsch-Gordan de todas estas tablas puede escribirse de la siguiente manera:
A modo de ejemplo, tomando una de las columnas en específico, la columna para la cual. j.=.2 y m.=.+1 (distinguida de color amarillo), se tiene la siguiente expansión:
Los cuadrados de los coeficientes Clebsch-Gordan representan probabilidades. A modo de ejemplo sobre esto último, suponiendo que se tienen dos partículas identificadas como 1 y 2 en reposo dentro de una caja, y suponiendo que el momento angular total del sistema es j.=.2 y que la proyección de la componente del momento angular sobre el eje-z es igual a m.=.+1, entonces una medición del momento angular llevada a cabo sobre la partícula 1 tendría una probabilidad de 1/3 de regresarnos un valor igual a 2ħ, una probabilidad de 1/6 de regresarnos un valor igual a ħ, y una probabilidad de 1/2 de regresarnos un valor igual a cero. Obsérvese cómo la suma de las probabilidades, o lo que es lo mismo, la suma de los cuadrados de los coeficientes Clebsch-Gordan, es igual a la unidad:
No es difícil comprobar que lo mismo resulta válido para las otras columnas de todas las tablas. En general, la suma de los cuadrados de los coeficientes Clebsh-Gordan de cualquier columna es igual a la unidad.
En algunas de las simbolizaciones dadas al principio de esta entrada para los coeficientes Clebsch-Gordan, el uso de paréntesis angulados puestos en los extremos así como de una barra vertical intermedia sugiere el uso del producto interno entre un bra y un ket mediante la notación bra-ket de Dirac para simbolizar a los coeficientes Clebsch-Gordan. Y así es, en efecto. Pero para lograr tal simbolización, hay que considerar el producto de los dos kets (en una expansión como la que se acaba de dar) reemplazándolo por un solo ket que representa dicho producto, de una manera como la siguiente:
Esta es una simbolización posible del producto de kets, muy utilizada en la literatura. Otra simbolización ampliamente utilizada es aquella en la cual se prescinde el uso de las comas dentro de los kets, y en la cual se prescinde también de la inclusión de j1 y j2.al considerarse dichos valores ya prefijados para una tabla de coeficientes Clebsch-Gordan cuando están dados los valores de m1.y m2::
De este modo, trabajando sobre el ejemplo que se acaba de dar, la expansión se puede escribir de la siguiente manera:
De nueva cuenta, al escribirse una expansión como esta en muchos textos se prescinde de los símbolos. j1 y j2.al considerarse dichos valores como números que quedan automáticamente prefijados al especificarse los valores de m1.y m2:
Ahora bien, si formamos bras a partir de los kets que aparecen en esta expansión, la hipótesis de la ortonormalidad en todos los productos bra-kets que se puedan formar para la expansión en el caso en el cual son. j1.=.2 y j2.=.1 (y para cualquier otro caso) sigue siendo válida:
De este modo, aplicando como bras cada uno de los tres kets usados en la expansión y usando las relaciones de ortonormalidad, se tienen entonces los siguientes coeficientes Clebsch-Gordan definidos en notación de productos internos bra-ket:
En muchos textos, y aunque de una manera algo superflua, se agrega a las definiciones simbólicas dentro de la parte bra como de la parte ket el par j1.j2:
Este tipo de simbolización es precisamente el primero que se dió como ejemplo al principio junto con otro tipo de simbologías de los coeficientes Clebsch-Gordan al hablar de la “torre de Babel”. De este modo, para el caso en el cual. j1.=.2 y j2.=.1 y para el ejemplo dentro de la tabla en donde. j.=.2 y m.=.+1, se tienen las siguientes equivalencias entre dos de las simbologías Clebsch-Gordan que se han introducido:
A continuación se presentan todas las tablas de los coeficientes Clebsch-Gordan para el caso en el que los momentos angulares son j1.=.3/2 y j2.=.1:
Esto presenta una buena oportunidad para demostrar la manera en la cual las tablas de los coeficientes Clebsch-Gordan funcionan en lo que viene siendo la transformación inversa. La relación que será aplicada es la siguiente:
A modo de ejemplo, tomando uno de los renglones en específico, el renglón para el cual m1.=.1/2 y m2.=.0 (distinguido de color amarillo), se tiene la siguiente expansión:
De nueva cuenta, tenemos operando aquí también el hecho de que los cuadrados de los coeficientes Clebsch-Gordan representan probabilidades. A modo de ejemplo sobre esto último, supóngase que se tienen dos partículas identificadas como 1 y 2 en reposo dentro de una caja. Suponiendo que la proyección sobre el eje-z del momento angular de la primera partícula es m1.=.1/2, y suponiendo que la proyección sobre el eje-z del momento angular de la segunda partícula es m2.=.0, entonces una medición del momento angular total del sistema de dos partículas tendría una probabilidad de 3/5 de regresarnos un valor igual a (5/2)ħ, una probabilidad de 1/15 de regresarnos un valor igual a (3/2)ħ, y una probabilidad de 1/3 de regresarnos un valor igual a 1/2. Obsérvese nuevamente cómo la suma de las probabilidades, o lo que es lo mismo, la suma de los cuadrados de los coeficientes Clebsch-Gordan, sigue siendo igual a la unidad:
No es difícil comprobar que lo mismo resulta válido para los otros renglones de todas las tablas. En general, la suma de los cuadrados de los coeficientes Clebsh-Gordan de cualquier renglón es igual a la unidad.
De este modo, tanto la suma de los cuadrados de los coeficientes Clebsch-Gordan llevada a cabo sobre cualquier columna, o llevada a cabo sobre cualquier renglón de cualquiera de las tablas, dá como resultado la unidad. Detrás de este hecho interesante, subyace otro hecho aún más fundamental:
Los coeficientes Clebsch-Gordan forman una matriz unitaria.
Al llevar a cabo el estudio introductorio del momento angular de spin S para una sola partícula, se encontró que la magnitud cuadrática S2 del momento angular de spin está dada por la relación:
en donde I es una matriz identidad 2×2. Esta relación es válida para dos partículas que están separadas a una distancia apreciable. ¿Y qué del caso en el cual ambas partículas son combinadas en proximidad cercana la una a la otra? En tal caso, cada una de ellas retendrá su propia magnitud S2 en virtud del principio básico de la conservación del momento angular. Esto nos permite definir para un sistema combinado de dos partículas 1 y 2:
Tratándose de la magnitud S2 de un sistema combinado de dos partículas, la definición apropiada se puede dar de la siguiente manera:
En la tercera línea de este desarrollo se ha hecho uso del conocimiento que se tiene de que los operadores de spins de dos partículas diferentes conmutan. Habiéndose dado ya previamente la definición para los primeros dos términos que aparecen en esta expresión, en lo que toca al tercer término éste puede ser definido en un sistema de coordenadas rectangulares Cartesianas con la ayuda de la definición del producto interno de dos vectores:
Si aplicamos este operador a un sistema combinado de dos partículas en el cual la primera partícula (1) tiene su spin apuntando “hacia arriba” y la segunda partícula (2) tiene su spin apuntando “hacia abajo”, entonces haciendo uso del hecho de que los operadores S1k sólo actúan sobre la primera partícula y los operadores S2k sólo actúan sobre la segunda partícula se tiene lo siguiente:
Del mismo modo, podemos obtener fácilmente el siguiente resultado:
Aplicando lo que acabamos de obtener sobre un ket del sistema especificado en la representación {s,m} usando para ello los valores s.=.1 y m.=.0, obtenemos entonces:
Con un procedimiento similar, obtenemos también lo siguiente:
De este modo, y haciendo un “gran resumen”, podemos deducir que el eigenket para s.=.1 y m.=.0 representa un eigenestado de S2 con un eigenvalor igual a 2ħ2:
Procediendo de modo semejante, podemos demostrar que el eigenket para s.=.0 y m.=.0 representa también un eigenestado de S2 con un eigenvalor igual a 0:
Repitiendo los pasos anteriores con cambios mínimos, se puede demostrar también que los eigenkets para s.=.1 y m.=.1 así como para s.=.1 y m.=.1 también son eigenestados de S2.
Al combinar dos partículas distintas, ambas con un momento angular de spin 1/2, para obtener un momento angular compuesto de 0 y de 1, se ha llevado a cabo la solución más sencilla de un problema mayor, el cual consiste en determinar el spin total que se obtiene al combinar un momento angular de spin s1 con otro momento angular de spin s2. Y la respuesta al problema es que se obtienen todos los valores posibles de spin desde hasta s1+s2 (el máximo valor posible) hasta |s1-s2|. El máximo valor posible de spin ocurre cuando los spins individuales de las partículas están alineados en la misma dirección (cuando son paralelos), y el menor valor posible ocurre cuando están alineados en direcciones opuestas (cuando son antiparalelos). De este modo, si ponemos en un mismo recipiente una particula cuyo spin sea 3/2 junto con otra partícula cuyo spin sea 2, podemos obtener un spin total de 7/2, 5/2, 3/2 o 1/2. Visto desde un punto de vista más abstracto, y usando los simbolos j1 y j2 para referirnos al momento angular en general en lugar de los símbolos s1 y s2 que hemos usado para representar al momento angular de spin, al considerar los valores posibles que pueda tomar cada uno de los parámetros que especifiquen a cierto coeficiente Clebsch-Gordan hay que recurrir a la regla de adiciones del momento angular desde el punto de vista mecánico-cuántico. Por el momento, convengamos en simbolizar los dos momentos angulares j1 y j2 a ser sumados en forma tal que j1≥ j2, lo cual es algo que siempre es posible hacer. Siendo así, el valor máximo que puede tomar la suma total m de las proyecciones sobre el eje-z de los momentos angulares, mmax, ocurrirá justo cuando ambos momentos angulares m1 y m2 en la configuración paralela tomen también sus valores máximos, los cuales son m1max, y m2max, que son j1 y j2, o sea:
Existe sólo una eigenfunción de onda (o lo que es lo mismo, en la notación bra-ket de Dirac, sólo un eigenket) que corresponde a este valor mmax, ya sea que se lleve a cabo la descripción en la representación {m1,m2} en términos del eigenket:
o en la representación {.j,m}. términos del eigenket:
En la primera base (la representación {m1,m2}) especificada mediante m1 y m2, hay únicamente dos kets que corresponden al eigenvalor de m que es mmax-1, siendo el primero aquél para el cual m1 es igual a m1max-1 y m2 es igual a m2max, y siendo el segundo aquél para el cual m1 es igual a m1max y m2 es igual a m2max-1. Esto implica que hay una doble degeneración en esta base, lo cual implica que también en la representación {.j,m} debe de haber una degeneración doble. ¿Y de dónde podría venir ésto? Claramente, m1max-1 es un valor posible de m para .j.=. j1+ j2. Pero también es un valor posible de m para .j.=. j1+ j2-1 (de hecho, el valor máximo de m para este caso). De este modo, .j1 y j2 pueden sumarse para dar dos valores de .j que son. j1+ j2 y. j1+ j2-1. Podemos continuar de este modo, y la degeneración irá aumentando a una degeneración triple, a una degeneración cuádruple, etc., pero resulta claro que la degeneración no puede aumentar indefinidamente. Y de hecho, para mmin igual a - j1- j2, se vuelve a tener un solo eigenket. La máxima degeneración es de (2 j2+1)-vías. Esto resulta más claro considerando el caso particular j1.=.2 y j2.=.1, en donde se muestran en la siguiente tabla las posibilidades para las distintas combinaciones de m1 y m2:
Por otro lado, para el caso j1.=.2 y j2.=.1/2, se tienen las siguientes posibilidades para las distintas combinaciones de m1 y m2:,
La degeneración de (2 j2+1)-vías está asociada con los 2 j2+1 estados .j:
Si levantamos la restricción j1≥ j2, obtenemos entonces la famosa regla del triángulo: