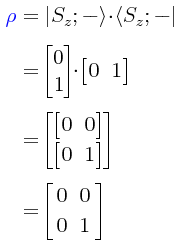Este valor esperado es el que podemos anticipar para una sola partícula que se encuentre en cierto eigenestado. ¿Y cómo habremos de manejar una situación en la cual en lugar de tener una sola partícula tenemos un ensamble compuesto de una gran cantidad de partículas semejantes? Para poder hacer frente a una situación como esta, tenemos que tomar un promedio estadístico sobre el ensamble de partículas, asignándole a cada partícula que se encuentre en cierto eigenestado un peso estadístico wi. Puesto que este promedio estadístico es un promedio que se toma sobre un conjunto de esperanzas matemáticas distintas, cada una de las cuales posee su propio peso estadístico, debemos tener alguna manera de poder distinguir este promedio estadístico del concepto de la esperanza matemática como lo hemos estado utilizando en la Mecánica Cuántica. Para ello, utilizaremos paréntesis cuadrados en lugar de los paréntesis angulados que hemos estado utilizando, de modo tal que el promedio del ensamble se puede conceptualizar de la siguiente manera:
Es muy importante tener presente que en esta definición el concepto probabilista entra por partida doble a través de dos rutas diferentes: la primera cuando hablamos de una probabilidad mecánico-cuántica para que pueda darse algúm eigen-valor que corresponda a cierta observable, y la segunda cuando hablamos de un factor de probabilidad wi para encontrar cada uno de los valores esperados que corresponden a los distintos estados mecánico-cuánticos del ensamble.
Puesto que toda función de onda, o bien, todo ket, puede ser expandido como una combinación lineal de estados de base como los siguientes:
esto nos permite escribir cada uno de los kets en forma expandida sobre la base de la manera siguiente:
Expresado en términos de la base ortonormal seleccionada, el promedio estadístico del ensamble queda expresado de la siguiente manera (obsérvese que tenemos que tomar el conjugado complejo de la expansión de los kets hecha sobre la base vectorial seleccionada para poder obtener la expansión de los bras sobre dicha base):
Si nos fijamos bien en lo que tenemos en el extremo derecho (entre los paréntesis angulados), convendremos en que esto es justo lo que nos entresaca al elemento matricial de Q que va puesto en el renglón .j y en la columa k de la matriz que representa a Q, o sea a Qjk:
Esto nos permite escribir la expresión para [Q] de la manera siguiente:
Qjk es el elemento matricial que le corresponde a un operador que en la forma matricial compacta que hemos estado utilizando con anterioridad escribimos como Q. Obsérvese que se ha introducido también en la simplificación simbólica que estamos llevando a cabo no sólo el enunciado de simplificación que damos con Qjk. Puesto que la doble sumatoria actúa también sobre lo que tenemos entre los paréntesis rectangulares, se le ha dado a ello también la interpretación matricial que le corresponde:
ρkj es el elemento matricial que le corresponde a un operador que en la forma matricial compacta que hemos estado utilizando escribimos como ρ. Por la forma en la cual están puestos los sub-índices en la doble sumatoria, una expansión de unos cuantos términos en la doble sumatoria deberá ser suficiente para convencernos de que lo que en realidad tenemos para la evaluación estadística [Q] es la traza del producto matricial de ρ y Q, definida la traza como la suma de los elementos que van puestos a lo largo de la diagonal principal de la matriz que resulta del producto de ρ y Q. En pocas palabras, lo que tenemos es lo siguiente:
Este resultado es completamente válido para cualquier tipo de ensamble que esté formado por cualquier tipo de partículas siempre y cuando se trate de las mismas partículas. Pero antes de seguir hablando en términos abstractos, generales, resulta instructivo aplicar el concepto del que estamos hablando sobre un caso sencillo, y el caso que estudiaremos consistirá en el de partículas de spin 1/2 tales como los electrones, para las cuales la descripción mecánico-cuántica está dada en función de las matrices de Pauli. Y antes de entrar de lleno en esto, resulta conveniente fijar algunas convenciones que serán utilizadas tanto en la evaluación del operador densidad ρ como en la evaluación del promedio estadístico de un ensamble .
La siguiente figura nos muestra un haz completamente polarizado de electrones moviéndose de izquierda a derecha, teniendo todos ellos sus spins apuntando hacia arriba en el sentido positivo del eje-z, siendo por lo tanto un estado puro:
Este flujo de partículas lo podemos tomar como uno de los dos haces que acaban de salir de un aparato Stern-Gerlach del cual se ha tomado la parte del haz de partículas que ha sido deflexionado “hacia arriba”. Por otro lado, la siguiente figura nos muestra un haz polarizado de electrones moviéndose también de izquierda a derecha, pero teniendo todos ellos sus spins apuntando “hacia abajo”, siendo por lo tanto también un estado puro:
En cambio, la siguiente figura nos muestra un haz de electrones moviéndose de izquierda a derecha teniendo algunos de ellos sus spins apuntando hacia arriba con los demás electrones teniendo sus spins apuntando hacia abajo. Esto no es ya lo que se considera un estado puro:
En esta última figura, si la tomamos como una muestra estadísticamente representativa del haz de electrones, podemos ver que hay el doble de partículas con sus spins apuntando hacia arriba (doce en total) que el número de partículas que hay con sus spins apuntando hacia abajo (seis en total). Siendo el número total de partículas en la muestra igual a 18, podemos asignarle a las partículas en el haz con sus spins apuntando hacia arriba un peso estadístico w1 igual a 2/3, mientras que las partículas en el haz con sus spins apuntando hacia abajo tienen un peso estadístico w2 igual a 1/3.
El principal instrumento para emprender el análisis de la Mecánica Estadística Cuántica sobre una base formal es lo que se conoce como la matriz densidad (descrita también en la literatura como el operador densidad), representada como ρ. Pero antes es conveniente estar de acuerdo en algunas convenciones que serán utilizadas aquí.
Para una familiarización con los conceptos básicos de la matriz densidad, es usual empezar por lo más sencillo describiendo los estados de spin de partículas como el electrón con un spin de 1/2, y para el tratamiento matemático estadístico de los ensambles de las partículas empleando la notación bra-ket de Dirac (este es el enfoque más moderno utilizado con mayor frecuencia), podemos empezar definiendo tentativamente a los kets que corresponden tanto a un electrón con su spin apuntando “hacia arriba” como a un electrón con su spin apuntando “hacia abajo” de la siguiente manera:
En conformidad con las convenciones de la notación bra-ket de Dirac, lo usual para representar el spin que está apuntando “hacia arriba” (positivo) y el spin que está apuntando “hacia abajo” (negativo) es recurrir a vectores columna como los siguientes:
Tomando la transpuesta del conjugado complejo de los vectores columna, obtenemos como vectores renglón los bras que son duales a los kets de arriba:
Un estado general de spin simbolizado como |χ> siempre puede ser escrito como una combinación lineal de los dos estados de base:
De lo anterior, obtenemos la representación del estado adjunto tomando la transpuesta del conjugado complejo obteniendo de este modo el bra que es el dual del ket de arriba:
En rigor de verdad, al hablar de partículas con sus spins apuntando “hacia arriba” y “hacia abajo” tomando al eje de referencia de la dirección del spin como el eje-z, no se ha tomado en cuenta la posibilidad de que haya también partículas que estén apuntando a lo largo del otro eje que es perpendicular al eje-z, o sea el eje-x. Tomar en cuenta esta posibilidad nos obliga a repasar las convenciones de uso común que son utilizadas para describir a las partículas que salen de un horno y pasan por el sistema de imanes que forman parte de un experimento Stern-Gerlach. El flujo de partículas en sí se va moviendo a lo largo de un eje horizontal, a lo largo de un eje-y. El campo magnético inhomogéneo separa al haz de partículas en dos haces cuyos spins estarán apuntando en una dirección perpendicular al eje de movimiento traslacional, el eje-z, el cual es en realidad un eje transversal. Pero hay otro eje transversal que es perpendicular al eje-z y tambiés es perpendicular al eje del movimiento de traslación de las partículas a lo largo del eje-y, es el eje-x:
Y así como el eje-z tiene dos direcciones para la clasificación de los spins, una positiva y una negativa, también el eje-x tiene dos direcciones, una positiva y una negativa. De este modo, mientras que en su esencia básica podemos tener caracterizada a una partícula con su spin apuntando “hacia arriba” o “hacia abajo” en relación al eje-z conforme la partícula se desplaza a lo largo del eje-y:
también podemos tener que la partícula debe ser caracterizada con su spin apuntando no “hacia arriba” ni “hacia abajo” sino en el sentido positivo del eje-x o en el sentido negativo del eje-x conforme la partícula se desplaza a lo largo del eje-y:
Como puede verse en las figuras de arriba, para mayor comodidad y claridad así como se ha representado previamente a una partícula con su spin apuntando “hacia arriba” a lo largo del eje-z (en el sentido positivo) de color azul o con su spin apuntando “hacia abajo”a lo largo del eje-z (en el sentido negativo) de color rojo, a una partícula cuyo spin esté apuntando en el sentido positivo del eje-x se le ha representado de color magenta, mientras que a una partícula cuyo spin esté apuntando en el sentido negativo del eje-x se le ha representado de color verde. Esto nos permite considerar un haz de partículas que contenga tanto electrones con sus spins apuntando “hacia arriba” o “hacia abajo” en relación al eje-z como electrones con sus spins apuntando tanto en el sentido positivo como en el sentido negativo del eje-x (el haz de partículas se sigue moviendo en el sentido del eje-y):
¿Y cómo podríamos obtener un haz tan “desordenado” (por así decirlo) de partículas conteniendo tal mescolanza? Pues la manera más fácil es utilizando cuatro aparatos Stern-Gerlach, uno para obtener un haz de partículas con sus spins apuntando “hacia arriba” en relación al eje-z, el segundo aparato se utilizaría para obtener un haz de partículas con sus spins apuntando “hacia abajo” en relación al mismo eje-z, el tercer aparato se utilizaría para obtener un haz de partículas con sus spins apuntando en la dirección positiva del eje-x, y el cuarto aparato se utilizaría para obtener un haz de partículas con sus spins apuntando en la dirección negativa del eje-x, tras lo cual se pueden juntar los cuatro haces en uno solo mediante otro arreglo apropiado de imanes.
PROBLEMA: Si en la última figura de arriba el haz fuese una muestra estadística representativa de las fracciones poblacionales de partículas que esperaríamos encontrar en una población mayor, ¿como están repartidos los porcentajes relativos de las partículas en el haz?
Hay 8 partículas azules, 9 partículas rojas, 6 partículas magenta y 6 partículas verdes, dando un total de 29 partículas. Entonces las fracciones relativas son:
w1(Sx+) = 6/29 = 0.2069 = 20.69 %
w2(Sx-) = 6/29 = 0.2069 = 20.69 %
w3(Sz+) = 8/29 = 0.2759 = 27.59 %
w4(Sz-) = 9/29 = 0.3103 = 31.03 %
Obviamente, la notación bra-ket introducida arriba no resultará suficiente para poder describir situaciones como ésta, la notación tiene que ser ampliada para considerar también la posibilidad de que las partículas puedan estar apuntando no sólo a lo largo del eje-z sino también a lo largo del eje-x en ambas direcciones (positiva y negativa). Una notación un poco más refinada es la siguiente:
Estando de acuerdo en estas cosas, si llamamos a un ensamble de partículas un estado puro siempre y cuando el ensamble contenga únicamente partículas de un solo tipo como uno de los cuatro que se han definido arriba, podemos escribir la matriz densidad para un ensamble puro de la siguiente manera empleando la notación de bras y kets:
Obsérvese con detenimiento que esta definición toma el producto externo de dos vectores, y en contraposición con la definición del producto interno de dos vectores que siempre nos produce un escalar (un número) el producto externo de dos vectores siempre nos producirá una matriz.
PROBLEMA: Demostrar que, para un estado puro, la matriz densidad es idempotente, esto es:
ρ2 = ρ
Usando la definición que se acaba de dar para la matriz densidad de un estado puro:
Usando la propiedad asociativa, podemos reagrupar los paréntesis de la siguiente manera fijando un orden distinto de operaciones:
Pero por ortonormarlidad se tiene que:
Entonces:
PROBLEMA: Obténgase la matriz densidad ρ para un estado puro conformado con partículas Sz+.
Utilizando la definición dada arriba para la matriz densidad de un estado puro, esta debe resultar del tomar el producto externo del ket y el bra para Sz+ en el siguiente orden:
Obsérvese que la suma de los elementos a lo largo de la diagonal principal de la matriz ρ es igual a la unidad:
1 + 0 = 1
Obsérvese también que hay una sola entrada en la diagonal principal con un valor diferente de cero, siendo todas las demás entradas iguales a cero, lo cual nos indica sin necesidad de saber la procedencia de la matriz que se trata de un estado puro.
PROBLEMA: Obténgase la matriz densidad ρ para un estado puro conformado con partículas Sz-.
Utilizando la definición dada arriba para la matriz densidad de un estado puro, esta debe resultar del tomar el producto externo del ket y el bra para Sz- en el siguiente orden:
Nuevamente, la suma de los elementos a lo largo de la diagonal principal de la matriz ρ es igual a la unidad:
0 + 1 = 1
Y nuevamente, hay una sola entrada en la diagonal principal con un valor diferente de cero como debe ser cuando se trata de un estado puro.
Tomando en cuenta lo que se ha visto en entradas anteriores concerniente a la orientación del spin del electrón, podemos definir matemáticamente un ket para partículas del tipo Sx+ de la siguiente manera:
Una vez definido el ket para Sx+, la definición del bra con el que se corresponde (su dual) se puede definir también de inmediato:
Podemos verificar que las definiciones dadas para el bra y el ket de Sx+ son correctas tomando el producto interno del bra y el ket, sabiendo de antemano que por la ortonormalidad de los mismos la respuesta esperada debe ser igual a la unidad:
Del mismo modo, podemos definir matemáticamente un ket para partículas del tipo Sx- de la siguiente manera:
Y una vez definido el ket para Sx-, el bra que es su dual debe ser entonces:
PROBLEMA: Obténgase la matriz densidad ρ para un estado puro conformado con partículas Sx+.
Utilizando la definición dada para la matriz densidad de un estado puro, esta debe resultar del tomar el producto externo del ket y el bra para Sx+ en el siguiente orden:
Efectuando las operaciones requeridas, esto nos produce el siguiente resultado:
Obsérvese que la suma de los elementos a lo largo de la diagonal principal de la matriz ρ es igual a la unidad:
Obsérvese también que hay dos entradas en la diagonal principal con un valor diferente de cero. Sin necesidad de ver el origen de la matriz ρ, esto nos indica que no representa un estado puro.
PROBLEMA: Obténgase la matriz densidad ρ para un estado puro conformado con partículas Sx-.
Utilizando nuevamente la definición dada para la matriz densidad de un estado puro, esta debe resultar del tomar el producto externo del ket y el bra para Sx- en el siguiente orden:
Efectuando las operaciones requeridas, esto nos produce el siguiente resultado:
Obsérvese que la suma de los elementos a lo largo de la diagonal principal de la matriz ρ es igual a la unidad:
Obsérvese también que hay dos entradas en la diagonal principal con un valor diferente de cero. Sin necesidad de ver el origen de la matriz ρ, esto nos indica que no representa un estado puro.
¿Y cómo habremos de manejar el caso de un ensamble que no representa un estado puro sino que puede estar conformado con partículas de tipos diversos? Considerando al ensamble mixto como una mezcla de ensambles puros. Esto equivale, en efecto, a descomponar la matriz densidad ρ de un ensamble aleatorio en la suma de dos o más matrices densidad (cuantas sean necesarias) cada una de las cuales corresponda a un estado puro:
En rigor de verdad, a cada estado puro en el cual pueda descomponerse una matriz densidad se le debe asignar un peso estadístico, tomando en cuenta que las partículas bajo consideración no necesariamente estarán repartidas en partes iguales. Esto nos lleva a escribir en la notación de bras y kets la siguiente definición general de la matriz densidad ρ para estados aleatorios que incluye como un caso especial a la matriz densidad para un estado puro:
en donde wi es el peso estadístico que va aparejado con cada ensamble puro. Las poblaciones fraccionales están, desde luego, restringidas a satisfacer la condición de normalización:
La matriz densidad contiene toda la información físicamente relevante que se pueda obtener acerca del ensamble que está siendo descrito.
PROBLEMA: Obténgase la matriz densidad ρ para un haz de partículas completamente aleatorio que está conformado con partículas Sz+ y Sz-.
Si el haz es completamente aleatorio, formado con un ensamble puro Sz+ y con un ensamble puro Sz-, ambos ensambles deben tener igual peso estadístico, esto es:
w1(Sz+) = 50 % = 1/2
w2(Sz-) = 50 % = 1/2
La matriz densidad para el estado mixto será entonces:
en donde ρ1 y ρ2 son las matrices densidad para los estados puros que corresponden a un ensamble Sz+ y a un ensamble Sz-, los cuales ya se habían obtenido previamente. Usando dichos resultados se tiene entonces:
PROBLEMA: Obténgase la matriz densidad ρ para un haz de partículas que está conformado con un 75% de partículas Sz+ y un 25% de partículas Sx+.
w1(Sz+) = 75 % = 3/4
w2(Sx+) = 25 % = 1/4
La matriz densidad para el estado mixto será entonces:
en donde ρ1 y ρ2 son las matrices densidad para los estados puros que corresponden a un ensamble Sz+ y a un ensamble Sx+, los cuales ya se habían obtenido previamente. Usando dichos resultados se tiene entonces:
Considérese ahora el siguiente ensamble cuya matriz densidad es la siguiente:
Esta matriz densidad se puede descomponer en dos estados puros de la siguiente manera:
siendo:
las matrices densidad que corresponden a un haz orientado en la dirección positiva del eje-x y a un haz orientado en la dirección positiva del eje-z. Esta descomposición nos indica que podemos considerar al ensamble conformado por una mezcla de cantidades iguales de electrones orientados en estas dos direcciones. Se trata de una descomposición posible. Sin embargo, no es la única. A modo de ejemplo, otra descomposición posible es la siguiente:
en donde:
representan un ensamble de partículas con sus spins orientados en el plano x-z a un ángulo de 45° con ambos eje-x y eje-z positivos, y otro ensamble con sus spins orientados en las direcciones opuestas. Esta última descomposición que se ha llevado a cabo representa por lo tanto una mezcla de electrones con fracciones:
(√2 + 1)/2√2
y:
(√2 - 1)/2√2
en las dos orientaciones señaladas.
En virtud de que, para un estado mixto, una matriz densidad puede ser descompuesta en más de una manera, habiendo por lo tanto cierta ambigüedad en la representación del ensamble para el estado mixto, esto puede dar lugar a confusiones. Un ejemplo de ello lo es la publicación que se hizo hace ya algún tiempo de papeles teóricos sobre el tema de la interferencia electrónica. En estos experimentos de interferencia electrónica, los electrones son emitidos por un filamento caliente al rojo vivo (como el de los viejos tubos electrónicos al vacío con los cuales se construían los aparatos de radio y televisión antes del advenimiento del transistor y la microelectrónica de semiconductores) que actúa como cátodo, siendo los electrones acelerados para formar con ellos un haz utilizado para bombardear laminillas delgadas de esparcimiento. Algunos investigadores en este campo trabajaban sobre la hipótesis de que los electrones son emitidos por el cátodo en la forma de paquetes de onda que tienen un “desparrame” de energía igual al “desparrame” de energía observado en el haz electrónico. Trabajando sobre esta hipótesis, se calculan los efectos de interferencia de los electrones utilizándose a los paquetes de onda como funciones de onda. Sin embargo, la matriz densidad ρ que describe al estado de los electrones emitidos desde el cátodo tiene una forma tal que puede ser descompuesta ya sea en estados monoenergéticos puros o en estados puros de paquetes de onda. Por lo tanto, la representación del ensamble del estado mixto es ambigua. Aunque podemos conceptualizar a los electrones como paquetes de onda emitidos desde el cátodo, no hay necesidad de hacer tal cosa. En virtud de que los cálculos de los efectos de interferencia se pueden llevar a cabo con mayor facilidad utilizando funciones de onda monoenergéticas, resulta más conveniente considerar a cada electrón como teniendo una energía definida. De cualquier manera, ambas descripciones son físicamente equivalentes.
Debe ser más claro ahora que, al hablar acerca del promedio estadístico de un ensamble A, al cual como ya se señaló al principio se le representa convencionalmente de la siguiente manera con paréntesis cuadrados:
no se le debe confundir con el concepto del valor esperado o esperanza matemática de una observable en su sentido mecánico-cuántico usual. En otras palabras:
Considérese al ensamble formado por diversas funciones de onda ψ1, ψ2, ψ3, ... etc. Una descripción completa del ensamble es proporcionada mediante la especificación de los números n1, n2, n3, ... etc., con cada uno de ellos representando los sistemas nj descritos por la función de onda ψj. Sin embargo, el conjunto de números nj puede contener información que no es de relevancia física alguna. Por ejemplo, como ha sido enfatizado en otras entradas previas, dos sistemas cuyas funciones de onda difieren únicamente en su (ángulo de) fase no pueden ser distinguidas. Obviamente, el incluír funciones de onda que difieren únicamente en fase en el conjunto de las ψj no es necesario ni deseable. Puede haber otras redundancias que también deben ser eliminadas.
Las únicas propiedades físicamente significativas de un ensamble son las funciones de distribución estadística (como las que ya hemos visto previamente en otras entradas) para cada una de las mediciones que se puedan llevar a cabo sobre el ensamble de sistemas. De este modo, si P(q) representa la función de distribución probabilista por unidad q de que una medición sobre una observable Q llevada a cabo sobre uno de los miembros del ensamble resultará en un valor q, entonces la función de distribución contiene toda la información físicamente significativa acerca del ensamble que pueda ser obtenida a partir de mediciones de Q.
Al principio de esta entrada, para la distribución estadística utilizada para el cálculo del promedio de un ensamble se supuso una distribución discreta, hecha efectiva mediante la aplicación de pesos estadísticos wi a cada uno de los estados del ensamble. Esto es válido para una cantidad moderada de partículas, pero para una cantidad sumamente grande de partículas resulta conveniente pasar de una distribución discreta a una función de distribución continua, lo cual requiere reemplazar la sumatoria con una integral. Como lo hemos visto en entradas anteriores, una función de distribución P(q) nos determina la esperanza matemática (el valor esperado, el valor promedio, etc.) de Q mediante la siguiente definición del promedio estadístico:
Y como ya lo hemos visto, esta definición es extensible a potencias (Qn) de Q:
De modo converso, estos valores promedio o momentos determinan la función de distribución estadística, como puede verificarse para funciones matemáticas de distribución “bien comportadas” (integrables cuadráticamente) mediante la introducción de una variable k, multiplicando la relación anterior por inkn/n! y efectuando la sumación sobre n:
Tomando la definición estadística que se le ha dado a [Qn] e introduciendo dicha definición en lo anterior, metiendo asimismo la sumatoria dentro de la integral:
Pero lo que se tiene en esto último dentro de los paréntesis es simplemente la definición en series del exponencial que hemos estado utilizando con bastante frecuencia:
Por lo tanto:
La función F(k) definida con la ayuda de la sumación anterior es entonces simplemente la transformada de Fourier de P(q). De este modo, la función de distribución P(q) puede ser determinada de la siguiente manera:
con lo cual podemos ver que una descripción física completa de un ensamble de sistemas semejantes está dada por los valores promedio de todas las observables del sistema (en este caso, las varias potencias de una cierta observable son consideradas como observables separadas).
Ahora bien, puesto que al evaluar la traza de un producto matricial el resultado obtenido no depende del orden en el cual se multipliquen las matrices, podemos tomar el producto en cualquier orden, ya sea como ρ·A o como A·ρ:
Bajo la superficie de esta peculiaridad matemática subyace la observación de que la traza es independiente del tipo de representación utilizada, y por lo tanto [A] puede ser evaluada sobre cualquier base vectorial que resulte conveniente, lo cual le dá a la fórmula una utilidad extraordinaria.
PROBLEMA: Demostrar que la traza del producto de dos matrices A y B es independiente del orden en el cual se tome el producto matricial.
Sea C la matriz que resulta de tomar el producto matricial A y B, en ese orden. La definición del producto matricial A·B, la cual debe ser utilizada siempre en este tipo de demostraciones, determina que cada elemento cij de la matriz C que resulte del producto debe ser obtenido de la siguiente manera:
Entonces, tomando la traza del producto matricial, lo cual consiste en sumar todos los elementos a lo largo de la diagonal principal de la matriz resultante, se tiene entonces que:
Se concluye entonces que la traza del producto de dos matrices es indiferente al orden en el cual se tome el producto matricial. Si la matriz A es una matriz cuyo tamaño es m×n, y si la matriz B es una matriz cuyo tamaño es n×m, entonces el producto matricial en el orden A·B producirá una matriz cuyo tamaño será m×m, entanto que el producto matricial en el orden B·A producirá una matriz cuyo tamaño será n×n, estando definido el producto matricial en ambas situaciones, aunque de cualquier modo esto no afectará a la traza de la matriz resultante.
PROBLEMA: Dadas las siguientes dos matrices A y B, obténgase el producto matricial A·B y calcúlese la traza de la matriz resultante, haciendo lo mismo con el producto matricial B·A:
El producto matricial A·B y la traza del mismo resultan ser:
El producto matricial B·A y la traza del mismo resultan ser:
De los resultados obtenidos, se puede ver que:
PROBLEMA: Usando los resultados de uno de los problemas anteriores, obténganse los promedios [Sx], [Sy] y [Sz] para un ensamble aleatorio de partículas que está conformado con cantidades iguales de partículas correspondientes al ensamble puro Sz+ y partículas correspondientes al ensamble puro Sz-.
Este es el caso para el cual los pesos estadísticos dados a cada estado puro del ensamble son:
w1(Sz+) = 1/2
w2(Sz-) = 1/2
habiendose obtenido para este ensamble la siguiente matriz densidad:
Utilizando el resultado que nos dá el promedio estadístico de un ensamble en función de la matriz densidad, tenemos por principio de cuentas para [Sx]:
En lo que respecta a [Sy], se tiene:
Obsérvese que los dos elementos que son reflejados con respecto a la diagonal principal son el conjugado complejo el uno del otro. Esto viene del hecho de que la matriz densidad es Hermitiana.
Y por último, en lo que respecta a [Sz], se tiene:
PROBLEMA: Usando los resultados de uno de los problemas anteriores, obténganse los promedios [Sx], [Sy] y [Sz] para un ensamble de partículas que está conformado con un 75% de partículas Sz+ y un 25% de partículas Sx+.
Este es el caso para el cual los pesos estadísticos dados a cada estado puro del ensamble son:
w1(Sz+) = 75 % = 3/4
w2(Sx+) = 25 % = 1/4
habiendose obtenido para este ensamble la siguiente matriz densidad:
Utilizando el resultado que nos dá el promedio estadístico de un ensamble en función de la matriz densidad, tenemos por principio de cuentas para [Sx]:
En lo que respecta a [Sy], se tiene:
Y por último, en lo que respecta a [Sz], se tiene:
PROBLEMA: Suponiendo que para un sistema que consta de partículas de spin 1/2 se conocen los valores de [Sx], [Sy] y [Sz]; ¿cómo se puede construír a partir de dicha información la matriz densidad ρ?
La matriz densidad ρ constará de cuatro entradas desconocidas, p, q, r y s, que tienen que ser determinadas a partir de los valores de [Sx], [Sy] y [Sz]. Esto lo podemos hacer de la siguiente manera:
Para el del ensamble [Sx]:
Para el caso del ensamble [Sy]:
Y para el caso del ensamble [Sy]:
Tenemos tres ecuaciones con cuatro incógnitas, p, q, r y s. Se requiere una ecuación adicional para poder resolver el sistema. Esta ecuación nos la dá la condición de normalización:
Resolviendo el sistema de ecuaciones, tenemos entonces que cada una de las cuatro entradas que corresponden a la matriz densidad se obtienen de las siguientes relaciones:
Cuando se trata de fermiones, que son partículas de spin 1/2, el tamaño de la matriz densidad es 2x2. Pero también hay partículas con spin 1, y para un ensamble que contenga una mezcla de tales partículas la matriz densidad será de tamaño 3x3:
Puesto que la matriz densidad ρ es Hermitiana, el reflejo de sus elementos con respecto a la diagonal principal debe mostrarlos como conjugados complejos, de modo tal que una representación un poco más realista de una matriz densidad 3x3 es la siguiente:
El requisito fundamental de que la traza de la matriz sea igual a la unidad sigue siendo válido, de modo tal que se debe cumplir la condición:
Una matriz densidad 3x3 que represente un ensamble puro tendrá una sola de sus entradas diagonales igual a la unidad, mientras que las otras dos entradas diagonales serán iguales a cero, como en el siguiente caso:
en tanto que una matriz densidad 3x3 que represente un ensamble mixto tendrá dos o más entradas diferentes de cero a lo largo de su diagonal principal, como en el siguiente caso:
Por último, para el caso en que la matriz densidad 3x3 represente un ensamble completamente aleatorio, todas sus entradas diagonales tendrán el mismo valor, y la suma de dichas entradas diagonales seguirá siendo igual a la unidad:
Extendiendo todo lo anterior hacia el caso más general, una matriz densidad para un ensamble puro tiene el siguiente aspecto:
en tanto que una matriz densidad para un ensamble completamente aleatorio tiene el siguiente aspecto:
La traza de una matriz densidad ρ para un estado puro siempre es igual a la unidad. Esta es la característica distintiva del estado puro. Si consideramos que un estado puro es un reflejo del mayor orden posible que se pueda lograr dentro de un sistema, con todas las partículas agrupadas en torno a un solo valor o característica, entonces podemos ver que en la matriz densidad ρ tenemos en cierta forma una medida del orden o del “desorden” que hay en un sistema. Esto es importante porque para la discusión de muchos problemas importantes en la Mecánica Estadística Cuántica se requiere de alguna medida del grado de orden o del desorden de un ensamble. Una definición cuantitativa utilizada ampliamente y la cual depende del concepto de la matriz densidad es la siguiente:
La evaluación del logaritmo natural de un operador matricial, en este caso la matriz densidad ρ, recurriendo a la definición usual empleada para este tipo de funciones matriciales (usando una serie de Maclaurin-Taylor) se antoja algo formidable e intimidante. Sin embargo, el significado de esta cantidad se vuelve manejable si recurrimos a una representación en la cual fincamos a la matriz ρ si seleccionamos una base de kets sobre la cual la matriz sea diagonal:
De este modo, para un ensamble completamente aleatorio (cuya matriz densidad representativa se ha bosquejado en la última figura matricial de arriba) se tiene:
siendo N el número de estados cuánticos posibles y teniendo la matriz densidad una dimensión NxN. Puesto que N es un entero positivo mayor (o igual) a la unidad, σ sólo podrá tomar valores positivos para un ensamble aleatorio. Por otra parte, para el caso de un ensamble puro, una de los elementos en la diagonal principal será igual a 1 mientras que todos los demás elementos serán iguales a cero. Y puesto que:
se concluye que para para un ensamble puro σ será igual a cero. De este modo, el ensamble para el cual σ.=.0 es aquél en el cual se encuentra el mayor orden posible, ya que todos sus miembros están caracterizados por el mismo ket de estado mecánico-cuántico, como las partículas en un ensamble que están apuntando todas hacia la misma dirección ó como los soldados que marchan en forma perfectamente sincronizada en un pelotón; en tanto que para un estado aleatorio σ tendrá un valor positivo diferente de cero, al ser todos los estados mecánico-cuánticos posibles igualmente probables, como las partículas en un ensamble que están apuntando al azar en todas las direcciones posibles sin una dirección preferida sobre las demás ó como un pelotón de soldados borrachos que caminan sin dirección fija. Para una colectividad de N partículas, el máximo valor de σ será ln(N). En pocas palabras, σ está acotado entre los siguientes límites dependiendo del orden o del desorden que haya en el sistema:
Habiéndose considerado matrices de densidad en un espacio de kets en donde los kets de base están etiquetados con los eigenvalores discretos de alguna observable, nos preguntamos cómo se puede generalizar el concepto de la matriz densidad a casos en los cuales los kets de base a ser utilizados están etiquetados por eigenvalores continuos, como en el caso en donde el espacio ket es abarcado con eigenkets de posición |x'>. El análogo de la distribución usada para el caso discreto en donde se recurrió a una sumatoria nos llevó a la relación fundamental:
está dado por una relación que tiene el siguiente aspecto:
en donde P(ψ) es la función que nos dá el peso estadístico propio para el ensamble. Puesto que la multiplicación con el operador identidad definido en la convención de Dirac mediante productos externos:
no alterará la expresión para el valor esperado del ensamble [A], la expresión se puede expandir utilizando una base ortonormal de kets de base (para el caso continuo) de la siguiente manera injertando al operador identidad en los lugares apropiados:
Esto se puede reescribir de la siguiente manera
Si definimos al operador densidad ρ de la siguiente forma:
tenemos entonces el siguiente resultado para el promedio del ensamble:
Esto, desde luego, es lo mismo que tomar la traza del producto matricial de la matriz densidad ρ con el operador A en su representación matricial:
La expresión no compactada se puede escribir también de la manera siguiente:
que es lo mismo que:
reafirmando lo dicho con anterioridad de que el producto matricial se puede tomar en cualquier orden.