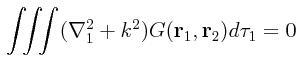La aproximación de Born I

Habiendo visto previamente el método de las ondas parciales aplicado al esparcimiento de partículas, veremos a continuación otro método, conocido como la aproximación de Born, el cual resulta de mucha utilidad en el análisis de ciertos casos especiales.

Haciendo a un lado los detalles matemáticos, la idea esencial detrás de la aproximación de Born es muy sencilla. Esta aproximación consiste en suponer que el potencial de repulsión V(r) que produce el esparcimiento de las partículas está localizado y es relativamente débil, lo cual permite suponer que no ocurre un esparcimiento muy apreciable de partículas lejos del centro de esparcimiento, y débil en el sentido de que la onda esparcida es mucho más débil que la onda incidente.

Antes de entrar a fondo en la cuestión matemática de la aproximación de Born, daremos un repaso a dos conceptos fundamentales que estaremos utilizando. El primero es el teorema de Green, el cual es una extensión de una relación importante que existe entre integrales de volumen e integrales de superficie para la cual recurrimos al concepto de la divergencia, el teorema de la divegencia conocido también como el teorema de Gauss, y el segundo es la función de Green que es esencialmente una alternativa elegante para obtener una solución al problema de una ecuación diferencial inhomogénea.

En prácticamente cualquier curso de Análisis Vectorial, se demuestra que la integral de volumen de la divergencia de un campo vectorial F, simbolizada como ∇·F y evaluada sobre cada uno de los elementos infinitesimales de volumen dτ, es igual al flujo neto del campo vectorial F que sale (o entra) a través de la superficie total que encierra al volumen bajo consideración (o sea, es igual a la integral de superficie de un campo vectorial F evaluada sobre una superficie cerrada):

La utilidad de este teorema conocido como el teorema de la divergencia o teorema de Gauss estriba precisamente en que permite convertir una integral de volumen en una integral de superficie, o viceversa.

Ahora bien, sean u y v dos funciones escalares. Entonces, por las reglas de la diferenciación del producto de dos funciones escalares (regla de Leibniz), las siguientes identidades deben ser ciertas:

Restando la segunda relación de la primera, llevando a cabo una integración volumétrica, y aplicando el teorema de Gauss, obtenemos la siguiente relación:

Podemos simplificar esto un poco con la ayuda del operador Laplaciano ∇².=.∇·∇, escribiendo entonces:

Esta relación es conocida como el teorema de Green.

Por otro lado, demos ahora un repaso de una de las relaciones fundamentales de la electrodinámica clásica, la ecuación de Maxwell que afirma que una carga eléctrica q para la cual la densidad de carga se simbolice como ρ, producirá en torno a la misma un campo eléctrico E cuya divergencia, en el sistema de unidades MKS-SI, estará dada por la siguiente relación:

La interpretación física más sencilla que le podemos dar a esto es que, en ausencia de una carga eléctrica, no hay divergencia de “líneas de fuerza” del campo eléctrico E, o sea que no hay ni una fuente ni un sumidero de líneas de fuerza, no hay campo vectorial alguno porque ρ es igual a cero. Obviamente, la carga eléctrica total encerrada dentro de cierto volumen se obtiene llevando a cabo la siguiente integración:

Una de las primeras cosas que aprende un estudiante de física es que es mucho más fácil lidiar con problemas escalares para los cuales las operaciones relacionadas con los campos escalares se llevan a cabo mediante sumas y restas, que tener que batallas con problemas vectoriales para los cuales las operaciones relacionadas con los campos vectoriales se tienen que llevar a cabo de acuerdo a las reglas más elaboradas del Análisis Vectorial. Es por esto que resulta definir el concepto del potencial eléctrico, que aquí simbolizaremos como Φ, cuyo gradiente ∇Φ nos produce un campo eléctrico E (se adopta por convención un signo negativo en la operación). Esto nos permite llevar a cabo el siguiente reemplazo en la relación de Maxwell dada arriba:

con lo cual obtenemos:

o lo que es lo mismo:

Si ρ fuera una simple constante numérica, entonces la ecuación diferencial resultante a causa de ello sería algo trivial. Sin embargo, y en un caso general, ρ puede ser una cantidad que depende de la distancia radial, o sea que en lugar de escribir ρ tendríamos que escribir ρ(r), en donde r es un vector tridimensional especificado en cualquier sistema de coordenadas. En tal caso, la ecuación general viene siendo:

Esta expresión es mejor conocida como la ecuación de Poisson, en honor al matemático Siméon Poisson que elaboró el primer trabajo serio sobre la misma. Matemáticamente hablando, esto representa ya una cosa más seria en virtud de que se traduce en una ecuación diferencial no-homogénea. Para fines comparativos, el caso general de una ecuación diferencial homogénea, linear, de segundo orden, se puede escribir de la siguiente manera:

Este tipo de ecuaciones puede resolver de manera directa con expansiones en serie (o sea, con el método de Frobenius, que una vez comprendido se puede aplicar de manera casi mecánica). En contraste, lo que tenemos en el caso de la ecuación de Poisson es una ecuación diferencial no-homogénea, representativa del tipo de ecuaciones diferenciales no-homogéneas que se pueden escribir de la siguiente manera:

Podemos obtener, por consideraciones de índole física, una solución al problema de la deteminación del potencial eléctrico Φ, la cual podemos usar como punto de referencia para desarrollar una metodología general para obtener soluciones a ecuaciones diferenciales homogéneas, y si tal metodología trabaja los resultados que produzca deben coincidir con aquellos que se obtengan a partir de consideraciones físicas.

Empezaremos con el hecho de que el potencial eléctrico, siendo una cantidad escalar (sin dirección y sentido), puede ser sumado aritméticamente a otro potencial eléctrico. Si cierto punto en el espacio está situado a una distancia r₁ de una carga eléctrica q₁ que produce un potencial eléctrico Φ₁ sobre dicho punto,  y si dicho punto está situado a una distancia r₂ de otra carga eléctrica q₂ que produce un potencial eléctrico Φ₂ sobre dicho punto, y así sucesivamente, entonces tal conjunto de cargas eléctricas discretas producirá un potencial total Φ que está dado (en el sistema de unidades MKS-SI) por la relación:

siendo r_i la distancia de cada carga eléctrica q_i  al punto en donde se está produciendo el potencial Φ.Si lo que tenemos es una distribución continua de carga eléctrica, entonces si el “centro de simetría” (el punto en el espacio en donde para fines de cálculo podemos considerar que está concentrada toda la carga) de dicha carga eléctrica está ubicado en una posición r₂ con respecto al origen del sistema de coordenadas (que supondremos de coordenadas rectangulares Cartesianas), y si el punto en donde se está produciendo el potencial Φ está ubicado en la posición r₁, la generalización de lo anterior nos dice que el potencial eléctrico Φ en el punto especificado en la posición r₁ debe estar dado por la siguiente relación:

siendo r₁₂ la distancia del  “centro de la carga eléctrica” al punto en donde está produciendo el potencial Φ. Puesto que estamos utilizando vectores posición r₁ y r₂:

r₁ = (x₁, y₁, z₁)

r₂  = (x₂, y₂, z₂)

entonces podemos escribir la relación anterior de la siguiente manera:

          (1)

en donde, desde luego:

Esta es precisamente la solución al problema de la ecuación de Poisson para una distribución de carga localizada, obtenida por consideraciones físicas. Pero, ¿podemos obtener el mismo resultado por consideraciones de índole meramente matemática sin recurrir a argumentaciones físicas? Antes de entrar en mayores detalles, daremos un repaso a varios resultados que son obtenidos bajo el Análisis Vectorial.

PROBLEMA.- Obténgase el gradiente de una función f(r) cualesquiera.

En un sistema de coordenadas rectangulares Cartesianas, la aplicación del operador diferencial vectorial nabla ∇ a la función para obtener el gradiente de la misma se hace de la manera siguiente:

Desde la perspectiva del cálculo multivariables, lo siguiente debe ser cierto:

Por otro lado:

Entonces:

con lo cual:

siendo r₀ (destacado en color azul) un vector unitario (r/r) que apunta en la dirección radial positiva. El gradiente de una función de r es por lo tanto un vector que apunta en una dirección radial.

PROBLEMA.- Demuéstrese que:

Usamos el resultado del problema anterior, haciendo:

Por lo tanto:

con lo cual queda demostrada la relación pedida.

PROBLEMA.- Demuéstrese que:

¿A qué resultado se reduce la expresión para n.=.-2?

Se tiene, por cálculo directo:

Usando los resultados anteriores, podemos hacer la siguiente generalización:

Haciendo en esto último f(r) = r^n-1, se tiene:

con lo cual se da por demostrada la relación pedida.

Reacomodando un poco lo anterior, se tiene:

Haciendo en esto n.=.-2, obtenemos el siguiente resultado importante que usaremos más abajo:

Basándonos en el resultado que acabamos de obtener, podemos tratar de aplicar el teorema de la divergencia (teorema de Gauss) conectando una integral de volumen con una integral de superficie de la siguiente manera:

Podemos entonces tratar de postular entonces algo como lo siguiente:

teniendo en mente, como lo resalta la segunda línea, de que la función específica utilizada en la derivación de los resultados previos fue:

Hay que ejercitar suma precaución en la forma en la cual aplicamos el teorema de la divergencia en un caso como este. La relación obtenida es válida siempre y cuando el volumen de integración no incluya al origen, esto es, el punto r.=.0 (lo cual implica que la superficie de integración excluye dicho punto). Si hemos de establecer una analogía con una situación física, la relación obtenida podría ser el equivalente de una carga eléctrica puntual situada en el origen de las coordenadas, o sea en el  punto r.=.0, y al usar una superficie de integración como la siguiente que no incluye dentro de la misma a dicha carga:

el resultado obtenido nos dice que el flujo neto de las líneas de fuerza que atraviesan a la superficie (y por ende al volumen encerrado por la superficie) es igual a cero. Sin embargo, si la superficie de integración incluye dentro de la misma el punto en el cual está situada la carga eléctrica, entonces se tiene ya un flujo neto de líneas de fuerza hacia afuera (una fuente de líneas de fuerza, cuando se trata de una carga eléctrica positiva) o un flujo neto de líneas de fuerza hacia adentro (un sumidero de líneas de fuerza, cuando se trata de una carga eléctrica negativa). Para poder manejar este segundo caso, recurrimos a un truco: encerramos la singularidad dentro de dos superficies esféricas de la siguiente manera:

y, manteniendo constante el radio b de la superficie esférica exterior, vamos disminuyendo el radio a de la superficie interior, el cual podemos hacer tan pequeño como queramos. A la vez que hacemos esto, hemos “conectado” a la superficie exterior de radio b con el casquete esférico interior de radio a con un tubito muy pequeño (no mostrado en la figura), de modo tal ambas esferas representan en realidad una sola superficie, con la curiosa característica de que la superficie externa apunta radialmente hacia afuera del origen del sistema de coordenadas, mientras que la normal de la superficie del casquete esférico interno apunta hacia adentro, hacia el origen del sistema de coordenadas. Llevando a cabo las integraciones en la forma debida mediante un sistema de coordenadas esféricas (en lugar de un sistema de coordenadas rectangulares), y efectuando la integración cubriendo un ángulo sólido Ω que abarque todo el volumen interno (o sea un ángulo de 4π estereoradianes), en el espíritu de la derivación del teorema de la divergencia se obtiene el siguiente resultado:

Ahora bien, para la resolución matemática de la ecuación de Poisson, postulamos una función, representativa de una familia de funciones conocidas como funciones de Green, la cual deberá satisfacer la ecuación de Poisson con una fuente puntual localizada en r₂:

∇²G(r₁,r₂) = - δ(r₁ - r₂)

Obsérvese que estamos invocando aquí la definición de la función delta de Dirac. Recuérdese que la función delta de Dirac carece de significado por sí sola, tiene que ser interpretada siempre bajo el signo de una integral:

Por convención, el “área bajo la curva” de la función delta de Dirac se define como igual a la unidad, esto es:

Esta definición puede ser extendida hacia tres dimensiones, en un sistema de coordenadas rectangulares Cartesianas:

En ocasiones, sobre todo cuando se está trabajando en problemas que involucran simetría esférica, resulta conveniente definir una función delta de Dirac δ(r) recurriendo a un sistema de coordenadas ortogonales esféricas (r,θ,φ):

Obsérvese que para esta definición de la función δ(r) bajo el signo integral se usa como elemento diferencial de volumen el que está definido así como tal en un sistema de coordenadas esféricas:

La definición dada para la función delta de Dirac bajo el signo de la integral en un sistema de coordenadas esféricas corresponde a una singularidad situada en el origen del sistema de coordenadas esféricas. Si la singularidad no está ubicada en el origen sino en otro punto definido por el vector posición  r₁, entonces en la definición anterior se tiene que efectuar el reemplazo:

δ(r) → δ(r₂ - r₁)

para tener así la siguiente definición:

Aunque la única interpretación posible para una función delta de Dirac es bajo el signo de la integración, podemos darle una interpretación “intuitiva” a la misma. En su interpretación más sencilla, la función delta de Dirac nos dá las coordenadas del punto preciso en donde está ubicada una singularidad, por ejemplo una carga eléctrica puntual. De este modo, si la singularidad está situada en:

(x, y, z) = (4, -1, 5)

entonces la función delta de Dirac que especifica dicha singularidad debe ser:

δ(x - 4)δ( y + 1)δ(z - 5)

Hemos llegado al punto apropiado en el cual podemos intentar justificar la función de Green dada arriba para la solución de la ecuación de Poisson. Y empezaremos haciéndolo recurriendo precisamente al teorema de Green que se obtuvo arriba al principio, de acuerdo al cual si tomamos como dos funciones escalares el potencial Φ y la función de Green G, podemos relacionarlas tanto bajo una integral de volumen como bajo una integral de superficie de la siguiente manera:

Supondremos ahora que en el lado derecho de esta ecuación, el integrando cae a una rapidez mucho mayor que r^-2, una aproximación válida en muchas situaciones del mundo real, con lo cual podemos tomar un volumen lo suficientemente grande para que la integral de superficie se desvanezca, esto es:

Siendo así, entonces se debe tener:

Enfoquémonos primero en la triple integral del lado izquierdo. Para la evaluación de la misma, se tiene:

Para la evaluación de esta triple integral, recurrimos a la quintaesencia de la función delta de Dirac, cuya definición nos dice que:

Entonces se debe tener:

Ahora enfoquémonos en la triple integral del lado derecho de la expresión que estamos simplificando, para la cual recurriendo a la ecuación de Poisson dada arriba se tiene:

Entonces, igualando las expansiones que llevamos a cabo en cada lado:

Por otra parte, de acuerdo a la ley de Gauss, cuando el volumen de la integración no incluye el origen (o sea, el punto en donde está situada la singularidad, y en el caso de la electrostática, el lugar en donde está ubicada la carga eléctrica puntual), se tiene que:

mientras que, cuando el volumen de la integración incluye el origen (aunque el origen es una singularidad, se le puede evadir considerando un volumen situado entre dos esferas, una de gran radio con centro en el origen y la de un radio pequeñismo también con centro en el origen pero que lo deja fuera del volumen de la integración), se tiene que:

Esto último lo podemos escribir de la siguiente manera:

El efecto de ambas relaciones puede ser combinado en uno solo de la siguiente manera si recurrimos a la definición de la función delta de Dirac:

En efecto, lo que estamos haciendo es lo siguiente (esta es una igualdad simbólica, teniendo en mente que la función delta de Dirac solo tiene sentido cuando se usa bajo un signo de integral):

Si la singularidad no está situada en el origen del sistema de coordenadas que está siendo utilizado, sino en una posición especificada por el vector posición r₂, entonces esto lo podemos tomar en cuenta modificando la expresión anterior de la siguiente manera:

Comparando esto último con la función de Green postulada arriba:

∇²G(r₁,r₂) = - δ(r₁ - r₂)

resulta evidente que para esto sea cierto, se debe tener:

o bien, escribiendo lo mismo pero de un modo más formal y elegante:

Hemos obtenido así de este modo la función de Green requerida para la solución general de la ecuación diferencial no-homogénea que estamos considerando. Introduciendo esta expresión en la relación derivada arriba para la función Φ(r₁), se tiene entonces lo siguiente:

Comparando esto que hemos obtenido con procedimientos puramente matemáticos con la expresión obtenida arriba mediante consideraciones físicas relativas a la electrostática, resulta evidente que ambas expresiones son iguales. Y en la obtención de la función de Green para la ecuación de Poisson, hemos desarrollado un procedimiento constructivo para poder llegar a ella, el cual consiste en invocar el teorema de Green. Esta es la razón del por qué para la clase de problemas que estamos considerando las funciones de Green están enlazadas de modo inseparable al teorema de Green.

Hay muchas funciones de Green para otros tipos de problemas. El que más nos interesa por el momento es el problema para el cual se necesita una función de Green G(r₁,r₂) que sirva como solución a la siguiente ecuación diferencial de Helmholtz:

No es un asunto muy difícil demostrar que, para este caso, la función de Green requerida es la siguiente:

Podemos comprobar, por substitución directa, que esta función de Green es realmente una solución para la ecuación diferencial de Helmholtz dada arriba. La interpretación que se debe dar a esto en base a la función delta de Dirac es cuando el volumen de la integración no incluye al punto especificado por el vector posición r₂, entonces se tiene lo siguiente:

mientas que cuando el volumen de la integración sí incluye al punto especificado por el vector posición r₂, entonces se tiene lo siguiente:

Teniendo a la mano la metodología matemática para hacerle frente a problemas que involucran ecuaciones diferenciales no-homogéneas, estamos en condiciones de poder hacerle frente a problemas mecánico-cuánticos de esparcimiento de partículas usando la aproximación de Born.

Una clase importante de problemas de esparcimiento pueden ser clasificados dentro de una misma categoría cuando se tiene un potencial débil y localizado, localizado en el sentido de que no ocurre un esparcimiento apreciable lejos del centro del dispersor, y débil en el sentido de que la onda esparcida ξ es mucho más débil que la onda incidente. Esto último puede ser especificado mediante la relación:

usando la siguiente condición:

En este punto, se vuelve necesario hacer una observación importante. La cantidad e^iX, sin importar lo que esté siendo representado por X, siempre será igual a la unidad, en virtud de la relación de Euler:

e^iX = cos(X) + isen(X)

En efecto:

siendo esto (en un plano complejo o plano de Argand) el equivalente geométrico de un círculo unitario, valor numérico que dicho sea de paso coincide con una probabilidad igual a 1 que es equivalente a la certeza. De este modo, la condición impone el requerimiento de que la amplitud de la onda esparcida ξ sea mucho menor que la onda incidente.

La condición que se ha impuesto es precisamente la aproximación de Born. Substituyendo el valor de ψ en la ecuación de Schrödinger:

obtenemos entonces el siguiente resultado:

o bien:

en donde:

Puesto que la cantidad U está siendo definida directamente en función del potencial V, si el potencial V es constante entonces la cantidad U también lo será. Por el contrario, si admitimos la posibilidad de que el potencial V pueda depender del punto seleccionado de acuerdo a algún vector posición r que parta del origen del sistema de coordenadas, esto es, que V sea una función del vector r representada como V(r), entonces la cantidad U también podrá depender del vector posición r y para mayor generalidad es válido utilizar la siguiente representación:

En este punto es donde entra nuevamente en acción la aproximación de Born. Si la función potencial V es relativamente débil, entonces el término U, siendo una función de V, también lo será, con lo cual el término Uξ destacado arriba en color magenta se puede eliminar. Entonces, en virtud de la aproximación de Born, lo que nos queda es lo siguiente:

Físicamente, esto equivale a decir que el esparcimiento ocurre como si parte del potencial de esparcimiento tuviera una onda de fuerza completa e^ikz incidiendo sobre el mismo, lo cual corresponde al supuesto de que el potencial de esparcimiento es débil. La ecuación dada arriba es una ecuación diferencial no-homogénea, y puede ser resuelta con la ayuda de una función de Green w que sea una solución a la siguiente ecuación:

En el desarrollo que sigue, la función-δ será considerada como cualquier función matemática apropiada que tenga un “pico” muy pronunciado en r.=.r'. El paso hacia el límite singular r.→.0 en donde se encuentra el “pico” es tomado en una etapa posterior en donde la función aparezca bajo una integral apropiada, que es en donde la función delta de Dirac adquiere su verdadero significado. Obsérvese con cuidado que en cualquier otro lado excepto en el punto r.=.r', esta ecuación diferencial construída sobre la función de Green w toma la forma:

que es una ecuación homogénea y que tiene una solución conocida. Bajo un límite adecuado, la solución a la ecuación diferencial no-homogénea que se acaba de proponer arriba resulta ser la siguiente función de Green:

Para una mayor claridad que suele ser obscurecida con la notación vectorial, si designamos la diferencia vectorial entre los vectores r y r' como R, y tomamos la magnitud de este último:

entonces la función de Green adquiere la siguiente forma que revela en forma más cercana su verdadero sentido:

Con la función de Green w, la solución ξ(r) a la ecuación diferencial no-homogénea:

puede ser escrita de la siguiente manera:

En esta expresión, dr’ simboliza un elemento diferencial de volumen (no se utilizó dV para no causar confusiones con la simbología utilizada para denotar a la función potencial V en la ecuación de Schrödinger), y se sobreentiende con esto que la integral que debe ser llevada a cabo bajo cualquier sistema de coordenadas que se utilice es una integral triple.

De que esto en efecto es así puede ser demostrado de la siguiente manera recurriendo al teorema de Green, empezando primero por el hecho de que de acuerdo a lo anterior:

Integrando sobre todo el espacio y aplicando el teorema de Green, podemos afirmar que:

Al hablar acerca de una integral en “todo el espacio” estamos hablando de una integral volumétrica, o sea una integral triple que se lleva a cabo sobre un espacio tridimensional, mientras que al hablar de una integral sobre una “esfera en R.=.∞” estamos hablando de una integral doble, una integral de superficie, en este caso la superficie es una esfera de radio grande que tiene como centro el núcleo repulsor que produce el esparcimiento de partículas. El radio de la esfera en realidad no lo consideramos infinitamente grande, sino lo suficientemente grande para que podamos llevar a cabo aproximaciones asintóticas. Se recalca que lo que hemos hecho aquí ha sido aplicar directamente el mismo teorema de Green cuya derivación fue dada arriba.

Para la evaluación de la integral volumétrica, podemos llevar a cabo los pasos siguientes:

Para pasar de la tercera línea a la cuarta línea, se utilizó la quintaesencia de la definición de la función delta de Dirac, es por ello que una vez evaluada la integral en vez de ξ(r) tenemos ξ(r’)

Ahora enfocaremos nuestra atención sobre la integral de superficie.

PROBLEMA: Dadas las siguientes dos relaciones:

demuéstrese que:

Para poder llevar a cabo lo que se pide aquí, haremos uso de la siguiente figura que nos muestra las relaciones geométricas que hay entre los vectores posición r y r’, siendo r el vector posición que parte desde el centro del sistema de coordenadas (tomado desde el centro del potencial de esparcimiento hasta el punto en el que la onda esparcida está siendo evaluada) y siendo r’ el vector posición de un punto en el potencial de esparcimiento, mientras que α es el ángulo entre los vectores r y r’:

con la cual podemos justificar las siguientes aproximaciones asintóticas para distancias radiales lo suficientemente grandes (no infinitas) como para que las aproximaciones que llevaremos a cabo puedan ser válidas:

Usando estas dos aproximaciones geométricas, podemos expresar la función de Green w de la siguiente forma:

A continuación, y para poder usar el teorema de Green (que es nuestro verdadero objetivo), recurrimos al operador ∇ expresado  no en un sistema de coordenadas rectangulares Cartesianas sino en un sistema de coordenadas ortogonales esféricas, el cual viene siendo:

en donde r₀, θ₀ y φ₀, son vectores unitarios ortogonales.

De este modo, haciendo uso del operador ∇ expresado en el sistema de coordenadas ortogonales esféricas, la evaluación de ∇w procede de la siguiente manera:

y puesto que:

se tiene entonces después de llevar a cabo las simplificaciones pertinentes:

Por otro lado, puesto que:

se tiene entonces con la aplicación del operador ∇:

Simplificando al máximo:

De este modo, la relación ξ∇w−w∇ξ después de hacer las simplificaciones pertinentes resulta ser:

Ahora bien, esta expresión vectorial es una función de los vectores unitarios esféricos θ₀ y φ₀, el vector unitario radial r₀ no aparece en ella. Pero si vamos a evaluar la siguiente expresión (que es en realidad una doble integral por llevarse a cabo sobre un elemento diferencial de superficie dS):

tenemos que tomar en cuenta que para estos cálculos a un elemento diferencial de superficie dS se le asigna vectorialmente dirección y sentido, dado por un vector unitario n normal a dicha superficie:

O sea que dS = ndS. Pero como estaremos llevando a cabo la integración sobre una superficie esférica, el vector unitario normal a cada elemento diferencial dS de superficie apunta radialmente “hacia afuera” de la esfera en cada punto de la esfera:

O sea que para el caso que nos ocupa, el vector unitario normal n debe ser lo mismo que el vector unitario radial r₀. Pero este vector unitario radial es ortogonal a los otros dos vectores unitarios esféricos θ₀ y φ₀, y puesto que son ortogonales el producto vectorial punto entre ellos debe ser igual a cero:

Esto implica necesariamente que en la evaluación de cualquier integral como la de arriba, todos los productos punto de cada elemento infinitesimal de superficie dS se desvanecerán cuando son tomados con cualquier función que contenga los vectores unitarios esféricos θ₀ y φ₀:

De este modo, se deduce que para una esfera de radio r suficientemente grande se obtiene el siguiente resultado:

Así pues, queda demostrado que la integral de superficie es igual a cero, y así pues queda demostrado también que  la solución ξ(r) haciendo uso de la función de Green w dada arriba es efectivamente una solución a la ecuación diferencial no-homogénea. En pocas palabras, hemos demostrado que:

es equivalente a:

Esta última relación la podemos escribir en la siguiente forma haciendo uso de las aproximaciones geométricas utilizadas arriba:

Simbolizando el vector de onda de la onda incidente como k₀ y al vector de onda de la onda esparcida como k (puesto que el momentum p es proporcional a ħk, en realidad estamos hablando del momentum de las partículas incidentes y del momentum de las partículas esparcidas), tenemos entonces (véase la figura de arriba):

kz’ = k₀ · r’

kr’cos(α) = k · r’

Con esto, podemos reescribir la relación asintótica para ξ del siguiente modo:

Podemos simplificar esto último un poco más, observando la diferencia vectorial que aparece en el exponencial, y definiendo un vector de onda K de la siguiente manera:

K = k₀ - k

Físicamente, la cantidad K representa (vectorialmente hablando) el cambio en el vector de onda de la partícula incidente ocasionado por el esparcimiento, y lo podemos llamar la “transferencia del momentum”, que es lo que realmente es. Es importante tener presente que k₀ y k tienen magnitudes iguales, o sea:

|k₀| = |k| = k

Lo que cambia vectorialmente (a causa del esparcimiento) es la dirección del momentum. Y puesto que k₀ y k son de igual magnitud, podemos entonces deducir del siguiente diagrama:

que:

Esta relación será usada más abajo.

Así pues, habiendo introducido el vector K, la relación asintótica para ξ se puede escribir de la siguiente manera:

Comparando esta expresión con la relación:

podemos deducir de inmediato que:

Si en vez de usar a U(r’) metemos en esta última expresión al potencial V(r’) en su forma explícita, lo anterior se puede escribir de la siguiente manera (representaremos aquí la integral como lo que realmente es, una integral triple llevada a cabo sobre elementos diferenciales volumétricos dr’):

Puede verse que, en esta aproximación de Born, la amplitud del esparcimiento es simplemente igual a la transformada de Fourier del potencial. Esto puede traer una reminiscencia de lo que ocurre en la difracción de Fraunhofer, en donde el patrón de difracción de una onda electromagnética (como la luz) está relacionado en forma sencilla a la transformada de Fourier de la apertura de la difracción.

Decir que la distribución del esparcimiento depende de los ángulos θ y φ es tanto como decir que depende de los vectores k₀ y k, y por ello es frecuente encontrar en varios textos una notación alterna, de la cual daremos aquí la equivalencia:

Obsérvese que se ha agregado el super-índice (1), que enfatiza el hecho de que esta distribución de esparcimiento fue lograda con una amplitud de Born de primer orden, la cual puede ser mejorada agregándole amplitudes adicionales de segundo orden, tercer orden, etcétera.

Puesto que, como ya lo vimos previamente, la sección transversal del esparcimiento está dada por la relación:

se tiene entonces que:

Como un primer ejemplo de la aplicación de la aproximación de Born, veremos el caso del esparcimiento de partículas de alta energía producido por un potencial esférico relativamente débil:

Esto lo podemos imaginar como una esfera de radio a dentro de la cual el potencial V es igual a V₀, y fuera de la cual el potencial V es igual a cero:

Dentro de la esfera de radio a, se tiene un potencial esférico constante y débil (débil en comparación con la energía de las partículas incidentes, las cuales se supone que son partículas de energía elevada) de magnitud V₀, razón por la cual la cantidad U(r’) definida arriba tomará un valor constante, mientras que fuera de la esfera de esparcimiento el potencial es igual a cero con lo cual U(r’) toma también un valor igual a cero fuera de la esfera de potencial. De este modo, puesto que:

sólo es necesario evaluar la integral dentro de la esfera. Para la evaluación de la integral, usaremos la siguiente figura como punto de referencia:

En base a esta figura, y reemplazando en el exponencial a |K| por la relación dada arriba así como a r’ en el producto punto de ambas cantidades, tomando para la integración la superficie anular 2πr’ entonces la integral dada arriba para la evaluación de σ(θ,φ) puede ser escrita de la siguiente manera:

Recurriendo a la relación de Eueler para convertir el exponencial a su forma trigonométrica, esta integral puede ser evaluada de inmediato como se muestra a continuación:

Para ángulos θ pequeños de esparcimiento tales que podamos usar las aproximaciones:

sen(θ) ≈ θ          cos(θ) ≈ 1

podemos ver que la integral se aproxima asintóticamente a lo siguiente:

La sección transvesal del esparcimiento resulta ser entonces:

o bien:

Esto nos dice que el esparcimiento para ángulos de esparcimiento θ pequeños aumenta mucho más rápido (¡en relación a la sexta potencia!) que la sección transversal geométrica conforme el radio del dispersor es aumentado.

Si k₀a » 1, entonces para todos los ángulos tales que k₀a.».1 el segundo término entre los paréntesis rectangulares de la integral dada arriba es el que domina el esparcimiento, y la integral se reduce a:

Esto corresponde a una sección transversal de esparcimiento igual a:

En esta expresión, y teniendo en cuenta que k₀a.».1 fue el criterio utilizado para derivarla, la sección transversal σ(θ) es una función que experimenta una fluctuación muy rápida en su variación con respecto a θ en virtud del factor:

Para poder apreciar la variación rapidísima de σ(θ) en función de θ, a continuación se presentarán dos gráficas de la relación con diferentes escalas para la variable independiente θ:

las cuales son:

La gráfica inferior nos muestra un comportamiento algo más elaborado que el comportamiento mostrado por la gráfica superior. Sin embargo, puesto que estamos considerando el comportamiento que ocurre a ángulos pequeños para los cuales el seno de un ángulo (expresado en radianes) es numéricamente igual al ángulo (esto es, sen(θ/2).≈.θ/2), podemos ignorar la gráfica inferior basándonos en el comportamiento mostrado por la gráfica superior que es esencialmente el comportamiento de una función cosenoidal cuadrática de oscila bruscamente dentro del rango de esos ángulos pequeños. Promediando sobre estas fluctuaciones rápidas, y en vista de que para ángulos pequeños para los cuales el seno de un ángulo θ expresado en radianes se puede substituir por el mismo ángulo θ expresado también en radianes, se puede obtener el siguiente resultado (véase la entrada previa titulada “El método de las ondas parciales I”):

De este modo, la promediación de la sección transversal de esparcimiento nos arroja la expresión:

La semejanza de este resultado con el resultado obtenido por Rutherford:

mediante consideraciones puramente clásicas resulta sorprendente. En verdad, las dos secciones transversales resultan ser idénticas si la altura del potencial esférico V₀ es seleccionada de modo tal que el potencial sea idéntico con la energía Coulómbica de la partícula incidente en el esparcimiento Rutherford cuando la partícula incidente esté a una distancia a (el radio del potencial esférico) del dispersor. Obsérvese que nos hemos aproximado al resultado clásico de Rutherford mediante las herramientas de la Mecánica Ondulatoria, algo que no funciona cuando se intenta hacer el procedimiento inverso. Es posible derivar la mecánica clásica a partir de la Mecánica Ondulatoria, pero no es posible obtener la Mecánica Ondulatoria a partir de los postulados clásicos. Sin embargo, los resultados clásicos muchas veces han servido como guía para proporcionar pistas sobre los resultados que se pueden esperar cuando las deducciones obtenidas por la vía de la Mecánica Ondulatoria son evaluadas en condiciones de aproximación para casos límite.