Una diferencia que destaca de inmediato entre la espectroscopía RMN y la espectroscopía RSE es la frecuencia de la radioseñal requerida en la espectroscopía RSE en comparación con la radioseñal requerida en la espectroscopía RMN. Mientras que en el análisis RMN la radioseñal típica requerida tiene una frecuencia en el rango de los Megahertz (por ejemplo, 60, 90, inclusive hasta 400 Megahertz), en el caso de la espectroscopía RSE la señal de estímulo está en el orden de los Gigahertz, una frecuencia tan elevada que no hace mucho tiempo era prácticamente inaccesible por las dificultades técnicas en obtener frecuencias tan elevadas con los dispositivos electrónicos disponibles, teniéndose que recurrir al uso de tubos klystron como los que se utilizan en los hornos de microondas.
PROBLEMA: Determínese la frecuencia de precesión de los electrones cuando son sometidos a un campo magnético de 1.5 Teslas.
De las relaciones dadas en la entrada anterior, se tiene para el caso del electrón:
En presencia de un campo magnético externo, se elimina la degeneración de la función de onda del spin para un electrón no-apareado, tomándose por convención al estado s.=.-1/2 como el más bajo en energía y al estado s.=.+1/2 como el más alto en energía. Cada uno de estos estados se desdobla en n+1 componentes para cada n núcleos equivalentes que tienen un spin nuclear presente en la molécula. Por convención, se supone que los estados de spin nuclear con spin positivo son más bajos que aquellos que tienen spin nuclear negativo en el estado s.=.-1/2, y viceversa en el estado s.=.±1/2. La regla de selección para transiciones permitidas es ΔmI.=.0, en donde:
mI = I, I - 1, I - 2, I - 3, ... , - I
e I.=.n(1/2).
La siguiente figura nos muestra el desdoblamiento energético ocasionado por un campo magnético sobre el spin de un electrón no-apareado así como el desdoblamiento posterior en niveles energéticos adicionales ante la presencia de un protón (H), así como el espectro resultante con tres picos de resonancia que van apareciendo conforme va aumentando la intensidad del campo magnético de izquierda a derecha:
Al igual que como ocurre con el desdoblamiento de los picos de resonancia RMN, se puede demostrar que las intensidades de los picos de resonancia RSE son proporcionales al número de combinaciones de spines nucleares los cuales crearán el valor de mI. Y del mismo modo, una manera sencilla de determinar las intensidades relativas de las líneas espectrales RSE es usar el triángulo de Pascal de coeficientes binomiales en donde los coeficientes de hileras adicionales se pueden determinar sumando los coeficientes de la derecha y de la izquierda en la hilera previa al coeficiente deseado. Es importante no confundir el desdoblamiento de líneas observado en la espectroscopía de resonancia magnética nuclear RMN con el desdoblamiento de líneas observado en la espectroscopía de resonancia del spin electrónico RSE. En la espectroscopía RMN, el desdoblamiento es un desdoblamiento spin-spin, mientras que en la espectroscopía RSE el desdoblamiento es conocido como desdoblamiento hiperfino (hyperfine splitting, en inglés).
PROBLEMA: Las separaciones que hay en las líneas en los espectros RSE pueden ser expresadas ya sea en unidades del campo magnético (Teslas) o en unidades de frecuencia (Megahertz), para lo cual se utiliza frecuentemente el siguiente factor de conversión:
1 Tesla = 2.80×104 Megahertz
Obténgase este factor de conversión.
De las relaciones dadas en la entrada anterior, se tiene para el caso del electrón:
Como un ejemplo sencillo del desdoblamiento hiperfino, considérese un radical libre con dos protones (H) que afectan los niveles de energía del electrón de maneras diferentes. La siguiente figura muestra los efectos de dos protones no-equivalentes (cuyas constantes de acoplamiento J son diferentes) sobre los niveles energéticos posibles de un electrón:
Ante la presencia de un campo magnético, el electrón no-apareado tiene dos niveles de energía, ms.=.+1/2 y ms.=.-1/2. Uno de los protones produce un primer desdoblamiento en ambos niveles, y el otro protón produce un segundo desdoblamiento en ambos niveles, de modo tal que el electrón no-apareado puede tener ocho niveles distintos de energía. En la resonancia del spin electrónico, el spin del electrón cambia de orientación (de “abajo” hacia “arriba” o de “arriba” hacia “abajo”), pero los spins nucleares no lo hacen. De este modo, al absorber energía en una transición RSE, el electrón va de un nivel de energía que corresponde al grupo bajo (ms.=.-1/2) a un nivel de energía que corresponde al grupo alto (ms.=.+1/2). Al ser incrementada la fuerza del campo magnético, las cuatro transiciones posibles van entrando sucesivamente en resonancia una a una, obteniéndose de este modo cuatro líneas en el espectro RSE. Puesto que los cuatro estados de spin nuclear (α1α2, α1β2, α2β1, y β1β2) son igualmente probables, las cuatro líneas son de igual intensidad. Las dos separaciones a1 y a2 pueden ser calculadas del espectro para quedar como se muestra a continuación:
Si los protones tienen la misma constante de acoplamiento J, esto es, si los protones son equivalentes, el espectro RSE tendrá tres líneas, y la línea central será dos veces más intensa que las otras dos porque representa dos transiciones posibles, como lo muestra la siguiente figura:
En este caso, el espectro RSE, deducido directamente de la figura que tenemos arriba, muestra el siguiente aspecto:
Dos o más protones que tienen el mismo acoplamiento a un electrón no-apareado siendo por ello equivalentes usualmente ocupan posiciones equivalentes en una molécula. Podemos describir el efecto de los dos spins de los protones (H) que hay en una molécula diciendo que el primer protón desdobla la línea de resonancia original del electrón no apareado en un doblete, y que el segundo protón se encarga de desdoblar posteriormente a las dos líneas en un cuadruplete. Como ya vimos, si los dos desdoblamientos hiperfinos son diferentes (esto es, si los dos protones no son equivalentes), se obtendrán cuatro líneas de absorción. Y si los dos desdoblamientos hiperfinos son iguales (esto es, si los dos protones son equivalentes), se obtendrán tres líneas. La siguiente figura nos muestra los desdoblamientos RSE que se producen cuando los protones (H) no son equivalentes:
mientras que la siguiente figura nos muestra los desdoblamientos RSE que se producen cuando los protones (H) son equivalentes:
En general, si n electrones equivalentes interactúan con un electrón no apareado, habrá n+1 líneas cuyas intensidades relativas estarán dadas por el triángulo de Pascal.
PROBLEMA: Si un electrón no-apareado en cierto compuesto dá el siguiente espectro de líneas RSE:
determínense las constantes del acoplamiento hiperfino a1 y a2 tanto en Teslas como en Megahertz.
Utilizando el factor de conversión obtenido en el problema previo con el cual se tiene que 1 Tesla es igual a 2.8×104 Megahertz, se tiene entonces que las constantes del acoplamiento hiperfino en el espectro RSE:
son, respectivamente:
a1 = 3×10-4 Teslas ó 8.40 Megahertz
a2 = 1×10-4 Teslas ó 2.80 Megahertz
PROBLEMA: Dibújese el espectro RSE que puede esperarse para un electrón no-apareado ante la presencia de tres protones cuando los protones no son equivalentes.
En la siguiente figura, la flecha (1) muestra el primer desdoblamiento causado por uno de los protones sobre la línea del pico de resonancia que corresponde a la transición energética entre los dos niveles posibles del spin del electrón no-apareado (entre ms.=.-1/2 y ms.=.+1/2), la flecha (2) muestra el segundo desdoblamiento causado por el otro protón no-equivalente, y la flecha (3) muestra el tercer desdoblamiendo causado por el tercer protón no-equivalente.
PROBLEMA: Dibújese el espectro RSE que puede esperarse para un electrón no-apareado ante la presencia de tres protones cuando los protones son equivalentes.
Siendo los tres protones equivalentes, los desdoblamientos sucesivos producirán tres líneas cuyas intensidades relativas estarán dadas por los coeficientes binomiales del triángulo de Pascal:
PROBLEMA: Dibújese el espectro RSE que puede esperarse para un electrón no-apareado ante la presencia de dos protones que son equivalentes y un tercer protón que no es equivalente a ninguno de ellos.
En este caso, los desdoblamientos conducen a un espectro RSE como el siguiente:
Como puede intuírse de lo anterior, y en forma parecida a como sucedió en el caso de la espectroscopía RMN, podemos generalizar que para una molécula que tiene n protones el pico de resonancia del electrón que corresponde a un espectro RSE se desdoblará en un conjunto de n+1 líneas con intensidades relativas como las dadas por el triángulo de Pascal, y en caso de que haya protones adicionales habrá desdoblamientos adicionales que aparecerán en el espectrograma final.
PROBLEMA: ¿Qué aspecto tendrá el espectro RSE del ión radical negativo benzosemiquinona cuya fórmula estructural es la siguiente?:
Como puede apreciarse de inmediato, los cuatro protones (hidrógenos H) son magnéticamente equivalentes. El espectro RSE del electrón no-apareado ocasionado por sus dos niveles energéticos (-1/2 y +1/2) será desdoblado por la acción de cualquiera de los cuatro protones, para ser desdoblado esto nuevamente por cualquiera de los tres protones restantes, para ser desdoblado nuevamente todo por cualquiera de los dos protones restantes, para ser desdoblado nuevamente todo por el cuarto protón. El espectro RSE de la molécula orgánica constará de cinco líneas:
n + 1 = 4 + 1 = 5 líneas
cuyas intensidades estarán dadas por la quinta línea triángulo de Pascal:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
siendo las intensidades relativas de las cinco líneas 1:4:6:4:1.
PROBLEMA: Descríbase el espectro RSE del ión negativo del benceno, C6H6-.
Bajo la aplicación de un campo magnético, la función de onda del spin para el electrón no-apareado se desdoblará en dos componentes. Los seis protones equivalentes (los seis hidrógenos H del benceno) dan:
I.=.6(1/2).=.3
De este modo, los dos niveles que fueron desdoblados por el campo magnético serán desdoblados cada uno en siete sub-niveles que corresponden a:
mI = 3, 2, 1, 0, -1, -2, -3
Por su parte, la regla de selección ΔmI.=.0 da siete picos de resonancia igualmente espaciados que tienen intensidades relativas de:
1 : 6 : 15 : 20 : 15 : 6 : 1
Por último, el núcleo de carbono 12C no tiene spin nuclear neto, y por lo tanto no contribuirá al espectro RSE. La siguiente figura nos muestra el desdoblamiento de los niveles de energía del spin del electrón no-apareado en el ión negativo de benceno al ser aplicado un campo magnético, así como el desdoblamiento posterior de cada uno de estos dos niveles en siete en virtud de los seis protones equivalentes (los seis hidrógenos H del benceno), posibilitando la aparición de siete picos de resonancia RSE que corresponderán a las transiciones (indicadas por las flechas rojas) que se pueden llevar a cabo entre los 14 niveles energéticos disponibles de acuerdo a la regla de selección dada anteriormente:
La siguiente figura nos muestra el espectro RSE del ión negativo del benceno así como las intensidades relativas de los picos de resonancia de acuerdo a lo que predicen los coeficientes binomiales del triángulo de Pascal (la escala mostrada es para dar la magnitud del campo magnético en mili-Teslas):
En contraste con el espectrograma RSE del benceno, el espectrograma RSE del ión negativo del naftaleno, C10H8-, resulta ser más complicado en virtud de que hay dos tipos diferentes de protones (H) que se pueden identificar en la fórmula estructural del naftaleno:
Los cuatro protones A por sí solos darían lugar a un espectro RSE con cinco picos de resonancia:
n + 1 = 4 + 1 = 5 líneas
Pero cada una de estas líneas es desdoblada posteriormente en cinco líneas de resonancia por los protones B dando lugar a un espectro de 25 líneas. El siguiente espectrograma del naftaleno nos muestra la identificación de tres de los varios grupos de líneas de resonancia que forman parte del espectro:
PROBLEMA: Descríbase el espectro RSE del ión negativo CH3·.
Obsérvese con cuidado el punto intermedio puesto a la derecha del radical metil, representando al electrón no-apareado que producirá un espectro RSE al ser desdoblada su línea de resonancia. Puesto que se tienen tres protones, el desdoblamiento producirá n+1 = 3+1 = 4 líneas, cuyas intensidades relativas serán 1:3:3:1 de acuerdo a lo que nos marcan los coeficientes binomiales del triángulo de Pascal. Las transiciones que hay detrás de los desdoblamientos son las siguientes de acuerdo a lo que marca la regla de selección:
PROBLEMA: ¿Cuáles son las intensidades relativas de las 25 líneas que corresponden al espectro RSE del anión naftaleno?
Haciendo referencia a la fórmula estructural dada arriba para el anión naftaleno, tenemos por principio de cuentas que los cuatro protones A producen 5 picos cuyas intensidades relativas de acuerdo al triángulo de Pascal son 1:4:6:4:1. Pero cada uno de estos picos es a su vez desdoblado en 5 picos cuyas intensidades relativas también serán 1:4:6:4:1, dando un total de 25 picos cuyas intensidades relativas podemos calcular de la siguiente manera:
Entonces habrá 4 picos de intensidad 1, 8 picos de intensidad 4, 4 picos de intensidad 6, 4 picos de intensidad 16, 4 picos de intensidad 24, y un pico de intensidad 36.
Como podrá suponerse al contemplar los traslapes que hay entre los tres grupos de líneas espectrales mostrados, en compuestos orgánicos aún más complejos que el benceno y el naftaleno la identificación de los grupos resulta más un arte refinado que una cuestión de metodología científica, y aunque el advenimiento de las computadoras ha simplificado los análisis de los espectrogramas, no faltan aquellas ocasiones en las que la determinación de una fórmula estructural puede resultar un desafío tal que en ocasiones el esfuerzo ha valido uno que otro Premio Nóbel otorgado a quienes no se han dejado vencer tan fácilmente. El siguiente espectrograma nos muestra algo que resulta un poco más legible para quienes se están iniciando en el arte de la lectura de los espectros RMN:
El desdoblamiento causado por otros núcleos magnéticos es similar al que se ha mostrado arriba para los espectros del ión negativo del benceno y el ión negativo del naftaleno, excepto que los núcleos con spin integral de 1 tales como el 14N producirán un desdoblamiento en tripletes de igual intensidad, puesto que el número cuántico para el núcleo 14N puede ser -1, 0 ó +1.
PROBLEMA: El espectro RSE de un radical cuya fórmula química condensada es C3H7· (el punto a la derecha de la fórmula representa el electrón no apareado cuyo pico de resonancia es desdoblado) mostró 14 picos de absorción con intensidades relativas de 1, 1, 6, 6, 15, 15, 20, 20, 15, 15, 6, 6, 1 y 1. Determínese si se trata de un radical n-propilo o de un isopropilo.
Un radical n-propilo, cuya fórmula estructural abreviada es:
CH3 - CH2 - CH2 ·
mostrará (yendo de derecha a izquierda para la contabilización de los desdoblamientos) 3 picos con intensidades relativas de 1:2:1; y cada uno de estos picos será desdoblado en tres picos de resonancia con intensidades relativas de 1:2:1, y a su vez cada uno de estos picos será desdoblado en 4 picos con intensidades relativas de 1:3:3:1, dando un total de 36 picos, lo cual no está de acuerdo con los datos experimentales proporcionados. En cambio, el radical isopropilo cuya fórmula estructural abreviada es:
CH3 - CH - CH3 ·
mostrará 2 picos con intensidades relativas 1:1 (primer desdoblamiento), siendo desdoblados cada uno de ellos en 7 picos con intensidades relativas 1:6:15:20:15:6:1, dando un total de 14 picos cuyas intensidades relativas serán:
lo cual concuerda con los datos proporcionados. Se concluye que el compuesto es un isopropilo.
PROBLEMA: Determínese la fórmula estructural para un radical orgánico que contiene dos carbonos y cuyo espectro RSE consistió de 12 líneas con intensidades relativas de 1, 2, 3, 1, 6, 3, 3, 6, 1, 3, 2 y 1.
La fórmula estructural más probable es la siguiente (el punto a la derecha de la fórmula representa el electrón no apareado cuyo pico de resonancia es desdoblado por ambos grupos):
CH3 - CH2 ·
en virtud de que los desdoblamientos CH3 dan n+1 = 3+1 = 4 picos con intensidades 1:3:3:1 mientras que los desdoblamientos CH2 dan un desdoblamiento adicional en n+1 = 2+1 = 3 picos con intensidades 1:2:1 resultando en 3(4) = 12 picos en total cuyas intensidades calculamos de la siguiente manera:
Hay 4 picos con una intensidad relativa de 1, 4 picos con una intensidad relativa de 3, 2 picos con una intensidad relativa de 2, y 2 picos con una intensidad relativa de 6, lo cual concuerda con los datos proporcionados, confirmando que la fórmula estructural propuesta es la que corresponde a las intensidades experimentales proporcionadas.
PROBLEMA: Dibújese el espectro RSE que podemos esperar para el siguiente radical etil para el cual se han determinado los desdoblamientos hiperfinos que se indican:
Este problema deriva esencialmente del problema anterior, excepto que aquí contamos ya con las magnitudes de los desdoblamientos hiperfinos que nos permiten construír el espectrograma RSE. El CH2 que consta de dos protones (H) equivalentes desdobla la línea de resonancia del electrón no apareado en 3 líneas separadas 2.238×10-3 Tesla con intensidades 1:2:1. Y a su vez, el CH3 que consta de tres protones (H) equivalentes desdobla cada una de estas tres líneas en 4 líneas con intensidades 1:3:3:1 separadas 2.687×10-3 Tesla. Podemos empezar a construír el espectrograma RSE indicando sobre una línea horizontal graduada las líneas del primer desdoblamiento separadas 2.238×10-3 Tesla (los números en color magenta indican las intensidades relativas):
Cada una de estas tres líneas es desdoblada a su vez en cuatro líneas con intensidades relativas 1:3:3:1 y separadas 2.687×10-3 Tesla, como la línea de la derecha (en color verde en el diagrama de arriba):
En el caso de la línea azul (la intermedia), el desdoblamiento será similar manteniéndose la misma separación entre los picos de resonancia (la figura muestra las áreas o intensidades relativas redimensionadas en sus alturas para mantener las proporciones obtenidas previamente de manera tal que la menor intensidad tenga un valor relativo igual a la unidad y todos los demás picos sean múltiplos de dicho valor):
El caso del desdoblamiento de la línea roja (la de la izquierda) es idéntico al de la línea verde, con las mismas proporciones. Usando papel graduado y manteniendo las proporciones, o bien superimponiendo los tres desdoblamientos finales (rojo, azul y verde) en una sola figura, se puede obtener de este modo en forma muy aproximada el aspecto que mostrará el espectro RSE de un radical como el analizado en este problema:
Se ha logrado determinar que el acoplamiento hiperfino entre el protón y el electrón dentro de un mismo átomo de hidrógeno es de 0.0507 Teslas. Este acoplamiento (debido principalmente a la interacción de contacto propuesta por Fermi, ya discutida anteriormente) es proporcional a la probabilidad de encontrar al electrón 1s en el núcleo del átomo (y al decir en el núcleo del átomo, estamos diciendo claramente dentro del núcleo del átomo, lo cual puede asombrar a quienes siempre se imaginaron al electrón como una partícula situada en el exterior del núcleo atómico como lo propone los modelos atómicos de Rutherford y de Bohr; recuérdese que el único lugar en donde la probabilidad de encontrar al electrón es exactamente igual a cero es en el centro geométrico del núcleo del átomo, en el punto r.=.0.)
PROBLEMA: Dibújese el espectro RSE de CD3· mostrando las intensidades relativas de las líneas que se pueden esperar para este radical.
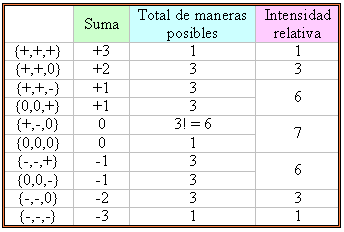
Obsérvese que en la fórmula proporcionada se ha substituído cada uno de los protones (H) por un átomo de deuterio (D), que no es más que el isótopo del hidrógeno pero con un neutrón agregado al núcleo del átomo. Esto significa que el spin del elemento insertado no será ya ±1/2 sino que podrá tomar cualquiera de tres valores posibles, -1, 0 y +1. Al igual que en el caso del radical metil o metilo CH3, podemos considerar a los deuterones en el radical magnéticamente equivalentes. Sin embargo, se vuelve necesario considerar las abundancias relativas de las combinaciones posibles de los spins en los tres deuterones. Esto no es muy diferente a los análisis estadísticos que llevamos a cabo para tres partículas distinguibles en la serie de entradas tituladas “Mecánica Estadística Cuántica”. Considérese por principío de cuentas la combinación en la cual los tres deuterones tiene spins tales que su suma dará 0. Esto no significa en lo absoluto que en el radical los spins de los núcleos se sumarán, siendo las partículas independientes y distinguibles, lo que se está haciendo aquí es únicamente para fines de poder determinar la abundancia estadística relativa de las combinaciones posibles de spins (se identificará por separado a uno de los deuterones como Da, a otro como Db, y al restante como Dc):
Procediendo de este modo, podemos construír la siguiente tabla que nos muestra las abundancias relativas de todas las combinaciones posibles:
De la cuarta columna en la tabla de arriba, podemos predecir de inmediato el número de líneas que podemos esperar obtener en el espectro RSE de CD3·, así como las intensidades relativas de las líneas:
A continuación se hará un bosquejo del esquema del funcionamiento básico de un espectrómetro de resonancia magnética, ya sea del tipo RMN o del tipo RSE:
Como nos lo muestra el dibujo esquemático, los componentes esenciales para llevar a cabo un análisis mediante resonancia magnética nuclear son: (1) un generador de ondas de radiofrecuencia (RF) las cuales son enviadas por un transmisor local y aplicadas a la muestra por una bobina, y (2) un campo magnético que sea lo más homogéneo posible. En su versión más básica, la señal de radiofrecuencia utilizada para estimular la muestra bajo observación es una señal que puede ser de 60 MHz o más en el espectógrafo RMN (los espectógrafos de mayor calidad ofrecen la capacidad de escoger entre otras frecuencias de operación disponibles), mientras que en el espectógrafo RSE se requieren frecuencias mucho más elevadas. Por varias razones como las ya citadas con anterioridad, es ventajoso usar campos magnéticos de la mayor intensidad posible, aunque hay grandes dificultades prácticas para obtener campos magnéticos por encima de los 7 Teslas que sean lo suficientemente estables y homogéneos para el trabajo de resonancia magnética de alta resolución. De hecho, con mucha frecuencia el factor limitante en la espectroscopía RMN de alta resolución es la inhomogeneidad del campo magnético. Puesto que en el caso de la espectroscopía RMN, los desplazamientos químicos δ están en el rango de las partes por millón (p.p.m.), el campo magnético tiene que ser constante a una parte entre 108 ó 109. La frecuencia fija de la señal de radiofrecuencia es controlada mediante cristales de cuarzo (los mismos que se utilizan en los relojes digitales) que dan una estabilidad a una parte en 109. La dirección del campo magnético constante B0 (el eje del electroimán) es tomada como el eje-z en torno al cual se lleva a cabo la precesión de los spins de los núcleos. Las transiciones entre las orientaciones posibles de un spin nuclear son producidas sometiendo a la muestra a ondas de radio a una frecuencia constante que son transmitidas por una bobina alrededor de la muestra con su eje perpendicular a la dirección-z. Es importante que el componente del campo magnético de la señal de radiofrecuencia (recuérdese que de acuerdo a la teoría electromagnética clásica toda señal electromagnética oscilante consta de un campo eléctrico oscilante y un campo magnético oscilante a la misma frecuencia) esté orientado en forma perpendicular al eje-z para poder obtener los efectos deseados, lo cual no es difícil de lograr ya que la bobina RF actúa como una pequeña antena transmisora que envía una señal polarizada de radiofrecuencia. El eje de la bobina transmisora es el eje-x, mientras que el eje de la bobina receptora es el eje-y, que es el eje del tubo que contiene la muestra del material bajo análisis. Cuando la señal de radiofrecuencia y la intensidad del campo magnético corresponden a una resonancia para cierto conjunto de núcleos, se absorbe energía de la bobina transmisora (al igual que como ocurre cuando sintonizamos un canal de televisión). Esta energía es radiada por los núcleos que están en precesión y captada por la bobina detectora que está orientada de modo tal (perpendicularmente) que no tome energía de la bobina transmisora.
Si nuestra tarea consiste en explicarle a un laboratorista la manera en la cual funciona un espectrómetro de resonancia magnética, seguramente empezaríamos por explicarle como ya lo hemos visto que el funcionamiento está basado en el hecho de que al ser aplicado un campo magnético uniforme el spin del protón, considerado como un pequeño electroimán, no puede alinearse jamás con el campo magnético que está siendo aplicado, lo cual significa que, al estar girando el protón en torno a su propio eje de simetría, el cual no se puede alinear con el eje de simetría del campo magnético aplicado (digamos, un campo magnético vertical), entonces hará lo mismo que lo que hace un trompo en el suelo que no está en una posición perfectamente vertical: llevará a cabo un movimiento de precesión giratorio en torno al eje vertical, producido sobre el trompo giratorio por el torque o momento de la gravedad de la tierra actuando sobre el centro de masa del trompo. Y así como la velocidad a la cual gira el trompo en torno a la vertical depende de la fuerza de la gravedad de la Tierra, en el caso del átomo la frecuencia de precesión en torno a la vertical dependerá de la magnitud del campo magnético aplicado. Esto significa que, si aplicamos a una muestra pura de material un campo magnético uniforme, cada uno de los átomos entrará en un movimiento de precesión a una frecuencia angular fija. Y si le aplicamos una señal de radiofrecuencia a la muestra cuya frecuencia sea muy cercana o igual a la frecuencia de precesión del “trompo atómico” poniendo ambas frecuencias en resonancia (así como ocurre cuando sintonizamos un canal de televisión o un canal de radio), entonces podremos esperar ver una caída en la potencia de la señal de radiofrecuencia que está siendo radiada hacia la muestra en virtud de la interacción energética causada por el efecto de la resonancia. Nuestra explicación al laboratorista continuaría señalando que aunque estamos acostumbrados a variar con una perilla la frecuencia del receptor de señales de radio AM/FM para poder “sintonizar” hacia una transmisora en particular que está radiando a la misma frecuencia a la cual estamos sintonizando, en la práctica en vez de aplicar un campo magnético uniforme y constante a la muestra de material variando la frecuencia de la radioseñal aplicada hacemos precisamente lo contrario, esto es, enviamos a la muestra una señal a una radiofrecuencia fija muy precisa, y lo que vamos variando es el campo magnético que le estamos aplicando a la muestra.
En realidad, el tarea dura no está en la operación de un espectógrafo de resonancia magnética, sino en la preparación del experimento y en la interpretación de los resultados.
Aunque están basados esencialmente en la misma explicación del mismo fenómeno cuántico pero aplicada a partículas diferentes, el espectrómetro RMN y el espectrómetro RSE operan en rangos de frecuencias muy distintas, ya que mientras que es posible echar a andar un espectrómetro RMN a una frecuencia relativamente modesta de 60 Megahertz (equiparable a las frecuencias a las que operan muchas estaciones de radio comerciales), el espectrómetro RSE requiere de frecuencias más elevadas, y si lo que se desea es obtener espectrogramas RSE de alta resolución, las frecuencias requeridas suelen ser aún mayores, superando el rango de los Gigahertz en el que operan los teléfonos celulares, como puede apreciarse en los siguientes dibujos de espectrogramas RSE de alta resolución sobre una misma muestra que contiene un radical nitróxido así como las frecuencias elevadas a las cuales se tiene que recurrir para poder obtener tales resoluciones:
La siguiente fotografía nos muestra un espectrómetro típico RSE de laboratorio en el cual podemos apreciar de manera sobresaliente el electroimán debajo de la mesa, entre cuyos polos se coloca la muestra a ser analizada:
Para llevar a cabo un análisis de resonancia magnética RSE en un entorno económico y rudimentario, a la vez que se mantiene fija la señal de radiofrecuencia se va variando gradualmente la intensidad del campo magnético moviendo alguna perilla con la cual se controla la corriente eléctrica que entra a la bobina del electroimán, aumentando el campo magnético hasta que vayan haciendo su aparición los picos de resonancia. Podemos equiparar esto con el proceso de sintonización de estaciones de radio “a la antigüita”, moviendo una perilla hasta que empezamos a captar una señal. En realidad, el concepto de “sintonización” es esencialmente el mismo tanto en la espectroscopía de resonancia magnética como en la búsqueda manual de estaciones de radio. Pero dado lo difícil que resulta llevar a cabo manualmente una variación constante del campo magnético del espectógrafo en forma tal que se mantenga un ascenso perfectamente lineal del campo magnético, la variación del campo magnético tiene que ser automatizada y puesta en manos de un “generador de barrido” de campo magnético que trabaje automáticamente, lo cual contribuye a que no hay dos espectrómetros de resonancia magnética iguales (ya sea de RMN o de RSE). Y a la necesidad de tener que agregarle a las muestras bajo análisis el estándard de calibración TMS usado como el punto de referencia cero para la ubicación de los desplazamientos químicos.
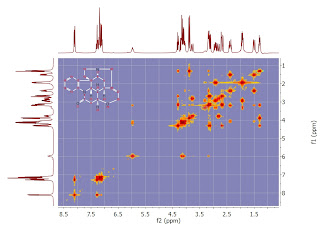
Si bien en sus inicios la espectroscopía RMN consistió en aplicar una sola señal de radiofrecuencia continua a una frecuencia fija, un avance significativo se logró cuando en vez de aplicarse una señal continua se optó por aplicar pulsos de radiofrecuencia con la frecuencia de los pulsos centrada a la mitad del espectro RMN accesible. Como bien sabemos, una tren periódico de pulsos puede ser construído mediante una suma grande armónicas de frecuencia utilizando los principios del análisis de Fourier. Esto equivale (matemáticamente) a aplicarle a la muestra una gama de radiofrecuencias en lugar de una sola centradas en torno a la frecuencia portadora, con el rango de excitación (conocido como el ancho de banda) siendo inversamente proporcional a la duración del pulso. Puesto que la transformada de Fourier de un tren de pulsos aproximadamente cuadrados contiene contribuciones de todas las frecuencias (armónicas) en torno a la frecuencia principal. El rango restringido de radiofrecuencias facilita el uso de pulsos de radiofrecuencia cortos (entre los milisegundos y los microsegundos) que son capaces de excitar el espectro RMN completo a la vez. Aplicando un pulso de señal en lugar de una onda continua a un conjunto de spins nucleares excita simultáneamente todas las transiciones cuánticas NMR. Este método, posibilitado gracias al desarrollo simultáneo de las técnicas matemáticas conocidas como la Transformada Rápida de Fourier (FFT, del Inglés Fast Fourier Transform) y la Transformada Discreta de Fourier (DFT, del Inglés Discrete Fourier Transform) desarrolladas por James Cooley y John Tukey así como el desarrollo de las computadoras digitales de alta velocidad y bajo costo, es conocido como Espectroscopía RMN por Transformada de Fourier, el cual fue concebido por Richard Ernst quien recibió el Premio Nóbel de Química por su descubrimiento. Ampliando el poder de dicha técnica mediante el uso de pulsos de señal de distintas formas, tamaños y duración, se logró llevar a cabo la espectroscopía RMN multidimensional, en la cual se utilizan por lo menos dos pulsos y el experimento es repetido al menos en una ocasión. En la espectroscopía RMN con Transformada de Fourier bi-dimensional (conocida como 2D FT), habrá una secuencia de pulsos y al menos un período de tiempo variable. En tres dimensiones, se variarán dos secuencias de tiempo, mientras que en cuatro dimensiones se variarán tres secuencias de tiempo. En todos estos experimentos el objetivo final es obtener un espectro de la muestra resultando en una serie de frecuencias y sus amplitudes relativas, sobre lo cual se puede aplicar un análisis de Fourier tomando en cuenta la naturaleza de los pulsos de señal utilizados para aplicarlos sobre la muestra. A continuación tenemos un ejemplo de un espectrograma RMN bi-dimensional llevado a cabo sobre una muestra de estricnina en base al procedimiento 2D FT (la imagen es una imagen de alta resolución, y puede ser amplificada sucesivamente para poder apreciar mejor los detalles del espectrograma así como la complejidad estructural de la molécula):
Hay otros tipos de espectroscopías RMN capaces de generar mapas bidimensionales como el que tenemos arriba, entre ellas la espectroscopía de correlación COSY (COrrelation SpectroscopY) y la espectroscopía de correlación total TOCSY. La espectroscopía por resonancia magnética no sólo puede ser mejorada mediante herramientas puramente teóricas como la transformada de Fourier y el procesamiento computacional de datos utilizado todo en conjunto para extraerle a los datos obtenidos la mayor información posible. También se puede recurrir a técnicas de construcción basadas en consideraciones teóricas para mejorar el equipo en sí. Una de tales técnicas es la espectroscopía de alta resolución MAS (HR-MAS spectroscopy), mejor conocida como la técnica magic angle spinning (MAS), utilizada con frecuencia para llevar a cabo experimentos en espectroscopías RMN no sobre muestras disueltas en algún solvente sino en muestras que están en estado sólido. Girando la muestra mecánicamente (por lo general a una frecuencia de 1 a 70 Hertz) estando situada al ángulo mágico θm de 54.74 grados (obtenido de la relación cos2θm.=.1/3) con respecto a la vertical que define la dirección del campo magnético aplicado a la muestra:
las líneas espectrales anchas se hacen más estrechas mejorándose la definición y la resolución de los datos obtenidos. Esto se debe a que la interacción nuclear dipolo-dipolo entre los momentos magnéticos de los núcleos (la causa principal del ensanchamiento de las líneas espectrales) se promedia a cero únicamente al ángulo mágico θm. En la siguiente figura podemos apreciar la mejora obtenida con respecto a varios alineamientos de la muestra en relación al ángulo mágico:
Los siguientes espectrogramas nos muestran comparativamente los resultados obtenidos sobre una muestra analizada mediante espectroscopía RMN convencional y espectroscopía mejorada con la incorporación de una giración de la muestra dada al ángulo mágico:
En las siguiente dos fotografías tenemos una (a) con el mecanismo rotor que se le agrega al espectrómetro para sostener la muestra bajo análisis, estando el rotor probador inclinado precisamente al ángulo mágico, mientras que la otra fotografía (b) nos muestra al rotor alineado verticalmente en la dirección del campo magnético (la variación del ángulo de inclinación le permite al laboratorista inclinar al rotor a ángulos diferentes con el objetivo de encontrar experimentalmente el ángulo mágico que dá los mejores resultados de resolución):
La espectroscopía por resonancia magnética es una rama científica tan enriquecida que su estudio requiere una actualización constante. La siguiente bitácora creada por la University of Ottawa de Canadá proporciona numerosos ejemplos y explicaciones sobre muchos de los tópicos que podemos esperar encontrar en esta ciencia de continuo crecimiento:
Las espectroscopías de resonancia magnética nos permiten entrar de lleno a lo que se conoce como la espectroscopía de moléculas poliatómicas. La resonancia magnética es un fenómeno de naturaleza eminentemente cuántica, no se le puede explicar de otra manera. Además de su enorme utilidad para la identificación de las fórmulas estructurales de los compuestos químicos propios de la química orgánica, su uso más extendido tal vez sea en el campo de la medicina en lo que comúnmente se conoce como la tomografía axial computarizada. Antes del advenimiento de la imagenología por resonancia (resonance imaging), lo único disponible para poder “ver” hacia el interior de un paciente sin recurrir a la cirugía era mediante el uso de los rayos-X, considerados de uso delicado y cuya exposición prolongada es considerada tan nociva para la salud como la exposición a materiales radioactivos. A diferencia de los rayos-X, los cuales son radiación ionizante (energía electromagnética con la suficiente intensidad para ionizar los materiales que van atravesando a su paso), la resonancia magnética nuclear proporciona un método no-invasivo que se puede aplicar cuantas veces se requiere sin tener que preocuparse por una exposición prolongada del paciente al tomógrafo, pudiéndose obtener en muchos casos imágenes de calidad superior y más detallada que la que puede obtenerse con los rayos-X convencionales que producen imágenes difusas que en el mejor de los casos requieren interpretación médica especializada. A continuación tenemos ejemplos de imágenes obtenidas con la ayuda de la resonancia magnética en el campo de la medicina clínica que hoy se conoce como MRI (Magnetic Resonance Imaging, cuya traducción al Castellano es Imagenología por Resonancia Magnética):
De este modo, la resonancia magnética con aplicaciones médicas convierte a la Mecánica Cuántica en un asunto de vida o muerte, hablando en el pleno sentido literal de la palabra, en algo con el potencial de poder ayudar a salvar muchas vidas gracias a las tomografías computarizadas que hoy son de uso común.
Con un poco de paciencia, es posible encontrar en Internet simulaciones interactivas dinámicas que pueden mostrar de manera un poco más amena el fenómeno de la Resonancia Magnética Nuclear así como la forma en la que trabaja la imagenología médica MRI, como la siguiente simulación dinámica interactiva presentada en la entrada suplementaria titulada “Recusos de software” que forma parte de esta obra: