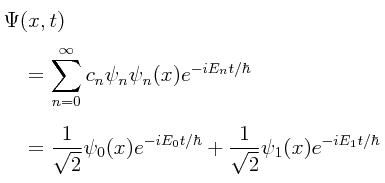Anteriormente en la entrada titulada “La ecuación de movimiento de Heisenberg” ya vimos cómo aunque el concepto Newtoniano de la fuerza no es empleado en lo absoluto dentro de la Mecánica Cuántica, ni en la Mecánica Matricial ni en la Mecánica Ondulatoria, aún así es posible definir un equivalente mecánico-cuántico de la segunda ley de Newton, conocido como el teorema de Ehrenfest, el cual generalmente es enunciado de la siguiente manera mediante la noción de las esperanzas matemáticas cuánticas:
habiéndose mencionado cómo con un poco de imaginación podemos reconocer el lado izquierdo como el equivalente de la fórmula Newtoniana masa×aceleración, y cómo también con un poco de imaginación podemos reconocer el lado derecho como el equivalente de la fuerza Newtoniana F al tomarse el negativo de la derivada de la energía potencial V con respecto a la posición como el equivalente de la fuerza clásica.
Puesto que el teorema de Ehrenfest que establece una equivalencia mecánico-cuántica de la segunda ley de Newton involucra de manera muy específica como parámetro libre a la variable del tiempo, anteriormente no habíamos tenido muchas oportunidades para comprobar la validez de dicho teorema al haber estado manejando estados “puros” como los de una partícula encerrada en una caja unidimensional en cuyos eigenvalores y eigenfunciones está notoriamente ausente la variable del tiempo. Sin embargo, en el tratamiento de estados mezclados en donde hay una superposición de estados, se tiene ya una variación temporal que puede ser analizada y estudiada, la cual a su vez tendrá consecuencias medibles en el laboratorio. Y para una investigación preliminar de este asunto, algo que se presta admirablemente como punto de inicio es el caso del oscilador armónico simple tomándose una mezcla de sus dos primeros estados, el estado basal (n.=.0) y el primer estado excitado (n.=.1).
PROBLEMA: Considérese una partícula que está sometida a un potencial que corresponde al de un oscilador armónico simple y que tiene la siguiente función de onda inicial que consta del estado fundamental y el primer estado excitado:
en donde A es una constante. Encuéntrese primero el valor de dicha constante normalizando con ello a la función de onda Ψ(x,0). Tras esto, encuéntrese la función de onda generalizada Ψ(x,t) y escríbase una expresión para |Ψ(x,t)|2. Con esta información, calcúlese la esperanza matemática de la posición de la partícula y calcúlese una expresión para la esperanza matemática del momentum de la partícula. Usando los resultados obtenidos, determínese si este sistema físico obedece lo que especifica el teorema de Ehrenfest.
Recurriremos a la entrada titulada “Oscilador armónico simple: solución ondulatoria”, para tomar de allí las eigenfunciones de onda que corresponden al estado fundamental y al primer estado excitado del oscilador armónico simple. Para el estado fundamental la función de onda ψ0 es:
mientras que la función de onda ψ1 para el primer estado excitado es:
La condición de normalización impone el siguiente requerimiento:
Llevando a cabo la multiplicación de términos y borrando los “términos cruzados” en virtud de que las funciones de onda ψ0 y ψ1 son ortogonales, obtenemos por principio de cuentas la constante de normalización:
Puesto que el sistema está formado por la mezcla de dos estados discretos, la función general de onda Ψ(x,t) viene siendo:
El cuadrado de la función de onda se obtiene entonces multiplicando esta función de onda por su conjugado complejo Ψ(x,t)*:
Aquí podemos hacer una simplificación en los exponentes definiendo la siguiente frecuencia angular:
De este modo, se tiene para |Ψ(x,t)|:
Usando lo anterior, la esperanza matemática de la posición viene siendo entonces:
Podemos evaluar las primeras dos integrales en forma directa tal y como lo haremos con la tercera integral y la cuarta integral. Sin embargo, podemos simplificar un poco nuestra labor sabiendo de antemano que las primeras dos integrales serán iguales a cero en virtud de la siguiente condición que se puede demostrar que es válida para funciones de onda que son descritas con polinomios de Hermite como es el caso de las funciones de onda que corresponden al oscilador armónico simple:
Así nos viene quedando únicamente lo siguiente:
Puesto que tanto ψ0 como ψ1 no poseen términos imaginarios ni complejos, siendo ambas funciones de onda reales en todos sentidos, se tiene entonces que ψ0*.=.ψ0 y ψ1*.=.ψ1, lo cual a su vez implica que:
Entonces podemos factorizar el término común quedándonos con:
Esto se puede simplificar algebraicamente aún más del modo siguiente:
Tenemos que evaluar ahora la integral que se muestra dentro de los paréntesis cuadrados. Desarrollando:
La integral remanente es una integral definida muy conocida que aparece prácticamente en todas las tablas de integrales disponibles en el mercado, siendo ésta:
Substituyendo el valor de la integral en lo anterior, se tiene por lo tanto:
De este modo, la esperanza matemática para la posición de la partícula viene siendo:
Obsérvese que a diferencia de lo que se había obtenido previamente en la entrada “Oscilador armónico simple: solución ondulatoria” para la esperanza matemática de la posición de un oscilador armónico simple en un estado “puro” (el estado fundamental), un valor esperado de la posición situado en promedio todo el tiempo justo en el origen de las coordenadas, en este caso la esperanza matemática de la posición no es igual a cero sino que va variando sinusoidalmente con el tiempo. La oscilación tiene una amplitud igual a √ħ/2mω y una frecuencia angular de oscilación ω igual a (E1-E0)/ħ.
Podemos llevar a cabo un cálculo del valor esperado del momentum de la manera siguiente:
Por último, investigaremos qué tan bien concuerda lo que hemos obtenido dentro de lo que estipula el teorema de Ehrenfest. Para ello, tomaremos el potencial parabólico V(x) que describe el comportamiento del oscilador armónico simple:
y obteniendo de esta expresión la razón de cambio del potencial V(x) con respecto a la posición:
a continuación evaluaremos la esperanza matemática de ∂V/∂x usando para ello la definición cuántica del valor esperado para una cantidad cualesquiera:
A continuación evaluaremos la otra parte que requerimos para la verificación del cumplimiento del teorema de Ehrenfest:
Comprobamos así que, efectivamente, se cumple el teorema de Ehrenfest para el caso de una partícula modelada con los dos estados mezclados del oscilador armónico simple.
Se había señalado ya al final de la entrada anterior que si bien la obtención de la función de onda Ψ(x,t) a partir de Ψ(x,0) para el caso discreto en el cual se tienen estados ligados es un asunto relativamente fácil, conceptualmente hablando, en contraste y en lo que compete al caso continuo como el que corresponde a las partículas libres los procedimientos que hemos estado empleando aquí resultan insuficientes, siendo necesario recurrir a otro tipo de estrategia para poder manejar el caso continuo. El procedimiento más metódico y directo consiste en tomar primero a la función de onda Ψ(x,0) que es una función de onda en el espacio posición y aplicarle una transformada de Fourier a dicha función de onda para expresarla en el espacio momentum, o sea el espacio-k:
Tras esto, tomamos la función de onda φ(k) y volvemos a aplicar una transformada de Fourier (o mejor dicho, la transformada inversa de Fourier) para regresar al espacio posición, en donde tendremos ya a la función de onda Ψ(x,t):
Una pregunta interesante que podemos formularnos relacionada con la evolución temporal de las ondas de materia es la manera en la cual se pueda verificar en un fenómeno de este tipo el cumplimiento del principio de incertidumbre de Heisenberg. Para ello, podemos usar algunas de las expresiones y conclusiones obtenidas previamente relacionadas con el principio de incertidumbre (véase la entrada “El principio de incertidumbre, revisitado”). Una de ellas es la relación:
Escogiendo la observable física Q.=.x, se tiene con ello:
Nuevamente, suponiendo que se tiene una partícula encerrada en una caja (o lo que es lo mismo, en un pozo de potencial con paredes infinitamente altas) cuya función de onda inicial sea la mezcla de los primeros dos estados estacionarios:
Metiendo en esto la constante de normalización en su forma explícita y reemplazando las eigenfunciones de onda por lo que corresponde a los primeros dos estados estacionarios de una partícula encerrada en una caja, se tiene para un tiempo t cualesquiera lo siguiente:
Aplicando repetidamente el operador Hamiltoniano H de energía en ambos lados (o sea, como H2), se tiene:
Ahora bien, por la ecuación de Schrödinger, se sabe que:
Del mismo modo:
El valor esperado (esperanza matemática) del cuadrado del Hamiltoniano es:
Lo último nos resulta en cuatro productos bra-ket, que se pueden simplificar moviendo los exponenciales de los bras hacia el lado de los kets (recuérdese que al efectuar esta operación se tiene que ejecutar el conjugado complejo) teniéndose entonces:
Por la ortonormalidad en los productos bra-ket, el segundo término y el tercer término se desvanecen, y lo que nos queda es, aplicando nuevamente la ortonormalidad:
Resulta más fácil aún comprobar que el valor esperado (esperanza matemática) del Hamiltoniano es:
De este modo, la incertidumbre en la energía se viene obteniendo de la siguiente manera:
con lo cual:
Falta por determinar σx para lo cual tenemos que determinar primero la esperanza matemática del cuadrado de x procediendo en una forma parecida (aunque no igual) a como lo hicimos arriba:
Desafortunadamente, en este caso no podemos usar la ortonormalidad para llevar a cabo simplificaciones como las que se llevaron a cabo un poco más arriba, y hay que proceder a llevar a cabo integraciones, para lo cual se requiere recurrir a las eigenfunciones de onda que corresponden a la partícula encerrada en una caja:
De este modo:
Recurriendo a la identidad trigonométrica que relaciona el producto de dos funciones senoidales, se tiene:
Se tienen hasta este punto dos integrales. Para desarrollarlas, obsérvese lo siguiente:
siendo k un entero diferente de cero. De este modo:
Por lo tanto, usando el resultado obtenido:
Hemos visto ya al llevar a cabo nuestros estudios sobre la partícula encerrada en una caja que para un cierto eigenestado la esperanza del cuadrado de la posición es:
Para los primeros dos eigenestados n.=.1 y n.=.2, se tiene:
Por lo tanto, juntándolo todo:
Podemos simplificar esto un poco más notando, con la ayuda de la fórmula de Euler, que:
Además:
Por lo tanto:
Esta es la esperanza matemática para el cuadrado de la observable posición, obviamente dependiente del tiempo al tratarse de estados mezclados. Para evaluar la dispersión estadística σx en la variable posición, necesitamos además la esperanza matemática de la observable posición que para la partícula encerrada en una caja ya ha sido obtenido en una entrada previa como:
De este modo, desarrollando y simplificando:
Estamos en condiciones de poder evaluar σ2H.σ2x, lo cual se lleva a cabo en forma directa con lo que tenemos a la mano:
Desarrollando y simplificando, llegamos a:
Puesto que queremos evaluar la validez de:
o lo que es lo mismo:
entonces, teniendo ya evaluado el lado izquierdo de la igualdad-desigualdad, procedemos a evaluar el lado derecho de la igualdad-desigualdad. Para ello, de lo que se ha obtenido para la variación de la esperanza matemática de la observable posición en lo que toca a los dos primeros eigen-estados mezclados de la partícula encerrada en una caja, se sabe ya que:
Usando lo siguiente:
se puede escribir entonces:
Haciendo caso omiso del factor (aħω)2 común a ambos lados de la igualdad-desigualdad, podemos ver que lo que se tiene que demostrar es que la relación:
debe ser mayor o igual en todo momento a la relación:
Explícitamente:
Para continuar con la simplificación de esto último, podemos despejar el término trigonométrico del lado izquierdo hacia el lado derecho:
De este modo, al final todo se reduce a la evaluación numérica del lado izquierdo y del lado derecho. Haciendo tal cosa, se tiene:
Esto último es evidentemente cierto, aplicándose el símbolo de desigualdad, ya que 0.2066818 es mayor que 0.1297822.
Hemos comprobado con este último ejemplo que el principio de incertidumbre se sigue sosteniendo en un sistema cuántico que evoluciona con el tiempo. De hecho, no ha sido posible encontrar hasta la fecha un solo ejemplo o un solo caso de un sistema cuántico que evolucione en el tiempo en el cual el principio de incertidumbre pierda su validez en algún momento, lo cual permite considerar a dicho principio como una ley de carácter universal.
Nota Bene: La columna izquierda en ésta página Web solo muestra los primeros 93 capitulos de ésta obra. La lista completa de enlaces hacia todos los capítulos de los que consta la obra se encuentra disponible por orden numérico en la primera entrada titulada "Indice"
Seguidores
Archivo del blog
-
▼
2009
(152)
-
▼
agosto
(152)
- Indice
- Prólogo
- El modelo atómico planetario de Bohr I
- El modelo atómico planetario de Bohr II
- La espectroscopía de rayos-X
- La extraña ecuación de Max Born
- Vectores y matrices I
- Vectores y matrices II
- El análisis de Fourier
- La regla de multiplicación de Heisenberg
- Observables compatibles e incompatibles
- Oscilador armónico simple: solución matricial
- Matrices y probabilidad
- El principio de incertidumbre I
- El principio de incertidumbre II
- El experimento Stern-Gerlach
- El spin del electron
- Momento angular: tratamiento matricial I
- Momento angular: tratamiento matricial II
- Momento angular: tratamiento matricial III
- La energía rotacional
- Matrices y sub-matrices
- Solución matricial del átomo de hidrógeno
- Funciones matriciales
- De la mecánica clásica a la mecánica matricial
- La matriz momentum como generadora de traslación
- La matriz generadora de rotación
- Rotaciones de las matrices de Pauli
- El aspecto estadístico de la Mecánica Matricial
- Evolución temporal de los sistemas físicos
- Matrices continuas
- Ondas de materia
- La ecuación de Schrödinger
- Solución matemática de la ecuación de onda
- Solución numérica de la ecuacion de Schrödinger
- Interpretación probabilista de ψ I
- Interpretación probabilista de ψ II
- Interpretación probabilista de Ψ III
- Operadores y esperanzas matemáticas I
- Operadores y esperanzas matemáticas II
- Oscilador armónico simple: solución ondulatoria
- La función delta de Dirac
- Transmisión y reflexión de partículas I
- Transmisión y reflexión de partículas II
- Transmisión y reflexión de partículas III
- Transmisión y reflexión de partículas IV
- El potencial delta de Dirac
- Ondas de simetría circular y esférica
- La notación bra-ket de Dirac
- El espacio de Hilbert I
- El espacio de Hilbert II
- Operadores Hermitianos
- Los operadores escalera I
- Los operadores escalera II
- El principio de incertidumbre, revisitado
- El acto de medición
- Momento angular orbital: análisis ondulatorio I
- Momento angular orbital: análisis ondulatorio II
- Momento angular orbital: funciones de onda I
- Momento angular orbital: funciones de onda II
- Polinomios de Legendre: aspectos matemáticos
- La función de onda radial
- La función de onda del momento angular del spin
- El principio de exclusión de Pauli
- El proceso de construcción Aufbau
- El acoplamiento LS
- La suma de momentos angulares
- Las reglas de selección
- Técnicas de aproximación I
- Técnicas de aproximación II
- Técnicas de aproximación III
- Técnicas de aproximación IV
- Perturbacion y estados degenerados I
- Perturbacion y estados degenerados II
- Modelos perturbativos para átomos hidrogenoides
- El efecto Stark I
- El efecto Stark II
- Corrección perturbativa relativista
- La estructura fina del hidrógeno
- Perturbaciones dependientes del tiempo I
- Perturbaciones dependientes del tiempo II
- Perturbaciones dependientes del tiempo III
- Interacción con un campo electro-magnético I
- Interacción con un campo electro-magnético II
- Interacción con un campo electro-magnético III
- El método de aproximación WKB I
- El método de aproximación WKB II
- El método de aproximación WKB III
- El método de aproximación WKB IV
- El enlace molecular I
- El enlace molecular II
- La hibridación de los orbitales atómicos
- La teoría de los orbitales moleculares
- Teoría del campo cristalino
- Operadores clase T
- El espacio-posición y el espacio-momentum I
- El espacio-posición y el espacio-momentum II
- El espacio-posición y el espacio-momentum III
- El espacio-posición y el espacio-momentum IV
- La partícula libre I
-
▼
agosto
(152)