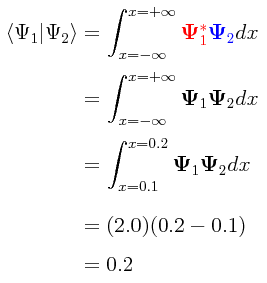en donde dr = dx·dy·dz representa un elemento infinitesimal de volumen (¡no es el diferencial de un vector!). Para poder hablar acerca de un flujo de probabilidad, tenemos que saber cómo varía con respecto al tiempo la probabilidad de encontrar a la partícula dentro de dicha región. Tomando la derivada con respecto al tiempo de la igualdad de arriba tenemos lo siguiente:
Metiendo la derivación con respecto al tiempo dentro del signo de la integral y aplicando la regla de la derivada del producto de dos funciones obtenemos:
La ecuación de Schrödinger para una región del espacio en la cual el potencial puede considerarse constante e igualado a cero es la siguiente:
Tomando el conjugado complejo de la ecuación de Schrödinger tenemos:
Despejando en ambos casos para la derivada con respecto al tiempo (obsérvese que los números imaginarios i pasan como recíprocos 1/i, convirtiéndose en i/i² = -i):
Substituyendo esto en nuestra expresión para el flujo de probabilidad:
Simplificando un poco sacando las constantes fuera de la integral:
La integral que tenemos es una integral de volumen, llevándose a cabo sobre el volumen de la región de interés. Esta integral puede ser convertida en una integral de superficie mediante una identidad que nos viene del análisis vectorial (conocida a veces como el teorema de Green) que nos permite hacer la siguiente substitución para poder llevar a cabo la conversión:
La superficie en cuestión es la misma que la que encierra al volumen del que estamos hablando. Con esta identidad tenemos entonces:
Lo que tenemos a la derecha de la igualdad es el producto escalar (o producto punto) de dos “vectores”. Esto nos sugiere hacer la siguiente definición tentativa del concepto de un flujo de probabilidad (también conocido como corriente de densidad de probabilidad) de la siguiente manera (obsérvese que el flujo de probabilidad es una cantidad vectorial):
De este modo, con esta definición obtenemos la siguiente relación:
Esto último tiene una interpretación muy sencilla: la razón del cambio de la probabilidad de encontrar a una partícula dentro de una superficie A será igual al negativo del flujo total de probabilidad que está atravesando la superficie A que acota un volumen V. A este flujo de probabilidad contribuye cada elemento infinitesimal de flujo de probabilidad que pasa a través de cada elemento infinitesimal del área de que consta dicha superficie:
Si nos limitamos a trabajar en una sola dimensión (en lugar de tres dimensiones como lo hicimos arriba), al flujo de probabilidad S considerado no solo como una función de la posición sino también como una función del tiempo se le puede escribir de la siguiente manera (en esta definición se ha invertido el signo, aunque en los cálculos finales esto carece de relevancia):
Una aplicación de esta fórmula posiblemente aclare un poco más las cosas. Considérese un haz de partículas libres que pueda ser considerado como una onda de materia plana senoidal viajando en una sola dirección, expresable mediante la siguiente función de onda:
Entonces el flujo de probabilidad será:
De acuerdo al resultado obtenido, en este caso el flujo de probabilidad tiene lugar en el sentido positivo del eje-x.
La interpretación probabilista de la función de onda dada por Max Born es de aplicación general y es completamente válida en cualquier sistema de coordenadas, trátese de coordenadas rectangulares Cartesianas, coordenadas esféricas, en fin, cualquier tipo de coordenadas. Tómese a modo de ejemplo un sistema de coordenadas cilíndricas (ρ,φ,z).
Con la transformación apropiada de coordenadas, podemos expresar una función de onda Ψ(x,y,z) en coordenadas cilíndricas Ψ(ρ,φ,z). De acuerdo con el criterio de Born, la densidad de probabilidad de la función de onda está dada por el producto de la función de onda Ψ y el conjugado complejo de la misma Ψ* en cualquier sistema de coordenadas, estando en absoluta libertad de poder escoger el sistema de coordenadas que más nos convenga para la resolución de un problema. Es muy posible (aunque ello no está garantizado de antemano) que dada una función de onda Ψ(ρ,φ,z) en coordenadas cilíndricas la podamos escribir mediante la técnica matemática de separación de variables como el producto de una función de onda radial R(ρ) con una función de onda Φ(φ) y con una función de onda Z(z). Siendo así, podemos expresar la densidad de probabilidad de la función de onda (por unidad de volumen) de la siguiente manera:
Si lo que queremos es encontrar la probabilidad de encontrar una partícula con tal función de onda en cierta región del espacio cuando nuestro sistema de medición está basado en coordenadas cilíndricas, un volumen cilíndrico como el siguiente:
en tal caso tenemos que multiplicar la densidad de probabilidad de la función de onda por tal volumen expresado en coordenadas cilíndricas. Puesto que un elemento infinitesimal de línea expresado en coordenadas cilíndricas está dado por:
en donde los símbolos destacados en color azul representan vectores unitarios de base (ortogonales, a ángulos rectos entre sí) que fijan la dirección a cada componente en el sistema de coordenadas cilíndricas, entonces el elemento infinitesimal de volumen en coordenadas cilíndricas será:
De este modo, la probabilidad de encontrar a una partícula con una función de onda Ψ(ρ,φ,z) dentro de cierto volumen infinitesimal del espacio bajo consideración viene siendo:
en donde se ha destacado con color magenta el elemento infinitesimal de volumen dentro del cual queremos obtener la probabilidad de poder encontrar a la partícula. En cualquier caso, bajo cualquier sistema de coordenadas, la probabilidad de encontrar a una partícula dentro de cierto volumen se obtiene multiplicando la densidad de probabilidad por el elemento de volumen bajo consideración:
en cuyo caso la densidad de probabilidad tiene que ser una densidad de probabilidad por unidad de volumen (en problemas unidimensionales, se usará una densidad de probabilidad por unidad de longitud, y en problemas en dos dimensiones se usará una densidad de probabilidad por unidad de área).
PROBLEMA: En la mecánica clásica lo que importa son las diferencias de energía ΔE y no tanto el valor absoluto que se le pueda dar a cierto valor de energía. De este modo el nivel de referencia que se le dá a la energía potencial dentro de la mecánica clásica es arbitrario. ¿Cuáles son los efectos sobre la función de onda y sobre la energía de añadirle un potencial constante a la ecuación de Schrödinger?
Para conocer el efecto de añadirle un potencial constante V0 a la función potencial V = V(x) que aparece en la ecuación de Schrödinger, podemos empezar con la versión unidimensional de la misma:
y agregarle un potencial constante a dicha ecuación:
Despejando para ∂Ψ/∂t de esta ecuación tenemos entonces:
Tomando el conjugado complejo de esta última ecuación obtenemos la siguiente:
Si substituímos estas dos relaciones en la expresión para dP/dt:
obtenemos entonces:
Simplificando esto último llegamos a lo siguiente:
Obviamente, los últimos cuatro términos se cancelan entre sí por pares, quedándonos únicamente:
Pero usando nuevamente la ecuación de Schrödinger para pasar los términos que involucran a las segundas derivadas de la función de onda Ψ con respecto a la coordenada-x poniéndolo todo en función de términos que involucran a la primera derivada de Ψ con respecto al tiempo, obtenemos nuevamente el punto de partida original que tendríamos si no se le hubiese añadido potencial constante alguno a la ecuación de Schrödinger. Se concluye por lo tanto que agregarle a la ecuación de onda de Schrödinger un potencial constante V0 no produce efecto observable alguno en las variables dinámicas, al menos no algo que podamos detectar experimentalmente en el laboratorio, y por lo tanto no se producirá efecto alguno en la esperanza matemática de la energía que calculemos para un sistema basada en su función de onda. Sin embargo, la ecuación de onda en sí recogerá un factor de fase exp(iV0t/ħ) como consecuencia de agregarle el potencial constante V0 a la ecuación de Schrödinger. Para demostrarlo, supóngase una solución a la ecuación de onda con la forma:
de lo cual obtenemos lo siguiente tomando derivadas de Ψ con respecto a la coordenada-x y con respecto al tiempo:
Substituyendo estas expresiones en la ecuación de onda tenemos entonces:
El factor exp(iV0t/ħ) es común a todo los términos, con lo cual podemos simplemente borrarlo para llegar así a lo siguiente:
Invirtiendo los pasos que utilizamos para llegar a esto último tenemos la demostración formal de que agregarle un potencial V0 a la ecuación de onda de Schrödinger equivale a tanto como añadirle a la ecuación de onda un factor de fase eiφ con φ = V0t/ħ, sin consecuencias medibles en el laboratorio porque el valor calculado para una observable física (a través de su esperanza matemática) no puede depender en la convención de la fase.
PROBLEMA: Tomando la divergencia para el vector flujo de probabilidad S demostrar que:
Tomando la divergencia vectorial de S tenemos lo siguiente:
Podemos simplificar esto usando la siguiente identidad vectorial en donde φ es una función escalar y f es una función vectorial:
Tenemos entonces:
El segundo y el cuarto término se cancelan dejándonos:
Usando la ecuación de Schrödinger en su forma usual y en su forma conjugada compleja la expresión se nos reduce a:
Si en el resultado que acabamos de obtener reemplazamos el producto ψ*ψ por lo que realmente representa, la probabilidad P, obtenemos lo siguiente:
Esto último es mejor conocido dentro de la Mecánica Cuántica como la ecuación de continuidad, en similitud con su contraparte clásica que se escribe de igual manera.
PROBLEMA: Considérese la siguiente ecuación para una onda plana:
en donde p es el vector momentum y r es el vector posición (no confundir el número imaginario i con el vector unitario de base i usado para el eje-x en las coordenadas Cartesianas):
p = (px, py, pz) = ipx + jpy + kpz
r = (x,y,z) = ix + jy + kz
r = (x,y,z) = ix + jy + kz
Una ecuación de este tipo no puede ser normalizada, de modo tal que el cuadrado de la amplitud de la función de onda sólo puede representar la probabilidad de poder encontrar a la partícula en cierto punto en el espacio. La densidad de probabilidad en este caso es independiente de la posición. Una forma de visualizar la función de onda proporcionada es como un enjambre móvil de partículas con una densidad promedio de una partícula por centímetro cúbico. En este caso, las partículas se están moviendo con un momentum p y tienen una velocidad v = p/m. Con esta velocidad y con una densidad promedio de una partícula por centímetro cúbico, v partículas por segundo estarán pasando a través de una área superficial de un centímetro cuadrado perpendicular a la dirección de movimiento de las partículas:
Esto constituye el flujo de probabilidad de la onda. Obténgase el flujo de probabilidad para este caso.
El gradiente para la función de onda dada ψ es:
Tomando cada una de las derivadas parciales sobre el exponencial y simplificando un poco:
Esto lo podemos simplificar aún más escribiéndolo como:
Simplificando un poco más:
Tomaremos a continuación el conjugado complejo de ambos lados de esto último, lo cual requiere reemplazar i por -i:
Esto nos resulta en lo siguiente:
Con lo que hemos obtenido podemos calcular ya la corriente de densidad de probabilidad:
Puesto que el exponencial de cero es igual a la unidad, tenemos finalmente el siguiente resultado:
Esto último está en concordancia con el resultado clásico para la razón a la cual un flujo de partículas atraviesa un centímetro cuadrado de área superficial por unidad de tiempo bajo estas condiciones.
PROBLEMA: Demuéstrese que el flujo de probabilidad se puede escribir de la siguiente manera:
en donde “Im” representa la parte imaginaria de la función de onda.
Una función de onda siempre puede ser representada como una función compleja separada en una parte real (Re) y una parte imaginaria (Im):
Tomando el conjugado complejo:
Del mismo modo:
Con esto obtenemos:
Del mismo modo se tiene lo siguiente:
Removiendo los paréntesis y llevando a cabo los productos:
Comparando estos resultados y combinándolo todo tenemos entonces que:
puede ser escrito como:
Retomaremos ahora un asunto que había quedado pendiente en las entradas anteriores y cuya discusión había sido postpuesta hasta tener en claro la interpretación probabilista de la función de onda Ψ que hemos estado viendo aquí. Regresemos al caso de una partícula encerrada dentro de una caja efectuando un movimiento unidimensional, rebotando de una pared a otra, la cual puede tener una plétora de estados cuánticos empezando por el estado fundamental que corresponde a n.=.1. La solución de la ecuación de onda de Schrödinger para este tipo de problemas arroja soluciones de tipo senoidal o cosenoidal, según sea el caso. El hecho de que estamos hablando de ondas de materia sugiere que al encontrarse la onda de materia que representa a la partícula aprisionada dentro de la caja se está llevando a cabo una oscilación conforme avanza el tiempo, y se nos puede venir a la mente una imagen como la siguiente que correspondería al estado cuántico n.=.4:
Esta visualización dinámica es desbancada de inmediato con ayuda de la interpretación probabilista de Ψ. Para ello, fijémonos bien en los puntos de color rojo de la figura anterior, o sea los nodos de la onda, que permanecen estacionarios todo el tiempo. Supóngase que con la ayuda de una “cámara fotográfica cuántica” logramos tomar una serie de instantáneas como las que se muestran a continuación:
Empecemos por lo más fácil. La naturaleza del problema es tal que para una partícula que se encuentra en el estado cuántico n.=.4 el interior de la caja se encuentra dividido en tres regiones (podemos imaginar cada división de la caja como un plano perpendicular a la onda). En un punto en donde Ψ.=.0, la probabilidad Ψ2 de encontrar a la partícula en dicho punto es exactamente igual a cero. Teóricamente, la partícula no puede ser encontrada jamás en un nodo.
¿Entonces cómo puede pasar la partícula de la Región 1 a la Región 2 y de allí a la Región 3? La partícula en la Región 1 estaría atrapada “cuánticamente” en lo que viene siendo una tercera parte de toda la caja, sin posibilidad alguna de poder pasar de una región a otra, y por lo tanto ¡sería imposible para la partícula el poder estar rebotando de una pared a otra dentro de la caja para lo cual tendría que pasar por dos lugares en donde la probabilidad de encontrarla es igual a cero! La partícula estaría confinada por siempre en una tercera parte de la caja. Esto desde luego no es lo que ocurre en el laboratorio, ni se ha encontrado tal cosa jamás. ¿Entonces qué es lo que sucede? El problema radica en querer darle una realidad física a un concepto puramente geométrico, un nodo de la onda, como algo que ocupa una dimensión en el espacio, y la realidad es que el nodo teórico de la onda (que es esencialmente un punto geométrico) tiene una longitud igual a cero. No se trata de algo que sea de un espesor infinitamente pequeño, ya que un espesor infinitamente pequeño implicaría algo que de cualquier manera tiene un grosor. En la práctica, el nodo es tan solo un punto geométrico de referencia, y no podemos tratar de darle un espesor al punto geométrico que por definición carece de espesor alguno. La partícula por lo tanto puede pasar de una región a otra sin problemas, aunque al efectuar mediciones de laboratorio no esperamos encontrar a muchas partículas (en el caso de que sean muchas partículas submicroscópicas y no una sola en un solo estado cuántico) en los lugares que identificamos como los planos nodales.
La otra observación es que, si la onda de materia realmente estuviera oscilando, después de que cada cresta de la onda ha alcanzado su amplitud máxima entonces la onda emparía a disminuír de tamaño (como ocurre con cualquier fenómeno oscilatorio) hasta que como vemos en la cuarta figura al fondo de las cuatro fotografías “instantáneas” que se han ido tomando, la función de onda Ψ se encuentra esencialmente convertida momentáneamente en una línea recta. Y si aplicamos en ese momento la interpretación probabilista de Ψ, o sea Ψ2.=.0 por doquier, ¡esencialmente, la partícula ha desaparecido y en ese momento se ha desvanecido de nuestro Universo! ¿Realmente la partícula desaparece y desaparece mágicamente? Desde luego que no. La partícula no va desapareciendo a medida que la onda senoidal (o cosenoidal) va perdiendo su amplitud hasta desaparecer por completo, porque la amplitud de la función de onda Ψ permanece todo el tiempo fija en su valor máximo. No hay pues ninguna “oscilación” dinámica con el paso del tiempo. A estas alturas, el lector podría pensar: ¿acaso no hay una ecuación de Schrödinger dependiente del tiempo? Sí la hay, pero para que muestre sus efectos es necesario cambiar la naturaleza del experimento, por ejemplo variando dinámicamente la longitud interior de la caja, o metiendo una segunda partícula con lo cual su función de onda puede interactuar con la función de onda de la primera partícula. Todo depende del experimento que se esté llevando a cabo, pero lo importante es que hay que tener presente en todo momento la interpretación probabilista de la función de onda para poder predecir o anticipar lo que ocurrirá al llevarse a cabo cierto experimento.
Lo que se acaba de ver se puede interpretar como un enunciado absoluto que puede ser usado ventajosamente en la resolución de problemas de Mecánica Cuántica, y se puede enunciar formalmente del modo siguiente:
| En todo momento, dada una función de onda normalizada Ψ(x,t) para cierto estado cuántico n, la probabilidad total |Ψ|2total de encontrar a la partícula en algún lado debe ser igual a la unidad, o sea la certidumbre total, y si la función de onda es de naturaleza tal que varía con el tiempo, entonces aquellas secciones de Ψ que hayan disminuído en alguna región o regiones del espacio deben ser compensadas de inmediato y en forma automática con un aumento o aumentos en la intensidad |Ψ|2 de Ψ en otras regiones del espacio de modo tal que la probabilidad total de encontrar a la partícula en algún lado siga siendo igual a la unidad, o sea a la certidumbre total, en conformidad con el principio de conservación de la masa-energía. |
En el siguiente gráfico animado tenemos en la columna izquierda varias configuraciones de dos funciones de onda, una de color azul y la otra de color rosa, que forman parte de un mismo sistema y que están variando con el tiempo tanto en magnitud como en su signo, y puede apreciarse en los primeros dos renglones que la densidad de probabilidad Ψ2 permanece en todo momento sin variación alguna; mientras que en el tercer renglón aunque la densidad de probabilidad Ψ2 es tal que sí varía con el tiempo (véase el recuadro en la esquina inferior derecha), las “pérdidas” en amplitud de Ψ en ciertas regiones son compensadas de inmediato con “ganancias” en otras de modo tal que la densidad de probabilidad total del sistema a lo largo de todo el eje coordenado horizontal seguirá siendo igual a la unidad en todo momento confirmando que aunque la probabilidad de encontrar la partícula en cierta zona va cambiando con el tiempo, la probabilidad de encontrar a la partícula en alguna parte de todo el eje coordenado horizontal (medida por el área total bajo la curva) es igual a la unidad, o sea a la certeza:
Pasaremos ahora a un tema de la mayor importancia. Trabajando en una sola dimensión, supóngase que se tienen dos funciones de onda φ y ψ normalizadas:
¿Qué interpretación podríamos darle entonces a algo como lo siguiente?
Podemos visualizar el traslape de ambas funciones de onda de la siguiente manera:
Como parece sugerirlo la figura de arriba, el traslape de las dos funciones de onda, representada por el área blanca que ambas funciones de onda tienen en común, representa la probabilidad conjunta de ambas funciones de onda. Esto es una consecuencia directa de las leyes de la probabilidad. Obviamente, a menos de que ambas funciones de onda φ y ψ sean iguales, esto es, φ.=.ψ, esta probabilidad conjunta será inferior a la unidad. La probabilidad representada por el traslape dependerá de qué tanto estén traslapadas ambas funciones de onda. Esta probabilidad conjunta tiene una importancia tan crucial dentro de la Mecánica Cuántica, que es frecuente emplear una notación para simbolizar el traslape (este tipo de notación lo estudiaremos más a fondo en la entrada “La notación bra-ket de Dirac”):
Considérese la siguiente función de onda Ψ1 para una partícula, función de onda que aunque ficticia nos puede ilustrar el concepto que queremos dejar en claro.
Esta función de onda ya se encuentra normalizada bajo el sistema de unidades que está siendo empleado en la figura, cumpliendo con el criterio esencial de normalización:
Obsérvese en la figura que se ha dado arriba que lo que se ha graficado es en realidad Ψ12 y no simplemente la función de onda Ψ1, con lo cual se está graficando realmente la densidad de probabilidad de la partícula a la largo del eje-x.
Supóngase ahora que se tiene otra función de onda posible Ψ1 para la misma partícula, cuya densidad de probabilidad es ligeramente diferente a lo largo del eje-x:
Esta es una función de onda que también se encuentra normalizada, como podemos verificarlo de inmediato:
Supóngase ahora que ambas funciones de onda Ψ1 y Ψ2 pueden coexistir a lo largo de la coordenada x, separadas entre sí mediante cierta distancia que impide que haya un traslape entre dichas funciones:
La pregunta que nos hacemos ahora es: ¿cómo puede pasar una partícula espontáneamente del estado del estado Ψ1 al estado Ψ2 o viceversa? La respuesta es: no puede, al menos no sin la presencia de algún estímulo exterior, porque no hay traslape alguno entre ambas funciones de onda, y la probabilidad de que la partícula se pueda encontrar entre ellas, o sea en el espacio comprendido entre la posición x.=.0.2 y x.=.0,5 es igual a cero.
Sin embargo, si ambas funciones de onda Ψ1 y Ψ2 están traslapadas como se muestra en la siguiente figura:
entonces el área común a ambas (de color café obscuro) es una región en la cual la partícula puede pertenecer al mismo tiempo a ambas funciones de onda, y a través del área común puede moverse a una posición en la cual no hay traslape alguno (como el área entre x.=.0.2 y x.=.0.6). Y de hecho, podemos determinar la probabilidad de que la partícula se pueda encontrar en el área común a ambas funciones de onda, mediante el área en donde están traslapadas, recurriendo a la prescripción con la cual se evalúa el área común conjunta a ambas funciones de onda:
Sin embargo, el traslape de dos funciones de onda distintas nos proporciona simplemente lo que se conoce como la amplitud del traslape de las funciones de onda. Para obtener la probabilidad proporcionada por dicho traslape, en concordancia con el criterio de Born, la probabilidad se obtiene mediante el cuadrado del traslape de las dos funciones de onda, o sea:
o más explícitamente, y resaltando la naturaleza tridimensional del cálculo:
De éste modo, la probabilidad de que una partícula se pueda mover espontáneamente de la región ocupada por la función de onda Ψ1 a la región ocupada por la función de onda Ψ2 o viceversa del estado del estado Ψ1 al estado Ψ2 en el ejemplo mostrado será igual a (0.2)2 o bien 4%. ¿Y qué es lo que determina el sentido del movimiento, o sea la dirección hacia la cual se moverá la partícula? Frecuentemente, las condiciones las impone la misma Naturaleza, específicamente el hecho de que todos los cuerpos buscan el estado de mayor estabilidad o de energía potencial mínima. En un átomo, esperamos que un electrón caiga espontáneamente de un estado excitado como la capa energética n.=.2 en el átomo de hidrógeno, hacia el estado basal n.=.1, emitiendo un fotón de luz en el proceso, y no al revés. Lo usual es que se requiera proporcionar un fotón de energía para sacar al átomo de su estado basal poniéndolo en un estado excitado.
El área común a ambas funciones de onda está resaltada en color rosa. Esta es el área que “conecta” ambas funciones de onda y a través de la cual una partícula que se encuentra en el estado Ψ1 puede pasar al estado Ψ2 o viceversa, ¿Y cómo habremos de saber cuál de los dos estados representa el lugar en el que preferentemente estará situada la partícula? Para ello, requerimos de otra información adicional: el nivel energético asociado a cada estado. La naturaleza dicta que el comportamiento de toda partícula es tal que siempre se moverá de un estado de mayor nivel energético a un estado de menor nivel energético, de hecho el menor nivel energético posible. Con estos dos datos, se puede obtener todo lo que se puede saber, y de hecho todo lo que la Mecánica Cuántica nos permite saber.
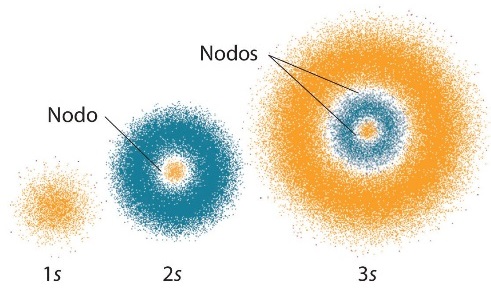
Lo anterior aclara una duda que de vez en cuando suelen tener quienes apenas están iniciando sus estudios en la Mecánica Ondulatoria, relacionada con los orbitales esféricos del modelo atómico planetario de Bohr situados en capas colindantes. Para cada número cuántico principal n del modelo atómico planetario de Bohr, se puede concebir una nube electrónica o nube de probabilidad esencialmente esférica, identificadas sucesivamente como 1s, 2s, 3s y así sucesivamente, Y entre cada nube de probabilidad, debe de haber una capa esférica nodal en donde la probabilidad de encontrar un electrón es igual a cero. A continuación tenemos un esquema que nos muestra las nubes de probabilidad para los estados 1s, 2s y 3s de un átomo de hidrógeno, indicando los nodos en donde la función de onda para el átomo de hidrógeno tiene un valor exactamente igual a cero:
A continuación se tiene otra ilustración de los contornos de probabilidad en donde podemos ver con mayor claridad la presencia de las capas esféricas nodales:
¿Entonces cómo puede brincar un electrón de una capa a otra, digamos de la capa n.=.2 a la capa n.=.1, al caer el electrón de un nivel energético superior a un nivel energético inferior, emitiendo además un fotón luminoso en el proceso, si no puede existir en una capa nodal en donde la probabilidad de encontrarlo es cero?
En primer lugar, aunque sí podemos hablar de una capa nodal esférica en donde la función de onda tendrá un valor igual a cero, tal capa nodal en principio tiene un espesor igual a cero, y no sería imposible para una partícula atravesar algo con un espesor igual a cero aunque en dicha capa la partícula teóricamente no pueda existir. Pero de cualquier modo resulta que, al estudiar las funciones de onda del átomo de hidrógeno en mayor detalle, las funciones de onda que corresponden a los estados 1s, 2s, 3s y otros semejantes para el átomo de hidrógeno se traslapan. Estas son las funciones de onda para estos primeros tres estados cuánticos:
Podemos observar claramente el traslape del cual estamos hablando, las tres funciones de onda están traslapadas, de modo tal que siempre hay un área en común y es posible para el electrón saltar de una capa a otra tal y como lo predice el modelo atómico planetario de Bohr.
La siguiente figura nos muestra con mayor claridad varios de los traslapes que se dan entre funciones de onda propios del átomo de hidrógeno:
Muchos fenómenos físicos que ocurren a niveles sub-microscópicos dependen precisamente de que haya este tipo de traslapes. Supóngase, por ejemplo, que se tienen dos partículas atrapadas en cajas separadas, siendo ambas cajas de las mismas dimensiones (con una distancia L de pared a pared), habiendo una partícula en cada caja que llamaremos A y B respectivamente. Si ponemos las dos cajas en proximidad cercana, una a un lado de otra, cabe preguntarnos: ¿qué probabilidad hay de que una partícula “salte” de una caja a otra? Si las paredes de ambas cajas son impenetrables (lo cual equivale a considerar cada partícula como situada en un pozo de potencial cuyas paredes son infinitamente altas), entonces aunque los espacios huecos de ambas cajas estén separados el uno del otro por unos cuantos milímetros la probabilidad de que una partícula se pase de una caja a otra es cero. Tal “brinco” no puede ser efectuado porque las paredes de ambas cajas son impenetrables, lo cual a su vez implica que las funciones de onda ψA y ψB de cada partícula no tienen ningún “traslape” en común:
Si queremos que haya una probabilidad así sea mínima de que una partícula pueda saltar del interior de una caja al interior de la otra es necesario que la pared que separa ambos interiores deje de ser impenetrable, es necesario que la barrera de potencial que separa ambas cajas deje de ser una barrera de altura infinita para ser una barrera de altura finita:
De este modo, inclusive aún si la energía de una partícula es inferior a la altura de la barrera finita de potencial que separa ambas cavidades, una partícula puede efectuar un tunelaje de una cavidad a otra (atravesando la barrera de potencial de altura finita), por el simple hecho de que ambas cavidades están interconectadas, lo cual implica que hay un traslape entre las funciones de onda que corresponden a una partícula ubicada en cada cavidad.
Aún tratándose de una sola partícula atrapada dentro de una caja, esto es, una partícula solitaria atrapada entre dos paredes de potencial infinitamente altas, para que haya una probabilidad de que una partícula pueda “saltar” de un nivel energético inferior a un nivel energético superior al suministrar una energía externa (por ejemplo, mediante un fotón luminoso), para que tal salto pueda ocurrir, es indispensable que entre el eigenestado que corresponde a cierta función de onda (por ejemplo, la función de onda ψ2 que corresponde al estado n.=.2) y el eigenestado hacia el cual queremos excitar a la partícula (por ejemplo, el estado que corresponde la función de onda ψ15 que a su vez corresponde al estado n.=.15), es indispensable que haya un traslape entre ambas funciones de onda (en este caso, un traslape entre ψ2 y ψ15) para que tal salto pueda tener lugar. Del mismo modo, para que una partícula pueda caer desde un nivel energético superior hacia un nivel energético inferior (emitiendo un fotón de energía luminosa) es también necesario que haya un traslape entre ambas eigenfunciones de onda. Esto implica que el fenómeno de las radiaciones originadas por fenomenología sub-atómica depende directamente del traslape de funciones de onda. Y la Mecánica Ondulatoria nos permite calcular en forma cuantitativa la probabilidad en cada caso. Estas probabilidades se reflejan a su vez en las intensidades relativas de las líneas espectrales obtenidas en los espectrogramas, se trata de cosas que podemos medir directamente en el laboratorio. De este modo, la interpretación probabilista de la función de onda es lo que le da aplicabilidad a la Mecánica Cuántica, es lo que nos permite sacar los conceptos del pizarrón hacia el mundo real.