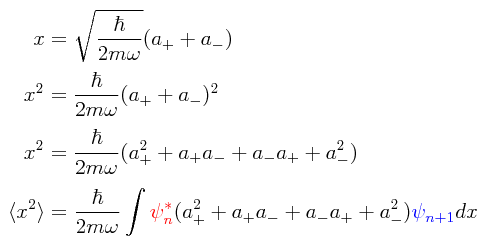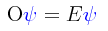Antes de entrar a fondo en algunos de los detalles de los estados Glauber, resulta instructivo atisbar de manera intuitiva aquello de lo que estamos hablando, y nada mejor que un simulador de estados Glauber para captar la esencia del tema, la mayoría de los cuales toma como punto de partida al oscilador armónico simple.
Hay disponibles en la Web varios simuladores dinámicos de lo que sucede en un oscilador armónico simple en el cual se tienen estados coherentes. Uno de tales simuladores fue diseñado en la Universidad de Bergen, la misma universidad en la cual se diseñó el simulador de la regla de oro de Fermi discutido en la entrada “Perturbaciones dependientes del tiempo II” que forma parte de ésta obra. El simulador de estados coherentes de la Universidad de Bergen, apoyado en la versatilidad de los applets del lenguaje Java (un lenguaje de programación que es compatible con la mayoría de los navegadores Web hoy en día), nos presenta un pozo de potencial parabólico del tipo V.=.ax2 en el cual se superponen hasta diez de los niveles de energía cuantizados que corresponden al oscilador armónico simple así como los cuadrados de las funciones de onda que corresponden a la probabilidad de encontrar a la partícula en alguna posición horizontal en alguno de los diez estados. Estos niveles de energía son seleccionados desde el teclado de la computadora mediante los botones “deslizantes” que se pueden mover hacia arriba (hasta llegar a la posición máxima en donde la barra vertical está completamente llena) y hacia abajo (en donde la barra vertical que indica la intensidad energética no indica nada):
Obsérvese que cada estado tiene en el lado izquierdo una etiqueta de texto con la leyenda que dice “Single state”. Podemos seleccionar un estado “puro” haciendo click en el número que corresponde al estado deseado y que está debajo de los botones deslizantes. Cada uno de éstos estados puros corresponde a cada una de las primeras diez funciones de onda del oscilador armónico. Las primeras cuatro funciones de onda para el oscilador armónico simple son las siguientes:
Lo interesante ocurre no cuando tenemos estados “puros” del oscilador armónico simple cuántico como los que se muestran arriba en forma alternada en el gráfico animado, sino cuando mezclamos distintos estados como en el siguiente caso en el cual los botones deslizantes se han movido verticalmente para situarlos en la manera mostrada produciendo el comportamiento que se muestra para la partícula representada como una nube de probabilidad desplazándose de un lado a otro (obviamente, para obtener éste tipo de comportamiento hay que recurrir a la ecuación de Schrödinger dependiente del tiempo, aplicada en un sistema que tiene estados mezclados):
Obsérvese que la simulación tiene una etiqueta de texto en el borde izquierdo del simulador que dice “Glauber state”. Obsérvese también algo extraordinario. El comportamiento de la partícula es idéntico al de la partícula clásica que usualmente asociamos con la partícula que exhibe el comportamiento típico del oscilador armónico simple, que en éste caso es el que corresponde a una partícula con un nivel energético n.=.4. Compárese nuevamente éste comportamiento dinámico de la función de onda de la partícula emulando lo que ocurre en la física del mundo macroscópico con el panorama completamente estático que se obtiene de la ecuación de Schrödinger independiente del tiempo para el estado n.=.4 del oscilador armónico y que regula lo que sucede cuando no hay estados mezclados y por lo tanto no hay dinámica alguna a ser observada:
No todas las combinaciones posibles de distintos estados energéticos del oscilador armónico simple nos resultan en un estado Glauber. La siguiente combinación de los diez estados disponibles en el simulador nos resulta en una superposición de estados (obsérvese que la simulación muestra una etiqueta que dice “Superposition”) que no exhibe ningún comportamiento interesante cuando la simulación es puesta en movimiento con el comando “run” del simulador:
El comportamiento de un estado Glauber nos motiva a regresar a la simulación en la cual la función de onda de la partícula se comportaba igual que el de una partícula clásica ligada al oscilador armónico simple (unidimensional) para ver en qué combinación de intensidades fueron seleccionados cada uno de los estados participantes. No se requiere de mucha imaginación para darse cuenta de que la distribución de intensidades (amplitudes de los coeficientes asociados a cada eigenvalor) de cada nivel energético es la que corresponde a una curva normal Gaussiana, con el pico máximo de la curva Gaussiana ubicado precisamente en la parte que corresponde al nivel energético n.=.4.
La mezcla de estados (o bien combinación especial de funciones de onda) del oscilador armónico simple para producir un estado coherente, llamémosla función de onda Glauber, está determinada por el requerimiento de que los coeficientes cn usados para producir la combinación linear de funciones de onda conducentes a un estado coherente Glauber tengan una distribución normal (Gaussiana):
De éste modo, un estado Glauber estará descrito por una función de onda como la siguiente:
y la probabilidad Ψ2 de encontrar a la partícula en algún lugar del espacio de volumen infinitesimal dr conforme el tiempo va transcurriendo, comportándose la partícula en su desplazamiento como un paquete de onda Gaussiano moviéndose clásicamente, será:
Ésto es en esencia lo que nos muestra el simulador de estados coherentes de la Universidad de Bergen para el estado n.=.4. Hay desde luego un estado coherente que corresponde al número cuántico n.=.2, y otro estado coherente que corresponde al número cuántico n.=.25, y así por el estilo. Lo verdaderamente importante es que la mezcla de estados se tiene que llevar a cabo con los coeficientes usados en la combinación linear de funciones de base obedeciendo rigurosamente una distribución Gaussiana. Jugando un poco con el simulador, es posible acercarse algo al estado coherente que corresponde al nivel energético n.=.5 mediante la siguiente distribución de “alturas” en las barras del simulador, y echando a andar la simulación con la opción “run”:
Aunque el resultado que se obtenga con el simulador para n.=.5 no sea exactamente un estado coherente en el sentido formal y riguroso de la palabra, al echar a andar la simulación se encontrará que el desplazamiento horizontal de la partícula se acerca al comportamiento clásico de la partícula para el estado coherente n.=.4, con algo de distorsión en la función de onda conforme se mueve de un lugar a otro al no ser las “alturas” lo que deben ser para generar el estado coherente que corresponde a n.=.5. De cualquier modo (y afortunadamente) el simulador de estados coherentes de la Universidad de Bergen permite generar los coeficientes de amplitud exactos para obtener cualquiera de los estados coherentes del oscilador armónico simple con solo hacer click con el Mouse dentro de la región de color blanco de la curva de energía potencial V; el estado coherente producido dependerá de la altura dentro de la curva de energía potencial en donde se haga el click. Para n.=.1, por ejemplo, se genera lo siguiente (obsérvese que la etiqueta de texto indica no “Superposition” sino “Glauber State”):
mientras que si se selecciona n.=.9 en el simulador se obtiene lo siguiente (no se muestran en la figura del simulador las amplitudes de los otros estados contribuyentes a cada estado coherente como n.=.11, n.=.12, etcétera necesarios para producir el estado coherente, aunque se sobreentiende que tras bambalinas se les incorpora para poder obtener el comportamiento correcto del desplazamiento del paquete de onda Gaussiano):
Puesto que las amplitudes relativas de las funciones de onda que son mezcladas tienen que seguir estrictamente un patrón Gaussiano, parecería que producir estados coherentes en el laboratorio debería ser una cosa endiabladamente difícil. Sin embargo, no es así, porque la misma Naturaleza se encarga de optimizar las cosas, sobre todo tomando en cuenta que la distribución Gaussiana es precisamente la que minimiza el producto de incertidumbres (algo parecido a lo que ocurre con el principio de mínima acción con el cual la Naturaleza misma encarga de buscar la ruta mínima cuando hay varias rutas menos eficientes posibles). Ésto facilita las cosas, ya que de no ser así el hombre no habría podido producir el rayo láser.
Los estados coherentes no fueron descubiertos por Roy Glauber. Hay que ir atrás a los tiempos de Erwin Schrödinger, precisamente el descubridor de la ecuación de onda cuántica, quien fue el que los encontró por vez primera en 1926 como el primer ejemplo de lo que se considera la dinámica cuántica basada en la ecuación de onda dependiente del tiempo. Schrödinger obtuvo sus estados coherentes como paquetes de onda Gaussianos de “incertidumbre mínima” (mínima en el sentido de que se pudiera minimizar el producto de las incertidumbres en la posición q y el momentum p que de acuerdo a lo que descubrió Werner Heisenberg puede ser igual o mayor a ħ/2 pero no puede ser menor que ħ/2) mientras buscaba soluciones a su ecuación de onda que satisfacieran el principio de correspondencia que afirma que los resultados obtenidos en la Mecánica Cuántica se deben ir aproximando más y más a las mismas ecuaciones y fórmulas de la mecánica clásica conforme van aumentando los números cuánticos n que describen al sistema submicroscópico, o sea conforme n tiende al infinito, o lo que es lo mismo, conforme el valor de la constante de Planck ħ es cambiado y se le hace tender a cero. En pocas palabras, Schrödinger estaba interesado en lograr sistemas cuánticos que para números cuánticos grandes reprodujeran los resultados ya conocidos en la mecánica clásica. Para los fundadores de la Mecánica Cuántica, era obvio que la Mecánica Cuántica no era un “caso especial” de la mecánica clásica, simple y sencillamente no había manera alguna de poder derivar la Mecánica Cuántica de la mecánica clásica, atribuíble filosóficamente al hecho de que ultimadamente todos los cuerpos macroscópicos están constituídos por átomos y moléculas, y en todo caso debería ser la mecánica clásica la que se pudiese derivar de la Mecánica Cuántica “para números cuánticos grandes”. Pero... ¿era posible lograr tal conexión teórica entre la teoría que rije los fenómenos del mundo submicroscópico, una teoría de índole esencialmente probabilista, con la mecánica Newtoniana que rije los fenónemos del mundo macroscópico, de índole cien por ciento determinista? En sus esfuerzos por lograr tal objetivo, Schrödinger daba por hecho que era necesario trabajar sobre sistemas y cosas que minimizaran la inevitable incertidumbre que trae consigo el principio de incertidumbre de Heisenberg. Y los estados coherentes para el oscilador armónico simple le parecieron a Schrödinger un punto ideal de partida, aunque no llegó más lejos dadas las limitaciones teóricas y tecnológicas de su época. De cualquier modo, desde aquél entonces el estado coherente fue establecido como un estado de incertidumbre mínima, con el único parámetero libre escogido para hacer la dispersión natural (la desviación estándard estadística σ en unidades naturales adimensionales) igual para la posición y el momentum, cada uno siendo igualmente pequeño a energías relativamente altas. Como vimos arriba en el ejemplo proporcionado por el simulador, en contraste con los eigenestados estáticos de energía del sistema, la evolución temporal de un sistema coherente está concentrada a lo largo de trayectorias clásicas. La dinámica del estado coherente del oscilador armónico cuántico linear surge inesperadamente en una amplia variedad de sistemas físicos, ocurriendo sobre todo en la teoría cuántica de la luz fundamentada en la electrodinámica cuántica.
Poco tiempo después de los esfuerzos de Schrödinger, la ruta teórica hacia el entendimiento de la coherencia de estados empezó en cierto modo cuando en 1927 Paul Adrien Maurice Dirac combinó la formulación Maxwelliana de la luz en su aspecto ondulatorio con el concepto del oscilador armónico cuántico obteniendo de éste modo una descripción cuántica de la radiación electromagnética mediante la cuantización del campo electromagnético. En general, las predicciones de la formulación de Dirac no empatan del todo con los resultados de Maxwell ya que corresponden a dos descripciones diferentes de un mismo sistema, aplicables cada una de ellas en extremos opuestos del comportamiento de la luz. Fue hasta en 1963 cuando Roy Glauber en su trabajo “The Quantum Theory of Optical Coherence” publicado en el Physical Review Letters propuso un modelo cuántico de la luz que permite hacer predicciones muy similares a las de Maxwell al tiempo que preserva la estructura teórica establecida por Dirac. De acuerdo con Glauber, la luz de Dirac debe producirse en estados de polarización coherentes si ésta ha de compararse con la luz Maxwelliana. Los estados coherentes de Glauber llamaron de inmediato la atención de la comunidad científica y fomentaron un sinfín de desarrollos teóricos y experimentales. Tomando en cuenta lo anterior, cabe preguntarse hasta dónde es posible dar una descripción cuántica de los sistemas macroscópicos. En 1935 Schrödinger dió a conocer su diseño de su famoso experimento Gedanken donde se involucran un inocente gato y la desintegración de un átomo (decaimiento atómico). Para mostrar las “aparentes contradicciones” de la teoría cuántica con el “concepto de realidad” Schrödinger primero le adjudica un estado cuántico al gato, después mezcla éste último con el estado cuántico del átomo para concluir que el gato estará vivo y muerto a la vez en tanto no lo “observemos”. Sorprendentemente, se pueden usar los estados coherentes de Glauber para representar al sistema cuántico del gato, incluso a nivel experimental.
El mérito de Roy Glauber, ganador del Premio Nóbel de Física en 2005, fue haber rescatado el tema de los estados coherentes del olvido dándoles el impulso teórico necesario para fundamentar sobre bases sólidas el campo científico hoy conocido como la óptica cuántica. En la óptica cuántica, el estado coherente se refiere a un estado del campo electromagmético cuantizado que describe una máxima especie de coherencia y una especie de comportamiento clásico. Hoy, estos estados del oscilador armónico, estados coherentes conocidos como estados Glauber, son considerados prototipos del campo electromagnético oscilante, siendo el modelo del campo de onda continuo del láser, o del campo electromagnético de una onda de radio no modulada.
Se han dado demasiadas generalidades arriba, y es momento de repasar los principios básicos que nos conducen a los estados coherentes.
Es un hecho que entre los estados del oscilador armónico simple, el único estado entre todos ellos que satisface en su carácter de igualdad el principio de incertidumbre de Heisenberg expresado ya sea en su forma convencional como el producto de la incertidumbre en la posición Δx y la incertidumbre en el momentum Δp:
o más correctamente en su versión estadística como una dispersión de valores σxσp:
es el estado basal n.=.0. Todos los demás estados del oscilador armónico simple tienen un producto en su incertidumbre en la posición y en su incertidumbre en el momentum mayor que ħ/2, dado por la relación:
Para el oscilador armónico simple, ya se ha visto previamente que para ir de un nivel energético inferior al nivel energético superior o viceversa, se pueden usar los operadores escalera conocidos ya sea como operadores de creación y aniquilación o bien como operadores de ascenso y descenso (en relación a ésto véanse las entradas tituladas "Los operadores escalera" que forman parte de ésta obra):
Los operadores de la posición x y el momentum p para el oscilador armónico simple pueden ser expresados en función de los operadores de ascenso y descenso de la siguiente manera:
La disponibilidad de operadores escalera para el versátil oscilador harmónico simple permiten calcular de una manera muy sui generis las esperanzas matemáticas de ciertas esperanzas matemáticas para el oscilador armónico, por ejemplo:
en donde se ha hecho uso de la ortogonalidad de las funciones de onda para el oscilador armónico simple (lo cual nos ahorra el trabajo de tener que llevar a cabo integración alguna). Del mismo modo:
Pero puesto que:
se tiene entonces, habiéndose recurrido de nuevo a la ortogonalidad de las funciones en aquellos casos en donde la integral conjunta de dos funciones diferentes se vuelve cero, y a la normalidad de las mismas cuando el producto interno produce la unidad, el siguiente resultado:
Del mismo modo, se puede demostrar que la esperanza matemática para el cuadrado del momentum es:
Es así como se puede obtener la dispersión (incentidumbre) σx para la posición:
y la dispersión (incentidumbre) σp en el momentum:
y con ello obtenemos el producto de ambas incertidumbres:
mostrando que el producto solo será igual a ħ/2 para n.=.0, o sea únicamente para el estado basal (fundamental) del oscilador armónico, confirmándose así que el único estado entre todos los estados del oscilador armónico simple que satisface en su carácter de igualdad el principio de incertidumbre de Heisenberg es el estado n.=.0, el estado de incertidumbre mínima. Y de hecho, para todos los demás estados la incertidumbre conjunta en el producto de la posición y el momentum irá aumentando conforme vaya aumentando el número cuántico n del eigenestado. Esto es lo mismo que encontró Schrödinger.
Como ya se señaló al discutir los ejemplos del simulador de la Universidad de Bergen relativos a estados coherentes, ciertas combinaciones lineares son capaces de poder minimizar el producto de incertidumbres en la posición y el momentum; estas combinaciones lineares son precisamente las que conducen a los estados coherentes. Y resulta que son eigenfunciones del operador de descenso
Efectuaremos ahora un ligero cambio en nuestra notación para que el lector no sea confundido con cierta notación que aparece en muchos textos y libros que hablan de los estados coherentes. Normalmente, cuando un operador O actúa sobre una función de onda Ψ produciendo un eigenvalor E, representamos tal cosa de la siguiente manera:
Pero hay una costumbre en la cual algo como lo anterior se escribe del siguiente modo usando la notación bra-ket de Dirac:
En efecto, se usa el mismo símbolo (la misma letra griega α) para la función de onda que el símbolo usado para representar el eigenvalor, prescindiendo por completo del símbolo ψ. Pero se sigue teniendo la misma equivalencia entre las notaciones:
Mientras que α representa el eigenvalor, |α〉 representa la eigenfunción de onda:
Aunque el uso del mismo símbolo α tanto en la designación del eigenvalor como en la designación de la función de onda es algo que al principio puede ocasionar alguna confusión, eventualmente es posible acostumbrarse a la diferencia notacional entre ambas cosas. En la notación que estaremos usando, la manera de distinguir entre el eigenvalor y la función de onda es que la función de onda es lo que aparece encapsulada entre la barra vertical izquierda y el paréntesis angulado derecho, y en ésto es en lo que hay que estar prevenidos.
Hecha la anterior aclaración, es el momento propicio para entrar en lo substancial del tema.
Una de las cosas interesantes de los estados coherentes, como ya se dijo arriba, es que los estados coherentes son eigenfunciones del operador de descenso:
Tómese ésto como una definición formal de los estados coherentes. Y para ésto, se dá por hecho que el operador de ascenso a+ es el conjugado Hermitiano del operador de descenso (o sea, el conjugado complejo). Estamos hablando de los mismos operadores de ascenso y descenso que se usaron arriba para el oscilador armónico, o sea:
Basándonos en éstos hechos, vamos a efectuar nuevamente el cálculo de las esperanzas matemáticas de la posición, el cuadrado de la posición, el momentum y el cuadrado del momentum para los estados Glauber del oscilador armónico simple. O sea que volveremos a efectuar los cálculos que se efectuaron arriba para el oscilador armónico, excepto que ahora lo haremos basándonos en el hecho que se acaba de enunciar de que los estados coherentes son eigenfunciones del operador de descenso además de recurrir nuevamente al uso de los operadores escalera.
En lo que toca a la esperanza matemática de la posición para un estado Glauber del oscilador armónico, se tiene lo siguiente:
Sorprendentemente, en comparación con la esperanza matemática〈x〉de la posición de la partícula del oscilador armónico cuántico, la cual fue evaluada arriba a cero en conformidad con la explicación de que la partícula pasa tanto tiempo “a la derecha” del origen x.=.0 (en donde los valores de la coordenada de la posición son positivos) como “a la izquierda” del origen x.=.0 (en donde los valores de la coordenada de la posición son negativos) indicando con ello que la probabilidad de encontrar a la partícula a la derecha del centro del movimiento oscilatorio es igual a la probabilidad de encontrar a la partícula a la izquierda del centro de oscilación, para el estado coherente la esperanza matemática de la posición no es igual a cero, al hacer su aparición un factor en el que se suman el eigenvalor α y su conjugado complejo α*.
Para calcular la esperanza matemática del cuadrado de la posición para un estado Glauber, haremos uso de un resultado intermedio. Del operador Hamiltoniano para el oscilador armónico simple:
se pueden demostrar las siguientes relaciones (en realidad, más que demostración, sería una simple verificación que el lector puede llevar a cabo por cuenta propia si así lo desea):
Restando una expresión de la otra para formar el conmutador de ellas, se tiene lo siguiente:
Éste resultado intermedio nos permite simplificar el siguiente desarrollo:
con el cual se puede obtener el cuadrado de la posición para el estado coherente Glauber:
Ahora pasamos a la evaluación de la esperanza matemática del momentum para el estado coherente Glauber del oscilador armónico, en un desarrollo que resulta casi idéntico al que fue efectuado para obtener la esperanza matemática de la posición:
De nueva cuenta, y sorprendentemente en comparación con la esperanza matemática〈p〉del momentum de la partícula del oscilador armónico cuántico que es evaluado a cero en conformidad con la explicación de que la partícula pasa tanto tiempo “moviéndose hacia la derecha” (con un momentum positivo) como moviéndose “hacia la izquierda” (con un momentum negativo) indicando con ello que en promedio el momentum de la partícula es igual a cero, el momentum promedio para el estado coherente no es igual a cero, haciendo su aparición un factor en el que se toma no la suma sin la diferencia entre el eigenvalor α y su conjugado complejo α*.
De igual manera, el desarrollo que se llevó a cabo para el cálculo de la esperanza matemática del cuadrado de la posición resulta ser casi idéntico al que se lleva a cabo para el cálculo de la esperanza matemática del cuadrado del momentum:
El tener a la mano las esperanzas matemáticas del cuadrado de la posición y del momentum nos posibilita obtener una expresión para el producto de las incertidumbres de ambos parámetros y ver cómo anda la situación en relación con el principio de incertidumbre de Heisenberg. Pero antes tenemos que obtener dichas incertidumbres como lo que son, dispersiones estadísticas:
De éste modo, se tiene:
El resultado obtenido nos dice algo importante: todos los estados coherentes para el oscilador armónico simple son estados de incertidumbre mínima en virtud de que se cumple la igualdad en la relación igualdad-desigualdad del principio de incertidumbre de Heisenberg. En efecto, de las dos posibilidades que ofrece el principio de incertidumbre de Heisenberg:
la posibilidad derecha, la de la igualdad, es la de la incertidumbre mínima. Esto contrasta diametralmente con el hecho demostrado arriba de que el único estado de incertidumbre mínima entre todos los estados del oscilador armónico simple es el estado n.=.0. ¡Todos los estados coherentes del oscilador armónico simple para cualquier valor de n son estados en los cuales hay incertidumbre mínima!
Como ya se ha hecho hincapié, todos los estados coherentes del oscilador armónico simple pueden ser expandidos en términos de las funciones de base que corresponden a los eigenestados de energía:
La relación básica que que nos indica cómo usar el operador de ascenso para ir generando las funciones de onda del oscilador armónico a partir de la función de onda para el estado fundamental ψ0 es la siguiente:
Ésta relación nos permite obtener los coeficientes de la expansión cn de la manera usual (obsérvese que en el desarrollo se usa la propiedad del operador Hermitiano):
La obtención de los coeficientes cn que nos dan las intensidades (amplitudes) de las contribuciones que debemos dar a cada una de las eigenfunciones de onda del oscilador armónico de acuerdo a lo anterior dependen de que se conozca previamente el coeficiente c0 que marca el punto de arranque para la generación de todos las demás coeficientes. Esto lo podemos obtener normalizando la función de onda α que corresponde al estado coherente, lo cual se logra de la siguiente manera:
Obsérvese algo importante aquí: empieza a hacer su aparición el factor exponencial que es precisamente el que corresponde a la generación de distribución estadística de una curva Gaussiana. Esto nos va señalando ya que en la distribución de la amplitud de los coeficientes asignados a las funciones de base del oscilador armónico para obtener un estado coherente Glauber se tendrá que seguir el patrón de una curva normal Gaussiana.
lo cual en nuestra notación abreviada equivale a hacer la substitución:
Haciendo tal cosa para obtener la evolución temporal de los eigenvalores de los estados coherentes del oscilador armónico, vemos que:
El factor de fase e-iθ/2 no afecta en nada la condición del estado coherente como una eigenfunción ψα del operador de descenso, ni cambia tampoco su eigenvalor α. En pocas palabras, la función de onda ψα(t) sigue siendo un estado eigen del operador de descenso, aunque el eigenvalor α evoluciona con el tiempo en la siguiente forma con un factor de fase mostrado en color magenta:
α(t) = e-iθ α
|α(t)〉se mantiene igual que antes, sigue siendo el |α〉original. Así pues, un estado que es coherente ses sigue manteniendo como estado coherente pese al transcurso del tiempo, y continúa minimizando el producto de incertidumbres. De éste modo, lo que vimos arriba en el simulador de estados coherentes confirma visualmente en cierto modo el comportamiento aparentemente clásico del paquete de onda Gaussiano con amplitud de probabilidad Ψ2 formado por la superposición de ondas estacionarias del oscilador armónico, que se mueve de izquierda a derecha y de derecha a izquierda sin que se deforme la onda mixta viajera.
Si regresamos al simulador de estados coherentes y tratamos de llevar a cabo la simulación con el estado fundamental n.=.0, obtenemos una sola “curva de campana” solitaria:
que al echar a andar la simulación permanece completamente estática sin mostrar ninguna dinámica, lo que nos puede llevar a sospechar que tal vez el estado basal no sea un estado coherente constituyéndose en la excepción. Sin embargo, ésto no es así, ya que por la propiedad del operador de descenso actuando sobre el estado fundamental, se tiene que:
de modo que también el estado fundamental del oscilador armónico es un estado coherente, cuyo eigenvalor α es igual a cero.
De éste modo, la aplicación de estados coherentes para poder proyectar “clásicamente” hacia el mundo macroscópico al menos una parte de la amplia fenomenología de sistemas cuánticos se amplía considerablemente, empezando por el enriquecimiento de la rama del saber conocida como la Electrodinámica Cuántica (una extensión de la Mecánica Cuántica que abandona la idea de los campos electro-magnéticos clásicos continuos y los reemplaza por campos discretizados) y la Óptica cuántica que prácticamente fue fundada por Roy Glauber con su ameno libro Quantum Theory of Optical Coherence. Y ésto es tan solo el principio. Se puede extender el modelo a un oscilador armónico en tres dimensiones, con lo cual podemos postular la existencia de un paquete de onda Gaussiano como un estado coherente moviéndose clásicamente en tres dimensiones.
Hay una razón importante del por qué hay que empezar a darle prioridad a partir de aquí al uso de los operadores escalera, de ascenso y de descenso. A partir de los trabajos pioneros de Dirac, se trata precisamente de la misma metodología que se utiliza como principal puerta de entrada hacia lo que se conoce dentro de la Electrodinámica Cuántica como la segunda cuantización que permite estudiar el campo electromagnético desde el punto de vista cuántico. En la serie de entradas tituladas “Interacción con un campo electro-magnético” que forman parte de ésta obra, se supuso a los campos electro-magnéticos como campos continuos (clásicos) sin discretización alguna, suponiendo a los campos electro-magnéticos bajo consideración como clásicamente continuos y lo suficientemente fuertes como para ser alterados en forma imperceptible por las partículas con carga eléctrica sobre las cuales actúan. En la Electrodinámica Cuántica se remueve tal limitación, y los campos electro-magnéticos también terminan siendo discretizados, y eventualmente no sólo el campo electro-magnético sino todos los campos de índole teórica relacionados con las interacciones de partículas en lo que se conoce como la Teoría del Campo Cuántico. Los operadores de creación y aniquilación en tales teorías tienen realmente un objetivo mucho más amplio: sirven para agregar o remover una partícula que forme parte de un sistema de muchas partículas en lo que es el problema de los muchos cuerpos en el estudio del campo cuántico, y están en el corazón del formalismo de la segunda cuantización, cerrando la brecha que hay entre los estados de primera cuantización y los estados en los que se ha llevado a cabo una segunda cuantización. Aplicando un operador de creación-aniquilación a una función de onda que ha sido objeto de una primera cuantización injertará o borrará un estado de una sola partícula de la función de onda de una manera simetrizada dependiendo de la estadística de partículas que se utilice, mientras que por otro lado todos los estados de segunda cuantización conocidos como estados Fock pueden ser construídos aplicando repetidamente los operadores de creación al estado del vacío. Los operadores de creación y aniquilación para los bosones originalmente fueron construídos bajo el contexto del oscilador armónico simple cuántico como los operadores escalera de ascenso y descenso, y posteriormente fueron generalizados a los operadores de campo en la Teoría del Campo Cuántico siendo fundamentales en la teoría del cuántica de los muchos cuerpos en el sentido de que cualquier operador de muchos cuerpos, incluyendo el Hamiltoniano en el sistema de muchos cuerpos y todas las observables físicas, pueden ser expresados en términos de dichos operadores de creación y aniquilación. No debe causar sorpresa pues de que, en el fondo, los estados coherentes del oscilador armónico o estados Glauber definidos arriba como los autoestados del operador de aniquilación del oscilador armónico sean escritos en términos de lo que ahora formalmente podemos llamar estados de Fock, lo cual resulta evidente arriba en la sumatorias empleadas.
Es necesario agregar que los estados coherentes no son los unicos estados de incertidumbre mínima que existen. La condición:
define una familia de estados de incertidumbre mínima a la que pertenecen los estados coherentes como un caso especial en el que la incertidumbre de ambas dispersiones es la misma, o sea:
como se muestra en la siguiente figura:
en donde el punto resaltado en la curva es el único que corresponde a los estados coherentes, mientras que el resto de la curva corresponde a los estados de incertidumbre mínima conocidos como estados “apachurrados” o estados squeezed siguiendo la designación introducida por vez primera por James Hollenhorst con su operador squeeze (en inglés “squeeze” significa “deformar”, “exprimir”, “retorcer”, y se pronuncia “squisd”). La designación de squeeze se debe a que si se representan los estados coherentes Glauber en un plano complejo asociado con las incertidumbres σx y σp se tendrá un círculo conocido como el círculo de incertidumbre centrado en〈a〉=.α y de radio:
mientras que si se hace lo mismo para un estado squeezed el círculo se verá deformado a una elipse. A continuación se muestra la representación de los estados coherentes en ése plano complejo en donde el desplazamiento α del estado coherente es mostreado en su desplazamiento en relación con el lugar que corresponde al estado del vacío (los estados squeezed fueron introducidos en úptica cuántica por la necesidad de disminuir el ruido producido en los interferometros utilizados para detectar ondas gravitacionales (una predicción de la Teoría General de la Relatividad confirmada experimentalmente):
