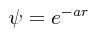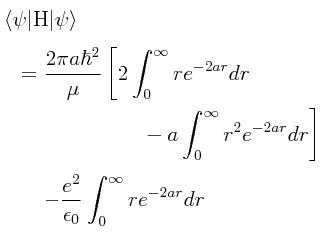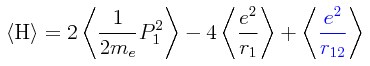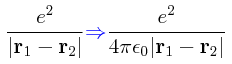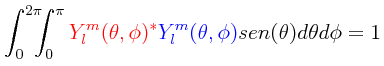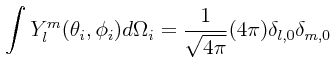PROBLEMA: Supóngase que la siguiente función de onda es una función de onda que se sospecha desde un principio que representa razonablemente a la función de onda verdadera del átomo de hidrógeno:
Calcúlese mediante el método de variación la energía del átomo de hidrógeno en su estado basal con esta función de prueba, y compárese el resultado obtenido con el resultado exacto.
Este es esencialmente un problema de simetría esférica y el cual no se presta para el uso de coordenadas Cartesianas rectangulares. Lo primero que haremos será utilizar la función de prueba para obtener la condición de normalización de la misma que será utilizado en el denominador de nuestro estimativo:
La integración debe llevarse a cabo sobre todo el espacio, y es una integración triple porque estaremos utilizando coordenadas esféricas (r,θ,φ). Metiendo la función de prueba proporcionada y considerando un elemento infinitesimal de volumen en coordenadas esféricas, tenemos entonces:
El elemento infinitesimal de volumen dV en coordenadas esféricas está dado por:
Entonces las integraciones que tenemos que llevar a cabo, ya con coordenadas esféricas, son las siguientes:
En la integración que corresponde a la coordenada , podemos hacer una pequeña simplificación:
De este modo, llevando a cabo la integración sobre la parte angular, lo anterior se reduce a:
Nos queda por resolver la parte radial. Esta integral la podemos llevar a cabo fácilmente consultando las tablas de integrales de donde obtenemos la siguiente prescripción:
De este modo, obtenemos el resultado mostrado:
Ahora enfocaremos nuestra atención para obtener la esperanza matemática del Hamiltoniano H que requeriremos en el numerador de nuestro estimativo, la cual estará dada por la definición básica de la esperanza matemática del Hamiltoniano usando la función de onda de prueba:
Para poder continuar adelante, necesitamos definir el Hamiltoniano que estaremos utilizando. Este Hamiltoniano no puede ser especificado en coordenadas Cartesianas rectangulares dada la simetría esférica del problema, tenemos que especificarlo en coordenadas esféricas. Para ello, utilizamos el operador Laplaciano expresado en coordenadas esféricas. Puesto que estamos interesados en la dependencia radial exclusivamente, nuestro Hamiltoniano tendrá dos términos, uno correspondiente a la energía cinética radial, y el otro correspondiente a la energía potencial de atracción eléctrica entre el electrón y el núcleo (estaremos utilizando la masa reducida μ del átomo en lugar de la masa del electrón para darle una mayor generalidad al asunto sin que ello implique esfuerzo adicional alguno de nuestra parte):
En unidades MKS-SI, la energía potencial V(r) de atracción eléctrica entre el electrón y el núcleo está dada por la fórmula:
Por su parte, el operador del momentum radial Pr que actuará sobre la función de onda debe ser el siguiente de acuerdo con la transformación del Laplaciano de coordenadas rectangulares a coordenadas esféricas:
Aplicando este operador del momentum radial a la función de prueba, tenemos entonces:
Llevando a cabo las dos diferenciaciones una tras otra obtenemos:
Entonces el Hamiltoniano, aplicado a la función de onda de prueba con sus dos términos incluídos, viene dando:
Habiendo obtenido lo anterior, la esperanza matemática del Hamiltoniano se puede llevar a cabo de la manera siguiente:
Nuevamente, el elemento infinitesimal de volumen dV, expresado en coordenadas esféricas, nos conduce a dos tipos de integraciones, una parte radial, y una parte angular. Por lo que obtuvimos previamente, la integración de la parte angular produce simplemente el factor 4π. Esto nos permite reducir la integración triple a una integración sencilla llevada a cabo sobre la parte radial:
La integración de la parte radial se puede “romper” en tres integraciones separadas:
Cada una de estas integrales se puede llevar a cabo fácilmente recurriendo a la prescripción citada arriba obtenida de las tablas de integrales de donde, según la cual:
De este modo, llevando a cabo las integraciones, obtenemos para la esperanza matemática del Hamiltoniano con la función de onda proporcionada lo siguiente:
Con esto tenemos ya lo que necesitamos para “llenar” el numerador y el denominador de nuestro estimativo de la energía del sistema con la función de onda de prueba proporcionada:
A continuación, tal y como nos lo pide el procedimiento que hemos estado llevando a cabo:
tomaremos la derivada de E con respecto a a para poder obtener así el valor de a que nos proporciona el mínimo, y el cual resulta ser:
Con este valor de a, substituyéndolo en E, obtenemos la expresión para nuestro estimativo de la energía mínima del estado fundamental de acuerdo con la función de onda proporcionada:
Comparando esta expresión con la expresión exacta obtenida mediante la solución de la ecuación de Schrödinger, encontramos que el resultado obtenido aquí no sólo es una aproximación, sino que es el mismo resultado. Esta extraordinaria coincidencia tiene su explicación en el hecho de que la función de onda de prueba que hemos usado aquí es de hecho proporcional a la función de onda “verdadera” que obtenemos como solución exacta a la ecuación de Schrödinger, la cual es también de tipo exponencial negativo para el estado basal del átomo de hidrógeno.
Otro problema importante que sólo puede ser tratado mediante una técnica de aproximación como el método de variación es el problema del elemento que le sigue al hidrógeno en orden de complejidad: el átomo de helio, un átomo que consta de dos protones y dos neutrones en su núcleo, con dos electrones orbitando en torno al núcleo como una nube de probabilidad que en el estado basal suponemos esférica aunque vulgarmente se le concibe bajo el esquema del modelo atómico planetario de Bohr:
Este problema fue resuelto por vez primera por Albrecht Unsöld en 1927, y la concordancia de su solución aproximada con los resultados obtenidos experimentalmente constituyó una de las primeras confirmaciones de que el modelo de Schrödinger estaba en el camino correcto en su explicación del comportamiento de los elementos de la tabla periódica.
PROBLEMA: Escríbase el operador diferencial Hamiltoniano para el átomo de helio.
Llamemos r1 y r2 a las distancias respectivas de cada uno de los dos electrones al núcleo del helio, y llamemos también r12 a la distancia que separa a ambos electrones:
Si consideramos al núcleo del helio como un centro fijo de fuerza central (sin experimentar movimiento alguno), y si además ignoramos los términos de interacción spin-órbita de cada uno de los electrones así como las interacciones de los momentos magnéticos de los dos electrones, entonces tomando en cuenta que el número atómico del helio es Z = 2 el operador diferencial Hamiltoniano H para el helio escrito en el sistema de unidades MKS-SI contendrá los siguientes términos:
en donde los operadores P1 y P2 son los operadores diferenciales usuales bajo el sistema de coordenadas que esté siendo utilizado (en este caso, un sistema de coordenadas esféricas). Los primeros dos términos del Hamiltoniano representan la energía cinética de cada uno de los electrones, los siguientes dos términos representan la energía potencial de atracción de cada electrón al núcleo del átomo, y el último término que se muestra en color azul representa la energía potencial de repulsión entre los dos electrones. Es precisamente el último término el que impide que al átomo de helio se le pueda dar una solución exacta mediante la ecuación de onda de Schrödinger, ya que no es posible recurrir a la separación de variables en este caso.
Dada la cantidad de símbolos que hay que manejar en un problema de este tipo cuando se trabaja dentro del sistema de unidades MKS-SI, resulta ventajoso hacer el cambio al sistema de unidades cgs-Gaussianas, y en tal caso el operador Hamiltoniano para el helio puede ser escrito de la siguiente manera:
Con el fin de poder un estimativo de la energía aproximada del átomo de helio cuando se encuentra en el estado basal (y al hablar de un estado basal para el átomo de helio la alusión es clara a que ninguno de sus dos electrones esté excitado a un nivel energético más alto), bajo el método de variación tenemos que proponer alguna función de onda razonable que pueda ser utilizada para obtener tal estimativo. Una posibilidad razonablemente buena consiste en usar para la función de onda del helio el producto de dos funciones de onda que correspondan al estado basal del átomo de hidrógeno, usando asimismo como parámetro libre que pueda ser variado a la variable Z que normalmente corresponde al número atómico. Esta selección nos permite utilizar la función de onda radial del hidrógeno para el estado basal (identificado como 1s) que ya había sido obtenida previamente en la entrada titulada “La función de onda radial”:
siendo σ = (Z/a0)r y siendo a0 el radio de Bohr. Nuestra función de onda tentativa, desconociendo una expresión analítica exacta para la función de onda del átomo de helio, será entonces (los números entre paréntesis en color rojo utilizados en los sub-índices son una referencia al electrón al cual está asociado cada función de onda):
ψ = ψ1s(1) · ψ1s(2)
Llevando a cabo el producto con las funciones de onda para el hidrógeno en su estado basal, tenemos entonces para nuestra función de onda de prueba lo siguiente:
Simplificando un poco:
Podemos justificar esta selección de función de onda de prueba para el helio en su estado basal argumentando que ésta sería una función de onda exacta si el término de interacción en el Hamiltoniano fuese descartado y si el número atómico Z fuese puesto igual a 2.
Si tomamos la esperanza matemática del Hamiltoniano, será igual en el lado derecho de su expresión a las esperanzas matemáticas de cada uno de los términos que corresponden a las energías cinética y potencial. Esto se puede simplificar aún más siendo razonable el suponer que en virtud de la simetría del Hamiltoniano y en virtud de la simetría de la función de onda de prueba, la esperanza matemática del término que corresponde a la energía cinética del electrón 1 es igual a la esperanza matemática del término que corresponde a la energía cinética del electrón 2, y se puede simplificar todavía más suponiento que también la esperanza matemática que corresponde a la energía potencial de atracción entre cada electrón y el núcleo son iguales, dándonos en consecuencia lo siguiente:
Las primeras dos esperanzas matemáticas de esta expresión pueden ser evaluadas recordando algo acerca de la energía promedio de un electrón moviéndose en un campo de fuerza coulómbico. Se puede demostrar mediante un teorema conocido como el teorema virial que para el movimiento clásico de cualquier partícula moviéndose en un campo de fuerza que obedece una ley de la inversa del cuadrado de la distancia que la energía cinética promedio de la partícula es igual al negativo de su energía total. Por lo tanto, la esperanza matemática de la energía cinética que aparece como el primer término puede ser evaluada simplemente tomando la energía de enlace de un átomo hidrogenoide en su estado basal con una carga Z en su núcleo y cambiando el signo:
Del mismo modo, el valor promedio de la energía potencial de un electrón en un átomo hidrogenoide será igual al doble de la energía de enlace del electrón en el estado basal:
De esta manera, la esperanza matemática del Hamiltoniano toma el siguiente aspecto:
La única integral que puede darnos problemas, sin lugar a dudas, es el último término, la integral del término de interacción, el mismo término que impide que se le pueda encontrar una solución exacta al átomo de helio. Resolveremos aquí esta integral de dos maneras distintas: una más intuitiva pero más laboriosa, y otra menos laboriosa pero que require de conocimientos matemáticos algo más avanzados que los que ordinariamente se tienen en un curso introductorio de Mecánica Cuántica (específicamente, una familiaridad con el teorema de adición de armónicas esféricas).
En el sistema de unidades cgs-Gaussiano, la integral del término de interacción entre los dos electrones se puede escribir de la siguiente manera:
Con el propósito de ejercitarnos en el manejo fluído de interconversión de unidades, haremos el cambio del sistema cgs-Gaussiano a MKS-SI, lo cual implica hacer:
En virtud de que |ψ1(r1)|2 y |ψ1(r2)|2 son solamente las probabilidades de encontrar al electrón 1 en la región volumétrica de r1 y al electrón 2 cerca de r2, se ve que en realidad la ecuación que estamos trabajando representa la energía de repulsión electrostática entre dos nubes de carga eléctrica, cada una de las cuales tiene una distribución de densidad de carga eléctrica dada por -e|ψ1(r1)|2. También se debe destacar el hecho de que en la ecuación para ψ1s la distribución tiene simetría esférica.
Considérese primero la interacción entre una capa esférica de la primera distribución de carga, de radio r1, con un elemento infinitesimal de volumen d3r2 de la segunda distribución de carga situada en r2, siendo r2 mayor que r1. Para puntos que se encuentren fuera de r1, la capa esférica interior actúa como si estuviera concentrada en el origen (del mismo modo en el que la fuerza de gravedad de la Tierra que actúa sobre un satélite actúa como si toda la masa de la Tierra estuviera concentrada en su centro), y la energía potencial infinitesimal dU entre la capa esférica interior y el elemento de carga en r2 es por lo tanto:
en donde ρ1 y ρ2 son las densidades de las dos distribuciones de carga eléctrica. Como esta relación es independiente de la posición angular del volumen infinitesimal d3r2, el potencial electrostático que actúa entre dos capas de radios r1 y r2 siendo r2 mayor que r1 es:
Una expresión similar substituyendo a r1 por r2 en el denominador de esta expresión indudablemente será válida en el caso de que r2 sea menor que r1. Se pueden considerar ambos casos simultáneamente escribiendo:
en donde:
es la mayor de r1 y r2.
Puesto que:
con algo similar para ρ2, empleando la función de onda para el orbital 1s se tiene:
Usando lo anterior, podemos obtener la esperanza matemática de la energía de interacción del modo siguiente:
Como esta integral es simétrica en r1 y r2, evidentemente se obtendrán contribuciones iguales cuando r1 sea menor que r2 y cuando r1 sea mayor que r2. Por lo tanto, se puede evaluar la integral anterior haciendo:
e integrando sobre r1 desde cero hasta infinito, y después integrando sobre r0 desde cero hasta infinito, y multiplicando por dos el resultado final. Efectuando estas substituciones, se tiene:
Esto se encuentra ya en una forma que puede ser consultada en tablas de integrales, en donde hallamos lo siguiente:
Empleando esto, al llevar a cabo la integración sobre r1 se llega a lo siguiente:
o lo que es lo mismo:
Empleando nuevamente la forma tomada de las tablas de integrales, para la integral sobre r0 se obtiene lo siguiente:
lo cual, expresado en el sistema de unidades cgs-Gaussianas, viene siendo:
Evaluaremos nuevamente el término de interacción, pero utilizando matemáticas un poco más avanzadas que sin embargo pueden abreviar los pasos. Empezaremos desde el principio con la evaluación de la esperanza matemática de lo siguiente:
en donde:
Y usando la función de onda de prueba que hemos definido arriba, tenemos la siguiente integral a ser evaluada en coordenadas esféricas, habiendo tanto una parte radial como una parte angular:
Si llamamos γ al ángulo entre los dos vectores radiales r1 y r2, entonces de acuerdo a la ley de los cosenos tenemos lo siguiente:
Siendo este un problema de simetría esférica, no nos queda más opción que recurrir al uso de las coordenadas esféricas. Esto significa que tendremos dos partes a ser evaluadas, una parte angular y una parte radial:
resultando al final de cuentas en una integración sextuple. Sacando fuera de la integración múltiple la cantidad constante Z6e²/πa0, lo que tenemos entre manos es lo siguiente:
La integración de la parte angular se debe llevar a cabo sobre toda la “esfera”. Podemos tratar de llevar a cabo la integración de la parte angular usando “fuerza bruta”, esto es, integración convencional ortodoxa. Afortunadamente, para este tipo de cosas hay atajos que nos simplifican un poco la vida. Por las mismas razones de conveniencia esgrimidas para recurrir al uso de las armónicas esféricas para resolver la parte angular de la ecuación de Schrödinger en la solución del potencial de simetría esférica que corresponde al átomo de hidrógeno, aquí también haremos uso de las armónicas esféricas para poder llevar a cabo la integración de la parte angular. Específicamente, estaremos haciendo uso del conocido teorema de la adición de armónicas esféricas (véase la entrada “Polinomios de Legendre: aspectos matemáticos”), el cual es una generalización de la identidad trigonométrica:
cos(θ’ − θ) = cos(θ’)cos(θ) + sin(θ)sin(θ’)
en donde el papel que desempeñan las funciones trigonométricas que aparecen en el lado derecho de la igualdad será llevado a cabo por las armónicas esféricas, y el papel que desempeña el lado izquierdo de la igualdad será llevado a cabo por los polinomios de Legendre. Considerando dos vectores x y y a los cuales les corresponden las coordenadas esféricas angulares (θ1,φ1) y (θ2,φ2), respectivamente, el teorema de la adición de armónicas esféricas enuncia lo siguiente:
siendo esta expresión válida tanto para armónicas esféricas reales como armonicas esféricas complejas, y en en donde Pl es un polinomio de Legendre de grado l. Se supone de inicio que las armónicas esféricas están normalizadas de la siguiente manera:
Obsérvese que la relación del ángulo γ que hay entre los dos vectores radiales r1 y r2, y los ángulos θ1, φ1, θ2 y φ2, viene siendo:
Lo que estamos haciendo es, en efecto, lo siguiente:
en donde los símbolos con sub-índices menor y mayor tienen los siguientes significados:
Para mayor claridad:
Expuesto lo anterior, vemos que la integración angular se puede llevar a cabo sin mayores problemas expresando a Pl.[cos(θ)] en términos de las armónicas esféricas Yml.(θ1,φ1) y Yml.(θ2,φ2) normalizadas:
Integrando sobre los ángulos sólidos dΩi = dθi,dφi (un ángulo sólido para cada par de coordenadas angulares), definidos cada uno como:
tenemos entonces el siguiente resultado para cada par de coordenadas angulares, un resultado que podría considerarse trivial
Obsérvese que se ha tomado en cuenta ya en la asignación de valores numéricos a los sub-índices que los dos electrones del átomo de helio están siendo considerados en el estado basal para el cual el número cuántico principal es n = 1 y los números cuánticos l y m son respectivamente iguales a cero. Obsérvese también que, para l = m = 0, el valor de la armónica esférica Yml viene siendo:
La integración de la parte radial:
es elemental y directa, razón por lo cual simplemente se dará el resultado de la misma con la finalidad de que no se pierda de vista el objetivo central:
Juntando los resultados para la parte angular y la parte radial tomando el producto de los resultados obtenidos, tenemos entonces para el término de interacción lo siguiente:
Esto es lo mismo que lo que se obtuvo anteriormente. Aparentemente, no hubo mucho ahorro en trabajo de cálculo, pero ello se debió a que se introdujeron explicaciones adicionales que usualmente se omiten para quienes tiene ya una familiaridad con el procedimiento que se ha empleado aquí.
Por si acaso el lector no se ha dado cuenta de ello, la razón por la cual el cálculo del término de interacción resulta algo elaborado es porque los orbitales cuasi-esféricos que corresponden al estado basal 1s y al primer estado excitado 2s, además de ser nubes de probabilidad que en este caso interpretamos como nubes de carga eléctrica, lejos de estar separados de manera bien definida el uno del otro se trata de orbitales “borrosos” que se traslapan el uno al otro en un mismo átomo de modo tal que no es posible afirmar categóricamente que en todo momento el electrón que corresponde al electrón 2s estará situado a una mayor distancia del núcleo del átomo que el electrón que corresponde al electrón 1s, y de hecho un electrón 2s puede estar situado más cerca del “interior” del átomo que un electrón 1s sobre el cual siempre hay una probabilidad (por pequeña que sea) de que esté situado a una distancia mucho más alejada del núcleo. Esto se vuelve más claro si comparamos la gráfica de la distribución de probabilidad del orbital 1s:
con la gráfica de la distribución de probabilidad del orbital 2s:
Sin necesidad de tener que llevar a cabo un redimensionamiento de una de las dos gráficas para poder superimponer una gráfica sobre la otra a una misma escala, resulta obvio que habrá un traslape entre ambos orbitales desde una distancia radial de cero.
Agregando el término de interacción a la esperanza matemática del Hamiltoniano y tomando la derivada de dicha esperanza matemática con respecto a Z para ser igualada a cero con la finalidad de encontrar el valor mínimo, tenemos entonces:
El valor mínimo resulta ser entonces:
Usando este mismo valor de Z en la expresión para la esperanza matemática del Hamiltoniano, obtenemos el valor aproximado de la energía de enlace E0 de un electrón en el estado basal del átomo de helio:
Esta es la energía necesaria para remover a los electrones del átomo de helio, esto es, la energía necesaria para poder obtener un átomo de helio doblemente ionizado.
En el problema que acabamos de resolver, vemos que las respuestas están dadas en múltiplos de e²/a0. Esta cantidad es una cantidad utilizada con tanta frecuencia en este tipo de problemas que se le ha dado un nombre especial, el Hartree (llamada así por el físico Douglas Hartree), definida como la energía potencial de repulsión de dos cargas eléctricas unitarias separadas una distancia equivalente a un radio de Bohr a0 la una de la otra.
PROBLEMA: Calcúlese la energía de un Hartree en unidades de electrón-volts.
De la definición del Hartree, en unidades MKS-SI:
Usando las constantes físicas:
e = 1.602 189 2×10-19 coulomb
ε0 = 8.854 187 82×10-12 coulomb²/newton·metro²
a0 = 5.291 770 6×10-11 metro
obtenemos:
Eh = 4.359 814 4×10-18 joule
Usando:
1 eV = 1.602 189 2×10-19 joule
para convertir a electrón-volts, tenemos entonces que la unidad del Hartree es:
Eh = 27.211 608 eV
Con este valor en electrón-volts para la cantidad e²/a0, la energía estimada del estado basal del átomo de helio con la ayuda del método de variación viene siendo:
E0 ≈ (- 2.848)(27.211 608 eV) ≈ -77.5 eV
Este valor estimado contrasta favorablemente con el valor experimental, el cual es -78.8 eV. De esta manera, aún sin contar con una función de onda para el átomo de helio en su estado basal, la concordancia entre la estimación teórica y el resultado experimental resulta ser excelente.
Habiendo resuelto el problema del átomo de helio con sus dos electrones en el estado basal, el siguiente problema en complejidad consiste en el mismo átomo de helio, pero con uno de sus dos electrones en el estado excitado más cercano, o sea el estado 2s. Con los dos electrones del átomo de helio situados en diferentes capas, podemos imaginarnos dos nubes borrosas de probabilidad albergando a cada electrón del siguiente modo:
Para poder tomar en cuenta la indistinguibilidad de los dos electrones del helio siguiendo las reglas de la Mecánica Cuántica, lo cual requiere que en una expresión que combine a las funciones de onda de cada electrón la expresión permanezca igual al intercambiar los índices (o sub-índices) usados para identificar a cada electrón (en este caso, el cambio será relativo a dos estados, 1s ↔ 2s), podemos escribir las siguientes dos funciones de onda espaciales (el factor 1/√2 es el factor de normalización):
ψ = (1/√2)[ψ1s(1)· ψ2s(2) + ψ1s(2)· ψ2s(1)]
ψ = (1/√2)[ψ1s(1)· ψ2s(2) - ψ1s(2)· ψ2s(1)]
en donde el símbolo 1s en el sub-índice es una referencia al estado basal y el símbolo 2s es una referencia al estado excitado, mientras que los números en rojo son una referencia al electrón 1 y al electrón 2. A continuación combinaremos ambas expresiones en una sola haciendo referencia al estado basal y al estado excitado a través de los tres números cuánticos n, l y m:
Estas funciones de onda espaciales deben ser combinadas con funciones de spin para tomar en cuenta el spin de cada electrón, algo que no había sido necesario cuando ambos electrones estaban en el estado fundamental en virtud de que en dicho estado los electrones deben estar necesariamente apareados. Cuando dos electrones están en orbitales diferentes, pueden tener sus spins apuntando en la misma dirección o en direcciones opuestas. Hay, por lo tanto, cuatro funciones posibles de spin:
α(1)α(2)___β(1)β(2)___α(1)β(2)___α(2)β(1)
Sin embargo, para proporcionar la indistinguibilidad de los electrones (al igual que como lo hicimos con las funciones de onda espaciales), las funciones de onda de spin deben ser escritas de la siguiente manera:
α(1)α(2)___β(1)β(2)
(1/√2)[α(1)β(2) + α(2)β(1)]___(1/√2)[α(1)β(2) + α(2)β(1)]
Cada una de estas cuatro funciones de spin puede ser usada para multiplicarla por las dos funciones de onda espaciales de arriba. Sin embargo, únicamente las siguientes cuatro funciones de onda son antisimétricas y por lo tanto útiles (de acuerdo al principio de exclusión de Pauli) para representar el primer estado excitado del helio (la parte espacial se ha representado de color azul y la parte de spin se ha representado de color magenta):
La parte espacial de Ψ1 es simétrica pero la parte de spin es antisimétrica, de modo tal que toda la función de onda es antisimétrica. Y las partes espaciales de Ψ2, Ψ3 y Ψ4 son antisimétricas, pero sus partes de spin son simétricas, de modo tal que también estas funciones de onda son antisimétricas. Puesto que, en la ausencia de un campo magnético, la energía de cada estado depende únicamente de la parte espacial de la función de onda, Ψ2, Ψ3 y Ψ4 constituyen un estado degenerado y forman un triplete (triplet) de spin, un estado con una multiplicidad de tres. Por su parte, Ψ1 posee una energía distinta, y no hay forma en la cual pueda constituírse en un estado degenerado, siendo por lo tanto un singulete (singlet) de spin, un estado con una multiplicidad de uno. En el estado basal del helio (1s), sus electrones están apareados, apuntando en direcciones contrarias, y la suma de los spins será igual a cero. Sin embargo, cuando uno de los electrones es excitado al siguiente nivel energético (2s), los electrones pueden estar apareados, como en el estado singulete representado por Ψ1, o desapareados, como en el estado triplete representado por Ψ2, Ψ3 y Ψ4. Las tres componentes del triplete tienen un spin total en la dirección-z de 0, -1 y +1, respectivamente. En la presencia de un campo magnético externo, al romperse la simetría del espacio con ello, el nivel singulete no se divide en bandas, pero el nivel triplete se subdivide en tres bandas. Más aún, los átomos de helio que se encuentran en el estado singulete son conocidos como parahelio, mientras que los átomos de helio que se encuentran en el estado triplete son conocidos como ortohelio (como es de esperarse, también hay parahidrógeno y ortohidrógeno).
Para el análisis del estado excitado, la energía del átomo de helio se evalúa de la siguiente manera suponiendo que se agrega una corrección ΔE a la suma de la energía E100 del electrón en el estado basal y la energía Enlm del electrón en el estado excitado:
E = E100 + Enlm + ΔE
En una primera instancia, la corrección ΔE es lo que se conoce como una perturbación de primer orden. La determinación aproximada del valor de ΔE requiere una evaluación de la esperanza matemática precisamente del mismo término que nos había presentado algunos problemas en la solución del problema que vimos arriba de la determinación de la energía del estado basal del átomo de helio, esto es, el término:
Para el caso del átomo excitado de helio, podemos tomar al término de la interacción entre los dos electrones como estando constituído ya sea por la suma de dos cantidades A y B:
o por la diferencia de las mismas dos cantidades A y B:
siendo dichas cantidades:
una integral conocida como la integral directa, en donde, como de costumbre:
y siendo:
una integral conocida como la integral de intercambio.
En el caso de la suma de A y B, esta condición es la que corresponde a la del estado singulete, mientras que en el caso de la diferencia de A y B esta condición es la que corresponde a la del estado triplete. Como ya se mencionó, lo que estamos haciendo aquí es tratar al término problemático ΔE como una perturbación de primer orden. La terminología que estamos empleando aquí debe sugerirle al lector correcciones más refinadas de orden mayor, tales como una perturbación de segundo orden, del mismo modo en el que en muchas series aritméticas infinitas podemos obtener una mayor precisión en una cantidad evaluada de modo aproximado entre más y más términos de la serie infinita sean incluídos en la evaluación de la aproximación. Todo esto es lo que nos lleva directamente a nuestra segunda técnica de aproximación que veremos a continuación, conocida precisamente como teoría de las perturbaciones.