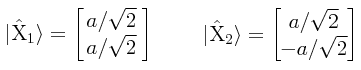Esto es en realidad una simplificación que se justifica al tomar la función general de onda que incluye tanto la parte temporal como la parte espacial:
asignándole a dicha función de onda un tiempo igual a cero. En pocas palabras, con lo que realmente hemos estado trabajando es con lo siguiente:
De este modo, con lo que hemos estado trabajando es con funciones de onda sobre las cuales tomamos una “instantánea fotográfica” en un tiempo igual a cero, lo cual es aceptable y suficiente cuando se trata de funciones de onda que corresponden a estados ligados en donde lo que tenemos son ondas estacionarias. Sin embargo, hay muchos problemas de interés en los cuales nos interesa obtener una idea sobre cómo evoluciona el comportamiento de una función de onda que representa a una partícula de materia de dimensiones sub-microscópicas. Para el análisis de muchos problemas de este tipo, un buen punto de partida para empezar a tomar en consideración el avance del tiempo lo es la ecuación de Schrödinger dependiente del tiempo que dada en notación bra-ket de Dirac tiene el siguiente aspecto:
tomando a Ψ como Ψ = Ψ(t), la parte temporal de la función de onda.
PROBLEMA: Supóngase que se tiene un sistema de dos estados para el cual el operador matricial Hamiltoniano de energía es el siguiente:
Tras obtener los eigenvalores y las eigenfunciones que corresponden a este operador Hamiltoniano, obténgase la función de onda dependiente del tiempo para este sistema.
Supondremos que el sistema tiene los siguientes dos estados linealmente independientes:
El estado más general para la función de onda dependiente del tiempo estará dada entonces por la siguiente combinación lineal normalizada:
siendo la condición de normalización:
Para obtener los eigen-valores λ del sistema y las eigen-funciones, montamos la eigen-ecuación:
Para un sistema de dos estados, el eigenvector será un vector columna de dos renglones:
Entonces la eigen-ecuación matricial viene siendo:
Llevando a cabo la multiplicación matricial:
lo cual nos produce un sistema de ecuaciones simultáneas:
o lo que es lo mismo:
Despejando x1 de la segunda ecuación:
Substituyendo este x1 en la primera ecuación y resolviendo para λ:
La solución de la ecuación cuadrática nos dá las raíces λ que son a su vez los eigenvalores del sistema:
Entonces los dos eigenvalores λ1 y λ2 del sistema son:
Los eigenvalores que acabamos de obtener nos conducen a dos eigenvectores:
Tenemos entonces los siguientes eigenvectores columna:
Estos eigenvectores no están normalizados. La normalización de los mismos nos conduce a los siguientes vectores columna normalizados:
Las combinaciones más sencillas se obtienen haciendo x1 = 1:
Haremos ahora uso de la parte temporal de la ecuación de Schrödinger:
Substituyendo la matriz H y el primer eigenvector columna normalizado, se tiene entonces la siguiente ecuación matricial (la ħ reducida de Planck se ha destacado de color magenta para evitar que pueda ser confundida con el elemento h de la matriz H):
Igualando ambos miembros del primer renglón, se tiene:
Integrando:
Con esto, la primera función de onda debe ser:
o bien:
El segundo eigenvector nos dá una segunda ecuación matricial que es la siguiente:
Llevando a cabo la multiplicación matricial e igualando ambos miembros del mismo renglón, se tiene:
Integrando:
Con esto, la segunda función de onda debe ser:
o bien:
La función general de onda para el sistema será igual a la suma de las dos funciones de onda que han sido obtenidas, o sea:
que viene dando:
o bien, expresando el resultado en notación bra-ket para mayor elegancia:
Ya hemos visto previamente que la función general de onda Ψ(x,t), que incluye tanto la componente espacial como la componente temporal, cuando se recurre al método de separación de variables aplicado en la ecuación de Schrödinger para separar la parte espacial ψ(x) de la parte temporal, quedará expresada como el producto de ψ(x) por un factor e-iHt/ħ siendo H el Hamiltoniano de energía, que para un estado fijo de energía E podemos escribir como:
Esto es válido cuando se tiene un solo estado energético. Sin embargo, el caso general considera no un solo estado aislado sino una cantidad infinitamente grande de estados discretos, montados sobre la estructura matemática del espacio vectorial de Hilbert, y si a cada uno de dichos estados le corresponde su propio factor e-iEt/ħ, entonces la fórmula más general que toma esto en cuenta debe ser la siguiente:
Sin embargo, esta relación como está dada está incompleta, ya que falta agregarle a cada término de la sumatoria su propia constante de amplitud cn, con lo cual la expresión para la función general de onda viene quedando como:
Si Ψ(x,t) está normalizada, las constantes de amplitud cn deben tener valores tales que la suma de los cuadrados de todas ellas será igual a la unidad, lo cual no es difícil de demostrar. Visto de otro modo, la expansión de una función de onda Ψ(x,0) como una sumatoria de funciones de base ortogonales:
es un caso especial de la expansión para Ψ(x,0) en la cual a la variable del tiempo se le ha dado un valor igual a cero, siendo cada término realmente:
Entonces si queremos obtener Ψ(x,t) a partir de Ψ(x,0) debemos restablecer el exponencial que va adjunto a cada término:
Puesto que ωn.=.En/ħ, una forma alterna aceptable de lo anterior es la siguiente:
Lo anterior nos indica el procedimiento general para obtener Ψ(x,t) a partir de Ψ(x,0) para aquellos sistemas físicos discretos que corresponden a estados ligados en los cuales se ha resuelto la ecuación de Schrödinger independiente del tiempo. Simplemente le anexamos a cada función de base su exponencial e-iEt/ħ, tras lo cual se puede intentar una simplificación o una evaluación de la expresión resultante.
PROBLEMA: Dada la función general de onda:
y suponiendo que dicha función de onda está normalizada, demuéstrese que:
Demuéstrese asimismo la validez de la siguiente expresión para el valor esperado del operador Hamiltoniano de energía para esta función general de onda:
Partiendo del hecho de que, por hipótesis, la función de onda Ψ(x,t) se encuentra ya normalizada a la unidad, podemos escribir entonces lo siguiente:
Reacomodando:
En virtud de que, debido a la ortonormalidad, los “términos cruzados” en la sumatoria para m.≠.n se cancelan, lo anterior se reduce a:
o lo que es lo mismo:
Puesto que cada una de las funciones ψn(x) se supone que está normalizada dentro del rango aplicable de la integración, entonces se obtiene:
Echando recurso de la definición aceptada para el valor esperado o esperanza matemática de un operador, para el caso del operador Hamiltoniano de energía se tiene:
Substituyendo en lo anterior la expresión para la función general de onda Ψ(x,t) así como su conjugado complejo Ψ*(x,t):
Reacomodando:
De nueva cuenta, y en virtud de la ortonormalidad, lo anterior se reduce a:
Sabemos ya que una de las eigen-ecuacines fundamentales de la Mecánica Cuántica es la siguiente:
Usando esta eigen-ecuación, obtenemos de este modo el resultado deseado:
Es muy importante tener presente el hecho de que para que se pueda utilizar la relación:
para obtener Ψ(x,t) a partir de Ψ(x,0), es necesario que las funciones ψn(x) formen parte de un conjunto de funciones ortogonales. De no ser así, la función que se esté utilizando para Ψ(x,0) tiene que ser “desintegrada” en una suma de términos ψn(x) que sean linealmente independientes (ortogonales) para poder aplicar la relación que nos dá Ψ(x,t).
PROBLEMA: Supóngase que se tiene una partícula atrapada en un pozo infinito de potencial cuya función de onda inicial es la siguiente:
Encuéntrese una expresión para Ψ(x,t) para dicha partícula.
Lo primero a notar es que la función de onda Ψ(x,0) es impar o antisimétrica, esto es:
Ψ(-x,0) = +Ψ(x,0)
Esto implica que las funciones de onda base ortogonales que sean utilizadas para construír la función Ψ(x,0) tendrán que ser también antisimétricas todas ellas.
Aunque se puede llevar a cabo la expansión de la función cúbica senoidal mediante series de Fourier, podemos recurrir a una identidad como la siguiente:
Elevando al cubo:
Simplificando:
Obtendremos primero el valor de la constante A mediante la condición de normalización:
Esta es una integral de la sexta potencia de un término senoidal. Para poder llevar a cabo la integración, tenemos que recurrir a una tabla de integrales para encontrar alguna forma convencional que nos permita abatir el orden cúbico del exponente. Una manera de hacerlo es la siguiente:
De esto se obtiene, para n.=.6:
A continuación recurrimos a la siguiente integral convencional también sacada de las tablas:
Con esto podemos llevar a cabo la integración del término cúbico senoidal tomando límites:
Por lo tanto, la constante de normalización A se obtiene como:
Para una partícula atrapada en un pozo de potencial con paredes infinitamente altas, los eigenvalores de energía están dados por la relación:
Obviamente, los eigenvalores que requerimos son los primeros dos eigenvalores impares, o sea:
Con esto, podemos escribir la función de onda generalizada Ψ(x,t) de la siguiente manera:
En el caso de un estado estacionario único para el cual la energía E está prefijada de modo unívoco, todas las esperanzas matemáticas son constantes, esto es, no varían con el tiempo. Para hacer que algo ocurra conforme va transcurriendo el tiempo, se debe tomar una combinación lineal de por lo menos dos estados estacionarios, y de hecho esta es la combinación más susceptible de un análisis simplificado; es lo que en la Mecánica Cuántica se conoce como el problema de los estados mezclados para el cual, cuando tenemos dos estados “puros” mezclados (designando a cada estado estacionario como un estado “puro”), la función general de onda viene siendo:
En esta expresión, se supone que las funciones ψ1(x) y ψ2(x) ya están normalizadas; las constantes a y b fijan la contribución individual de cada función de onda al total de la función de onda compuesta Ψ(x,t), la cual a su vez tendrá que ser normalizada en función de las magnitudes de a y b con la finalidad de que se le pueda dar también una interpretación probabilista a ||Ψ(x,t)||2. Puesto que las funciones espaciales de onda ψ1(x) y ψ2(x) son ortogonales, esto es, de frecuencias distintas, podemos imaginar una “instantánea fotográfica” en la cual ambos términos “puros” de Ψ(x,t) se suman dando algo como lo que se muestra en las siguientes figuras:
Para el caso en el cual se tienen dos estados estacionarios que se encuentran mezclados:
Suponiendo que tanto a y b como ψ1(x) y ψ2(x) son reales, desarrollando y simplificando lo anterior se obtiene:
Siendo ||Ψ(x,t)||2Δx la probabilidad de encontrar a la partícula dentro de un intervalo Δx en un cierto tiempo, la expresión anterior que involucra el tiempo explícitamente nos dá una imagen dinámica del movimiento de la partícula, o mejor dicho, de la onda de materia. Siendo el argumento cosenoidal ωt igual a (E2-E1)t/ħ, entonces con:
obtenemos en forma aproximada para el período de oscilación τ del sistema:
Como un chequeo sobre el principio de incertidumbre, tomando ΔE.=.E2-E1 y Δt.=.τ, se tiene entonces que:
y puesto que el producto es mayor que ħ/2, el principio de incertidumbre se cumple en este caso.
Analizaremos ahora el comportamiento dinámico de ||Ψ(x,t)||2 para dos estados mezclados, habido el hecho de que esta es una función de onda que va evolucionando con el tiempo. Supondremos que los dos estados mezclados son los que corresponden a los primeros dos estados energéticos E0 y E1 de un oscilador armónico simple (el estado fundamental y el primer estado excitado), cuyas eigenfunciones ψ0(ξ) y ψ1(ξ) de acuerdo a lo que se vió previamente en la entrada titulada “Oscilador armónico simple: solución ondulatoria” son las siguientes en función de la variable adimensional ξ que podemos tomar como la posición de la partícula (se dejarán pendientes para la siguiente entrada los cálculos más detallados requeridos en el análisis de este problema de dos mezclados del oscilador armónico simple, esto con la finalidad de enfocarnos aquí sobre un aspecto importante de lo que sucede):
La gráfica (estática) que junta cada una de estas dos eigenfunciones (usando x en lugar de ξ para mayor claridad en la especificación de la posición) es la siguiente:
En contraste con las gráficas de estas dos eigenfunciones “puras” para el oscilador armónico simple, la gráfica de la densidad de probabilidad ||Ψ(x,t)||2 será diferente conforme vaya avanzando el tiempo. La función de onda compuesta que estaremos utilizando para el graficado será la siguiente:
Los factores 1/√2 que aparecen multiplicando cada término no tienen nada que ver con normalización alguna sobre ψ0 y ψ1 ya que se supone que ambas funciones de onda están normalizadas. Son los factores de normalización de Ψ(x,t) para darle una contribución en partes iguales a cada estado “puro” dentro de Ψ(x,t) manteniendo a esta última normalizada. Para analizar el efecto del tiempo, podemos prescindir en los graficados de los cuadrados de las eigenfunciones, o sea de |ψ1(x)|2 y |ψ2(x)|2, en virtud de que ambas cantidades son invariantes con el tiempo, concentrando nuestra atención sobre la parte que varía con el tiempo. Sin entrar en los detalles específicos de los cálculos numéricos, encontramos que la gráfica de para un tiempo t.=.0 tiene el siguiente aspecto:
mientras que para un tiempo tal que ωt.=.π/4 la gráfica correspondiente será la siguiente:
Para un tiempo tal que ωt.=.π/2, la gráfica correspondiente será la siguiente:
Para un tiempo tal que ωt.=.3π/4, la gráfica correspondiente será la siguiente:
Para un tiempo tal que ωt.=.π, la gráfica correspondiente será la siguiente:
Para un tiempo tal que ωt.=.5π/4, la gráfica correspondiente será la siguiente:
Y para un tiempo tal que ωt.=.3π/2, la gráfica correspondiente será la siguiente:
No es necesario obtener más graficados para darnos cuenta del comportamiento oscilatorio del cuadrado de la función de onda ||Ψ(x,t)||2 para este sistema físico con dos estados mezclados. Suponiendo que las dos funciones de base corresponden a los primeros dos estados (el estado fundamental y el primer estado excitado) de un oscilador armónico simple unidimensional, esto nos permite darnos una idea sobre cómo el comportamiento del oscilador armónico simple cuántico se puede asemejar al de una partícula clásica. Ya hemos visto previamente cómo el comportamiento del oscilador armónico simple cuántico puede ser muy diferente del comportamiento que predice la mecánica clásica. Desde el punto de vista cuántico y para un estado definido de energía, la probabilidad de encontrar una partícula en un punto dado es independiente del tiempo. Clásicamente, sin embargo, la partícula del oscilador armónico simple oscila de tal manera que la probabilidad de que una partícula se encuentre dentro de cierto elemento pequeño de volumen en cierto lugar del espacio es diferente de un instante de tiempo a otro. De hecho, la probabilidad es igual a cero o a la unidad, ya que clásicamente hablando la partícula está allí o no lo está. Del mismo modo, clásicamente, el momentum del oscilador armónico simple está cambiando continuamente con el tiempo. La descripción del momentum de acuerdo con formalismo mecánico-cuántico es tal que para un estado de energía definida hay una distribución estadística de los momentums que corresponden a varias ondas planas en las cuales la función de onda puede ser expandida. Cada onda plana corresponde a un estado definido de momentum, con el carácter estacionario de cada estado implicando que la probabilidad de que cierto momentum será obtenido es constante y permanece invariable con el tiempo. La pregunta que nos hacemos entonces es: ¿cómo puede ser el formalismo clásico equivalente al formalismo mecánico-cuántico, o bien un caso especial de este último? La conexión entre el formalismo clásico y el formalismo cuántico aparece cuando se considera el movimiento de un paquete de onda de materia. En el comportamiento que hemos obtenido arriba para el caso de dos estados mezclados, puede verse en las figuras que la función de onda tiene un comportamiento que se parece mucho al de una partícula oscilando con un movimiento armónico simple clásico. La frecuencia de la oscilación es la que corresponde a la frecuencia observada en el caso de la oscilación clásica. Parece razonable suponer entonces que si se llevara a cabo la superposición de un gran número de estados de energía, nos acercaríamos más y más a lo que vendría siendo un paquete de onda Gaussiano que oscilaría de una manera muy parecida a la manera en la que se mueve una partícula clásica. Desde esta perspectiva, la descripción clásica del movimiento de una partícula es aquella para la cual se pueden especificar simultáneamente tanto la posición como el momentum de la partícula con cierto grado de precisión (más no con precisión ilimitada). El estado del sistema es descrito por un paquete de ondas de materia cuya posición más o menos especifica la posición de la partícula y obedece las reglas clásicas dentro de los límites del error de medición. Es importante que la energía no esté completamente especificada, porque si el sistema está en un estado de energía definida la función de onda no puede describir un movimiento oscilatorio.
El siguiente gráfico animado nos muestra, dinámicamente, el comportamiento oscilatorio de ||Ψ(x,t)||2 para los dos estados mezclados del oscilador armónico simple:
PROBLEMA: Usualmente, el agregar un factor global de fase eiφ (en donde φ es una constante) a una función de onda no tiene significado físico alguno ya que se cancela al momento de efectuar los cálculos de los valores esperados de las observables físicas. Sin embargo, si se le agrega un factor de fase local a uno de los coeficientes de expansión en un sistema de dos estados de la manera que se muestra a continuación:
se encuentra que eventualmente dicho factor de fase sí se hace presente en los cálculos finales de las esperanzas matemáticas de las observables físicas. Obténganse la constante de normalización A y la función de onda general Ψ(x,t) así como el cuadrado de la función de onda ||Ψ(x,t)||2 para el caso de una partícula atrapada en un pozo de potencial con paredes infinitamente altas. Usando esto, obténgase la esperanza matemática de la posición de la partícula, esto es:
Empezaremos con la condición de normalización:
El producto de la función Ψ(x,t) por su conjugado complejo Ψ(x,t)* viene siendo:
Llevando a cabo los productos:
La integración de lo anterior viene quedando entonces como:
Puesto que las funciones de base ψ1(x) y ψ2(x) son ortogonales, se tiene entonces que:
Por lo tanto:
Usando para la expansión el estado fundamental E1 y el primer estado excitado E2, para una partícula atrapada en un pozo de potencial infinito, se tiene entonces la siguiente función de onda generalizada:
Substituyendo en esta expresión la constante de normalización A así como las eigenfunciones que corresponden a las de los primeros dos estados cuánticos de una partícula atrapada en un pozo de potencial infinito, se tiene entonces:
Simplificando:
Factorizando para simplificar aún más llegamos a la siguiente expresión aceptable para cálculos posteriores:
Usando lo anterior, ahora calcularemos ||Ψ(x,t)||2 usando la definición:
con lo cual:
Efectuando los productos y utilizando:
así como:
se tiene entonces:
Usando la definición de la esperanza matemática de la posición de la partícula, se tiene ahora:
Tenemos tres integrales a resolver. Para llevar a cabo la primera integración, recurrimos a las tablas de integrales que nos proporcionan la siguiente forma convencional:
Por lo tanto:
Usando la misma forma convencional, se obtiene:
Nos falta la evaluación de la integral que corresponde al tercer término, de la cual podemos sacar fuera del signo integral el factor cos(3ωt-φ):
Para la evaluación de esta integral, haremos recurso de la siguiente identidad trigonométrica:
Haciendo α = πx/a y β = 2πx/a, se tiene entonces:
A continuación, procedemos a integrar ambos miembros de esta igualdad:
Tenemos ahora del lado derecho de la igualdad dos integrales que llamaremos integral # 1 e integral # 2. Para poder continuar adelante, echando mano de una tabla de integrales obteniendo la siguiente forma convencional:
De este modo la integral # 1 termina siendo evaluada como:
Por otro lado, la integral # 2 resulta ser:
De este modo, juntando las integrales # 1 y # 2, se tiene lo siguiente:
Entonces, juntando los resultados de las tres integrales, se tiene lo siguiente:
que podemos simplificar un poco más como:
Este es un resultado interesante y extraordinario, porque nos dice que la esperanza matemática de la posición de la partícula, lejos de estar especificada todo el tiempo justo a la mitad de la distancia que hay entre ambas paredes, está variando con el tiempo. Una gráfica de esta expresión para un pozo de potencial de anchura a.=.5 usando un ángulo de fase igual a φ.=.π/4 presenta el siguiente aspecto (la gráfica está dada de modo tal que en el eje vertical se está representando el avance del tiempo a partir de un tiempo igual a cero, mientras que el eje horizontal muestra cómo la esperanza matemática de la posición oscila de un lado al otro con respecto a la línea central imaginaria de color verde que divide al pozo de potencial en dos partes iguales):
En general, la obtención de la función de onda Ψ(x,t) a partir de Ψ(x,0) para el caso discreto en el cual se tienen estados ligados es un asunto relativamente fácil, conceptualmente hablando, que se lleva a cabo de manera casi mecánica. Sin embargo, en lo que compete al caso continuo, como el que corresponde a las partículas libres, la prescripción que se ha dado no se suficiente, y es necesario recurrir a artillería más potente para poder manejar el caso continuo.