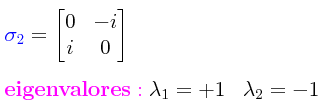Ahora bien, podemos hablar del valor promedio de una matriz o la esperanza matemática de una matriz si tomamos simplemente el promedio aritmético de sus eigenvalores. Si hacemos tal cosa en el caso de la matriz Sz (o la matriz Sx, que al fin y al cabo ambas tienen los mismos eigenvalores), podemos ver que su esperanza matemática será:
Es muy importante no confundir los eigenvalores de una matriz con el concepto de las esperanzas matemáticas. La esperanza matemática o valor esperado en una medición puede tomar, en principio, cualquier valor real. En cambio, el eigenvalor de Sz sólo puede tomar uno de dos valores, -ħ/2 y +ħ/2. El hecho de que la esperanza matemática de la matriz Sz sea igual a cero nos indica que, en promedio, hay tantas probabilidades de obtener saliendo del horno partículas cuyo spin está apuntando “hacia arriba” (↑) como de obtener partículas cuyo spin está apuntando “hacia abajo” (↓). Hay otra forma alterna en la cual podemos representar el procedimiento de cálculo anterior, que es la siguiente:
Esta forma se acerca aún más a la interpretación probabilista de obtener los eigenvalores físicos que codifica la matriz. Lo que tenemos en la segunda línea nos dice que hay una probabilidad p1 igual a 1/2 de obtener el eigenvalor λ1, y que hay una probabilidad p2 también igual a 1/2 de obtener el eigenvalor λ2. Esto es importante, porque las probabilidades de obtener cada eigenvalor físico corresponden directamente con las intensidades de las líneas espectrales observadas en el laboratorio. En este caso, la intensidad registrada del haz de las partículas cuyo spin está apuntando “hacia arriba” será igual a la intensidad registrada del haz de las partículas cuyo spin está apuntando “hacia abajo”. ¿Y si las intensidades fueran diferentes? En tal caso, esto se verá reflejado en la diferencia que habrá en los eigenvalores de la misma matriz. Si un eigenvalor de una matriz resulta ser dos veces mayor que otro, entonces tendrá una intensidad mayor al ser medida dicha cantidad en el laboratorio. A fin de cuentas, toda la información física que estamos buscando del sistema viene saliendo del interior de la matriz que describe al sistema. Esta es la esencia filosófica de la Mecánica Matricial.
Hasta aquí hemos hablado de un solo aparato Stern-Gerlach que está recibiendo un haz de partículas que están saliendo de un horno orientadas al azar, el cual subdivide a las partículas en dos haces opuestos. Pero es posible en principio llevar a cabo experimentos con dos aparatos Stern-Gerlach en sucesión, uno tras otro. Supóngase que se tiene un primer aparato Stern-Gerlach alineado verticalmente (paralelo al eje-z) que recibe a las partículas, subdividiéndolas en dos haces. ¿Qué sucedería si el segundo aparato Stern-Gerlach lo alineamos en la misma dirección que el primero, pero le metemos un haz de partículas cuyo spin ya sabemos que apunta en cierta dirección, digamos “hacia arriba” (↑)? En tal caso, ya no habrá una subdivisión posterior del haz, porque todas las partículas que le están entrando al segundo aparato, con su spin apuntando “hacia arriba” (↑) saldrán del segundo aparato con su spin apuntando también “hacia arriba” sin haber partículas cuyo spin esté apuntando “hacia abajo”. En este caso, con la medición llevada a cabo con el segundo aparato, ya no se tienen dos haces con probabilidades repartidas en partes iguales. Se tiene un solo haz de partículas, las partículas cuyo spin está apuntando “hacia arriba” (↑) con una probabilidad p1 igual a la unidad (la certeza estadística) de obtener tales partículas, no habiendo partícula alguna cuyo spin esté apuntando “hacia abajo” (↓), siendo la probabilidad p2 de que tal cosa ocurra igual a cero, lo cual podemos representar del modo siguiente:
Ahora bien, si en un experimento con un solo aparato Stern-Gerlach giramos el aparato 90° hacia cualquiera de los otros dos ejes coordenados rectangulares Cartesianos, el haz de partículas que están saliendo del horno se seguirá subdividiendo en dos haces, -ħ/2 y +ħ/2. Estando descrita la situación física para cada uno de los tres ejes coordenados por igual con cada una de las matrices de Pauli, esto implica necesariamente que en algo sí son definitivamente iguales las tres matrices de Pauli: cada una de las tres matrices de Pauli tiene los mismos dos eigenvalores que la otra (esto lo podemos comprobar fácilmente montando la ecuación secular en cada caso con la finalidad de obtener los eigenvalores para cada matriz de Pauli):
Aquí cabe formular una pregunta de mérito: ¿Cómo es posible que la matriz de Pauli σ2, pese a tener entradas imaginarias, se las arregla de algún modo para que sus valores propios eigen sigan siendo valores reales susceptibles de ser medidos y confirmados con un aparato de laboratorio? Desde el punto de vista puramente matemático, la respuesta a esta interrogante la podemos apreciar mejor tomando primero el conjugado complejo de la matriz de Pauli obteniendo de este modo σ*, tras lo cual tomamos la transpuesta de esta matriz conjugada compleja (intercambiando los renglones de la matriz por las columnas y viceversa) obteniendo (σ*)T, a lo cual hemos dado en llamar el transconjugado complejo de la matriz, representándolo en este caso como σ2†. Hecho esto, si comparamos σ2 con σ2† vemos ambas son idénticas:
En pocas palabras, la matriz σ2 (al igual que las otras dos matrices de Pauli) es una matriz Hermitiana. Y la característica principal que distingue a toda matriz Hermitiana (al menos la de mayor importancia para los científicos) es que está garantizado plenamente que sus valores eigen siempre serán valores reales, jamás serán valores imaginarios o complejos (esto ya lo vimos previamente en la entrada titulada “Vectores y matrices II”). Esto pone a la matriz σ2 a la par con las matrices σ1 y σ3, lo cual significa que la asignación de cada una de las tres matrices de Pauli a cada una de las tres coordenadas rectangulares Cartesianas (x,y,z) es completamente arbitraria. Así como podemos hacer:
igualmente podemos hacer sin ningún problema:
aunque en la gran mayoría de los textos introductorios se acostumbra reservar la matriz de Pauli σ2 cuyas entradas son imaginarias para el eje-y con la finalidad de no minimizar malentendidos y confusiones.
De las tres matrices de Pauli dadas arriba, sólo una de ellas (σ3) es una matriz diagonal. Sin embargo, y como lo hemos visto previamente en otras entradas, una vez que se han obtenido los eigenvalores de una matriz M dicha matriz puede ser diagonalizada de modo tal que sus eigenvalores aparezcan como las entradas puestas a lo largo de la diagonal principal. Podemos efectuar esto con una transformación de semejanza obteniendo primero una matriz X (construída con los eigenvectores de la matriz a ser diagonalizada) y con ello su adjunta la matriz X† con lo cual pre-multiplicando y post-multiplicando ya sea como X·M·X† ó como X†·M·X (el resultado final sigue siendo el mismo en ambos casos) se obtiene la matriz equivalente M’ diagonalizada (esto también fue cubierto en la entrada “Vectores y matrices II”). Esta es una manera de diagonalizar cualquier matriz. Pero hay otra manera más expedita de hacerlo, la cual consiste simplemente en escribir los eigenvalores de la matriz M a lo largo de su diagonal principal llenando de ceros las otras entradas de la matriz, en virtud de que toda matriz M que es diagonalizada termina siendo invariablemente una matriz M’ cuyas entradas son precisamente los eigenvalores de la matriz M (ambas matrices M y M’ poseen los mismos eigenvalores, precisamente en ello radica la semejanza de dos matrices tal y como se define en el Álgebra Lineal). Esto implica que todas las matrices de Pauli pueden ser diagonalizadas hacia una misma matriz diagonal, cuyas entradas +1 y -1 codifican los dos valores posibles del momento angular de spin:
Todo esto explica el por qué, matricialmente hablando, no importa que el aparato Stern-Gerlach pueda ser girado en la forma descrita y de cualquier modo se sigan obteniendo dos haces de partículas, un haz con un valor observable igual a +ħ/2 y el otro haz con un valor observable igual a -ħ/2, con el signo menos (-) en el segundo caso simplemente indicando que uno de los haces saldrá en una dirección al otro haz al pasar por el aparato Stern-Gerlach. Las tres matrices de Pauli son semejantes; sin embargo, no son iguales. Tienen los mismos valores eigen, pero no es posible obtener una a partir de la otra o una a partir de una combinación lineal de las otras dos mediante operaciones matriciales elementales en virtud de que son linealmente independientes (obsérvese que aquí estamos estirando el concepto de dos vectores linealmente independientes al concepto de dos matrices linealmente independientes, de este tipo de generalizaciones y abstracciones es precisamente de lo que tratan las matemáticas). Lo que se quiere decir con esto es que si se trata de llevar a cabo algo como lo siguiente:
se puede confirmar casi de inmediato que las únicas constantes a y b para las cuales lo anterior se cumple es para el caso trivial en el cual ambas constantes son iguales a cero.
Al salir un haz de partículas del horno, antes de entrar a un aparato Stern-Gerlach, el momento angular de spin de cualquiera de las partículas puede estar orientado en cualquier dirección, no habiendo dos haces perfectamente definidos. Esto significa que, al pasar el haz de partículas por el aparato Stern-Gerlach, algo ocurre desde el punto de vista mecánico-cuántico que produce una especie de “colapso” que altera en forma radical el aspecto aparentemente caótico en las direcciones de los spins de las partículas que están saliendo del horno. Este “colapso” que identificamos con el proceso de observación llamado frecuentemente el acto de medición nos proporciona cierta información sobre el sistema. Sin embargo, si intentamos extraer información adicional del sistema, el acto de medición se resiste tozudamente a proporcionarnos información adicional. Cualquier información nueva que se obtenga llegará al costo de destruír información obtenida previamente. Esto es inherente a las matemáticas matriciales usadas para describir al sistema. El experimento lo único que hace es confirmarnos lo que las matemáticas nos advierten de antemano que va a suceder, y no hay manera en la cual sea posible cambiar esto. Una manera de ilustrar esto es la siguiente:
Una vez efectuada la medición (la observación del sistema), en este caso cualquier medición posterior en circunstancias similares nos seguirá produciendo dos haces de partículas (o un solo haz, en caso de que los aparatos Stern-Gerlach adicionales tengan una salida para sólo uno de los haces bloqueando el otro haz). Al haberse llevado a cabo la medición, la descripción matemática del sistema está anclada sólidamente a la matriz. Pero hay que hacerse a la idea de que el comportamiento que se está observando está siendo llevado a cabo sobre un gran número de partículas (al cual se le suele dar el nombre de ensamble), no sobre una partícula individual. La matriz nos refleja un comportamiento estadístico. No existe matriz alguna para tratar el comportamiento de una sola partícula. Esto marca una fisura con la física clásica Newtoniana en la cual es posible en principio describir el comportamiento físico de cualquier fenómeno de manera completamente determinística. Es posible predecir con bastante precisión con las leyes de Newton el movimiento de los planetas, los eclipses lunares y los vuelos de los cometas. Pero todos los intentos de extender la validez de las leyes clásicas hacia lo infinitamente pequeño eventualmente se topan con una barrera infranqueable.
Ahora retomaremos un asunto que había quedado pendiente en la entrada anterior, el asunto de lo que sucede cuando se utilizan dos aparatos Stern-Gerlach, el primero de los cuales (SG1) toma un haz colimado de partículas acabadas de salir del horno separando dicho haz en dos haces de partículas que podemos indentificar de varias maneras como (+,↑,+1/2,“spin apuntando hacia arriba”, etc.) y como (-,↓,-1/2,“spin apuntando hacia abajo”, etc.), uno de las cuales ingresa al segundo aparato Stern-Gerlach (SG2) que también tiene dos salidas como el primer aparato para separar el haz polarizado de partículas que entra al segundo aparato, tomándose ahora en cuenta la posición relativa que guarda el segundo aparato con respecto al primero.
Al pasar las partículas (acabadas de salir del horno) por el primer aparato Stern-Gerlach SG1 que supondremos que está alineado para medir el momento angular de spin Sz, hay tantas probabilidades (50%) de obtener partículas cuyo spin esté apuntando “hacia arriba” como de obtener partículas cuyo spin esté apuntando “hacia abajo”. Supóngase que tomamos el haz de partículas cuyo spin está apuntando “hacia arriba” (↑) ingresando dichas partículas al segundo aparato Stern-Gerlach SG2 que también tiene dos canales de salida. ¿Cuales serán las probabilidades de obtener a la salida del segundo aparato partículas cuyo spin esté apuntando en cierta dirección y de obtener partículas cuyo spin esté apuntando en la dirección opuesta? Esto depende del ángulo relativo de orientación que hay entre los dos aparatos, al cual llamaremos φ. Supóngase que inicialmente se tiene a los dos aparatos Stern-Gerlach perfectamente alineados el uno con respecto al otro, en forma paralela a la vertical para medir Sz, de modo tal que el ángulo φ entre sus orientaciones relativas es igual a cero. En tal caso, la situación que se tiene es la siguiente:
En este caso, puesto que no está entrando al segundo aparato SG2 una sola partícula cuyo spin esté apuntando “hacia abajo”, la probabilidad de obtener partículas saliendo de su canal “-” al medir Sz es igual a cero. Todas las partículas que ingresen al segundo aparato saldrán por el canal “+”, habiendo una probabilidad del 100% de obtener partículas cuyo spin esté apuntando “hacia arriba” de las partículas que están ingresando al segundo aparato.
Ahora supóngase que, manteniendo fijo el primer aparato SG1, giramos el segundo aparato con respecto al primero, en un ángulo φ de 90°, en forma tal que el segundo aparato SG2 quedará alineado perpendicularmente con respecto al primero, en una posición justa para medir Sx en lugar de Sz. En tal caso, la informacion que se tenía sobre el conocimiento de Sz se pierde, y habrá probabilidades iguales (50%) de obtener partículas cuyo spin está apuntando en cierta dirección y de obtener partículas cuyo spin está apuntando en la dirección opuesta. La situación es ahora la siguiente:
Puesto que, al llevarse a cabo el experimento, el laboratorista no está limitado a girar el segundo aparato SG2 de forma tal que quede alineado con respecto al primer aparato SG1 en ángulos de cero grados y de 90°, sino que puede girar el segundo aparato SG2 a cualquier ángulo φ comprendido entre los cero grados y los noventa grados, ¿qué es lo que sucede dentro de ese gran intervalo? ¿Cómo se reparten las probabilidades? ¿Cómo pasamos de una situación en la que las probabilidades están repartidas en 100% y 0% (aparatos alineados ambos para medir Sz) a la situación en la que las probabilidades están repartidas en 50%-50% (primer aparato alineado para medir Sz y segundo aparato alineado para medir Sx)? ¿Cuál deberá ser la matriz que represente una situación así? Obviamente, en la región comprendida entre φ.=.0° y φ.=.90°, las probabilidades para los canales de salida “+” y “-” serán diferentes. Esperamos que, para un ángulo relativo φ entre los dos aparatos, digamos de 60°, se tenga una situación como la siguiente:
A estas alturas, resulta conveniente definir un vector de probabilidad que sea capaz de variar sus componentes en forma tal que las probabilidades relativas se reduzcan a los casos especiales φ.=.0° y φ.=.90° que tenemos arriba, pero que de algún modo la probabilidad total (al sumarse las probabilidades relativas) codificada en dicho vector se mantenga igual a la unidad (al 100%). Considerando la naturaleza del asunto, no es necesario ir muy lejos para encontrar un vector de probabilidad que se puede ajustar a los requerimientos de esta situación, siendo dicho vector de probabilidad (enunciado como vector columna) el siguiente:
La comprobación de que este vector de probabilidad es un vector unitario se lleva a cabo tomando el producto interno (producto punto) de dicho vector v consigo mismo, para lo cual usamos la transpuesta vT del vector y efectuamos el producto como si fuese un producto matricial:
Puesto que los valores eigen de cualquiera de las tres matrices de Pauli son +1 y -1, todas ellas son semejantes a una matriz diagonal σ cuyas entradas son -1 y -1. Podemos usar esta matriz diagonal σ para incorporar el ángulo de rotación φ (y con ello el aspecto probabilista en función de dicho ángulo) a la nueva descripción del sistema de dos aparatos Stern-Gerlach secuenciales de la siguiente manera:
En base a lo discutido arriba, al término que tenemos en la última línea le podemos dar la siguiente simbolización:
En el lado izquierdo de la igualdad se tiene la simbolización que se le ha dado a todo como la esperanza matemática del momento angular del spin para partículas cuyo spin se designa como 1/2, y en el lado derecho de la igualdad se tiene lo que es en esencia una interpretación probabilista de los valores esperados en la obtención de los valores.
Es importante tener en mente en todo momento que aquí se está manejando una situación en la cual se tiene no uno sino dos aparatos Stern-Gerlach en cascada.
La “prueba de fuego” es, desde luego, si la expresión obtenida puede reducirse a los resultados que esperamos para los casos especiales φ.=.0° y φ.=.90°. Para φ.=.0° la expresión se reduce a:
Esto es precisamente lo que esperamos cuando se tienen los dos aparatos Stern-Gerlach alineados el uno con respecto al otro a un ángulo φ.=.0° en la posición para medir Sz, el segundo aparato SG2 debe producir un haz al 100% en su canal de salida “+” y cero partículas en su canal de salida “-”, dando una esperanza matemática igual a +ħ/2. Para φ.=.90° la expresión se reduce a:
Esto también es justo lo que esperamos cuando se tienen los dos aparatos Stern-Gerlach alineados el uno con respecto al otro a un ángulo φ.=.90°, con el primer aparato SG1 en la posición requerida para medir Sz y con el segundo aparato SG2 en la posición requerida para medir Sx, destruyéndose la información producida por el primer aparato y terminando con una situación en la cual el segundo aparato SG2 produce dos haces con las probabilidades repartidas en partes iguales en ambos canales de salida “+” y “-”.
Ahora bien, para un ángulo intermedio como φ.=.60°:
Esta es precisamente la situación reflejada en la última figura de arriba.
Designando como p1 a la probabilidad cos2(φ/2) de que la partícula tenga un valor característico eigen igual a +1 y como p2 a la probabilidad sen2(φ/2) de que la partícula tenga un valor característico eigen igual a -1, para un sistema combinado de dos aparatos Stern-Gerlach en el cual el segundo aparato SG2 vaya siendo girado a un ángulo φ con respecto a la posicion del primer aparato, si hacemos una gráfica de estas probabilidades en función del ángulo de rotación φ obtendremos una gráfica dual como la siguiente:
De acuerdo con esta gráfica dual, al principio cuando ambos aparatos Stern-Gerlach SG1 y SG2 están alineados el uno con respecto al otro a un ángulo φ.=.0° la probabilidad p1 de obtener un haz de partículas del canal de salida “+” es igual a la unidad (la certeza), mientras que la probabilidad p2 de obtener un haz de partículas del canal de salida “-” es igual a cero. Conforme el segundo aparato va siendo girado con respecto al primero, la probabilidad de obtener partículas del canal de salida “+” va disminuyendo mientras que la probabilidad de obtener partículas del canal de salida “-” va aumentando, hasta que en cierto punto para un ángulo φ.=.90° las probabilidades de obtener partículas saliendo por ambos canales se igualan al 50%. ¿Y qué del caso en el cual el segundo aparato Stern-Gerlach sigue siendo girado más allá de los 90°, de modo tal que el aparato SG2 termine quedando en una posición vertical opuesta por completo a su posición original, a un ángulo φ.=.180°, de modo tal que mientras que el primer aparato SG1 mide +Sz el segundo aparato medirá -Sz? La gráfica dual de arriba parece indicarnos que las curvas probabilistas se extenderán suavemente más alla de los 90° en la forma mostrada. Y en tal caso, la evaluación de la expresión del sistema nos arroja el siguiente resultado:
Pero aquí nos enfrentamos a una aparente paradoja si consideramos que el aparato Stern-Gerlach es tan solo un instrumento de medición incapaz de invertir el momento angular de spin de las partículas. Si trabajamos sobre esta hipótesis y se continúa girando el segundo aparato más allá de los 90°, haciéndolo llegar incluso hasta los 180° lo que se tendría en principio es una situación como la siguiente:
En este esquema, las partículas cuyo spin está apuntando “hacia arriba” que entran al segundo aparato SG2 seguirían saliendo por el canal de salida del segundo aparato marcado como “+”, no pudiendo salir del segundo aparato particula alguna con su spin apuntando “hacia abajo” porque no entró al segundo aparato partícula alguna con su spin apuntando “hacia abajo” La única diferencia sería que la posición de los canales de salida “+” y “-” se han invertido como consecuencia del giro de rotación. Pero si esto fuera así, la gráfica dual dada arriba para las probabilidades p1 y p1 parecería perder su validez para un giro superior a los 90°. Habría de hecho dos situaciones posibles, ambas desagradables desde el punto de vista estético. En la primera situación, para un giro del segundo aparato SG2 superior a los 90°, los haces de partículas mantendrían sus valores de +ħ/2 y -ħ/2 hasta que el giro llegara a los 270°, en donde por simple simetría un giro mayor restablecería la situación previa:
La otra posibilidad es que tras el filtrado de partículas llevado a cabo por el primer aparato SG1, simple y sencillamente no haya partículas apuntando “hacia abajo” disponibles para nada, no obteniéndose haz alguno de partículas para ángulos de giro superiores a los 90°:
La paradoja se puede resolver si se considera que al hablar de dos “canales” de salida en realidad se ha estado hablando en forma artificiosa, como si hubiera un duende dentro del aparato separando las partículas que apuntan “hacia arriba” de las partículas que apuntan “hacia abajo” y echando cada una por su respectivo canal. Después de todo, lo que hay en el interior de un aparato Stern-Gerlach es simplemente un par de imanes configurados para producir un campo magnético no homogéneo. Al invertir por completo el segundo aparato SG2 con respecto al primero, el gradiente del campo magnético (-∂B/∂z) del segundo aparato está invertido con respecto al gradiente del primer aparato (∂B/∂z). Si prescindimos de la idea de que se tienen dos canales de salida disponibles, entonces habrá una sola gráfica probabilista para el experimento Stern-Gerlach secuencial, como la siguiente:
Con la finalidad de que el lector pueda adquirir una mayor familiaridad en la resolución de la aparente paradoja, se le recomienda visitar la siguiente página elaborada por el Profesor David M. Harrison de la Universidad de Toronto en Canadá, en la cual el lector puede “conectar” en cascada secuencial hasta tres aparatos Stern-Gerlach, pudiendo girarlos independientemente en cualquier ángulo (sobre el mismo plano-xz perpendicular al haz que viaja sobre el eje-y) desde 0° hasta 360° (la demostración requiere que el navegador esté equipado con el “add-on” Flash de Macromedia):
Volvamos ahora al caso en el cual se tiene un solo aparato Stern-Gerlach. Puesto que (estadísticamente hablando) hay tantas partículas saliendo del aparato con su spin apuntando “hacia arriba” como partículas saliendo del aparato con su spin apuntando “hacia abajo”, la suma de las probabilidades en ambos casos debe ser igual a la unidad ya que cualquier partícula debe corresponder a uno de ambos tipos:
De acuerdo a la definición probabilista que se le ha dado a la esperanza matemática de una matriz en función de sus valores eigen, la esperanza matemática de la matriz de Pauli σ1 viene siendo:
En base a esta definición estadística que se le ha dado al valor promedio de una matriz, representando como p1 a la probabilidad de que la partícula tenga un valor característico eigen igual a +1 y como p2 a la probabilidad de que la partícula tenga un valor característico eigen igual a -1, se puede afirmar lo siguiente:
siendo esta la probabilidad de que las partículas salgan del aparato Stern-Gerlach con su spin apuntando “hacia arriba”, mientras que por otro lado:
siendo esta la probabilidad de que las partículas salgan del aparato Stern-Gerlach con su spin apuntando “hacia abajo”. Iguales conclusiones se pueden obtener de inmediato para las otras dos matrices de Pauli σ2 y σ3. Esto nos indica que las probabilidades están determinadas por la esperanza matemática (valor promedio) de la matriz. En el caso de las matrices de Pauli, las esperanzas matemáticas de las tres son iguales a cero, lo cual arroja como resultado que las probabilidades p1 y p2 sean ambas iguales a 1/2. Sin embargo, ¿qué ocurriría para un sistema físico en el cual la esperanza matemática de la matriz que representa sus eigenvalores no sea igual a cero? En tal caso, las probabilidades serán diferentes, y las relaciones dadas arriba nos dán la clave para obtener dichas probabilidades. Y esto es precisamente lo que ocurre en el caso de un experimento combinado en el que se utilizan dos aparatos Stern-Gerlach.
Si la esperanza matemática de una matriz 2×2 es igual no a cero sino a +1, entonces p1 (que mide la probabilidad para el eigenvalor +1) debe ser igual a 1 y p2 (que mide la probabilidad para el eigenvalor -1) debe ser igual a cero. La cantidad física que representa la matriz tendrá un valor bien definido de 1. En cambio, si la esperanza matemática de una matriz 2×2 es igual no a cero sino a -1, entonces p1 debe ser igual a cero y p2 debe ser igual a 1. La cantidad física que representa la matriz tendrá un valor bien definido de -1. Y en el caso de que la esperanza matemática de la matriz sea igual a cero, entonces la probabilidad p1 debe ser igual a 1/2 y la probabilidad p2 también debe ser igual a 1/2, de forma tal que los dos valores posibles son igualmente probables.
Los valores promedio (en función de los valores eigen) para las matrices de Pauli σ1, σ2 y σ3 no son independientes como pudiera parecer a primera vista. Estos valores promedio están limitados por la siguiente desigualdad:
Para demostrar esta desigualdad, considérense tres números reales x1, x2 y x3. Hágase:
Considérese ahora una cantidad representada por la siguiente matriz (a través de uno de los valores eigen de la matriz así definida):
El cuadrado de esta cantidad es:
Podemos simplificar esto si recurriemos a las siguientes relaciones que se pueden verificar de inmediato por multiplicación matricial directa:
Desarrollando y simplificando, se tiene:
De este modo, la cuadrado de la cantidad solo puede tener el valor r2, lo cual implica que la cantidad en sí sólo puede tener los valores -r y r. Su valor medio tiene que estar comprendido entre -r y r. Por lo tanto:
Puesto que la esperanza matemática de una suma de cantidades es igual a la suma de las esperanzas matemáticas de dichas cantidades:
se tiene entonces:
Con esto:
Esto último es válido para números reales x1, x2 y x3 cualesquiera. En particular, si se hace:
entonces:
lo cual implica que:
y que a su vez implica lo siguiente:
Para un experimento llevado a cabo con un solo aparato Stern-Gerlach, descrito por cualquiera de las tres matrices de Pauli, la experanza matemática en los tres casos será igual a cero, reflejando con ello el hecho de que el haz de partículas que entran al aparato es subdividido en proporciones iguales. Sin embargo, para un experimento llevado a cabo con una combinación de aparatos Stern-Gerlach, no hay razón alguna para esperar que las esperanzas matemáticas de la matriz que describe tal sistema sean iguales a cero excepto en casos especiales. En una situación así, dejamos de utilizar las matrices de Pauli σ1, σ2 y σ3, simbolizando a las matrices que describen cada una de las tres coordenadas rectangulares Cartesianas del sistema como Ω1, Ω2 y Ω3. De cualquier modo, mucho de lo que se ha descrito arriba sigue siendo válido. La esperanza matemática probabilista de cualquiera de estas matrices, como Ω1, sigue siendo dada matemáticamente en función de los dos eigenvalores λ1 y λ2 de la matriz Ω1 de la manera usual:
La relación obtenida previamente que conecta las esperanzas matemáticas de las tres matrices Ω1, Ω2 y Ω3 debe ser también:
Del mismo modo, también lo que sigue debe seguir siendo válido:
Esto nos permite tratar de hacer frente a problemas propios de experimentos en los cuales no se está utilizando un solo aparato Stern-Gerlach.
PROBLEMA: Supóngase que para cierto sistema físico las esperanzas matemáticas en dos de los ejes coordenados resultan ser las siguientes:
Encuéntrense las seis probabilidades para los haces que se espera que ocurran en las tres coordenadas.
Para la primera coordenada (1), las dos probabilidades de los haces de partículas son:
Para la segunda coordenada (2), las probabilidades de los dos haces de partículas son:
Por último, para la coordenada (3) puesto que:
se concluye que el único valor posible para la esperanza matemática de la matriz Ω3 debe ser:
Esto implica que, para la cantidad física representada por la matriz Ω3, hay probabilidades iguales de 1/2 para los dos haces de partículas.
Al hablar acerca del momento angular intrínseco de las partículas, el momento angular de spin que posee una partícula ya de por sí aún cuando la partícula no se está desplazando hacia ninguna parte, hemos estado enfocados arriba sobre partículas cuyo spin es igual a 1/2, tales como el electrón y el protón. Sin embargo, también hay partículas cuyo spin es igual a 1. Esto se sabe porque al someter a tales partículas a un campo magnético inhomogéneo el haz que entra al aparato separa el haz entrante en tres haces en lugar de dos. Uno de esos haces continúa en la misma dirección con la cual entró al aparato, mientras que los otros dos haces se encaminarán en direcciones opuestas.
La pregunta ahora es: ¿cómo podemos manejar matemáticamente esta nueva situación en la cual, matricialmente hablando, se requieren tres eigenvalores en lugar de dos?
Así como hay matrices 2×2 (las matrices de Pauli σ1, σ2 y σ3) que a través de sus valores propios eigen pueden describir sobre cualquiera de los tres ejes coordenados Cartesianos la subdivisión de un haz de partículas en dos haces distintos revelando la existencia del momento angular de spin de partículas identificadas con un momento angular intrínseco igual a 1/2, también hay matrices 3×3 que a través de sus valores propios eigen pueden describir sobre cualquiera de los tres ejes coordenados Cartesianos la subdivisión de un haz de partículas en tres haces distintos revelando la existencia del momento angular de spin de partículas identificadas con un momento angular intrínseco igual a 1. Como ejemplo de ello, tenemos las siguientes tres matrices:
Cada una de estas tres matrices 3×3 tiene los mismos eigenvalores que la otra, lo cual podemos comprobar fácilmente montando la ecuación secular en cada caso con la finalidad de obtener los eigenvalores para cada matriz que resultan ser los siguientes:
Las matrices Σ1, Σ2 y Σ3 son semejantes, pero no iguales. Y cada una de estas matrices puede ser asignada a uno de los ejes coordenados Cartesianos, por ejemplo:
Σ1 = Σx , Σ2 = Σy , Σ3 = Σz
Teniendo las tres matrices los mismos eigenvalores, esto explica el por qué, matricialmente hablando, no importa que el aparato Stern-Gerlach pueda ser girado en la forma descrita y de cualquier modo se sigan obteniendo los tres haces de partículas siempre separados de la misma manera.
Al igual que como se hizo en el caso de las partículas con spin 1/2, podemos calcular los promedios aritméticos de las matrices Σ1, Σ2 y Σ3 a traves de sus eigenvalores. Por ejemplo, para el caso de la matriz Σ1, la esperanza matemática de la misma es:
Esto nos dice que, además de las partículas con momento angular de spin igual a cero que no son deflexionadas por el campo magnético inhomogéneo, hay tantas partículas que están siendo desviadas “hacia arriba” como partículas que están siendo desviadas “hacia abajo” (tomaremos prestadas las expresiones usadas para el caso de las partículas con spin 1/2). Hay otra forma alterna en la cual podemos representar el procedimiento de cálculo anterior, la forma probabilista, que es la siguiente:
Lo que tenemos en la tercera línea nos dice que hay una probabilidad p1 igual a 1/3 de obtener el eigenvalor λ1, hay una probabilidad p2 también igual a 1/3 de obtener el eigenvalor λ2, y hay una probabilidad p3 igual a 1/3 de obtener el eigenvalor λ3. En pocas palabras, las probabilidades de que cualquier partícula tomada al azar pueda tener cualquiera de los tres eigenvalores son iguales, lo cual a su vez implica que las intensidades registradas de los tres haces sobre la placa fotográfica serán iguales (de no serlo, en base a resultados de laboratorio, habría que incorporar la discrepancia a la matriz junto con alguna explicación teórica capaz de explicar la discrepancia).
Por multiplicación matricial directa, se puede verificar que para las matrices Σ1, Σ2 y Σ3 que se acaban de dar se cumple la siguiente relación:
El hecho de que las matrices Σ1 y Σ2 no conmutan revela de inmediato que son observables incompatibles. Al igual que como ocurrió para las partículas cuyo spin es igual a 1/2 y cuyos valores posibles eigen de momento angular están contenidos esencialmente por las tres matrices de Pauli σ1, σ2 y σ3, para las partículas cuyo spin es igual a 1 y cuyos valores posibles eigen de momento angular están contenidos esencialmente por las tres matrices Σ1, Σ2 y Σ3 no es posible medir simultáneamente el momento angular de una partícula sobre una coordenada rectangular Cartesiana como el eje-z (Σz) y medirlo también sobre otra coordenada rectangular Cartesian ortogonal a la primera como el eje-x (Σx).
Así como hay matrices 3×3 (como las matrices Σ1, Σ2 y Σ3 dadas arriba) que a través de sus valores propios eigen pueden describir sobre cualquiera de los tres ejes coordenados Cartesianos la subdivisión de un haz de partículas en tres haces distintos revelando la existencia del momento angular de spin de partículas identificadas con un momento angular intrínseco igual a 1, también hay matrices 4×4 que a través de sus valores propios eigen pueden describir sobre cualquiera de los tres ejes coordenados Cartesianos la subdivisión de un haz de partículas en tres haces distintos revelando la existencia del momento angular de spin de partículas identificadas con un momento angular intrínseco igual a 3/2. Como ejemplo de ello, tenemos las siguientes tres matrices 4x4:
Cada una de estas tres matrices 4×4 tiene los mismos eigenvalores que la otra, lo cual podemos comprobar fácilmente montando la ecuación secular en cada caso con la finalidad de obtener los eigenvalores para cada matriz que resultan ser los siguientes:
Las matrices Σ1, Σ2 y Σ3 dadas arriba para describir el comportamiento experimental de partículas con un momento angular de spin igual a 3/2 son semejantes, pero no iguales. Y de nueva cuenta, cada una de estas matrices puede ser asignada a uno de los ejes coordenados Cartesianos, por ejemplo:
Σ1 = Σx , Σ2 = Σy , Σ3 = Σz
Teniendo las tres matrices los mismos eigenvalores, esto explica el por qué, matricialmente hablando, no importa que el aparato Stern-Gerlach pueda ser girado en la forma descrita y de cualquier modo se sigan obteniendo los cuatro haces de partículas siempre separados de la misma manera.
Al igual que como se hizo en el caso de las partículas con spin 1, podemos calcular los promedios aritméticos de las matrices Σ1, Σ2 y Σ3 de partículas con un momento angular de spin igual a 3/2 a traves de sus eigenvalores (¡siempre a través de los eigenvalores!). Por ejemplo, para el caso de la matriz Σ1, la esperanza matemática de la misma es:
Esto nos dice que hay tantas partículas que están siendo desviadas “hacia arriba” como partículas que están siendo desviadas “hacia abajo”. Obsérvese con cuidado que ahora tenemos dos haces de partículas que están siendo desviadas hacia arriba y dos haces de partículas que están siendo desviadas hacia abajo. La forma alterna en la cual podemos representar el procedimiento de cálculo anterior, la forma probabilista, es la siguiente:
Lo que tenemos en la tercera línea nos dice que hay una probabilidad p1 igual a 1/4 de obtener el eigenvalor λ1, hay una probabilidad p2 también igual a 1/4 de obtener el eigenvalor λ2, y hay una probabilidad p3 igual a 1/4 de obtener el eigenvalor λ3, y hay una probabilidad p4 igual a 1/4 de obtener el eigenvalor λ4. En pocas palabras, las probabilidades de que cualquier partícula tomada al azar pueda tener cualquiera de los cuatro eigenvalores son iguales, lo cual a su vez implica que las intensidades registradas de los cuatro haces sobre la placa fotográfica serán iguales (de no serlo, en base a resultados de laboratorio, habría que incorporar la discrepancia a la matriz junto con alguna explicación teórica capaz de explicar la discrepancia).
Las siguientes figuras nos muestran el aspecto que produce sobre una placa fotográfica el desdoblamiento que ocurre al pasar un haz de partículas a través de un aparato Stern-Gerlach, dependiendo de que el momento angular de spin de las partículas sea igual a 1/2, sea igual a 1, o sea igual a 3/2. En el extremo derecho se tiene la impresión fotográfica de una línea espectral de partículas acabadas de salir del horno que no han sido sometidas a deflexión por campo magnético alguno, mientras que las demás tiras muestran los desdoblamientos que son detectados de acuerdo al momento angular intrínseco de las partículas:
Al igual que como ocurre con el aparato Stern-Gerlach que recibe y separa partículas para las cuales su momento angular de spin es igual a 1/2, y el cual al ser girado en un plano perpendicular al haz entrante de partículas seguirá separando el haz entrante en dos haces diferentes encaminados siempre en direcciones opuestas, cabe esperar que suceda lo mismo cuando se trata de partículas cuyo spin es igual a 1, esto es, el haz entrante será separado en tres haces, y al ser girado el aparato sobre un mismo plano el haz entrante seguirá siendo subdividido en tres haces. Y cabe esperar que suceda también lo mismo cuando se trata de partículas cuyo spin es igual a 3/2, esto es, el haz entrante será separado en cuatro haces, y al ser girado el aparato sobre un mismo plano el haz entrante seguirá siendo subdividido en cuatro haces. En este punto, cabe meditar sobre la posibilidad de poder construir operadores matriciales de rotación para las matrices Σ1, Σ2 y Σ3 que sean capaces de “convertir” (girar) a estas matrices que pueden ser 3×3, 4×4, en fin, lo que se nos venga a la imaginación, convirtiendo (por ejemplo) a la matriz Σ2 en la matriz Σ1. ¿Cómo podemos construír tales operadores? En las entradas “La matriz generadora de rotación” y “Rotaciones de las matrices de Pauli”, tenemos una pista para ello. En realidad, la respuesta es sencilla y directa: si queremos construír operadores matriciales de rotación para girar matrices como Σ1, Σ2, y Σ3, usamos las mismas matrices Σ1, Σ2, y Σ3 en la forma exponencial que ya se ha tratado con anterioridad.
Una situación más elaborada aún es aquella en la cual un aparato Stern-Gerlach es girado primero en torno a uno de los ejes (por ejemplo, en torno al eje-y, lo cual implica girar el aparato en torno al plano x-z), y tras esto girar el aparato en torno a otro de los ejes (por ejemplo, en torno al eje-x, lo cual implica girar el aparato en torno a un plano y-z). El giro combinado ya no es un giro bidimensional, sino un giro tridimensional, el cual requiere la especificación de dos ángulos de rotación (por ejemplo, α y β) con respecto a los ejes seleccionados para el giro combinado. Este tipo de problema se puede tratar mediante la Mecánica Matricial. Sin embargo, es más común tratar un problema de este tipo bajo la Mecánica Ondulatoria, en donde se puede recurrir e incluír sin mayores problemas algo como las rotaciones de Euler, razón por la cual este tipo de problemas no será cubierto aquí bajo la óptica de la Mecánica Matricial.