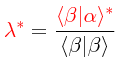En la figura de arriba, los vectores i, j y k son vectores unitarios (cuya longitud es igual a la unidad) de base que fijan las direcciones de las proyecciones del vector a sobre los tres ejes coordenados, estando especificado dicho vector por sus tres componentes de la manera siguiente:
a = (ax , ay , az)
Estamos acostumbrados también a definir operaciones con vectores, tales como la multiplicación de un vector por una constante numérica k (la cual aumenta la longitud del vector si la constante k es mayor que la unidad o disminuye la longitud del vector si la constante k es menor que la unidad) o como la adición de dos vectores a y b:
ka = (kax , kay , kaz)
a + b = (ax + bx , ay + by , az + bz )
Estos conceptos son conceptos esenciales que se ven en cualquier curso introductorio de física o en un curso de Análisis Vectorial. Concebidos no tanto como un concepto físico sino como un concepto matemático, los vectores suelen ser definidos con más de las tres componentes a las que están limitados los vectores en un espacio Euclideano tridimensional, por ejemplo, a un espacio de cinco dimensiones:
a = (a1 , a2 , a3 , a4 , a5 )
ka = (ka1 , ka2 , ka3 , ka4 , ka5 )
a + b = (a1 + b1 , a2 + b2 , a3 + b3 , a4 + b4 , a5 + b5 )
Estos espacios generalizados, los cuales son el tema central de estudio del Algebra Lineal, son conocidos como espacios vectoriales.
No son pocos los que resultan sorprendidos cuando toman conocimiento de que los vectores pueden ser relacionados con todo lo que se estudia en la Mecánica Ondulatoria. ¿Y qué tienen que ver los vectores y los espacios vectoriales con la Mecánica Ondulatoria en donde lo que se maneja son funciones de onda?, se preguntarán algunos. Para responder esta pregunta, tómese la siguiente función de onda que es una solución particular de la ecuación de Schrödinger independiente del tiempo que corresponde al caso de una partícula encerrada en una caja unidimensional para n.=.1.
Esta es una solución particular a la ecuación diferencial de Schrödinger independiente del tiempo. Pero ya vimos que hay otras soluciones particulares a este mismo problema, como la siguiente (n.=.2):
y la siguiente (n.=.3):
No habiendo un límite superior al valor que pueda tomar el entero positivo n para este problema, hay una cantidad infinitamente grande de soluciones particulares posibles a la ecuación diferencial de Schrödinger. Es un principio básico de la teoría de las Ecuaciones Diferenciales que cualquier combinación lineal de soluciones particulares a una ecuación diferencial lineal también será una solución a dicha ecuación diferencial, como la siguiente combinación que también será una solución:
La solución general a una ecuación diferencial lineal está dada por la combinación lineal de todas las soluciones particulares a dicha ecuación diferencial. Esto significa que si tomamos todas y cada una de las soluciones particulares al problema de una partícula encerrada en una caja unidimensional y las sumamos representando dicha suma como Ψ(x):
entonces Ψ(x) será la solución general a la ecuación de Schrödinger para el caso de una partícula encerrada en una caja unidimensional. Podemos representar la anterior suma infinita de una manera un poco más compacta usando el símbolo de la sumatoria:
Siendo todas las funciones senoidales de cada uno de los términos de esta serie infinita ortogonales en el sentido de que el producto interno de cualquier par de ellas será igual a cero, esto se parece mucho a una serie de Fourier. Sin embargo, no lo es, ya que las amplitudes de todos los términos son iguales, y si fuéramos sumando en una gráfica cada uno de los términos de la serie no tardaríamos en obtener amplitudes aproximándose a valores infinitamente grandes. No hay convergencia alguna dentro de intervalo alguno de la serie. Sin embargo, esto no representa ningún problema desde el punto de vista de la interpretación física, porque aunque en principio todos los términos conviven juntos de alguna manera, al llevarse a cabo el acto de medición la función de onda Ψ(x) se colapsará aleatoriamente hacia uno y solo uno de los términos de la serie. En realidad, en la suma de términos que representa la solución general a la ecuación de Schrödinger, el símbolo “+” debe tomarse más como un “separador” de los términos de la sumatoria que una adición real a ser llevada a cabo. Hay otra forma más apropiada en la cual podemos agrupar las soluciones particulares a la ecuación de Schrödinger manteniéndolas separadas pero incluyéndolas a todas:
Esto empieza a parecerse demasiado a un vector. Y en realidad, ¿por qué no considerarlo como un vector en el pleno sentido matemático de la palabra? No hay nada que nos impida hacer tal cosa, excepto por el hecho inquietante de que se trata de un vector con una cantidad infinitamente grande de componentes. Y todavía hasta principios del siglo XX, los matemáticos no se sentían cómodos con una propuesta de esta índole. Pero con el advenimiento de la Mecánica Cuántica, se vió aquí una oportunidad dorada para concretar como una realidad con aplicaciones inmediatas lo que vendría siendo un espacio vectorial capaz de servir como andamiaje a la estructura matemática de la Mecánica Cuántica, asentándola sobre una base rigurosa y formal. Esto, desde luego, requería agallas, porque no cualquier matemático está dispuesto a zambullirse en cuestiones que tienen que ver con el infinito y que frecuentemente conducen a paradojas si se da un paso en falso. Se requería de un matemático de primer nivel con el coraje suficiente para adentrarse en terrenos hasta entonces desconocidos, un matemático de la talla de David Hilbert.
El espacio de Hilbert es un espacio vectorial infinitamente grande. En su momento, esto fue una idea revolucionaria, en virtud de que todos los espacios vectoriales, inclusive los espacios matemáticos abstractos, eran finitos. Pero afortunadamente en su trabajo sobre ecuaciones integrales llevado a cabo en 1912 David Hilbert tuvo la visión suficiente para captar la necesidad de tener que postular un espacio vectorial infinitamente grande para poder proyectar todo el aparato matemático de la Mecánica Cuántica sobre una base rigurosamente formal. Y quince años después correspondió a otro matemático igualmente brillante, el matemático húngaro John von Neumann, el darle en 1927 una definición axiomática al espacio vectorial de Hilbert en su ya famosa obra Mathematische Grundlagen der Quantenmechanik. Pero Hilbert no solo propuso un espacio vectorial infinitamente grande. Propuso también que los componentes de los “vectores” pudiesen ser números imaginarios o números complejos sin estar limitados a ser números reales, redefiniendo a la vez el concepto del producto interno de dos vectores para que dicho producto pudiese seguir siendo un número real con significado físico.
Habiendo sido introducidos ya a la notación bra-ket de Dirac, manteniéndonos aún en el problema de la partícula encerrada en una caja unidimensional llevaremos a cabo el siguiente cambio en la simbolización:
Habiendo convenido en la notación anterior, encontramos que la expansión de la función de onda Ψ(x) representada como un ket queda simbolizada de la siguiente manera en función de los kets de base:
Como una operación válida, podemos premultiplicar ambos miembros de esta igualdad por un bra que es el dual a cualquiera de los kets de base:
Al igual que como ocurre con las funciones de base ψ1, ψ2, ψ3, etc., las cuales son funciones de base normalizadas, en el lado derecho de la igualdad cada uno de los productos bra-ket será igual a cero excepto para el caso en el cual a.=.b, con lo cual en el lado derecho nos viene quedando un solo término de la sumatoria infinita:
En esto último podemos intercambiar b por a sin que ello implique diferencia alguna excepto puramente notacional, ya que seguimos refiriéndonos a los mismos kets de la sumatoria, escribiendo así:
Obsérvese con detenimiento lo que tenemos en el lado derecho de la igualdad, puesto que se trata de una nueva interpretación que se le está dando aquí al producto bra-ket de Dirac. Si el bra representa uno de los eigenkets de la sumatoria infinita, entonces al aparearlo con un ket que representa la suma de todos los términos de la sumatoria el resultado que esperamos obtener es la constante que va adjunta al ket seleccionado, teniéndose en cuenta que a cada ket le corresponde su propia constante con la cual va apareado.
Si substituímos lo que obtuvimos para el coeficiente ca en la expansión previa del ket en función de kets de base, se tiene:
Fijándonos en los dos kets que están uno tras otro, podemos utilizar el hecho de que tratándose de kets el orden en el que están escritos es indiferente (conmutatividad de kets):
lo que nos permite escribir lo anterior del modo siguiente:
Fijémonos bien ahora en un hecho importante que destacaremos resaltando parte de la expresión anterior en color magenta:
Cualquier matemático, viendo lo anterior, de inmediato concluirá que en el lado derecho de la igualdad lo que se está haciendo es simplemente premultiplicar al ket por el número 1, o mejor dicho, por un operador identidad (que representaremos como I) que deja al ket sin cambio alguno.
Puesto que el ket es un ket arbitrario, esto significa que podemos dar por hecho la siguiente definición:
Esta última relación es conocida ya sea como la relación de completitud o la relación de cerradura. La definición del operador identidad I puede ser ampliada del modo siguiente:
e igualmente del modo siguiente:
No hay límite alguno a las ampliaciones que podemos llevar a cabo de la definición del operador identidad bajo el contexto de la notación bra-ket. Lo que acaba de ser definido resulta de una utilidad extraordinaria tomando en cuenta que el operador identidad I puede ser “injertado” en cualquier parte dentro de una expresión que involucre bras y kets, permitiendo manipulaciones posteriores para obtener resultados que algunas veces no son tan obvios. Como un ejemplo sencillo de esto, considérese el siguiente desarrollo en el cual injertaremos el operador identidad y llevaremos a cabo algunos reacomodos válidos siguiendo las reglas del juego:
Lo que tenemos en las dos últimas líneas encierra una conclusión importante, ya que nos dice que si un ket |α> está normalizado, con lo cual el producto interno del ket consigo mismo debe ser igual a la unidad, entonces los coeficientes que se han utilizado en la expansión deben satisfacer:
Esto, desde luego, tiene una interpretación probabilista, precisamente la interpretación probabilista que le hemos estado dando a la función de onda en la Mecánica Cuántica.
PROBLEMA: Demuéstrese que la traza de un operador X es independiente de la representación, o sea, independiente del conjunto de kets de base utilizados para describir el espacio vectorial.
Tomaremos como punto de partida la definición de la traza de un operador e injertaremos en la definición dos operadores identidad I e I del modo siguiente:
A continuación, seleccionaremos el par bra-ket que está al final de esta relación, el cual por ser una constante numérica y no un operador que actúe sobre algo podrá ser movido libremente dentro de la relación:
Relocalizaremos el par bra-ket colocándolo al principio de la relación (pero siempre dentro de las sumatorias):
Ahora seleccionaremos un par ket-bra de la manera siguiente:
Obsérvese que todo lo que se ha resaltado de color magenta en esta última expresión constituye un operador identidad I, lo cual nos permite borrar de un solo golpe todo lo que está resaltado de color magenta dejándonos lo siguiente:
Nuevamente, podemos seleccionar otro par ket-bra que será resaltado de color azul:
Y de nueva cuenta, todo lo que se ha resaltado de color azul en esta última expresión constituye un operador identidad I, lo cual nos permite borrar de un solo golpe todo lo que está resaltado de color azul dejándonos lo siguiente:
Se supone, por hipótesis, que tanto el bra como el ket que aparecen en esta última expresión fueron tomados de otro conjunto de kets de base, y sin embargo en el lado derecho de la igualdad seguimos teniendo la misma relación que nos define la traza del operador X, esta vez mediante otro conjunto de kets de base. Se concluye entonces que la traza de un operador es independiente de la representación.
PROBLEMA: Demuéstrese siguiendo las reglas del álgebra bra-ket que la traza del producto de dos operadores X y Y permanece invariante si se toma la traza del producto de los operadores en el orden inverso.
Empezaremos por aplicar rigurosamente la definición de la traza de la siguiente manera a lo que vendría siendo la traza de un producto de operadores X y Y:
Las reglas del álgebra bra-ket nos permiten injertar un operador identidad I entre los operadores X y Y de la siguiente manera:
Pero por lo que vimos anteriormente, es válido reemplazar este operador identidad I por lo siguiente:
Ahora resaltaremos de color magenta lo siguiente:
Lo que está resaltado de color magenta (del mismo modo que lo que quedó de color negro) no es un operador; en todo caso es un elemento matricial extraído del operador X, y por lo tanto se puede mover libremente como se hará a continuación:
Ahora resaltaremos de color azul lo siguiente:
Lo que tenemos de color azul es obviamente un operador identidad I, razón por la cual podemos escribir lo anterior del modo siguiente:
Esto último se reduce a:
Se concluye entonces que la traza del producto de dos operadores X y Y permanece invariante si se toma la traza del producto de los operadores en el orden inverso.
En el estudio de los espacios vectoriales finitos, un concepto que se utiliza mucho es el de la norma de un vector, que viene siendo lo mismo que la longitud de un vector a y que simbolizaremos aquí como ||a||. Considérese el siguiente vector v en un espacio de dos dimensiones cuyas componentes están orientadas sobre dos ejes rectangulares Cartesianos de acuerdo con las direcciones indicadas por los vectores unitarios de base ex y ey:
Entonces la longitud ||v|| del vector será:
Si dividimos al vector v entre la magnitud ||v|| de su longitud, obtendremos un vector v normalizado cuya longitud será igual a la unidad:
En general, para un espacio n-dimensional, la norma de un vector a:
a = (a1 , a2 , a3 , a4 , a5 , ... , an)
está dada como:
Obsérvese que en la segunda línea la norma del vector a está especificada como la raíz cuadrada del producto escalar punto del vector a consigo mismo. Procediendo por analogía, podemos definir la norma de la siguiente manera:
Es importante aprovechar la ocasión para aclarar de una vez por todas que las dobles barras verticales utilizadas arriba para denotar la norma de un vector cuyo cuadrado:
en el caso de un vector tridimensional Euclideano :representa la suma de los cuadrados de las componentes del vector en un sistema de ejes rectangulares Cartesianos (en conformidad con el teorema de Pitágoras extendido a tres dimensiones):
representa esencialmente el mismo concepto que el que hemos estado utilizando para definir con barras verticales sencillas el producto de una función por su conjugado complejo:
Las dobles barras verticales tienen una ventaja sobre las barras verticales sencillas en el sentido de que estas últimas pueden ser confundidas por los principiantes con el símbolo usual que se le dá en las matemáticas al valor absoluto, por ejemplo |-47|.=.+47. En vez de unificar en esta obra toda la notación hacia el uso exclusivo de las dobles barras verticales o las barras verticales sencillas, se seguirán usando ambos tipos de notación sin que ello implique un nuevo significado de una notación sobre otra, esto con el fin de acostumbrar al lector a ambos tipos de notación usados indistintamente en el grueso de la literatura técnica y científica.
Procediendo también por analogía, extenderemos la definición de un vector normalizado a la de un ket normalizado de la siguiente manera dividiendo al ket entre la norma:
Si los teoremas que se descubren y se demuestran en el Algebra Lineal de aplican sin cambio alguno a la ecuación diferencial de Schrödinger, entonces hay ya muchos teoremas que podemos explotar y que no es necesario derivar nuevamente dentro de la Mecánica Cuántica. Uno de ellos es el proceso de ortogonalización Gram-Schmidt, cuyo objeto es tomar un conjunto de vectores de base (linealmente independientes, lo cual implica que no se puede obtener uno de los vectores mediante una combinación lineal de los demás) y construír un conjunto ortonormal de vectores de base.
El hecho de que los kets (y por ende, también los bras) puedan ser considerados como vectores y manejados como vectores al ser considerados como componentes de un espacio vectorial implica que se pueden establecer muchas analogías con toda cosa que tenga que ver con el Algebra Lineal y con el Análisis Vectorial. Una fórmula que puede parecer un poco curiosa e inclusive extraña para los principiantes es la que se puede definir en notación bra-ket de Dirac generalizando el concepto del producto escalar o producto punto de dos vectores. Bajo la geometría elemental Euclideana se define el producto punto de dos vectores tridimensionales como el producto de las magnitudes de dichos vectores por el coseno del ángulo que forman entre sí ambos vectores. Considerando kets en lugar de vectores, la fórmula que se obtiene en la Mecánica Cuántica para el coseno del ángulo entre dos kets viene siendo:
Aunque el numerador puede ser simplificado, se ha dejado así porque fija un orden a los cálculos que se tienen que llevar a cabo. Compárese la fórmula anterior con su contraparte vectorial para dos vectores a y b:
Es un hecho que el coseno de un ángulo cualquiera puede ser menor o igual que la unidad, pero nunca puede ser mayor que la unidad, siendo esto válido también para el cuadrado del coseno de un ángulo, o sea:
Aplicando este hecho a la penúltima expresión, esto implica que:
Lo que aparece en la segunda línea es una relación extremadamente importante, conocida como la desigualdad de Schwarz. Esta desigualdad puede resultar algo familiar, ya que se trata de la misma desigualdad utilizada para obtener el principio de incertidumbre de Heisenberg a partir de la “extraña ecuación” de Max Born, ya sea en su versión matricial o desde la perspectiva de las funciones de onda de la Mecánica Ondulatoria. Aunque la hemos obtenido recurriendo a analogías y conceptos propios del Análisis Vectorial, podemos formalizar un poco la obtención de la misma sin tener que recurrir a vías indirectas.
PROBLEMA: Demuéstrese, empleando la notación bra-ket de Dirac para ello, la desigualdad de Schwarz (los colores han sido dados para mayor claridad):
Como ya se mencionó previamente, aunque no parezca obvio a primera vista esta desigualdad tiene su símil en el espacio tri-dimensional Euclideano, la desigualdad que nos dice que “los productos de los cuadrados de las magnitudes de dos vectores a y b será mayor o igual al cuadrado de la magnitud que resulta de tomar el producto escalar entre ambos vectores”:
Para llevar a cabo la demostración, partiremos primero del hecho de que cualquier ket premultiplicado por el bra que es su dual exacto siempre será un número real positivo, esto es, mayor o igual a cero:
Del mismo modo, si premultiplicamos la suma de dos kets:
por la expresión que corresponde a su dual:
el producto también debe seguir siendo un número real positivo:
Esto se puede generalizar aún más cuando en la suma de los kets le agregamos una constante λ (que puede ser compleja) a uno de los kets:
Al formar el producto bra-ket sobre esto último, debemos tener entonces (λ* es el conjugado complejo de λ):
Removiendo los paréntesis, se tiene entonces que la expresión en el lado izquierdo de la desigualdad es:
Por la forma en la cual fue definida de inicio, la desigualdad será válida para cualquier valor positivo o negativo, real o complejo, que tome λ, y debe seguir siendo válida cuando le damos a λ el siguiente valor (la razón para esta definición será obvia más adelante):
El conjugado complejo de lo anterior será:
Recordando que:
se tiene entonces:
Substituyendo tanto a λ como a λ* en la desigualdad anterior:
Habiéndose destacado arriba de color magenta algo que puede ser cancelado, resulta evidente que tanto el tercer término como el cuarto término se anulan (esta fue la razón para haberse definido a λ en la forma en la cual fue definido) dejándonos únicamente el primer término y el segundo término, con lo cual se tiene:
De este modo, la desigualdad viene quedando como:
lo cual prueba la desigualdad de Schwarz. Obsérvese que en el último paso se utilizó en el lado derecho de la desigualdad la simbolización para la magnitud del producto bra-ket (elevada al cuadrado) <α|β> que viene representando lo mismo que:
PROBLEMA: Obténgase el ángulo entre el siguiente par de kets cuyas componentes sobre los ejes coordenados rectangulares Cartesianos están dadas empleándose el conjunto usual de vectores unitarios de base {i,j,k} (véase la figura al principio de esta entrada):
Los cálculos intermedios son los siguientes:
Obsérvese que <β|α> resulta ser el conjugado complejo de <α|β>, lo cual era de esperarse, razón por la cual el producto de ambos siempre será un número positivo real. Usando la fórmula dada arriba, se tiene entonces:
No resulta muy prudente intentar darle un significado físico a este resultado, habido el hecho de que algunos de los componentes de ambos kets son números imaginarios o complejos. Sin embargo, no deja de ser interesante el hecho de que se pueda trabajar con algo tan peculiar obteniendo como resultado final un número positivo real.
Ahora bien, partiendo de un conjunto de eigenfunciones de base independientes no necesariamente ortogonal:
se desea construír a partir de dicho conjunto otro conjunto de eigenfunciones ortogonales:
Para empezar con la construcción de la base ortogonal de funciones u1, tómese el producto interno de la función u1 consigo misma y hágase lo siguiente:
Obsérvese que aquí tenemos en esencia el mismo procedimiento al cual hemos estado recurriendo para normalizar funciones de onda. Ahora, tomando el producto interno de las funciones u1 y ψ2, desígnese el resultado de dicho producto como una constante c12. Entonces:
Como parte del procedimiento de ortogonalización, constrúyase a la siguiente función u2 del modo siguiente:
Tómese ahora el producto interno de ambos lados de esta igualdad con la función u1 integrando sobre todo el espacio bajo consideración, lo cual se lleva a cabo premultiplicando todo por u1* y aplicando la integración sobre los productos que hay en cada lado de la igualdad:
Usando lo que tenemos previamente, se tiene entonces que:
Este resultado nos dice claramente que las primeras dos funciones de nuestro nuevo conjunto, u1 y u2, son ortogonales, ya que se está cumpliendo en forma precisa la definición de ortogonalidad para dos funciones diferentes. Tenemos ya pues un conjunto de dos funciones ortogonales:
Alentados por la ortogonalización que hemos logrado, extenderemos el procedimiento usado previamente con miras a obtener u3, el cual esperamos que sea ortogonal con u1 y u2. Para ello, tómese el producto interno de la función u2 consigo misma y hágase lo siguiente:
Ahora, tomando el producto interno de las funciones u1 y u2 con la función ψ3, desígnese el resultado de dichos productos como una constante c13 y como una constante c23. Entonces:
Como parte del procedimiento de ortogonalización, constrúyase a la función u3 del modo siguiente:
Aquí tenemos dos opciones, y empezaremos con la primera opción, tomando el producto interno de ambos lados de esta igualdad con la función u1 integrando sobre todo el espacio bajo consideración, lo cual se lleva a cabo premultiplicando todo por u1* y aplicando la integración sobre los productos que hay en cada lado de la igualdad:
Usando lo que tenemos previamente, se tiene entonces que:
Este resultado nos dice claramente que la función u1 de nuestro nuevo conjunto y la función u3 son ortogonales, ya que se está cumpliendo en forma precisa la definición de ortogonalidad para dos funciones diferentes.
Ahora trabajaremos sobre la segunda opción, tomando el producto interno de ambos lados de la igualdad de arriba con la función u2 integrando sobre todo el espacio bajo consideración, lo cual se lleva a cabo premultiplicando todo por u2* y aplicando la integración sobre los productos que hay en cada lado de la igualdad:
Usando lo que tenemos previamente, se tiene entonces que:
Este resultado nos dice claramente que la función u1 de nuestro nuevo conjunto y la función u3 son ortogonales, ya que se está cumpliendo en forma precisa la definición de ortogonalidad para dos funciones diferentes. Tenemos ya entonces un conjunto de tres funciones ortogonales:
El procedimiento que hemos utilizado se puede extender para ir obteniendo el resto de las funciones ortogonales. En el caso de u4, haríamos:
y construiríamos a la función u4 de la manera siguiente:
El conjunto de funciones:
ciertamente es ortogonal, pero no es ortonormal. Sin embargo, ello no representa problema alguno, ya que en la obtención de las funciones de base ortogonales hemos ido obteniendo las constantes necesarias para llevar a cabo la normalización de cada una de las funciones.
La notación usada arriba en la delineación del procedimiento, apegada estrictamente a la notación usada en la Mecánica Ondulatoria para designar las funciones de onda, está en conformidad con lo que se acostumbra utilizar en muchos textos y publicaciones científicas. Sin embargo, un enfoque más moderno se basa en hacer un cambio de notación empleando la notación bra-ket de Dirac. Con la finalidad de familiarizar al lector con esta tipo de notación, haciendo una transición suave hacia el análisis y la solución de problemas en donde esta simbología es utilizada, se repetirá el procedimiento utilizado arriba, pero “traduciendo” los pasos adaptándolos a la notación bra-ket de Dirac, y usando el mismo lenguaje que se utiliza cuando se emplea dicha notación, de forma tal que en vez de hablar acerca de eigenfunciones estaremos hablando de eigenkets. Partiendo de un conjunto inicial de kets:
los cuales ni están normalizados ni son ortogonales, nuestro propósito será construír un conjunto ortonormal de kets de base en el cual el producto interno de dos eigenkets distintos sea igual a cero y el producto interno de cualquiera de los eigenkets consigo mismo sea igual a la unidad, un conjunto que simbolizaremos como:
El único requisito que se le impondrá al conjunto inicial de kets es que los kets sean linealmente independientes, esto es, que cualquiera de los kets del conjunto no pueda ser obtenido mediante una combinación lineal de algunos (o todos) los demás kets del conjunto, lo cual equivale a exigir que no haya constantes multiplicativas tales que pueda ocurrir lo siguiente:
a menos de que todas las constantes multiplicativas sean iguales a cero. Tomaremos el primer ket del conjunto inicial de kets, y normalizaremos dicho ket obteniendo un ket normalizado, el primer ket que formará parte del nuevo conjunto:
El producto interno bra-ket de este ket consigo mismo es igual a la unidad, lo cual se comprueba de una manera sencilla:
Por lo tanto el primer ket de nuestro nuevo conjunto está normalizado. Los kets:
siguen siendo linealmente independientes puesto que lo único que se hizo con el primer ket del conjunto inicial fue dividirlo entre una constante.
Como parte del procedimiento de ortogonalización, constrúyase del modo siguiente el segundo ket que formará parte del nuevo conjunto de kets (se han destacado todos los kets de color azul con la finalidad de minimizar cualquier confusión que se pueda dar):
Este ket no es un ket normalizado (la comilla utilizada como super-índice resalta este hecho), pero sí es un ket que es ortogonal (“perpendicular”, parafraseando el término que se utiliza al referirse en la física a dos vectores que son perpendiculares entre sí) al ket dado previamente. Esto lo podemos comprobar fácilmente del modo siguiente premultiplicando todo lo que hay en ambos miembros de la igualdad por el bra que es dual al primer ket como se muestra a continuación (lo que no está puesto de color azul en la expresión de arriba, entre paréntesis ordinarios, es una simple constante multiplicativa por resultar del producto interno de un bra y un ket):
Entonces el segundo ket construído de acuerdo con la prescripción dada con anterioridad es ortogonal al primer ket. Pero el segundo ket no es un ket normalizado, lo cual se puede remediar fácilmente del mismo modo en el que fue normalizado el primer ket:
El conjunto intermedio de kets en nuestro procedimiento constructivo consta ya de dos kets normalizados y ortogonales:
Ahora iremos tras el tercer ket repitiendo la misma receta “constructiva” dada anteriormente:
Aunque este tercer ket de base no está normalizado, es ortogonal tanto al primer ket como al segundo ket obtenidos previamente. La comprobación de que el tercer ket es ortogonal al primer ket se lleva a cabo del modo siguiente premultiplicando todo lo que hay en ambos lados de la igualdad por el bra que es dual al primer ket:
Y la comprobación de que el tercer ket es ortogonal al segundo ket se lleva a cabo del modo siguiente premultiplicando todo lo que hay en ambos lados de la igualdad por el bra que es dual al segundo ket:
El tercer ket por lo tanto es ortogonal tanto al primer ket como al segundo ket. Sin embargo, no está normalizado, lo cual se puede remediar fácilmente del mismo modo en el que fueron normalizados el primer ket y el segundo ket:
El conjunto intermedio de kets en nuestro procedimiento constructivo consta ya de tres kets normalizados y ortogonales:
De este modo, repitiendo el mismo procedimiento constructivo que hemos estado utilizando, obtenemos el siguiente conjunto ortonormal de kets de base:
cumpliendo todos los kets del conjunto la condición de ortonormalidad especificada con la ayuda del delta de Kronecker:
Es de resaltarse el hecho de que el empleo de la notación bra-ket de Dirac simplifica un poco los desarrollos y las demostraciones, escondiendo símbolos del cálculo infinitesimal que una vez entendidos resultan algo superfluos y hasta tediosos en procedimientos extensos en donde cualquier economía de escritura es bienvenida, siempre y cuando se entienda bien que la “taquigrafía” no está introduciendo ningún concepto nuevo.
El procedimiento constructivo de una base ortonormal de kets mediante el procedimiento de ortogonalización Gram-Schmidt discutido arriba supuso un espacio dimensional finito de dimensión n. Sin embargo, no tenemos por qué limitarnos a suponer que el procedimiento es válido únicamente para espacios vectoriales finitos. Podemos extender la validez del procedimiento hacia espacios vectoriales infinitos, esto es, espacios de Hilbert. Considerando que todo lo que tiene que ver con el infinito es un terreno que los matemáticos suelen pisar con mucha cautela e inclusive muchos matemáticos experimentados han sucumbido cometiendo errores inadvertidos de razonamiento al proyectar sus suposiciones desde un espacio finito hacia un espacio infinito, podría parecer osado y aventurado suponer que el procedimiento Gram-Schmidt seguirá siendo válido para espacios de Hilbert. Sin embargo, considerando que no existe en principio limitación alguna a que el procedimiento constructivo que ha sido detallado sea aplicado a espacios vectoriales finitos de dimensiones astronómicas, ya que para cualquier entero n el procedimiento constructivo sigue siendo el mismo, damos por hecho que el procedimiento seguirá siendo válido para espacios vectoriales de Hilbert, de extensión infinita.