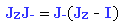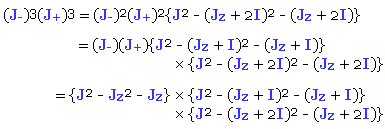Ambos operadores escalera frecuentemente son representados en una sola relación que puede tomar cualquiera de las siguientes dos formas:
Con la finalidad de adquirir un poco de práctica en el uso de los operadores escalera, se presentarán a continuación algunos ejercicios con este propósito.
PROBLEMA: Demuéstrese la siguiente relación:
La solución del problema para el caso L+L- es directa y procede de la siguiente manera;
Procediendo de la misma manera obtenemos:
Resumiendo ambos resultados en uno solo obtenemos la relación pedida en el encabezado de este problema.
PROBLEMA: Demuéstrese la siguiente relación:
Aplicando la definición del conmutador en el lado izquierdo, expandiendo y simplificando, tenemos lo siguiente:
Procediendo de la misma manera obtenemos:
Resumiendo ambos resultados en uno solo obtenemos la relación pedida en el encabezado de este problema.
Resulta obvio a estas alturas que en cualquier desarrollo posterior que llevemos a cabo estaremos arrastrando la ħ reducida de Dirac a menos de que hagamos algún tipo de simplificación. Al tratar el tema de “El spin del electrón”, vimos que podíamos definir los componentes matriciales del spin Sx, Sy y Sz en función de las matrices de Pauli σx, σy y σz las cuales no incluyen la constante ħ reducida de Dirac. Aquí podemos hacer lo mismo, y en lugar de insistir en seguir utilizando las matrices del momento angular Lx, Ly y Lz podemos definir unas matrices Jx, Jy y Jz de la siguiente manera:
Lx = ħJx___Ly = ħJy___Lz = ħJz
Estas matrices J no deben ser confundidas en ningún momento con las matrices J que serán estudiadas cuando llegue el momento de cubrir el tema de la adición vectorial de momentos angulares en donde estaremos utilizando el mismo símbolo para representar la resultante vectorial de una suma de momentos angulares.
PROBLEMA: Obtener la matriz que representa a J², la “magnitud” de la “suma vectorial” de las matrices Jx, Jy y Jy.
Procediendo en forma similar a como procedemos con la definición vectorial para la magnitud de un vector formado a partir de la suma vectorial de sus proyecciones cuando estas son magnitudes de variables continuas a lo largo de los ejes coordenados, la definición pedida será:
J² = Jx² + Jy² + Jz²
Puesto que las matrices Jx, Jy y Jz son obtenidas de las matrices Lx, Ly y Lz mediante el simple expediente de la remoción de la constante ħ reducida de Dirac, lo siguiente que asevera la conmutatividad de J² con Jx, Jy y Jz debe ser cierto:
[J², Jx] = [J², Jy] = [J², Jz] = O
Igualmente, de la relación:
LxLy - LyLx = iħLz
tenemos:
lo cual es más fácil de manipular, ya sin las ħ. Procediendo de igual manera, obtenemos las otras dos relaciones:
Definidas las matrices J de la manera en que acabamos de hacerlo, la definición de los operadores escalera J+ y J- procede de la misma manera quedando todo prácticamente igual que antes excepto que no estaremos arrastrando ya a la constante ħ reducida de Dirac:
PROBLEMA: Evaluar las siguientes cuatro relaciones:
[Jz, J+]___[Jz, J-]___J+J-___J-J+
Aprovechando los resultados previos ya obtenidos para las matrices L, pero prescindiendo de la constante ħ, obtenemos las siguientes respuestas:
Ahora bien, usando el primer resultado del problema se obtiene:
Del mismo modo obtenemos también lo siguiente:
Con estas últimas dos relaciones podemos sacar a relucir una propiedad interesante de los operadores escalera tratando de obtener (J+)3(J-)3 a partir de (J+)²(J-)² de la siguiente manera (póngase atención y cuidado en los lugares en donde el operador escalera J+ es desplazado de derecha a izquierda ejerciendo el efecto de meter a la matriz identidad durante el proceso de corrimiento):
Esta forma en la cual obtuvimos (J+)3(J-)3 a partir de (J+)²(J-)² puede ser generalizada para cualquier exponente de la siguiente manera por medio de la exponenciación repetida de los operadores escalera y aprovechando la conmutatividad en donde la haya:
La razón del por qué se conoce a los operadores J+ y J- como los operadores escalera empieza a resultar clara con lo que acabamos de obtener. Tomando la exponenciación de cualquier matriz al exponente cero como igual a la matriz identidad I (al igual que como ocurre con la exponenciación de los números ordinarios), entonces a partir del exponente n = 0 podemos obtener (J-).n(J+).n para cualquier exponente n. Procediendo del mismo modo obtenemos:
Trabajando “hacia abajo” a partir de cualquier exponente, se puede apreciar el hecho de que tanto (J-).n(J+).n como (J+).n(J-).n representan cantidades que eventualmente se pueden obtener de las cantidades representadas por las matrices J² y Jz. Tal es el caso para (J-)3(J+)3:
A estas alturas, es necesario hacer una distinción clara entre los dos tipos de momento angular que puede haber. El primero es el momento angular orbital, el cual puede corresponder a un cuerpo o partícula que está en órbita alrededor de otro cuerpo o partícula de masa mucho mayor (es así como hablamos clásicamente del momento angular que tiene la Luna como consecuencia de su movimiento de rotación alrededor de la Tierra, multiplicando la distancia r que hay de la Luna a la Tierra por el momentum lineal p de la Luna en producto vectorial cruz r×p ) o a dos cuerpos o partículas de masas comparables que giran en torno a su centro de masa común; y el segundo es el momento angular de spin que posee un cuerpo como consecuencia de su rotación en torno a su propio eje. Esto significa que, al hablar del spin del electrón desde el punto de vista de la Mecánica Cuántica, en realidad siempre estuvimos hablando de su momento angular de spin. El trabajo previo que ha sido desarrollado es mucho más amplio, porque si bien en el momento angular del spin del electrón dicho momento angular está cuantizado en valores fraccionarios de ħ, esperamos que los resultados matriciales previos sean válidos también para el caso en el cual el momento angular está cuantizado en múltiplos enteros de ħ.
En el caso del spin del electrón, las matrices básicas que son utilizadas son las matrices de Pauli σx, σy y σz. Utilizando estas matrices como matrices fraccionarias para definir las matrices Jx, Jy y Jz. correspondientes, podemos efectuar evaluaciones sobre las mismas de acuerdo a las relaciones que fueron desarrolladas previamente.
PROBLEMA: Si a partir de las matrices de Pauli σx, σy y σz se definen las matrices Jx, Jy y Jz de la siguiente manera:
obténganse las siguientes matrices siguiendo como lineamiento las definiciones dadas previamente:
Asimismo, verifíquese con los resultados obtenidos que se cumplen las siguientes igualdades para las matrices del momento angular del spin:
Empezaremos con la evaluación del operador escalera J+ para el spin del electrón:
A continuación evaluaremos el operador escalera J-:
Con los dos resultados obtenidos, podemos calcular J-J+:
Del mismo modo, obtenemos para lo siguiente:
Continuamos con la evaluación de J²:
La evaluación de J²-Jz²-Jz resulta en lo siguiente:
Por otro lado, la evaluación de J²-Jz²-Jz produce lo siguiente:
Comparando resultados, podemos verificar que se cumplen cabalmente dos de las igualdades que se habían obtenido previamente para el momento angular matricial:
A continuación evaluaremos todos los productos (J+) n(J-) n que sea posible obtener para cualquier valor del exponente n:
Resulta obvio que en este caso el producto (J+).n(J-).n será igual a la matriz cero O para cualquier exponente n mayor que 2. El resultado obtenido debe despertar nuestras primeras sospechas de que este producto también será igual a la matriz cero para todas las demás matrices propias del momento angular. En otras palabras, no sólo el momento angular está cuantizado, sino que, a diferencia de la cuantización observada en los niveles de energía del átomo en el modelo atómico planetario de Bohr en donde el número cuántico principal puede tomar cualquier valor posible de una gama infinita de valores enteros positivos, en el caso del momento angular sólo habrá una cantidad finita posible de valores distintos.
Volviendo a las matrices más generales que corresponden al momento angular orbital, partiremos del supuesto de que tanto la matriz J² como la matriz Jz posee cada una de ella sus propios autovalores eigen. Habiendo comprobado que tanto (J-).n(J+).n como (J+).n(J-).n representan (a través de sus autovalores eigen) cantidades reales positivas (susceptibles de poder ser medidas u observadas en el laboratorio con algún aparato) que eventualmente se pueden obtener de las cantidades (también reales y positivas) representadas por las matrices J² y Jz, debemos estar convencidos de que para cualquiera de los valores posibles representados por las matrices s J² y Jz habrá valores correspondientes para las cantidades representadas por las matrices (J-).n(J+).n y (J+).n(J-).n. Ahora bien, si a y b representan cantidades reales y positivas, entonces:
a² + b²
también representará una cantidad real y positiva. Y no importa que llevemos a cabo la factorización:
(a + ib)(a - ib)
de cualquier modo a y b seguirán representando cantidades reales y positivas. Y si la cantidad a es uno de los autovalores propios eigen de la matriz A, y si también la cantidad b es uno de los autovalores propios eigen de la matriz B, entonces el siguiente producto matricial:
representará una cantidad real positiva si las matrices A y B representan cantidades reales y positivas. Del mismo modo, si las matrices C, D y E representan cantidades reales y positivas, entonces el siguiente triple producto matricial:
también representará una cantidad real y positiva. Se deduce entonces que:
así como:
también representarán cantidades reales y positivas si (J-).n(J+).n y (J+).n(J-).n también representan cantidades reales y positivas. En base a esto, trataremos de determinar los valores (eigen) que pueden tener las cantidades representadas por las matrices J² y Jz haciendo uso de las igualdades matriciales arriba obtenidas para los operadores escalera. Supóngase que para algún estado en particular las matrices J² y Jz toman respectivamente los valores g y k. Entonces el valor de la cantidad representada por la matriz:
deberá ser:
g - (k + n)² - (k + n)
Sin embargo, para valores finitos de g y de k, esta cantidad eventualmente se convertirá en una cantidad negativa conforme n va aumentando hacia arriba. Un valor negativo para esta cantidad y un valor positivo para la cantidad representada por (J-).n(J+).n implican que la cantidad representada por (J-).n+1(J+).n+1 tendría también un valor negativo. Pero ya vimos que la cantidad representada por (J-).n+1(J+).n+1 no puede tomar un valor negativo, y la cantidad representada por (J-).n(J+).n ciertamente tendrá un valor positivo cuando n es igual a cero. Esta contradicción lógica nos deja como única posibilidad el que para algún valor muy específico del exponente n el valor de la cantidad representada por (J-).n+1(J+).n+1 será necesariamente igual a cero. En tal caso, todas las cantidades con un exponente superior tales como (J-).n+2(J+).n+2, (J-).n+3(J+).n+3, (J-).n+4(J+).n+4, ... tendrán todas un valor igual a cero. Debe existir algún número n, el cual debe ser un entero como 0, 1, 2, 3 ... en donde tal cosa ocurre, con lo cual si bien la cantidad representada por (J-).n(J+).n no será igual a cero la cantidad representada por (J-).n+1(J+).n+1 sí lo será. Esto implica que en ese “punto crítico” en el cual podemos hacer n = n1 el valor (eigen) representado por la matriz:
será igual a cero, lo cual nos permite escribir dicho valor de la siguiente manera:
g - (k + n1)² - (k + n1) = 0
g = (k + n1)² + (k + n1)
g = (k + n1)² + (k + n1)
Procediendo de la misma manera con el producto (J+).n(J-).n, podemos afirmar categóricamente que la cantidad representada por la matriz:
tendrá un valor real y positivo dado por la cantidad respectiva:
g - (k - n)² + (k - n)
Esta cantidad eventualmente también se volverá negativa conforme n va aumentando hacia arriba. Puesto que la cantidad representada por el producto matricial (J+).n+1(J-).n+1 no puede tener un valor negativo para ningún valor del exponente n (de ocurrir tal cosa, no representaría algo que pueda ser medido en el laboratorio), la única posibilidad es que para algún exponente n que aquí identificaremos como n = n2 el valor (eigen) representado por la matriz:
será igual a cero, lo cual nos permite escribir lo siguiente:
g - (k - n2)² + (k - n2) = 0
g = (k - n2)² - (k - n2)
g = (k - n2)² - (k - n2)
en donde de nueva cuenta n2 debe ser un entero positivo.
De las relaciones que hemos obtenido para n1 y n2 podemos escribir lo siguiente:
g = g
(k + n1)² + (k + n1) = (k - n2)² - (k - n2)
(k + n1)² + (k + n1) = (k - n2)² - (k - n2)
Podemos llevar a cabo en ambos lados la siguiente factorización:
(k + n1)(k + n1 + 1) = (n2 - k)(n2 - k + 1)
Ahora bien, en el lado derecho la ecuación cuadrática resultante tiene dos soluciones posibles, siendo la primera:
n2 - k = k + n1
que podemos verificar de la siguiente manera trabajando en el lado izquierdo de la penúltima igualdad:
(n2 - k)(n2 - k + 1) = (k + n1)(k + n1 + 1)
y siendo la segunda:
n2 = - n1 - 1
que también podemos verificar de igual manera. Sin embargo, puesto que n1 sólo puede tomar valores enteros positivos, la segunda solución implicaría que n2 puede tomar valores negativos, razón por la cual desechamos la segunda solución quedándonos con la primera.
Haciendo:
j = k + n1 = n2 - k
tenemos entonces que:
j = (n1 + n2)/2
y también que:
k = j - n1 = - j + n2
Lo anterior implica que j debe ser uno de los siguientes números:
j = 0, 1/2, 1, 3/2, 2, 5/2, ...
y que k debe ser uno de los siguientes números:
k = - j, - j + 1, - j + 2, - j + 3, ... , j - 3, j -2, j - 1, j
Estos son los únicos valores que las cantidades representadas por las matrices J² y Jz pueden tener. En el caso del número k, esto implica que el momento angular orbital medido en el eje-z que corresponde a alguno de los valores (eigen) posibles de la matriz Jz debe ser un múltiplo del entero k el cual puede variar desde -j hasta +j. No hay por lo tanto un rango continuo de valores posibles para cualquiera de las cantidades representadas por las matrices J² y Jz, los valores están cuantizados. Puesto que J² y Jz, representan observables compatibles, cualquiera de los valores que pueda tomar la matriz J² puede ocurrir con cualquiera de los valores que pueda tomar la matriz Jz, no hay cosa que lo impida.
Para el momento angular orbital, los valores j y k siempre son ambos números enteros, no hay valores fraccionarios permitidos. En cambio, para el momento angular del spin, puesto que:
J² = Jx² + Jy² + Jz² = (3/4) I
tal y como lo vimos en el problema de arriba, en valores eigen esto equivale a:
para j = 1/2. De este modo, los únicos valores posibles de la cantidad representada por Jz (para el momento angular del spin del electrón) serán:
k = + 1/2__(spin “hacia arriba”)
k = - 1/2__(spin “hacia abajo”)
k = - 1/2__(spin “hacia abajo”)
puesto que los valores que puede tomar k están restringidos al rango:
k = - j, + j