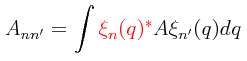Para alguien que haga comparaciones superficiales entre la Mecánica Matricial y la Mecánica Ondulatoria las diferencias y las similitudes entre ambas parece ser una cosa interesante que bien pudiera deberse a simples coincidencias. Tómese por ejemplo el contraste que hay entre el operador matricial utilizado para describir al momento angular orbital, y el mismo operador tal y como se utiliza en la Mecánica Ondulatoria:
Sin embargo, el lector que haya seguido de cerca aquí el estudio de la Mecánica Ondulatoria de Schrödinger tras haber leído con atención lo que se ha detallado acerca de la Mecánica Matricial de Heisenberg sin lugar a dudas se habrá dado cuenta ya de otras numerosas coincidencias que hay entre ambas ramas científicas. Tómese por caso la esperanza matemática de una cantidad física representada por una matriz Ξx la cual ya vimos en nuestro estudio matricial previo de “El spin del electrón” que se puede definir de la siguiente manera:
Compárese esta definición con la definición para la esperanza para una cantidad física como el operador de energía Hamiltoniano H usándose como mecanismo de evaluación una función de onda ψ no necesariamente normalizada:
Por otra parte, ya vimos en un principio que el problema del oscilador harmónico simple se puede resolver utilizando la Mecánica Matricial de Heisenberg. Pero también se puede resolver utilizando la Mecánica Ondulatoria de Schrödinger. Y en ambos casos obtenemos exactamente el mismo resultado. Pese a que un procedimiento recurre al uso de matrices mientras que el otro procedimiento recurre al uso de ecuaciones diferenciales, técnicas matemáticas por completo diferentes, el hecho de obtener los mismos resultados utilizando dos técnicas diversas nos puede llevar a sospechar de que, en el fondo, aquí no se trata de ninguna coincidencia fortuita, y que existe una equivalencia entre ambas técnicas que nos permite usar la una o la otra sin que haya diversidad alguna en el resultado final. En pocas palabras, sospechamos que hay una correspondencia directa entre la Mecánica Matricial y la Mecánica Ondulatoria. Esto mismo sospechó Schrödinger, y no le llevó mucho esfuerzo el comprobar que efectivamente la correspondencia entre la Mecánica Matricial y la Mecánica Ondulatoria es tal que podemos utilizar cualquiera de las dos técnicas para resolver cualquier problema soluble de Mecánica Cuántica. Mientras que en la Mecánica Ondulatoria el problema físico a resolver está fundamentado sobre ecuaciones diferenciales que describen el comportamiento del sistema, en la Mecánica Matricial el problema físico está fundamentado sobre la matriz que describe el comportamiento del sistema:
Otro punto de coincidencia entre la Mecánica Matricial y la Mecánica Ondulatoria es el hecho de que en ambas se recurre con harta frecuencia a las funciones ortogonales. Lo que en la Mecánica Matricial es un vector, en la Mecánica Matricial es una función, y así como un vector cualquiera casi siempre puede ser expandido sobre una base vectores ortogonales del mismo modo la gran mayoría de las funciones matemáticas periódicas pueden ser expandidas sobre una base de funciones ortogonales a través de las series de Fourier. Y de hecho esta expansión mediante funciones ortogonales es lo que nos proporciona la ruta de entrada para la demostración formal de la equivalencia plena entre ambas ramas de la Mecánica Cuántica.
Se puede establecer casi de inmediato la equivalencia total entre la Mecánica Matricial y la Mecánica Ondulatoria tomando como guía el siguiente precepto al cual se le puede dar validez matemática rigurosa:
| Dada cualquier función matemática f(x), siempre es posible encontrar una representación matricial M para dicha función si se usa para ello un conjunto de funciones ortogonales ψ(x) que sean linealmente independientes. |
El método para demostrar lo anterior es constructivo, y lo único que se requiere es que las funciones de base ψa(x) sean ortogonales (ni siquiera se requiere que estén normalizadas a la unidad, esto es, que sean ortonormales, tal requerimiento lo impone el criterio de Born usado para darle una interpretación física a las funciones de onda como estimadoras de la probabilidad de encontrar una partícula en cierto lugar del espacio):
Cada elemento matricial de la matriz M a ser construída será obtenido de la siguiente manera:
PROBLEMA: Dada la siguiente función:
bosquejar la manera de construír la representación matricial de dicha función usando para ello el conjunto de funciones de onda del oscilador armónico simple.
Las primeras cuatro funciones de onda del oscilador armónico simple (cuántico) son las siguientes:
Usando tales funciones de onda como funciones de base o vectores de base, se pueden obtener los elementos matriciales que se muestran a continuación:
Resulta evidente que si en vez de usarse las funciones de onda del oscilador armónico simple se usan las funciones de onda de una particula atrapada en una caja de longitud L:
la matriz que así se obtenga será completamente diferente a la matriz anterior. Cada conjunto de funciones de onda ortogonales genera una matriz diferente.
Si el conjunto de funciones de base ortogonales es un conjunto finito, obviamente la matriz que se construya será una matriz cuadrada finita, pero si en caso contrario se trata de un conjunto de funciones de base infinitamente grande, la matriz generada será una matriz infinitamente grande. Afortunadamente, no se requieren todos los elementos de una matriz infinitamente grande para poder explicar muchos fenómenos físicos, en la mayoría de los casos basta con obtener unos cuantos elementos matriciales.
Con la prescripción que se acaba de dar, se puede en principio ir construyendo una matriz calculando cada elemento matricial de la misma, uno por uno. Así pues, podemos ir fácilmente de la Mecánica Ondulatoria a la Mecánica Matricial sin problema alguno. Pero... ¿podemos llevar a cabo el procedimiento opuesto? El asunto ya no es tan fácil, empezando por el hecho de que si se nos presenta una matriz M ya construída, las funciones de onda han desaparecido por completo en la evaluación de los elementos matriciales, no queda nada de ellas, y casi tendríamos que ser adivinos para intuír la naturaleza matemática de las funciones usadas para construír la matriz que se nos proporciona. Es fácil imaginar que en los inicios de la Mecánica Matricial se obtuvieron resultados importantes que no pudieron ser trasladados de la Mecánica Matricial a la Mecáncia Ondulatoria, teniéndose que comenzar de cero para poder obtener el símil de cierto resultado matricial.
De cualquier modo, viendo la facilidad con la cual se puede construír una matriz a partir de alguna función matemática si se cuenta de antemano con un conjunto de funciones de onda que pueda ser usado como base, el mismo descubridor de la ecuación de onda para las ondas de materia, Erwin Schrödinger, fue de los primeros en asentar por escrito la equivalencia plena entre la Mecánica Ondulatoria y la Mecánica Matricial. Es justo poner las ideas expuestas arriba de una manera un poco más formal para darle gusto a los matemáticos que prefieren el simbolismo riguroso de aplicación general, y tal cosa es lo que vamos a hacer a continuación.
Así pues, es muy fácil dar el salto formal desde el entorno matemático de la Mecánica Ondulatoria en donde manejamos funciones de onda continuas y ecuaciones diferenciales hacia la Mecánica Matricial en donde no se ven funciones continuas ni ecuaciones diferenciales. Desde el aspecto matemático, para llevar a cabo la transición lo único que necesitamos son dos cosas:
1) Un operador continuo (un operador diferencial, un operador integral, una combinación de operadores, etc.)
2) Un conjunto de funciones ortogonales (no necesariamente ortonormales).
PROBLEMA: Constrúyase una matriz X que represente al operador posición:
utilizando como pie de base el siguiente conjunto de funciones ortogonales:
válido en el intervalo -1.≤.x.≤.+1
A partir del conjunto de kets que nos es proporcionado (los cuales no están normalizados), podemos formar el dual a este conjunto de kets, que viene siendo el siguiente conjunto de bras:
con todo lo cual podemos definir una matriz X del modo siguiente:
Para el caso en el cual i.=.j, podemos ver que:
en virtud de que -1 elevado a cualquier entero par es igual a +1. Esto se traduce en una matriz para la cual todas las entradas a lo largo de su diagonal principal son iguales a cero. Esto lo podemos ver más claramente dándoles tanto a los enteros i como a los enteros j un valor máximo igual a 5 con lo cual tenemos la siguiente matriz 5x5 en base a la relación obtenida:
Una matriz así no puede ser diagonalizada, ni siquiera en principio, ya que no podemos montar una ecuación característica que no nos conduzca más que a raíces repetidas de cero. La explicación del fracaso radica en el hecho de que el operador posición no es un operador que represente a una observable física que pueda ser discretizada; la posición no puede ser cuantizada, y punto. No habrá matriz que sea capaz de corresponderse con el operador posición a través de sus eigenvalores, no a menos de que se trate de una matriz continua para cuya representación diagonalizada se utilice la función δ de Dirac en lugar del delta de Kronecker.
La moraleja en esto es clara. Aunque podamos contruír una matriz para cualquier operador continuo utilizando cualquier conjunto de funciones ortogonales, no todas las funciones ortogonales que podamos concebir serán útiles para tal propósito. De hecho, las únicas funciones ortogonales que servirán para construír una matriz que se corresponda con un operador continuo serán aquellas que también sean eigenfunciones del operador.
PROBLEMA: Constrúyase una matriz D que represente al operador derivativo:
utilizando como pie de base el siguiente conjunto de funciones ortogonales:
válido en el intervalo -1.≤.x.≤.+1
A partir del conjunto de kets que nos es proporcionado (los cuales no están normalizados), podemos formar el dual a este conjunto de kets que viene siendo el siguiente conjunto de bras:
Un elemento matricial típico Dij que nos representa al operador diferencial d/dx está dado entonces por:
Simplificando un poco más, tenemos la expresión que nos dá todos los elementos de la matriz construída para representar al operador derivativo:
Nuevamente, se comprueba aquí que la selección del conjunto de funciones ortogonales utilizadas para construír una matriz para cierto operador impactará directamente en la forma que tomará la matriz final.
PROBLEMA: Constrúyase para el operador derivativo dado en el problema anterior una matriz utilizando para la construcción de la matriz el siguiente conjunto de funciones ortogonales:
Para este conjunto ortogonal de kets, el conjunto correspondiente de bras será el siguiente (obsérvese cómo tenemos que tomar el conjugado complejo):
Entonces los elementos del operador matricial Dmn serán:
Recurriendo a la fórmula de Euler, esto lo podemos escribir como:
Llevando a cabo ambas integraciones (en el segundo término el producto de dos números imaginarios i nos dá una unidad positiva cuyo signo es invertido a causa del signo negativo introducido por la integración de la función cosenoidal):
que es lo mismo que:
Tomando límites, resulta obvio que el segundo término se desvanece por ser una función par, quedándonos únicamente el primer término que tras la toma de límites nos viene dando:
Por hipótesis, tanto m como n son enteros. La expresión anterior no es válida para m.=.n ya que nos produce una indeterminación. Suponiendo que m y n son diferentes, entonces la evaluación del término senoidal tendrá como argumento un múltiplo entero de π, y siendo así entonces el término senoidal tendrá que ser necesariamente igual a cero. Por otro lado, cuando m y n son iguales, la integración al principio procede de la siguiente manera:
Podemos juntar ambos resultados tanto para m y n diferentes como para m y n iguales en una sola expresión con la ayuda del delta de Kronecker:
Obsérvese que a diferencia de la matriz que se obtuvo en el problema anterior, esta es una matriz diagonal cuyas entradas son imaginarias. El hecho de haber obtenido aquí una matriz con entradas imaginarias nos debe poner a reflexionar sobre una cosa muy importante: para un problema físico en el cual cierta cantidad observable sea uno de los eigenvalores que puede tomar la ecuación diferencial cuántica que describe al sistema físico bajo el contexto de la Mecánica Ondulatoria, la matriz que se corresponda con la ecuación diferencial tiene que tener los mismos eigenvalores. Sin entrar en mayores detalles, resulta obvio que una matriz diagonal con entradas imaginarias no podrá describir ningún sistema físico en el cual vamos a medir cantidades reales. El dilema que confrontamos aquí es que no sólo el operador derivativo es un operador lineal en toda la extensión de la palabra en el sentido de que:
sino que cada uno de los kets de la base ortonormal de eigenkets que utilizamos aquí en este problema es también una eigenfunción del operador derivativo (los kets del problema anterior no lo eran); esto es, si D es el operador derivativo, entonces eikx será una eigenfunción del operador derivativo puesto que D(eikx).=.ikeikx (el exponencial real ekx también es una eigenfunción, pero puesto que explota hacia cantidades infinitamente grandes para valores grandes de la variable independiente, no está comprendido dentro del espacio de Hilbert y por lo tanto no lo consideramos). Las eigenfunciones normalizables del operador derivativo D son precisamente eikx (así como e-ikx), y el operador derivativo es un operador lineal. Aparentemente, todo debería haber funcionado a la perfección, pero no fue así. ¿Entonces que fue lo que nos salió mal aquí? Puesto que la propia naturaleza de las eigenfunciones que van aparejadas con el operador derivativo hace descender al número imaginario i cuando se lleva a cabo la diferenciación, todos los eigenvalores terminan siendo imaginarios. Esto trae a colación el hecho de que puesto que el resultado de cualquier observación física debe ser un valor real, también debe serlo el eigenvalor del operador, y ya hemos visto previamente que sólo los operadores Hermitianos pueden tener eigenvalores reales. Esta es la importancia de los operadores Hermitianos en la Mecánica Cuántica. Con este breve argumento, y sin necesidad de tener que entrar en detalles finos, hemos demostrado que el operador derivativo D no es un operador Hermitiano. Es, de hecho, lo que se conoce como un operador anti-Hermitiano. ¿Hay algo que podamos hacer para que el operador:
que no es Hermitiano pueda de alguna manera ser convertido en un operador Hermitiano? La respuesta es afirmativa, y para lograr tal cosa todo es tan sencillo como premultiplicar el operador derivativo por el número imaginario i definiendo de este modo el siguiente operador:
Esto hace que todos los eigenvalores se vuelvan reales, convirtiendo al operador no-Hermitiano D en un operador Hermitiano Q. De hecho, si cambiamos un poco la constante pre-multiplicadora, podemos obtener el siguiente operador:
Este es el mismo operador Hermitiano que hemos estado utilizando previamente como el operador diferencial cuántico del momentum.
Lo que acabamos de ver tiene una contraparte en la Mecánica Matricial. Así como en la Mecánica Ondulatoria hablamos de operadores diferenciales Hermitianos y operadores diferenciales anti-Hermitianos, en la Mecánica Matricial hablamos de matrices Hermitianas y matrices anti-Hermitianas. Lo uno se corresponde directamente con lo otro. Recuérdese que definimos una matriz Hermitiana como toda aquella matriz M cuya transpuesta de su conjugado complejo, o bien su transconjugada simbolizada como M†, es igual a la misma matriz M. Ahora, del mismo modo, definimos a una matriz anti-Hermitiana (en los textos en inglés es frecuente encontrar el apelativo skew-symmetric matrix que resulta más críptico y menos iluminante) como toda aquella matriz cuya transconjugada es igual al negativo de la matriz original:
____Matriz Hermitiana: M† = M
____Matriz anti-Hermitiana: M† = - M
En síntesis, el requisito primordial que debe satisfacer un operador mecánico-cuántico para que dicho operador sea de utilidad correspondiéndose con observables físicas es que dicho operador sea Hermitiano, estando expresada dicha condición para un operador Q cualquiera mediante la siguiente igualdad que ya fue postulada previamente en la entrada “Operadores Hermitianos”:
De este modo, y ya no desde el punto de vista puramente matemático sino también desde el aspecto físico, para llevar a cabo la transición de la Mecánica Ondulatoria a la Mecánica Matricial, lo único que necesitamos son dos cosas:
1) Un operador continuo que sea Hermitiano.
2) Un conjunto de funciones ortogonales que estén normalizadas.
Obsérvese que se ha agregado otro requisito fundamental, el requisito de que el conjunto de funciones ortogonales consista de funciones también normalizadas, esto es, que sea un conjunto de funciones orto-normales. Ha sido necesario agregar este segundo requisito para poder satisfacer el criterio de Born que le dá una interpretación probabilista al cuadrado de la función de onda. Las dos condiciones que han sido agregadas y que han sido resaltadas en letras itálicas no son requerimientos matemáticos, son requerimientos físicos para que lo que estamos manejando pueda tener algún sentido.
Si bien a estas alturas resulta obvio cómo podemos brincar de la Mecánica Ondulatoria a la Mecánica Matricial, quizá no sea tan obvio cómo podemos dar el salto contrario, esto es, de la Mecánica Matricial a la Mecánica Ondulatoria. Esto se dilucidará procediendo con la demostración formal de la equivalencia plena que hay entre la Mecánica Matricial y la Mecánica Ondulatoria.
La idea detrás de la demostración formal de la equivalencia entre la Mecánica Cuántica y la Mecánica Ondulatoria es en realidad una idea muy sencilla. Así como las matrices infinitas que sean diagonalizables poseen una cantidad infinitamente grande de valores propios discretos, sus valores eigen, también ciertas ecuaciones diferenciales poseen una cantidad infinitamente grande de valores que son soluciones a dichas ecuaciones. Cuando las soluciones son equivalentes, la solución general puede ser representada matemáticamente como la suma vectorial de todos esos valores discretos.
Antes de llevar a cabo la demostración formal de la equivalencia que hay entre la Mecánica Matricial y la Mecánica Ondulatoria, repasaremos primero el concepto de los operadores lineales. Nos referiremos al resultado de aplicar en forma secuencial la operación d/dx = Dx a una función arbitraria f(x) en ese orden simplemente como el producto del operador d/dx = Dx por la función f(x). Del mismo modo, a la función x.f(x) que se obtiene de aplicarle el operador x a la función f(x) en ese orden se le llamará simplemente el producto del operador x por la función f(x). Para hablar con mayor generalidad, podemos representar a los operadores lineales con letras mayúsculas, A, B, C, etc. De este modo, la operación de obtener la función g(x) a partir de la función f(x) con la aplicación de un operador lineal A sobre la función f(x) se puede simbolizar de la siguiente manera:
g(x) = Af(x)
Tratándose de operaciones sencillas tales como la diferenciación (simbolizada como d/dx), podemos expresar sin riesgo de confusión alguna al operador lineal correspondiente utilizando los mismos símbolos con los cuales se suele escribir dicho operador (como d/dx) sin necesidad de tener que recurrir al uso de letras mayúsculas.
Definimos al producto de dos operadores lineales A y B, escrito en el orden AB, como el operador que al ser aplicado a una función f(x) nos dá el mismo resultado que si el operador A es aplicado al producto Bf(x). En símbolos, este producto queda definido mediante la siguiente relación:
(AB) f(x) = A(Bf(x))
Por otro lado, definimos a la suma de dos operadores lineales A y B de la siguiente manera:
(A + B)f(x) = Af(x) + Bf(x)
Decimos que dos operadores lineales son iguales cuando aplicados sobre una función arbitraria f(x) nos producen el mismo resultado:
Af(x) = Bf(x)
representándose esta relación de igualdad de la manera siguiente:
A = B
La relación mediante la cual se define formalmente un operador lineal que puede actuar sobre cualquier selección de funciones arbitrarias .f1(x) y .f2(x) es la siguiente:
A{c1.f1(x) + c2.f2(x)} = c1Af1(x) + c2Af2(x)
siendo c1 y c2 constantes.
PROBLEMA: Demostrar que un operador A que reemplaza a una función f(x) por el cuadrado de dicha función no es un operador lineal.
Por la forma en la cual está definido el operador A, debemos tener lo siguiente cuando aplicamos dicho operador sobre dos funciones .f1(x) y .f2(x):
A f1(x) = f1(x)²
A f2(x) = f2(x)²
A f1(x) + A f2(x) = f1(x)² + f2(x)²
Por otro lado, tenemos que:
A{.f1(x) + .f2(x)} = {.f1(x) + .f2(x)}² = f1(x)² + 2f1(x)f2(x) + f2(x)²
Obviamente:
A{.f1(x) + .f2(x)} ≠ A f1(x) + A f2(x)
Entonces el operador A no es un operador lineal.
Entre los operadores lineales, además de los operadores diferenciales tenemos a lo que se conoce comunmente como los operadores integrales. Dada una función de dos variables G(x,x’) conocida como “núcleo” o kernel, a partir de una función f(x) podemos construír una nueva función g(x) mediante la operación:
PROBLEMA: Demostrar que el operador integral es un operador lineal.
El operador integral es claramente un operador lineal en virtud de que:
Dicho sea de paso, se recuerda aquí que recurriendo a la definición de la función delta δ(x) de Dirac se puede expresar al operador diferencial d/dx en la forma de un operador integral con el simple hecho de hacer lo siguiente:
G(x,x’) = δ’(x’)
del mismo modo en que podemos expresar al operador posición también en la forma de un operador integral haciendo:
G(x,x’) = x δ’(x’)
La interpretación que se debe dar a un operador lineal exponenciado consiste en aplicar el mismo operador sobre un operando tantas veces como lo indique el exponente. De este modo, el operador (d/dx)² equivale a dos operaciones sucesivas de d/dx, mientras que el producto con el operador posición x² se debe interpretar como dos multiplicaciones sucesivas con el operador posición. De este modo, las expresiones simbólicas (d/dx)² y x² en la eigenecuación:
estarán en concordancia con nuestra definición de operadores y productos, y el símbolo + también puede ser entendido como la adición de operadores sumandos.
A continuación investigaremos las propiedades de los operadores x y (ħ/i)(d2/dx2), para lo cual multiplicaremos primero una función arbitraria f(x) con el operador posición tras lo cual aplicaremos el operador lineal d/dx para así obtener el siguiente aplicando la regla de Leibniz para la diferenciación del producto de dos cantidades:
Pasando el segundo término que está en el lado derecho de la igualdad hacia el lado izquierdo de la igualdad y factorizando operacionalmente el lado izquierdo de la igualdad de acuerdo a nuestras definiciones de suma y producto de operadores, lo anterior se puede expresar de la siguiente manera:
Multiplicando ambos miembros de la igualdad por el factor constante ħ/i, obtenemos entonces:
Puesto que esta ecuación es válida para cualquier función arbitraria f(x), podemos enfocarnos directamente sobre la parte operacional de la misma enunciando lo siguiente:
Si comparamos esta expresión con la ecuación de Max Born tal y como la vimos desde un principio para el caso en el cual empezamos manejando matrices que corresponden al operador matricial momentum P y al operador matricial posición Q, podemos ver que hay una correspondencia directa si reemplazamos al vector η y las matrices P y Q que actúen sobre dicho vector con la función f(x) y con los operadores x y (ħ/i)(d2 /dx2). La clave de esta extraordinaria coincidencia radica en el hecho de que tanto la ecuación matricial como la ecuación diferencial con la cual se corresponde tienen el mismo conjunto de eigenvalores. Y se trata de una correspondencia que vá más allá de algo meramente formal, ya que el efecto de:
sobre un vector η es exactamente el mismo que el efecto de:
sobre una función Φ(x). Sin embargo, no debemos quedarnos conformes con un enunciado vago acerca de “efectos”. Tenemos que colocar la razón que hay detrás de esta coincidencia sobre un andamiaje matemático rígido. Esto fue lo que hizo Schrödinger y a continuación haremos lo mismo siguiendo una línea de demostración muy parecida a la que fue utilizada por el mismo Schrödinger.
La demostración formal de la correspondencia entre funciones y vectores y entre operadores lineales y matrices, respectivamente, depende del hecho de que, mediante un conjunto de funciones ortonormales apropiadas (de las cuales ya hemos visto bastantes en las entradas previas), se puede establecer una correspondencia biunívoca (de uno-a-uno) entre funciones y vectores y entre operadores lineales y matrices. La base matemática para la coincidencia entre la Mecánica Matricial y la Mecánica Ondulatoria está sustentada en esta correspondencia.
La equivalencia entre la Mecánica Matricial y la Mecánica Ondulatoria se puede empezar a demostrar de dos maneras: (1) partiendo de los postulados y las técnicas utilizadas en la Mecánica Matricial para obtener los postulados utilizados en la Mecánica Ondulatoria, y (2) partiendo de los postulados y las técnicas utilizadas en la Mecánica Ondulatoria para obtener los postulados utilizados en la Mecánica Matricial. Por cuestiones pedagógicas, empezaremos por la segunda vía de demostración.
Considérese un conjunto completo de funciones ortonormales:
ξ1(q), ξ2(q), ξ3(q), ... , ξn(q), ...
satisfaciendo los requisitos usuales de ortonormalidad para dos funciones cualesquiera del conjunto:
que podemos simplificar simbólicamente con la notación bra-ket de Dirac y con el delta de Kronecker de la siguiente manera:
Para mayor simplicidad, supondremos que todas las funciones ξk(q) = {ξ1, ξ2, ξ3, ...} se desvanecen para |q|→∞ (recuérdese el requerimiento de que la función de onda ψ se desvanezca en el infinito para que la solución a la ecuación de onda de Schrödinger pueda tener un sentido físico).
Puesto que el conjunto de funciones ortonormales {ξk(q)} = {ξ1, ξ2, ξ3, ...} es un conjunto completo, es posible expandir una función f(q) cualesquiera (que sea “bien comportada”, desde luego) en términos del conjunto de funciones ortonormales que ha sido seleccionado:
siendo cada una de las constantes ηn (representadas con la letra griega eta η) los “coeficientes de Fourier” que deben ser utilizados para que la suma infinita de términos pueda ser capaz de reproducir fielmente la función f(q).
De acuerdo a lo que hemos visto previamente en otras entradas acerca de las expansiones en series de Fourier, podemos ir obteniendo cada uno de los coeficientes ηn mediante una simple integración que va descartando todos los términos de la serie infinita excepto aquél cuyo coeficiente será evaluado:
siempre y cuando todas las integrales converjan para todos los valores de n. Cada ξn* nos “entresacará” un número ηn de la suma infinita de términos.Esto mismo desde luego puede ser expresado de modo más elegante y compacto con la notación bra-ket de Dirac:
La expansión de Fourier (1) determina de manera unívoca la función f(q) cuando se ha proporcionado previamente un conjunto de números η1, η2, η3, etc. Y “a la inversa”, la relación (2) determina en forma unívoca el conjunto de números η1, η2, η3, etc. cuando se proporciona una función f(q) cualquiera. Si consideramos al conjunto de números η1, η2, η3, ... como los componentes de un vector η, podemos afirmar entonces que existe una correspondencia entre funciones y vectores, en cuyo caso el conjunto Fourier de funciones ortonormales {ξ1, ξ2, ξ3, ...} nos sirve meramente como una especie de “intermediario” para poder establecer la correspondencia. Puesto que hemos visto que hay muchos conjuntos de funciones ortonormales que pueden ser utilizadas para tal efecto, no estando limitados a únicamente a las funciones trigonométricas con las que trabajó Jean-Baptiste Fourier, y puesto que cualquier conjunto de funciones puede ser utilizado siempre y cuando cumpla la condición de ortonormalidad, resulta claro que las diferentes representaciones Fourier que se pueden llevar a cabo sobre una misma función f(q) serán prácticamente infinitas, aunque el resultado final siga siendo el mismo.
El tipo de operaciones que encontramos frecuentemente en la Mecánica Ondulatoria es de la forma:
Aψ = ψ’
en donde A es un operador diferencial (como el operador Hamiltoniano de energía) que se aplica sobre una función de onda. La función de onda ψ es aquí la función generalizada f(q) que hemos estado manejando arriba, y como tal la podemos tomar. Expandiendo tanto la función ψ como la función ψ’ mediante el conjunto de funciones ortonormales {ξk(q)} que estemos utilizando en (1) arriba, la relación de arriba toma el siguiente aspecto:
Multiplicando ambos miembros de esta igualdad por ξm(q)*:
e integrando sobre todo el espacio bajo consideración:
podemos ver que, por la ortonormalidad de las funciones de base, el único coeficiente que sobrevivirá a la integración término-por-término en el lado derecho de la igualdad (obsérvese que tras la expansión de la sumatoria se tendrá una suma infinita de integrales y cada η’ se puede sacar fuera de cada una de estas integrales por ser una constante) es aquél para el cual m = n, o sea:
Trabajando sobre el lado derecho de la igualdad, e intercambiando el orden de la sumación y la integración (matemáticamente hablando, tal vez esto no sea permisible en todos los casos, pero no entraremos en detalle sobre esos casos patológicos especiales con mayor relevancia en las matemáticas puras que en la física), tenemos lo siguiente:
que podemos destacar como:
Esto tiene ya una forma que nos debe ser familiar. Recurriendo a la notación bra-ket de Dirac, podemos escribir lo anterior como:
Considerando a lo que tenemos en el bra-ket como un elemento matricial que nos simboliza a los elementos matriciales Amn, podemos escribir lo anterior de una manera más compacta aún:
y puesto que, si bajo un símbolo de sumatoria al intercambiar el orden de los sumandos el resultado de la suma sigue siendo el mismo, esto es:
entonces podemos juntar esto con el resultado previo que habíamos obtenido para el lado derecho de la igualdad escribiendo lo siguiente:
Puesto que los elementos Amn pueden ser acomodados ordenadamente dentro de una matriz:
y puesto que tanto el conjunto de números {η} como el conjunto de números {η’} se pueden escribir acomodándolos como vectores:
entonces podemos escribir lo siguiente:
Aη = η’
Esta es una ecuación matricial, que involucra una matriz A = (Amn) y dos vectores (η y η’). Tras el proceso de conversión tenemos ya una ecuación propia de la Mecánica Matricial y no de la Mecánica Ondulatoria.
La correspondencia entre funciones y vectores tiene la propiedad común de linealidad: si un vector η se corresponde con una función f(q) y un vector τ se corresponde con una función g(q), entonces el vector η+τ se corresponde con la función f(q)+g(q), y viceversa.
También por lo que se ha afirmado previamente en otras entradas, en virtud de las relaciones de ortonormalidad se puede demostrar que que:
Esto último se puede expresar con una mayor generalidad involucrando no el producto de una función f(q) consigo misma sino el producto de dos funciones distintas f(q) y g(q) de la siguiente manera:
en donde ηn* se corresponde con f(q)* y τn se corresponde con g(q), siendo esto consecuencia también de las relaciones ortonormales que hay entre los ξ. Bajo este punto de vista, podemos empezar por tratar de encontrar al vector que se corresponde con el “producto” entre el operador lineal A con la función f(q) (en realidad, el operador lineal A actuando sobre la función f(q) aunque la costumbre nos hace llamar a la operación un “producto”), y podemos imaginar que empezamos trabajando desde el ámbito de la Mecánica Ondulatoria en donde lo que se manejan son funciones y operadores diferenciales lineales. Siendo así, lo que queremos hacer es encontrar al vector que se corresponde con el “producto”. Si simbolizamos al vector que se corresponde con la función f(q) como η, y simbolizamos al vector que se corresponde con el “producto” Af(q) como τ, entonces, de acuerdo con (2), τn está determinado y puede ser obtenido mediante la siguiente relación:
lo cual se convierte, en virtud de la relación (1), en:
Puesto que A es un operador lineal, lo podemos meter dentro de la sumación para actuar sobre cada ξ:
De este modo, intercambiando el orden de la sumación y la integración, llegamos a lo siguiente:
Esta última ecuación es la que nos proporciona la relación que hay entre el vector τ y el vector ξ. Si definimos a los elementos matriciales Ann' de la siguiente manera:
que también puede ser representada de manera un poco más compacta mediante la notación bra-ket de Dirac:
entonces tenemos a la relación que nos establece una correspondencia directa entre operadores lineales y matrices, lo cual se vuelve aún más obvio al poder escribir lo siguiente en base a lo anterior:
Esto último nos indica que el vector τ = (τn) está dado por el producto de la matriz A = (Ann') y el vector η. Y de hecho, como podemos apreciarlo en la definición que se ha dado para Ann', los elementos matriciales Ann' están determinados única y exclusivamente por el operador A y por las funciones ortonormales ξ en forma independiente del vector η. De nueva cuenta, llegamos al resultado que habíamos obtenido previamente, estableciendo firmemente la existencia de una correspondencia entre operadores lineales y matrices. Siempre que tengamos un operador lineal entonces habrá una matriz que se corresponderá directamente con dicho operador. Obsérvese que el elemento central para poder llevar a cabo la demostración fue el uso de funciones ortonormales.
Procediendo “a la inversa”, podemos demostrar que cuando se nos proporciona una matriz entonces existe un operador lineal que corresponderá a la matriz proporcionada. Esta es la otra vía de demostración mencionada previamente para empezar a probar la equivalencia entre la Mecánica Matricial y la Mecánica Ondulatoria, partiendo de los postulados y las técnicas utilizadas en la Mecánica Matricial para obtener los postulados utilizados en la Mecánica Ondulatoria. Para ello, supóngase que tenemos una matriz M y dos vectores η y τ están relacionados de la siguiente manera:
τ = Mη
Sean f(q) y g(q) las funciones que se corresponden directamente con los dos vectores η y τ. Se debe demostrar entonces que la función g(q) se puede obtener como el producto de la función f(q) por cierto operador lineal que está pendiente aún de ser determinado. Este operador lineal queda definido exclusivamente en términos de la matriz M junto con las funciones ortonormales utilizadas para establecer la correspondencia, siendo independiente de f(q) y g(q).
La relación en notación matricial compacta:
τ = Mη
escrita en notación matricial explícita (usando sumatoria) tiene el siguiente aspecto:
Por lo tanto, la función g(q) que se corresponde con el vector τ puede ser escrita como:
y en virtud de que tenemos:
la expresión para g(q) puede ser escrita como:
Definiendo G(q, q') de la siguiente manera:
e intercambiando el orden de la integración y las sumatorias (esto es, metiendo los dos símbolos Σ dentro del signo de la integral), obtenemos el siguiente resultado conciso:
Por la definición que le hemos dado a la función de dos variables G(q,q'), vemos que está determinada única y exclusivamente por la matriz M = (Mnn') conjuntamente con las funciones de base ξk(q), y es independiente de f(q). Ahora bien, el último resultado que acabamos de obtener nos dice que g(q) es el resultado de la multiplicación de una función f(q) por un operador integral que está especificado mediante el núcleo o kernel G(q,q'). Siendo la integración -al igual que la diferenciación- una operación lineal en el sentido de que la integral de una suma (o diferencia) de integrandos es igual a la suma (o la diferencia) de los integrandos, esto nos establece la correspondencia biunívoca entre operadores lineales y matrices. Esta correspondencia es de la siguiente naturaleza: sea g(q) la función que obtenemos al llevar a cabo el “producto” de un operador lineal M por una función f(q), y sean τ el vector que se corresponde con la función g(q) y η el vector que se corresponde con la función f(q). Entonces el vector τ está dado por el producto de la matriz que se corresponde con el operador M y el vector τ. Esto es, si denotamos a la matriz en cuestión como M, entonces la relación:
τ = Mη
es una consecuencia directa de la relación:
g(q) = M f(q)
En lo general, se ha utilizado aquí el símbolo A para denotar a un operador lineal, y el símbolo A para denotar a una matriz. En algunos textos sin embargo se utiliza un mismo símbolo para representar ambas cosas, lo cual puede dar origen a confusiones. Pero no habrá confusión alguna si se interpreta al símbolo que va puesto adelante de una función como un operador lineal, y al símbolo que puesto adelante de un vector como una matriz.
Pese a lo que se acaba de demostrar arriba es trascendente, lo que se ha hecho no es suficiente. Tenemos que investigar también cómo se corresponde la suma de dos matrices con la suma de dos funciones, y tenemos que demostrar también cómo se corresponde el producto de dos matrices con el producto de dos funciones. Empezaremos por lo primero.
Tómese una función arbitraria f(q), y sea η el vector con el cual se corresponde:
f(q) ↔ η
Entonces el vector Aη se corresponde con la función Af(q) y el vector Bη se corresponde con la función Bf(q).
Af(q) ↔ Aη
Bf(q) ↔ Bη
Sin lugar a dudas, la suma de vectores correspondientes se corresponde con la suma de las funciones. Esto es, el vector Aη+Bη se corresponde con la función Af(q)+Bf(q):
Af(q) + Bf(q) ↔ Aη + Bη
En virtud de las definiciones de lo que es una suma de operadores y una suma matricial:
(A + B) f(q) = Af(q) + Bf(q)
(A + B)η = Aη + Bη
se concluye que la suma de las matrices se corresponde directamente con la suma de operadores, y viceversa:
A + B ↔ A + B
Esto que acabamos de concluír puede ser verificado mediante operaciones explícitas. Por ejemplo, denotando al operador suma de dos funciones (A+B) como C, usando la siguiente relación derivada arriba:
obtenemos lo siguiente:
Aplicando la definición de lo que debe ser el operador suma, esto se nos convierte en lo siguiente:
Esto último lo podemos expresar en una forma un poco más elegante y sofisticada mediante la notación bra-ket de Dirac:
Ahora veremos cómo se corresponde el producto de dos matrices con el producto de dos funciones. De nueva cuenta, tómese una función arbitraria f(q) junto con el vector η con el cual se corresponde:
f(q) ↔ η
Entonces el vector Bη se corresponde con la función Bf(q) y el vector A(Bη) se corresponde con la función A(B(f(q))):
Bf(q) ↔ Bη
A(B(f(q)))↔ A(Bη)
En virtud de las definiciones de lo que debe ser un producto de operadores -conocido frecuentemente como operador producto- y lo que es un producto de matrices:
(AB) f(q) = A(Bf(q))
(AB)η = A(Bη)
se concluye que el producto de las matrices correspondientes se corresponde con el producto de dos operadores lineales:
AB ↔ AB
Esto que acabamos de concluír también puede ser verificado mediante operaciones explícitas. Para ello, tomando en cuenta que:
con lo cual:
entonces, denotando a la matriz que corresponde al operador producto AB como C, tenemos entonces que:
lo cual, usando la relación dada arriba:
se nos convierte en lo siguiente:
Pero ya habíamos visto en una entrada previa al tratar a manera de repaso acerca del tema de vectores y matrices que una sumatoria de este tipo es precisamente la definición del producto de dos matrices A y B, en el orden AB. Se concluye entonces que la matriz C es igual al producto de la matrices A y B, y se concluye en consecuencia que el producto de dos operadores lineales se corresponde con el producto de las dos matrices correspondientes.
Hemos visto, pues, que hay una correspondencia cercana entre funciones y vectores, y entre operadores lineales y matrices, en tal forma que entre funciones y vectores la suma se corresponde con la suma, y entre operadores lineales y matrices se corresponde con la suma y el producto con el producto. Más aún, la correspondencia es tal que el producto de un operador lineal por una función se corresponde con el producto correspondiente de la matriz correspondiente y el vector correspondiente. De estos hechos concluímos que si hay una relación algebraica entre operadores lineales diversos A, B, C, D, etc., y dos funciones f(q) y g(q) de la forma:
F(A, B, C, D, ...) f(q) = G(A, B, C, D, ...) g(q)
El análisis anterior ha establecido correspondencias de índole puramente matemática, pero nos ha proporcionado las herramientas para clarificar las relación que existe entre la Mecánica Matricial por un lado y la Mecánica Ondulatoria por el otro.
Ya se ha visto previamente dentro de los confines de la Mecánica Ondulatoria que, definido de la siguiente manera el operador diferencial del momentum especificado para cierta coordenada generalizada q:
la siguiente ecuación diferencial algebraica es una ecuación perfectamente válida:
Procediendo como lo hemos hecho arriba, si tomamos un conjunto completo de funciones ortonormales {ξ1, ξ2, ξ3, ...} siempre podemos construír dos matrices:
que se correspondan directamente con los operadores q y Pq. Los elementos matriciales que van dentro de tales matrices están dados respectivamente por:
y por:
Esto mismo lo podemos expresar de una manera un poco más elegante y sofisticada recurriendo a la notación bra-ket de Dirac:
Puesto que la ecuación diferencial algebraica de Born dada con anterioridad es válida para los operadores q y Pq, entonces debe ser también igualmente válida para sus contrpartes matriciales, lo cual equivale a decir que las matrices Q y P también satisfacen la relación de Born. Esto nos proporciona el punto fundamental común entre la Mecánica Matricial y la Mecánica Ondulatoria:
Se puede demostrar que las matrices Q y P obtenidas de los operadores q y Pq son Hermitianas, esto es, los elementos matriciales de ambas satisfacen las condiciones:
La demostración para el caso de la matriz momentum P procede de la siguiente manera: primero tómese el conjugado complejo de la ecuación:
e intercámbiese el orden de los subíndices n y n’, obteniendo de este modo lo siguiente:
Llevando a cabo una integración por partes y aplicando en este proceso el hecho de que la función ξn se desvanece cuando la coordenada generalizada q tiende hacia el infinito, o sea |q|.→.∞, encontramos entonces que:
lo cual nos comprueba que la matriz momentum P es verdaderamente Hermitiana. La demostración de que la matriz posición Q también es Hermitiana procede de la misma manera y no será necesario llevarla a cabo.
Ahora bien, el problema fundamental en la Mecánica Matricial, cuando se tiene un operador Hamiltoniano de energía H que es una función de las matrices momentum P y posición Q, o sea H = H(P,Q), consiste en la resolución de la ecuación matricial:
Las matrices P y Q pueden ser seleccionadas arbitrariamente siempre y cuando cumplan con la condición de ser Hermitianas y que satisfagan la ecuación canónica de conmutación (la ecuación de Born). Por lo tanto, podemos utilizar las matrices obtenidas mediante las relaciones:
que corresponden a los operadores q y Pq de la Mecánica Ondulatoria. En base a todo lo anterior, la función matricial H(P,Q) que se corresponde con el operador lineal H(q,Pq) de la Mecánica Ondulatoria será:
Esto lo podemos escribir de una manera un poco más concisa y tal vez más entendible mediante la notación bra-ket de Dirac:
Definiendo a la función φ(q) que se corresponde con el vector χ de la misma manera que lo hemos hecho anteriormente mediante la relación (1) dada arriba:
teniendo desde luego:
podemos concluír en base a las discusiones anteriores que para el operador lineal H(q,Pq) propio de la Mecánica Ondulatoria así como para la función φ(q) debe de haber una relación de la misma forma que la relación matricial:
teniéndose por lo tanto lo siguiente:
El problema de encontrar una solución a esta ecuación diferencial propia de la Mecánica Ondulatoria es por lo tanto equivalente a la resolución de la ecuación matricial con la que se corresponde. Si podemos resolver esta última relación podemos entonces construír el vector χ a partir de φ(q) recurriendo para ello a un conjunto adecuado de funciones ortonormales, y del mismo modo (procediendo a la inversa) podemos obtener la función φ(q) a partir del vector χ si podemos resolver primero la ecuación matricial del sistema. Más aún, en virtud de la relación:
se requiere normalizar a la función φ(q) mediante el procedimiento usual para obtener las constantes de normalización:
Habiendo dos alternativas para llevar a cabo la solución de problemas mecánico-cuánticos, la cuestión sobre cuál de las dos alternativas utilizar es muchas veces una cuestión de conveniencia o incluso de necesidad, ya que un problema fácilmente soluble mediante las técnicas de la Mecánica Ondulatoria puede ser sumamente laborioso de resolver mediante las técnicas de la Mecánica Matricial, y viceversa. En muchos casos podemos seleccionar las matrices P y Q de modo tal que la función matricial H(P,Q) sea de orden finito en P, la mayoría de las veces de un orden no mayor que el segundo, y correspondientemente el operador lineal H(q,Pq) involucrará una diferenciación de orden finito, en muchos casos no mayor del segundo orden. Siendo así, la ecuación diferencial será una ecuación de orden finito, y la ecuación matricial puede ser reemplazada por la ecuación diferencial correspondiente, lo cual es una situación ventajosa puesto que la ecuación diferencial es una herramienta con la cual los físicos en su mayoría están mejor familiarizados que con la ecuación matricial que puede involucrar una cantidad una cantidad infinita de valores desconocidos. Dada su enorme utilidad, la ecuación diferencial:
es la que se utiliza con mayor frecuencia en la Mecánica Cuántica, siendo precisamente esta ecuación la ecuación de Schrödinger con la que estamos ya familiarizados.
Aunque hemos hablado de sistemas dinámicos en los cuales hay un solo grado de libertad, no resulta difícil generalizar los argumentos anteriores de modo tal que se puedan aplicar a sistemas dinámicos con varios grados de libertad. Si simbolizamos a las matrices de la posición como Q1, Q2, ..., Qr, y a las matrices del momentum como P1, P2, ..., Pr, en donde r es el número de grados de libertad, entonces las relaciones de conmutación de Born vienen siendo las siguientes:
QaQb - QbQa = O
PaPb - PbPa = O
QaPb - PbQa = iħδabI
Y dadas las correspondencias, cada conjunto de ecuaciones matriciales se corresponderá con un conjunto de ecuaciones diferenciales. De nueva cuenta, la conveniencia de trabajar para la solución de algún problema dentro de la Mecánica Matricial o dentro de la Mecánica Ondulatoria tendrá que ser tomada en cuenta para cada caso en particular.
La equivalencia plena que existe entre la Mecánica Matricial y la Mecánica Ondulatoria nos permite tomar el caudal de conocimientos acumulados en una de ellas para “transcribirlos” directamente a la otra, duplicando en cierta forma nuestro caudal de conocimientos con una inversión mínima de esfuerzo, siendo éste en realidad el principal objetivo de toda generalización o abstracción (en los años veintes del siglo XX, cuando la Mecánica Cuántica estaba aún en pañales, los proponentes de ambas filosofías estaban duplicando mucho del trabajo que estaban haciendo los del “bando contrario” sin darse cuenta de que en realidad estaban volviendo a reinventar la rueda). De cualquier manera, la duplicidad no es total, y es frecuente el poder obtener resultados nuevos que no sería fácil poder obtener de otra manera. Un ejemplo entre muchos que podríamos citar sería el de la “regla de Dirac” que consiste en tomar el conmutador clásico de los corchetes de Poisson, y con el solo hecho de multiplicarlo por el factor iħ obtener así la relación mecánico cuántica que va aparejada con el conmutador de la relación de Born:
Para mayor comodidad, reproduciremos aquí la definición clásica del corchete de Poisson tal y como se utiliza en la mecánica clásica:
En la entrada “De la mecánica clásica a la Mecánica Matricial”, ya vimos algunos ejemplos de cómo se utiliza la “regla de Dirac” para el caso en el cual lo que estaremos manejando son matrices. Aquí haremos lo mismo, excepto que no daremos brinco alguno a la Mecánica Matricial, los resultados que obtendremos estarán confinados a la Mecánica Ondulatoria.
Supóngase que en el corchete de Poisson definido arriba, haremos la cantidad A igual a la variable de la posición sobre la coordenada-x, y que la cantidad B la haremos igual a una función F del momentum a lo largo de la misma coordenada:
A = x
B = F(px)
B = F(px)
Con esto tenemos entonces lo siguiente:
Obsérvese arriba que, puesto que la variable de la posición es independiente de la variable del momentum medido sobre la misma coordenada, o sea ∂x/∂px = 0, lo que está de color rojo es cero anulándose así el segundo término.
Usando ahora la “regla de Dirac”, podemos obtener de la expresión clásica la ecuación mecánico cuántica correspondiente que viene siendo:
Supóngase ahora que la función F está dada por la siguiente expresión:
Reemplazando esto en la expresión de arriba y desarrollando tenemos entonces:
Esto, tal y como está escrito, puede ser considerado como un operador mecánico cuántico, un operador que podemos aplicar sobre una función de onda ψ puesta a su derecha sobre la cual actúa:
Desarrollando el conmutador en el lado izquierdo de la igualdad de acuerdo a su definición, y simplificando lo que resulta:
Podemos dar a este último resultado una interpretación desde el punto de vista estricto de la Mecánica Ondulatoria sin apelar a concepto matricial alguno, considerándolo como una eigen-ecuación. Lo que tenemos es ni más ni menos un operador posición (x) que actúa sobre el siguiente eigen-estado del operador posición:
y para esta eigen-ecuación el valor eigen de la misma será:
x - a
Esto equivale a una operación de traslación a lo largo de la coordenada x, en una distancia a.
Compárese lo que hemos obtenido con la operación matricial de traslación que vimos en la entrada “La matriz momentum como generadora de traslación”.
La equivalencia plena que hay entre la Mecánica Matricial y la Mecánica Ondulatoria es lo que nos permite también el poder combinar libremente operadores matriciales y operadores diferenciales para poder construír nuevas definiciones y conceptos que, pese a la mescolanza, tienen plena validez dentro de la Mecánica Cuántica. Y es aquí precisamente cuando puede ocasionarse una confusión cuando no se tiene perfectamente claro en mente si aquello de lo que estamos hablando son matrices o son operadores diferenciales, algo lamentablemente escondido muchas veces en la simbología compacta a la que muchos autores de hoy en día son tan afectos.
PROBLEMA: Para una partícula de masa m, defínase el siguiente operador:
en donde P es el operador del momentum y σ es un vector formado por las matrices de Pauli.
(1) Obténgase una expresión matricial para el operador T1/2 y demuéstrese a partir de la misma mediante un cálculo directo que el operador de energía cinética es igual a T = (1/2m)p²I.
(2) Demuéstrese que el operador T1/2 tiene los eigenvalores ±E1/2, siendo E la energía cinética de la partícula.
(1) Expresado en coordenadas Cartesianas rectangulares, el operador diferencial vectorial P puede ser escrito de la siguiente manera apropiada para la Mecánica Cuántica:
Por otro lado, si σ es un vector construído usando como sus componentes a las matrices de Pauli, entonces tenemos en coordenadas Cartesianas rectangulares:
siendo las matrices de Pauli las siguientes: aa
Tenemos entonces:
Con esto, el operador T1/2 resulta ser:
El operador de energía cinética T será entonces:
En virtud de que, de la definición operacional usada en la Mecánica Ondulatoria, se tiene que:
o lo que es lo mismo:
se deduce entonces lo siguiente:
(2) Supóngase un eigenvalor A y un eigenvector α = (α1, α1) que vaya aparejado con tal eigenvalor. Entonces, de la eigen-ecuación matricial:
T1/2α = Aα
obtenemos:
Este sistema es equivalente al determinante que lo resuelve:
De este modo, obtenemos para los eigenvalores del operador T1/2:
Un hecho histórico interesante es que, al poco tiempo de ser descubierta la Mecánica Matricial, Max Born le sugirió a Heisenberg convertir sus manejos matriciales a ecuaciones diferenciales con la finalidad de explorar la posibilidad de que se pudiesen simplificar algunos de los problemas que estaba estudiando Heisenberg tal como el de los niveles de energía del átomo de hidrógeno. Aunque Heisenberg no siguió este consejo, de haberlo hecho muy posiblemente habría terminado creando también la Mecánica Ondulatoria.
En no pocos historiadores de la ciencia ha surgido la duda de que Schrödinger pudiera haber “hecho trampa” tomando los trabajos de Heisenberg haciendo la conversión de los mismos a su formato en ecuaciones diferenciales para terminar obteniendo de este modo por una vía no tan indirecta su famosa ecuación. Después de todo, Schrödinger era un matemático experimentado que estaba al tanto sobre la equivalencia plena entre los procedimientos matemáticos matriciales y los procedimientos matemáticos utilizados en la solución de ecuaciones diferenciales. También es cierto que el descubrimiento de la Mecánica Matricial fue un hecho previo al descubrimiento de la Mecánica Ondulatoria por cuestión de unos cuantos meses. Y también es cierto que fué el mismo Schrödinger el que posteriormente demostró de manera formal la equivalencia entre la Mecánica Matricial y la Mecánica Ondulatoria. Sin embargo, la Mecánica Ondulatoria descansa sobre bases filosóficas distintas a las bases filosóficas utilizadas por Heisenberg el cual no se apoyó en la relación de Louis de Brogile para el análisis de ondas de materia. Mientras que a Heisenberg lo único que le interesaba eran las observables desechando todo aquello que no pudiera ser medido u observado así fuese indirectamente (como el radio de un electrón en su órbita circular en torno al núcleo atómico o la velocidad del electrón moviéndose alrededor del núcleo), la ecuación de onda de Schrödinger fue desde un principio una ecuación de onda elaborada para ondas de materia, inspirada en las ecuaciones de onda del electromagnetismo clásico y en la propuesta de De Broglie. Simple y sencillamente no hay punto de comparación entre ambas bases filosóficas. Si Schrödinger realmente hizo “trampa”, cubrió tan bien sus huellas que sólo con una declaración suya para tal efecto se podría despejar la duda, algo que ciertamente nadie en el lugar de Schrödinger haría.