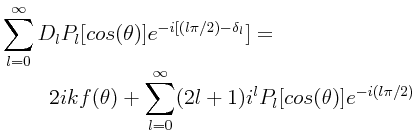El modelo nuclear de Rutherford precedió al advenimiento de la Mecánica Cuántica en sus dos vertientes, la Mecánica Matricial de Heisenberg y la Mecánica Ondulatoria de Schrödinger. Y sin embargo, Rutherford y sus colaboradores obtuvieron una concordancia excelente entre su modelo teórico basado en consideraciones puramente clásicas (considerando a las partículas sub-atómicas como algo equivalente a objetos corpusculares sólidos) y los resultados experimentales, sin sospechar ni siquiera remotamente que aquello con lo que estaban trabajando eran ondas de materia. Y el modelo de Rutherford sigue tan válido hoy como ayer.
¿Qué fue lo que sucedió?
La respuesta a esto último nos lleva directamente al pilar fundamental de la Mecánica Cuántica, la dualidad onda-partícula. Un ente sub-atómico se las arregla de alguna manera para tener dos rostros en uno solo, comportándose como una onda bajo ciertas condiciones experimentales, y comportándose como una partícula bajo otro conjunto de condiciones experimentales. Esta es la gran paradoja de la física cuántica que choca directamente con nuestra lógica Aristotélica basada en el principio del tercero excluído según el cual una cosa no puede ser y no ser al mismo tiempo, y es lo que le permitió a Rutherford y a sus colaboradores el poder salirse con la suya, porque afortunadamente para ellos los experimentos que llevaron a cabo eran de tal naturaleza que lo que imperaba era el “rostro” de la partícula sobre el “rostro” de la onda. De haber ocurrido a la inversa, Rutherford y sus colegas jamás habrían podido obtener concordancia en nada.
Hemos visto ya que los electrones, a los cuales usualmente nos imaginamos como partículas parecidas a los perdigones de los fusiles, exhiben las propiedades ondulatorias de difracción e interferencia; el experimento de Davisson y Germer fue el primero en dejar esto definitivamente en claro y no nos queda ya duda alguna al respecto. Por otro lado, la luz, a la cual usualmente imaginamos como una onda electromagnética, exhibe propiedades corpusculares en experimentos tales como el del efecto fotoeléctrico (cuya explicación teórica suponiendo a la luz no como una onda electromagnética sino por un enjambre viajero de cuantos luminosos le valió a Albert Einstein el Premio Nóbel) y el efecto Compton. Todos los fenómenos del mundo sub-microscópico (electrones, átomos, luz, sonido, etcétera) tienen las características onda y partícula, y es por ello que se dice, por ejemplo, que el electrón es onda y partícula a la vez, lo cual resulta algo confuso, porque en la física clásica los conceptos de ondas y partículas son mutuamente excluyentes. Una partícula clásica se comporta como el perdigón de un fusil. Puede ser localizada y esparcida de un lugar a otro, y es capaz de intercambiar de súbito energía con otras partículas, obedeciendo las leyes de conservación de energía y momentum en colisiones, pero no exhibe interferencia y difracción. Por otro lado, una onda clásica se comporta como una onda viajera en la superficie de un estanque de agua, exhibiendo patrones de difracción e interferencia , y tiene su energía esparcida continuamente en el espacio y el tiempo. Nada puede ser al mismo tiempo una partícula clásica y una onda clásica.
Hasta el siglo XX, se creía que la luz era una onda clásica y que el electrón era una partícula clásica. Sin embargo, los conceptos de ondas clásicas y partículas clásicas no describen adecuadamente ningún fenómeno en el mundo sub-microscópico. Hemos visto ya que cualquier fenómeno del mundo sub-microscópico puede ser descrito mediante una función de onda que es a su vez la solución de la ecuación de onda de Schrödinger. De cualquier modo, y dependiendo de la naturaleza del experimento que se está llevando a cabo, podemos enunciar lo siguiente:
Todo fenómeno se comporta como una onda clásica cuando se considera una propagación, y como una partícula clásica cuando se consideran intercambios de energía.Para poder determinar el lugar más probable en el cual se pueda encontrar un electrón, tenemos que encontrar la función de onda por métodos semejantes a los que se utilizan en la teoría ondulatoria clásica. Pero cuando el electrón (o la luz) interactúa intercambiando energía y momentum, entonces la función de onda tiene que cambiar como resultado de la interacción. La interacción puede ser descrita con la teoría clásica de las partículas (usando los principios de conservación de la energía y el momentum) tal y como se hace en la descripción teórica del efecto Compton.
Hay ocasiones en las cuales la teoría de partículas clásicas y la teoría ondulatoria clásica dan los mismos resultados. Si la longitud de onda es mucho más pequeña que cualquier objeto o apertura, la teoría corpuscular puede ser usada tan bien como la teoría ondulatoria para describir la propagación porque los efectos de interferencia y difracción son demasiado pequeños como para poder ser observados. El ejemplo más común es la óptica geométrica, que en realidad es una teoría corpuscular, y la propagación de pelotas de beisbol en un campo deportivo. Si uno está interesado únicamente en los promedios en el tiempo de los intercambios de energía y momentum, la teoría ondulatoria clásica trabaja tan bien como la teoría de partículas clásicas. Un ejemplo de ello es la manera en la que la teoría ondulatoria de la luz predice correctamente que la corriente electrónica total en el efecto fotoeléctrico es proporcional a la intensidad de la luz.
En lo que cabe al experimento de Rutherford, el análisis clásico que supone a las partículas sub-microscópicas como partículas puntuales sólidas dá una buena concordancia con los resultados experimentales. Sin embargo, ¿qué sucede cuando, trabajando bajo el contexto de la Mecánica Ondulatoria, consideramos a cualquiera de las partículas de Rutheford que son usadas como “balas de perdigón” no como partículas sino como paquetes de onda viajeros? De lo que estamos hablando aquí es que, en principio, debería ser posible obtener las mismas explicaciones teóricas que las que obtuvo Rutherford, pero recurriendo a la ecuación de onda de Schrödinger en vez de recurrir a relaciones sencillas basadas en un modelo corpuscular de las partículas sub-atómicas. Esta es una de esas situaciones en las que lo único que puede dar resultados es la Mecánica Ondulatoria, porque la Mecánica Matricial de Heisenberg por la forma en la que fue construída sólo nos sirve para la descripción de sistemas ligados (electrones situados en una de las capas de un átomo, partículas atrapadas dentro de una caja, etc.) y no para sistemas en los que tenemos ondas viajeras (las partículas esparcidas por un centro de repulsión) moviéndose libremente de un lado a otro.
¿Y por qué razón habríamos de entrar en las complejidades involucradas en meter la ecuación de onda de Schrödinger para efectos de análisis siendo que el modelo teórico de Rutherford relativamente mucho más sencillo ha funcionado tan bien?
Podemos tomar esto último como un reto intelectual. Si la Mecánica Cuántica es consistente, entonces en principio debe ser posible obtener las mismas relaciones teóricas que obtuvo Rutherford pero sin recurrir a las relaciones clásicas usadas por Rutherford para intercambio de energía y momentum. Por otro lado, podemos esperar que bajo ciertas condiciones experimentales el modelo clásico de Rutherford terminará derrumbándose, y no nos quedará más remedio que recurrir a la Mecánica Cuántica Ondulatoria para poder explicar teóricamente los resultados experimentales. A partir de este punto, de lo que estaremos hablando es del esparcimiento de partículas según la Mecánica Cuántica y no del esparcimiento de partículas según el modelo de Rutherford el cual es un modelo puramente clásico.
Entendiblemente, el objetivo que nos estamos fijando aquí resulta ser algo pesado, y eventualmente se tiene que recurrir a herramientas matemáticas que por su sofisticación no pueden resultar tan agradables como las relaciones algebraicas sencillas que vimos en el análisis clásicos del esparcimiento de partículas. Pero aquí no nos queda mucha opción, porque es eso, o nada.
Afortunadamente, no es necesario inventar la rueda desde el principio. Puesto que la Mecánica Ondulatoria es esencialmente un estudio del comportamiento de ondas de materia, resulta muy difícil resistir a la tentación de echar mano del amplio arsenal de recursos que fueron desarrollados en el siglo XIX y a principios del siglo XX para el análisis de los fenómenos propios del electromagnetismo, o sea la electrodinámica clásica. La única diferencia es que en vez de estar tratando con una onda electromagnética estaremos tratando con una onda de materia Ψ, fuera de eso podemos simplemente tomar libros y tratados del electromagnetismo clásico, y con algunos cambios triviales de símbolos y nomenclatura, escribir de inmediato resultados aplicables al esparcimiento de partículas desde la perspectiva de la Mecánica Cuántica. Y puesto que la luz es una onda electromagnética, al hablar acerca del esparcimiento de las “ondas de luz” estamos hablando también del esparcimiento de las ondas electromagnéticas en general, lo cual incluye las ondas emanadas de las estaciones de radio y televisión así como las repetidoras de señal para los teléfonoes celulares que también son ondas electromagnéticas y las cuales están cuantizadas a nivel sub-microscópico., razón por la cual aunque pueda parecer extraño nos permite hablar de los fotones de las señales de radio y televisión que llegan a nuestros receptores.
Al empezar el estudio de la Mecánica Ondulatoria, y en especial al llevar a cabo el análisis de un haz de partículas caracterizadas en su conjunto por una función de onda Ψ la cual pasaba, por ejemplo, de una región de potencial V1 a otra región de potencial V2, o la cual estaba confinada dentro de un pozo de potencial de altura finita, estos casos tratados en forma unidimensional estaban limitados a la discusión de ondas en donde la función de onda dependía de una sola coordenada rectangular, usualmente la coordenada-x, tratándose por lo tanto de ondas planas moviéndose en una misma dirección como lo muestra la siguiente figura:
Como hemos visto previamente en capítulos anteriores, un haz de partículas monoenergéticas (esto es, todas ellas tienen la misma energía) puede ser descrito dentro de la Mecánica Cuántica mediante una función de onda que representa una onda plana. Tal onda plana se extiende infinitamente en ambas direcciones. Sin embargo, un haz de partículas utilizado en cualquier experimento de esparcimiento está necesariamente limitado a una extensión finita en la dirección transversal, y por lo tanto de acuerdo al principio de incertidumbre no puede estar compuesto de partículas libres cuyos momentums y energía se conocen con exactitud. Sin embargo, esto no destruye la utilidad de la descripción de un haz monoenergético mediante una onda plana, porque para haces cuya sección transversal es de dimensiones macroscópicas (y no de dimensiones sub-microscópicas), la incertidumbre en el momentum se vuelve insignificante.
La restricción al caso unidimensional no fue artificial, porque como hemos visto ya, hay muchos problemas importantes que pueden ser analizados bajo estos términos. Si uno restringe la región de interés para que ésta tenga dimensiones suficientemente menores que la distancia hacia la fuente de la radiación, entonces la aproximación basada en el supuesto de ondas planas resulta muy adecuada para muchas aplicaciones. En la electrodinámica clásica, un dipolo eléctrico oscilante generará ondas electromagnéticas esféricas, del mismo modo que una esfera vibrante que es sumergida en un medio uniforme e isotrópico como el agua generará ondas esféricas de presión emanando del centro de la radiación. Pero si observamos la radiación a una distancia lo suficientemente grande de la fuente y sobre una región limitada del espacio, las ondas pueden ser consideradas esencialmente planas, como podemos verlo en la siguiente figura en la cual a una distancia lo suficientemente cercana del centro de la radiación (en el lado izquierdo de la figura) las ondas son esféricas mientras que a una distancia lo suficientemente lejana (en el lado derecho de la figura) las ondas son esencialmente planas:
Si lo que queremos hacer es llevar a cabo un análisis sobre el campo entero de la radiación, no quedará más alternativa que abandonar la aproximación puramente planar y recurrir a un análisis basado en algo que necesariamente involucrará ondas esféricas.
En las dos figuras dadas arriba de una onda plana y una onda esférica, la función de una onda plana de carácter senoidal que se extiende unidimensionalmente hacia el infinito en ambas direcciones contrarias se puede representar mediante alguna función matemática como las siguientes:
y = Asen(kx -ωt) y = Acos(kx - ωt) y = ei(kx -ωt)
mientras que para la representación de una onda esférica se requiere de funciones matemáticas más elaboradas, específicamente, funciones de Bessel de un tipo especial conocidas como las funciones de Hankel y de Neumann.
Claramente, una onda plana y una onda esférica y una onda esférica son dos cosas diferentes. Sin embargo, los matemáticos del siglo antepasado descubrieron algo sumamente interesante. Así como podemos representar cualquier función matemática que se repita periódicamente (por ejemplo, una función de onda cuadrada, o una función de onda triangular) con una suma (usualmente infinita) de términos que representan funciones trigonométricas de frecuencias que son múltiplos (armónicas) de una frecuencia fundamental, es posible representar una onda plana como la suma de un número infinito de ondas esféricas (dándole desde luego una amplitud apropiada a cada onda esférica). En efecto, esto equivale a darle un giro completamente nuevo al análisis de Fourier. Esta idea fundamental puede ser enunciada en palabras de la siguiente manera:
Este avance matemático fue precisamente lo que se utilizó para llevar a cabo el análisis del esparcimiento de una onda electromagnética que choca contra un obstáculo, el cual sería utilizado posteriormente en la Mecánica Ondulatoria para llevar a cabo el análisis mecánico-cuántico del esparcimiento de partículas bajo un método conocido como el método de las ondas parciales.
Por razones pedagógicas, resulta más conveniente empezar nuestro análisis con ondas esféricas escalares. Al hacer esto, aunque podremos obtener muchos resultados importantes, tales análisis no serán correctos en los “detalles finos” puesto que la radiación en realidad tiene un carácter vectorial y no escalar.
En la electrodinámica clásica, la ecuación de onda escalar básica es la siguiente:
Recurriendo al método matemático de la separación de variables, esta función de onda Ψ(r,t) puede ser separada en el producto de una función espacial ψ(r) y una función temporal e-iωt:
Con esto, y designando al número de onda k.=.ω/v, se tiene entonces:
Esta ecuación de onda independiente del tiempo es conocida en la electrodinámica clásica como la ecuación de Helmholtz, así llamada en honor de su descubridor Hermann von Helmholtz.
Pero hemos visto ya que, gracias al análisis de Fourier, una función de onda que varía con el tiempo (expresada en el dominio tiempo) puede ser expresada en el dominio frecuencia de la siguiente manera:
en donde cada componente ψ(r,ω) satisface la ecuación de Helmholtz.
Al manejar este tipo de problemas, es casi inevitable que el sistema de coordenadas predilecto sea un sistema de coordenadas esféricas (r,θ,φ), con el cual podemos expresar a ψ(r) [o, más apropiadamente, a ψ(r,ω)] como la suma de productos de funciones radiales y armónicas esféricas:
En este caso, la ecuación diferencial que corresponde a la parte radial es la siguiente:
Si efectuamos la substitución:
entonces la ecuación diferencial para la parte radial se convierte en:
la cual, con el cambio de variable u.=.kr, nos produce lo siguiente:
Esta ecuación es la ecuación diferencial de Bessel. Las soluciones de esta ecuación diferencial resultan ser las funciones de Bessel de medio orden integral, representadas frecuentemente del siguiente modo:
y las funciones de Neumann de medio orden integral, representadas frecuentemente del siguiente modo:
Así, una solución particular para la ecuación diferencial de Bessel dada arriba viene siendo:
en donde Al y Bl son constantes que pueden ser arbitrarias o bien determinadas por la naturaleza del sistema físico que se está describiendo (varios de estos detalles matemáticos serán discutidos más a fondo en una entrada posterior). Dividiendo estas constantes arbitrarias entre √k , se puede escribir:
Se acostumbra definir las función esférica de Bessel de la siguiente manera (obsérvese el uso de una letra minúscula en lugar de una letra mayúscula):
A modo comparativo, se muestra la siguiente gráfica de la función esférica de Bessel de orden cinco:
mientras que la siguiente gráfica nos muestra la función esférica de Bessel de orden 50:
Del mismo modo, se acostumbra definir la función esférica de Neumann de la siguiente manera:
Se puede demostrar que las primeras funciones esféricas de Bessel están dadas por las siguientes relaciones:
De modo semejante, se puede demostrar que las primeras funciones esféricas de Neumann están dadas por las siguientes relaciones:
Los valores límite (asintóticos) de las funciones esféricas de Bessel y Neumann para kr.«.l vienen siendo:
mientras que los valores límite de las funciones esféricas de Bessel y Neumann para kr.».l vienen siendo:
En las relaciones para los valores límite dadas arriba, hemos utilizado la definición del doble factorial:
(2l + 1)!! = 1 · 3 · 5 · 7 ····· (2l + 1)
Hermann Hankel se fijó en un hecho interesante. Puesto que las funciones senoidal y cosenoidal de un mismo argumento pueden ser combinadas en una función exponencial de acuerdo a la relación de Euler:
eix = cos(x) + isen(x)
entonces, puesto que las funciones esféricas de Bessel y Neumann involucran senos y cosenos, también pueden ser combinadas para formar exponenciales, lo cual da origen a las funciones esféricas de Hankel (introducidas en 1869, mucho antes del advenimiento de la Mecánica Cuántica):
hl(1)(kr) = jl.(kr) + inl.(kr)
hl(2)(kr) = jl.(kr) - inl.(kr)
en donde los super-índices (1) y (2) simplemente identifican el signo aritmético entre los dos términos.
Es obvio que, para valores reales de kr, hl(1)(kr) y hl(2)(kr) son conjugados complejos el uno del otro:
hl(1)(kr) = hl(1)*(kr)
Así pues, las primeras funciones (esféricas) de Hankel deben ser:
La forma asintótica correspondiente la función de Hankel para el caso kr.».l viene siendo:
Las expresiones correspondientes para las funciones hl(2)(kr) se obtienen tomando los conjugados complejos de las funciones hl(1)(kr) siempre y cuando kr tenga un valor real.
Si usamos a ξl.(kr) para representar a cualquiera de las funciones jl.(kr), nl.(kr), hl(1)(kr) y hl(2)(kr), se puede demostrar que las siguientes relaciones recursivas se cumplen:
Podemos escribir la expresión general para la función de onda (electromagnética) ψ(r) dada arriba en coordenadas esféricas incorporando las soluciones linealmente independientes jl.(kr) y nl.(kr) de la siguiente manera:
o bien, puesto que las funciones hl(1) y hl(2) son linealmente independientes, podemos escribir:
teniendo cuidado de observar que las constantes arbitrarias Alm y Blm son diferentes en las dos expresiones generales.
Ahora bien, de acuerdo a la relación asintótica:
dada arriba, la forma asintótica de ψ(r) tiene la variación radial:
para valores reales de kr. Entonces, para valores de r tales que r→∞, la función de onda completa debe tener la siguiente forma asintótica:
Podemos ver que, tal y como ocurre en el caso de las ondas planares, tenemos una combinación de dos frentes de onda, una onda saliente representada por exp[-i(ωt-kr)] y una onda entrante representada por exp[-i(ωt+kr)]. El factor 1/kr toma en cuenta la expansión esférica de la onda conforme aumenta la distancia radial r. Debemos entonces identificar aquella porción de la función de onda que depende de hl(1)(kr) como una onda saliente, y aquella parte que depende de hl(2)(kr) como una onda entrante.
Habiendo expuesto lo anterior, veremos ahora cómo es posible representar matemáticamente una onda plana como una combinación de ondas esféricas. Para el caso( más común) en el que hay una simetría con respecto al vector normal al frente de onda planar, una expansión en términos de armónicas esféricas se reduce a una expansión que se lleva a cabo usando los polinomios de Legendre, los cuales ya hemos utilizado previamente al discutir la solución ondulatoria al problema del átomo de hidrógeno, y podemos escribir, para una onda planar que viaja en la dirección del eje-z:
La expansión del lado derecho usando las funciones de Legendre es la siguiente:
Para poder obtener una expresión para las constantes Cl.(r), tenemos que multiplicar primero esta ecuación por Pl’ [cos(θ)] (obsérvese la comilla puesta en la l.) y llevar a cabo la integración sobre el rango -1.≤cos(θ).≤1, obteniendo:
Para poder continuar simplificando, tenemos que recurrir a la relación de ortogonalidad para los polinomios de Legendre (pondremos aquí los dos tipos de notación de uso corriente para la función δ de Dirac):
Con esta medida simplificadora, se tiene entonces:
Por lo tanto:
Recurriremos a otra simplificación, la cual consiste en usar la siguiente representación integral de las funciones esféricas de Bessel (la derivación de la misma se puede encontrar en muchos tratados de matemáticas así como en Internet):
De este modo, la constanteCl.(r) puede ser expresada como:
Y así, la expansión de una onda plana en ondas esféricas está dada por la siguiente relación:
Este tipo de expansión es lo que nos conducirá directamente a lo que en la Mecánica Cuántica se le conoce como el método de las ondas parciales, aplicado a las ondas de materia consideradas como ondas esféricas.
Estamos ahora en condiciones de poder discutir el efecto producido sobre una onda plana electromagnética por un objeto dispersor que actúa como el obstáculo que produce el esparcimiento de la onda, el cual podemos suponer inicialmente como un objeto esférico. Tomando al eje-z como el sentido de propagación de la onda plana, la componente Fourier de la onda incidente (inc) a la cual le corresponde una frecuencia ω puede ser representada como:
ψinc = Aeikz
que describe una onda plana de amplitud A moviéndose en la dirección positiva del eje-z. La interacción de la onda plana con la esfera de esparcimiento producirá ondas salientes que a grandes distancias parecerán ondas esféricas, y que por ello mismo deben tener asintóticamente la forma hl(1)(kr). Si incluímos un factor f.(θ) para describir cualquier dependencia angular que haya en la intensidad de la onda esparcida (esp), debemos tener, asintóticamente:
en donde se ha supuesto que hay una simetría (angular) en torno a la dirección que es normal al frente de la onda plana.
Por el principio de la superposición linear, la función de onda completa es:
ψ(r) = ψinc(r) + ψinc(r)
y cuya forma asintótica (a distancias radiales suficientemente grandes) debe ser:
Podemos introducir ahora en el panorama la definición ondulatoria de la sección transversal diferencial de esparcimiento:
que es igual a la energía esparcida hacia un ángulo sólido dΩ por unidad de tiempo, dividido todo entre la energía incidente por unidad diferencial de área por unidad de tiempo. Esta definición es esencialmente igual a la definición clásica, y esperamos eventualmente obtener resultados iguales o parecidos ya sea bajo un tratamiento clásico o un tratamiento ondulatorio (cuántico).
La densidad de energía en una onda es proporcional al cuadrado de la magnitud de la función de onda, tanto en la electrodinámica clásica como en la Mecánica Ondulatoria. De este modo, la potencia por unidad de área en la onda incidente (planar) debe ser proporcional a:
|ψinc(r)|2 = |A|2
La densidad de potencia en la onda esparcida es proporcional a:
de modo tal que la potencia de la onda electromagnética esparcida por unidad de ángulo sólido es esta cantidad multiplicada por r2. Siendo así, la sección transversal diferencial de esparcimiento debe ser:
de lo cual se obtiene que:
La sección transversal total es entonces:
en donde se ha utilizado la simbolización 4π al pie del símbolo integral para indicar que la integración se llevará a cabo sobre el equivalente de un ángulo sólido que abarca el equivalente de una esfera completa cuya superficie es 4πr2.
Hasta aquí, hemos tomado la función de onda total que describe la interacción entre el campo de radiación (el campo electromagnético incidente) y el objeto que produce el esparcimiento de las ondas, y hemos separado esta función de onda en dos partes que describen una onda incidente y una onda esparcida. Claramente, esta es una separación que resulta útil hacer, y puede ser entendida apelando a nuestra intuición física de la siguiente manera. La función de onda debe satisfacer ciertas condiciones de frontera impuestas por la presencia del objeto que produce la dispersión; esto es, la función de onda, o posiblemente su derivada, tienen que tomar cierto valor en la superficie del objeto dispersor, un valor dictado por la naturaleza física de la situación. Por lo general, una onda plana no cumplirá con tales condiciones, y se vuelve necesario introducir una onda adicional para que la interferencia entre ambas produzca el resultado deseado en la superficie del objeto esparcidor. Claramente, esta onda adicional debe ser una onda saliente y, puesto que debemos dar cuenta de la energía que es retirada de esta manera, la onda saliente debe ser una porción de la onda incidente que es reflejada por el objeto dispersor.
En las últimas dos ecuaciones de arriba, se han expresado las secciones transversales para el esparcimiento en los términos de un factor f(θ) que ocurre en aquella porción de la función de onda que identificamos como la onda esparcida. Puesto que ambas porciones de la función de onda total se extienden hacia todo el espacio, surge la pregunta sobre cómo se puede efectuar una medición únicamente sobre la porción esparcida para poder determinar experimentalmente la sección transversal. Esto será posible sólo si limitamos la extensión de la onda incidente, por ejemplo, pasándola por una apertura de una pantalla impenetrable a cierta distancia del objeto dispersor como lo muestra la siguiente figura:
De este modo, la onda resultante ya no será una onda plana pura, pero si las dimensiones de la apertura son relativamente grandes en comparación con la longitud de onda, entonces la distorsión de la onda incidente no será significativa. Mediante esta táctica se vuelve posible excluir la onda incidente de las regiones del espacio en donde se llevaran a cabo las mediciones.
Queremos expresar a continuación las secciones transversales en función del número de onda k de la onda incidente y el radio de una esfera que supondremos que actúa como un objeto dispersor.
Una forma suficientemente general para la porción radial de la función de onda total ψ(r) para un valor particular de l puede ser escrito como:
en donde escogemos a Al y Bl como números reales, y tomamos en consideración cualquier factor complejo o imaginario que aparezca con la inclusión de la constante Cl. Si definimos:
y hacemos:
tenemos entonces:
en donde δl es real pero Dl puede ser un número complejo o imaginario. Si usamos las definiciones dadas arriba para las funciones esféricas de Bessel y de Neumann, la solución radial asintótica para valores suficientemente grandes de r viene siendo:
o bien, simplificando un poco:
Puesto que las armónicas esféricas son las funciones de Legendre usuales siempre y cuando haya simetría esférica, podemos escribir de la siguiente manera la forma asintótica de la función de onda total:
en donde se considera que las constantes Dl incorporan los factores constantes que aparecen en la definición de las armónicas esféricas Ylm. De este modo, la función de onda ψ(r) tiene la apariencia normal de una onda esférica, pero con una fase que es diferente en una cantidad δl. Esta cantidad δl es conocida como el desplazamiento de fase y, como veremos, es característico del número de onda de la onda incidente y las propiedades del objeto dispersor, incluyendo el tipo de condiciones de frontera impuestas en la superficie del objeto dispersor.
La función de onda asintótica también está dada por:
ψ(r) = ψinc(r) + ψinc(r)
y podemos utilizar la expansión de una onda plana dada por:
para escribir:
Las dos formas asintóticas dadas arriba para ψ(r) tienen que ser, desde luego, idénticas, así que, expresando las funciones senoidales como exponenciales con la ayuda de la relación de Euler, se tiene:
Puesto que los exponenciales eikr y e-ikr son linearmente independientes, los coeficientes en estos términos tomados separadamente deben ser iguales. Para los términos que involucran e-ikr, se tiene:
Si multiplicamos esta ecuación por Pl’[cos(θ)], encontramos que:
Los términos que involucran a eikr producen:
Substituyendo el resultado anterior obtenido para Dl y usando el hecho de que:
se tiene por lo tanto:
o bien:
Por lo tanto, la sección transversal diferencial de esparcimiento dσ/dΩ está dada por la expresión:
De lo anterior se deduce que la sección transversal de esparcimiento es:
En virtud de la ortogonalidad de Pl.[cos(θ)], las integrales de todos los términos “cruzados” en la suma cuadrática se desvanecen, y por lo tanto:
Usando la siguiente relación de ortogonalidad para los polinomios de Legendre:
se obtiene el siguiente resultado importante:
Para poder completar el cálculo de las secciones transversales dado por las últimas expresiones que acabamos de obtener arriba, se vuelve necesario encontrar los desplazamientos de fase δl. Esto se puede lograr imponiendo la condición de frontera apropiada sobre la función de onda en la superficie del objeto dispersor. La form exacta de la condición de frontera dependerá en la naturaleza física de la onda y el objeto. Por ejemplo, si estamos considerando el esparcimiento de una onda electromagnética por un conductor perfecto, entonces requerimos que la función de onda (esto es, el campo eléctrico) se desvanezca en la superficie. Por otro lado, si tenemos una onda acústica que incide sobre un objeto perfectamente rígido inmerso en un medio fluido, entonces la onda de presión no se desvanecerá en la superficie, pero la velocidad del medio lo hará, y por lo tanto en este caso se requiere el desvanecimiento de la derivada normal de la función de onda en la superficie. Estos son dos ejemplos que excluyen por completo la función de onda del interior del objeto. Podríamos, sin embargo, considerar una onda luminosa siendo esparcida por un objeto refractivo o una onda acústica esparciéndose de un objeto no rígido. En estos casos habría alguna penetración de la función de onda hacia el interior, y la condición de frontera apropiada es que la función de onda y su derivada sean continuas en la superficie. (Obsérvese que en este último caso tenemos que desarrollar una solución para el interior basado por completo en las funciones de Bessel, puesto que las funciones de Neumann no pueden ser utilizadas en una región que incluye el origen.)
Consideremos primero el caso de una onda incidiendo sobre una esfera impenetrable en donde la función de onda se desvanezca en la superficie. Esta es nuestra condición de frontera. Entonces, si el radio de la esfera es a, se tiene:
Rl.(ka) = 0
y por la ecuación:
se tiene:
Ahora bien, en la discusión de ondas con longitudes de onda largas (o sea, con un número de onda k muy pequeño) de modo tal que ka.«.1, es fácil calcular los δl de las expresiones asintóticas para jl.(kr) y nl.(kr). De este modo:
o, puesto que ka es pequeño:
Por lo tanto:
De este modo, en el límite de las longitudes de onda largas, los desplazamientos de fase para l.>.1 son insignificantes en comparación con δ0. Como consecuencia de ello, la sección transversal puede ser aproximada en forma cercana por el término l.=.0:
y así:
Observamos que en el límite de ondas con longitudes de onda largas, la sección transversal σ es aproximadamente igual a cuatro veces la sección transversal geométrica de la esfera πa2. La razón para esto es que hemos impuesto la condición de que la función de onda se desvanezca en r.=.a. Por lo tanto, puesto que las distorsiones de la función de onda se tienen que llevar a cabo de una manera continua, el hecho de forzar a ψ(r) a que tenga un valor definido en la superficie de la esfera afecta la función de onda inclusive a cierta distancia alejada de la esfera. Esta extensión de la región efectiva de interacción incrementa la sección transversal en un factor de cuatro tantos.
La expresión general para la sección transversal diferencial es, por lo general, algo complicada, puesto que involucra el cuadrado absoluto de una suma de términos. Sin embargo, si únicamente el término l.=.0 es importante, entonces notamos que el esparcimiento es esféricamente simétrico, como lo indica el resultado dσ(θ)/dΩ.≈.a2 que obtuvimos arriba.
Hemos obtenido la solución para el problema del esparcimiento de una onda electromagnética plana por una esfera para el caso en el cual las condiciones de frontera requieren el desvanecimiento de la función de onda en la superficie de la esfera. Debemos inquirir ahora acerca de los problemas físicos que serán descritos de esta manera. Se había señalado antes que el esparcimiento de ondas electromagnéticas por un conductor perfecto requiere el desvanecimiento de ψ(r) en la superficie del objeto dispersor. El resultado que hemos obtenido no es sin embargo aplicable a este problema, puesto que el campo electromagnético es un campo vectorial en contraste con el campo escalar que hemos supuesto explícitamente al seleccionar la función de onda ψ(r,t) para describir nuestro problema. Una de las diferencias que surgen en el tratamiento del esparcimiento de ondas electromagnéticas es que el término sen2(δl) en la expresión dada arriba (encerrada en recuadro negro) para la sección transversal total σ es reemplazada por:
sen2(δl) + sen2(εl)
en donde los desplazamientos de fase δl y εl para los campos eléctrico y magnético son, por lo general, diferentes.
Otra diferencia importante en nuestros resultados cuando se consideran ondas electromagnéticas es el término l.=.0. La onda electromagnética puede ser expandida en términos de multipolos, con el índice l indicando el orden del multipolo: monopolo (l.=.0), dipolo (l.=.1), cuadrupolo (l.=.2), etc. El término de monopolo proviene de la carga eléctrica total en el conductor. De este modo, si la esfera conductora es aislada, no hay carga eléctrica neta alguna, y el término l.=.0 simple y sencillamente no existe. El término de orden más bajo en la sección transversal involucra por lo tanto a l.=.1, y encontramos para la sección transversal total:
Puesto que el número de onda k es igual a 2π/λ, tenemos entonces:
haciéndose la advertencia de que para el caso electromagnético, el coeficiente de 1/λ4 es algo ligeramente diferente a lo que se da aquí debido a la naturaleza particular del campo electromagnético.
Consideremos ahora otra condición de frontera posible para una esfera impenetrable, aquella en la cual lo que se requiere que se desvanezca en la superficie de la esfera es la derivada de la función de onda, esto es:
o bien, limitándonos a usar la parte radial de la función de onda, la función de onda radial Rl :
Diferenciando la función de onda radial dada arriba:
e igualando a cero al aplicar la condición de frontera de que sea la derivada de la función de onda lo que se desvanezca en la superficie, se tiene:
en donde la comilla puesta como super-índice indica que este nuevo desplazamiento de fase está basado en una condición de frontera impuesta sobre la derivada de la función de onda radial, y en donde las otras comillas indican una diferenciación con respecto a r. Por lo tanto:
Las derivadas de las funciones de Bessel y Neumann pueden ser evaluadas usando la relación recursiva dada arriba:
Para l.=.0 encontramos:
De este modo, tenemos el resultado de que el desplazamiento de fase l.=.0 para el caso en el que la derivada normal se desvanece en la superficie es igual al desplazamiento de fase l.=.1 para el desvanecimiento de la misma función de onda. Tenemos, en la aproximación de onda larga:
y la sección transversal total viene siendo:
Habiendo considerado el caso en el que la longitud de onda de la onda plana incidente es grande en comparación con el tamaño del objeto que provoca la dispersión, consideraremos ahora el caso contrario en el cual la longitud de onda es pequeña en comparación con las dimensiones del objeto esparcidor, o sea ka.».1. Previamente, se había argumentado que forzar a la función de onda a desvanecerse en la superficie de la esfera dispersora distorsionaba la función de onda a cierta distancia de la esfera y que, por lo tanto, la sección transversal total de esparcimiento era más grande que la sección transversal geométrica. En la aproximación de longitudes de onda cortas, esperamos que este efecto sea pequeño y, como consecuencia, podemos anticipar que esta sección transversal de esparcimiento sea casi geométrica. Más aún, en este límite, anticipamos una sombra razonablemente bien definida que se forme detrás de la esfera, tal y como ocurre cuando un objeto opaco es puesto en el camino de un haz luminoso. Como veremos, esto último resulta ser correcto, pero lo primero requiere de alguna modificación.
De las expresiones asintóticas para jl.(kr) y nl.(kr), encontramos con:
la siguiente aproximación asintótica en el limite ka.».l:
y la siguiente aproximación asintótica en el limite ka.«.l:
Por lo tanto, los desplazamientos de fase δl son aproximadamente iguales a:
- ka + (lπ/2)
para l menor que ka. Para l mayor que ka, los factoriales en el denominador aumentan más rápidamente con l que lo que lo hace la potencia de ka en el numerador, de modo tal que los desplazamientos de fase tienden a volverse bastante pequeños. Si hacemos a un lado los valores posteriores de δl, la expresión para la sección transversal total obtenida arriba:
se vuelve:
Ahora bien, en vista de la aproximación asintótica que está siendo invocada arriba, se tiene:
en donde el término “cruzado”, el que involucra a sen(lπ/2)cos(lπ/2) se desvanece para todos los valores integrales de l. Se tiene así entonces:
Al recorrer l los valores 0, 1, 2, ..., los términos sen2(lπ/2) y cos2(lπ/2) se desvanecen alternativamente o se vuelven l, y se tiene entonces:
Esto lo podemos agrupar de la siguiente manera:
Ahora usaremos la siguiente bien conocida serie aritmética:
en donde L es el último término:
Para nuestro caso:
L = 2ka + 1
de modo tal que:
n = (ka/2) +1
y por lo tanto:
puesto que ka.».1. El mismo resultado se obtiene para la serie que es el coeficiente de cos2(ka). El hecho de que ka no es, por lo general, un entero, introducirá un error despreciable si ka es grande. Por lo tanto, tenemos aproximadamente:
de modo tal que la sección transversal es el doble de la sección transversal geométrica. Para poder entender este resultado, observamos que en el límite de las longitudes de onda cortas, la porción de la onda incidente que impacta a la esfera tenderá a ser reflejada en la dirección contraria. La sección transversal para la reflexión será aproximadamente geométrica. Pero para que se pueda formar una sombra en la dirección frontal (detrás del esparcidor) tiene que haber interferencia destructiva entre dos ondas. Consecuentemente, además de la onda reflejada para la cual la sección transversal es πa2, tiene que haber una cantidad igual que es esparcida hacia la dirección frontal (detrás del esparcidor), la onda forjadora de la sombra, que se cancele con la onda incidente para producir la región de sombra. De este modo, la sección transversal total de esparcimiento debe ser aproximadamente 2πa2. Tenemos por lo tanto que πa2 es removido de la onda incidente y aparece en la onda reflejada, pero además de esto cantidades iguales de onda incidente y onda reflejada (πa2) interfieren detrás del objeto esparcidor para producir una región de sombra. Encontraremos el mismo resultado cuando llevemos a cabo el estudio del esparcimiento de las ondas de materia.
Para poder medir la sección transversal total de esparcimiento, es necesario detectar la onda esparcida en todos los ángulos de esparcimiento, llevando a cabo una integración de los resultados. Si una porción considerable de la onda esparcida cae en la dirección frontal, entonces, como un asunto práctico, se vuelve cada vez más difícil separar esta onda de la onda incidente conforme nos acercamos a θ.=.0°. De hecho, conforme ka tiende hacia el infinito, toda la onda causante de la sombra se acerca más y más a θ.=.0°, de modo tal que en el límite se vuelve imposible separar las dos ondas experimentalmente, y la sección transversal medida será igual a σ/2, o la sección transversal geométrica.
Hemos visto lo que ocurre con el esparcimiento de las ondas de luz, analizado todo el asunto desde la perspectiva del electromagnetismo clásico. Con ello, estamos preparados para trasladar el análisis que hemos visto aquí a todo lo que concierne a las ondas de materia. Pero antes en la siguiente entrada se dará un repaso a la obtención de algunos resultados de índole matemática que nos pueden ayudar a comprender mejor este asunto del esparcimiento de partículas consideradas no como partículas clásicas sino como ondas de materia.