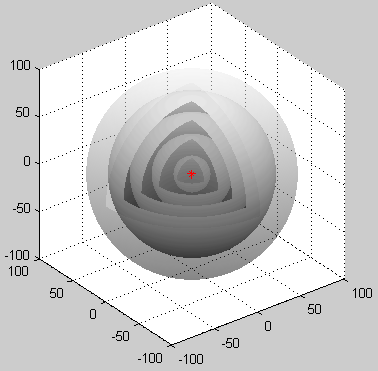
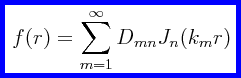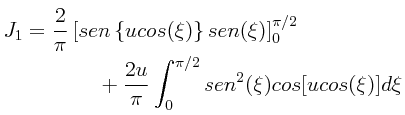Cualquier niño que haya arrojado una piedra a un estanque de agua está familiarizado ya intuitivamente con el concepto de las ondas esféricas al ver los rizos de anillos concéntricos sobre la superficie del agua que se van ampliando y se van alejando del punto en donde cayó la piedra:
Extendiendo este concepto de las ondas esféricas hacia un espacio verdaderamente tridimensional, aunque resulta más difícil representar este clase de ondas en tres dimensiones podemos hacer una esquematización como la siguiente en donde el centro generador de las ondas esféricas está representado como una pequeña cruz roja (se puede apreciar en Wikipedia una demostración dinámica en tres dimensiones de estas ondas esféricas conformen se van expandiendo hacia el exterior):
Puesto que la esfera, simétricamente hablando, es el cuerpo más perfecto que existe en la Naturaleza, parecería a primera vista que la representación matemática de las ondas esféricas debería ser algo realmente sencillo. Sin embargo, a diferencia de las ondas senoidales unidimensionales, no lo es, y los matemáticos de antaño fueron los primeros en darse cuenta de ello. Esta es la razón por la cual nos vemos casi obligados a elevar el grado de complejidad en cualquier análisis que involucre este tipo de fenómenos.
En la entrada previa abarcamos algunos tópicos de naturaleza puramente matemática sin entrar en mayor detalle sobre los mismos. Aquí exploraremos un poco más a fondo tales detalles, con la finalidad de darle alguna justificación a las bases que estamos cimentando. Mantendremos, por lo pronto y al igual que como se hizo en la entrada previa, el análisis clásico de este tipo de fenómenos en la forma en que se lleva a cabo en el campo de la electrodinámica clásica.
Empezaremos por repasar la ecuación differencial de Bessel. Decimos que cualquier ecuación diferencial que pueda ser escrita en la forma:
es una ecuación diferencial de Bessel. Observando que esta ecuación diferencial es singular en el punto u.=.0, en la búsqueda de una solución a dicha ecuación diferencial el camino más expedito consiste en buscar una solución con una expansión en una serie de términos de R(u) con respecto a este punto, escribiendo lo siguiente:
Tomando diferenciales de esta expansión, se tiene entonces:
Substituyendo estas expresiones en la ecuación diferencial de Bessel, vemos que:
Puesto que las distintas potencias de u son linearmente independientes, el coeficiente de cada potencia se debe desvanecer separadamente. Por lo tanto, igualando a cero el coeficiente de uk+b, encontramos que:
[(k + b)(k + b - 1) + (k + b) - n2] ak + ak-2 = 0
o lo que es lo mismo:
[(k + b)2 - n2]ak + ak-2 = 0
Para el caso en el quel k.=.0 (obsérvese que a-2.=.0) obtenemos la ecuación indicial:
b2 - n2 = 0
la cual tiene dos raíces sencillas:
b1 = n (siendo n ≥ 0 )
b2 = - n
Para el caso en el cual k.=.1, se tiene:
[(b + 1)2 - n2]a1 = 0
De esto se deduce que a1 es igual a cero para ambas de las raíces b1 y b2.
Si usamos b1 = n en la expresión:
[(k + b)2 - n2]ak + ak-2 = 0
entonces se produce la relación:
Esta es precisamente la relación recursiva para la ecuación de Bessel. Puesto que ya encontramos que a1.=.0 , esta última expresión requiere que todos los ak para los cuales k sea impar también se desvanezcan. Por lo tanto, k está restringido a tomar valores pares. Si hacemos la substitución de 2λ por k en la expresión, entonces podemos permitir que λ tome los valores 0, 1, 2, etcétera:
Por lo tanto, para λ = 1:
y para λ = 2, haciendo uso de la recursividad para meter el resultado obtenido arriba:
De este modo, llegamos a la siguiente relación general:
De este modo, para el caso b1 = n, la solución es:
Excepto para algunos valores especiales de n, esta no es una función elemental. Se acostumbra definir a a0 como 1/(2nn!). Cuando esto se hace, entonces R1(u) se convierte en una función de Bessel de orden n:
Históricamente, aunque fue Friedrich Bessel el primero que dió en 1824 un tratamiento sistemático a la ecuación diferencial que lleva su nombre y a este tipo de soluciones, estas funciones fueron estudiadas por vez primera por Leonhard Euler en 1764 en sus estudios sobre la vibración de las membranas circulares.
Si recurrimos a la definición matemática de la función gamma Γ, podemos darle a lo anterior una forma un poco más compacta:
En cualesquier caso, la expansión de la función de Bessel como una serie infinita de términos está dada por la siguiente relación general:
De acuerdo a esta relación, las primeras dos funciones de Bessel J0(u) y J1(u) se pueden escribir de la siguiente manera:
A estas alturas, resulta instructivo graficar estas funciones de Bessel para los órdenes 0 y 1 junto con las funciones de Bessel para otros órdenes superiores:
Si tomamos la función de Bessel de orden cero, y la hacemos girar en torno al eje vertical, la gráfica tridimensional resultante revela nítidamente la manera en la que estas funciones son precisamente la clave para la representación de ondas esféricas:
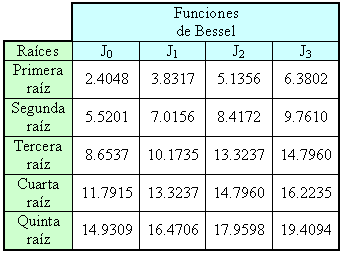
Los puntos en los cuales una función de Bessel cruza del eje vertical positivo al eje vertical negativo (o viceversa) son conocidos como los ceros o las raíces de la función de Bessel. La primera raíz de la función de Bessel de orden cero J0(u) es igual 2.4048, como podemos verlo arriba. La siguiente tabla nos da los valores de varias raíces para las primeras cuatro funciones de Bessel:
Un resultado obtenido por George Stokes en 1850 indica que conforme el orden n de la función de Bessel se vuelve muy grande, el valor de la ν-raíz está dado aproximadamente por la relación:
νπ + [n - (½ )](π/2)
Comparando (con la ayuda de una calculadora de bolsillo) los valores obtenidos mediante la fórmula de Stokes con los valores dados en la tabla de arriba revela que la aproximación de Stokes es precisa con un margen de error inferior al 10% inclusive para n.=.2.
Las funciones de Bessel, extendiéndose en ambas direcciones del argumento ( tanto en la dirección positiva hacia la derecha como en la dirección negativa hacia la izquierda), pueden ser simétricas o antisimétricas, como puede apreciarse en la siguiente gráfica:
Pero si las funciones de Bessel van a ser utilizadas para representar ondas de materia esféricas, ¿cómo podemos adecuar a un sentido físico real los valores negativos de tales funciones de onda? Esto no ofrece problema alguno, porque al igual que como ocurre en la Mecánica Cuántica en donde no es la función de onda Ψ sino el cuadrado de la función de onda, o sea Ψ2, lo que dá una medida de la densidad de probabilidad para encontrar una partícula en cierta región del espacio (el criterio probabilista de Born), en la electrodinámica clásica lo que proporciona la intensidad de la magnitud (energética) de una onda electromagnética no es la magnitud de la onda electromagnética sino el cuadrado de la amplitud de la onda electromagnética, lo cual se deshace del signo negativo. La siguiente gráfica nos muestra los cuadrados de algunas funciones de Bessel:
Todas las funciones de Bessel son de carácter oscilatorio con una amplitud decreciente conforme va aumentando el orden de la función. La siguiente gráfica en donde abarcamos más “ciclos” de las funciones de Bessel resalta el carácter oscilatorio de las mismas:
En la gráfica anterior podemos observar que en el extremo izquierdo de la misma las funciones de Bessel parecen comportarse como ondas senoidales puras. Este es precisamente el comportamiento asintótico de una función de Bessel, y no se requieren valores extremadamente grandes de r (la condición r→∞) para que pueda usarse dicha aproximación, esto llega después de una cantidad moderada de ciclos, y es lo que permite que a distancias relativamente grandes las ondas esféricas representadas mediante funciones de Bessel puedan ser consideradas (aproximadamente) como ondas planares. Esto lo podemos destacar con mayor claridad mediante la gráfica extendida de una sola de ellas (J0):
La solución para la raíz b2.=.- n viene siendo:
Hasta aquí hemos hablado de funciones de Bessel de orden integral. Pero como lo vimos en la entrada previa, no sólo hay funciones de Bessel de orden integral, también hay funciones de Bessel de medio orden integral. Si n no es un entero, entonces Jn(u) y J-n(u) son soluciones linearmente independientes. Sin embargo, si n es un entero, las soluciones son linearmente dependientes como lo demostraremos a continuación.
PROBLEMA: Demuéstrese que:
J-m(u) = (-1)mJm(u)
Para resolver este problema, podemos empezar con la definición de una función de Bessel Jn(u) mediante la serie infinita:
Haciendo la substitución n.→.-m, se tiene:
Ahora bien, la función gamma Γ es divergente para:
λ - m + 1 ≤ 0
λ ≤ m - 1
Por lo tanto, el primer término de la sumación que sobrevive es λ.=.m. Substituyendo (en la sumatoria) un nuevo sub-índice:
μ = λ - m
la sumatoria se vuelve entonces:
Usando la serie para Jn(u) y el hecho de que Γ(k+1).=.k! por las propiedades de la función Gamma, todo lo anterior se reduce al resultado deseado:
PROBLEMA: Si Zn(u) simboliza ya sea una función de Bessel Jn(u) o una función de Neumann Nn(u), demuéstrese que:
La expresión proporcionada expresa la derivada de una función de Bessel o de Neumann en la forma de una relación recursiva. Para resolver este problema en lo que toca a las funciones de Bessel, recurrimos a la siguiente expansión en series:
Diferenciando el producto unu2 se tiene entonces:
El primer término puede ser factorizado de la siguiente manera:
En lo que toca al segundo término, podemos redefinir de la siguiente manera el índice de la sumatoria:
λ - 1 → μ
Con esto, el segundo término se convierte en lo siguiente:
El término μ = -1 en la primera sumatoria es cero en virtud de que 0/0! = 0/1 = 0. Por lo tanto:
La metodología para demostrar la validez de la relación recursiva general en el caso de las funciones de Neumann es exactamente la misma, y no es necesario repetirla aquí.
Las funciones de Bessel que hemos visto hasta este punto son funciones de Bessel del primer género. Para el caso en el cual n sea un entero (e inclusive para el caso en el cual n no sea un entero), la solución general de la ecuación diferencial de Bessel usualmente se escribe en función de las funciones linearmente independientes Jn(u) y Nn(u), en donde las Nn(u) son las funciones de Neumann. Las funciones de Neumann también son llamadas frecuentemente funciones de Bessel del segundo género, de modo tal que la solución general de la ecuación diferencial de Bessel está dada por una combinación linear de funciones de Bessel del primer género y del segundo género. (Advertencia: las funciones de Bessel del segundo género frecuentemente se representan como Yn(u), pero nos abstendremos aquí de hacer tal cosa porque esto se presta a confusiones con la notación que hemos estado utilizando para simbolizar a las armónicas esféricas que aunque son un concepto similar no se trata de la misma cosa). Las funciones de Neumann se definen formalmente mediante la siguiente relación:
De este modo, la solución general Rn(u) = Rn(kr) de la ecuación diferencial de Bessel se puede expresar en forma sencilla de la siguiente manera:
Las funciones de Bessel Jn(kr) son regulares en el origen, y para valores pequeños de kr (esto es, kr«1), éstas varían de acuerdo a la relación:
Por el otro lado, las formas asintóticas para valores relativamente grandes de kr (esto es, kr»1) están dadas por (la expresión asintótica para J0 fue obtenida en 1817 por Poisson, mientras que el resultado general para cualquier n fue obtenido por Jacobi):
Las funciones de Bessel, por lo tanto, exhiben una variación asintótica senoidal a medida que aumenta kr, pero con una disminución en la amplitud al ir creciendo kr. La región de transición entre la aproximación para valores pequeños de kr y la aproximación para valores grandes de kr es cercana al punto kr.≈.n.
A estas alturas, resulta instructivo echarle un vistazo a las gráficas de varias funciones de Neumann para varios órdenes:
Lo primero que resalta es que todas las funciones de Neumann son irregulares en el origen, en donde su valor se va hacia el infinito (negativo). Es por ello que debemos usar mucha precaución en los usos que le demos a estas funciones en problemas de la física, y es por ello que en virtud de esta irregularidad de las funciones Nn(kr) escogemos únicamente a las funciones Jn(kr) en problemas en los que el origen esté involucrado.
Para valores pequeños de kr (esto es, kr«1) y para n.=.0, la función de Neumann varía de la siguiente manera:
Para valores pequeños de kr (esto es, kr«1) y para cualquier otro valor de n difefente de n.=.0, la función de Neumann varía de la siguiente manera:
Las expresiones asintóticas de las funciones de Neumann para valores relativamente grandes de kr (esto es, kr»1) son:
Conforme nos alejamos de la singularidad en el origen, todas las funciones de Neumann son de carácter oscilatorio con una amplitud decreciente conforme va aumentando el argumento de la función. La siguiente gráfica en donde abarcamos más “ciclos” de las funciones de Neumann resalta el carácter oscilatorio de las mismas:
Compárese la forma asintótica algebraica de las funciones de Neumann con la forma asintótica de las funciones de Bessel del primer género. Son casi la misma cosa, ambas con la misma amplitud, excepto que una forma es senoidal y la otra cosenoidal.
Se ha afirmado que es posible llevar a cabo la representación de una onda plana mediante una suma (infinita) de ondas esféricas. De la quintaesencia del análisis de Fourier, sabemos ya que para que esto se pueda llevar a cabo las funciones que representan cada onda esférica necesariamente tienen que ser ortogonales entre sí. Afortunadamente, esto está garantizado, porque se puede demostrar que las funciones de Bessel Jn(kr) son ortogonales. Si kmρ es la m-raíz de Jn(kr), esto es, Jn(kmρ).=.0, entonces la condición de ortogonalidad sobre las funciones de Bessel dentro de cierto intervalo 0.≤.r.≤.ρ afirma que:
Es un hecho que las funciones de Bessel forman un conjunto ortogonal completo de funciones para la expansión de una función f(r) en el intervalo 0.≤.r.≤.ρ:
PROBLEMA: Obténganse los “coeficientes Fourier” Dmn para la expansión de una función de r en términos de una serie (infinita) de funciones de Bessel.
Si multiplicamos ambos miembros de la expansión anterior por:
y llevamos a cabo la integración en el intervalo 0.≤.r.≤.ρ, se tiene entonces:
El lado derecho puede ser evaluado usando la condición de ortogonalidad dada arriba:
Por lo tanto:
Obviamente, las series que son generadas de esta manera son conocidas como series Fourier-Bessel.
Aunque la evaluación numérica de las funciones de Bessel usando una expansión en series pueda parecer algo sencillo y directo recurriendo un programa de computación para el cálculo numérico de dichas series, la lentitud en la convergencia hacia una respuesta con un grado aceptable de precisión (digamos cuatro o cinco cifras significativas) hace que tal procedimiento sea de valor escaso para argumentos que sean muy superiores a la unidad. No entraremos a fondo en los detalles de las dificultades enfrentadas en una situación de este tipo ya que, afortunadamente, tales detalles en la evaluación de cómputos numéricos pueden ser solventados recurriendo a lo que se conoce como las representaciones integrales de las funciones de Bessel:
PROBLEMA: Demuéstrese que:
es equivalente a la relación recursiva:
Llevando a cabo la diferenciación indicada y usando la relación recursiva, se tiene:
PROBLEMA: Usando el resultado del problema previo junto con la representación integral para la función de Bessel J0(u), obténgase la representación integral para la función de Bessel J1(u). Generalícese el procedimiento para obtener la representación integral de cualquier función de Bessel demostrando que, en general:
Usando el resultado previo haciendo n.=.0, y recurriendo a la representación integral para la función de Bessel J0(u), se tiene que:
Podemos diferenciar bajo el signo de la integral para obtener lo siguiente (los colores son para resaltar las partes con las cuales se llevará a cabo una substitución de variables con la finalidad de facilitar el proceso de integración por partes):
Es evidente que las variables “monigote” son tales que lo siguiente debe ser cierto:
Llevando a cabo la integración por partes, se tiene entonces:
El término “uv” se desvanece en ambos límites. Procediendo de modo similar repitiendo la técnica de integración por partes, obtenemos:
Cada subsecuente integración por partes va recogiendo los factores adicionales sen2(ξ), u, y un coeficiente en la progresión 1/3, 1/5, 1/7, etc. Por lo tanto, la generalización deseada es:
La representación integral de J0(u) se puede demostrar llevando a cabo la expansión del integrando en una serie de potencias, llevando a cabo la integración término por término, y efectuando la comparación con la expansión en series para J0(u).
PROBLEMA: Utilícense los resultados vistos previamente para demostrar las siguientes relaciones:
De lo que se ha visto con anterioridad, se tiene que:
Para n.=.1/2, se vuelve necesario recurrir a las propiedades de la función Gamma en la forma en la que se aplica para argumentos de medio orden integral. En este caso, consultando la bibliografía matemática, se tiene que:
De este modo, la serie toma el siguiente aspecto:
De modo semejante, para n.=.-1/2:
Entonces para este caso la serie toma el siguiente aspecto:
Un procedimiento alterno de solución consiste en recurrir a la siguiente substitución:
tomando n.=.±1/2 en la ecuación diferencial de Bessel, lo cual reduce la ecuación a la forma familiar:
PROBLEMA: Obténganse expresiones para las siguientes funciones de Bessel y de Neumann de medio orden integral:
Las funciones de Bessel J+1/2 y J-1/2 pueden ser obtenidas directamente de la expansión en series dada arriba:
Puesto que ya se obtuvieron J+1/2 y J-1/2 en el problema anterior, no será necesario repetir aquí la solución de los mismos.
En lo que respecta a la función de Bessel J+3/2, esta puede ser obtenida con la ayuda de la relación recursiva:
Usando los resultados obtenidos arriba,
Por otra parte, para J-3/2, se tiene:
Para valores medios integrales de n, la relación:
nos conduce a:
Por lo tanto:
Del mismo modo:
Usando los factores de normalización e indexación que corresponden propiamente a las funciones esféricas de Bessel, tenemos primero que:
Del mismo modo:
En lo que toca a las funciones esféricas de Neumann, se tiene primero que:
Del mismo modo:
PROBLEMA: Usando la relación:
demuéstrese lo siguiente:
Usando la expresión así obtenida, demuéstrese que:
Finalmente, utilícese la expresión anterior para demostrar que:
Obténganse de esta última relación las primeras tres funciones esféricas de Bessel, y compruébese que se obtiene lo mismo que lo que había sido dado previamente.
Utilizaremos el muy conocido procedimiento de inducción matemática para demostrar lo primero. Para m.=.0, la relación a ser demostrada se reduce al siguiente resultado que es trivialmente cierto:
Suponemos ahora que la relación es válida para cualquier valor de m. Tenemos que demostrar que ello implica que será válida también para m+1. Si el teorema a ser demostrado es válido para m, entonces para m+1 se tiene:
Esto se reduce a la forma:
al llevar a cabo el reemplazo n→n+m. Puesto que hemos demostrado la validez de la hipótesis para m.=.0 y para m+1, será válida para cualquier valor entero de m, con lo cual se dá por concluida la demostración.
Ahora bien, hágase n.=.1/2 y m→l. La relación demostrada se vuelve entonces:
Pero:
y se tiene también que:
Entonces, para la función de Bessel de medio orden integral:
Y en lo que respecta a la función esférica de Bessel correspondiente:
Para l = 0, 1 y 2, esta última relación que acabamos de obtener nos produce las primeras tres funciones esféricas de Bessel que resultan ser idénticas a lo dado previamente:
PROBLEMA: Verifíquese por integración directa que la expresión:
produce las primeras tres funciones esféricas de Bessel.
La ecuación proporcionada es una forma integral de las funciones esféricas de Bessel, que con un ligero cambio en la notación toma el siguiente aspecto:
Usando los polinomios de Legendre:
se tiene entonces por principio de cuentas:
Del mismo modo, y llevando a cabo una integración por partes:
Finalmente:
PROBLEMA: Las funciones generadoras para las funciones esféricas de Bessel y Neumann son las siguientes:
en donde, por ejemplo, operacionalmente hablando:
y así sucesivamente para valores crecientes de l. Utilícense estas funciones generadoras para obtener las primeras tres funciones esféricas de Bessel y de Neumann.
Las funciones jl para l.=.0, 1, y 2 fueron obtenidas en uno de los problemas resueltos arriba precisamente por este procedimiento. Podemos escribir la función generadora de la siguiente manera:
Por lo tanto:
Las funciones esféricas nl pueden ser obtenidas de las funciones esféricas de Bessel jl mediante la substitución (el signo negativo viene del signo negativo extra en la función generadora):
sen(u) → - cos(u)
y la substitución (el signo es invertido por el signo negativo adicional en la diferenciación hacia el coseno):
cos(u) → + sen(u)
Así, por ejemplo:
Sin entrar en tanto detalle en torno a las funciones esféricas de Bessel y Neumann, resulta posible entender cómo siempre debe ser posible representar una onda plana (escrita ya sea como una función senoidal o cosenoidal multiplicada por un factor que representa la amplitud de la onda) mediante una combinación en serie (infinita) de funciones de Bessel, en virtud de las siguientes relaciones matemáticas cuya demostración puede ser encontrada en Internet y en muchos textos de matemáticas propias de la física:
Si es posible representar una onda plana en función de una combinación de un número infinito de ondas esféricas, puede surgir entonces la pregunta: ¿será posible hacer lo opuesto, esto es, representar una onda esférica utilizando ondas planas? La respuesta, como pudiera sospecharse, es afirmativa. En efecto, y utilizando como referencia la definición para una transformada de Fourier en una dimensión:
pero extendida a tres dimensiones, se encuentra que una onda esférica definida como Ylm.j(kr) puede ser expandida en términos de ondas esféricas mediante el cálculo de los coeficientes A(k) de la siguiente relación:
Lo que se lleva a cabo, en efecto, es una transformada de Fourier en el sentido inverso. Aunque el lector posiblemente ya sospechaba desde un principio que esta era la forma de llevarlo a cabo.