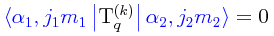En la entrada previa “El momento de cuadripolo”, se vió casi al final de la misma lo que se conoce como el tensor de cuadripolo, un tensor Cartesiano definido en coordenadas Cartesianas rectangulares:
que consta de nueve elementos Qij y que en ocasiones es simbolizado como Q, los cuales podemos agrupar en un arreglo rectangular como el siguiente:
El tensor de cuadripolo, por estar especificado con nueve elementos Qij, parecería poder proporcionar más información que la que proporciona el tensor esférico momento de cuadripolo de segundo orden el cual consta de tan solo cinco elementos (los cuales pueden ser definidos a su vez empleando armónicas esféricas):
Sin embargo, esto no es así. Ninguno puede proporcionar más información que el otro, porque si bien el tensor Cartesiano de cuadripolo consta de nueve elementos, por ser simétrico (esto es Qij.=.Qji) en realidad solo contiene seis elementos independientes. Pero tomando en cuenta además que la traza del tensor de cuadripolo es igual a cero, esto es:
con lo cual dados dos elementos cualesquiera de la traza podemos obtener de inmediato el tercero, en realidad el número de elementos independientes se reduce a cinco, justo la misma cantidad de componentes de que consta el tensor esférico para el momento de cuadripolo. ¿Entonces por qué razón usar un tensor esférico en lugar de usar de usar de usar el tensor de cuadripolo definido en coordenadas Cartesianas rectangulares? Porque, como ya se señaló en la entrada “Operadores tensoriales”, los tensores esféricos son irreducibles (esto es una consecuencia directa del hecho de que estén definidos en base a las armónicas esféricas, las cuales también son irreducibles) mientras que los tensores Cartesianos no lo son, lo cual los vuelve sumamente atractivos.
Los conceptos delineados en la entrada “El momento de cuadripolo” forman parte de las bases que fueron asentadas para el advenimiento de lo que puede llamarse la espectroscopía nuclear. La física atómica nació de la necesidad de entender los espectros atómicos, sus hermosas líneas con los colores del arco iris y sus espaciamientos inmutables para cada átomo. Los espectros atómicos permanecieron incomprendidos por buen tiempo hasta que Niels Bohr sugirió en 1913 que las líneas espectrales correspondían a transiciones entre dos estados del átomo, y que eran rayos luminosos emitidos cuando un electrón brincaba de una capa energética superior a una capa energética inferior. Lo que vino siendo conocido como espectroscopía atómica consistió en determinar los estados de un átomo y sus propiedades que eran determinadas por sus funciones de onda. En contraste, la espectroscopía nuclear empezó mucho tiempo después, en los años cincuentas. Su objetivo era determinar también los estados del núcleo atómico, y sus propiedades, lo cual equivale a determinar eventualmente las funciones de onda que corresponden al estado del núcleo, lo cual resultó ser más difícil de lograr en el caso del átomo porque las interacciones que encadenan a los nucleones al átomo son menos conocidas. Sin embargo, el modelo de capas nuclear postulado por Maria Goeppert-Mayer y por Hans Jensen, extendido por Aage Bohr y Ben Mottelson con su concepto del núcleo deformado (elipsoidal en vez de esférico) proporcionó un modelo teorico sólido para comprender la estructura interna del núcleo atómico. Fue precisamente en noviembre de 1952 y en marzo de 1953 cuando Bohr y Mottelson enviaron dos cartas ya clásicas a la publicación Physical Review. En la primera demostraron que las transiciones rápidas en el estado basal del núcleo pueden ser explicadas si uno supone que el núcleo en lugar de tener una forma esférica (una creencia que prevalecía desde los tiempos en los que Ernest Rutherford postuló su modelo del átomo nuclear para explicar los resultados obtenidos en experimentos de esparcimiento de partículas) en realidad es un núcleo deformado, e inclusive estimaron momentos de cuadripolo que eran más o menos cercanos a los valores obtenidos experimentalmente, mientras que en su segunda carta insistieron en la acumulación de evidencias experimentales para apoyar su hipótesis. Al concluir 1953, resumieron sus conclusiones en un trabajo de 173 páginas titulado “Collective and individual-particle aspects of nuclear structure ” publicado en el Mathematics and Physics Communications of the Royal Society of Sciences of Denmark (Det Kgl. Danske videnskabernes selskab. Matematisk-fysiske meddelelser) que describe un modelo unificado de la estructura nuclear que terminó convirtiéndose en una referencia importante para una generación de físicos nucleares alrededor del mundo.
Antes de entrar en detalles sobre la necesidad y la utilidad de recurrir a un teorema como el teorema Wigner-Eckart, resulta conveniente repasar algunos detalles que solo se exploraron superficialmente en la entrada “El momento de cuadripolo”. La definición misma del momento de cuadripolo implica que el meollo del asunto en su descripción mecánico-cuántica se basa en la evaluación de algo como lo siguiente:
en donde α es una función radial que relacionada con la función de onda total que describe el estado del sistema:
α = α(r)
y J y m son las variables relacionadas con el momento angular y por lo tanto representan la evaluación (usualmente en coordenadas esféricas) de la parte angular de la función de onda. Si enfocamos nuestro interés exclusivamente sobre la parte angular haciendo a un lado la parte radial, entonces lo que se quiere evaluar es lo siguiente (obsérvese que se ha eliminado la referencia a α):
Sobre el supuesto de que la evaluación de la parte angular se lleva a cabo recurriendo a armónicas esféricas Ylm, el bra de la expresión anterior (destacado en color magenta) necesariamente mete en la evaluación una armónica esférica. Pero por otro lado, el ket (destacado en color azul) también mete otra armónica esférica en la integral a ser evaluada (por el momento supondremos que una armónica esférica es el conjugado complejo de la otra). El asunto se complica cuando tomamos en cuenta la siguiente relación (véase la entrada “Operadores tensoriales”):
Haciendo la substitución, tenemos entonces para evaluar una doble integral (en coordenadas esféricas, llevada a cabo sobre los ángulos θ y φ) que involucra el producto de tres armónicas esféricas:
Hasta aquí hemos supuesto que tanto el bra como el ket son conjugados complejos el uno del otro. Sin embargo, el asunto se puede complicar aún más si suponemos que el número cuántico m en el bra posee un cierto valor (llamémoslo m1) que es diferente del número cuántico m en el ket (llamémoslo m2). Esto nos pide la evalación de una doble integral sobre el producto de tres armónicas esféricas. Este tipo de integrales ha sido bien estudiado y hay bastante literatura sobre el tema. En su quintaesencia, la evaluación de una integral de este tipo posee una solución conocida que se puede expresar recurriendo a los símbolos 3-j de Wigner del siguiente modo:
Hay disponibles en Internet varios sitios de ayuda que nos proporcionan el valor de un símbolo 3-j de Wigner para cualquier combinación de los números cuánticos que estemos manejando. También hay paquetes de programas computacionales que incluyen el cálculo de los símbolos 3-j, uno de ellos es Mathematica con el comando:
ThreeJSymbol[{.j1, m1}, {j2, m2}, {m3, m3}]
que a manera de ejemplo, se usa de la siguiente manera:
ThreeJSymbol[{6, 0}, {4, 0}, {2, 0}]
regresándonos el siguiente valor:
De este modo. lo que a primera vista se antoja como una integral sumamente intimidante llevada a cabo sobre el producto de tres armónicas esféricas queda reducida a un asunto trivial. Esto debe ser motivación más que suficiente para asimilar las matemáticas que pueden simplificar de tal modo un asunto de esta naturaleza. En este punto, es igualmente importante destacar el hecho de que los símbolos 3-j de Wigner están relacionados con los coeficientes Clebsch-Gordan (véanse las entradas tituladas “Los coeficientes Clebsch-Gordan”) de la siguiente manera permitiéndonos obtener un número 3-j de Wigner de un coeficiente Clebsch-Gordan:
siendo la relación inversa (que nos permite obtener un coeficiente Clebsch-Gordan de un número 3-j de Wigner):
Un operador tensorial esférico, por la manera en la que está definido, es también un operador matricial. Precisamente en la entrada anterior titulada “El momento de cuadripolo” vimos un ejemplo aplicado de un operador tensorial esférico, el operador momento de cuadripolo Q(J)m desarrollado inicialmente a partir de una definición electrostática clásica del momento de cuadripolo eléctrico. Como se vió arriba, podemos definir elementos matriciales para este operador tomando la esperanza matemática de dicho operador tensorial para varias combinaciones de eigenestados. Haciendo tal cosa exclusivamente sobre la parte angular (ignorando la parte radial) de la función de onda, en la notación bra-ket de Dirac se tienen elementos matriciales como los siguientes:
De hecho, para representar estos elementos matriciales en un arreglo matricial convencional es necesario recurrir a matrices y submatrices (véase la entrada “Matrices y sub-matrices”). No todos los elementos matriciales que podamos evaluar serán diferentes de cero; algunos de ellos serán necesariamente igual a cero. Para poder determinar de antemano aquellos elementos matriciales que serán iguales a cero, existe una regla de selección conocida como la regla de selección m, la cual nos dice lo siguiente:
El elemento matricial:
del operador tensorial T(k)qes igual a cero, a menos de que:
La aplicación de este criterio, cuando se está empleando la notación bra-ket de Dirac, resulta extremadamente sencilla, y se puede llevar a cabo visualmente en forma directa sin mayores problemas:
Con solo ir viendo cada uno de los elementos matriciales del operador tensorial, se puede decir de inmediato cuáles son iguales a cero y cuáles no lo son.
Se vuelve necesario justificar rigurosamente la regla de selección m. Esto lo haremos a continuación partiendo de la siguiente relación fundamental:
Tomaremos lo anterior y lo aprisionaremos entre un bra de estado y un ket de estado a manera de “sandwich”:
Lo anterior puede ser desarrollado de la siguiente manera:
Para poder continuar adelante, recurriremos a la eigenecuación básica que nos describe la acción del operador del momento angular Jz sobre un eigenestado del momento angular, actuando sobre un ket que representa a dicho estado, regresándonos un eigenvalor que multiplica al ket sobre el cual actuó el operador Jz (en esta relación no se incluye la parte radial α de la función de onda porque el operador Jz sólo actúa sobre la parte angular):
Con esto, el segundo término de la expresión previa se puede desarrollar de la siguiente manera:
En lo que respecta al primer término, recurriremos nuevamente a la eigenecuación básica que nos describe la acción del operador del momento angular Jz sobre un eigenestado del momento angular, pero esta ocasión actuando sobre el bra que está a su izquierda y que representa a dicho estado, regresándonos un eigenvalor que multiplica al bra sobre el cual actuó el operador Jz:
Con esto, el primer término de la expresión en la que estamos trabajando se puede desarrollar de la siguiente manera:
Así pues, la expresión viene quedando del modo siguiente:
Recurriendo a simples factorizaciones algebraicas, lo anterior se reduce a:
Esto nos dice en forma directa algo innegable: el elemento matricial del operador tensorial necesariamente es igual a cero:
a menos de que se cumpla la siguiente condición:
Estamos ahora en condiciones de poder enunciar, en su forma más sencilla, el teorema Wigner-Eckart (también referido en la literatura simplemente como el teorema WE):
Los elementos matriciales de operadores tensoriales (irreducibles) pueden ser factorizados como el producto de una constante de acoplamiento (la cual resulta ser un coeficiente Clebsch-Gordan) y un factor que es independiente de números cuánticos magnéticos m.Expresado simbólicamente, el teorema Wigner-Eckart toma la siguiente forma (obsérvese que el coeficiente Clebsch-Gordan está siendo resaltado en color magenta):
En el enunciamiento simbólico anterior del teorema Wigner-Eckart, se ha utilizado una notación que es común para la representación de los coeficientes Clebsch-Gordan, los cuales son estudiados más a fondo en la serie de entradas tituladas [recisamente “Los coeficientes Clebsch-Gordan”. Desafortunadamente, y como ya se ha señalado en dichas entradas, la notación empleada para la simbolización de los coeficientes Clebsch-Gordan no está estandarizada, y hay una verdadera torre de Babel en lo que concierne a dicha notación, lo cual se presta a confusiones al pasar de un texto a otro de diferentes autores. Aquí emplearemos una notación que resalta el hecho de que los coeficientes Clebsch-Gordan son simples constantes numéricas, enunciando el teorema Wigner-Eckart de la siguiente forma alterna:
El lector observador se habrá dado cuenta en esto último de que en el bra y el ket que describen los eigenestados del sistema no se ha incluído referencia a función radial alguna. Dejando abierta la posibilidad de que el operador tensorial esférico pueda cambiar también los números cuánticos no-rotacionales (esto es, la función radial), si representamos dos estados de la función radial como α y β, esto es:
α = α(r) , β = β(r)
entonces el elemento matricial general se puede representar como:
tal y como lo hemos estado haciendo arriba (en donde antes se había supuesto por simplicidad que α es igual a β e independiente de la acción del operador tensorial que actúa únicamente sobre la parte angular que es la que tiene que ver con el momento angular).
Veamos ahora el factor que en el teorema Wigner-Eckart es independiente de los números cuánticos magnéticos m, poniendo atención especial en el elemento que aparece en el numerador mejor conocido como elemento matricial reducido y también como el elemento matricial doble-barra (obsérvense las barras paralelas dobles empleadas al escribir dicho elemento, las cuales han sido destacadas de color rojo):
Como puede verse, el sub-índice m2 que aparece en el elemento matricial del operador tensorial T(k)q (al hacerse q.=.m2 en el teorema Wigner-Eckart) está ausente en el elemento matricial doble barra. No aparece por lo tanto allí referencia a número cuántico magnético m alguno. Pero no solo allí se ha eliminado cualquier referencia a números cuánticos magnéticos en el operador tensorial. También en lo que parece ser un bra y un ket se ha eliminado la referencia a m y m1 que aparece en la representación matricial del operador tensorial. Esto significa que el factor al que se hace mención en el teorema Wigner-Eckart que a su vez multiplica al coeficiente Clebsch-Gordan es una constante independiente de los números cuánticos magnéticos m, m1 y m2. Pero si este factor, específicamente el elemento matricial doble-barra, no hace referencia a número cuántico magnético alguno, ¿entonces cómo lo vamos a evaluar? La respuesta es que no es posible evaluar directamente un elemento matricial doble-barra, tiene que ser evaluado indirectamente. Esto implica que hay que evaluar primero un elemento matricial por la “vía difícil”, llevando a cabo un proceso de integración múltiple de la manera usual. Hecho esto, como un segundo paso se substituye el resultado en el teorema Wigner-Eckart, y se lleva a cabo un despeje para el elemento matricial doble barra, obteniéndolo así de esta manera. Sin embargo, una vez obtenido el elemento matricial doble-barra, no es necesario evaluarlo de nuevo. Podemos evaluar otros elementos matriciales recurriendo únicamente a los coeficientes Clebsch-Gordan que serán diferentes para cada elemento matricial. En rigor de verdad, aunque por su aspecto el elemento matricial doble-barra parece ser algo así como una esperanza matemática representada en notación bra-ket de Dirac, no lo es, lo cual al principio puede dar lugar a confusiones. Pero una vez desarrollada la metodología para resolver problemas con la ayuda del teorema Wigner-Eckart, la confusión se desvanece con el aprendizaje de este nuevo símbolo.
Obsérvese también en el enunciado simbólico del teorema Wigner-Eckart otro hecho importante: en el coeficiente Clebsch-Gordan no aparece operador tensorial alguno. Como preludio de la aplicación del teorema Wigner-Eckart, se recurrió al momento de cuadripolo Q expresado como un operador tensorial esférico. Sin embargo, hay otras observables físicas además del momento de cuadripolo, como las que tienen que ver con la interacción de los electrones orbitales de un átomo con un campo electromagnético, las cuales también son expresables como operadores tensoriales. Sin embargo, en el coeficiente Clebsch-Gordan no aparece referencia alguna a ningún tipo de operador tensorial. Y como en el factor que hemos llamado elemento matricial doble-barra no aparece número cuántico magnético m alguno, estos dos hechos por sí solos hacen que el teorema sea de aplicabilidad casi universal.
El teorema Wigner-Eckart está tan íntimamente ligado al concepto de los coeficientes Clebsch-Gordan, que antes de continuar adelante daremos aquí un breve repaso sobre lo que son dichos coeficientes.
Supóngase que se tienen dos sistemas cuyos momentos angulares totales e individuales son:
j1 = 4 , j2 = 1
Por las reglas fundamentales de la Mecánica Cuántica (obtenidas de la solución de la parte angular de la función de onda Ψ(r,θ,φ) con la ecuación diferencial de Schrödinger expresada en tres dimensiones en coordenadas esféricas), el primer sistema tiene nueve subestados magnéticos posibles:
m1 : -4 , -3 , -2 , -1 , 0 , 1 , 2 , 3 , 4
mientras que el segundo sistema tiene tres subestados magnéticos posibles:
m2 : -1 , 0 , 1
Si el primer sistema está en un estado que podemos representar con el siguiente ket:
y si el segundo sistema está en un estado que podemos representar con el siguiente ket:
entonces el estado combinado de los dos sistemas será el siguiente estado que podemos simbolizar con un solo ket:
Por combinatórica elemental, hay, en total, 9×3.=.27 estados combinados, entre los cuales se encuentran los siguientes:
Los valores posibles de j para el sistema combinado formado por j1.=.4 y j2.=.1 son:
j : 3 , 4 , 5
al estar dados por la regla del triángulo (así llamada porque j1.y j2 y j van formando los tres lados de un triángulo conforme van variando los valores de j1.y j2) simbolizada como Δ( j1 j2. j) y la cual nos dice que dos momentos angulares j1.y j2 solo pueden ser combinados de modo tal que sean compatibles con un triángulo de adición vectorial:
o sea, cada valor de j solo puede ir tomando uno de los valores:
j1 + j2
j1 + j2 - 1
j1 + j2 - 2
...
| j1 - j2 |
El problema de la adición de los momentos angulares consiste en tomar los 27 estados:
formando con ellos combinaciones lineares “en ciertas maneras” para formar 27 nuevos estados, requiriéndose rigurosamente que todos esos nuevos estados sean eigenestados de los operadores J2 y Jz (estos son los operadores para el sistema combinado) que a su vez tengan los eigenvalores j(.j+1) y m que corresponden a los valores observados en el laboratorio para el sistema combinado. Habrá un total de siete nuevos estados con el eigenvalor j.=.3, habrá un total de nueve nuevos estados con el eigenvalor j.=.4, y habrá un total de once nuevos estados con el eigenvalor j.=.5; en total habrá 27 nuevos estados, el mismo número que el número de estados |4,1,m1,m2>, lo cual no es ningún accidente, ya que los estados |.j,m> deben cubrir y abarcar (en la literatura inglesa en el lenguaje del Algebra Linear, la palabra usada es “span”) el mismo espacio que el espacio que cubren y abarcan los estados |4,1,m1,m2>, y ese espacio tiene 27 dimensiones. Los once estados posibles cuando el eigenvalor del sistema combinado es j.=.5 son los siguientes:
Podemos ver casi de inmediato que exactamente dos de los 27 estados |4,1,m1,m2> son ya de por sí eigenestados de J2 y Jz, ellos son:
Obsérvese que. en todos los demás casos, los estados |4,1,m1,m2> utilizados para formar las combinaciones lineares están premultiplicados por un coeficiente numérico. Estos coeficientes numéricos son precisamente lo que hoy llamamos coeficientes Clebsch-Gordan. Premultiplicando algunos de los kets |5,m> por los bras adecuados y usando en las expansiones que aparecen al lado izquiedo de las igualdades la propiedad de ortogonalidad que indica que:
podemos extraer individualmente cada uno de dichos coeficientes numéricos Clebsch-Gordan:
Esto es precisamente lo que inspira la siguiente convención de notación para los coeficientes Clebsch-Gordan (la única diferencia entre ambas es que en la primera los números cuánticos del momento angular para el sistema combinado se escriben en minúsculas mientras que en la segunda se escriben en mayúsculas, pero se sigue representando lo mismo):
En muchas ocasiones, por razones de espacio, resulta conveniente recurrir a formas tipográficas más compactas para representar los coeficientes Clebsch-Gordan. Una de tales convenciones es la siguiente:
La utilidad práctica en el laboratorio de todo esto para la interpretación de los resultados experimentales obtenidos se obtiene al tomar los productos internos bra-ket <j,m|.j,m>, por ejemplo:
Efectuando todas las multiplicaciones requeridas y desechando aquellos términos que contienen productos bra-ket que serán iguales a cero al aplicarles el principio de ortogonalidad, se tiene entonces:
Lo que se obtiene, en efecto, es la magnitud de la probabilidad para cada subestado del sistema, lo cual se verá reflejado en las intensidades relativas de las líneas obtenidas mediante experimentos de espectroscopía. Puede observarse que en el ejemplo que se acaba de dar el subestado intermedio tendrá la mayor probabilidad de ser observado, una probabilidad de 24/45.=.53.33%, mientras que el tercer subestado tendrá una probabilidad de de 15/45.=.33.33%, y el primer subestado tendrá una probabilidad relativamente escasa del 6/45.=.13.33% de ser observado. Resulta fácil comprobar que la suma de las probabilidades relativas es igual a la unidad:
Así pues, viendo la tabla completa dada arriba con todas las combinaciones posibles, resalta de inmediato que en el caso del ejemplo del sistema combinado con j1 = 4 y con j2 = 1, de entre los 11 estados posibles del sistema combinado hay dos estados singlete (o singulete) que solo pueden darse de una sola manera (con una probabilidad igual a la unidad o la certeza), hay dos estados doblete que pueden darse de dos maneras distintas (en cada caso, uno de ellos con una probabilidad de 4/5 y el otro con una probabilidad de 1/5), y el resto de los 7 estados posibles son estados triplete cuyas probabilidades se obtienen tomando el cuadrado del coeficiente Clebsch-Gordan que va anexado a cada sub-estado. No hay que olvidar que el número de combinaciones posibles para cada sub-estado está dado por las reglas de selección en base a las proyecciones del vector momento angular J2 sobre el eje-z, como tampoco hay que olvidar que en un espacio tridimensional cada vector del momento angular J2 está situado en la superficie de un cono, habiendo un cono diferente para cada combinación de números cuánticos magnéticos m. A manera de ejemplo, mostraremos otros casos usando valores diferentes de j1 y j2 (para la notación simbólica del producto bra-ket en cada caso puesto arriba de cada figura se usará una notación algo más superflua que la que fue dada arriba pero que suele encontrarse con frecuencia en la literatura, la cual agrega j1 y j2 al ket aunque ello no es necesario por estar especificados ya j1 y j2 en el bra):
Resulta cosa fácil obtener la definición notacional que se ha dado arriba para los coeficientes Clebsch-Gordan llevando a cabo una expansión del ket |.j,m> recurriendo para ello al operador identidad (relación de cerradura) aplicado dos veces al mismo, una vez para los números cuánticos magnéticos m1 y la segunda para los números cuánticos magnéticos m2:
Todo lo que tenemos que hacer ahora es reagrupar (esto se puede llevar a cabo mentalmente) dándole una intepretación al producto bra-ket que tenemos a la derecha, llegando precisamente a la misma convención notacional dada arriba:
El problema se reduce ahora al cálculo de los coeficientes Clebsch-Gordan. Afortunadamente, no tenemos necesidad de hacer tal cosa. Además de haber disponibles numerosos textos así como sitios Web en los cuales podemos consultar tablas que nos proporcionan los coeficientes Clebsch-Gordan para cada combinación de valores de j1, j2, m1 y m2>, existen programas computacionales que tienen tales constantes numéricas en su base de datos; el programa computacional Mathematica nos los proporciona con el comando:
ClebschGordan[{.j1, m1}, {j2, m2}, { j, m}]
que a manera de ejemplo, si se usa de la siguiente manera:
ClebshGordan[{1, 0}, {1, 0}, {2, 0}]
nos regresa como respuesta correcta √2/3. De cualquier modo, en el dudoso caso en el cual resulte difícil si no imposible el poder encontrar algún coeficiente Clebsch-Gordan en particular, hay dos relaciones recursivas que nos permiten partir de coeficientes Clebsch-Gordan ya conocidos para poder llegar a los coeficientes Clebsch-Gordan que estamos buscando. Estas relaciones que fueron descubiertas por el físico Giulio Racah son las siguientes:
A manera de ejemplo sobre el uso de las relaciones recursivas, obtendremos con la ayuda de las mismas el coeficiente Clebsch-Gordan:
La primera de las dos relaciones recursivas nos dice que:
Simplificando un poco:
Damos por conocido el coeficiente Clebsch-Gordan que aparece del lado derecho (podemos leerlo directamente en la tabla de expansiones que fue puesta arriba), el cual es:
Por lo tanto:
lo cual podemos verificar que concuerda con los valores que tenemos tabulados arriba en las expansiones.
Si tomamos la segunda relación recursiva para coeficientes Clebsch-Gordan dada arriba y hacemos una reagrupación de lo que aparece bajo la raíz cuadrada, podemos escribir la segunda relación recursiva de la siguiente forma alterna:
Podemos hacer algo similar con la primera relación recursiva para los coeficientes Clebsch-Gordan, y podemos ir un poco más lejos juntando ambas relaciones en una sola como se muestra a continuación:
Usando los signos aritméticos superiores en donde aparecen los signos dobles se recupera una de las relaciones recursivas, y usando los signos aritméticos inferiores se recupera la otra. Usaremos esto último más abajo para la demostración que llevaremos a cabo del teorema Wigner-Eckart.
Habiéndose dado ya un ejemplo sobre la utilidad práctica de los coeficientes Clebsch-Gordan para la interpretación de los resultados experimentales obtenidos en un laboratorio con experimentos de espectroscopía. dándonos las probabilidades de encontrar a los subestados de un sistema, tal vez haya quien se pregunte sobre la utilidad teórica que justifique el invertir algo de tiempo en el aprendizaje del teorema Wigner-Eckart. Para poder apreciar la utilidad teórica del teorema Wigner-Eckart, resultará provechoso recurrir a un ejemplo ilustrativo.
Supóngase que se quiere evaluar la siguiente integral:
que involucra el producto de tres armónicas esféricas, siendo la primera de ellas portadora de tres unidades de momento angular, siendo la segunda de ellas portadora de dos unidades de momento angular, y siendo la tercera de ellas portadora de una unidad de momento angular. Este tipo de integrales aparecen repetidamente en problemas de espectroscopía al intentar aclarar situaciones en los que la parte angular de la función de onda tiene efectos relevantes en el análisis de los resultados obtenidos en el laboratorio. El elemento infinitesimal es el que corresponde a un ángulo sólido que en coordenadas esféricas está dado por la relación:
La evaluación de la integral para la combinación de números cuánticos:
m1 = m2 = m3 = 0
resulta ser laboriosa. Usando las armónicas esféricas:
entonces se tiene el siguiente producto triple:
con lo cual se puede proceder a la evaluación de la integral (en coordenadas esféricas, sobre un ángulo sólido completo, esto es, sobre el interior angular sólido de toda la esfera unitaria; la integral sobre el ángulo φ es trivial siendo igual a 2π, mientras que la integral sobre el ángulo θ es la que requiere el trabajo pesado de evaluación y simplificación que no se muestra en detalle):
Y esto es apenas el principio de la dura tarea. Puesto que la primera armónica esférica es portadora de tres unidades de momento angular, m1 puede tomar siete valores distintos:
m1 = 3 , 2 , 1 , 0 , -1 , -2 , -3
Por su parte, la segunda armónica esférica es portadora de dos unidades de momento angular, con lo cual m2 puede tomar cinco valores distintos:
m2 = 2 , 1 , 0 , -1 , -2
Y la tercera armónica esférica es portadora de una unidad de momento angular, pudiendo por ello m3 tomar tres valores distintos:
m3 = 1 , 0 , -1
Esto significa que hay 7×5×3 = 105 combinaciones distintas de m1, m2 y m3, ¡105 integrales a evaluar! Aún con la ayuda de la regla de selección m para desechar de antemano aquellas integrales que terminarán siendo iguales a cero, el trabajo a llevarese a cabo se antoja duro y laborioso.
El teorema Wigner-Eckart nos permite escribir lo siguiente para la integral de las tres armónicas esféricas:
Puesto que la integral ya fue evaluada (laboriosamente), el trabajo efectuado nos permite evaluar el elemento matricial doble-barra del siguiente modo:
De este modo, todas las demás integrales a ser evaluadas, para cualquier combinación de números cuánticos magnéticos m1, m2 y m3, se pueden obtener del siguiente modo con la aplicación del teorema Wigner-Eckart:
En pocas palabras, el trabajo hercúleo de evaluación de todas las demás integrales restantes se reduce al cálculo de coeficientes Clebsch-Gordan, para lo cual hay disponibles muchas tablas y sitios de Internet así como programas computacionales.
Expuesta la mecánica del teorema Wigner-Eckart y expuestas las razones del por qué nos debe interesar tomar conocimiento del tema, procederemos a demostrar dicho teorema. El teorema será demostrado en una forma parecida a como se llevó a cabo arriba la demostración de la regla de selección m, excepto que en vez de utilizar el operador Jz del momento angular usaremos los operadores escalera J± del momento angular. El punto de partida es la siguiente relación fundamental (véase la entrada “Operadores tensoriales”):
Nuevamente, tomaremos lo anterior y lo aprisionaremos entre un bra de estado y un ket de estado a manera de “sandwich”:
En este punto, se vuelve necesario hacer un alto para reflexionar sobre lo que tenemos en el lado izquierdo de la expresión. Tenemos un operador escalera del momento angular J± (en realidad, dos operadores escalera, uno de ascenso y el otro de descenso) que puede actuar sobre un ket a su derecha elevando (o disminuyendo, en su caso) en una unidad el número cuántico magnético m del ket. Pero el operador escalera del momento angular J± también puede actuar sobre un bra a su izquierda elevando (o disminuyendo, en su caso) en una unidad el número cuántico magnético m del bra. Para llegar a esto, procediendo del mismo modo en que lo hicimos para demostrar la regla de selección m podemos desarrollar el conmutador de Born que aparece en el lado izquierdo de la expresión de arriba, obteniendo:
Trabajaremos primero sobre el segundo término de esto último recurriendo a la relación general que nos describe la acción del operador escalera J± sobre un estado del momento angular actuando sobre el ket que representa a dicho estado, (en esto no tomaremos en cuenta la parte radial α de la función de onda porque el operador escalera J± sólo actúa sobre la parte angular):
Adecuando esta relación general a la notación que estamos empleando, se tiene:
dándonos:
Por otro lado, trabajando ahora sobre el primer término de la expresión recurriendo a la misma relación general que nos describe la acción del operador escalera J± sobre un estado del momento angular actuando ahora sobre el bra que representa a dicho estado y que está a su izquierda, se tiene (¡precaución!, obsérvese la manera diferente en la que actúan los operadores escalera al hacerlo sobre un bra en comparación a como lo hacen cuando actúan sobre un ket):
dándonos:
De este modo, juntándolo todo y cancelando el factor ħ que es común a todos los términos, se llega a lo siguiente:
Esta es una expresión recursiva (de hecho, son dos expresiones recursivas, una de ellas se obtiene usando los signos aritméticos superiores en donde aparecen los signos dobles y la otra se obtiene usando los signos aritméticos inferiores) que nos permite obtener diversos elementos matriciales del operador tensorial partiendo de elementos matriciales ya conocidos. Y el lector astuto se habrá dado cuenta ya de que esta relación se parece mucho a las relaciones recursivas dadas arriba para los coeficientes Clebsch-Gordan (encerradas en un recuadro verde). Con la finalidad de evitar confusiones en virtud de que símbolos similares aparecen en lugares diferentes en los pares conjuntos de relaciones recursivas, modificaremos un poco la doble relación recursiva obtenida arriba para los elementos matriciales del operador tensorial T(k)q, escribiéndola de la siguiente manera (sigue siendo esencialmente la misma expresión):
El parecido entre ambas relaciones en verdad es sorprendente. Aunque se trata de cosas diferentes, podemos establecer de inmediato las siguientes correspondencias usando como punto común de referencia los factores que aparecen bajo las raíces cuadradas:
Hay una correspondencia directa uno-a-uno entre los coeficientes Clebsch-Gordan recursivos y los elementos matriciales recursivos:
Por otro lado, si en la relación que nos dá las dos expresiones recursivas para los coeficientes Clebsch-Gordan substituímos los números que se evalúan con las raíces cuadradas por K1, K2 y K3, obtenemos lo siguiente:
Esto nos genera una serie de ecuaciones lineares (de primer orden) homogéneas con coeficientes constantes. El conjunto completo de ecuaciones lineares nos dá la solución completa del sistema, con lo cual todos los coeficientes quedan especificados y con ello los subestados del sistema combinado de momentos angulares. Las ecuaciones lineares que se obtienen son de la forma:
Siempre que tenemos algo como:
no es posible resolver individualmente para los xj (o los yj). Sin embargo, podemos resolver para dos cocientes, de modo tal que:
o bien:
siendo c un factor universal de proporcionalidad. En este punto cabe observar que el cociente de dos coeficientes Clebsch-Gordan cualesquiera es un número independiente de los números cuánticos magnéticos m. Esto lo vimos claramente en el ejemplo dado arriba en donde:
En las relaciones recursivas Clebsch-Gordan, el objetivo es calcular un coeficiente Clebsch-Gordan cuando se conoce otro o cuando se conocen otros dos. En el caso del teorema Wigner-Eckart, el asunto es al revés, ya que se supone que todos los coeficientes Clebsch-Gordan son conocidos o se pueden obtener de algún lado sin necesidad de tener que evaluarlos, mientras que el objetivo aquí es calcular los elementos matriciales de un operador tensorial usando coeficientes Clebsch-Gordan y un elemento matricial doble-barra calculado convencionalmente una sola vez tras lo cual el cálculo de los elementos matriciales restantes del operador tensorial se reduce al cálculo de cocientes de coeficientes Clebsch-Gordan multiplicados por el elemento matricial doble-barra. Esto lo podemos hacer en virtud de que las relaciones recursivas para los elementos matriciales del operador tensorial T(k)q tienen esencialmente la misma forma y estructura que las relaciones recursivas para el cálculo recursivo de los coeficientes Clebsch-Gordan. Poniendo especial atención en la correspondencia:
y en base a las anteriores consideraciones, podemos reemplazar la correspondencia entre los coeficientes Clebsch-Gordan contiguos y los elementos matriciales del operador tensorial contiguos por una igualdad metiendo una constante de proporcionalidad que, siendo una constante, necesariamente debe ser independiente de los números cuánticos magnéticos (se ha actualizado la notación del coeficiente Clebsch-Gordan para que la correspondencia pueda tener sentido como igualdad):
De este modo, y en pocas palabras, un elemento matricial del operador tensorial:
tomado entre dos eigenestados del momento angular es igual a una constante de proporcionalidad universal que es independiente de los números cuánticos magnéticos m, q y m', o sea, el elemento matricial doble-barra, lo cual esencialmente demuestra el teorema Wigner-Eckart.
En rigor de verdad, el teorema Wigner-Eckart fue obtenido por vez primera de una manera más rigurosa y formal que como lo hemos hecho aquí (aunque menos fácil de entender) recurriendo a la Teoría de Grupos, las matemáticas de la simetría; ese fue el gran mérito de Eugene Wigner consignado en su libro clásico Gruppentheorie publicado en 1931, el darse cuenta que los operadores de rotación del momento angular tienen su contraparte en la representación matricial de un grupo, lo cual al emplear los grupos continuos de Sophus Lie lleva al empleo del lema de Schur y al eventual descubrimiento de los coeficientes Clebsch-Gordan como el recurso con el cual se pueden metodizar las propiedades básicas grupales de los operadores mecánico-cuánticos de rotación. La metodología empleada aquí en la derivación del teorema Wigner-Eckart está en cierto modo sobresimplificada, pero es suficiente para nuestros propósitos didácticos extrayendo de la teoría las ideas centrales que suelen ser obscurecidas innecesariamente por notación críptica y poco común.