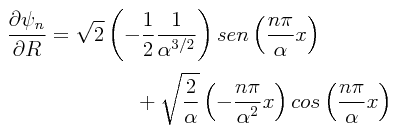Si el triángulo no es un triángulo geodésico, esto es, un triángulo que pueda ser acomodado sin hueco alguno sobre la superficie de una esfera (o sobre la superficie de un elipsoide, o sobre la superficie de un huevo, o sobre cualquier otro tipo de superficie que tenga una curvatura tridimensional), si el triángulo es un triángulo plano que pueda ser acostado por completo sobre una superficie de dos dimensiones como el siguiente triángulo escaleno:
entonces el plano de oscilación del péndulo de Focault no experimentará cambio alguno al llevarlo por la ruta ABCA, lo cual es fácil de verificar. Al llevar un péndulo de Focault oscilante a lo largo de una línea recta (en la figura de arriba, de A a B) y no a lo largo de una geodésica que puede ser un arco de un círculo máximo (un meridiano, por ejemplo), el plano de oscilación no experimenta cambio alguno (en el sentido más absoluto de la palabra), y lo mismo ocurre al tranportar el péndulo de Focault a lo largo de una trayectoria cerrada de cualquier superficie plana. La curvatura en el espacio tridimensional es el ingrediente esencial que permite que el plano de oscilación de un péndulo de Focault al ser transportado a lo largo del perímetro de un triángulo esférico vaya cambiando en forma detectable. Y resulta que este hecho tiene una contraparte directa en la Teoría de la Relatividad (véase la obra de este mismo autor bajo tal título). En un espacio-tiempo plano (de cuatro dimensiones) en donde no hay curvatura alguna, lo que rige es la Teoría Especial de la Relatividad, y el marco de referencia es lo que se conoce como Lorentziano, caracterizado por la ausencia total de gravedad. A partir del momento en el que hace su aparición un cuerpo con una gran cantidad de masa introduciendo gravedad en el espacio-tiempo, el espacio-tiempo que era plano adquiere una curvatura que antes era igual a cero, y la Teoría Especial de la Relatividad pierde su validez, teniendo que ser reemplazada por la Teoría General de la Relatividad. Puesto que, al igual que la fase de Berry en donde todo depende de la geometría, en la Teoría General de la Relatividad también todo depende de la geometría, a dicha teoría Einsteniana de la gravitación se le ha hecho pasar a formar parte de lo que se conoce como una geometrodinámica. El hecho de que la geometría y en particular la curvatura en el espacio multidimensional esté pasando a formar parte importante no sólo de la Teoría de la Relatividad sino también de la Mecánica Cuántica hace sospechar y suponer que aquí puede haber mucho mar de fondo más que simples coincidencias en base al entorno geométrico.
Se había mencionado también en la entrada anterior que algo extraordinario del péndulo de Focault es que con dicho péndulo se tiene, sin necesidad de tener que salir al espacio exterior en una nave para ver globalmente a la Tierra desde fuera, una manera de determinar la existencia de la curvatura de la superficie terrestre con observaciones puramente locales. En principio, y especificando los tres vértices de un triángulo de gran tamaño sobre la superficie de la Tierra (lo cual hace al experimento algo impráctico), es posible descubrir la existencia de la curvatura de la Tierra localmente con el solo hecho de desplazarse de uno a otro vértice hasta recorrer el perímetro completo del triángulo. Esto fue de hecho lo que descubrió el famoso matemático Carl Gauss con su theorema egregium, lo cual posiblemente habrá sorprendido al mismo Gauss, y se rumora incluso que Gauss llevó a cabo el experimento (aunque sin mucho éxito, en virtud de las distancias involucradas y la precisión instrumental requerida para poder detectar diferencias significativas). De este modo, además de la Geometría Analítica que nos describe globalmente la curva de una circunferencia de radio a con una fórmula como la siguiente:
x2 + y2 = a2
se tiene un nuevo esquema en el que la misma curva puede ser descrita localmente en la Geometría Diferencial con ecuaciones locales (sin recurrir en lo absoluto a ningún sistema específico de coordenadas) empleando diferenciales como los que se utilizan en las fórmulas de Frenet-Serret que afijan vectores unitarios a cada punto local de la curva, tales como el vector unitario tangente T a la curva y el vector unitario normal N. Para quienes han estado acostumbrados toda su vida a trabajar con ecuaciones algebraicas que tienen una representación gráfica directa en el sistema tridimensional de coordenadas rectangulares Cartesianas (o coordenadas esféricas, o coordenadas de cualquier otro tipo), la transición a la Geometría Diferencial puede ser desconcertante al desaparecer del horizonte las fórmulas con las cuales se puede jugar metiendo números directamente en las mismas, números que tienen una ubicación en el espacio tridimensional. Para dar una idea de la enorme diferencia que hay entre la Geometría Analítica y la Geometría Diferencial, considérese una curva espacial muy común, la hélice, como la siguiente:
Usando un sistema de coordenadas rectangulares Cartesianas, el vector posición r(t) que va trazando en el espacio la hélice mostrada en la figura está definido como:
siendo {i,j,k} vectores unitarios definidos a lo largo de los ejes Cartesianos {x,y,z} respectivamente. El caso más general de cualquier hélice de este tipo está dado por:
De lo anterior podemos obtener de inmediato las ecuaciones paramétricas de la hélice, definidas en un sistema de coordenadas rectangulares Cartesianas como:
Tenemos aquí, para todo el espacio, la colección entera posible de tripletes ordenados de números que definen cada punto en el espacio tridimensional por donde pasa la curva. En contraste, usando los métodos de la Geometría Diferencial, no cuesta mucho trabajo demostrar que la misma hélice puede ser definida mediante solo dos parámetros: su curvatura κ y su torsión τ:
Para el ejemplo que se tiene arriba, a.=.4 y p.=.1, con lo cual la curvatura y torsión de dicha hélice son:
Obsérvese que no hay referencia alguna a ningún “punto de origen” de referencia en el espacio como tampoco hay referencia a nada que nos pueda definir un triplete ordenado de números (x,y,z) que se ubicarían en relación al punto de origen O usual de las coordenadas rectangulares Cartesianas, y de hecho no hay referencia alguna a ningún tipo de coordenadas. Es una nueva geometría por completo, con nuevas reglas del juego. Obsérvese que si en el ejemplo hacemos la torsión p igual a cero, entonces la curva resulta ser una curva cerrada, una círculo de radio a, con una curvatura κ.=.1/a. En general, una curva es una curva plana si y solo si su torsión es igual a cero.
La importancia actual de la Geometría Diferencial es tal que ha adquirido un nivel de sofisticación superior al evolucionar hacia lo que hoy es conocido como el Cálculo Exterior o Cálculo de las Formas Diferenciales, siendo el concepto de la forma diferencial una generalización sobre ideas previas como el gradiente, la divergencia, el rotacional, etc., con la notación moderna empleada en el estudio de las formas diferenciales debido a Elie Cartan introduciendo el uso de conceptos tales como el producto cuña, la derivada exterior, las 1-formas y las 2-formas, material matemático que puede ser intimidante para quien lo enfrenta por vez primera sin la ayuda y los consejos de un buen instructor. Desafortunadamente, con la creciente sofisticación matemática se corre el riesgo de ir perdiendo de vista el “gran panorama” pudiéndose pasar por encima de cosas de importancia fundamental, a grado tal que en unas cinco décadas alguien podría estar diciendo lo siguiente sobre algo importante que está siendo pasado por alto hoy por estar ahogados en un exceso de rigorismo notacional: “esto debería haber sido descubierto hace 50 años”.
Si bien el ejemplo comunmente citado relacionado con el transporte paralelo de un péndulo de Focault se basa en un recorrido con el péndulo oscilante a lo largo del perímetro de un triángulo geodésico, la trayectoria en realidad puede ser cualquier tipo de trayectoria cerrada C que se lleve a cabo sobre la superficie de la esfera, una trayectoria como la siguiente:
En la entrada anterior vimos el caso de una partícula encerrada en una caja, una de cuyas paredes se va moviendo lentamente aumentando la anchura de la caja. Retomaremos aquí dicho ejemplo, y partiendo de la relación:
determinaremos el cambio que tiene lugar en la fase geométrica cuando la caja se expande adiabáticamente de una anchura α1 a una anchura α2. Empezaremos con la función de onda para dicha caja:
En este caso, en la aplicación de la fórmula para la obtención de γn(t), se tiene R.=.α. Con esto, tomando diferenciales, podemos afirmar que:
Por lo tanto:
Para simplificar, podemos recurrir a la identidad trigonométrica con la cual se puede escribir:
De este modo:
Por lo tanto, se deduce que γn(t).=.0. En palabras, la fase geométrica se desvanece. En esto tuvo algo que ver el hecho de que las eigenfunciones de onda ψn(x) para una partícula encerrada en una caja son eigenfunciones de onda reales, esto es, no tienen anexado un factor de fase como en el caso de la siguiente función de onda:
Obsérvese que inclusive si la función de onda es puramente imaginaria al aplicar el criterio de Born para determinar la densidad de la probabilidad lo imaginario deja de tener relevancia, lo cual permite incluir en cualquier análisis funciones de onda imaginarias o complejas y no solamente funciones de onda reales:
Será formalizado más abajo el hecho de que si las eigenfunciones de onda son reales (como en este ejemplo), la fase geométrica se desvanece. Habiendo calculado el cambio en la fase geométrica que resultó ser igual a cero, ahora calcularemos el cambio el cambio de la fase dinámica θn(t) suponiendo para ello que la expansión de la anchura de la caja ocurre a una velocidad constante:
Tomando como punto de partida la definición de la fase dinámica:
se tiene entonces para la partícula encerrada en una caja que:
Efectuando un cambio de variable, se tiene entonces:
Obviamente por lo que vimos en este problema, si la anchura de la caja es regresada adiabáticamente (lentamente) a su tamaño original, la fase de Berry para este ciclo será igual a cero.
Veamos ahora otro ejemplo, el del pozo de potencial delta definido como:
Este pozo de potencial admite un (y solo uno) estado ligado. Calcularemos el cambio en la fase geométrica cuando el factor α (que no debe ser confundido con la anchura de la caja que usamos en el ejemplo anterior) cambia de α1 a α2. Para el pozo de potencial δ, una vez que se ha resuelto la ecuación de Schrödinger para este potencial, se tiene como eigenfunción de onda ψ(x) y como el eigenvalor de energía lo siguiente:
En este caso, en la aplicación de la fórmula para la obtención de γn(t), se tiene R.=.α. Con esto, tomando diferenciales, podemos afirmar que:
Desarrollando:
Por lo tanto:
y nuevamente, como en el ejemplo anterior, se tiene que γn(t).=.0, y la fase geométrica se desvanece. También para este ejemplo se cumple que si las eigenfunciones de onda son reales, la fase geométrica se desvanece. ¿Es esto algo que se aplica únicamente para estos dos ejemplos, o hay mar de fondo en ello? Mientras reflexionamos sobre ello, calcularemos el cambio de la fase dinámica θn(t) suponiendo que el cambio de de α1 a α2 ocurre a una velocidad constante:
para lo cual, usando el valor de la eigenenergía para el único estado ligado que hay en este sistema, se tiene:
Se ha visto en los dos ejemplos anteriores que si las eigenfunciones de onda son reales, la fase geométrica se desvanece. Procederemos a demostrar este hecho a continuación recurriendo a la definición general de la fase geométrica que se obtuvo en la entrada anterior:
Usaremos el hecho de que, en todo momento, el conjunto base de funciones ortonormales permanece ortonormal:
Aplicando el operador nabla ∇R (tal y como se definió para el espacio-R) sobre esta igualdad, se tiene con la ayuda de la regla del producto:
Para que esto sea cierto, se requiere que:
sea puramente imaginario, y si la función de onda ψn es real, entonces debe ser no imaginario sino cero. Pensando en tal posibilidad, le anexaremos a la función de onda ψn que consideramos real un factor de fase como el que se muestra a continuación formando una nueva función de onda ψ’n que ya no será real:
Aplicamos el operador ∇R a ambos lados de esta relación obteniendo nuevamente con la ayuda de la regla del producto:
Formando un producto interno bra-ket con esto, se tiene:
Por lo tanto:
De esto podemos sacar una conclusión inmediata: para una trayectoria que se lleve a cabo sobre un bucle cerrado entonces:
El resultado obtenido también nos dice que:
Esto nos confirma que la función de onda terminó recogiendo un factor de fase hasta cierto punto trivial cuyo único papel fue el de cancelar el factor de fase que habíamos anexado manualmente como:
De este modo, podemos afirmar finalmente lo siguiente para la evolución temporal del estado del sistema:
Por todo lo anterior, se puede ver que para poder obtener una fase de Berry que no sea idénticamente igual a cero se requieren dos cosas: (1) que haya más de un parámetro dependiente del tiempo en el Hamiltoniano, y (2) que el Hamiltoniano sea uno capaz de generar no eigenfunciones de onda reales sino eigenfunciones imaginarias o complejas como soluciones a la ecuación de Schrödinger.
Puesto que, más que alguna dependencia explícita del Hamiltoniano en la variable tiempo, lo relevante es una dependencia del Hamiltoniano en parámetros (simbolizados aquí como R) que a su vez varían con el tiempo, una notación algo más correcta que H(t) vendría siendo H(R) o simplemente H(R) cuando en lugar de un vector R de varios parámetros que varían con el tiempo hay un solo parámetro R que está variando con el tiempo.
siendo f(t) una función general a ser especificada. Obsérvese que, por la forma en la que está definida, la función f(t) tiene las dimensiones de longitud. Como ya hemos visto, en la Mecánica Cuántica no se manejan los conceptos de las fuerzas, se utilizan las energías, los campos y los Hamiltonianos. En este caso, para el oscilador armónico simple que está siendo sometido a una fuerza como la que se acaba de definir, el Hamiltoniano viene siendo:
Como puede verse, la inclusión de una fuerza externa hace que el Hamiltoniano varíe con el tiempo. Supondremos que la fuerza f(t) comienza a ser aplicada al oscilador en un tiempo t.=.0, lo cual implica que f(t).=.0 para t.≤.0. Empezaremos por comprobar que, si el oscilador se encuentra en la posición inicial x(0).=.0 en un tiempo t.=.0, y si la velocidad inicial es dx(0)/dt.=.0, entonces la posición clásica en cualquier tiempo t estará dada por:
Esta relación ciertamente cumple con lo que se pide para t.=.0:
Para la velocidad instantánea se tiene (¡precaución!: obsérvese que se está derivando una expresión que contiene un símbolo integral, teniéndose que aplicar la regla de la cadena en forma adecuada por haber dos funciones derivables dentro del símbolo integral, la función f(t) y la función senoidal):
de lo cual vemos que se cumple la otra condición requerida para la velocidad instantánea:
Tomando la segunda derivada con respecto al tiempo de la posición clásica, se tiene para la aceleración:
En base a las leyes del movimiento de Newton, la ecuación del movimiento para el oscilador armónico simple forzado debe ser:
De acuerdo a lo que se obtuvo aquí con la solución xclasica propuesta, se tiene:
Se concluye entonces que la expresión xclasica propuesta es realmente una solución exacta al problema clásico del oscilador armónico simple forzado.
A continuación analizaremos la misma situación, pero usando un enfoque mecánico-cuántico. Veremos primero que la solución a la ecuación de Schrödinger dependiente del tiempo para este oscilador, suponiendo que empezó en el n-avo eigenestado del oscilador armónico simple antes de que le fuera aplicada la fuerza externa, o sea:
Ψ(x,0) = ψn(x)
estará dada ahora por la siguiente expresión (por cuestiones de espacio y para evitar complejidad innecesaria, usaremos la abreviatura “clas” en lugar de “clasica”):
Puesto que arrastrar el término exponencial de esta relación en una derivación resulta engorroso y superfluo, efectuaremos la siguiente simbolización simplificadora:
También, por cuestiones de espacio y para evitar complejidad innecesaria, haremos la siguiente substitución de variable:
ξ = x - xclas
con lo cual:
ψn(x - xclas) = ψn(ξ)
Para confirmar que la expresión proporcionada arriba para Ψ(x,t) realmente es una solución legítima a la ecuación de Schrödinger:
hay que evaluar ∂Ψ/∂t, ∂Ψ/∂x y ∂2Ψ/∂x2. Empezaremos con ∂Ψ/∂t:
Los términos ubicados dentro de los paréntesis rectangulares pueden ser simplificados a lo siguiente:
Por lo tanto:
Ahora procederemos con ∂Ψ/∂x:
Tomando la segunda deriva de lo anterior, ∂2Ψ/∂x2, se tiene:
Tenemos ya todo lo que necesitamos para poder calcular la acción del operador Hamiltoniano H sobre la función de onda Ψ:
Teniendo en cuenta que:
estamos por fin en condiciones de recurrir a la ecuación de Schrödinger:
para comprobar la validez de la solución mecánico-cuántica propuesta para el oscilador armónico simple cuando es sometido a la acción de una fuerza externa:
Esto se puede simplificar a lo siguiente:
que a su vez se puede simplificar a:
Pero esto último es precisamente la condición que se había estipulado arriba. Se concluye que la solución dada al inicio es una solución mecánico-cuántica al oscilador armónico simple cuando es sometido a la acción de una fuerza externa.
Si escribimos el operador Hamiltoniano como:
y desplazamos el origen del sistema de coordenadas de la siguiente manera:
μ = x - f
el Hamiltoniano relocalizado se puede escribir entonces como:
El término destacado en color azul es un oscilador armónico simple en la variable μ, mientras que el término destacado en color magenta es una constante (con respecto a la variable posición definida como μ). De este modo, las eigenfunciones de onda son simplemente ψn(μ), y no varían explícitamente con el tiempo, pudiendo escribirse entonces como:
ψn(x,t) = ψn(x - f)
mientras que los eigenvalores de energía son los que corresponden al oscilador armónico simple redefinido menos lo que viene siendo una energía constante:
A continuación veremos que, en la aproximación adiabática, la posición clásica:
se reduce a xclasica(t).≈.f(t). Para ello, usaremos el hecho de que:
con lo cual:
Llevando a cabo una integración por partes tomando en cuenta para ello que f(0).=.0:
Para que el comportamiento del oscilador armónico simple bajo la acción de una fuerza externa pueda ser considerado adiabático, se requiere que df/dt sea muy pequeño, o lo que es lo mismo, para todos los valores de t’ comprendidos entre t.=.0 y t.=.t:
Esto hace que lo que se obtenga con el procedimiento de integración sea despreciable en comparación con f(t), teniéndose por lo tanto:
Podemos darle una interpretación física a esto, tomándolo como el equivalente a jalar (o empujar) ligeramente el resorte del oscilador armónico simple de modo tal que no se introducen oscilaciones acopladas adicionales al modo de oscilación fundamental, de modo tal que la masa m se mueve como si estuviera unida a una cuerda de longitud fija.
Metiendo la aproximación obtenida xclasica(t).≈.f(t) en la solución mecánico-cuántica del problema del oscilador armónico simple que se encuentra bajo la influencia de una fuerza externa, se tiene:
Para la fase dinámica se tiene:
Comparando expresiones, resulta evidente que la función de onda Ψ(x,t) puede escribirse como:
viéndose que la fase geométrica está dada por:
Aquí puede surgir una duda, ya que las eigenfunciones de onda no son imaginarias ni complejas, son reales, y por lo tanto de acuerdo a lo que se ha estado discutiendo arriba, la fase geométrica debería ser igual a cero. Lo que cabe destacar aquí es que, en el límite de la aproximación adiabática, df/dt es muy pequeño, y por lo tanto en este límite la expresión:
con lo cual la fase geométrica toma el valor de cero al menos en la región de x en donde ψn(x,t) es diferente de cero.
Antes de que se conociera todo lo que se ha discutido aquí, estábamos acostumbrados a pensar que la fase de una función de onda es arbitraria porque las cantidades físicas que se observan en el laboratorio tienen que ver con la densidad de probabilidad |Ψ|2 en cuya evaluación se cancela el factor de fase. Por esto mismo, se suponía que la fase geométrica carecía de significado físico habido el hecho de que la fase de ψ(x) es arbitraria. El mérito de Michael Berry consiste en haberse dado cuenta de que si el Hamiltoniano es transportado a lo largo de una trayectoria cerrada devolviéndolo a su forma original, la fase relativa al inicio y al final del proceso no es arbitraria y de hecho es algo susceptible de ser medido en el laboratorio. Supóngase que tomamos un haz de partículas y lo sub-dividimos en dos fases, de modo tal que uno de ellos pase a través de un potencial adiabáticamente cambiante mientras que el otro no. Al ser recombinados los dos hacer, la función total de onda es:
siendo ψ0 la función de onda inalterada y siendo Γ la fase adquirida, en parte dinámica y en parte geométrica, adquirida por el haz sometido al Hamiltoniano variante. En tal caso:
De este modo, buscando puntos de interferencia constructiva e interferencia destructiva en donde Γ es un múltiplo par o impar de π, respectivamente, se puede medir Γ con facilidad. Aunque Berry y otros manifestaron una preocupación de que la fase geométrica pudiera ser fuertemente opacada por la fase dinámica, ha sido posible arreglar las cosas de modo tal que se puedan separar ambos efectos. Suponiendo que el espacio paramétrico R de la fase de Berry sea tridimensional, o sea:
R = (R1, R2, R3)
entonces la fórmula para la fase de Berry:
es reminiscente de la relación para el flujo del campo magnético B expresado en función del potencial vectorial A. La fórmula demostrada en la teoría electromagnética nos dice que el flujo Φ a través de una superficie S acotada por una cuva de contorno C es:
siendo da un elemento infinitesimal de superficie atravesada por el campo magnético en esa región infinitesimal. Esto lo podemos ver mejor ilustrado en la siguiente figura:
Si escribimos al vector campo magnético B en función del potencial vectorial A de la manera siguiente:
obteniéndolo mediante la operación que en el Anásisis Vectorial se conoce como el rotacional del campo vectorial A, entonces podemos escribir el flujo Φ como la siguiente integral de superficie:
La integral de superficie, usualmente de engorrosa evaluación, puede ser reemplazada con una integral de línea o integral de contorno apelando al teorema de Stokes:
Por lo tanto:
Estableciendo comparaciones, esto nos permite imaginarnos a la fase de Berry como una especie de “flujo de campo magnético Berry”:
llevando a cabo la integral de línea a lo largo de una trayectoria cerrada en el espacio paramétrico R. Esto a su vez implica que debe ser posible escribir la fase de Berry en un caso tridimensional como una integral de superficie:
Veamos ahora otro ejemplo, esta vez el de un electrón en reposo situado en el origen de un sistema de coordenadas rectangulares Cartesianas, que es sometido a la acción de un campo magnético cuya magnitud B0 es constante pero cuya dirección describe un cono a una velocidad angular ω con un ángulo de apertura α:
Este es un caso que ya estudiamos con anterioridad en la entrada “La funcion de onda del momento angular del spin”. Usando el conjunto usual de vectores unitarios de base {i,j,k}, el vector campo magnético B(t) se puede describir de la siguiente manera:
Usando las matrices de Pauli σx , σy y σz, el operador Hamiltoniano H del sistema se puede expresar del siguiente modo:
en donde:
Para escribir las dos funciones de onda que corresponden como soluciones al Hamiltoniano de arriba, usaremos la letra griega χ (.ji) que se acostumbra usar para las funciones de onda del spin o espinores:
las cuales representan respectivamente al spin apuntando “hacia arriba” y al spin apuntando “hacia abajo” a lo largo de la dirección instantánea del vector de campo magnético B(t). Los eigenvalores de energía correspondientes son:
Suponiendo que en el tiempo t.=.0 para B(0) el electrón se encuentra en el estado en que su spin está apuntando “hacia arriba”, se tiene:
Para el Hamiltoniano dado arriba, y procediendo del mismo modo como se procedió para verificar la validez de la solución a la ecuación de Schrödinger dependiente del tiempo para el oscilador armónico simple sometido a una fuerza externa, no cuesta mucho trabajo verificar que la solución a la ecuación de Schrödinger en este caso es:
en donde por razones de simplicidad se ha definido a λ como:
La función de onda espinorial puede ser expresada del siguiente modo emplando a los espinores de base:
La probabilidad de que ocurra una transición de la condición del spin apuntando “hacia arriba” a la condición del spin apuntando “hacia abajo” está dada por:
De acuerdo al teorema adiabático, esta probabilidad de transición de un estado a otro debe desvanecerse en el límite Text.».Tint en donde Text es el tiempo “exterior” característico para que ocurran los cambios en el operador Hamiltoniano y que en este caso viene siendo 1/ω, y Tint es el tiempo “interior” para que ocurran cambios en la función de onda y que en este caso viene siendo:
Y todo esto implica que la condición para la validez de la aproximación adiabática viene siendo ω.«.ω1, en cuyo caso el campo magnético que describe al cono gira lentamente en comparación con la fase de las funciones de onda espinoriales no-perturbadas. Para el caso contrario, ω.».ω1, con la consecuente λ.≈.ω, el sistema rebota periódicamente de la condición de spin apuntando “hacia arriba” a la condición de spin apuntando “hacia abajo”.
En el régimen adiabático ω.«.ω1, cuando el campo magnético efectúa lentamente un movimiento de precesión en torno al eje-z, de lo anterior se tiene:
con lo cual se tiene a la vez:
Conforme ω/ω1.→.0, el segundo término se vuelve insignificante, y lo que se obtiene coincide con la forma adiabática anticipada que hemos estado encontrado anteriormente en donde un exponencial representa la fase dinámica y el otro exponencial representa la fase geométrica:
Estableciendo comparaciones, podemos ver que la fase dinámica es:
en donde E+ es el eigenvalor de energía dado más arriba para el estado en el que el spin está apuntando “hacia arriba”, y continuando con las comparaciones, se deduce que la fase geométrica está dada por:
Para un período (o ciclo completo) T.=.2π/ω, la fase de Berry será:
A continuación consideraremos el caso más general en el cual la punta del vector del campo magnético recorre una curva arbitraria sobre lo que vendría siendo la superficie de una esfera de radio B0. En tal caso, puede demostrarse que el eigenestado que corresponde al spin “apuntando hacia arriba” a lo largo de B(t) está dado por:
en donde como puede verse se está recurriendo ahora a coordenadas esféricas en lugar de coordenadas rectangulares Cartesianas. Obsérvese que, siendo el radio de la esfera constante, las coordenadas esféricas θ y φ ambas son funciones del tiempo. Aplicando a la función de arriba el operador nabla para obtener el gradiente, se tiene:
Por lo tanto, formando el producto bra-ket de esto último con χ+, se tiene:
El rotacional vectorial de esta cantidad es:
De este modo, recurriendo a la expresión obtenida arriba (enmarcada en recuadro verde) para la evaluación de la fase de Berry:
se tiene:
La integral se lleva a cabo sobre una superficie “barrida” y encapsulada por el contorno de la trayectoria sobre una ruta cerrada de la punta del vector del campo magnético B que se desplaza sobre la superficie de la esfera en el transcurso de un ciclo completo, de modo que:
Se concluye por lo tanto que:
Este resultado nos dice, de una manera sencilla, que si tomamos un imán y movemos adiabáticamente el spin de un electrón en una trayectoria arbitraria (siempre y cuando se trate de una trayectoria cerrada, sin brechas), el cambio neto en la fase geométrica será igual a menos un medio del ángulo sólido que es cubierto por el movimiento del vector de campo magnético. Aquí podemos formularnos una pregunta interesante: ¿Cuál sería el resultado obtenido para una partícula cuyo spin sea igual a 1 en lugar del electrón cuyo spin es igual a 1/2? Para responder a ello, usamos nuevamente el campo magnético rotatorio:
pero en esta ocasión recurrimos a las matrices Sx , Sy y Sz definidas de la siguiente manera:
con las cuales el operador Hamiltoniano H del sistema se puede expresar del siguiente modo:
Montando la eigenecuación para la función de onda espinorial :
con el siguiente vector columna de tres componentes (a ser evaluados) para la representación de los elementos del eigenespinor:
la eigenecuación nos produce entonces:
o bien:
Esto nos conduce directamente a un conjunto de tres ecuaciones simultáneas:
Al resolver el conjunto de ecuaciones simultáneas, se encuentra que una de ellas es redundante. Normalizando los componentes obtenidos para el eigenespinor tenemos como solución posible:
De este modo, se tiene como eigenespinor al siguiente vector columna:
Evaluando sucesivamente primero ∇χ+ y tras esto el producto interno bra-ket que necesitamos usando a χ+ como bra, se tiene:
y:
Por lo tanto, recurriendo nuevamente a la expresión obtenida arriba (enmarcada en recuadro verde) para la evaluación de la fase de Berry:
se obtiene:
Se pueden generalizar los resultados obtenidos para una partícula de spin s.=.1/2 y una partícula de spin s.=.1 hacia una partícula cualquiera de spin s, enunciando que la fase geométrica para una partícula tal será:
Veamos algo que posiblemente había quedado pendiente como interrogante en la entrada anterior al recurrir al péndulo de Focault para establecer comparaciones. Vimos que el plano de oscilación de un péndulo de Focault manifestará un giro completo de 360° (regresando a su alineación original con el meridiano terrestre al cual estaba alineado al empezar) en el transcurso de una rotación completa de la Tierra cada 24 horas si mantenemos el péndulo fijo en el espacio mientras la Tierra va girando debajo del péndulo. Y el plano de oscilación del mismo péndulo permanecerá igual si el péndulo es colocado sobre el Ecuador terrestre. ¿Pero qué sucede si se coloca un péndulo de Focault en algún lugar situado entre el polo Norte y el Ecuador?:
El sentido común nos dice que al completarse un ciclo diurno de 24 horas, el plano de oscilación habrá girado un cierto ángulo comprendido entre cero grados y 360°, ¿pero qué tanto? Más que indagar sobre el ángulo de giro en sí del plano de oscilación del péndulo, resulta conveniente percatarse de que al completarse un giro completo de la Tierra, lo cual coloca al péndulo sobre el mismo punto geográfico con el que coincidía 24 horas antes, en virtud de la rotación se habrá abarcado un ángulo sólido Ω que a su vez define un cono:
Si usamos un sistema de coordenadas esféricas, entonces definiendo como θ al ángulo subtendido entre un lado del cono y el eje central del cono (que vendría siendo el polo Norte):
entonces podemos calcular la magnitud del ángulo sólido Ω del cono que se genera cuando el péndulo está situado a una distancia angular θ del polo Norte cuando se ha efectuado una trayectoria completa, cerrada y sin brechas al haber girado la Tierra 360°:
De este modo, relativo a la Tierra al haber dado ésta un giro completo, podemos ver que la precesión diaria del plano de oscilación d un péndulo de Focault es igual a 2πcos(θ0). De acuerdo a este resultado, si el ángulo θ0 es igual a cero (con el plano de oscilación del péndulo justo encima del polo Norte), entonces la precesión diaria será igual a 2π radianes cada 24 horas, justo lo que esperaríamos, y si el ángulo θ0 es igual a 90 grados, entonces no habrá precesión alguna, el plano del péndulo se mantendrá todo el tiempo en la misma posición original en la que estaba. En los textos de mecánica clásica este mismo resultado se obtiene de manera muy rebuscada apelando a las fuerzas de Coriolis (las cuales dicho sea de paso en realidad son fuerzas ficticias inventadas para compensar por los efectos no-inerciales debidos a la rotación de la Tierra), aunque como puede verse todo es cuestión de geometría. En la primera figura dada arriba (al principio de esta entrada) se usó como trayectoria cerrada un triángulo geodésico trazado sobre la superficie de la Tierra para marcar el recorrido del péndulo de Focault cuyo plano de oscilación termina desfasándose al completarse una trayectoria cerrada sobre el perímetro del triángulo geodésico, mientras que aquí la trayectoria cerrada se lleva a cabo sobre un círculo. En realidad, cualquier recorrido cerrado llevado a cabo sobre la superficie de la Tierra generará un ángulo sólido Ω, aunque el espacio angular sólido subtendido no tenga forma de cono, como en el caso de la siguiente trayectoria llevada a cabo sobre el perímetro de un cuadrángulo esférico:
Otra trayectoria interesante es la de una lúnula:
La lúnula mostrada puede ser considerada como formada por dos triángulos geodésicos, el triángulo esférico APF cuyo recorrido genera un desfase ΩF, y el triángulo esférico PSA cuyo recorrido genera un desfase ΩS. Se puede sospechar desde un principio que el desfase total Ω para la trayectoria ASPFA será el mismo que el desfase para la trayectoria APSAFPA, aunque algo como esto tiene que ser demostrado, usando provechosamente las herramientas de cálculo proporcionadas por la Geometría Diferencial, como también puede indagarse qué relación pueda haber entre ΩF, ,ΩF y Ω. Relaciones de este tipo pueden ser puestas a prueba en experimentos de laboratorio, principalmente con haces luminosos polarizados.
Lo importante en todo caso es la trayectoria cerrada que se lleve a cabo sobre la superficie de la Tierra que definirá a su vez la amplitud del desfase angular entre el inicio y el final del recorrido. Lo que en estos ejemplos que hemos estudiado en los que el sistema físico no regresa a su mismo estado original (idéntico, sin desfasamientos) al completarse un recorrido cerrado a lo largo de un bucle es conocido como un sistema no-holonómico.
PROBLEMA: Usando como referencia la primera figura dada al principio de esta entrada, determínese el ángulo de fase que se pueda acumular cuando sobre el triángulo geodésico ABC se lleva a cabo uno de los siguientes deplazamientos: (1) de A a C y de C a A; (2) a lo largo de la trayectoria ACBABCA.
(1) El recorrido de A a C y de regreso de C a A constituye una trayectoria cerrada, puesto que al final del recorrido se vuelve al punto de partida. Sin embargo, a tal trayectoria no corresponde ángulo sólido Ω alguno. Siendo Ω igual a cero, el ángulo de fase es también igual a cero.
(2) El recorrido a lo largo de la trayectoria ACBABCA (recorriendo los vértices del triángulo geodésico en ese orden) se puede subdividir en la suma acumulada de dos trayectorias cerradas. La primera es la trayectoria cerrada ACBA, debajo de la cual hay un ángulo esférico Ω; seguida de la trayectoria cerrada ABCA debajo de la cual hay un ángulo esférico de la misma magnitud pero de signo contrario. Al sumar ambos ángulos sólidos, el ángulo sólido neto es por lo tanto igual a cero:
(+Ω) + (-Ω) = 0
y por lo tanto la fase acumulada es también igual a cero. Esto significa que -suponiendo un globo terráqueo estático- si se lleva un péndulo de Focault del Ecuador al Polo Norte a lo largo de cierto meridiano, bajando posteriormente al Ecuador a lo largo de otro meridiano para recorrer tras esto el Ecuador regresando así al punto de partida, y se recorre la misma ruta pero al revés, al final del recorrido combinado el plano del péndulo de Focault estará en la misma alineación que tenía antes de llevarse a cabo el recorrido combinado. Esto nos muestra la importancia que pueden tener los signos que se le asignen a los ángulos sólidos Ω que formen parte de un recorrido combinado en la evaluación del ángulo de fase cumulativo.
En la entrada anterior se había mencionado que el físico hindú Shivaramakrishnan Pancharatnam se había adelantado al trabajo de Michael Berry basándose en la esfera de Poincaré en sus estudios de lo que hoy conocemos como la fase geométrica relacionados con el comportamiento de haces polarizados de luz. Si Pancharatnam se hubiera aferrado rigurosamente al concepto mecánico-cuántico de la dualidad onda-partícula y basándose en el modelo cuántico de las ondas electromagnéticas como fotones discretos de luz, postulando en base a ello la validez de su obra para partículas de materia, posiblemente habría acaparado de inmediato la atención de muchos científicos de su era. De cualquier modo, su obra continúa siendo ampliamente utilizada en trabajos técnicos especializados de óptica. La siguiente figura nos muestra lo que es esencialmente una esfera de Poincaré así como los ejes Cartesianos que denotan la polarización luminosa P en cada eje:
No debe causar extrañeza que al cono que abarca el ángulo sólido en esta figura se le conozca como cono de Berry.
La aplicación del teorema adiabático no debe llevarse a cabo ciegamente en todos los tipos de situaciones bajo la creencia de que está a prueba de fallos. En trabajos tales como el de Karl-Peter Marzlin y Barry C. Sanders publicado en arXiv en agosto de 2004 bajo el título “Inconsistency in the application of the adiabatic theorem” (en donde con un ejemplo de un sistema de dos niveles con una evolución exactamente soluble los autores demuestran la inaplicabilidad de la aproximación adiabática para cierto Hamiltoniano que varía lentamente pero en el cual el cambio en el eigenestado es significativo lo cual impacta en la validez y aplicabilidad de la aproximación adiabática), se puede apreciar que habrá casos en los cuales la aproximación adiabática se cae por tierra, lo cual no le resta su utilidad en muchos otros casos en donde ha probado ser de gran utilidad. Otros trabajos como el elaborado por Mario Frasca bajo el título “Consistency of the adiabatic theorem and perturbation theory” publicado también en arXiv en julio de 2011 hacen ver que la aproximación adiabática debe ser considerada como el término de orden mayor de una serie de perturbación, y que es capaz de sostenerse en el régimen de una perturbación que se extiende hasta el infinito, de modo tal que las condiciones para su validez se deben obtener yendo a términos de órdenes mayores en la expansión y removiendo los términos seculares, o sea los términos que se van hasta el infinito conforme va aumentando el tiempo. Esto ha sido formalizado de manera rigurosa y puesto sobre bases matemáticas firmes en obras tales como el libro “Adiabatic Perturbation Theory in Quantum Dynamics” de Stefan Teufel (publicado por la editorial Springer en 2003).
Así pues, como lo hemos visto, la holonomía cuántica es el análogo cuántico del efecto de rotación que ocurre cuando un vector es transportado paralelamente (o para mayor claridad, cuando un péndulo de Focault es desplazado de un punto a otro sobre la superficie de un globo terráqueo, con el plano del péndulo conteniendo el vector imaginario que es transportado imaginariamente junto con el péndulo) a lo largo de un bucle cerrado no sobre una superficie plana sino sobre una superficie curva. Tal rotación global sin rotación local es la holonomía ocasionada por la curvatura del espacio subyacente. En la Mecánica Cuántica, como lo hemos visto ya, los estados son representados como vectores (bras y kets) en un espacio de Hilbert, y las rotaciones de tales vectores se obtienen aplicándoles matrices unitarias o factores de fase. Tal y como ocurre en el caso de la Geometría Diferencial, un vector de estado cuántico puede ser transportado a lo largo de una trayectoria-bucle cerrada en algún espacio paramétrico cuántico sin producirle rotación local alguna, y la transformación resultante tiene el mismo efecto sobre el vector de estado que la aplicación de una matriz unitaria.
Además de los ejemplos ya mencionados, hay otro fenómeno cuántico al cual se le puede dar una explicación recurriendo a la fase de Berry. Se trata del efecto Aharonov-Bohm, en donde una partícula con carga eléctrica que está confinada dentro de una caja sellada adquiere una fase geométrica al llevarla lentamente alrededor de un flujo magnético, siendo este un fenómeno detectable experimentalmente. Tal y como ocurre en las holonomías de otros tipos, esta fase surge en la evolución adiabática para eigenespacios no-degenerados de los operadores Hamiltonianos. De hecho, la fase de Berry puede ser visualizada como una holonomía cuántica adiabática restringida a un eigenespacio unidimensional de energía.
Poco tiempo después del anuncio del descubrimiento del factor de fase de Berry, en un trabajo elaborado por Yakir Aharonov (uno de los descubridores del efecto Aharonov-Bohm) y Jeeva Anandan bajo el título “Phase change during a cyclic quantum evolution” publicado el mes de abril de 1987 en el Physical Review Letters, la fase de Berry fue redefinida y generalizada para cualquier evolución cíclica de un sistema cuántico con un nuevo factor de fase geométrico que es independiente de los vectores de estado inicial y final así como del Hamiltoniano. Esta nueva definición utiliza el hecho de que las fases geométricas también se pueden acumular en procesos que no sean adiabáticos, como en casos en donde los parámetros en el Hamiltoniano (por ejemplo, el campo magnético producido por un sistema de spin 1/2) varían rápidamente con el tiempo, provocando transiciones entre distintos niveles de energía. Estas fases son determinadas por propiedades geométricas de bucles en el espacio de estados, tales como el espacio que representa la dirección del spin cuántico, en lugar de bucles en un espacio en donde los parámetros varían lentamente como la dirección del campo magnético en rotación en el escenario de fase Berry que corresponde al ejemplo del sistema spin 1/2.
Si la aproximación adiabática puede ser considerada como el primer término de una serie adiabática para los coeficientes cm(t) de la ecuación:
entonces en una forma parecida a la manera en la cual en el estudio del esparcimiento de partículas la aproximación de Born pudo ser mejorada considerándola como una primera aproximación y mejorando dicha aproximación con una aproximación de segundo orden y puede ser mejorada aún más con una aproximación de tercer orden y así sucesivamente en lo que se conoce como una serie de Born (véase la entrada “La aproximación de Born III”), podemos empezar con el hecho de que un sistema que empieze en el n-avo eigenestado en la aproximación adiabática se mantendrá en el n-avo estado y recogerá además un factor de fase de la siguiente manera:
Substituyendo esto en el lado derecho de la relación que ya se obtuvo previamente:
se obtiene lo que puede considerarse como una “primera corrección” a la adiabaticidad:
Integrando:
La obtención de estos coeficientes nos permite calcular las probabilidades de transición en un régimen casi adiabático. Podemos obtener una aproximación adiabática de segundo orden insertando este último resultado en el lado derecho de la relación:
repitiendo el mismo proceso en forma iterativa para obtener correcciones de tercer orden, de cuarto orden, y así sucesivamente.
No se ha hablado mucho sobre lo que pueda suceder en el caso en el que se tengan niveles de energía degenerados. El caso sencillo de la partícula atrapada en una caja rebotando unidimensionalmente de una pared a otra no tiene degeneraciones, cada nivel discreto de energía de la partícula dentro de la caja es único. Sin embargo, en el caso tridimensional de una partícula realmente atrapada en una caja del mundo real, se presentan degeneraciones (y muchas de ellas) de estados de energía del mismo valor pero descritos por combinaciones diferentes de los tres números cuánticos nx, ny y nz. ¿Qué de esto? La fase geométrica, determinada únicamente por la forma de la ruta seguida, en su forma más sencilla es un número real. Sin embargo, si un sistema tiene niveles de energía degenerados, las transformaciones geométricas de estado tienen que ser descritas ya no con números sino con matrices, conocidas como holonomías no-Abelianas (no conmutativas, obviamente), y uno de los efectos más sorprendentes es que el efecto depende del orden en el que se tomen dos trayectorias consecutivas. En pocas palabras, en un sistema con niveles de energía degenerados, si se toma primero la ruta A y después la ruta B, la fase geométrica que se obtiene es diferente de la que se obtiene cuando se toma primro la ruta B y después la ruta A. En rigor de verdad, esto es anticipable en un sistema cuya descripción se lleva a cabo mediante matrices, las cuales no son conmutativas.
Se había asentado en la entrada anterior que los orígenes del teorema adiabático pueden ser rastreados a la aproximación Born-Oppenheimer, la cual considera que el movimiento de los electrones en torno a un núcleo ocurre a una rapidez mucho mayor que el movimiento del núcleo (o de los núcleos, tratándose de un compuesto formado por dos o más elementos), lo cual se puede ilustrar mediante la siguiente figura:
en la cual el movimiento del núcleo de un átomo (representado con un círculo azul grande, y el cual ocurre siguiendo la trayectoria cerrada de color verde) situado a cierta distancia instantánea R del origen de un sistema de coordenadas se lleva a cabo a una velocidad mucho menor que la velocidad a la cual se desplaza un electrón de valencia (representado con un círculo rojo pequeño) en torno al núcleo, con el electrón situado a una cierta distancia instanténea x del origen. En una situación así, la aproximación adiabática requiere que la velocidad instantánea dR/dt sea mucho menor que la velocidad instantánea dx/dt. Puesto de otra manera, en un proceso adiabático la variable R atraviesa por un cambio lento regresando a su valor inicial completando una trayectoria cerrada en el espacio-R (un recorrido análogo al que efectúa un péndulo de Focault que es transportado a lo largo de un triángulo esférico regresando al punto de partida). Puesto que el cambio en R es gradual, podemos suponer que el sub-sistema (el electrón) permanece todo el tiempo en su eigenestado original. Al completarse el recorrido de R, esperamos que la función de onda del electrón recupere su valor inicial. El teorema de Berry agrega un hecho que Max Born y Robert Oppenheimer desconocían en su tiempo: el hecho de que la función de onda del electrón adquiere además una fase geométrica que es el análogo del ángulo de fase que adquiere un péndulo de Focault cuando es transportado sobre una superficie curva a lo largo de una trayectoria cerrada.
Eventualmente se llega a un punto en el cual la aproximación Born-Oppenheimer tal y como fue enunciada originalmente se agota y se requiere recurrir a consideraciones adicionales para poder continuar adelante, extendiéndola de alguna manera para poder obtener mejor concordancia con los resultados experimentales. Esto fue lo que motivó una modificación posterior de la aproximación Born-Oppenheimer, llevada a cabo por el físico teórico chino Huan Kung, el cual colaboró estrechamente con Max Born para forjar un nuevo tipo de aproximación matemática, la aproximación Born-Huang. Esta aproximación es lo que viene siendo una “corrección diagonal” a la aproximación Born-Oppenheimer, y tiene implicaciones para la reactividad de los compuestos químicos en el área de la física molecular, tomando en cuenta la importancia de efectos no-adiabáticos. En forma simplificada, puede ser enunciada mediante la siguiente fórmula:
siendo Hnuclear el operador matricial de la representación del operador Hamiltoniano de energía cinética nuclear en las funciones de base electrónicas de la aproximación Born-Oppenheimer, y el cual (obsérvese el δ en el lado derecho de la expresión) es un operador diagonal. De este modo, la aproximación Born-Oppenheimer relaja algo las restricciones impuestas por la aproximación Born-Oppenheimer, incluyendo algunos elementos matriciales, pero al mismo tiempo manteniendo su estructura diagonal en las ecuaciones de movimiento nuclear, y como consecuencia de ello los núcleos permanecen moviéndose en superficies aisladas, un efecto obtenido con una corrección ligera a lo que en la fisicoquímica se conoce como superficies de energía potencial (SEP, ó PES en inglés).
Generalmente hablando, cuando no es posible mantener las matrices diagonales (como ocurre en el caso de sistemas con niveles de energía degenerados), los efectos interactivos ocasionados por los elementos no-diagonales no permiten una aplicación de la aproximación adiabática salvo casos especiales, y en situaciones de esta naturaleza no queda más opción que tratar de recurrir a soluciones numéricas en ausencia de soluciones analíticas exactas o de aproximaciones inexistentes e inaplicables.
Si hemos de buscar algún criterio que nos permita fijar las condiciones bajo las cuales un proceso cuántico evolucionando en el tiempo pueda considerarse adiabático o tenga que considerarse como diabático, podemos empezar con el vector de estado (ket) de un sistema que en un tiempo t pueda ser escrito de la siguiente manera:
en donde la función de onda espacial sea la proyección del vector de estado hacia uno de los eigenestados del operador posición (recuérdese que de acuerdo a las convenciones que hemos estado usando, lo que el producto bra-ket en el lado derecho de la siguiente expresión representa es la función de onda ψ(t) en el espacio posición):
Considérese un sistema cuyo operador Hamiltoniano H atraviesa un cambio continuo desde un valor inicial H0 en un tiempo t0 hasta un valor final H1 un tiempo t1 en donde:
τ = t1 - t0
En una representación de Schrödinger, la evolución temporal del sistema puede ser descrita mediante un operador de evolución del tiempo U (véase la entrada “El operador de evolución del tiempo”) que podemos definir mediante la siguiente ecuación de Schrödinger:
siendo lo anterior equivalente a:
siendo la condición inicial (desde luego):
Cuando se conoce la forma de la función de onda en un tiempo t0, ya hemos visto que la evolución del sistema en un tiempo posterior t puede ser obtenida usando:
El problema en determinar la adiabaticidad de un proceso dado es equivalente a establecer la dependencia temporal de U(t1,t0) en τ.
Para determinar la validez de la aproximación adiabática para un proceso dado, podemos calcular la probabilidad de encontrar al sistema en un estado (o eigenestado) distinto al estado (o eigenestado) en el cual comenzó. Para ello, defínase como ζ a esta probabilidad. Para mayor simplicidad, podemos emplear la notación bra-ket usando la siguente definición notacional:
Con esto, escribiremos lo siguiente definiendo a ζ:
Usando una expansión en serie de perturbación, podemos llevar a cabo la expansión del operador de evolución del tiempo de la siguiente manera:
En el límite perturbativo, podemos tomar los primeros dos términos ignorando los términos restantes de la serie infinita, substituyendo en la expresión para ζ la aproximación perturbativa al operador de evolución del tiempo, usando además como medida simplificadora el hecho de que el valor promediado en el tiempo del operador Hamiltoniano H, estadísticamente hablando, se puede definir del siguiente modo:
De este modo, se tiene:
Desarrollando y recolectando términos (el procedimiento es directo y no requiere mayor explicación), se tiene:
lo cual podemos compactar aún más de la siguiente manera:
si convenimos en acordar que ΔH es, estadísticamente hablando, la desviación raíz media cuadrática del Hamiltoniano del sistema evaluada en el intervalo temporal de interés (entre t1 y t0). La aproximación obtenida es válida cuando ζ.«.1 (esto es, cuando la probabilidad de encontrar al sistema en un estado o eigenestado distinto al estado o eigenestado en el cual comenzó es cercana a cero), en cuyo caso la condición de validez está dada por:
Esta relación debe resultar familiar. Es ni más ni menos el principio de incertidumbre de Heisenberg, expresado en la forma tiempo-energía.
El régimen diabático ocurre en el límite τ.→.0, para el cual:
En este caso, la forma funcional del sistema permanece inalterada:
En el límite τ.→.∞, tenemos una transición adiabática, lenta, adaptándose a las condiciones cambiantes, de forma tal que:
que refrenda lo que se había afirmado desde un principio en la entrada anterior, o sea el caso para el cual un sistema que inicialmente se encuentra en un eigenestado del Hamiltoniano H(t0) después de un lapso de tiempo τ habrá pasado al eigenestado correspondiente de H(t1).
La validez de la aproximación que se utilice para cierto proceso puede ser determinada mediante la probabilidad de que el estado final del sistema sea diferente del estado inicial:
P = ζ
Para la determinación de la probabilidad ζ en la región comprendida entre el régimen diabático y el régimen adiabático, obviamente se vuelve necesario tomar más términos de orden superior en la serie de perturbación, lo cual puede volver el problema difícil de manejar a menos de que se recurran a procedimientos numéricos con la ayuda de una computadora.