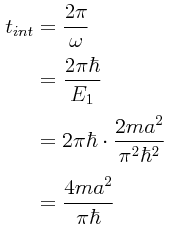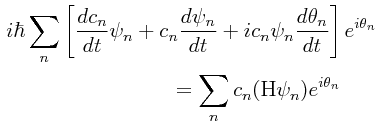Si el análisis de los orbitales atómicos como nubes de probabilidad que cumplan con la ecuación de Schrödinger independiente del tiempo se antojan ya de por sí algo elaborados para el caso de elementos químicos individuales tomando como base lo que ocurre en los átomos hidrogenoides, desde un principio se aceptó y se supuso que el análisis mecánico-cuántico de moléculas formadas por dos o más elementos sería algo para lo cual invariablemente se tendría que recurrir a métodos de aproximación.
La aproximación Born-Oppenheimer (¡la cual no debe ser confundida en ningún momento con la aproximación de Born empleada en el análisis de los fenómenos del esparcimiento de partículas) propuesta por vez primera por Max Born y Robert Oppenheimer en un trabajo publicado en 1927 en el volumen 84 del Annalen der Physik (que se puede encontrar traducido al inglés bajo el título “On the Quantum Theory of Molecules”) fue concebida precisamente para hacer frente al problema de tener que extender las herramientas de la Mecánica Cuántica hacia el análisis del comportamiento de las moléculas, las cuales también producen espectros de emisión y absorción cuando son bombardeadas con haces luminosos de alta energía, espectros que pueden proporcionar mucha información sobre la estructura interna de las moléculas. Es importante subrayar que la aproximación Born-Oppenheimer no consideró la posibilidad de que las nubes de probabilidad de un mismo átomo se pudieran mezclar entre sí para dar origen a nuevos orbitales híbridos capaces de formar enlaces químicos con otros átomos, el mérito de tal idea correspondería a Linus Pauling, y el tema fue tratado ya a partir de la entrada titulada “La hibridación de los orbitales atómicos”.
Considérese el siguiente operador Hamiltoniano completo (¡y exacto!) para una molécula poliatómica que incluye todas las contribuciones energéticas posibles, en el sistema de unidades MKS-SI:
en donde el primer término representa la energía cinética de todos los núcleos, el segundo término representa la energía cinética de todos los electrones, el tercer término representa la energía potencial (eléctrica) de repulsión nuclear entre todos los núcleos, el cuarto término representa la energía potencial (eléctrica) de atracción de cada núcleo a todos los electrones, y el quinto término representa la energía potencial (eléctrica) de repulsión entre cada electrón y el resto de los electrones. En su quintaesencia, la aproximación Born-Oppenheimer consiste en suponer que los núcleos de los átomos se mueven mucho más lentamente que los electrones. Esto permite de inmediato hacer al término de energía cinética nuclear (el primer término) igual a cero, haciéndose además el término de repulsión nuclear igual a una constante:
De este modo, para un sistema poliatómico que conste únicamente de dos átomos (dos núcleos) a y b, el término de repulsión nuclear en donde rab es la distancia internuclear:
se considera constante. Y si los dos átomos son átomos de hidrógeno formando una molécula de hidrógeno H2, con un electrón asociado a cada núcleo, el operador Hamiltoniano para la molécula de hidrógeno puede escribirse entonces como (se ha destacado en color azul la parte que representa la repulsión eléctrica entre los dos núcleos, los dos protones; y se ha destacado en color magenta la parte que representa la repulsión eléctrica entre los dos electrones):
Esto representa algo mucho más manejable con aplicaciones prácticas.
El hecho importante en la aproximación Born-Oppenheimer consiste en suponer que algo ocurre con mucha mayor lentitud que otra cosa. La aproximación que estudiaremos aquí es conocida en un buen número de textos como la “aproximación adiabática”, y es una extensión de esta suposición hacia otras situaciones; en muchos textos se considera a la aproximación Born-Oppenheimer y a la aproximación adiabática como sinónimos aunque en realidad no lo sean por ser un concepto una extensión del otro.
El empleo de la palabra “adiabática” tal vez sea algo infortunado porque puede dar la impresión de que esto tiene que ver con la aplicación de conceptos termodinámicos cuando esto no es así, las herramientas utilizadas son herramientas propias de la Mecánica Cuántica, no de la termodinámica. El concepto termodinámico de lo que es adiabático (la palabra deriva de los sufijos griegos a que significa “no”, dia que significa “a través” y bainein que significa “pasar”, siendo por lo tanto el derivado etimológico una palabra compuesta que significa “impasable”, en referencia a la idea en el cual hay una ausencia de transferencia de calor porque el sistema está aislado en forma tal que la conducción de calor de una región a otra es mínimo o imposible) no tiene mucho que ver con la idea central que hay detrás de la aproximación, de índole puramente mecánico-cuántica. Tras la publicación del trabajo “On the Quantum Theory of Molecules” en 1927, lo que hoy se conoce como el teorema adiabático fue propuesto conjuntamente al año siguiente en su forma original por Max Born y por Vladimir Fock en el trabajo titulado “Beweis des Adiabatensatzes” (Prueba de la Razón Adiabática) publicado en el volumen 51 del Zeitschrift für Physik A.
Para entender todas las motivaciones que hay detrás de lo que hoy conocemos como la aproximación adiabática, resulta conveniente salir momentáneamente del ámbito de la Mecánica Cuántica para ver lo que sucede en la mecánica clásica a la que estamos acostumbrados intuitivamente.
Es bien sabido que si a un sistema físico se le altera lentamente, el estado posterior del sistema físico se adapta suavemente a su nuevo entorno sin alteraciones bruscas. Tómese como ejemplo el caso de un péndulo de longitud L que se encuentra fijo en cierto lugar, oscilando a lo largo de un plano con el típico período clásico igual a T.=.2π√L/g :
Si metemos al péndulo dentro de una caja poniendo en acción el movimiento pendular, mientras la caja permanezca inmóvil asentada en un mismo sitio se tendrá algo igual a lo que se tiene arriba. ¿Y qué sucede si levantamos la caja hacia arriba? Todo depende. Si el movimiento de ascenso es rápido, entonces el modo de oscilación del péndulo cambiará. Sin embargo, si la caja es levantada lentamente, el movimiento del péndulo relativo a la caja permanecerá sin cambios.
Obsérvese que en la figura del péndulo metido dentro de una caja se destaca un pedazo pequeño del hilo del péndulo sobresaliendo de la parte superior de la caja, con el fin de sugerir que el experimento se puede llevar a cabo de otra manera. En lugar de ir levantando la caja, con la caja reposando sobre una mesa se puede ir jalando el péndulo lentamente sacando el hilo poco a poco hacia afuera. Este es un experimento sencillo que cualquiera puede hacer en su propia casa. Si se jala el hilo con suficiente lentitud, aunque el período del péndulo irá variando como T.=.2π√L(t)/g en virtud de que la longitud del hilo dentro de la caja es una función del tiempo, o sea L(t), el movimiento pendular permanecerá en el mismo plano de oscilación sin exhibir otro tipo de alteración. En cambio, si se jala el hilo bruscamente, la alteración del movimiento pendular será incluso impredecible (como ya se dijo, este experimento por la forma en la que se lleva a cabo puede ser realizado por el lector con una inversión mínima de tiempo y recursos, y la realización del experimento puede ser muy instructiva). Obsérvese que para el caso del movimiento de una caja dentro de la cual está metido un péndulo oscilante se puede hablar de dos tiempos, un “tiempo interno” y un “tiempo externo”. El “tiempo interior” tint representa el movimiento interno del sistema en sí, que en este caso viene siendo el período T de las oscilaciones del péndulo (en otros tiempos de antaño antes del advenimiento de la electrónica y los circuitos microminiaturizados, los períodos de las oscilaciones de un péndulo eran tan confiablemente repetitivos que era muy popular el “reloj del abuelo” para medir la hora del día, y todavía se pueden ver algunos de tales péndulos en uso), mientras que el “tiempo exterior” text vendría siendo algo así como el movimiento de la plataforma (o de la caja) en la cual está montado el péndulo, asociado con parámetros del sistema que pueden cambiar en forma apreciable sin tener en lo absoluto nada que ver con el tiempo interno que es propio al mismo péndulo.
Las figuras anteriores posiblemente no ilustren exactamente la idea que se está tratando de transmitir aquí, y por ello se dará otro ejemplo más apropiado a la Mecánica Cuántica. Tomaremos como ilustración el caso de una partícula encerrada en un pozo de potencial con paredes infinitamente altas (o lo que es lo mismo, una partícula encerrada en una caja). Para mayor simplicidad, usaremos como punto de referencia el estado basal de una partícula encerrada en una caja, para el cual la función de onda ψ(x) tiene una extensión de media longitud de onda de De Broglie, o sea λ/2. Un problema frecuentemente citado en muchos textos introductorios de Mecánica Cuántica es aquél en el cual una de las paredes (verticales) del pozo de potencial contra la cual está rebotando elásticamente la partícula es jalada rápidamente de modo tal que la distancia que tiene que recorrer la partícula es el doble de la distancia original. El enunciado del problema está formulado casi siempre de modo tal que la pared vertical móvil es jalada de forma casi instantánea, de forma tal que la función de onda no tiene tiempo suficiente de “estirarse” por sí sola acomodándose a las nuevas dimensiones. Se tiene entonces lo que es esencialmente una nueva función de onda, formada por una sección en la que se tiene media longitud de onda, y otra sección esencialmente plana. El siguiente gráfico animado nos muestra en forma dinámica lo que sucede:
Para aquellos que han estudiado electrónica la función de onda es el símil de lo que se obtiene al pasar una corriente sinusoidal alterna a través de un diodo rectificador, obteniéndose lo que se llama una rectificación de media onda. Sin embargo, no hay que confundirse, porque aquí de lo que estamos hablando es de una onda de materia.
La nueva función de onda, desde el punto de vista puramente matemático, definitivamente ya no es una cosa tan sencilla como la media onda senoidal original. Puede ser construída mediante una expansión en series de Fourier, o sea una serie infinita con el estado fundamental definido con una cierta longitud de onda y las armónicas de amplitudes distintas definidas con múltiplos enteros de la “frecuencia” que corresponde a tal longitud de onda. La función de onda que corresponde a la media onda senoidal periódica, representada mediante una expansión matemática en series de Fourier, es la siguiente:
Ya vimos en la entrada “Interpretación probabilista de ψ II” lo que sucede cuando una de las paredes es movida rápidamente, dándose un avance de lo que veremos aquí. Siempre motivados por la esperanza de poder entender otro tipo de situaciones así como de simplificar un poco más las cosas, formulémonos ahora una pregunta importante: ¿Qué sucedería si en lugar de separar bruscamente las paredes verticales contra las cuales está rebotando la partícula las separamos lentamente, muy lentamente? En tal caso, esperamos que la función de onda se vaya acomodando paulatinamente a las nuevas dimensiones internas horizontales de la caja, de forma tal que en vez de tener algo inusual como el equivalente de una media función de onda seguiremos teniendo el equivalente de un estado fundamental de la partícula pero de menor amplitud aunque de mayor longitud de onda λ. Volviendo al caso de arriba en el cual una de las paredes (verticales) de un pozo de potencial contra la cual está rebotando elásticamente la partícula es movida lentamente en lugar de ser jalada rápidamente de modo tal que la distancia que tiene que recorrer la partícula sea el doble de la distancia original, entonces la situación que se antoja posible es la siguiente:
Si suponemos que no hay transferencia alguna de energía hacia el exterior ni proveniente del exterior (la partícula, después de todo, sigue rebotando elásticamente dentro de la caja), entonces la energía de la partícula debe seguir siendo la misma que la que tenía antes de que las paredes del recipiente fueran separadas. Y esto se debe reflejar en el operador Hamiltoniano de energía de la partícula. La función de onda ψ(x) de la partícula en su estado basal ya no es la misma, ha cambiado, pero sigue teniendo una extensión de media longitud de onda de De Broglie, o sea λ/2. Es precisamente aquí en donde entra lo “adiabático” del asunto, el saber aprovechar inteligentemente en el análisis de la aproximación que se llevará a cabo a través del Hamiltoniano modificado el hecho de que no hay transferencia de energía aunque la función de onda haya cambiado.
Otro ejemplo que se puede citar para enfatizar la naturaleza de la aproximación que se pretende desarrollar aquí es el de un oscilador armónico cuántico simple cuya “constante del resorte” k pueda ser variada de alguna manera. Clásicamente, esto equivale a irle aumentando al resorte su dureza, mientras que cuánticamente esto equivale a ir “cerrando” la curva (parabólica) del potencial en el Hamiltoniano del sistema. Si k es incrementada adiabáticamente, lo cual equivale a estipular:
En tal caso, el sistema en un tiempo t se encontrará en un eigenestado instantáneo ψ(t) del operador Hamiltoniano H(t) para ese instante de tiempo. Para el caso especial de un oscilador armónico cuántico descrito por el número cuántico n en el que se encuentre, esto significa que el número cuántico seguirá siendo el mismo al irse variando k. Sin embargo, para un caso en el cual la constante k aumenta rápidamente:
el sistema experimenta lo que pudiéramos llamar un proceso no-adiabático o proceso diabático en el cual el sistema no tiene tiempo suficiente para adaptar su forma funcional a las condiciones rápidamente cambiantes. Mientras que la densidad de probabilidad del estado final tiene que verse idénticamente igual a la densidad de probabilidad del estado inicial:
|ψ(t)|2 = |ψ(0)|2
para un proceso que ocurre rápidamente dentro de cierto intervalo de tiempo, no habrá ningún eigenestado que corresponda al nuevo Hamiltoniano H(t). El estado final estará compuesto por una superposición linear de muchos eigenestados diferentes de H(t) que se suman para reproducir la forma del estado inicial. De este modo, podemos resumir de la siguiente manera la diferencia entre un proceso diabático y un proceso diabático:
Proceso diabático.- Las condiciones rápidamente cambiantes le impiden al sistema adaptar su configuración durante el proceso, y por lo tanto su densidad de probabilidad permanece inalterada. Típicamente, no hay un eigenestado del Hamiltoniano final que posea la misma forma funcional que la que tenía el estado inicial. El sistema termina siendo una combinación linear de estados que se suman para reproducir la densidad de probabilidad del estado inicial.Estamos en condiciones de poder enunciar el teorema adiabático en una de sus formas más conocidas, tal y como fue postulado por Max Born y Vladimir Fock:
Proceso adiabático.- Las condiciones gradualmente cambiantes le permiten al sistema adaptar su configuración, y por lo tanto la densidad de probabilidad es modificada durante el proceso. Si el sistema comienza en un eigenestado del Hamiltoniano inicial, permanecerá en el eigenestado correspondiente del Hamiltoniano final.
Un estado físico permanece en su eigenestado instantáneo si la perturbación que actúa sobre él es suficientemente lenta y hay una brecha entre su valor propio y el resto del espectro del Hamiltoniano.Por “el resto del espectro del Hamiltoniano” debemos entender el resto de los demás eigenestados del Hamiltoniano en los cuales puede encontrarse el sistema. Si suponemos que el Hamiltoniano del sistema se encuentra inicialmente en el eigenestado que corresponde a la eigenenergía E3 que forma parte de un sistema físici que puede admitir una cantidad infinitamente grande de estados discretos, entonces “el resto del espectro del Hamiltoniano” comprenderá el conjunto de eigenestados del Hamiltoniano en los cuales se tiene a E1, E2, E4, E5, etcétera, en fin, todos los demás eigenestados posibles, excepto el eigenestado E3. Poniendo lo mismo de otra manera, supóngase que el Hamiltoniano del sistema se encuentra en un valor inicial Hinicial y que el Hamiltoniano cambia gradualmente a otro valor Hfinal. El teorema adiabático nos afirma que si una partícula se encontraba inicialmente en el n-avo eigenestado de Hinicial, entonces bajo la ecuación de Schrödinger será llevada al n-avo estado del Hamiltoniano Hfinal. El estado-0 del Hamiltoniano Hinicial es llevado al estado-0 del Hamiltoniano Hfinal, el estado-1 del Hamiltoniano Hinicial es llevado al estado-1 del Hamiltoniano Hfinal ,El estado-2 del Hamiltoniano Hinicial es llevado al estado-2 del Hamiltoniano Hfinal, y así sucesivamente, conservándose el ordenamiento.
La estrategia básica de la aproximación adiabática en el análisis de un problema consiste en resolver primero el problema con los parámetros externos fijos (en forma convencional, con la finalidad de determinar las eigenfunciones de onda y los eigenvalores propios del sistema cuando no lo afecta perturbación alguna), y únicamente después de este cálculo se les permite variar con el tiempo, preferentemente en el estado fundamental (basal) inicial del sistema.
El caso mostrado arriba de una partícula encerrada en una caja una de cuyas paredes (en este caso, la pared derecha) se desplaza a una velocidad constante es tratado en un artículo titulado “Infinite Square-Well Potential with a Moving Wall”, publicado en la revista American Journal of Physics en diciembre de 1969. Este caso tiene una solución exacta para la ecuación de Schrödinger, la cual es:
siendo:
la anchura instantánea de la caja (la distancia inicial de pared a pared es a) y siendo:
el n-avo nivel de energía de la caja en el tiempo inicial t.=.0. Para comprobar que en efecto se tiene una solución exacta a la ecuación de Schrödinger, podemos comenzar por simplificar el exponente del modo siguiente:
de lo cual se tiene:
De este modo se tiene la siguiente relación simplificada para la función de onda:
Diferenciando esta función de onda con respecto al tiempo, se tiene:
en donde para factorizar hacia afuera a Ψn se usó:
Usaremos lo obtenido en el lado derecho de la ecuación fundamental de Schrödinger cuya integridad queremos probar:
De este modo:
Para la evaluación del lado izquierdo de la ecuación de Schrödinger, tomaremos ahora la derivada de la función de onda Ψn con respecto a la coordenada x:
Derivando con respecto a la coordenada x el parámetro θ que se ha definido arriba se tiene:
Por lo tanto:
Volviendo a tomar la derivada de la función de onda Ψn con respecto a la coordenada x y simplificando:
Esto nos permite llevar a cabo la evaluación de la acción del operador Hamiltoniano H sobre la función de onda Ψn:
Estamos en condiciones de poder juntar todo en la ecuación fundamental de Schrödinger, y si la solución que se ha dado al principio es en efecto una solución genuina, entonces ambos lados evaluados con la solución propuesta deben ser iguales:
Comparando términos equivalentes en ambos lados, se puede ir verificando de inmediato que son en efecto iguales. En lo que respecta a los términos cotangentes se tiene:
En lo que toca a los otros términos trigonométricos del lado derecho, se tiene:
Por último, se tiene para comprobar que esta relación:
debe ser igual a la siguiente:
dLa verificación de ello procede en forma directa:
De este modo, queda confirmado que la solución Ψn(x,t) proporcionada satisface en efecto a la ecuación de Schrödinger. La solución general estará dada por una combinación linear de las Ψn(x,t) de la siguiente manera:
Recuérdese que para una partícula encerrada en una caja con ambas paredes fijas, en un tiempo t.=.0, la función de onda para el n-avo estado era:
En el caso que nos ocupa, cuando una de las paredes es móvil, también para un tiempo t.=.0 la función de onda para el n-avo estado será:
Intentaremos obtener la función de onda general para el caso presente, lo cual en nuestro caso equivale al problema de determinar las constantes cn. Se tiene como punto de partida que:
Multiplicando por:
e integrando, se tiene:
usando la ortonormalidad de las funciones de base. Por lo tanto:
Ahora bien, puesto que para el caso presente:
se tiene entonces:
Definiendo una nueva variable ξ de la siguiente manera:
se tiene con ello:
Por lo tanto, la relación que nos proporciona los coeficientes cn se puede escribir de la siguiente manera simplificada:
en donde se ha definido a β como:
Desafortunadamente, la integral obtenida no puede ser evaluada en términos de funciones elementales. Pero es aquí en donde la aproximación proporcionada para este problema por el teorema adiabático nos puede ayudar. Supóngase ahora que le permitimos a la caja aumentar su distancia de pared a pared de a a 2a, de modo tal que lo que pudiéramos llamar “tiempo exterior” text quede definido por:
La determinación de dicho tiempo en función de la velocidad a la cual se mueve la pared es entonces:
Por otro lado, y de acuerdo a lo que hemos visto en entradas anteriores, en la solución exacta completa del problema incorporando el factor:
se tiene que tener ciertamente:
Definiendo un “tiempo interior” tint tomándolo como el período del factor exponencial dependiente del tiempo, se tiene entonces que:
La aproximación proporcionada por el método adiabático requiere que:
o lo que es lo mismo:
Esto último que se acaba de obtener es la condición que encapsula el espíritu de la aproximación adiabática para este problema, y la condición implica que:
sobre el dominio en el cual se llevará a cabo la integración para proceder a obtener los coeficientes cn de la expansión, la cual resulta sencilla al tomar en cuenta la ortonormalidad de las funciones de base:
De este modo, habiendo obtenido una expresión sencilla para los coeficientes de la expansión, podemos proceder a construír una expresión para Ψ(x,t) de la siguiente manera:
la cual, ignorando momentáneamente el factor de fase resaltado en color magenta, nos proporciona la función de onda instantánea (no solo para el caso t.=.0) del estado basal de la caja o pozo de potencial con paredes infinitamente altas de anchura instantánea α, tal y como lo especifica el teorema adiabático. Obsérvese que para x.=.a el primer término del exponente puede considerarse despreciable en virtud de que :
y por lo tanto puede ser borrado al ser tomada la aproximación adiabática.
A continuación se demostrará que la función de onda Ψ(x,t) puede ser escrita mediante la simbolización:
en donde:
es el eigenvalor instantáneo en un tiempo t. Para ello se tiene que:
De modo que, despreciando el primer término del exponencial por la razón que se acaba de exponer arriba, y teniendo en cuenta que:
se puede afirmar entonces que para Ψ(x,t):
ésta se puede escribir como:
resaltándose la naturaleza del factor de fase destacado en color magenta. El resultado obtenido es justo lo que se podría haber esperado; para una caja con ambas paredes fijas e inmóviles se tendría:
mientras que para una caja (o pozo de potencial con paredes de potencial infinitamente altas) una de cuyas paredes se está alejando de la otra adiabáticamente, basta con reemplazar la distancia a (fija) de pared a pared con la distancia variable α, observándose que ahora E1 es dependiente de la variable tiempo, llevando a cabo una integración para el cálculo del factor de fase acumulado.
Sabemos por lo que hemos visto en entradas previas que la densidad de probabilidad evaluada de acuerdo al criterio de Born como ψ*ψ por su propia naturaleza hará que los factores de fase se nulifiquen en virtud de la operación:
Sin embargo, para el caso del ejemplo que se acaba de resolver, esto no cambiará el hecho de que la amplitud de la función de onda de una partícula dentro de una caja con una pared móvil, por estar dada dicha amplitud no como √2/a (siendo a constante) sino como √2/α siendo α una función que varía linealmente con el tiempo, esto tendrá un impacto directo en el resultado final al calcularse la densidad de probabilidad, la cual ya no se mantendrá constante conforme transcurre el tiempo. ¿Significa esto que los factores de fase no aparecerán en resultado final alguno de lo que se mida en el laboratorio? Esto era lo que se creía hace buen tiempo, hasta el descubrimiento de un factor de fase muy peculiar que se las arregla para aparecer de modo tal que puede ser evaluado y detectado experimentalmente en un laboratorio, lo cual veremos más a fondo más adelante.
entonces al haber transcurrido un tiempo t la partícula permanecerá en dicho eigenestado, recogiendo en el camino un factor de fase (véase la entrada “El operador de evolución del tiempo”):
Sin embargo, si el operador Hamiltoniano H es dependiente del tiempo, entonces tanto las eigenfunciones como los eigenvalores se vuelven también dependientes del tiempo:
De cualquier manera, se da por hecho que en cualquier instante las eigenfunciones siguen constituyendo un conjunto ortonormal completo, esto es:
Siendo así, la solución general de la ecuación de Schrödinger dependiente del tiempo:
puede ser expresada como una combinación linear de las eigenfunciones de base:
en donde al hacerse:
se tiene una generalización del factor de fase convencional estático al caso en el cual el eigenvalor En varía con el tiempo. Esta es precisamente la razón por la cual a esto último se le conoce como la fase dinámica.
Substituyendo la expansión en funciones de base de Ψ(t) en la ecuación de Schrödinger dependiente del tiempo, se tiene:
Podemos simplificar esta notación recurriendo a la notación del punto puesto encima para indicar que se trata de algo que está siendo diferenciado con respecto al tiempo:
Esto es lo mismo que:
Los términos destacados en color rojo se cancelan mutuamente en virtud de las dos relaciones:
De este modo, todo lo que nos queda es lo siguiente:
Tomando el producto interno de ambos lados con ψm e invocando la condición de ortonormalidad de las eigenfunciones instantáneas dada arriba, se tiene:
de lo cual:
Por otro lado, diferenciando con respecto al tiempo la eigen-relación dada arriba para el operador Hamiltoniano instantáneo H(t) y manteniendo la notación del “punto encima”, se tiene:
Si tomamos nuevamente el producto interno de ambos lados con respecto a ψm, se tiene entonces:
En virtud de la hermiticidad del operador Hamiltoniano de energía H, podemos hacerlo actuar sobre un bra que está a la izquierda, permitiéndonos obtener :
Entonces, para m.≠.n, se tiene que:
Poniendo esto último en la ecuación y suponiendo que no hay estados degenerados de energía:
se tiene entonces:
Hasta este punto, lo que se ha obtenido es exacto; no se ha recurrido a ninguna aproximación. Es en este punto en donde entra la aproximación adiabática, suponiendo que dH/dt es extremadamente pequeño, lo cual nos permite tomar ignorar el segundo término. La demostración de esta suposición que se está tomando no es trivial, y puede verse más sobre ello en un trabajo elaborado por un equipo de teóricos brasileños bajo el título “Comment on the adiabatic condition”, publicado en el American Journal of Physics en octubre de 2000. Llevando a cabo la aproximación adiabática, todo lo que nos queda es:
Esto tiene como solución:
en donde se ha hecho la siguiente definición:
En el caso particular en el cual una partícula comienza en el n-avo eigenestado, lo cual implica una selección de coeficientes cm(t) tales que para m.≠.n se tiene cm(0).=.0 y cn(0).=.1, entonces de la ecuación:
se tiene que:
Esto significa que en una situación en la cual la aproximación adiabática sea válida, una partícula que se encuentre en el n-avo estado del operador Hamiltoniano conforme este va evolucionando con el tiempo permanecerá en dicho eigenestado, recogiéndose en el camino un par de factores de fase que no estaban presentes en el tiempo t.=.0.
Asociado íntimamente con el teorema adiabático, e independiente por completo de lo que hemos llamado arriba la fase dinámica, se tiene un concepto conocido comunmente como la fase geométrica, la cual es conocida en la Mecánica Cuántica alternadamente como la fase Pancharatman-Berry y como la fase de Berry (el efecto de la geometría espacial sobre haces de luz polarizada fue descubierto primero en 1956 por el físico hindú Shivaramakrishnan Pancharatnam y publicado por The Proceedings of the Indian Academy of Sciences con el trabajo titulado “Generalized Theory of Interference, and its Applications” en donde se recurre como herramienta de trabajo a un artificio matemático conocido como la esfera de Poincaré utilizada en óptica como herramienta gráfica para visualizar distintos tipos de luz polarizada, que dicho sea de paso es conocida en la física de la materia condensada como esfera de Bloch) y posteriormente redescubierto independientemente en 1983 por el físico inglés Michael Berry, aunque sólo con el redescubrimiento hecho por Berry y con la atención que recibió el tema a partir de su confirmación experimental se logró sacar el tema del olvido en que se encontraba dándole la importancia que merecía).
El haber comenzado la discusión del tema del teorema adiabático poniendo como ejemplo al péndulo ordinario no fue cosa fortuita, porque resulta que el péndulo tiene una importancia pedagógica enorme para la apreciación del teorema adiabático, por cosas que tienen que ver más con la geometría que con los asuntos de índole mecánica.
Una de las explicaciones más sencillas de lo que es la fase de Berry está basada en el péndulo de Focault. Para quienes no están muy familiarizados con dicho péndulo, baste con señalar que el péndulo de Focault proporciona una de las demostraciones más convincentes que pueda haber de la rotación de la Tierra sobre su propio eje. El péndulo de Focault es esencialmente un peso colgado de un cordón delgado lo suficientemente largo (por lo menos unos quince o veinte metros) para mantenerse oscilando de un extremo a otro durante el curso de varias horas manteniéndose intacto el plano de oscilación del péndulo, teniendo debajo del mismo el trazado de una rosa de los vientos. Para mayor claridad, podemos considerar al péndulo colgado de un globo aerostático fijo en el cielo a gran altura, “desconectado” (por así decirlo) por completo de la Tierra. Para una persona que esté posicionada con un péndulo de Focault justo en el Ecuador terrestre con el plano del péndulo apuntando en dirección hacia el Polo Norte, conforme la Tierra va girando el plano del péndulo parecerá mantenerse siempre a 90 grados con respecto a la línea del Ecuador, y esto lo confirmará la persona manteniendo su vista todo el tiempo sobre la rosa de los vientos que esté dibujada debajo del péndulo. Sin embargo, para una persona que esté posicionada justo en el Polo Norte, conforme la Tierra va girando sobre su eje el plano del péndulo parecerá ir girando paulatinamente también, y de hecho girará 360 grados hasta regresar a su misma dirección cuando hayan transcurrido 24 horas. Las siguientes dos figuras muestran lo que ven ambos observadores al empezar sus observaciones y lo que verán después de que hayan transcurrido unas seis horas:
Entre un extremo y otro, esto es, entre el Ecuador en donde el péndulo no manifiesta giro alguno, y el Polo Norte en donde el plano del péndulo parece estarse desplazando, hay una zona intermedia en donde el péndulo girará con mayor lentitud conforme el péndulo es movido desde el Polo Norte hacia el Ecuador. De este modo, si empezamos desde el Polo Norte:
entonces, al mover el péndulo bajándolo a una latitud situada entre el Polo Norte y el Ecuador, el plano del péndulo parecerá ir girando (aunque mayor lentitud) con respecto a la rosa de los vientos dibujada debajo del mismo:
Finalmente, al llegar al Ecuador, el péndulo parecerá permanecer estático con su plano de oscilación invariable con respecto a la rosa de los vientos que se ha dibujado debajo del péndulo:
Lo más espectacular de este experimento relativamente sencillo de llevar a cabo es que una persona que esté encerrada dentro de un cuarto sellado sin ventanas y sin ninguna referencia externa (como el movimiento aparente de las estrellas o como la experiencia del cambio del día a la noche) podrá enterarse sin duda alguna del movimiento de rotación de la Tierra. En otros tiempos, para comprobar la redondez de la Tierra, era necesario que un navegante se subiera a una carabela navegando a gran distancia (descubriendo de paso un nuevo continente) para poder convencer a los incrédulos de que la Tierra no es plana sino redonda. Y para comprobar que la Tierra se mueve sobre su propio eje y no el cosmos en torno a la Tierra, en otros tiempos era necesario desafiar a la misma Inquisición (sin mucho éxito, dicho sea de paso). ¡Hubiera bastado un péndulo de Focault para convencer hasta los más escépticos, inclusive en esos tiempos! Como ya se vió arriba, no es necesario trasladarse hasta el Polo Norte para ver al plano del péndulo de Focault ir girando con respecto a la rosa de los vientos dibujada debajo del péndulo. En cualquier otro punto situado entre el Polo Norte y el Ecuador el plano del péndulo de Focault parecerá ir girando con respecto a la rosa de los vientos dibujada debajo del mismo, aunque a una velocidad menor. De hecho, en principio es posible determinar con un péndulo de Focault la latitud en la cual está situado uno con el péndulo (sin necesidad de tener que ver las estrellas de noche) de acuerdo al tiempo que le lleva al péndulo efectuar una rotación completa. En el Polo Norte el plano del péndulo girará 360° en 24 horas mientras que en el Ecuador el plano del péndulo permanecerá estático, de modo tal que si el plano del péndulo tarda 87 horas en girar con respecto a la rosa de los vientos dibujada debajo del mismo, entonces con la ayuda de algunas fórmulas relativamente sencillas podemos calcular la latitud en la cual estamos ubicados. Inclusive hasta podemos determinar en qué hemisferio estamos situados (en un hemisferio el plano del péndulo girará en sentido de las manecillas del reloj, mientras que en otro hemisferio el plano del péndulo girará en sentido contrario).
Hay otro tipo de experimento que podemos llevar a cabo con un péndulo de Focault, para el cual ni siquiera necesitamos que la Tierra tenga un movimiento de rotación. En efecto, para el experimento que se describirá a continuación, supongamos que la Tierra está fija y que carece de movimiento de rotación.
Supóngase que hay dos personas con dos péndulos de Focault situadas en el Ecuador en el punto A de la figura que se muestra a continuación:
A continuación, una de las personas toma su péndulo de Focault y empieza a moverse lentamente hacia el Polo Norte (identificado como N) siguiendo un arco de círculo máximo terrestre. Al ir de A a N, las flechas que marcan el desplazamiento del observador móvil estarán situadas en el mismo plano que el plano de oscilación del péndulo de Focault del observador móvil. Habiendo llegado al Polo Norte, el observador móvil empieza a descender nuevamente hacia el Ecuador pero en otra dirección, hacia donde está el punto B en el Ecuador, siguiendo un arco de círculo máximo terrestre, haciéndolo lentamente. Obsérvese en la figura como el plano de oscilación del péndulo sigue fijo, no habiendo razón alguna para que cambie. Habiendo llegado al punto B, el observador móvil se desplaza de B hacia A para encontrarse con el otro observador fijo, siguiendo el arco del círculo máximo que llamamos Ecuador. Y es aquí que cuando ambos al encontrarse se topan con la enorme sorpresa de que los planos de oscilación de sus péndulos están desfasados, ya no coinciden. Este efecto que para los dos observadores puede parecer sorprendente no es más que una consecuencia de lo que llamamos un transporte paralelo a lo largo de geodésicas (en este caso, las geodésicas son los arcos de círculos máximos de la Tierra). Lo más extraordinario en todo esto es que se tiene, sin necesidad de tener que salir al espacio exterior en una nave para ver globalmente a la Tierra desde fuera, una manera de determinar la existencia de la curvatura de la superficie terrestre con observaciones puramente locales.
La fase de Berry es el equivalente mecánico-cuántico del experimento puramente clásico con péndulos de Focault que se acaba de describir.
El ejemplo introductorio a la fase de Berry basado en el péndulo de Focault es el resultado de una aplicación a la mecánica clásica del ángulo de Hannay, así llamado en referencia al matemático John H. Hannay (el cual imparte cátedra en la misma universidad a la que pertenece Michael Berry inspirándose en el descubrimiento de Berry para buscar el equivalente en la mecánica clásica de la fase de Berry) quien escribió un trabajo publicado en 1985 en el volumen 18 del Journal of Physics A: Mathematical and General bajo el título “Angle variable holonomy in adiabatic excursion of an integrable Hamiltonian”, justificando sobre bases rigurosas al péndulo de Focault como el análogo clásico de la fase de Berry.
La importancia de la fase de Berry es que en virtud de ella hay muchas situaciones en las cuales el estado de un sistema cuántico depende no solamente de la situación local y los parámetros físicos, sino también de la historia previa del sistema. Tales sistemas, como lo dijera Berry, tienen una memoria.
Recordemos ahora que en la mecánica clásica el nivel de referencia usado para la energía potencial es arbitrario, y lo único que termina siendo relevante en cualquier situación son las diferencias de energía potencial y no el valor absoluto que arbitrariamente les podamos asignar a las mismas. Un problema elemental estudiado en muchos cursos introductorios de Mecánica Cuántica consiste en demostrar que si al potencial V(x) se le agrega un potencial constante V0, el único efecto final que esto tendrá en la solución general proporcionada por la ecuación de Schrödinger será el de desplazar la función de onda en un factor de fase e-iφ siendo φ.=.V0t/ħ. Sin embargo, no se acostumbra darle significado físico alguno a tal factor de fase porque el valor calculado de una observable física no puede depender de la convención de fase, y en efecto al efectuar la operación ψ*ψ multiplicando una función de onda ψ por su conjugado complejo ψ* las fases se desvanecen del panorama. Sin embargo, al entrar la geometría en acción, nos topamos inevitablemente con ciertas fases que no se desvanecen sino que aparecen al final dentro de las fórmulas. Veamos nuevamente la última figura dada arriba en la cual un observador móvil se traslada con su péndulo de Focault de A hasta N, y supongamos que una vez en N en lugar de desplazarse hacia B se regresa nuevamente de N a A siguiendo la misma ruta de regreso. En tal caso, al encontrarse con el péndulo de Focault del observador fijo en A, no habrá diferencia alguna en los planos de oscilación de ambos péndulos. Esto sería a grosso modo el equivalente mecánico-cuántico de las fases que se cancelan entre sí sin ninguna diferencia observable al final del experimento. Sin embargo, si el observador móvil toma la ruta ANBA, entonces la diferencia entre los planos de oscilación de ambos péndulos será notoria e inocultable. Esto es a grosso modo el caso de la fase que inclusive puede ser medida experimentalmente. Y demuestra que la geometría puede jugar un papel importante en la Mecánica Cuántica.
La historia de la fase de Berry es interesante. En 1983, al estar impartiendo una cátedra en los Estados Unidos, el Profesor Michael Berry de la Universidad de Bristol se topó con problemas para darle una respuesta satisfactoria a uno de sus alumnos acerca del comportamiento de cierto tipo de funciones de onda cuando se viola la simetría en el revertimiento del tiempo. Dos semanas después de estar pensando sobre el asunto, Michael Berry descubrió lo que él llamó la fase cuántica adiabática, aunque hoy en día se le llama simplemente la fase de Berry. En el mismo año en el que Michael Berry anunciara su descubrimiento, un trabajo posterior titulado “Holonomy, the Quantum Adiabatic Theorem and Berry’s Phase” de Barry Simon publicado en diciembre de 1983 en el Physical Review Letters reformuló el resultado de Berry en el lenguaje compacto de la Geometría Diferencial proporcionando fórmulas simples de cálculo que hacen más sencillos los cómputos, y subrayando la conexión estrecha que hay entre la geometría y la física teórica moderna, en donde las propiedades topológicas de las superficies curvas han tomado una importancia decisiva. El mismo Barry Simon declaró en ese entonces al hablar de la fase de Berry que “debió de haber sido descubierta desde hace 50 años”. Bueno, de hecho ya había sido descubierta casi 30 años atrás por S. Pancharatnam, pero la enorme importancia del descubrimiento pasó desapercibida en aquél entonces como seguramente entre las toneladas de materiales científicos que se publican año tras año tal vez haya resultados de enorme importancia que permanecen acumulando polvo en los anaqueles a espera de ser redescubiertos. Al ser enterado Michael Berry del trabajo pionero de S. Pancharatnam, elaboró otro trabajo posterior titulado “The adiabatic phase and Pancharatnam’s phase for polarized light” publicado en 1987 en el Journal of Modern Optics en donde usando elementos básicos del álgebra espinorial y matrices Hermitianas 2×2 se estableció la relación precisa entre la fase óptica de Pancharatnam y el cambio de fase para sistemas cuánticos ciclados con la suficiente lentitud como para que se les pueda aplicar el teorema adiabático. Específicamente, el resultado central de Pancharatnam cuando es expresado simétricamente concierne un haz luminoso que es regresado a su estado inicial de polarización a través de dos polarizaciones intermedias, demostrándose que la fase no regresa a su valor original sino que aumenta en:
siendo Ω el área (el ángulo sólido) abarcado en la esfera de Poincaré por el triángulo geodésico cuyos vértices son las tres polarizaciones. De hecho, Pancharatnam confirmó él mismo experimentalmente su propia teoría detectando los desplazamientos de fase a través del fenómeno de la interferencia.
La primera confirmación experimental de la fase de Berry fue el seguimiento a un experimento propuesto por Raymond Y. Chiao y Yong-Shi Wu en un papel publicado en el Physical Review Letters en agosto de 1986 bajo el título “Manifestations of Berry’s Topological Phase for the Photon”, en el cual se recurre a una propiedad compartida por la luz y otras partículas que carecen de masa en reposo, el hecho de que la dirección de un rayo de luz (compuesto por fotones) y su momento angular de spin tienen que estar siempre alineados. Para hacer que la dirección del spin de un haz de luz polarizada dé una vuelta produciéndose un cambio en la fase lo único que hay que hacer es doblar físicamente (en el espacio) el camino del recorrido de un rayo de luz. Raymond Chiao y Akira Tomita llevaron a cabo el experimento en 1986 usando una fibra óptica recubierta con una capa de Teflon enrollándola a la forma de una hélice para meter en un extremo de la fibra óptica un rayo de luz polarizada como se muestra en la siguiente figura en la cual el haz de luz polarizada es metido por el lado derecho saliendo por el lado izquierdo de la figura:
La fase de las ondas de luz es medida a través de la polarización de las ondas (véase la entrada “El acto de medición”) comparando la polarización de la luz a la entrada con la polarización de la luz a la salida (en una fibra óptica recta sin doblez alguno no hay cambio de fase entre el vector de polarización de la luz que entra por un extremo de la fibra óptica y el vector de polarización de la luz que sale por el otro lado de la fibra, siendo en tal caso cero el ángulo de cambio de fase de Berry). La diferencia encontrada resultó ser exactamente la misma diferencia de fase predicha por la teoría. El siguiente par de figuras conlleva la idea de la relación geométrica que hay en un vector de polarización conforme el fotón luminoso se va desplazando a lo largo de la fibra óptica:
El hecho de que la fase de Berry exhiba las características de una memoria, y el hecho de que lo haga a niveles sub-microscópicos obedeciendo las reglas de la Mecánica Cuántica, ha encendido los “focos rojos” entre los científicos e ingenieros del campo de la informática que tratan de hacer realidad lo que podría ser considerado el proyecto más ambicioso de todos los proyectos en ciencias computacionales: la computación cuántica. Entre la literatura cada vez más numerosa que hay al respecto, y tomando al azar uno de los cada vez más frecuentes trabajos publicados sobre el tema, encontramos el trabajo titulado “Observation of Berry’s Phase in a Solid State Qubit” publicado en 2007 en la revista Science, en el cual el equipo ETH del Instituto Federal de Tecnología en Zurich, Suiza, reporta el éxito obtenido por vez primera en la realización de una operación geométrica en un bit cuántico creado en un microchip. Se trata, en esencia, del uso de la geometría para llevar a cabo computaciones cuánticas.
Ahora que tenemos una idea más firme sobre la importancia geométrica de la fase de Berry, podemos repasar nuevamente lo que se obtuvo arriba, cuando se vió que si una partícula cuyo Hamiltoniano sea H(t) comienza en un eigenestado de H(0) entonces bajo condiciones adiabáticas tal partícula se mantendrá en el n-avo eigenestado de H(t), recogiendo en el camino un factor de fase que dependerá del tiempo. Vimos que la función de onda será:
En el exponencial se tienen en realidad dos factores de fase. El primero de ellos está dado por:
que hemos dado en llamar aquí la fase dinámica y la cual es una generalización del factor:
al caso en el cual En es ahora dependiente de la variable tiempo. Por otro lado, tenemos a:
que llamaremos aquí la fase geométrica.
Ahora bien, ψn(t) depende de la variable tiempo porque algo en el operador Hamiltoniano H de energía está cambiando con el tiempo, algún parámetro que llamaremos R(t). En el caso de la partícula encerrada en una caja con una pared móvil que vimos arriba en detalle, el parámetro R(t) era la anchura creciente de la caja que simbolizamos como α(t). Tomando esto en consideración, podemos escribir lo siguiente:
De este modo, se tiene entonces:
siendo Rinicial y Rfinal los valores inicial y final de R(t). Hay un caso especial en el cual después de un cierto tiempo T el operador Hamiltoniano H(t) regresa a su forma original, lo cual implica que Rfinal.=.Rinicial. En el caso de la partícula encerrada en una caja con una pared móvil, esto equivaldría a la situación en la cual la pared es ampliada adiabáticamente desde a hasta 2a, y tras esto la pared es devuelta adiabáticamente a su posición original, para lo cual γn(T).=.0. En el caso del péndulo de Focault, esto equivaldría a llevar el péndulo de Focault móvil a lo largo de la ruta ANBA, regresando tras esto siguiendo el camino ABNA (véase la figura de arriba) quedando nuevamente los planos de oscilación del péndulo móvil y del péndulo fijo alineados nuevamente en el mismo plano.
Se supuso que solo hay un parámetro R(t) en el Hamiltoniano que está cambiando con el tiempo. Ampliaremos esta suposición considerando que puede haber N parámetros que pueden estar cambiando con el tiempo, o sea R1(t), R2(t), R3(t), etcétera. Podemos ampliar lo anterior para tomar esto en cuenta, teniendo entonces:
siendo:
y siendo:
Esto nos deja con lo siguiente:
Si el operador Hamiltoniano H ha de regresar a su forma original después de transcurrido un tiempo T (lo cual equivale a efectuar un recorrido completo), el cambio geométrico de fase neto será:
Esta es una línea de contorno llevada a cabo sobre una trayectoria cerrada en el espacio paramétrico, y por lo general no es igual a cero. Esta es la ecuación que fue obtenida por Michael Berry en 1983, y γn(T) es lo que conocemos como la fase de Berry. Como puede verse, la fase de Berry depende únicamente del recorrido seleccionado para llevar a cabo la trayectoria, y no de qué tan rápido la trayectoria pueda haber sido recorrida, siempre y cuando se lleve a cabo con suficiente lentitud para que la aproximación adiabática pueda sostenerse como válida. En contraste, lo que llamamos la fase dinámica definida como:
es algo que como puede verse depende en forma total del tiempo que ha transcurrido.
Puesto que, como se señaló arriba, estamos acostumbrados a pensar que la fase de la función de onda es tan insignificante como arbitraria en virtud de que las cantidades físicas involucran a |Ψ|2 y el factor de fase se cancela al ser multiplicada la función de onda por su conjugado complejo, todavía hasta tiempos recientes había muchos que suponían que la fase geométrica no tenía relevancia física alguna. La importancia del descubrimiento de Berry fue el haberse dado cuenta de que si el Hamiltoniano es llevado a través de una trayectoria cerrada (sin brechas) llevándolo de vuelta a su forma original, la fase relativa al inicio del proceso y al final del mismo no es arbitraria, y de hecho puede ser medida, tal y como lo hicieran Raymond Chiao y Akira Tomita en 1986.
Para quienes recuerden lo más relevante de los temas tratados en las entradas tituladas “Evolución temporal de las ondas de materia”, posiblemente en algunos lectores pueda haber alguna confusión sobre la relevancia de los factores de fase que hemos tratado aquí con el papel que puede jugar un factor de fase en el fenómeno de los estados mezclados. Suponiendo que comenzamos con una partícula encerrada en una caja cuya función de onda sea una mezcla en partes iguales de las dos funciones de onda que corresponden a los primeros eigenestados de la partícula encerrada en una caja:
Después de determinarse la constante de normalización como A.=.1/√2 y de insertarse los dos primeros eigenestados para una partícula encerrada en una caja, se tiene para la función de onda total Ψ(x,t):
de la cual obtenemos la densidad de probabilidad como:
con lo cual se pueden obtener los valores esperados en las observables físicas tales como el valor esperado en la posición de la partícula:
encontrándose en esta situación que se trata de una observable física que está oscilando con el tiempo. Si le anexamos un factor de fase a cualquiera de las dos eigenfunciones de onda, por ejemplo:
entonces, repitiendo los cálculos, se tiene para la función de onda total Ψ(x,t):
de la cual se obtiene la densidad de probabilidad:
y de la cual se obtiene para el valor esperado de la posición de la partícula:
La única diferencia entre este valor esperado para la posición y el valor anterior es que el efecto consiste en un desfasamiento que desplaza el tiempo t.=.0 empezando el conteo del tiempo en un tiempo distinto, siendo debatible el que algo así pueda ser detectado en un experimento de laboratorio.
Sin embargo, este caso de dos eigenestados mezclados supone que el operador Hamiltoniano H permanece invariable con el transcurso del tiempo, y lo que varía es la función de onda Ψ(x,t) de acuerdo a la prescripción dada por la ecuación de Schrödinger. En cambio, para el fenómeno que hemos estudiado aquí en esta entrada, la suposición fundamental es que el operador Hamiltoniano varía con el tiempo, si bien lo hace lentamente. Más aún, para que pueda darse el fenómeno de la fase geométrica no se requiere de eigenestados mezclados, y de hecho la suposición fundamental es que los estados propios permanecen separados sin mezclarse en lo absoluto; tal es la filosofía esencial del teorema adiabático, así que no puede haber confusión alguna entre lo que hemos tratado aquí y lo que se ha tratado previamente, se trata de cosas completamente diferentes, y lo que tenemos aquí es algo completamente nuevo cuya naturaleza esencial es de carácter geométrico.
Algo interesante que cabe mencionar en lo que toca a la aplicabilidad de la aproximación adiabática es lo que se conoce comúnmente como el caso del cruce evitado. Considérese un sistema atómico hipotético de dos niveles 1 y 2 que designaremos como:
usando la notación bra-ket de Dirac. La función de onda del sistema puede ser representada como una combinación linear de estos dos estados:
Podemos considerar a los dos estados de base como estados del momento angular, cada uno con su propia geometría. En ausencia de cualquier influencia exterior, la separación energética entre ambos estados será igual a ħω0, y la energía inicial de cada estado será:
Supóngase que ahora aplicamos y vamos incrementando lentamente un campo magnético B al sistema. La energía del estado 1 irá aumentando paulatinamente mientras que la energía del estado 2 irá disminuyendo paulatinamente. Supóngase ahora que la dependencia del campo magnético es linear y que la matriz Hamiltoniana H del sistema con el campo magnético aplicado puede ser escrita de la siguiente manera:
en donde μ es el momento magnético del átomo que se supone igual para ambos estados, y a es algún factor de acoplamiento independiente del tiempo entre los dos estados. Los elementos diagonales son las energías E1(t) y E2(t) de ambos estados. Sin embargo, puesto que la matriz no es una matriz diagonal, estos dos estados no son eigenestados del nuevo Hamiltoniano que incluye la contribución del campo magnético.
Los eigenvectores de la matriz Hamiltoniana H son los eigenestados del sistema que podemos simbolizar como:
Recurriendo a las técnicas expuestas previamente, podemos determinar que los eigenvalores que corresponden a estas eigenfunciones de onda son:
Es importante tomar nota de que los eigenvalores λ1(t) y λ2(t) son los únicos valores de salida para cualquier medición individual de la energía del sistema, mientras que las energías E1(t) y E2(t) corresponden a los valores esperados para la energía del sistema en los estados 1 y 2.
La siguiente figura nos muestra lo que puede ocurrir conforme se va incrementando la intensidad del campo magnético:
Obviamente, nuestro sistema hipotético no es uno en el que los dos estados representen al spin del electrón (un estado con el spin apuntando “hacia arriba” y el otro estado con el spin apuntando “hacia abajo”), porque en un experimento clásico tipo Stern-Gerlach en ausencia de un campo magnético los niveles energéticos de los dos estados tienen un mismo valor y por lo tanto son estados degenerados, algo a lo cual no se le puede aplicar la aproximación adiabática, y al ir aumentando el campo magnético se rompe la degeneración y los dos niveles de energía se van separando linearmente, lo cual no ocurre en la gráfica que tenemos aquí. Obsérvese (de las fórmulas para λ1(t) y λ2(t) obtenidas arriba) que para un acoplamiento que sea diferente de cero, esto es, a.≠.0, los eigenvalores del Hamiltoniano no pueden ser degenerados, y por lo tanto tenemos un cruce evitado, la curva superior azul no puede “tocar” a la curva inferior roja, las curvas no se pueden cruzar, y por lo tanto no puede haber un “brinco” de un estado a otro al ir aumentando el campo eléctrico. Si un átomo se encuentra inicialmente en el estado 1 en ausencia total de un campo magnético, entonces un incremento en el campo magnético B que obedezca la condición adiabática variando lentamente con respecto al tiempo:
logrará que el sistema permanezca en el eigenestado ψ1(t) a través del proceso siguiendo la línea roja en la figura. Sin embargo, un incremento rápido en el campo magnético que corresponda a la condición diabática:
causará que el sistema siga la línea diagonal sólida (de color negro en la figura) ocasionando un cambio del estado ψ1 al estado ψ2. En pocas palabras, habrá un cruce de un estado a otro. Una forma (parcialmente correcta) de visualizar esto es imaginando que al variar el campo magnético B rápidamente la partícula lleva una suficiente inercia propia para poder dar el brinco del estado inferior al estado superior en la zona de mayor proximidad entre ambas curvas, mientras que si el campo magnético es variado lentamente entonces no se le imparte a la partícula suficiente inercia como para que pueda dar el salto en la zona en la cual ambas curvas casi se tocan pero sin tocarse. Las siguientes dos figuras nos muestran el caso de una partícula que brinca del estado 0 al estado 1 al ser aumentado rápidamente el campo magnético (proceso diabático) y otra partícula que permanece en el mismo estado 0 al ser aumentado lentamente el campo magnético (proceso adiabático):
¿Y qué ocurrirá entre estos dos extremos? En tal caso, cuando:
habrá una probabilidad para encontrar al sistema en cualquiera de los dos eigenestados ψ1 y ψ2. La primera solución analítica al problema de calcular las probabilidades de transición de un estado a otro en el caso especial clasificado entre lo diabático y lo adiabático fue obtenida independientemente en 1937 por Lev Landau y por Clarence Zener para el caso especial de una perturbación (una variación en el campo magnético, por ejemplo) cuya variación es linear y en la cual el parámetro que varía con el tiempo no acopla los estados relevantes (el trabajo más conocido es el de Zener bajo el título “Non-Adiabatic Crossing of Energy Levels” publicado en septiembre de 1932 en los Proceedings of the Royal Society), lo cual está consignado bajo la fórmula de Landau-Zener. En las figuras de arriba, el lugar más probable en el cual podrá ocurrir un cruce de un estado a otro será en donde la curva azul está en su punto mínimo y la curva roja está en su punto máximo, o sea en donde hay la menor distancia de separación entre las dos curvas. Esta distancia mínima es la brecha significativa entre los dos estados del sistema. En general, dada una ecuación de Schrödinger con un Hamiltoniano que varíe lentamente con el tiempo, la condición de validez para que el sistema se siga manteniendo en un mismo eigenestado evolucionando apropiadamente en el tiempo (aproximación adiabática) puede ser expresada mediante el cociente entre la razón de cambio del Hamiltoniano y la brecha que debe existir entre los eigenvalores instantáneos de energía conforme los eigenvalores también van evolucionando con el tiempo. La condición de que esta brecha entre los eigenestados se mantenga en todo momento (aunque pueda irse cerrando o ampliando) es de enorme importancia, y esto fue corroborado formalmente por Tosio Kato en 1950 en su trabajo titulado “On the Adiabatic Theorem of Quantum Mechanics” publicado por el Journal of the Physical Society of Japan. El estudio detallado de las transiciones que ocurren cuando salimos fuera del régimen de la aproximación adiabática requiere entrar a fondo en otros detalles técnicos que suelen ser tratados en obras tales como el libro “Nonadiabatic Transition: Concepts, Basic Theories and Applications” de Hiroki Nakamura. El régimen no-adiabático en la cual no solo hay cruces (brincos, saltos) de un estado a otro sino inclusive las mismas curvas de eigenestados diferentes se tocan y hasta se traslapan es de enorme importancia porque las reacciones químicas y varios procesos espectroscópicos de moléculas son inducidos en su gran mayoría precisamente porque hay “cruces” no sólo de curvas de energía potencial sino inclusive de superficies de energía potencial (estas superficies son definidas como superficies equipotenciales por corresponder cada una de ellas a un mismo valor de energía potencial). Sin los “cruces” y traslapes no-adiabáticos seguramente habría muy poca química de qué hablar.