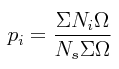En el denominador, si en el factor eα se le permite a α tomar un valor negativo, entonces en virtud de la operación:
e-α·eE/kT = e-α+E/kT
es posible en principio encontrar para cualquier valor de E/kT (a cualquier energía E y a cualquier temperatura T) un valor de α capaz de reducir el exponente a cero, con lo cual se tiene e0.=.1, lo cual a su vez hace cero el denominador de FMB haciendo que FMB tome un valor físico sorprendente, un valor infinito (esto es precisamente lo que ocurre en la condensación Einstein que veremos después, cuando todas las partículas terminan yéndose hacia el estado de más baja energía, el estado fundamental). Pero peor aún, si se le permite a α tomar un valor negativo, FMB podría tomar también un valor negativo, algo carente de sentido. Es obvio que la mayor densidad posible de partículas corresponde a un valor de α igual a cero. Sin embargo, si α es igualado a cero, y la distribución energética de partículas que se esté considerando (por ejemplo, una caja cúbica hueca de paredes impenetrables sellada por fuera) es integrada sobre todos los valores posibles de energía como se ha hecho en problemas anteriores, se obtiene entonces una densidad finita de partículas, y no una densidad infinita. Aparentemente, el formalismo que se ha desarrollado es incapaz de justificar la precipitación que ocurre en los gases Bose de alta densidad. Sin embargo, este no es el caso. La confusión surge del considerar a una distribución energética como un continuum de estados cuando esto, estrictamente hablando, no es así. Considerando los estados del gas ideal como discretos, la distribución discreta:
nos muestra que es posible tener una densidad infinita de partículas asociadas únicamente con el estado energético más bajo, el cual es Ei.=.0 (en la condensación Bose-Einstein, a fin de cuentas siempre habrá un número finito de partículas, las cuales al irse todas hacia un solo estado energético crean la ilusión de un infinito). Esto destaca la enorme importancia de tener siempre presente en la mente la diferencia que hay entre una distribución discreta y una distribución continua, sobre todo cuando se están manejando situaciones extremas en el laboratorio a temperaturas sumamente bajas o densidades muy elevadas de partículas como ocurre con todo lo que tiene que ver con la condensación de Bose. El mismo Erwin Schrödinger consideró este asunto sutil lo suficientemente importante como para discutirlo en detalle en su libro Statistical Thermodynamics. Pese a la sencillez del modelo matemático descubierto por Boltzmann, basado en las reglas más sencillas que hay en la combinatórica, puede decirse que la gran mayoría de las confusiones y malentendidos que hay en la Mecánica Estadística junto con todos los aparentes infinitos y paradojas que hacen su aparición de cuando en cuando tienen su origen en la incapacidad para distinguir claramente lo que ocurre al pasar de una distribución discreta hacia una distribución continua y viceversa.
PROBLEMA: Supóngase que se tiene un sistema que consta de cuatro partículas indistinguibles. Supóngase además que la energía total del sistema es igual a 12 unidades de energía, y que el sistema está subdividido en los siguientes niveles:
E0 = 0, E1 = 1, E2 = 2, ..., En = n
Encuéntrese la energía promedio para tal sistema. ¿Tiene sentido la respuesta obtenida?
Una partícula que se encuentre en el estado E0 no contribuirá con energía alguna para el sistema, mientras que una partícula que se encuentre en el estado E3 contribuirá con tres unidades de energía para el sistema. De este modo, adoptando la convención:
(E0, E1, E2, E3, E4, E5, E6, E7, E8, E9, E10, E11, E12, ...)
se tiene que cuatro partículas repartidas de la siguiente manera:
(1,0,0,0,2,0,0,0,0,0,0,1,0,...)
darán una energía total igual a 19 unidades de energía:
1·0 + 0·1 + 0·2 + 0·3 + 2·4 + 0·5 + 0·6
+0·7 + 0·8 + 0·9 + 0·10 + 1·11 + 0·12
= 8 + 11
= 19
Sin embargo, si la energía del sistema debe ser igual a un total de 12 unidades de energía, la combinación considerada arriba que proporciona 19 unidades de energía no es una distribución aceptable. Esto limita severamente las distribuciones posibles. Y aunque haya una cantidad infinitamente grande de “cajas” de energía disponibles, una sola partícula en la “caja” E13 excedería con sus trece unidades de energía el tope máximo disponible de 12 unidades aunque las otras tres partículas estén en el nivel E0, sin dar contribución energética alguna, razón por la cual podemos ignorar todos los niveles energéticos superiores a E12. Más aún, por ser las partículas indistinguibles, cada combinación como:
(0,1,0,1,2,0,0,0,0,0,0,0,0)
sólo se puede dar de una sola manera y no de varias. De este modo, manteniendo las restricciones de una cantidad constante de partículas y una energía total invariable para un sistema aislado, podemos agrupar las distintas posibilidades en una tabla como la siguiente:
Si tomamos, por ejemplo, la combinación que corresponde al noveno renglón, podemos verificar que dicha combinación produce las 12 unidades de energía:
1·E0 + 1·E1 + 1·E2 + 1·E9 = 1·0 + 1·1 + 1·2 + 1·9 = 12
La suma de los números en la tercera columna nos servirá para calcular la probabilidad p2 de que pueda darse el estado energético E2 con el sistema sujeto a las restricciones usuales. Este número es igual a 20. Pero necesitamos también el gran total obtenido de la suma de los totales de las demás columnas, el cual es:
27 + 23 + 20 + 18 + 14 + 10 + 8 + 5 + 4 + 3 + 2
= 136
Entonces la probabilidad que corresponde al estado E2 es:
p2 = 20/136 = 0.147
A continuación se enlistan las probabilidades que corresponden a todos y cada uno de los estados energéticos posibles del sistema:
p0 = F0 = 27/136 = 0.198
p1 = F1 = 23/136 = 0.169
p2 = F2 = 20/136 = 0.147
p3 = F3 = 18/136 = 0.132
p4 = F4 = 14/136 = 0.102
p5 = F5 = 10/136 = 0.735
p6 = F6 = 8/136 = 0.588
p7 = F7 = 5/136 = 0.0367
p8 = F8 = 4/136 = 0.0294
p9 = F9 = 3/136 = 0.022
p10 = F10 = 2/136 = 0.0147
p11 = F11 = 1/136 = 0.0074
p12 = F12 = 1/136 = 0.0074
Si multiplicamos cada uno de los valores energéticos que corresponden a los estados Ei por sus respectivas probabilidades pi, obtendremos así la contribución energética probabilista de cada uno de ellos a la energía total del sistema:
F0E0 = 0
F1E1 = 0.169
F2E2 = 0.294
F3E3 = 0.396
F4E4 = 0.408
F5E5 = 0.3675
F6E6 = 0.3528
F7E7 = 0.2569
F8E8 = 0.2352
F9E9 = 0.198
F10E10 = 0.147
F11E11 = 0.0814
F12E12 = 0.0888
Y si sumamos cada una de estas contribuciones, obtendremos entonces la energía promedio del sistema:
Esta es la energía promedio por partícula. Puesto que el sistema consta de cuatro partículas, entonces al tener cada una de estas partículas una energía promedio de tres unidades de energía la energía total del sistema debe rondar en las 12 unidades de energía. Esto es justo lo que esperaríamos. Por lo tanto, la respuesta obtenida tiene sentido.
La distribución Bose-Einstein es mucho más fácil de manipular en virtud de que dicha distribución considera que las partículas bajo consideración son indistinguibles, a diferencia de la distribución Maxwell-Boltzmann que considera a las partículas distinguibles. Es por ello que resulta instructivo repetir el problema anterior pero suponiendo que las partículas son distinguibles, con el fin de comparar ambos procedimientos y resultados.
PROBLEMA: Supóngase que se tiene un sistema que consta de cuatro partículas distinguibles. Supóngase además que la energía total del sistema es igual a 12 unidades de energía, y que el sistema está subdividido en los siguientes niveles:
E0 = 0, E1 = 1, E2 = 2, ..., En = n
(1) Encuéntrese la energía promedio para tal sistema. (2) Hágase una gráfica de la distribución de las probabilidades que se deben asignar a cada estado energético. (3) Hágase una gráfica que muestre la forma en la cual están repartidos sobre una base probabilista los estados energéticos mostrando la amplitud de cada contribución energética a la energía del sistema. (4) ¿Tiene sentido la respuesta obtenida?
Este problema es muy parecido al anterior, excepto que ahora se tienen cuatro partículas distinguibles que se pueden etiquetar como A, B, C y D. Esto significa que cada combinación mostrada en la tabla de arriba en cada uno de los 34 renglones no será única sino que tendrá (generalmente hablando) varias formas de ser realizada. Esto requiere tomar la tabla de arriba agregándole una columna adicional bajo el rubro “Ω” que nos dá la cantidad de maneras en las cuales se puede realizar cada una de las combinaciones, obteniéndose así una tabla como la siguiente en la cual en la parte inferior (fuera de la tabla) se dá la suma total de todos los Ω:
Así, por ejemplo, el número total de formas en las cuales se puede lograr la combinación mostrada en el primer renglón, con cuatro partículas distinguibles, es:
En esta combinación, una de las cuatro partículas se encuentra en el nivel E12 contribuyendo con las 12 unidades de energía para el sistema, mientras que las otras tres se encuentran en el nivel E0 sin aportar energía alguna al sistema. Y en el segundo renglón, el número total de formas en las cuales se puede lograr la combinación mostrada es:
en donde dos de las partículas en el nivel cero E0 no contribuyen con energía alguna al sistema, una partícula en el nivel E1 contribuye con una unidad de energía, y la cuarta partícula en el nivel E11 contribuye con 11 unidades de energía para dar un total de 12 unidades de energía, habiendo 12 maneras diferentes de lograrlo reacomodando las cuatro partículas en los niveles.
Si tomamos la tabla de arriba y multiplicamos para cada uno de sus renglones las entradas que ven en dicho renglón por el valor de Ω que corresponde al renglón, sumando tras esto los subtotales para cada columna (como lo hicimos en la entrada “Mecánica Estadística Cuántica I” para el caso en el que se tienen tres partículas distinguibles A, B y C con un sistema con una energía total de 8 unidades), se obtiene la siguiente tabla derivada en donde las cantidades destacadas en color verde claro abajo de la tabla (los subtotales) muestran la característica propia de la distribución de Boltzmann:
Teniendo estos valores, y siendo que ΣΩ que es igual a 455 multiplicado por 4 (el número de partículas) es igual a 1820, podemos obtener las fracciones probabilistas tal y como se hizo cuando se estudio el problema similar que corresponde a tres partículas, dividiendo cada una de estas entradas entre 1820. Por ejemplo, para p2:
p2 = 264/1820 = 0.145
Otra manera un poco más elegante para calcular la probabilidad relativa de ocurrencia que se debe asignar a cada estado energético consiste en recurrir a la fórmula que ya había sido obtenida (y utilizada) en la entrada titulada “Mecánica Estadística Cuántica I”:
siendo Ns el número de partículas que hay en el sistema (4). El cálculo numérico para p0 (recorriendo la primera columna de la primera tabla de arriba hacia abajo formando los productos parciales con los Ω respectivos) usando la fórmula se muestra a continuación:
A continuación se enlistan las probabilidades que corresponden a todos y cada uno de los estados energéticos posibles del sistema:
p0 = F0 = 364/1820 = 0.20
p1 = F1 = 312/1820 = 0.1714
p2 = F2 = 264/1820 = 0.145
p3 = F3 = 220/1820 = 0.121
p4 = F4 = 180/1820 = 0.098
p5 = F5 = 1441820 = 0.0791
p6 = F6 = 112/1820 = 0.0615
p7 = F7 = 84/1820 = 0.046
p8 = F8 = 60/1820 = 0.03297
p9 = F9 = 40/1820 = 0.022
p10 = F10 = 24/1820 = 0.0132
p11 = F11 = 12/1820 = 0.0066
p12 = F12 = 4/1820 = 0.0022
Después de estos cálculos numéricos, es prudente a estas alturas hacer una verificación sumando todas estas probabilidades sabiendo de antemano que la suma de las mismas debe ser igual a la unidad (la certeza):
Σ.pi =1
La gráfica de estas probabilidades nos muestra una caída del tipo exponencial como la que se podría esperar de una distribución Maxwell-Boltzmann:
Obsérvese que, en contraste con la gráfica obtenida en la entrada titulada “Mecánica Estadística Cuántica I” para el caso de tres partículas, la gráfica para el caso de cuatro partículas muestra a la curva exponencial decreciente de una manera más clara y pronunciada. En realidad, no se requieren de muchas partículas para darse cuenta del patrón que siguen este tipo de estadísticas. Para el caso de un sistema con una gran cantidad de partículas (como un mol de partículas de cualquier gas), la gráfica discreta se vuelve tan densa que resultará imposible el poder distinguirla de una función continua, y esto es precisamente lo que permite recurrir a los procedimientos del cálculo infinitesimal para poder obtener la relación de Boltzmann.
Multiplicando en el problema que nos concierne aquí para cuatro partículas cada una de las probabilidades pi obtenidas con los valores energéticos con los que se corresponden los estados Ei, se obtiene así la contribución energética probabilista de cada uno de ellos a la energía total del sistema:
F0E0 = 0
F1E1 = 0.1714
F2E2 = 0.2901
F3E3 = 0.3626
F4E4 = 0.3956
F5E5 = 0.3956
F6E6 = 0.3692
F7E7 = 0.3230
F8E8 = 0.2637
F9E9 = 0.1978
F10E10 = 0.1319
F11E11 = 0.2176
F12E12 = 0.0264
lo cual cuando es graficado nos produce la siguiente distribución:
Y si sumamos cada una de estas contribuciones energéticas, obtendremos entonces la energía promedio del sistema:
Este resultado tiene sentido, ya que si consideramos a la energía promedio por partícula, habiendo cuatro partículas entonces la energía total del sistema será igual a 12 unidades de energía, que es precisamente lo que se había postulado desde el principio como una de las restricciones del sistema.
Elaborando sobre los dos problemas anteriores en los cuales se obtuvo la energía promedio para un sistema de cuatro partículas tanto para una distribución Maxwell-Boltzmann FMB del tipo clásico como para una distribución Bose-Einstein FBE del tipo cuántico, si lo que queremos es obtener una distribución cuántica Fermi-Dirac FFD para el mismo sistema de cuatro partículas entonces las modificaciones que hay que hacer en los cálculos son mínimas, y de hecho la distribución Fermi-Dirac resulta ser la más sencilla de todas. Todo lo que tenemos que hacer es tomar la tabla que ya fue elaborada arriba para la distribución Bose-Einstein, y eliminar las combinaciones en las cuales hay más de dos partículas (indistinguibles) por “caja” de energía, ya que cada “caja” solo permite dos fermiones en virtud del principio de exclusión de Pauli; lo cual requiere eliminar los siguientes renglones destacados en color verde claro:
Con esto, nos queda la siguiente tabla en la cual podemos repetir los cálculos en una forma parecida a como se llevaron a cabo en el caso de la distribución Bose-Einstein:
Análogamente, las semejanzas de origen que hay en derivación de las tres distribuciones estadísticas que hemos estado utilizando posibilita la realización de desarrollos que no difieren mucho el uno del otro. Como muestra de ello, primero se obtendrá una expresión para la energía total de un gas de bosones, tras lo cual se obtendrá la energía total de un gas de fermiones.
En el caso de un gas de bosones, usando la distribución Bose-Einstein FBE tenemos el siguiente desarrollo en el cual se utilizará un cambio de variable utilizando a q para representar a E/kT:
La integral está expresada en una forma ampliamente estudiada por los matemáticos, para la cual la solución en forma cerrada es la siguiente siempre y cuando α sea mayor o igual que cero:
siendo ε = ±1, siendo p>0 y siendo Γ(x) la función gamma para la cual algunos valores y propiedades útiles de la misma son los siguientes:
y para la cual en el caso especial en el que α = 0 y ε = +1 la integral se convierte en:
siendo ζ(x) la función zeta de Riemann definida como:
De este modo, con lo anterior se llega a lo siguiente:
en donde Z = e-α.
Por otro lado, en el caso de un gas de fermiones, usando la distribución Fermi-Dirac FFD tenemos el siguiente desarrollo en el cual también se utilizará un cambio de variable utilizando a q para representar a E/kT:
Recurriendo nuevamente a la misma integral estándard dada arriba, se tiene:
lo cual se puede simplificar aún más para llegar al siguiente resultado:
en donde nuevamente Z = e-α.
Además de la explicación formal desde el punto de vista de la Mecánica Estadística Cuántica que se puede dar a la distribución espectral de la radiación del cuerpo negro y la explicación del comportamiento de la capacidad calorífica molar de los sólidos a bajas temperaturas bajo el modelo de Debye, otra aplicación interesante de la distribución Bose-Einstein es la que se le dá al helio líquido. En un intento por darle una explicación a las increíbles propiedades del helio a bajas temperaturas, en 1938 el físico Fritz London sugirió algo que entonces parecía una idea osada: considerar al helio líquido como si fuese un gas que obedece la distribución Bose-Einstein.
Cuando el helio líquido es enfriado a temperaturas sumamente bajas, a una temperatura aproximada de unos 2.17 °K ocurre un cambio sorprendente. En 1924, el físico holandés H. Kamerlingh Onnes y su colaborador J. Boks midieron la densidad del helio líquido en función de la temperatura, obteniendo una transición brusca en la variación de la densidad precisamente a dicha temperatura. Posteriormente, en 1928, Willem Hendrik Keesom y Mieczyslaw Wolfke, descubridores del helio II, sugirieron que la discontinuidad era el resultado de una transición de fase, usando los términos helio I para describir el comportamiento del líquido arriba de la temperatura crítica de los 2.17 °K y helio II para describir el comportamiento del líquido por debajo de dicha temperatura crítica. Algún tiempo después, en 1932 Keesom y Klaus Clusius midieron el calor específico del helio en función de la temperatura, obteniendo una gráfica como la siguiente:
Por su parecido con la letra griega lambda (λ), a la transición que ocurre a la temperatura crítica se le conoce como el punto lambda. Las siguientes tres gráficas (tomadas de The Nature of the λ-Transition: Progress in Low Temperature Physics de M. J. Buckingham y W. M. Fairbank publicado en 1961 por North-Holland Publishing Company) muestran en órdenes crecientes de “resolución” (magnificación) el comportamiento del punto lambda:
Justo arriba del punto lambda, el helio hierve vigorosamente conforme se evapora. Las burbujas de la evaporación desaparecen en el punto lambda, aunque la evaporación continúa. Este efecto es debido al aumento brusco en la conductividad térmica del helio en el punto lambda.
Las mediciones de la conductividad térmica muestran que el helio II conduce el calor mejor que el helio I por un factor de más de un millón; y de hecho el helio II es un mejor conductor del calor que cualquier metal. Este proceso de conducción térmica es muy diferente del proceso usual, en virtud de que el calor conducido no es proporcional a la diferencia de temperaturas. Si se mide la viscosidad del helio líquido II pasando el líquido a través de un tubo capilar fino, el resultado depende del tamaño del tubo capilar; la viscosidad medida se acerca a una viscosidad igual a cero conforme el diámetro del capilar disminuye. Sin embargo, si se utiliza otro método de medición de la viscosidad conocido como el método del disco rotatorio, la viscosidad obtenida no difiere mucho de la viscosidad del helio I.
En lugar de mencionar otras propiedades interesantes del helio líquido II, hablaremos brevemente acerca de la teoría propuesta por Fritz London en 1938 y refinada posteriormente por Laszlo Tisza quien fue el que propuso formalmente que el helio II fuera considerado como un gas ideal de Bose degenerado. De acuerdo con esta teoría, imaginamos al helio II como si consistiera de dos partes; una de ellas con propiedades similares a las del helio I, y la otra un superfluído con propiedades drásticamente diferentes. De este modo, la densidad ρ del helio líquido II consiste en la suma de las densidades del superfluído y el fluído normal:
ρ = ρs + ρn
Conforme la temperatura es disminuída aún más desde el punto lambda, la densidad del superfluído aumenta mientras que la del fluído normal disminuye hasta que, a la temperatura del cero absoluto, lo único que queda es superfluído. Se supone que el superfluído corresponde a moléculas de helio que están en el estado cuántico más bajo posible, el estado fundamental. Estas moléculas no son excitadas a niveles superiores de energía, de modo tal que el superfluído no puede hacer contribución alguna a la viscosidad. Cuando se mide la viscosidad del helio II con el método del disco rotatorio, únicamente la componente normal de fluído ejerce una fuerza viscosa sobre el disco. Conforme al temperatura es disminuída, la fracción de helio en su componente normal disminuye de un 100 por ciento en el punto lambda a un cero por ciento a la temperatura del cero absoluto. Por lo tanto, la viscosidad debe aumentar rápidamente con un aumento en la temperatura, en conformidad con los resultados experimentales.
Entre las propiedades asombrosas del helio líquido II destaca un efecto conocido en la literatura popular como el efecto “Rollin creepin film” (llamado así en honor a su descubridor Bernard V. Rollin) que es una capa delgadísima (film) de unos 30 nanometros de espesor que escala las paredes del recipiente contenedor hasta salir fuera del mismo:
La fotografía que sigue nos muestra cómo el helio líquido II sale del recipiente escalando por las paredes delmismo para formar la gota que aparece en la parte inferior del contenedor:
Algo que no es obvio del todo es que el helio líquido pueda y deba comportarse como un gas ideal. Los átomos de helio sí ejercen fuerzas entre sí, aunque estando razonablemente separados a grandes distancias (relativamente hablando, a escalas atómicas) como lo confirma la baja viscosidad, estas fuerzas son bastante débiles. Se utiliza el modelo del gas ideal por su relativa sencillez y porque dá una visión sobre el comportamiento del helio líquido a muy bajas temperaturas.
Si consideramos una constante de normalización AHe de 3.5×10-6 para el gas helio a la temperatura ambiental (300 °K), esto implica que habrá muy pocas partículas por estado cuántico, permitiéndonos utilizar como medida simplificadora a la distribución Maxwell-Boltzmann. La densidad del helio líquido es de aproximadamente 0.145 gramos/cm3, con lo cual el volumen de un mol será:
V = (4 gramos/mol)/(0.145 gramos/cm3) = 27.6 cm3/mol
Usando este volumen en una ecuación que ya había sido obtenida previamente:
en lugar de 22.4 ×103 cm3 (el volumen de un gas ideal a temperatura y presión estándard), podemos calcular AHe para el helio líquido. A una temperatura aproximada de 2.°K, el resultado es AHe.≈.5, y por lo tanto la distribución Maxwell-Boltzmann no sería una buena aproximación para este “gas”. Veamos a continuación cómo la estadística de Bose-Einstein está relacionada con el modelo de los dos fluídos para el helio líquido. Supondremos que el helio líquido es un gas ideal de N átomos que sigue la distribución Bose-Einstein, para el cual el número de moléculas en el estado i es:
Como ya se mencionó previamente arriba al principio, la constante α no puede tomar un valor negativo, porque si así fuese ni podría volverse negativo para valores de Ei/kT menores que |α|. Mantendremos nuestra escala de energías de modo tal que la energía más baja continúe etiquetada como E0.=.0. Ya hemos visto que para un gas de N partículas en una caja contenedora macroscópica los estados energéticos son numerosos y muy cercanos el uno al otro, lo cual nos permite considerarlo como un continuum que nos permite reemplazar a gi (el número de estados con energía Ei) con la densidad de estados g(E)dE (el número de estados en el intervalo de energía dE). Ya habíamos visto previamente que la densidad de estados para este problema está dada por la expresión:
Se debe notar que el reemplazar a la distribución discreta de estados con una distribución continua hace que se ignore al estado fundamental, aunque se trabaja sobre la base de que por tratarse de un solo estado esto no será de consecuencias mayores. Por el momento, se ignorará a este estado, aunque veremos que esta suposición eventualmente conduce a dificultades, y será necesario considerar a este estado de manera explícita.
La constante α está fijada por la condición de normalización que ya ha sido utilizada previamente, con la cual se tiene:
en donde en la última línea se ha hecho x.=.E/kT. La integral es una función de que puede ser tabulada o graficada. Con fines de simplicidad, se acostumbra escribir la ecuación anterior de la siguiente manera:
en donde:
La gráfica de F(α) es la siguiente:
La función F(α) es una función monotónicamente decreciente para valores positivos de α, y tiene un valor máximo para α.=.0 el cual es F(0).=.2.612, el cual está destacado en la gráfica de arriba con una línea horizontal azul. Todo lo anterior implica que:
Poniéndolo todo en términos de la temperatura crítica Tc, definida como:
se puede afirmar que:
Si usamos para el volumen V el volumen molar V = 27.6 cm3 que corresponde a una densidad máxima de 0.145 gramos/cm3, encontramos de esto último la siguiente temperatura crítica:
Tc ≈ 3.1 °K
Para temperaturas que están por debajo de este punto crítico, no es posible satisfacer la condición de normalización. Podemos ver aquí que en tal situación ya no es posible ignorar al estado fundamental, al estado de más baja energía. Evidentemente, una cantidad significativa de moléculas deben encontrarse en el estado basal a temperaturas extremadamente bajas, siendo dicho número:
en donde se ha hecho g0 = 0 para este estado único y E0 = 0. Este número se vuelve muy grande al volverse α pequeño. Tomando en consideración este estado fundamental, la condición de normalización (corregida) se vuelve:
Esta ecuación se puede satisfacer para cualquier temperatura y densidad con un valor apropiado de α. Se puede recurrir a varios métodos de aproximación para encontrar el número relativo de moléculas que se encuentran en el estado fundamental. Usando la definición dada previamente para la temperatura crítica Tc, esto último se puede escribir de la siguiente manera:
Para una temperatura T inferior a la temperatura crítica Tc, se puede comprobar que la solución de esta ecuación para α es del orden de α.≈.N-1que a su vez será mucho menor que la unidad. Si con esto en mente utilizamos la aproximación F(α)/F(0).≈.1, se tiene entonces:
Así pues, para temperaturas inferiores a la temperatura crítica, el número de moléculas en el estado fundamental se vuelve importante. Considerando que los cálculos que se llevaron a cabo están basados en la presunción de que el helio líquido se comporta como un gas ideal, el valor obtenido para la temperatura crítica Tc de 3.1 °K está bastante cercano a la temperatura del punto lambda Tc.=.2.17 °K. Este proceso de las moléculas yéndose en masa hacia el estado basal conforme la temperatura es dismuída por debajo de la temperatura crítica es la condensación Einstein también como condensación Bose-Einstein, predicha por Einstein en 1924, aunque en aquél entonces no había evidencias experimentales de que tal fenómeno pudiera ocurrir, era una predicción puramente teórica. La obtención y confirmación de un condensado gaseoso cuántico “puro” sólo pudo ser lograda experimentalmente 70 años después por Eric Cornell y Carl Wieman en el laboratorio NIST-JILA (National Institute of Standards and Technology-Joint Institute for Laboratory Astrophysics) utilizando un gas de átomos de rubidio-87 congelados a una temperatura de 170 grados nano-Kelvin.
Las siguientes figuras nos muestran cómo pasamos de una distribución de partículas propias del helio líquido I puesto a una temperatura mayor que la temperatura crítica Tc (figura de la izquierda) a una distribución de partículas propias del helio líquido II puesto a una temperatura menor que la temperatura crítica (figura de la derecha), con casi todas los átomos de helio yéndose al estado energético fundamental:
De una manera un poco más sofisticada, lo siguiente nos muestra una perspectiva tridimensional contemporánea del proceso de condensación Bose-Einstein en tres etapas (de izquierda a derecha) conforme la temperatura va disminuyendo:
Al llegar a estos extremos sumamente bajos de temperatura, el condensado Bose-Einstein no es lo único que se puede formar. Pueden hacer también su aparición en el condensado vórtices cuánticos, los cuales se pueden obtener ya sea “agitando” al condensado Bose-Einstein con rayos láser o girando la trampa de confinamiento. Para poder explicar teóricamente el por qué se forman los vórtices cuánticos, es necesario recurrir a una ecuación ondulatoria de Schrödinger ampliamente utilizada para el análisis teórico de estos fenómenos, conocida como la ecuación Gross-Pitaevskii, la cual contiene un término no-lineal que es precisamente el término que dá origen a los vórtices cuánticos. Aunque estamos acostumbrados a imaginar un vórtice como algo que tiene un “sumidero” en su centro absorbiendo materia o energía (como los vórtices de los embudos que caracterizan a los huracanes, o los vórtices que caracterizan al agua que se va por el tubo en el centro de un lavadero o de un sanitario), es importante entender que estos vórtices son vórtices “perfectos” en los cuales no hay nada que se esté yendo al centro de los mismos en un sumidero como tampoco hay nada que esté saliendo fuera del centro del vórtice; la rotación angular de estos vórtices está caracterizada por círculos y no por una espiral que vaya hacia el centro del vórtice o que salga del centro del vórtice:
De la condición esencial para la cuantización del momento angular:
sabemos que la velocidad a lo largo de cualquiera de las líneas de circulación debe ser inversamente proporcional a la distancia radial hacia el centro del vórtice. Más formalmente, de acuerdo a las consideraciones teóricas presentadas por Lars Onsager en 1949 en Nuovo Cimento y por Richard Feynman en 1955, la condición de cuantización para un vórtice está dada por la siguiente relación:
en donde la integral se toma a lo largo de una trayectoria cerrada siendo m es la masa de un átomo de helio. El descubrimiento de la cuantización del movimiento de los vórtices en el helio superfluídico fue logrado por vez primera en 1958 por el Profesor W. F. Vinen utilizando técnicas estrictamente clásicas para resolver un problema cuántico de enorme dificultad en una época en la cual muchos científicos no estaban convencidos de que los vórtices cuánticos pudieran existir, o que habrían apostado que serían inobservables. La formación de vórtices cuánticos fue confirmada posteriormente en 1969 por Richard E. Packard y su colaborador T. M. Sanders Jr. utilizando el método cuántico y técnicas experimentales sofisticadas, no habiendo duda alguna tras otros experimentos numerosos que se han llevado a cabo alrededor del mundo acerca de la existencia de este fenómeno peculiar de naturaleza cien por ciento cuántica.
La siguiente simulación computarizada nos muestra los pasos de formación de vórtices cuánticos dentro de un condensado Bose-Einstein atrapado en un contenedor de confinamiento magnético:
Y la siguiente simulación computarizada nos dá una mejor perspectiva sobre la formación de los vórtices en un condensado Bose-Einstein conformado por 200 mil átomos de rubidio contenidos dentro de una trampa magnética:
Otra consecuencia espectacular del condensado Bose-Einstein es la posibilidad de crear con el mismo lo que se conoce como un átomo láser. Inspirado en el mismo principio en el que se fundamentan los rayos láser que funcionan a base de fotones luminosos, y concebido en base a la dualidad onda-partícula que nos dice que del mismo modo en el cual los fotones luminosos se pueden comportar como una onda o como una partícula también los átomos deben poder hacer lo mismo con lo cual debe ser posible en principio la construcción de un láser en el cual las partículas coherentes (en fase) no sean fotones sino átomos, el átomo láser es un estado coherente de átomos que se propagan formando un haz coherente que se comporta en forma muy parecida a una onda. Aunque la física de un átomo láser es semejante a la de un láser óptico convencional, las diferencias principales radican en que los átomos interactúan consigo mismos, no pueden ser creados en la misma forma en la cual se pueden crear los fotones coherentes mediante un par de espejos reflectores, y los átomos poseen una masa a diferencia de los fotones que no poseen una masa en reposo. El primer átomo láser (emitiendo pulsos de partículas coherentes) fue logrado en el Instituto Tecnológico de Massachusetts en noviembre de 1996 por el profesor Wolfgang Ketterle, tras lo cual un equipo de investigadores en el Instituto Max Planck para Optica Cuántica en Munich (Bloch, Haensch, and Esslinger) lograron obtener en 1999 un átomo láser operando en forma continua. La realización del átomo láser ha resultado ser crucial para la creación de otro campo nuevo de investigación, la holografía átomo, la cual es semejante a la holografía convencional en su uso de la difracción de átomos. En virtud de que la longitud de onda de De Broglie de los átomos es mucho más pequeña que la longitud de onda de la luz visible, el átomo láser es capaz de crear imágenes holográficas de mucha mayor resolución que la conocida hasta ahora, y puede ser utilizada para proyectar patrones de circuitos integrados complejos de tan sólo unos cuantos nanometros en escala, algo que puede resultar crucial para la construcción de computadoras cuánticas cuya potencia haría palidecer la capacidad de procesamiento informativo del que gozamos hoy en día. Otra aplicación que se podría beneficiar mucho con el átomo láser es la interferometría átomo, lo cual podría resultar crucial en el camino hacia la construcción de una teoría de la gravedad cuántica. Todo esto posibilitado por un fenómeno mecánico cuántico de naturaleza estadística que hace casi un siglo atrás se contemplaba por muchos científicos como una mera curiosidad.