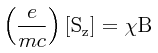Si post-multiplicamos lo de arriba por la derecha por la adjunta Hermitiana de la función de onda matricial ψ*, tendremos lo siguiente:
Obsérvese que siendo H una matriz, ésta opera únicamente sobre ψ y no sobre ψ*. Tomando la adjunta de la ecuación antepenúltima (tomando la transpuesta del conjugado complejo de ambos miembros de la igualdad) y pre-multiplicando por la izquierda por ψ nos produce ahora:
Restando esta ecuación de la anterior obtenemos entonces:
Si formamos ahora el promedio del ensamble usando ρ = [ψ·ψ*] llegamos a lo siguiente (los paréntesis rectangulares son utilizados a continuación no para representar el promedio de un ensamble sino el conmutador de Born):
De lo anterior podemos escribir:
Puesto que el tamaño de la matriz ρ es fijo en invariable, al hablar acerca de algo como ∂ρ/∂t de lo que se está hablando realmente es de un reacomodo de los elementos de la matriz a lo largo de su diagonal principal, siempre dando una suma igual a la unidad. Obsérvese que esto tiene un signo contrario al que corresponde a la evolución temporal de un operador Heisenberg en la ecuación del movimiento de Heisenberg, lo cual no debe de sorprendernos en virtud de que el operador densidad ρ ha sido construído utilizando kets y bras de Schrödinger que evolucionan en el tiempo de acuerdo con la ecuación de onda de Schrödinger; y además ρ no es una observable dinámica en la representación de Heisenberg. La ecuación que hemos obtenido es el análogo cuántico de un teorema propio de la Mecánica Estadística clásica, el teorema de Liouville, el cual describe la evolución temporal de sistemas clásicos idénticos tales como muchas “cajas” rellenas cada una con la misma cantidad de gas y estando todas ellas a la misma temperatura, pero con coordenadas de posición y valores de momentums distintos (aleatoriamente) para los átomos individuales. En el caso clásico, cada caja puede ser descrita como un punto individual en un gigantesco espacio dimensional que posee seis dimensiones para cada átomo (tres para la posición, y tres para el momentum, ignorándose los posibles grados internos de libertad); y el ensamble completo es entonces un gas de estos puntos en este espacio gigantesco, estando dada la razón de cambio para este gas clásico por la expresión ∂ρ/∂t.=.-{ρ,H} de acuerdo con la ecuación de Hamilton (los corchetes son los mismos conocidos en la mecánica clásica como los corchetes de Poisson). Esta es la razón por la cual el resultado cuántico que hemos obtenido aquí es mejor conocido como la ecuación Liouville-von Neumann, al haber sido el matemático John von Neumann el primero que desarrolló en 1927 este formalismo introduciendo el concepto de la matriz densidad.
La relación nos dá en forma correcta la ecuación de movimiento para el valor promedio de una observable. Esto lo podemos ver mejor a través de las siguientes operaciones en donde en la tercera línea del desarrollo utilizamos el resultado anterior (aquí se utiliza también la propiedad de la invarianza de la traza tr de un producto matricial al orden en el cual se toma el producto):
en donde con {Q,H} estamos usando el corchete de Poisson para Q y H.
PROBLEMA: Demuéstrese que en la representación de Schrödinger, la evolución temporal de la matriz densidad está dada por la siguiente expresión:
Empezaremos con la definición de la matriz densidad ρ modificada un poco bajo la suposición que los kets para cierto eigenestado evolucionan de alguna manera con el tiempo siendo por lo tanto ρ también una función del tiempo:
Supóngase ahora que el operador que actúa sobre un ket llevándolo de un tiempo incial t0 hacia otro tiempo t es el operador unitario U(t,t0), lo cual podemos representar de la manera siguiente:
Entonces, tras tomar el conjugado complejo de lo anterior, lo que sigue debe ser cierto al reemplazar las dos expresiones en el operador densidad ρ(t):
Metiendo la sumatoria hacia la derecha, lo anterior lo podemos escribir de la siguiente manera:
Pero lo que tenemos adentro es precisamente la definición que se había dado para ρ(t), válida para un tiempo inicial t0. Por lo tanto, llegamos a lo que se deseaba demostrar:
PROBLEMA: Demuéstrese que si empezamos con un ensamble puro, el ensamble seguirá siendo puro siempre y cuando la evolución del sistema sea descrita por la ecuación de Schrödinger.
Usando el resultado del problema anterior en el cual obtuvimos la evolución temporal de la matriz densidad bajo la representación de Schrödinger, podemos afirmar lo siguiente:
Ya se había demostrado en un problema anterior que la matriz densidad para un estado puro es idempotente, razón por la cual al empezar en un tiempo inicial con un estado puro lo que sigue debe ser cierto:
Del mismo modo, una vez que ha transcurrido cierto tiempo, la idempotencia de la matriz densidad de un estado puro, si es que sigue siendo puro debe permite afirmar que:
Usando la idempotencia de la matriz densidad para un tiempo inicial, tenemos entonces:
lo cual nos confirma que un estado puro se sigue manteniendo puro bajo una representación de Schrödinger con el transcurso del tiempo.
En el estudio de muchos problemas estadístico-cuánticos importantes, una medida del orden ó del desorden de un sistema está dada por:
σ = - tr(ρln(ρ))
Un ensamble está en su estado de mayor orden posible cuando todos sus miembros se encuentran en el mismo estado puro, cuando todas las entradas de la matriz densidad ρ a lo largo de la diagonal principal son cero exceptuando una de ellas que representa al eigenestado puro la cual debe ser igual a la unidad. En este caso, ya vimos que σ.=.0. Por el otro lado, para un estado completamente aleatorio, se tiene que:
σ = - ln (1/N) = + ln (N)
siendo N el número posible de estados cuánticos, teniendo la matriz densidad las dimensiones NxN, lo cual constituye un límite máximo al valor que puede tomar σ.
Si todos los miembros de un ensamble son sometidos a una misma perturbación, σ permanecerá igual sin alteración alguna. Suponiendo que las fuerzas que están relacionadas con un Hamiltoniano H independiente del tiempo actúan por igual sobre los miembros de un ensamble, a causa de la interacción la función de onda ψ(0) de cada miembro del ensamble evolucionará temporalmente en la representación de Schrödinger de acuerdo con la relación:
ψ(t) = e-iHt/ħψ(0)
Y por lo que acabamos de ver, la interacción hará evolucionar a la matriz densidad de la siguiente manera:
ρ(t) = e-iHt/ħρ(0)eiHt/ħ
Esto constituye una transformación unitaria sobre ρ. Y si el Hamiltoniano H es dependiente del tiempo, puede ser descompuesto en una secuencia (infinita) de segmentos independientes del tiempo. La transformación global es entonces el producto de estas transformaciones unitarias, y por lo tanto será también unitaria. Sin embargo, puesto que la traza de una matriz permanece invariante bajo una transformación unitaria, σ permanece inalterada por una perturbación que sea aplicada por igual a todos los miembros del ensamble. Por lo tanto, es imposible el poder introducir orden o desorden en un ensamble actuando sobre cada miembro del ensamble con el mismo campo de fuerza. Sin embargo, si los miembros de un ensamble reciben la acción de fuerzas distintas, hay una tendencia general a que se introduzca un mayor desorden dentro del sistema. Podemos ver esto mejor si consideramos el caso especial de un ensamble representado en una representación de energía a través de una matriz densidad estacionaria:
ρnn = 1
ρpq = 0__para p ≠ q__ó__p = q ≠ n
Un ensamble puro de este tipo tiene a todos sus miembros en el n-avo estado de energía. Consideremos el efecto sobre todos los miembros del ensamble de una perturbación instantánea en un tiempo t.=.t0. Esta perturbación puede ser representada en sus efectos en el ensamble mediante la transformación unitaria:
Uρ(t0)U-1 = Uρ(t0)U* = ρ'(t0)
Si la n-ava columna de la transformación unitaria U tiene elementos a1, a2, a3, etc., entonces ρ'( tiene la forma:
en donde la condición de normalización para la matriz densidad sigue siendo:
La matriz ρ'(t0) representa a la matriz densidad en un tiempo t.=.t0 después de que ha ocurrido la perturbación. Un tiempo después, la matriz densidad tendrá los elementos:
en donde:
Imaginemos ahora que distintos miembros del ensamble son perturbados en tiempos distintos, y que todas las perturbaciones está distribuídas aleatoriamente en el tiempo. Los elementos que resulten para la matriz densidad son obtenidos de la penúltima relación promediando sobre t0. No habiendo estados de energía degenerados, todos los elementos fuera de la diagonal principal terminan promediados a cero. Si hay degeneraciones, tales degeneraciones pueden ser separadas por otras perturbaciones, lo cual nos llevará a las mismas conclusiones.
Una perturbación aleatoria que actúe sobre varios miembros de un ensamble producirá un nuevo ensamble estacionario caracterizado por una matriz diagonal en una representación de energía. Los miembros individuales del ensamble pueden por lo tanto ser considerados estando en estados de energía bien definidos. Se puede decir que tales perturbaciones aleatorias simplemente producen transiciones de cambio entre los varios niveles de energía que hay en el sistema, habido el hecho de que las matrices densidad están caracterizadas por completo por las poblaciones relativas de partículas que hay entre los distintos niveles de energía. A continuación tenemos una matriz densidad diagonalizada que evoluciona en sus tres etapas desde un estado puro a un estado completamente aleatorio, pudiendo apreciarse cómo los niveles poblacionales son simplemente redistribuídos conforme el ensamble avanza espontáneamente del orden hacia el desorden:
Si la matriz densidad original ρ que caracteriza a un sistema es diagonal en una representación de energía, ya vimos que puede ser descompuesta sin dificultad alguna en una suma de matrices que representan estados puros. Podemos ver en la matriz que tenemos arriba para ρ'(t0) que después de una serie de perturbaciones aleatorias ρ se convierte en ρ' con sus elementos diagonales dados por:
Aquí Pkl representa la probabilidad de transición (positiva) entre los estados k y l debida a la perturbación. Obsérvese que cada término en la sumatoria en esta ecuación sirve para incrementar a ρkk si ρll es mayor que ρkk. Del mismo modo, ρll es entonces disminuído por esa misma cantidad por el término correspondiente en su suma. En todo caso, los valores son redistribuídos a lo largo de la diagonal principal. Obsérvese también que la suma:
es incrementada por una transferencia de la población del estado l al estado k (cuando ρll es mayor que ρkk). Consecuentemente, podemos ver mediante una iteración del argumento anterior que el parámetro σ es incrementado por perturbaciones aleatorias. Puesto de otra manera:
Las perturbaciones aleatorias introducen desorden en un ensamble. Es razonable suponer que las interacciones que ocurren entre cualquier sistema y un “baño de calor” constituyen tales perturbaciones aleatorias que incrementan el valor de σ.
Si una perturbación aleatoria individual produce sólo un cambio pequeño en ρ, entonces la ecuación:
se puede escribir de la siguiente manera como una ecuación diferencial:
Esta ecuación tiene un aspecto que tal vez resulte familiar para algunos lectores, porque se trata de una ecuación de difusión. La solución de la ecuación diferencial demuestra que hay una “difusión” de los miembros de los ensambles entre sus varios niveles energéticos, hasta que todos los niveles energéticos que puedan ser acoplados por las perturbaciones (para los cuales Ckl.≠.0) están igualmente poblados. Es sólo bajo esta condición que las derivadas de tiempo se desvanecen en esta última ecuación. Por lo tanto, los sistemas para los cuales la ecuación de arriba es válida tienden a aproximarse a la distribución aleatoria típica del mayor desorden posible:
ρ = (1/N) I
cuando los sistemas son objeto de una serie de perturbaciones aleatorias.
Es obvio del comportamiento del parámetro σ que es utilizado para la medición del orden que dicho parámetro está relacionado de alguna manera con esa variable de estado termodinámica conocida como la entropía. Se puede demostrar de hecho que la siguiente definición es una definición mecánico-cuántica correcta y apropiada para la entropía de un ensamble:
S = kσ
en donde k es la constante de Boltzmann.
Es posible obtener la matriz densidad para un ensamble una vez que dicho ensamble haya llegado a un equilibrio termodinámico. La suposición esencial para justificar este paso es que la naturaleza siempre tiende a maximizar espontáneamente la entropía S de un sistema (lo cual equivale a maximizar a σ), condición que desde luego sujetamos a la restricción de que la energía promedio (o Hamiltoniano) del ensamble se mantenga en cierto valor prescrito. Termodinámicamente hablando, todo sistema se mueve espontáneamente de cierto grado de orden (o del máximo orden que puede tener) hacia el desorden mayor que pueda lograr, lo cual ocurre cuando el sistema se encuentra en el equilibrio termodinámico. Una vez que se ha establecido el equilibrio termodinámico, la matriz densidad debe mantenerse más o menos invariable conforme avanza el tiempo:
Y en virtud del resultado obtenido arriba para la variación de la matriz densidad ρ con respecto al tiempo:
esto significa que cuando se ha logrado una situación de equilibrio termodinámico (máxima entropía) tanto el operador Hamiltoniano H como la matriz densidad ρ pueden ser diagonalizados simultáneamente, de modo tal que los kets que se utilicen para escribir a σ pueden ser considerados como eigenkets de energía. La maximización de σ se logra requiriendo que la variación de σ sea igual a cero en el punto de equilibrio termodinámico:
δσ = 0
Ya vimos que la matriz densidad ρ para un ensamble completamente aleatorio es proporcional a la matriz identidad I. Tiene por lo tanto la propiedad importante de que puede conmutar con cualquier operador Hamiltoniano de energía H y consecuentemente siempre será estacionaria, lo cual significa que no hay manera alguna en la cual un mismo campo de fuerza que actúe sobre todos los miembros de un ensamble aleatorio pueda introducir orden en el sistema. Decimos que un sistema que está caracterizado por una matriz densidad estacionaria se encuentra en una condición de equilibrio. Una condición necesaria y suficiente para que un sistema sea estacionario es la conmutación de la matriz densidad ρ que lo describe con el Hamiltoniano H. Una condición suficiente es que ρ sea alguna función de H:
ρ = ρ (H)
Los ensambles estacionarios son de especial importancia para sistemas que interactúan con un “baño de calor”; tales sistemas se aproximan a un estado estacionario caracterizado por la temperatura del baño. Otra aplicación importante de un ensamble estacionario es la representación de un sistema para el cual lo único que se conoce es su energía. Si hay muchos estados de la misma energía, es razonable darle a priori a cada estado una misma probabilidad. La matriz densidad tendrá entonces los mismos elementos sobre la diagonal principal únicamente para estos estados. De modo semejante, un sistema para el cual no hay información alguna se puede suponer que se encuentra en un estado completamente aleatorio. Todos estos ensambles están caracterizados por matrices densidad que son estacionarias que conmutan con el Hamiltoniano.
Como se discutió arriba, el ensamble completamente aleatorio es aquél para el cual todos los estados de energía son igualmente probables. En forma alterna, se le puede definir como aquél para el cual σ es maximizado sin condición física auxiliar alguna que pueda actuar como restricción del sistema. Por lo tanto, puede ser determinado con el requerimiento de que la variación δσ se desvanezca:
δσ = δ{tr(ρ)·ln(ρ)}= 0
La única condición auxiliar es, desde luego, la condición de normalización:
tr(ρ) = 1
Puesto que estamos considerando matrices densidad diagonales, tomando la variación δσ en forma similar a como se lleva a cabo con un diferencial se tiene entonces:
Las variaciones sobre cada .j son arbitrarias, sujetas únicamente a la condición:
Esta condición auxiliar puede ser introducida mediante la técnica matemática que ya vimos previamente en la obtención de distribuciones tales como la distribución de Boltzmann, el método de los multiplicadores de Lagrange. Si multiplicamos la condición por una constante λ y añadimos esto a la ecuación en la que estamos trabajando, tenemos entonces:
Esto representa en realidad un conjunto de .j condiciones, una para cada valor de .j. Podemos escoger a λ de modo tal que hagamos que cualquiera de los términos entre corchetes se desvanezca. Puesto que los restantes δρjj pueden ser variados independientemente, todos los demás términos entre corchetes también se deben desvanecer. Por lo tanto, podemos enunciar lo siguiente:
ln(ρjj) = constante
Si simbolizamos a tal constante como C, entonces se deduce que:
Cada uno de los elementos que van puestos en la diagonal principal de la matriz densidad ρ deben ser entonces eC. Usando la condición de normalización que nos indica que la suma de dichos elementos debe ser igual a la unidad, el siguiente desarrollo es válido:
Entonces, de acuerdo con esto, la matriz densidad toma el siguiente aspecto:
Esto es precisamente lo que estábamos esperando para el ensamble al ser dicho ensamble completamente aleatorio.
A diferencia de lo que hemos visto en donde no hay condición de restricción alguna salvo la condición de normalización, el ensamble canónico, por su parte, es definido mediante la condición de que σ sea maximizado sujeto a la condición de que la energía promedio del sistema tome algún valor preasignado. El ensamble canónico resulta útil en aquellos casos en los cuales se ha permitido a los miembros del ensamble interactuar con un “baño de calor” a cierta temperatura T. La energía promedio del ensamble, después de que se ha establecido un equilibrio termodinámico, está determinada por esta temperatura. Tenemos pues que tomar en cuenta la restricción de que el promedio del Hamiltoniano del ensamble tenga cierto valor prescrito, invariable. Usando el lenguaje que es propio a la Mecánica Estadística, podemos indentificar al valor promedio del ensamble [H] como la energía interna por constituyente, simbolizándola como U:
[H] = tr(ρ·H) = U
Además de esto, tenemos que tomar en cuenta la condición de normalización para la matriz densidad que nos requiere que la suma de los elementos de la misma a lo largo de su diagonal principal, su traza, sea igual a la unidad:
De este modo, lo que buscamos es obtener la condición para que la variación δσ sea igual a cero sujeta a las dos restricciones:
Procediendo como lo hicimos anteriormente, recurrimos nuevamente al método de los multiplicadores de Lagrange que nos lleva a lo siguiente:
La única manera en la cual se puede cumplir lo anterior para una variación arbitraria es si:
lo cual podemos escribir también como:
De la condición de normalización se tiene:
Entonces la matriz densidad tiene la siguiente forma, factorizando fuera de la matriz la constante e-(γ+1) que es común a cada término ρkk:
Resulta obvio entonces que cada elemento de la matriz densidad está dado por la siguiente relación:
La suma de exponenciales que tenemos en el denominador es lo que se define como la función de partición. Ya la hemos visto previamente desde antes de que se llevara a cabo la derivación de la distribución Maxwell-Boltzmann:
Se puede redactar la matriz densidad sobre lo que acabamos de obtener de una manera un poco más elegante. Para ello, utilizaremos la representación matricial explícita del operador de energía Hamiltoniano H con los eigenvalores puestos a lo largo de la diagonal principal (para mayor claridad, prescindiremos de las demás entradas matriciales por ser ceros):
De esta matriz H, el operador matricial exponencial e-βH debe ser:
La traza de esta matriz es:
Pero esto es precisamente la definición de la función de partición, lo cual nos permite afirmar que:
Con lo que tenemos hasta este punto, estamos posibilitados para dar enunciar lo siguiente:
Esta es una de las relaciones más fundamentales de las cuales proviene prácticamente todo lo demás. Mediante ella podemos obtener el promedio estadístico [Q] de un ensamble para una observable:
De acuerdo con esta última relación, la energía interna por constituyente del ensamble viene siendo:
Repasando las entradas anteriores relacionadas con la Mecánica Estadística Cuántica, se puede ver que el parámetro β está relacionado con la temperatura T de la siguiente manera:
siendo k la constante de Boltzmann. Es así como la energía promedio de un ensamble puede ser relacionada con la temperatura de un “baño de calor” al cual está sometido el ensamble. Considérese un ensamble de osciladores armónicos unidimensionales. De acuerdo a lo que acabamos de ver, la energía promedio del ensamble es:
Puesto que la energía de un oscilador armónico simple está dada por la relación:
se tiene entonces que:
Podemos efectuar aquí un poco del álgebra reminiscente de los pasos llevados a cabo cuando se trató el tema del modelo cuántico de Einstein para explicar la capacidad calorífica molar de los cristales:
Para un ensamble de osciladores armónicos unidimensionales, con la ayuda de la condición de normalización que nos indica que la traza de la matriz densidad ρ debe ser igual a la unidad podemos escribir lo siguiente:
Si substituímos esto en lo anterior, encontraremos que:
En el límite de frecuencias muy bajas, lo cual equivale a hacer tender a la frecuencia angular ω a cero, lo anterior se reduce a:
En este límite, los resultados clásicos resultan ser aplicables, y uno de tales resultados de la Mecánica Estadística clásica para un ensamble de partículas es el siguiente:
[E] = kT
Entonces se tiene lo siguiente:
La validez de este resultado, habiendo sido obtenido al haberse tomado un límite extremo para el caso de osciladores armónicos de bajas frecuencias, parecería estar muy limitada. Sin embargo, su cobertura es más amplia de lo que parece ser. Considérese un sistema compuesto de dos sub-sistemas que no interactúan entre sí, y sea uno de estos subsistemas un oscilador lineal de baja frecuencia. El sistema combinado puede ser considerado ya sea como un sistema único o como dos sistemas independientes. En cualquier caso, las últimas dos relaciones que tenemos arriba son válidas para el oscilador. Pero considerado como un sistema único, sólo puede haber un λ, determinado por λ.=.1/kT para el sistema combinado.
Frecuentemente, el número total de partículas en un sistema nos es desconocido, como ocurre en el caso de un gas. En consecuencia, a veces resulta conveniente considerar otro tipo de ensamble estacionario, aquél en el cual sus miembros varían en el número total de partículas. Si el número total de partículas en un sistema es introducido formalmente como una variable dinámica con un operador N que tenga los valores 0,1,2,...,.etc., se puede ver que para los sistemas no-relativistas que están siendo considerados, el número total de partículas es una constante del movimiento. N por lo tanto conmuta con el operador de energía Hamiltoniano H, y la matriz densidad puede ser tomada simultáneamente diagonal tanto en H como en N. En una manera semejante a como se hace para el ensamble canónico, el parámetro de desorden σ puede ser maximizado sujeto a las condiciones de que tanto la energía como el número de partículas (que ha dejado de ser una constante) tomen algún valor promedio prescrito. Esto equivale a buscar:
δσ = δ{tr(ρ·ln(ρ)) = 0
sujeto a las siguientes tres condiciones:
tr(ρ) = 1____tr(ρ·H) = [E]____tr(ρ·N) = [N]
Por lo tanto:
0 = tr{ln(ρ) + λH + νN - ln(A)}δρ
de lo cual:
ln(ρ) + λH + νN - ln(A) = 0
ln(ρ/A) = - (λH + νN)
ρ = Ae-(λH+ νN)
en donde A, λ y ν son constantes. Para una representación en la que H y N son simultáneamente diagonalizables, ρ también es diagonal. Un ensamble representado por una matriz densidad que tenga la forma de esta última ecuación es conocido como un gran ensamble canónico.
Yendo un poco más atrás, vemos que a la temperatura del cero absoluto, lo cual equivale a hacer β.=.∞, los coeficientes de probabilidad:
son todos iguales a cero excepto para el estado fundamental: el sistema se encuentra entonces en un estado puro, y la matriz densidad ρ tiene todos sus elementos iguales a cero excepto por un solo elemento en su diagonal principal. Es por esto que al hablar de un condensado Bose-Einstein estamos hablando de un estado puro, porque todos los átomos se van hacia un solo estado energético, el estado fundamental. ¿Pero que acaso no es la tendencia de todo el ir espontáneamente del orden hacia el desorden? En realidad, para poder obtener un condensado Bose-Einstein, es necesario invertir una buena cantidad de energía en los sistemas de refrigeración requeridos para poder obtener las temperaturas tan bajas que se necesitan para lograr tal cosa, y considerando todo dentro del sistema, tanto el orden máximo logrado en la obtención del estado puro de un condensado Bose-Einstein como el desorden inevitable inducido por el gasto externo de energía (por ejemplo, la quema de combustibles fósiles) la entropía total aumenta de modo inevitable e irreversible. Por otro lado, y en el extremo contrario, a una temperatura muy grande (infinita) todos los wi son iguales: la matriz densidad ρ es simplemente igual a 1/N veces times la matriz identidad, en donde N es el número total de estados disponibles para el sistema.
Una aplicación práctica de lo que hemos visto consiste en la determinación de la susceptibilidad magnética (usualmente simbolizada como χ en las fórmulas) de un material habido el hecho de que el magnetismo es un fenómeno debido exclusivamente al spin de cada electrón que forma parte de un ensamble. Considerando al ensamble canónico constituído por una multitud de electrones en el cual cada sistema tiene un momento magnético eħ/2mc (siendo e la carga del electrón y m su masa), al aplicar un campo magnético uniforme en una dirección usualmente tomada en la dirección del eje-z ya hemos visto previamente que el momento angular de spin Sz conmuta con el Hamiltoniano H, con lo cual la matriz densidad para este ensamble canónico es diagonal en la base Sz. Para un ensamble de este tipo, la matriz densidad está dada de la manera siguiente:
en donde Z es lo que conocemos comúnmente como la función de partición. Haciendo la siguiente compactación como algo intermedio que facilite nuestro desarrollo:
se tiene entonces:
Del mismo modo se puede verificar que:
[Sx] = 0____[Sy] = 0
Por la definición de lo que es la susceptibilidad magnética, podemos escribir lo siguiente:
Entonces la susceptibilidad magnética está dada por la siguiente expresión:
Esta fórmula es mejor conocida como la fórmula de Brillouin.
Otra aplicación interesante relacionada con ensambles de spins de electrones es la que se ve en el estudio de la espintrónica (este es un neologismo derivado de las palabras “spin” y “electrónica”), conocida también como magnetoelectrónica), es una tecnología en desarrollo que explota tanto la carga del electrón como su spin que se manifiesta como un estado de energía magnética débil que puede tomar sólo los valores +ħ/2 y -ħ/2. El primer requisito para construir un dispositivo espintrónico es disponer de un sistema que pueda generar una corriente de electrones “spin polarizados” (es decir, que tengan el mismo valor para su spin) y de otro sistema que sea sensible a esa polarización. Un paso más radical consiste en tener una unidad intermedia que realice algún tipo de procesamiento en la corriente, de acuerdo con los estados de los spines.
Un dispositivo espintrónico simple debe permitir la transmisión de un par de señales por un único canal usando electrones “spin polarizados” y produciendo una señal diferente para los dos valores posibles, duplicando así el ancho de banda del cable. El método más simple de que una corriente sea “spin polarizada” es hacerla pasar a través de un material ferromagnético, que debe ser un cristal único, de forma tal de que filtre a los electrones de manera uniforme. Y si se dispone el filtro frente a un transistor, éste se convertirá en un detector sensible a los spines. Probablemente el dispositivo espintrónico más exitoso hasta el momento haya sido la válvula spín, un dispositivo con una estructura de capas de materiales magnéticos que muestra enorme sensibilidad a los campos magnéticos. Cuando uno de estos campos está presente, la válvula permite el paso de los electrones, pero en caso contrario sólo deja pasar a los electrones con un spin determinado. Desde el año 2002 ha sido común su uso como transductor en cabezas de discos duros. La espintrónica puede tener un impacto radical en los dispositivos de almacenamiento masivo; científicos de IBM anunciaron en el año 2002 la compresión en un área diminuta de cantidades enormes de datos, alcanzando una densidad de aproximadamente 155 mil millones de bits por cm².
Una gran cantidad de aplicaciones de interés de la matriz densidad presentan el problema de que, al entrar en mayores detalles, la obtención de una solución así sea por la vía exclusiva del análisis numérico resulta ser algo formidable desde el punto de vista del cálculo computacional. Las dificultades matemáticas involucradas en la evaluación numérica de la matriz densidad inclusive para casos relativamente sencillos en los cuales tenemos una retícula de unos cuantos miles o inclusive unos cuantos cientos de partículas fueron parcialmente solventadas en 1992 cuando Steven R. White recurriendo a un viejo truco utilizado previamente en el desarrollo de la Teoría del Campo Cuántico (y en especial en la Electrodinámica Cuántica) conocida como la renormalización introdujo una técnica de renormalización grupal conocida como la técnica DMRG (Density Matrix Renormalization Group), y desde entonces esta metodología ha sido extendida a la solución de una gran variedad de problemas en todos los campos de la física así como de la química cuántica (desde 1992 cuando la técnica fue introducida hasta finales del año 2008 se habían publicado más de 1300 papeles científicos sobre el tópico de la renormalización de la matriz densidad). En aplicaciones a sistemas de retículas cuánticas, DMRG consiste en una truncación sistemática del espacio de Hilbert del sistema, conservando un número pequeño de estados importantes en una serie de subsistemas de tamaño creciente para construír de este modo funciones de onda del sistema completo. En DMRG los estados retenidos para la construcción de la transformación de un grupo de renormalización son los eigenestados más probables de una matriz densidad reducida en lugar de los estados de más baja energía en un cálculo NRG (numerical renormalization group). Las técnicas DMRG para sistemas fuertemente correlacionados han sido mejoradas substancialmente desde su introducción en 1992, y han demostrado ser extremadamente precisas y de amplia aplicabilidad en problemas con un número bajo de dimensiones, permitiendo cálculos numéricamente exactos (casi tan buenos como el lograr la obtención de diagonalizaciones matriciales exactas) sobre grandes retículas que estén formadas por algunos miles de partículas y sitios, en contraste con algunas decenas cuando se trata de diagonalizaciones exactas. Aunque originalmente DMRG fue considerada como un método de renormalización grupal, más recientemente se ha enfatizado la interpretación de DMRG como un “estado de producto-matricial”, un punto de vista bajo el cual DMRG se convierte en un algoritmo para optimizar una función de onda variacional con la estructura de un estado de producto-matricial. Esta formulación de DMRG a su vez ha revelado la conexión profunda que hay entre la renormalización de la matriz densidad y la teoría de la información cuántica, traduciéndose en el descubrimiento y el desarrollo de algoritmos eficientes para la simulación de la evolución temporal de sistemas cuánticos de muchos cuerpos (many-body) desde el 2004.