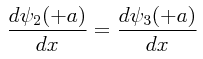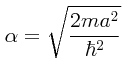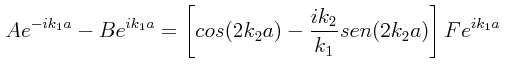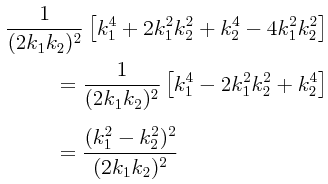¿Caerá dentro del pozo y quedará atrapada dentro del mismo? ¿Pasará por el pozo sin cambio alguno? Podríamos sospechar de antemano que la respuesta a estas preguntas dependerá de la profundidad del pozo de potencial y de la energía que lleve la partícula, y que posiblemente de un enjambre de partículas que pasen por el pozo de potencial habrá alguna probabilidad de que algunas de ellas queden atrapadas dentro del pozo y otras de ellas pasarán por el mismo sin quedar atrapadas.
El pozo de potencial rectangular de profundidad finita resuelve un problema que teníamos en el estudio del pozo de potencial de profundidad infinita (que es esencialmente el de una partícula atrapada en una caja con paredes rígidas) y que hasta ahora habíamos relegado. Si vamos a suponer el caso hipotético de una partícula en una caja con paredes impenetrables, ¿cómo entonces llegó a dar adentro de la caja la partícula si le es tan imposible entrar en la caja como salir de ella? El pozo de potencial rectangular de profundidad finita abre la posibilidad de que una partícula viajera libre que pase por dicho pozo de potencial pueda quedar atrapada. O puesto de otra manera, en términos probabilísticos, con un pozo de potencial de profundidad finita cierta cantidad X de partículas que pasen por dicho pozo dejarán una cantidad Y de partículas que quedarán atrapadas en el mismo, siendo la probabilidad de quedar atrapadas igual a Y/X.
Si bien, para el caso de una partícula atrapada entre dos paredes rígidas (un potencial infinitamente grande), la cantidad posible de estados cuánticos era teóricamente infinita:
en el caso de una partícula atrapada en un pozo de potencial de profundidad finita el número posible de estados cuánticos deberá ser necesariamente finito:
El caso de una partícula que pasa por la cercanía de un pozo de potencial rectangular es similar al de una partícula que pasa por una barrera de potencial rectangular de altura finita y de anchura finita, excepto que en este caso el potencial es -V0 en lugar de +V0. Para la solución mecánico-cuántica a este problema desde el aspecto ondulatorio, recurriremos nuevamente a la ecuación de onda de Schrödinger independiente del tiempo.
PROBLEMA: Supóngase una partícula viajera libre que pasa por un pozo de potencial rectangular especificado de la siguiente manera:
Descríbase lo que ocurre en un caso así resolviendo el sistema mediante la aplicación de la ecuación de onda de Schrödinger, suponiendo que la energía de la partícula es positiva (la partícula pasa por encima del pozo de potencial) siendo mayor que el potencial -V0, o sea que E > -V0.
Nuevamente, para la resolución del problema aplicando la ecuación de onda de Schrödinger, tenemos que subdividir el espacio bajo consideración en las siguientes tres regiones que deben ser tomadas en consideración:
De acuerdo con el planteamiento del problema, la colocación correcta de las coordenadas de la energía potencial V(x) en función de la coordenada horizontal para este pozo rectangular de anchura 2a es la siguiente:
El problema anterior tiene que ver con una situación en la que las partículas libres viajeras pueden venir desde la izquierda pasando por encima del pozo de potencial con una energía positiva E. Pero una variante interesante la tenemos en el caso en el que la energía de las partículas es negativa, aunque mayor que -V0.
PROBLEMA: Supóngase una partícula cuyo movimiento es de izquierda a derecha pasa por un pozo de potencial rectangular especificado de la siguiente manera:
Descríbase lo que ocurre en un caso así resolviendo el sistema mediante la aplicación de la ecuación de onda de Schrödinger, suponiendo que la energía de la partícula es negativa (la partícula se encuentra dentro del pozo de potencial) siendo de cualquier manera la energía mayor que el potencial -V0, o sea que -E > -V0.
Subdividiendo el espacio bajo consideración en tres regiones que deben ser tomadas en consideración tenemos entonces la siguiente situación:
Usaremos la misma colocación de las coordenadas que la que utilizamos en la resolución del problema anterior. Para la región x<-a en donde el potencial V(x) es igual a cero, la ecuación de Schrödinger independiente del tiempo para las regióm x<-a (región #1) en donde la energía potencial es igual a cero y la energía es negativa está dada por:
siendo:
una cantidad real y positiva (en virtud de que la energía es negativa, el signo dentro del radical termina siendo positivo). La solución matemática general en la región # 1 de la ecuación diferencial de onda viene siendo:
Para la región x<-a, el primer término se convierte en una exponencial decreciente, mientras que el segundo término explota exponencialmente al tomar la exponencial un signo positivo constante para cuando x tiende hacia un valor infinitamente negativo. El primer término es por lo tanto una solución físicamente admisible mientras que el segundo término no lo es ya que hace crecer a la función de onda ψ1(x) sin límite. Por lo tanto, tenemos que asignar al coeficiente B un valor de cero, con lo cual la única solución físicamente admisible en la primera región viene siendo:
En lo que cabe a la región intermedia -a<x<+a (la región # 2), en donde la energía E de la partícula es negativa aunque mayor que la energía potencial (negativa) V0 dentro del pozo de potencial, la ecuación de Schrödinger independiente del tiempo para esta región |x|<a es igual a:
siendo:
Es importante señalar que, aunque la energía E de la partícula es negativa, para un estado ligado (con la partícula atrapada dentro del pozo de potencial) dicha energía tiene que seguir siendo mayor que -V0. La solución general para la ecuación diferencial de onda que corresponde a la región intermedia puede ser enunciada como:
Tenemos por último a la región # 3 en donde el potencial vuelve a ser igual a cero. La solución matemática general de la ecuación de onda para esta región viene siendo:
Para la región x>+a, el primer término se convierte en una exponencial decreciente, mientras que el segundo término explota exponencialmente al tomar la exponencial un valor exponencialmente creciente para x→+∞. El primer término es por lo tanto una solución físicamente admisible mientras que el segundo término no lo es ya que hace crecer a la función de onda ψ3(x) sin límite. Por lo tanto, tenemos que asignar al coeficiente G un valor de cero, con lo cual la única solución físicamente admisible en la primera región viene siendo:
para x mayor que a.
El siguiente paso consiste en la imposición de las condiciones de frontera, las cuales son para este problema de tres regiones:
Podemos simplificar la resolución del problema dándonos cuenta de que el potencial V(x) es una función par, esto es:
V(x) = V(-x)
lo cual debe ser obvio ya que V(+a) = V(-a). Esto nos permite deducir de antemano que las soluciones deben ser ya sea pares o impares, lo cual nos permite imponer las condiciones de frontera en únicamente uno de los lados del pozo de potencial, ya sea el lado a en el sentido negativo o el lado a en el sentido positivo, obteniéndose el otro lado en forma automática ya que:
ψ(-x) = ± ψ(x)
en donde el signo de más/menos es tomado como positivo para el caso de funciones pares mientras que es tomado como negativo en el caso de funciones impares. De este modo, la función cosenoidal es una función par:
mientras que la función senoidal es impar:
Todas las funciones de onda impares tienen un nodo en el centro de simetría de las mismas (lo cual implica que para x.=.0 la función de onda ψ toma un valor igual a cero en dicho punto) mientras que para las funciones de onda pares ocurre lo contrario. Este contraste lo podemos apreciar mejor con las siguientes ilustraciones:
Se había visto arriba que la solución general para la ecuación diferencial de onda que corresponde a la región intermedia puede ser enunciada como:
Las soluciones pares se obtienen usando la función coseno, esto es, haciendo C.=.0, mientras que las soluciones impares se obtienen usando la función seno, esto es, haciendo D.=.0, combinando esto con los resultados obtenidos para las otras dos regiones. En el caso de las funciones pares, el requisito de continuidad de la función de onda en x.=.a requiere que:
Por otro lado, el requerimiento de continuidad de las derivadas dψ/dx en los puntos de transición de una región a otra requiere que:
Por lo tanto:
Dividiendo las ecuaciones obtenidas con las dos condiciones de continuidad, se llega de inmediato a lo siguiente:
Esta es una ecuación trascendental que nos sirve para obtener las energías permisibles (en virtud de que tanto k1 como k2 son funciones de la energía E) , la cual no tiene solución analítica exacta. Podemos tratar de resolverla mediante métodos numéricos o métodos gráficos. Más aún, esta ecuación trascendental puede tener no únicamente una sino dos o más soluciones, siendo dichas soluciones los valores propios eigen que corresponden a los estados discretos de energía de una partícula atrapada dentro del pozo de potencial. Para obtener los valores discretos de la energía, resulta conveniente simplificar esto un poco adoptando una notación más compacta. Hágase:
Metiendo aquí las expresiones para la energía E, se obtiene de modo directo lo siguiente:
con lo cual:
Por lo tanto:
Si hacemos:
entonces, trazando sobre una misma gráfica ambas funciones, los puntos en los cuales se cruzen tales funciones corresponderan a las soluciones de valores propios eigen que estamos buscando para la ecuación trascendental. Se recalca que esto es válido para las funciones pares.
A continuación tenemos un ejemplo de la solución gráfica de la ecuación trascendental en donde podemos apreciar tres puntos de intersección (la curva en color rojo corresponde a la fórmula en color rojo mientras que las curvas en color azul corresponden a la fórmula en color azul):
Específicamente, lo que queremos obtener de la gráfica son los valores de z en los cuales se “cruzan” las dos funciones f(z) y g(z). Hay tres de ellos. El más bajo ocurre un poco debajo de π/2. El que sigue ocurre entre π y 3π/2. Y el tercero ocurre entre 2π y 5π/2. Como ya se dijo, esta gráfica es válida para las funciones de onda pares. En este caso, puede verse que de acuerdo a los puntos de intersección obtenidos en la gráfica se obtienen tres energías propias eigen, por lo que el pozo de potencial admite solo tres estados discretos de paridad par.
En lo que toca a las funciones de onda impares, el procedimiento de solución es muy similar, excepto que en lugar de obtenerse una función tangente se obtiene una función cotangente de signo negativo:
Esto viene del hecho de que la primera condición de continuidad es:
siendo el requerimiento de continuidad de las derivadas dψ/dx en los puntos de transición de una región a otra:
Dividiendo las ecuaciones obtenidas con las dos condiciones de continuidad, se llega de inmediato a la relación cotangente dada arriba.
De nueva cuenta, podemos hacer:
Trazando sobre una misma gráfica ambas funciones, los puntos en los cuales se cruzan tales funciones (destacados como círculos de color rosa) corresponderán a las soluciones de valores propios eigen que estamos buscando para la ecuación trascendental, recalcándose que esto es válido para las funciones de onda impares:
A continuación se muestra una gráfica (se recomienda ampliar la imagen) mostrando tanto las soluciones pares (curvas de color azul) como las soluciones impares (curvas de color rojo) para un pozo de potencial que admite seis estados discretos de energía, para lo cual se ha supuesto una anchura del pozo 2a igual a 0.4 nanometros (a.=.0.2 nm) y una profundidad del pozo de potencial fijada en 75 eV:
Como puede verse en la figura, para las condiciones especificadas hay seis estados eigen posibles. Obsérvese también un detalle muy curioso: a las funciones de onda pares les corresponden números cuánticos n impares (n.=.1,3,5,...), mientras que a las funciones impares de onda les corresponden números cuánticos n pares (n.=.2,4,6,...). Esto se verá con mayor claridad en la siguiente ilustración que será dada más abajo.
De las soluciones gráficas para las funciones de onda pares, es posible apreciar que si z0 tiene un valor suficientemente grande (representando un pozo algo amplio y algo profundo), entonces las intersecciones ocurrirán por debajo de:
con lo cual se tiene entonces que:
Al ir disminuyendo el valor de z0 (con el punto z0 recorriéndose cada vez más y más hacia la izquierda en las figuras de arriba), habrá menos estados ligados, hasta que finalmente cuando z0 toma un valor inferior a π/2 (con lo cual desaparece el estado impar más bajo) solo quedará un estado discreto disponible dentro del pozo de potencial. Resulta sorprendente que, no importa qué tan débil sea el pozo de potencial, siempre habrá por lo menos un estado discreto.
La siguiente figura corresponde a la de un pozo de potencial rectangular que admite cuatro estados ligados. Los estados n.=.1 y n.=.3 corresponden a las soluciones pares de la ecuación de onda en el interior de la región 2 (la región intermedia en donde la partícula se la pasa la mayor parte del tiempo), mientras que los estados n.=.2 y n.=.4 corresponden a las soluciones impares de la ecuación de onda (confirmando lo que se asentó un poco más arriba al afirmarse que a las funciones de onda pares les corresponden números cuánticos n impares mientras que a las funciones impares de onda les corresponden números cuánticos n pares):
En la ilustración resalta el hecho notable de que una partícula atrapada dentro de un pozo de potencial rectangular de profundidad finita, por tratarse de una onda de materia, es capaz de “penetrar” en las paredes del pozo, algo que no podía hacer en el caso de un pozo de potencial rectangular con paredes infinitamente grandes. Esto es algo que la mecánica clásica es ya incapaz de predecir, y se trata de un comportamiento puramente mecánico-cuántico. Por otro lado, una partícula atrapada dentro de un pozo de potencial rectangular en cualquiera de los estados de energía admisibles dentro del pozo puede ser sacada del mismo suministrándole suficiente energía para que pueda subir por encima del nivel de energía potencial V(x).=.0. Si la partícula atrapada es un electrón, entonces la energía se la suministraríamos enviando adentro del pozo un fotón con la energía suficiente para liberar a la partícula del mismo.
Otro ejemplo instructivo de análisis, el cual aunque también requiere de solución numérica o de solución gráfica al no tener solución exacta la ecuación de Schrödinger para las condiciones del mismo resulta un poco más sencillo de resolver que el caso del pozo de potencial rectangular, es el caso del pozo de potencial semi-infinito, el cual consiste de un pozo de potencial una de cuyas paredes es impenetrable (infinitamente alta) y otra de las cuales tiene una altura finita. Podemos especificar un potencial de este tipo de la siguiente manera:
Puesto que la función de onda se desvanece por completo en la pared vertical izquierda al ser impenetrable, hay una ligera simplificación en los cálculos. Las soluciones, obtenidas resolviendo la ecuación independiente del tiempo de Schrödinger para cada región requiriéndose continuidad tanto para las funciones de onda como para las primeras derivadas en los puntos de encuentro entre regiones distintas, conducen a una ecuación trascendental de la forma:
en donde:
Quizá la forma más expedita de resolver la ecuación trascendental consiste en recurrir a soluciones gráficas, trazando en una misma gráfica las funciones tangente y la función cuadrática que nos permite determinar las energías eigen en los puntos de cruce entre ambas gráficas. Para el caso en el cual V0.=.1.5, se encuentra que hay cuatro energías discretas (las curvas de la función tangente se muestran de color obscuro mientras que la gráfica de la función cuadrática se muestra de color verde):
mientras que para el caso en el cual V0.=.0.5 se encuentra que hay dos energías eigen discretas:
de lo cual se concluye, como era de esperarse, que para el pozo de potencial semi-infinito entre mayor sea la profundidad del pozo tanto mayor será la cantidad posible de estados discretos que el pozo pueda contener.
Habiendo visto todo lo anterior, estamos en mejores condiciones para poder tratar en detalle el caso de transmisión de partículas sobre un pozo de potencial cuando la energía E de la partícula es superior al nivel de potencial V.=.0:
Para x menor que a negativo en la región 1 en donde tenemos partículas libres, la función de onda ψ1(x) en su forma más general está dada por la relación:
en donde, al igual que como se hizo arriba:
En la región intermedia, la función de onda ψ2(x) está dada por:
en donde, al igual que como se hizo arriba:
Y por último, para x>a en la tercera región (se usa k1 al igual que en la primera región):
En la línea de transición de la primera región a la segunda región, la condición de continuidad requerida de la función de onda al pasar de una región a otra especifica lo siguiente:
Por otro lado, en el mismo lugar, la condición de continuidad de que la derivada de la función de onda ψ1(x) sea igual a la derivada de la función de onda ψ2(x) (ambas deben tener la misma pendiente) especifica lo siguiente:
En lo que toca a la frontera de transición de la región 2 a la región 3 en donde se “conectan” las funciones de onda ψ2(x) y ψ3(x), la condición de continuidad de las mismas especifica lo siguiente:
Y por último, la condición de continuidad de que la derivada de la función de onda ψ2(x) sea igual a la derivada de la función de onda ψ3(x) especifica:
La solución del conjunto de ecuaciones obtenidas no es asunto difícil, aunque es algo tedioso requieriendo de cierta paciencia e ingenio. Una forma de llevarlo a cabo consiste en usar dos de las ecuaciones obtenidas para eliminar C y D, y usar las otras dos ecuaciones para B y F. Para ello, tomamos la ecuación:
y la multiplicamos por sen(k2a). Asimismo, tomamos la ecuación:
y la multiplicamos por cos(k2a)/k2, sumando ambas:
para obtener:
Del mismo modo, multiplicando:
por cos(k2a) y multiplicando:
y la multiplicamos por sen(k2a)/k2, y sumando ambas, se obtiene:
Poniendo ambas relaciones para C y D en la ecuación:
y simplificando, se obtiene:
Asimismo, llevando a cabo un procedimiento similar sobre la relación:
se obtiene:
Sumando las dos relaciones obtenidas eliminando el término con B, se tiene entonces:
de lo cual, despejando para F:
Del mismo modo, si en vez de sumar las relaciones las restamos, obtenemos lo siguiente para B:
El coeficiente de transmisión T para un flujo de partículas que van de izquierda a derecha, expresado en función de las densidades de probabilidad, es:
Sin embargo, por conveniencia tipográfica (y únicamente por esta razón), resultará más conveniente expresar lo anterior de la siguiente manera:
Usando lo obtenido anteriormente para F, vemos que:
Pero puesto que:
y usando la siguiente simplificación intermedia:
se tiene:
Por otro lado, usando las relaciones explícitas para k1 y k2 en función de la energía y el potencial, se tiene:
con lo cual:
para así llegar finalmente a la siguiente relación:
Usando el resultado obtenido, podemos construir una gráfica típica del coeficiente de transmisión de partículas a través del pozo de potencial en función de la energía para cierta combinación de valores de las constantes físicas involucradas es la siguiente:
A grosso modo, la interpretación de la gráfica obtenida es sencilla: en el momento en el que la energía E toma valores superiores a V0, hay una transmisión casi total de partículas que se aproxima al cien por ciento cuanto mayor sea la energía, pero para valores de la energía E inferiores a V0, la transmisión de partículas desciende abruptamente, lo cual es lógico ya que las partículas son atrapadas dentro del pozo. De la fórmula obtenida para el coeficiente de transmisión T, resulta evidente que cuando el término senoidal es exactamente igual a cero el pozo de potencial se vuelve invisible para el haz de partículas incidentes. La condición para que esto ocurra es:
Las energías discretas En para las cuales hay una transmisión perfecta de partículas se pueden apreciar en la gráfica de arriba para T(E), son los puntos en los que la curva “toca” a la línea horizontal T.=.1. Cada una de estas energías discretas corresponde a cierta longitud de onda para la onda de materia, lo cual significa que si la longitud de onda de De Broglie es la correcta, la transmisión de partículas se vuelve perfecta. Esto en realidad no es más que una manifestación del fenómeno de resonancia. Despejando para En de esta última fórmula, se tiene:
Pero resulta que estas son precisamente las energías discretas para un pozo de potencial infinito.
No hay que olvidar que en los análisis sobre-simplificados de los fenómenos de transmisión y reflexión de partículas llevados a cabo hasta este punto se ha supuesto que la función de onda Ψ(x) representa un haz de partículas de la misma energía que avanzan sincronizadas en fase una junto a la otra. En la práctica, no resulta nada fácil obtener un haz de partículas que tengan todas ellas la misma energía, y lo más usual en el mejor de los casos es tener un haz de partículas para el cual “la misma energía” E en realidad es tan sólo el máximo de la curva de distribución energética de partículas en donde podemos encontrar una mayor cantidad de partículas que tengan “más o menos” la misma energía (hablando en términos estadísticos). Y de hecho, en base a esto, se vuelve necesario para poder obtener una mayor concordancia entre los resultados teóricos y los resultados experimentales caer en la cuenta de que un haz de partículas en realidad está compuesto por partículas separadas e individuales que deben ser consideradas cada una de ellas como un paquete de onda. Esto lo veremos con mayor detenimiento en entradas posteriores.
El caso contrario al caso de la doble barrera de potencial es el caso del pozo de potencial doble. Esencialmente, son dos pozos de potencial separados por una barrera de potencial intermedia. A continuación se muestra una ilustración de un potencial de este tipo en donde ambos pozos que supondremos rectangulares tienen la misma anchura a y la barrera intermedia de separación entre ambos pozos tiene una anchura b (en un análisis más elaborado, cada pozo de potencial puede tener una anchura diferente, y del mismo modo cada pozo de potencial puede tener una profundidad diferente):
Intuitivamente, podemos suponer que dentro de cada pozo de potencial rectangular se podrá admitir una cantidad finita de estados discretos de energía, con el estado de energía basal en cada pozo ocupando el nivel más bajo (cerca del fondo del pozo). La cantidad de estados discretos de energía dependerá de la profundidad de los pozos, con un gran número de estados discretos cuanto mayor sea la profundidad del pozo. Del mismo modo, intuitivamente, podemos suponer que en el caso en el cual la anchura de la barrera que separa ambos pozos tiende a cero hasta el punto de desvanecerse, o sea cuando b.→.0, se tendrá el equivalente de un solo pozo de potencial de anchura 2a. Y si la anchura de la barrera que separa ambos pozos es muy grande, o sea cuando b.→.∞, se tendrán dos pozos de potencial
Sin entrar a fondo en los detalles matemáticos que se nos revelan mediante la solución de la ecuación de Schrödinger, y tomando el caso en el cual la anchura de la barrera es igual a cero, se tiene un solo pozo de potencial rectangular. Suponiendo que la profundidad de dicho pozo sea suficiente para admitir dos estados discretos, el estado basal (fundamental) E1 y el primer estado excitado E2, al estado basal le corresponderá una función de onda ψ1(x) que dentro del pozo debe ser el equivalente aproximado de una media longitud de onda (correspondiendo a una solución par de la ecuación de onda, sin un nodo en el punto intermedio central del pozo en donde la función de onda pudiera tomar el valor de cero), mientras que al primer estado excitado le corresponderá una función de onda ψ2(x) que dentro del pozo debe ser el equivalente aproximado de una longitud de onda completa (correspondiendo a una solución impar de la ecuación de onda, con un nodo en el punto intermedio central del pozo en donde la función de onda toma el valor de cero). Puesto que el pozo de potencial de anchura 2a no tiene las paredes verticales infinitamente altas, “algo” de la función de onda ψ1(x) así como de la función de onda ψ2(x) deberá “escaparse” hacia los lados fuera del pozo. Esto es lo que corresponde a una solución que en el exterior del pozo tiene un decaimiento exponencial mientras que en el interior del pozo tiene un comportamiento cosenoidal para ψ1(x) y senoidal para ψ2(x). En las figuras que se muestran a continuación, las regiones de color azul claro son las que corresponden a la solución de decaimiento exponencial:
Supóngase que ahora se interpone una barrera de potencial de anchura muy pequeña en el centro del pozo de potencial, una barrera casi inexistente pudiendo tomarse como una línea vertical imaginaria. El pozo de anchura 2a queda efectivamente subdividido en dos mitades iguales de anchura a cada una de ellas. Cada mitad tendrá dos niveles energéticos E1 y E2 por encima del potencial V0, iguales en magnitud a los niveles energéticos del pozo de anchura 2a. Las energías para los estados discretos de un pozo de potencial de anchura 2a pueden ser aproximadas mediante la relación que se obtuvo arriba:
La energía del estado basal será:
mientras que la energía del primer estado excitado será:
siendo:
Para el caso en el cual la barrera de separación entre ambos pozos no es muy grande, ni siquiera grande, por ejemplo cuando b.≈.a, la solución general debe ser tal que al ir aproximando los dos pozos de potencial rectangulares se van “uniendo” las funciones de onda de cada estado fundamental propio de los pozos separados para formar la nueva función de onda que corresponde al estado fundamental del doble pozo con dos “jorobas”. Esta es la solución par del doble pozo de potencial que corresponde a la función de onda ψ1 del doble pozo de potencial (¡no confundir!). La solución impar del doble pozo de potencial es la que llamaremos ψ2. A continuación, y a modo comparativo, se muestran en la parte superior las funciones de onda ψ1(x) y ψ2(x) para cada uno de los pozos separados, mientras que en la parte inferior se muestran las funciones de onda que corresponden al doble pozo de potencial:
De este modo, la solución para el estado fundamental del pozo de potencial doble es una función par (sin un nodo intermedio central) con decaimiento exponencial fuera de las paredes del pozo, senoidal dentro de cada pozo, y una función de tipo coseno hiperbólico dentro de la barrera intermedia para “conectar” ambos pozos. Del mismo modo, la solución para el primer estado excitado del pozo de potencial doble es una función impar (con un nodo intermedio central) con una función de tipo seno hiperbólico dentro de la barrera intermedia para “conectar” ambos pozos.
Conforme va aumentando la anchura de la barrera intermedia de potencial que separa ambos pozos, la situación, la función de onda del estado basal así como la función de onda para el primer estado excitado del pozo doble de potencial muestran el siguiente aspecto:
Al ocurrir esto, se tienen esencialmente dos pozos de potencial aislados, ψ1(x) y ψ2(x) para el pozo de potencial doble se traducen en dos niveles degenerados de energía (teniendo el mismo valor) que vienen siendo esencialmente las combinaciones lineares par e impar de los estados basales de los dos pozos de potencial separados.
Desde el punto de vista energético, lo que va ocurriendo conforme pasamos del pozo de potencial de anchuera 2a a dos pozos de potencial de anchura a interponiento una barrera intermedia de separación, es lo siguiente (obsérvese que cuando b es igual a cero los niveles de energía actuales E1 y E2 por encima del potencial V0, sin recurrir a aproximaciones en los cálculos, serán algo inferiores a Q y a Q/4 respectivamente):
Conforme aumenta la distancia de separación b entre ambos pozos de potencial, las dos energías discretas en ambos pozos de potencial se van acercando hacia un solo nivel de energía en cada pozo que se encontrará un poco debajo del nivel de energía dado por:
Esto lo podemos ver ilustrado mejor en el siguiente gráfico animado (la línea intermedia de color gris que aparece en cierto momento representa la nueva energía discreta E1 (sumada a V0) hacia la cual se encaminan las energías las energías discretas E1 y E2 (sumadas a V0 también) de cada pozo conforme va aumentando el espesor de la barrera de potencial en concordancia con la gráfica anterior:
En rigor de verdad, este gráfico animado no representa lo que realmente queremos representar en virtud de que al ir avanzando la animación podemos ver que la anchura a de cada pozo individual va disminuyendo siendo que esta anchura a debería de permanecer constante todo el tiempo, representándose dos pozos de anchura a fija que se van separando al mismo tiempo que la distancia de separación entre ambos se incrementa al ir aumentando b. El siguiente gráfico animado muestra en forma más fidedigna la situación que se trata de representar:
Resulta instructivo visualizar el proceso contrario, o sea lo que sucede cuando dos pozos de potencial ambos de anchura a se van aproximando hasta fusionarse para formar un solo pozo de potencial de anchura 2a, lo cual es mostrado por el siguiente gráfico animado:
El doble pozo de potencial puede ser considerado como un modelo muy primitivo unidimensional para el potencial experimentado por un electrón que es compartido por los dos átomos de una molécula diatómica, con cada uno de los dos pozos de potencial representando la fuerza atractiva de los núcleos atómicos sobre dicho electrón. Si ambos núcleos están en libertad de moverse, se dá por hecho que adoptarán una configuración que corresponderá a la configuración de la energía mínima, habido el hecho de que es una propiedad fundamental de la Naturaleza que todos los sistemas físicos tienden a acomodarse en la configuración de energía mínima. Nos preguntamos ahora: en base a las conclusiones presentadas arriba, ¿el electrón compartido tenderá a unir los átomos o tenderá a empujarlos haciéndolos que se separen? (ignoraremos por lo pronto el asunto de la repulsión internuclear, lo cual es un asunto que debe tratarse por separado). De lo que se tiene arriba, la energía del estado fundamental (función de onda par) es menor en la configuración para la cual b.→.0, de modo tal que el electrón tiende a “jalar” ambos núcleos atómicos acercándolos el uno al otro, promoviendo de este modo el enlace atómico. En contraste, el primer estado excitado (función de onda impar) el electrón tiende a “empujar” ambos núcleos atómicos separándolos el uno del otro. Al estudiar más a fondo el enlace atómico, veremos que en efecto hay dos tipos de orbitales atómicos, un orbital enlazante, y un orbital antienlazante, de modo que este modelo primitivo no está muy alejado de la realidad que se obtiene al recurrir a modelos (tridimensionales) más sofisticados.
Podemos considerar otras variantes de lo anterior. Una de ellas supone un doble pozo de potencial en el cual la barrera de potencial intermedia sobresale por encima del nivel V.=.0, siendo por lo tanto no solo una barrera de potencial intermedia sino una verdadera barrera de potencial:
Para partículas con energía E superior a un potencial V.=.0 como lo indica la figura, la barrera de potencial en el centro de la figura representa un potencial repulsivo. Los potenciales repulsivos puros no son capaces de formar estados ligados, puesto que “repelen” a las partículas incidentes, aunque dependiendo de la energía E de las partículas y la altura V de la barrera encontrada, habrá una probabilidad de que un porcentaje de partículas incidentes desde el lado izquierdo puedan “pasar” al lado derecho de la barrera atravesándola, mientras que otras partículas serán “reflejadas” en sentido contrario. En cambio, los dos pozos de potencial actúan como potenciales atractivos. Los potenciales atractivos puros son capaces de formar estados ligados, formando una cantidad de estados discretos que dependerá de la energía E de las partículas así como de la profundidad del pozo de potencial. Esto lo podemos resumir de la siguiente manera:
Los potenciales positivos son potenciales repulsivos.
Los potenciales negativos son potenciales atractivos.
Todos los casos que hemos tratado en esta serie de entradas acerca de la transmisión y reflexión de partículas sobre pozos de potencial o barreras de potencial han sido casos unidimensionales, en las cuales la onda de materia (o el haz de partículas-onda) se mueve a una velocidad constante en una sola dimensión, usualmente escogida a lo largo del eje-x. Y las paredes que representan cambios de potencial son paredes verticales. Las conclusiones obtenidas mediante este tipo de aproximaciones suelen ser válidas en una amplia variedad de casos tales como los que ocurren en semiconductores de estado sólido. Sin embargo, si se trata de un haz de partículas libres que es lanzado hacia un centro de esparcimiento en donde el “blanco” puede ser otra partícula que ejerce algún efecto de atracción o repulsión sobre las partículas del haz de tipo Coulómbico, el problema necesariamente se vuelve más complejo, ya que la descripción del comportamiento de las partículas dispersadas se debe llevar a cabo en un espacio tridimensional, y de la simple coordenada unidimensional Cartesiana tenemos que echar mano necesariamente de las coordenadas esféricas. En virtud de que este tipo de análisis requiere de otras técnicas mátemáticas más elaboradas que no hemos cubierto aún, una discusión más a fondo sobre esta situación se dejará postpuesto para otras entradas bajo títulos tales como “Esparcimiento clásico de partículas”, “Esparcimiento de las ondas de luz”, “El método de las ondas parciales” y “La aproximación de Born”.
¿Será solo posible, de acuerdo a lo que se ha discutido arriba, tener estados ligados únicamente dentro de pozos de potencial, atractivos por naturaleza, al ser repulsivas las barreras de potenciales positivos? Interesantemente, también es posible tener estados ligados en situaciones que involucran únicamente barreras de potencial. Un ejemplo sencillo de esto es la doble barrera de potencial rectangular. Dentro de una doble barrera de potenciales rectangulares finitos podemos tener el equivalente de partículas “semi-atrapadas” en cualquiera de una cantidad finita de niveles bien definidos de energía. Un caso sumamente interesante ocurre cuando las partículas que inciden sobre una doble barrera de potencial poseen la misma energía que cualquiera de las energías que corresponden dentro de la doble barrera a estados ligados, algo equivalente desde el punto de vista mecánico-cuántico a “sintonizar” un radio a cierta estación:
Como podemos ver en la primera figura, si la energía de una partícula que incide desde la izquierda sobre la doble barrera de potencial no tiene una energía cercana a la energía que corresponde a uno de los estados ligados del interior de la doble barrera, la partícula tendrá una probabilidad muy pequeña de atravesar la doble barrera. Sin embargo, como podemos verlo en la segunda figura, si la energía de la partícula que incide desde la izquierda sobre la doble barrera de potencial tiene una energía cercana o igual a la energía que corresponde a uno de los estados ligados del interior de la doble barrera, entonces la partícula tendrá una probabilidad muy buena de atravesar la doble barrera, con una transmisión casi perfecta, un efecto que es conocido como una resonancia. La solución del problema de una doble barrera de potencial requiere subdividir el espacio en cinco regiones como lo hemos hecho anteriormente, montando cinco sistemas de ecuaciones. Aunque las matemáticas son elaboradas, en realidad se pueden obtener resultados cualitativos bastante aproximados usando lo que ya se tiene para un pozo de potencial y una barrera de potencial considerados por separado. A continuación tenemos un ejemplo de cómo para una doble barrera de potencial con tres estados ligados interiores hay una transmisión casi perfecta, igual a la unidad, confirmada por la gráfica puesta del lado derecho en la que tenemos graficada la relación que hay entre el coeficiente de transmisión T en función de la energía E de las partículas que inciden sobre la doble barrera de potencial:
El fenómeno de la resonancia volverá a surgir nuevamente después de la entrada “Esparcimiento clásico de partículas” cuando llevaremos a cabo el estudio de la transmisión y la reflexión de partículas considerando el esparcimiento de las partículas hacia un espacio radial tridimensional con el centro de esparcimiento actuando como un radiador de ondas esféricas, lo cual obviamente requerirá que veamos herramientas matemáticas más sofisticadas que las que hemos estado utilizando aquí. La resonancia en sí es un tema propio de lo que suele ser conocido como las “Resonancias de esparcimientos”. Las enormes implicaciones de la resonancia como consecuencia de fenómenos de esparcimiento de partículas son tales que precisamente a estos efectos se deben los mismos fenómenos gracias a los cuales tenemos los hornos de microondas, los rayos láser, y la energía eléctrica no-contaminante generada en reactores nucleares.
Todos los casos que han sido cubiertos hasta aquí de transmisión y reflexión de partículas pueden ser combinados de nuevas maneras para obtener una gran variedad de situaciones interesantes que sirven para predecir o explicar fenómenos de amplia utilidad en áreas tales como la microelectrónica y en la construcción de rayos láser de estado sólido.