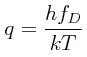El siguiente dibujo nos muestra un acomodo aleatorio de partículas indistinguibles en varias cajas de energía distinguibles como ocurre en el caso de los bosones:
Al empezar nuestro estudio de las relaciones combinatóricas básicas utilizadas en la Mecánica Estadística, ya vimos que el total de maneras posibles de colocar N objetos indistinguibles en g posiciones distinguibles sin restricciones en la ocupación es:
No cuesta mucho trabajo descubrir el origen de esta relación combinatórica. Supóngase que en el nivel de energía Ei existen gi estados por los efectos de la degeneración. Supóngase también que en ese nivel hay ni partículas. Este nivel puede representarse como ni partículas en filas (horizontales) divididas arbitrariamente en gi estados mediante gi-1 líneas. El número de formas diferentes en que los ni bosones pueden ubicarse en los gi estados, sin limitación en el número de partículas por estado y considerando por el momento que las partículas son distinguibles, es igual al número de maneras diferentes:
en que las partículas y las líneas que las dividen pueden permutarse, esto es:
dividido por el número de formas:
en las que las líneas pueden permutarse:
o sea:
Pero en virtud de que las partículas son indistinguibles unas de otras, de modo tal que el intercambio de dos partículas entre dos niveles de energía distintos da como resultado la misma distribución, la expresión anterior se tiene que dividir entre ni! formas diferentes en que pueden permutarse las partículas para obtener el número real de maneras diferentes en las que puede formarse el i-ésimo nivel de energía:
Por lo tanto, el número total X de formas diferentes que hay para organizar los n1, n2, n3, ... etc. bosones en los niveles de energía E1, E2, E3, ... etc. si existen ni!, ni!, ni!, ... etc. estados en cada nivel es:
Si queremos obtener la distribución más probable, al igual que como ocurrió con las distribuciones de Maxwell-Boltzmann y Fermi-Dirac tenemos que maximizar a X. El procedimiento sigue esencialmente la misma ruta que la que fue utilizada para obtener la distribución de Boltzmann. Al igual que como ocurrió para dicha distribución, aquí resulta matemáticamente más accesible llevar a cabo la maximización recurriendo al logaritmo natural de la función a ser maximizada. Aquí la expresión a ser maximizada se toma como:
sujeta a las restricciones de que el número total de partículas pueda ser considerado constante y que la energía total de las partículas se mantenga constante:
Después de las diferenciaciones de rigor, empleo de la fórmula de Stirling y el método de los multiplicadores de Lagrange, eventualmente se encuentra que las condiciones necesarias para un máximo son:
Para un sistema en el cual se tiene una gran cantidad de partículas y una gran cantidad de estados, se puede suponer que:
Con esto se tiene entonces:
En virtud de que ni es el número de bosones con energía Ei y gi es el número de estados con energía Ei, el número promedio de bosones en un estado con energía Ei es ni/gi. De este modo, ni/gi es la función de distribución Bose-Einstein que simbolizamos como FBE:
Obsérvese que aquí tenemos un problema potencial de una posible división entre cero, de cuyo manejo e interpretación hablaremos posteriormente.
PROBLEMA: Supóngase que se tiene un gas formado por un flujo de N bosones en un recipiente cuyo volumen es V. Demuéstrese que la variable α que aparece en la distribución Bose-Einstein es una función creciente de la temperatura absoluta T.
Teniéndose n = n(E), la condición de normalización está dada por:
que suponemos que debe ser un número fijo, constante. Introduciendo la densidad de estados g(E), lo anterior viene siendo:
Introduciendo explícitamente la distribución Bose-Einstein FBE, se tiene:
Haremos ahora una simplificación con el cambio de variables q.=.E/kT, escribiendo lo siguiente:
Podemos ver que esta ecuación nos define a α como una función de la temperatura absoluta T. Conforme la temperatura aumenta, el coeficiente de la integral también aumenta, y puesto que N es una cantidad fija entonces en la medida que la integral decrece el valor de α debe de crecer.
Consideraremos ahora el problema de la radiación del cuerpo negro desde un punto de vista diferente de la metodología utilizada por Max Planck para presentar su ya famosa ecuación que no sólo fue capaz de describir el comportamiento de la radiación del cuerpo negro sino que introdujo por vez primera la idea de la discretización de la energía en “cuantos”. En rigor de verdad, Planck llegó a su fórmula de una manera casi forzada, después de haber agotado todas las ideas y posibilidades que le ofrecían la termodinámica y la electrodinámica clásica. No podemos decir que su fórmula fue el producto de la casualidad o de un afortunado golpe de suerte, ya que su trabajo le costó obtenerla. El mismo Planck afirmó haber llegado a dicha fórmula como un acto final de desesperación además de haber sido acosado hasta el final de sus días por la inquietud del por qué en el mundo sub-microscópico la Naturaleza prefiere avanzar en “cuantos” en vez de hacerlo de una manera suave y continua.
Puesto que los fotones son bosones de spin S.=.1, consideraremos un gas de fotones.
Empezaremos con la relación de Louis de Broglie:
Puesto que la longitud de onda λ está relacionada con el número de onda k como k.=.2π/λ, se tiene entonces:
En un sistema tridimensional de coordenadas rectangulares Cartesianas, el momentum debe ser manejado como un vector de tres componentes, teniéndose entonces:
Supóngase ahora que tenemos un contenedor de paredes sólidas completamente sellado, con la forma exterior de un cubo y hueco por dentro con dimensión L en cada lado interno de la cavidad interior que también tiene la forma del cubo externo. Ahora supóngase que tenemos un “gas” de fotones encerrado dentro de la cavidad interior del cubo. Esto se antoja algo difícil de lograr, ya que lo primero que se nos viene a la mente es que el interior hueco del cubo debe estar completamente a obscuras, sin capacidad para poder contener un solo fotón luminoso, y menos aún cuando estamos acostumbrados a concebir al fotón individual como algo en movimiento que forma parte de un rayo de luz que se traslada de un lado a otro y que al llegar a un pared sólida desaparece en su interacción con la materia. Entonces, ¿cómo podemos sostener un gas de fotones dentro de la cavidad hueca del cubo? La respuesta a esto: de la única manera en la que es posible lograr tal cosa, que consiste en calentar al cubo hasta una temperatura elevada en la cual empiece a radiar energía electromagnética. Podemos imaginar al cubo como un cubo metálico calentado hasta ponerse al rojo vivo. Al ocurrir esto, sabemos que la energía radiante producida por el cubo tiene que ser energía producida por el mismo cubo como consecuencia del proceso de calentamiento. Y si las paredes interiores del cubo están a la misma temperatura que las paredes exteriores, entonces en el interior del cubo, dentro de la cavidad hueca, también debe de haber radiación luminosa, sólo que esta radiación luminosa, a diferencia de la radiación externa, no puede escapar hacia afuera al ser incapaz de poder atravesar las paredes sólidas del cubo; se trata de radiación confinada por completo al interior del cubo. Para indagar la naturaleza de esta radiación electromagnética interior, podemos hacer un agujerito muy pequeño en una de las paredes del cubo, lo suficientemente pequeño como para que pueda escapar algo de la radiación interna hacia el exterior en donde pueda ser analizada con un espectrómetro, como lo muestra la figura en la cual se ha hecho invisible la tapa superior de una caja metálica de paredes delgadas:
Si el agujerito de lo que puede ser considerdo literalmente como un horno es lo suficientemente pequeño, la luz exterior que cae sobre el cubo no contaminará apreciablemente la “luz” interna ocasionada por el calentamiento del cubo a altas temperaturas. Cuando se tiene una situación así, tenemos lo que se llama un cuerpo negro, y la radiación interna es lo que se conoce como la radiación del cuerpo negro. A la temperatura del cero absoluto, en el interior del cubo no esperamos que haya radiación interna alguna, y el interior del cubo realmente será “negro”. Pero conforme lo vamos calentando hasta llevarlo al rojo vivo (o al “blanco vivo”, esto depende de la magnitud de la temperatura), el interior ya no será tan negro, y de hecho habrá bastante “luz interna”. El cubo en sí, visto desde el exterior, en ningún momento es “negro”, ni siquiera a la temperatura ambiente. Si es de cobre, entonces tendrá un color cobrizo cuando es visto desde el exterior a la temperatura ambiente, y si es visto desde el interior no mostrará color alguno a la temperatura ambiente porque no hay luz externa que pueda reflejar para mostrarnos el color del cobre. Esto nos sugiere ya que la radiación interna que se obtenga a elevadas temperaturas del cubo de cobre no tiene absolutamente nada que ver con el “color” del cobre ya que no se trata de una luz reflejada por las paredes del material sino de una luz generada dentro del mismo material. Y de hecho esta “luz interna” no depende para nada del material del que esté hecho el cubo, depende únicamente de la temperatura.
Considerada la “luz interna” dentro del cubo como una radiación electromagnética aprisionada dentro del cubo, y considerada clásicamente dicha radiación en su aspecto ondulatorio, sabemos ya que para que puedan existir ondas luminosas estacionarias dentro del cubo la longitud de onda de cada fotón debe “caber” en un múltiplo enteros de medias longitudes de onda dentro de las paredes de la cavidad. Si designamos como L a la longitud de cada lado en el interior de la cavidad cúbica, entonces esto equivale a imponer sobre cada fotón la condición:
Un hecho comprobado experimentalmente desde un principio es que la radiación del cuerpo negro no consiste de una sola frecuencia luminosa; consiste de toda una gama de frecuencias distintas que desde luego tienen que cumplir con la condición anterior. Esto nos permite visualizar de la siguiente manera lo que ocurre en el interior de la cavidad de un cuerpo negro en donde tenemos tres frecuencias luminosas distintas además de un agujerito pequeño que permite escapar una fracción pequeñísima de la radiación al exterior para su análisis:
Queda desde luego una duda. Si al cubo que contendrá el “gas” de fotones se le hace un orificio pequeño para permitir una salida de la radiación interna, ¿no afectarán los resultados de la observación llevada a cabo sobre el haz emergente de fotones el estado normal de cosas que se tendría en una caja cúbica completamente sellada al haber una cantidad menor de fotones a causa de los fotones que se estarán escapando? Esto no nos debe de preocupar, porque mientras la caja se mantenga a una temperatura elevada, en las paredes internas de la cavidad cúbica se seguirán produciendo rápidamente más fotones para reponer a los que se pierdan al salirse por el orificio. Pero si esto ocurre, ¿que pasa entonces dentro de una caja sellada herméticamente de la cual no pueda escapar un solo fotón de los que se están produciendo en el interior, si continuamente se están produciendo nuevos fotones? Tampoco nos debe preocupar que el interior de una caja sellada herméticamente pueda “rebosar” de fotones hasta llenarse en exceso de ellos, porque no se producirán en el interior más fotones de los que sean permitidos para mantener por dentro el equilibrio termodinámico.
Siendo el número de onda tridimensional, entonces al tener lo siguiente:
debemos tener también números enteros nx, ny y nz que, en cumplimiento con la condición dada anteriormente:
o lo que es lo mismo:
con lo cual se tiene:
Esto último es similar a lo que se tuvo en el desarrollo que nos llevó previamente a la distribución de Fermi-Dirac para fermiones. Tomando en cuenta que nx, ny y nz son números enteros positivos, y haciendo:
en donde tomamos a N como el radio R de una esfera imaginaria, tenemos lo siguiente:
Puesto que, para un fotón luminoso, su energía E y su momentum p están relacionados de la siguiente manera:
entonces la energía para el gas de fotones debe estar dada por la expresión:
Tras lo anterior, en lugar de tratar de encontrar el número de estados enteros (nx, ny, nz) que corresponden a un N dado, podemos tratar de utilizar una aproximación continua para encontrar el número de puntos en una concha esférica de radio N y de espesor dN en el primer octante del espacio. La razón para limitarnos a un octante del espacio es la misma que la que se dió en la obtención de la distribución de Fermi-Dirac: tanto nx como ny como nz son enteros positivos y ninguno de ellos admite valores negativos. Una concha esférica de radio N y de espesor dN contiene un “volumen” infinitesimal dV que contiene el número de estados que hay entre N y N+dN, el cual es igual a:
Pero tenemos que tomar en cuenta de que hay dos direcciones posibles de polarización independientes para cada modo, de modo que tenemos que multiplicar lo anterior por dos para poder obtener el número de estados entre N y N+dN viene siendo:
Imaginemos ahora que con el número N podemos asociar fotones con una longitud de onda λ0, que a su vez corresponda con una frecuencia propia de la radiación electromagnética de dichos fotones. Entonces, considerados como un modo típico de vibración que dentro de la caja también solo puede existir en algún múltiplo entero de medias longitudes de onda, se puede escribir lo siguiente:
de lo cual:
Pero la longitud de onda de cualquier fotón multiplicada por la frecuencia del mismo debe ser igual a la velocidad a la cual se desplaza el fotón que sabemos que es la velocidad de la luz. Entonces:
Tomando infinitesimales sobre esto último:
El número de estados entre N y N+dN debe ser igual al número de estados en el intervalo de frecuencia correspondiente de f a f+df. Entonces combinando esto con lo que habíamos obtenido previamente se obtiene:
De este modo, como se ha destacado arriba, la densidad de estados de fotón en el intervalo de frecuencia df es:
Considerando a la cavidad como un recipiente que contiene un “gas” de fotones, los cuales son bosones de spin 1, podemos utilizar la función de distribución Bose-Einstein para fotones con α.=.0, obteniendo así el número infinitesimal de fotones dnf con frecuencias comprendidas entre f y f+df del modo siguiente:
De lo que hemos visto previamente en otras entradas, sabemos que la energía de cada fotón es E.=.hf. Entonces la energía infinitesimal dEf transportada por los dnf fotones tiene que ser:
Esto lo podemos abreviar como:
en donde se ha definido a la distribución espectral F(.f.) del modo siguiente:
Esta demostración fue obtenida por vez primera en 1924 por el físico hindú Satyendra Nath Bose, y el resultado es el mismo resultado que el que obtuvo Max Planck para explicar la naturaleza de la radiación electromagnética producida por un cuerpo negro calentado a una temperatura T, excepto que Planck utilizó otros argumentos para llegar a ella. Por lo que puede verse, esta ley es una consecuencia directa de la Mecánica Estadística Cuántica que está basada en argumentos combinatóricos. Aún si Planck no hubiera sido el primero en lograr el descubrimiento de tal expresión introduciendo firmemente con ella el concepto de la discretización de la energía que dió nacimiento a la Mecánica Cuántica, el descubrimiento de la misma era tan solo una cuestión de tiempo. De cualquier modo, vale la pena hacer un breve repaso de la forma en la cual Planck obtuvo la ley para describir la radiación del cuerpo negro. Tras haber fracasado en la obtención de una fórmula por medio de argumentos propios de la electrodinámica clásica, lo primero que hizo fue buscar una fórmula que pudiera ser ajustada a los datos experimentales, lo cual logró, tras lo cual buscó una manera en la cual la función pudiera ser explicada. Descubrió que esto podía lograrse si para los osciladores electromagnéticos resonantes que se suponía que debía de haber dentro de la cavidad del cuerpo negro se calculaba la energía promedio por modo de oscilación de la siguiente manera empleando la distribución de Boltzmann (la cual ya para entonces le era conocida):
Este postulado implica necesariamente que en lugar de tomar el procedimiento usual de suponer que la energía era continua, la energía estaba discretizada. Este fue precisamente el paso que a Boltzmann no se le ocurrió tomar o posiblemente no se atrevió a dar. En la época de Planck, no había ninguna razón alguna para proponer tal cosa, y era una proposición extremadamente osada para su tiempo, pero no había otra manera de poder obtener una fórmula que pudiese explicar los datos experimentales. De este modo, Planck encontró que podía ajustar los datos experimentales si suponía que la energía era discontinua estando dada por la siguiente relación sencilla:
en donde n es un entero, f es la frecuencia, y h una constante de proporcionalidad a ser determinada a partir de los datos experimentales, la misma constante que hemos estado utilizando desde un principio y que hoy es conocida como la constante de Planck.
El cálculo matemático de la sumación dada arriba para obtener la energía promedio es esencialmente similar al cálculo llevado a cabo por Einstein para poder obtener una expresión para la capacidad calorífica molar CV de los sólidos cristalinos que ya se vió en detalle en una entrada anterior, razón por la cual no será necesario repetir aquí dichos cálculos. El resultado obtenido por Planck para la energía promedio por modo de oscilación resulta ser:
Con esto, era ya posible obtener la función de la distribución espectral del cuerpo negro, que Planck encontró que era:
A continuación se tiene una gráfica de la distribución espectral F(.f.) para el gas de fotones que hay dentro de la cavidad de un cuerpo negro para cinco temperaturas diferentes (esta distribución es independiente del tipo de material con el que haya sido fabricada la cavidad, ya sea níquel, oro, cobre, plata o cualquier otro tipo de materia prima):
Es precisamente con la ayuda de la distribución de la energía espectral radiante que nos llega de las estrellas como podemos saber la temperatura de las mismas.
Si tomamos la función de la distribución de energía espectral obtenida por Planck y recurrimos a una aproximación para longitudes de onda λ grandes, entonces de la expansión en series de Maclaurin-Taylor del exponencial:
ex = 1 + x + ...
tenemos que para x.«.1 en donde x.=.hc/λkT:
con lo cual obtenemos la siguiente aproximación para valores grandes de λ:
Esta es la fórmula Rayleigh-Jeans, obtenida por argumentos puramente clásicos y la cual ya era conocida antes de que Planck obtuviera su fórmula exacta. El problema con la fórmula de Rayleigh-Jeans es que conforme λ se aproxima a cero dicha fórmula predice que la distribución espectral se vuelve infinitamente grande (esto porque el número de modos posibles de oscilación se vuelve infinito), en contraposición a los resultados experimentales que mostraban que la distribución espectral tiende a cero conforme λ se aproxima a cero. Esta disparidad era conocida como la catástrofe del ultravioleta, y permaneció como un misterio y como un reto hasta que Planck logró encontrar una explicación lógica al asunto fundando con ello a la Mecánica Cuántica.
PROBLEMA: Obténgase una expresión para la ley Stefan-Boltzmann que establece que la energía electromagnética total dentro de una cavidad cuyas paredes están a una temperatura T es igual a la cuarta potencia de la temperatura. Obténgase asimismo el valor de la constante de proporcionalidad.
De acuerdo a lo que se obtuvo previamente, la energía total en el interior de la cavidad está dada por:
Usando la integral:
con p = 4 tenemos entonces (de las tablas) que el valor de la integral es:
Entonces, usando las siguientes constantes físicas dentro del sistema de unidades MKS-SI:
k = 8.617.×.10-5 eV/°K
hc = 12.4.×.10-7 eV·m
en lo siguiente:
se obtiene la constante de proporcionalidad buscada:
E = (4.71.keV/°K4·m3)VT4
PROBLEMA: En las gráficas de distribuciones espectrales dadas arriba para diferentes temperaturas, se puede observar que el pico máximo de cada curva de distribución espectral se va desplazando en frecuencia con la temperatura. Si designamos a la longitud de onda que corresponde a un máximo como λmax, demuéstrese que:
λmaxT = constante
Usando la función de distribución espectral F(.f.) que se obtuvo arriba para un gas de fotones y tomando la derivada de la misma con respecto a la frecuencia, se tiene:
El máximo de la curva F(.f.) se cumple con la condición:
Por lo tanto:
Entonces la condición necesaria para un máximo es:
Haciendo y = hfmax, esto se puede representar de una manera un poco más compacta como sigue:
ey(3 - y) - 3 = 0
Esta es una ecución trascendental que tiene que resolverse por algún método de aproximación. Sin entrar en mayores detalles, la solución dá como resultado una constante con la cual se puede escribir lo siguiente:
Y puesto que fmax = c/λmax, entonces, agrupando la constante anterior en otra constante que incluya a las otras constantes físicas (constante de Planck, constante de Boltzmann, velocidad de la luz), llegamos al resultado:
La conclusión obtenida en este problema es conocida comúnmente como la ley de desplazamiento de Wien, en honor del físico Wilhelm Wien quien fue el primero que descubrió esta relación.
Un concepto equivocado entre muchos principiantes es aquél que supone que la Mecánica Cuántica empezó con la propuesta del modelo atómico planetario hecha por el físico danés Niels Bohr, pero esto es incorrecto. Si bien es cierto que Bohr, inspirado en las teorías de Rutherford, propuso la existencia de órbitas cuantificadas suponiendo que el electrón circundando en torno al núcleo atómico no podía tomar cualquier valor posible de energía permitido clásicamente sino que sólo podía tomar ciertos valores de energía bien definidos, lo cual a su vez requiere que el momento angular orbital del electrón esté cuantizado, Bohr presentó su modelo en 1913, trece años después de que Planck había introducido ya el concepto crucial de la discretización de la energía. Sin intención alguna de restarle mérito a las contribuciones de Bohr, lo que hizo Bohr fue tomar la idea esencial introducida por Planck y suponer que así como la energía estaba discretizada en el fenómeno de la radiación térmica emitida por el cuerpo negro, del mismo modo la energía que puede tener un electrón que se encuentre ligado a un átomo tampoco puede tomar cualquier valor ya que también debe estar discretizada. Inclusive Bohr usó para sus “cuantos” de energía la misma expresión que había sido propuesta por Planck:
El concepto de la energía discretizada es lo que abrió la puerta de entrada para todo lo demás. Es posible que la razón por la cual muchos suponen que la Mecánica Cuántica empieza a partir de Niels Bohr se deba a que en muchos textos en vez de seguirse el orden cronológico histórico se comienza a partir del modelo atómico planetario de Bohr (como se ha hecho en esta misma obra). Pero esta inversión en el orden de cosas se debe a que el modelo atómico planetario de Bohr es mucho más intuitivo y fácil de entender (relativamente hablando) que el análisis de la radiación del cuerpo negro para el cual, como hemos visto, se requiere de conocimientos esenciales previos sobre la Mecánica Estadística de Boltzmann, algo que muy pocos estudiantes poseen en su primer contacto con la Mecánica Cuántica.
Resumiendo lo que hemos visto, las dos funciones de distribución cuánticas pueden ser expresadas de la siguiente manera:
n(E)dE = g(E)FFDdE___(Fermi-Dirac)
n(E)dE = g(E)FBEdE___(Bose-Einstein)
Tenemos por lo tanto tres tipos de distribuciones estadísticas matemáticamente posibles, la primera (clásica) válida para partículas distinguibles puestas en “cajas de energía” distinguibles, y las otras dos (cuánticas) válidas para partículas indistinguibles puestas en “cajas de energía” distinguibles:
Algo que resalta como obvio es que para valores de E mucho mayores que kT tanto FFD como FBE se aproximan al factor de Boltzmann FMB. Una comparación de las tres distribuciones nos sugiere también que la distribución clásica Maxwell-Boltzmann puede ser una buena aproximación a ambas distribuciones cuánticas si BeE/kT es mucho mayor que la unidad, o lo que es lo mismo, si Ae-E/kT es mucho menor que la unidad, en donde A es la constante de normalización A.=.1/B calculada a partir de la distribución Maxwell-Boltzmann representando el número de partículas por estado en un intervalo infinitesimal de energía dE. De este modo, si el número de partículas por estado es mucho menor que la unidad, las distribuciones cuánticas difieren muy poco de la distribución clásica, de modo que esta condición equivale a la condición de que el número de partículas sea mucho menor que el número de estados disponibles. Esta condición siempre se cumple para gases ordinarios (que cumplan aproximadamente con la ley del gas ideal) en virtud de las grandes masas atómicas (en comparación con la masa del electrón) y las bajas densidades de los gases, pero casi nunca se cumple para gases de electrones. Para energías del orden kT, la distribución Maxwell-Boltzmann será una buena aproximación en el caso en el que A tiene un valor muy inferior a la unidad. Ya hemos visto que para un metal que contiene un electrón libre por átomo, el número de estados de energía que hay entre la energía que corresponde al estado fundamental y la energía kT es mucho menor que el número de electrones a menos de que la temperatura T sea muy grande.
Para poder ver cuándo podemos utilizar la más sencilla distribución clásica en lugar de las distribuciones cuánticas, todo lo que tenemos que hacer es suponer una distribución clásica y calcular el valor de A. La distribución clásica será válida si Ae-E/kT es mucho menor que la unidad. Calcularemos a continuación A para N partículas dentro de un cubo de lado L cuyo volumen será V = L3. Si las partículas son electrones, la densidad de estados en base a lo que hemos obtenido previamente puede ser escrita de la siguiente manera:
Si las partículas de las que estamos hablando son átomos de helio, por ejemplo, la densidad de estados es la misma excepto que la masa a ser utilizada es la masa del átomo de helio no habiendo un factor de 2 introducido porque no se tienen los dos estados que corresponden al spin del electrón (apuntando “hacia arriba” y apuntando “hacia abajo”). Utilizando la letra M mayúscula para representar a la masa del átomo de helio (este es un cambio mímimo e inconsecuente) con el fin de distinguirla de la letra m minúscula utilizada para representar a la masa del electrón, tenemos entonces que la densidad de estados para el átomo de helio cuyo spin es igual a cero y que obedece la estadística Bose-Einstein debe ser:
Podemos calcular la constante de normalización A para estos dos casos a partir de la condición:
Para el caso de los electrones, tenemos lo siguiente:
o bien:
Procediendo del mismo modo, obtenemos para el caso de los átomos de helio:
A continuación se realizarán algunos cálculos tanto para un gas de electrones (en el cual la estadística de distribución Fermi-Dirac es válida) como para un gas formado por átomos de helio (en el cual la estadística Bose-Einstein es válida). Suponiendo que hay un electrón libre en cada átomo de cobre, se tienen 6.023.×.1023 electrones (el número de Avogadro) en un mol de átomos de cobre, que tomaremos como el número N de partículas. Siendo la densidad ρ del cobre igual a 8.9.gramos/cm3 y siendo la masa m de un mol de átomos de cobre igual a 63.5.gramos/mol, el volumen que ocupa un mol de cobre (mismo volumen que ocupa aproximadamente el “gas” de electrones) es entonces:
V = m/ρ = (63.5 gramos/mol)/(8.9 gramos/cm3) = 7.13 cm3/mol
Con esto, la densidad de los átomos de cobre (que viene siendo la misma que la densidad de los electrones) se puede tomar como:
N/V = 8.5.×.1022 electrones/cm = 8.5.×.10-2 electrones/Å3
A la temperatura ambiente T = 300 °K, usando para el electrón:
kT = 0.0258 eV
mc2 = 0.511.×.106 eV
hc = 12,400 eV·Å
(hc/2)3 = 9.533.×.1011 eV3 ·Å3
entonces, con la fórmula para Ae modificada un poco para facilitar los cálculos numéricos:
se obtiene para el gas de electrones:
(2π · 0.511.×.106 eV · 0.0258 eV)-3/2 = 4.194 ×.10-8/eV3
Ae = (8.5.×.10-2)(9.533.×.1011)(4.194 ×.10-8)
Ae ≈ 3,398
y con esto vemos que la aproximación A«1 no es válida. Esto concuerda con lo que se había visto previamente: si los electrones obedecieran una distribución Maxwell-Boltzmann, habría muchos electrones por estado cuántico, violándose con ello el principio de exclusión de Pauli que impone un tope absoluto de dos electrones por estado.
En cambio, el cálculo llevado a cabo en forma similar para los átomos de helio, también a la temperatura ambiente, produce el siguiente resultado:
AHe ≈ 3.5.×.10-6
Este resultado es mucho más pequeño porque la masa del helio es unas ocho mil veces mayor que la masa del electrón, y por lo tanto:
(M/m)3/2 ≈ 106
Además, la densidad del helio es más pequeña, ya que un mol de gas helio ocupa un volumen aproximado de 22.4 litros (22.4.×.103 cm3), comparado con un volumen de 7.1 cm3 para el mol de cobre en donde reside el gas de electrones. Podemos ver que para el gas ligero helio hay únicamente uno de cada 106 estados que están ocupados a la temperatura ambiente, o lo que es lo mismo, a una energía E.≈.kT. Por lo tanto, la distribución Bose-Einstein difiere muy poco de la distribución Maxwell-Boltzmann, dando con ello la distribución Maxwell-Boltzmann una aproximación excelente a la distribución Bose-Einstein en prácticamente cualquier caso de interés. Sin embargo, no es una buena aproximación a la distribución Fermi-Dirac en la mayoría de los casos de interés, razón por la cual se amerita inspeccionarla más a fondo.
Al igual que como se hizo en la distribución Bose-Einstein arriba, en la distribución Fermi-Dirac la constante B se obtiene de la condición:
En virtud de que esta integral no es fácil de computar, obtendremos una aproximación para B que resulta útil para un rango amplio de temperaturas. Usando los resultados obtenidos previamente cuando se trató el tema de la distribución de Fermi-Dirac, escribiremos la densidad de estados g(E) en términos de la energía de Fermi:
Como hemos visto que para poder recurrir a la distribución de Maxwell-Boltzmann tenemos que tener un valor para A mucho mayor que la unidad (o lo que es lo mismo, un valor para B mucho menor que la unidad) a temperaturas que no sean demasiado elevadas, supongamos que BeE/kT es insignificante para todas aquellas energías hasta la energía para la cual BeE/kT.=.1, y arriba de esta energía supondremos que BeE/kT es muy grande con lo cual el integrando se vuelve despreciable. Esto equivale a llevar a cabo una integración desde E.=.0 hasta E.=.E1 definido E1 mediante:
Entonces con estas simplificaciones se puede llevar a cabo el siguiente proceso de integración aproximado (BeE/kT se desprecia al ser considerado insignificante dentro del rango de la integración):
De esto obtenemos de inmediato E1.≈.EF, dándonos para la constante B el siguiente resultado aproximado:
En virtud de que la energía de Fermi EF tiene un valor situado entre 1 y 7 eV para la mayoría de los casos de interés, la cantidad:
será pequeña hasta la temperatura de Fermi TF = EF/k, la cual es de alrededor de 81,000.°K. Por lo tanto, la aproximación que estamos haciendo es razonable. El factor de Fermi se vuelve entonces:
Conforme la temperatura T se va acercando al cero absoluto:
y:
Por lo tanto:
lo cual está de acuerdo con lo que se ha estado discutiendo con anterioridad.
La aproximación:
es válida cuando la energía de Fermi EF es definida a la temperatura del cero absoluto. Sin embargo, es rutinario definir a la energía de Fermi para cualquier temperatura tomando la expresión anterior como exacta, lo cual simplemente implica escribir a la constante de normalización como:
con lo cual se le dá una definición formal a la energía de Fermi. Debemos entonces utilizar algún otro tipo de notación para simbolizar a la energía de Fermi a la temperatura del cero absoluto, por ejemplo EF(0), ó mejor aún EF0. Podemos aproximar a EF con EF0 sobre un amplio rango de temperaturas. De la ecuación para el factor de Fermi FFD, podemos ver que la energía de Fermi se define como aquella energía para la cual la probabilidad de que un estado se encuentre ocupado es de 1/2.
Las tres distribuciones estadísticas que nos interesan pueden ser escritas de la siguiente manera haciendo resaltar explícitamente lo que representa la constante de normalización (B.=.eα) en las relaciones dadas arriba:
Obsérvese que en el caso de la distribución de Fermi-Dirac la constante de normalización está prefijada por el valor de la energía de Fermi EF.
Resulta instructivo comparar cuantitativamente las tres distribuciones dadas arriba para el caso de un gas ideal en el cual las moléculas están confinadas a los estados de energía que corresponden a los de una caja cúbica tridimensional, tanto para un gas poco denso como para un gas mucho más denso, manteniendo la temperatura constante (a un mismo valor) para las tres distribuciones. Esto se puede lograr seleccionando cuidadosamente los valores de α en forma tal que las tres distribuciones correspondan a la misma densidad total de partículas (lo cual requiere evaluar α para cada distribución sujeta a la condición de que la densidad total de las partículas sea la misma que en las otras dos distribuciones). Para un gas de baja densidad, la gráfica compuesta es la siguiente (para la abcisa que corresponde a la energía E se han utilizado múltiplos de kT):
Obsérvese que, excepto para los estados energéticos más bajos, los efectos peculiares producidos por la indistinguibilidad de las partículas en los dos casos cuánticos (Fermi-Dirac y Bose-Einstein) son prácticamente insignificantes. Sin embargo, si se aumenta la densidad del gas para que sea unas 150 veces más denso de lo que es en la figura de arriba, el contraste entre las tres distribuciones se vuelve notable:
Los efectos de la degeneración cuántica de los estados se vuelven notorios en los estados energéticos más bajos de las tres distribuciones. En el caso de la distribución Bose-Einstein, hay una tendencia marcada a que los estados energéticos más bajos (sobre todo el estado energético más bajo) estén mucho más poblados que los estados energéticos más altos. Este es precisamente el efecto de la condensación Bose-Einstein. Bajo estas condiciones de densidad elevada (correspondiendo a un α pequeño), un aumento posterior en la densidad simplemente resultará en una concentración mayor de las partículas de baja energía. La presión del gas no aumenta de modo apreciable. En este sentido, un gas de Bose se comporta como lo que se conoce como un vapor saturado: un aumento en la cantidad de substancia simplemente producirá un aumento en la cantidad de materia que se encuentra en la fase “condensada” sin que ello se traduzca en un aumento en la presión. Por su parte, en el gas de Fermi los estados energéticos inferiores muestran una tendencia a formar una población abnormalmente baja en comparación con las otras dos distribuciones. Aunque las tres curvas en cada caso fueron realizadas manteniendo la temperatura constante, cualitativamente hablando la forma general de las curvas también corresponde al efecto de ir disminuyendo paulatinamente la temperatura a la vez que se mantiene constante la densidad de las partículas (cuantitativamente los resultados serán diferentes, desde luego).
Un asunto que había quedado pendiente en una entrada anterior era la obtención de la fórmula de Debye para explicar el comportamiento de la capacidad calorífica de los sólidos, basada en un modelo más refinado que el modelo empleado por Einstein, en virtud de que el modelo empleado por Debye requiere considerar a las cuasi-partículas de vibración térmica cuantizada conocidas como fonones comportándose como lo que vendrían siendo dentro de una distribución estadística apropiada para partículas indistinguibles de las cuales puede haber cualquier cantidad de ellas en cualquiera de las “cajas de energía” distinguibles disponibles, o sea, bosones.
En el modelo de Debye, consideramos a los fonones como “ondas sonoras” que viajan en un sólido, perfectamente análogas a las oscilaciones de los fotones en la cavidad del cuerpo negro. Siguiendo los mismos razonamientos que hemos estado utilizando anteriormente, el número de modos de vibración dM con frecuencias en el intervalo comprendido entre f y f+df es:
para cada tipo de vibración, siendo c la velocidad de propagación de la onda en el medio (la cual no debe ser confundidad con la velocidad de la luz). Si se consideran los dos grados de libertad vibratoria para las ondas transversales, y el único grado de libertad para las ondas longitudinales, el número de estados vibratorios dS con una frecuencia en el intervalo comprendido entre f y f+df es:
De este modo, la densidad de estados en el intervalo de frecuencia df es:
En el modelo de Debye, existe un tope máximo a la frecuencia a la cual pueden vibrar los átomos que forman parte del sólido cristalino, la frecuencia de Debye f.D. Puesto que el número posible de estados es finito e igual a 3N, se tiene entonces:
Despejando de lo anterior, podemos ver que la densidad de estados tiene por lo tanto la forma:
si suponemos que la energía acústica es transportada a través de una estructura cristalina monoatómica en cantidades cuantizadas de valor hf por las cuasi-partículas que hemos dado en llamar fonones, las cuales son bosones cuyo número total, como el de los fotones, no está fijo, entonces si designamos al número de fonones con frecuencias en el intervalo comprendido entre f y f+df como dnf, entonces de acuerdo a la distribución Bose-Einstein este número será:
en donde g(.f.) es la función que fue obtenida arriba. En virtud de que cada fonón tiene una energía igual a hf, la energía dE que poseen los dnf fonones es:
La energía total Etotal del sólido será igual a la suma de las energías de todos los fonones, la cual podemos obtener mediante el proceso de integración que se deberá llevar a cabo hasta la frecuencia máxima posible que admite el modelo de Debye:
en donde:
es la definición de la temperatura de Debye, y en donde se ha hecho:
En virtud de que no existe un procedimiento analítico de solución que nos permita obtener una solución simbólica exacta en forma cerrada de la integral, esta integral tiene que ser calculada numéricamente mediante procedimientos de aproximación. De cualquier modo, se pueden llevar a cabo algunas simplificaciones para obtener resultados simbólicos tanto a temperaturas relativamente altas como a temperaturas relativamente bajas con respecto a la temperatura de Debye ΘD.
PROBLEMA: Usando el modelo de Debye, obténgase el calor específico molar a volumen constante para temperaturas que sean mucho más bajas que la temperatura de Debye.
Para temperaturas mucho más bajas que la temperatura de Debye, se puede poner en la integral de arriba lo siguiente:
y en tal caso la integral se aproxima a π4/15. De este modo, la energía total Etotal en su forma integral dada arriba se puede simplificar a lo siguiente:
Y recurriendo a la definición de la capacidad calorífica CV a volumen constante, se tiene entonces:
Para bajas temperaturas, se ha encontrado experimentalmente que la capacidad calorífica varía en razón directa al cubo de la temperatura absoluta tal y como lo predice el modelo de Debye, algo que no coincide con lo predicho por el modelo de Einstein, confirmándose de este modo la superioridad del modelo de Debye sobre el modelo de Einstein.
PROBLEMA: Demuéstrese que a temperaturas mucho mayores que la temperatura de Debye, el modelo de Debye predice una capacidad calorífica molar constante que coincide con lo que afirma la ley de Dulong y Petit.
Tomando el resultado obtenido arriba en forma integral para la energía total Etotal, para una temperatura que es mucho mayor que la temperatura de Debye se tiene:
y por lo tanto se puede hacer la aproximación:
sobre el intervalo de integración. De este modo:
y de acuerdo con la definición de la capacidad calorífica molar a volumen constante:
Esta es precisamente la ley de Dulong y Petit.
PROBLEMA: Obténgase una expresión sobre el modelo de Debye para la capacidad calorífica a volumen constante que sea válida a cualquier temperatura.
Tomando en cuenta que la frecuencia de Debye permanece constante cuando el volumen es constante:
Usando las simplificaciones simbólicas dadas arriba, esto último lo podemos escribir de la manera siguiente:
Las gráficas de la capacidad calorífica molar CV para el aluminio (Al), la plata (Ag) y el plomo en el modelo de Debye junto con sus respectivas temperaturas Debye son las siguientes que han sido superimpuestas en una sola gráfica:
Al igual que como ocurre con el modelo de Einstein, una característica importante de la fórmula obtenida por Debye para CV es que las curvas de las capacidades caloríficas para todos los sólidos monoatómicos deben “traslaparse” una encima de la otra si en vez de hacer las gráficas de en función de la temperatura absoluta T hacemos dichas gráficas en función de la temperatura reducida T/ΘD (para mayor simplicidad se ha escrito la temperatura de Debye como TD, una práctica seguida en muchos libros de texto). Si hacemos tal cosa con las tres gráficas mostradas en la figura de arriba, tendremos entonces que las tres gráficas se traslapan en una sola: