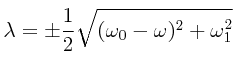Suponiendo que, antes de que se le diese una explicación al experimento Stern-Gerlach postulando para el electrón un momento angular intrínseco, ya hubiésemos resuelto el problema del momento angular orbital para el electrón que forma parte de un átomo de hidrógeno, ¿cómo deberíamos interpretar los resultados que se obtienen con una cantidad par de haces en el experimento Stern-Gerlach? Aquí resulta conveniente establecer analogías, considerando el caso clásico en el que se tiene un momento angular orbital y un momento angular intrínseco. La Tierra tiene un momento angular orbital debido a su órbita en torno al Sol, y tiene además un momento angular intrínseco debido a su rotación sobre su propio eje. Ambos momentos angulares son cantidades vectoriales, con componentes en tres direcciones, sus proyecciones sobre el eje-x, el eje-y y el eje-z, como vectorial es también el momento angular total producido al sumar el momento angular orbital de la Tierra en torno al Sol y el momento angular intrínseco de la Tierra debido al movimiento de rotación de la misma. Además, no existe diferencia alguna entre estas formas de momentos angulares con respecto a sus propiedades dinámicas, todas las formas clásicas de momento angular tienen la misma ecuación de movimiento:
en donde J es el momento angular y T es un par aplicado. Por lo tanto es de esperarse que los operadores del momento angular en la Mecánica Cuántica tengan propiedades iguales o similares, independientemente del tipo de momento angular al que se esté haciendo referencia.
Al estudiar la forma de los operadores del momento angular orbital, habíamos llegado a las siguientes relaciones:
LxLy - LyLx = iħLz
LyLz - LzLy = iħLx
LzLx - LxLz = iħLy
Estas son relaciones algebraicas de índole mecánico-cuántica entre los operadores del momento angular orbital que aceptamos como válidas. Si vamos a extender estos resultados al momento angular del spin del electrón, se supone que una relación de este tipo también será válida entre las componentes de los operadores que representen a cualquier forma del momento angular. Si simbolizamos a las componentes de estos operadores generalizados como Jx, Jy y Jz, se postula que deben obedecer la siguiente relación:
JxJy - JyJx = iħJz
JyJz - JzJy = iħJx
JzJx - JxJz = iħJy
Este trío de relaciones es suficiente para determinar los eigenvalores ó valores propios de Jz y de J² (definido como Jx² + Jy² + Jz²) mediante operaciones algebraicas que ya hemos visto con anterioridad. El resultado de un análisis de este tipo es que los valores propios de J² están dados por J(J+1)ħ en donde J es un entero (es decir, 0, 1, 2, etc.) o un semientero (es decir, 1/2, 3/2, 5/2, etc.), y los valores propios de Jz, para un valor dado de J, van en pasos enteros desde -J hasta +J en unidades de ħ. Así, las propiedades algebraicas de los operadores del momento angular permiten tener valores enteros o semienteros del momento angular, y es el requisito adicional, en el caso del momento angular orbital, de que la función de onda tenga un solo valor, lo que limita a los números cuánticos a tomar sólo valores enteros. Esto último nos lleva a una observación importante. Desde de que la Mecánica Ondulatoria empezó a dar sus primeros pasos, la función de onda Ψ se mantuvo como un ente indivisible, algo que no podía ser sub-dividido. Y de hecho, la función de onda para una onda de materia, independientemente del hecho de que pueda ser manipulable tanto espacial como temporalmente, en sí viene siendo a fin de cuentas una roca sólida que no es susceptible de ser particionada. Excepto, claro está, al momento de intentar darle una explicación al experimento de Stern-Gerlach bajo la Mecánica Ondulatoria. Es un hecho que la ecuación de Schrödinger, por sí sola, es incapaz de predecir un momento angular intrínseco para el spin del electrón, y es por lo tanto incapaz de predecir de antemano el resultado de un experimento como el experimento Stern-Gerlach. Para poder explicar el experimento Stern-Gerlach, fue necesario postular en la Mecánica Ondulatoria dos componentes discretas de la misma función de onda, necesarias para explicar las dos bandas bien definidas que aparecen en dicho experimento. Esto es sorpresivo e inesperado, porque anteriormente en todos los casos en los que hemos trabajado inclusive en el tratamiento del momento angular orbital, la función de onda era considerada como algo indivisible, sólido, que no podía ser separada en dos o más partes excepto al hacerlo sobre coordenadas ortogonales por el método matemático de la separación de variables. El por qué de esto sólo encontró una explicación cuando al físico teórico británico Paul Adrien Maurice Dirac se le ocurrió combinar la Mecánica Cuántica con la Teoría Especial de la Relatividad para poder obtener así una ecuación de onda relativista. Y al hacer tal cosa, de manera casi obligada desde el punto de vista matemático la función de onda Ψ perdió su status de indivisibilidad pasando a ser una función de onda que en el caso del momento angular intrínseco del electrón consta de dos componentes, la cual podemos representar simbólicamente como un vector columna:
Y de hecho, la ruptura de la función de onda en dos partes discretas resulta ser la gran puerta de entrada hacia la Teoría del Campo Cuántico, en donde la función de onda es cuantizada (a lo cual se le conoce como la segunda cuantización), pasando a ser considerada como un campo, un campo cuántico.
Lo anterior significa que, inevitablemente, vamos a terminar utilizando operadores matriciales en el estudio de la función de onda del momento angular del spin, ya que se requieren matrices para poder manipular matemáticamente un vector de forma tal que podamos obtener algún resultado útil en una eigenecuación de valores propios. De este modo, en caso de haber intentado postular inicialmente un operador de onda de spin S para una función de onda de spin ψs con el propósito de montar la siguiente eigenecuación con eigenvalores λ:
habríamos tenido que ampliar la definición considerando al operador de onda de spin como una matriz y a la función de onda de spin como un vector, algo que no habíamos hecho en el estudio del momento angular orbital en el átomo de hidrógeno:
Esto a primera vista parecería ser suficiente. Pero no es suficiente, al menos no en un espacio tridimensional en donde requerimos de tres operadores de spin, de forma tal que en un sistema de coordenadas rectangulares Cartesianas tendríamos el siguiente sistema de eigenecuaciones:
¿Y cuál vendría siendo la naturaleza de estos tres operadores de spin? No tenemos que esforzarnos mucho para encontrar la respuesta, si recurrimos a lo que ya vimos con anterioridad bajo el contexto de la Mecánica Matricial en la entrada “El spin del electrón”. El camino para el análisis desde la perspectiva de la Mecánica Ondulatoria del momento angular intrínseco del electrón son los mismos operadores matriciales del momento angular del spin expresados de la siguiente manera para los tres ejes coordenados rectangulares Cartesianos:
en función de las matrices σx, σy y σz, las matrices de Pauli.
PROBLEMA: Obténgase el resultado de la siguiente evaluación:
Sx · Sy - Sy · Sx
generalizando el resultado obtenido para los demás casos posibles.
La evaluación directa nos dá el resultado siguiente:
El lado izquierdo de la igualdad nos debe resultar familiar, ya que se puede simplificar simbólicamente si recurrimos al conmutador de Dirac:
En su forma explícita y removidos los embellecimientos tipográficos, esto es lo mismo que:
SxSy - SySx = iħSz
SySz - SzSy = iħSx
SzSx - SxSz = iħSy
Se recalca que estas relaciones no son las que corresponden al momento angular orbital; corresponden al momento angular del spin. Y sin embargo, ambas son idénticas en su estructura. Esto nos revela que en el mundo sub-microscópico, en su quintaesencia, está operando algo muy fundamental sobre todos los fenómenos cuánticos, y la relación de Born es la piedra angular sobre la cual descansa todo el edificio.
Al tratar el momento angular orbital desde el punto de vista de la Mecánica Ondulatoria, se había demostrado que no es posible conocer simultáneamente con precisión ilimitada las tres componentes del momento angular orbital, signo inequívoco de la acción omnipresente del principio de incertidumbre. Con los operadores del momento angular del spin en nuestras manos, podemos demostrar formalmente lo mismo sin dificultad alguna para el momento angular del spin.
PROBLEMA: Demostrar que no es posible conocer simultáneamente las tres componentes del momento angular del spin.
Por multiplicación matricial directa, podemos comprobar que:
Sx · Sy = - Sy · Sx
Sx · Sy + Sy · Sx = 0
Los operadores del momento angular del spin obviamente anticonmutan. Este es el rastro inequívoco de dos observables incompatibles. Si medimos la componente del momento angular del spin que corresponde a la coordenada-x, la medición con precisión ilimitada de la componente del momento angular del spin que corresponde a la coordenada-y queda fuera de nuestro alcance. Y puesto que:
Sx · Sz = - Sz · Sx
Sx · Sz + Sz · Sx = 0
tampoco podemos medir con precisión ilimitada ambas componentes del momento angular del spin para el eje-x y el eje-z. Se concluye entonces que no es posible medir con precisión ilimitada las tres componentes del momento angular del spin.
El resultado del problema anterior nos demuestra que podemos medir con precisión teóricamente ilimitada solo una de las tres componentes del momento angular de spin, generalmente aquella relacionada con el operador Sz, y una vez hecho esto no es posible medir con precisón ilimitada cualquiera de las otras dos componentes por el hecho de ser observables incompatibles. ¿Hay algo más que se pueda medir junto con la observable que corresponde al operador Sz? La respuesta es afirmativa, como lo demostrará el siguiente ejercicio.
PROBLEMA: (1) Evalúense los operadores cuadráticos Sx2, Sy2 y Sz2. (2) Evalúese la suma directa de estos tres operadores cuadráticos.
(1) Empezaremos con el operador Sx:
Tenemos entonces:
Llevando a cabo las mismas operaciones con los operadores Sy y Sz, obtenemos para Sy2 y Sz2 el mismo resultado que obtuvimos para Sx2 a partir de Sx.
(2) Designando como S2 a la suma de los tres operadores cuadráticos Sx2, Sy2 y Sz2, obtenemos lo siguiente:
Puesto que S2 es igual a una constante numérica que multiplica a la matriz identidad I la cual a su vez conmuta con cualquier matriz del mismo tamaño que le pongan enfrente, queda claro que el operador S2conmuta con cualquiera de los operadores Sx, Sy y Sz:
Esto significa que podemos medir simultáneamente con precisión teóricamente ilimitada una de las tres componentes del momento angular intrínseco (generalmente se escoge la componente-y) que será igual a ±ħ/2, y además podemos medir también al mismo tiempo con precisión ilimitada la magnitud total S2 del momento angular del spin que podemos ver arriba que será igual a √3ħ/2. ¿Y qué se puede decir acerca de lo que podamos saber entonces de las otras dos componentes? Que para ellas los operadores cuadráticos deberán estar combinados en todo momento de manera tal que se cumpla la relación a la cual le podemos dar una interpretación vectorial ya que se presta para ello:
Nótese algo importante: la relación que hay entre Sx2 y Sy2 se asemeja mucho a la de la ecuación del círculo que se estudia en Geometría Analítica:
Esto es lo que nos permite considerar a los operadores Sx2 y Sy2 combinados produciendo un vector radial de magnitud constante ħ/√2 perpendicular al eje-z y que puede encontrarse apuntando al azar en cualquier dirección del plano x-y en el que está ubicado, habiendo probabilidades iguales de encontrarlo apuntando en cualquier dirección de dicho plano.
El hecho de que, operacionalmente, podamos manejar a S2 como si fuese el cuadrado de la magnitud |S| de un vector, nos sugiere que podemos considerar a S en sí como un vector, específicamente como un vector de operadores matriciales (aunque se ha puesto una flecha encima de S para destacar su naturaleza vectorial, normalmente tal cosa no se suele hacer, sobreentendiéndose a S como un vector prescindiendo de la flecha):
Obsérvese que para partículas de spin semi-entero, específicamente, de spin 1/2, únicamente hay dos orientaciones posibles (eigenestados) del spin con respecto a una dirección fija en el espacio, usualmente tomada a lo largo del eje-z. Estas orientaciones comúnmente son referidas como las orientaciones en las cuales el spin es paralelo o antiparalelo al eje-z. Sin embargo, al hablar de estos dos valores, en realidad estamos hablando de la proyección del momento angular de spin sobre el eje-z. Considerado como un vector, el momento angular de spin (que nunca está alineado totalmente sobre eje alguno) es mucho mayor que su proyección sobre el eje-z. Esta situación puede ser visualizada con la ayuda de un modelo vectorial como el siguiente:
En la figura de arriba se muestra que, cuando la proyección del momento angular de spin (simbolizada como Sz) es positiva, el vector del momento angular de spin S yace en algún lugar sobre la superficie de un cono, aunque no sea posible especificar con exactitud la componente-x ni la componente-y. De hecho, los valores esperados (las esperanzas matemáticas) de Sx y Sy para el estado que está caracterizado por Sz.=.+ħ/2 son iguales a cero. Sin embargo, en este caso las esperanzas matemáticas tanto para la observable Sx2 como para la observable Sy2 relacionadas con los operadores Sx2 y Sy2 no son cero sino que son iguales a ħ2/4.
El hecho de que al electrón, una partícula de carga eléctrica negativa, se le considere como algo que tiene una rotación, implica necesariamente que se comportará como un pequeño electroimán:
o que exhibirá algún tipo de interacción con un campo magnético externo que le sea aplicado (como ocurre en el experimento Stern-Gerlach).
Antes de seguir tratando el caso mecánico-cuántico del spin del electrón, resulta conveniente repasar el tipo de comportamiento que podríamos esperar clásicamente de un electrón cuyo momento angular de spin es el resultado de la rotación de la masa cargada del electrón en torno a un eje que pasa por su centro, cuando le es aplicado un campo magnético externo uniforme. El efecto de la aplicación de un campo magnético externo a una carga eléctrica en rotación es el de producir un torque que tiene a alinear el eje del spin del electrón paralelamente al campo magnético externo que le está siendo aplicado. Este torque produce una precesión del eje del spin en torno de la dirección del campo magnético externo al igual que como ocurre con un trompo en giración que una vez sujeto a la acción de la gravedad de la Tierra en vez de caer empieza a dar vueltas en torno a la vertical. Puesto de otra manera, la partícula actúa como un giroscopio como consecuencia de su momento angular de spin. Cualquier torque que tienda a alinear el eje del spin y el campo magnético externo sólo puede resultar en una precesión del spin en torno al campo magnético. La situación clásica es la siguiente:
En este caso, el cono mostrado en esta figura que describe al vector momento angular de spin S cuando entra en precesión no debe ser confundido con el cono que tenemos en la figura anterior en ausencia total de un campo magnético externo, ya que mientras el cono de precesión es un cono dinámico sobre cuya superficie cónica el vector S está girando en cierto sentido (ya sea en el sentido de las manecillas del reloj o en sentido contrario cuando es visto desde arriba), el cono en ausencia de un campo magnético es un cono estático que simplemente nos dá una superficie probabilista sobre la cual podemos encontrar al vector S en cualquier posición al azar sobre el cono al llevar a cabo una medición, con probabilidades iguales de localización repartidas sobre toda la superficie. Obsérvese también en la figura que el vector momento magnético μ para el spin del electrón y el vector momento angular S apuntan en direcciones opuestas. Esto en virtud del signo negativo en la fórmula (en unidades MKS-SI) que relaciona ambas cantidades:
Viendo hacia atrás, esta fórmula es muy parecida a la fórmula que nos relaciona el momento magnético orbital del electrón producido por el movimiento del electrón girando en torno a un núcleo atómico (siendo L el momento angular orbital):
Sin embargo, ambas fórmulas son diferentes, porque en la fórmula para el momento magnético intrínseco del electrón aparece un factor g que se ha destacado de color magenta. Aunque en la Mecánica Cuántica Relativista se le asigna un valor un valor igual a 2, de hecho el factor-g está dado por la siguiente relación:
siendo:
Para obtener esta fórmula exacta para el factor-g (la cual de hecho es una serie infinita), la Mecánica Cuántica que hemos estado viendo no es suficiente, ni siquiera la Mecánica Cuántica Relativista nos permite obtener dicha fórmula. Para ello, es necesario recurrir a la Teoría del Campo Cuántico (específicamente, a la Electrodinámica Cuántica). La medición experimental del factor-g, uno de los más grandes triunfos de la ciencia moderna por ser uno de los valores más precisos que se conocen (con una exactitud igual o mayor a 12 cifras significativas) representa una de las confirmaciones más contundentes de la solidez de la teoría cuántica de la materia. La primera medición experimental de alta precisión del valor del factor-g fue llevada a cabo por H. Richard Crane y sus colaboradores. El valor experimental actual aceptado del factor-g para el electrón es:
2.0023193043622 ± 0.0000000000015
El valor del factor-g está tan cercano a 2 que usualmente se le toma como 2, lo cual permite simplificar un poco la fórmula para el momento magnético debido al spin del electrón:
La expresión anterior es válida en el sistema de unidades MKS-SI. Sin embargo, al trabajar en problemas relacionados con las cuestiones cuánticas del campo magnético, es frecuente trabajar en las unidades del sistema cgs-Gaussiano. En este sistema alternativo de unidades, la expresión para el momento magnético del spin del electrón se escribe de la siguiente manera:
Si tomamos la magnitud del vector S (prescindiendo de la notación vectorial, pero reteniendo el signo negativo como se acostumbra hacerlo) referenciándolo al eje-z, entonces siendo S.=.ħ/2 el momento magnético del spin del electrón en el sistema de unidades cgs-Gaussiano será simplemente:
A escalas atómicas, y en unidades del sistema MKS-SI, el momento magnético del electrón (tanto el orbital como el debido al spin del electrón) es expresado en múltiplos de la siguiente unidad:
conocida como el magnetón de Bohr. En unidades cgs-Gaussianas, la misma cantidad se define de la siguiente manera:
PROBLEMA: Calcúlese, en el sistema de unidades MKS-SI, el valor de un magnetón de Bohr.
Puesto que se trata del electrón aquello de lo cual estamos hablando, utilizaremos las siguiente constantes físicas:
e = 1.602.×.10-19 coulomb
ħ = h/2π = (6.626.×.10-34 joule·seg)/2π = 1.0546.×.10-34 joule·seg
me = 9.1095.×.10-31 Kg
Entonces, de acuerdo a la definición:
μ0 = (1.602.×.10-19)(1.0546.×.10-34)/2(9.1095.×.10-31)
μ0 = 1.602.×.10-19 joule/Tesla
PROBLEMA: Calcúlese, en el sistema de unidades cgs-Gaussianas, el valor de un magnetón de Bohr.
En este caso, tenemos que utilizar las siguiente constantes físicas para el electrón:
e = 4.8.×.10-10 esu
ħ = h/2π = (6.626.×.10-27 erg·seg)/2π = 1.0546.×.10-27 erg·seg
me = 9.1095.×.10-28 gramos
c = 3.×.1010 cm/seg
Entonces, de acuerdo a la definición:
μ0 = (4.8.×.10-10)(1.0546.×.10-27)/2(9.1095.×.10-28)(3.×.1010)
μ0 = 9.27.×.10-21 erg/Oersted
Consideraremos ahora el tratamiento mecánico-cuántico desde el aspecto ondulatorio de un electrón en presencia de un campo magnético B. Como se indicó arriba, un electrón tiene un momento magnético paralelo a su spin aunque apuntando en dirección contraria, expresado en el sistema cgs-Gaussiano como:
Si consideramos despreciables todas las demás contribuciones a la energía del electrón (tales como la energía cinética de su movimiento de traslación) y consideramos únicamente la interacción entre el momento magnético S del electrón y el campo magnético externo B que le está siendo aplicado, la expresión para la energía, que podemos tomar como el Hamiltoniano del sistema, está dada por:
En el caso particular de un campo magnético uniforme y estático B0 que apunte en la dirección del eje-z, esto se convierte en lo siguiente:
Por razones que pronto serán obvias, la cantidad
que tiene unidades de frecuencia angular será tomada realmente como una frecuencia angular ω0, (llamémosla la frecuencia natural del sistema) de forma tal que esto nos permita hablar de algo como:
Los valores para la energía del spin en este campo magnético están dados por la ecuación de Schrödinger independiente del tiempo:
Puesto que los valores de Sz son ±ħ/2, las dos energías posibles para el spin son como las que se indican en la siguiente figura:
Los estados correspondientes de energía en presencia de un campo magnético son aquellos para los cuales el spin del electrón es paralelo o antiparalelo al campo magnético.
Con la finalidad de investigar la analogía mecánico-cuántica del movimiento de precesión del spin del electrón en torno al eje-z cuando el spin no está alineado inicialmente en la dirección del eje-z, supóngase que en un tiempo inicial t.=.0 se mide la componente del momento angular de spin que sea paralela al eje-x, obteniéndose como resultado de la medición el valor ħ/2. Esto significa que que en este tiempo inicial la función de onda del spin debe ser una eigenfunción del operador Sx, con eigenvalor ħ/2:
Supóngase que las componentes del vector función de onda sean ψ = ψ(a,b). Entonces, utilizando el operador matricial Sx definido en función de la matriz de Pauli correspondiente, podemos establecer la ecuación matricial que nos lleve a la especificación de las componentes de la función de onda:
Esto es una igualdad entre dos vectores columna (habiéndose pasado el vector columna del lado derecho de la igualdad al lado izquierdo, en el lado izquierdo nos queda el vector columna cero). Siendo a.=.b la única condición a cumplir, podemos utilizar los valores que queramos siempre y cuando ambos sean iguales. Resulta conveniente escoger los valores a = b = 1/√2 de forma tal que:
La selección de valores que se acaba de hacer tiene la ventaja obvia de que si tomamos el producto vectorial punto de la función de onda de spin ψ por su conjugado complejo de spin ψ* (lo cual lo podemos hacer representando ambos vectores como matrices, en cuyo caso tenemos que tomar la transpuesta de uno de ellos además de tomar el conjugado complejo de sus componentes) obtendremos un resultado normalizado a la unidad:
Esta selección de valores no es accidental. Fue hecha teniendo en mente la interpretación probabilista de Born dada al cuadrado de una función de onda como |ψ|2 = ψ*ψ que permite darle un significado a la ubicación del electrón, con la novedad de que la función de onda es ahora un vector.
Lo que hemos obtenido es válido para un tiempo inicial t.=.0. Sin embargo, la función de onda tiene que ser algo cuyos dos componentes manifiesten algún tipo de dependencia con la variable del tiempo, de preferencia algo que se reduzca a lo que acabamos de obtener para t.=.0. Además (aquí es donde entra en el panorama la ecuación de Schrödinger), la ecuación de Schrödinger dependiente del tiempo:
debe ser satisfecha por cualquier solución que se proponga para la función de onda del electrón. Se propondrá la siguiente solución:
PROBLEMA: Demuéstrese que la función de onda propuesta arriba es una solución aceptable para la ecuación de Schrödinger dependiente del tiempo.
Por un lado tenemos que:
mientras que por el otro lado tenemos lo siguiente:
Comparando ambos resultados, vemos que son iguales. Entonces la función de onda propuesta arriba sí es una solución aceptable para la ecuación de Schrödinger dependiente del tiempo.
PROBLEMA: Evalúese la función de onda propuesta arriba como función de onda para el spin del electrón en los tiempos t.=.0, t.=.π/2ω, t.=.π y t.=.3π/2.
Para el tiempo t.=.0 la función de onda del spin viene siendo:
Este resultado concuerda con lo que se había estipulado anteriormente para un tiempo inicial t.=.0.
Para el tiempo t.=.π/2ω la función de onda del spin viene siendo:
Para un tiempo t.=.π/ω la función de onda del spin viene siendo:
Y finalmente, para un tiempo t.=.3π/2ω la función de onda del spin viene siendo:
Lo anterior significa que, en primer lugar, en un tiempo t.=.0 el spin estará alineado en la dirección positiva del eje-x bajo la función de onda propuesta. Aprovechando el resultado que obtuvimos para la función de onda del spin en el tiempo t.=.π/2ω, y usando la expresión matricial del operador Sy, vemos que:
lo cual se puede resumir como la siguiente eigenecuación:
Esta eigenecuación que se cumple para el operador Sy para un tiempo t.=.π/2ω nos dice que, un tiempo después, el momento angular intrínseco estará apuntando en la dirección positiva del eje-y (el eigenvalor es - +ħ/2) en dicho tiempo. Por otro lado, aprovechando el resultado que obtuvimos arriba para la función de onda del spin en el tiempo t.=.π/ω y usando la expresión matricial del operador Sx, obtendremos lo siguiente:
lo cual se puede resumir como la siguiente eigenecuación:
Esta eigenecuación que se cumple para el operador Sx para un tiempo t.=.π/ω nos dice que el momento angular intrínseco estará apuntando en la dirección negativa del eje-x (el eigenvalor es - ħ/2) en dicho tiempo. Por último, aprovechando el resultado que obtuvimos arriba para la función de onda del spin en el tiempo t.=.3π/2ω y usando la expresión matricial del operador Sy, obtendremos lo siguiente:
lo cual se puede resumir como la siguiente eigenecuación:
Esta eigenecuación que se cumple para el operador Sy para un tiempo t.=.3π/2ω nos dice que el momento angular intrínseco estará apuntando en la dirección negativa del eje-y (el eigenvalor es - ħ/2) en dicho tiempo.
En resumen, si al principio el spin está apuntando en la dirección positiva del eje-x, un tiempo después estará apuntando en la dirección positiva del eje-y, tras lo cual estará apuntando en la dirección negativa del eje-x, para posteriormente estar apuntando en la dirección negativa del eje-y. Esto es precisamente lo que nos describe un movimiento de precesión en torno al eje-z.
En analogía con lo que hemos visto con anterioridad, podemos definir el valor esperado (la observable susceptible de poder ser medida en el laboratorio) para el operador mecánico-cuántico de la componente del momento angular de spin sobre el eje-x de la siguiente manera (el numerador de la expresión es en sí la esperanza matemática, mientras que el denominador viene siendo la constante de normalización):
siendo ψ(t) la función de onda del momento angular del spin y siendo ψ*(t) el conjugado complejo de la misma. Es importante tener en cuenta de que, puesto que la función de onda es multicomponente, al manejarse como un arreglo vectorial es necesario tomar la transpuesta tras haberse tomado el conjugado complejo para poder llevar a cabo en forma correcta las operaciones. Usando la función de onda que se ha definido arriba, el numerador viene quedando evaluado como:
mientras que el numerador resulta ser:
Entonces el valor esperado de Sx (su esperanza matemática) es:
¿Y cuál vendría siendo el valor esperado de Sz? La respuesta es trivial:
por la sencilla razón de hay tantas probabilidades de encontrar al spin apuntando hacia arriba (+ħ/2) como de estar apuntando hacia abajo (-ħ/2).
Lo que hemos obtenido podemos verlo de otra manera definiendo un operador “combinado” como el siguiente (inspirado en lo que en Geometría Analítica y en el Análisis Vectorial se conoce como las ecuaciones paramétricas del círculo):
que representa la componente del momento angular intrínseco en el plano x-y a lo largo de una línea rotando con una frecuencia circular ω en torno al eje-z. Por substitución directa podemos comprobar que la función de onda de spin:
es una eigenfunción del operador combinado S0, esto es:
Esta eigenecuación nos dice que el spin tiene una componente constante de ħ/2 a lo largo de la línea de rotación.
PROBLEMA: Evalúese (S0)2 y dése una interpretación física al resultado.
Usando las expresiones matriciales para los operadores Sx y Sy, tenemos lo siguiente:
Entonces evaluando (S0)2 = S0·S0 y simplificando:
Considerando a la magnitud de S0 como (S0)2, confirmamos que el spin tiene una componente constante de magnitud ħ/2 en el plano x-y en el cual se lleva a cabo la rotación. Obsérvese que el eigenvalor de (S0)2 es igual tanto al eigenvalor de Sx2 como al eigenvalor de Sy2 (y como al eigenvalor de Sx2).
PROBLEMA: Demuéstrese que el operador S0, tal y como se ha definido arriba, actúa como el operador de la eigenecuación:
para la función de onda:
Tomaremos a S0 evaluado en el problema anterior:
y haremos una simplificación en sus dos elementos que no son cero recurriendo a la identidad eiθ = cos(θ)+isen(θ):
Con esto podemos aplicar directamente el operador S0 sobre el vector función de onda de spin:
Llevando a cabo la multiplicación matricial y simplificando, obtenemos entonces:
Se concluye que el operador S0 es operador de una eigenecuación, siendo ħ/2 el eigenvalor de la misma.
PROBLEMA: Obténgase por evaluación directa las expresiones equivalentes para los operadores escalera del momento angular del spin:
El primer operador escalera para el momento angular del spin será:
Y el segundo operador escalera vendrá siendo:
A continuación estudiaremos un problema un poco más elaborado pero más interesante, el caso de un sistema de spins de electrón inmersos en un campo magnético uniforme y estático B0 (que apunta en la dirección del eje-z) con un campo magnético oscilante B1 que es perpendicular al campo magnético estático. Investigaremos las transiciones entre los estados de energía ocasionados por el campo oscilante, o en otras palabras, la probabilidad de que emisiones y absorciones de fotones conduzcan a saltos en un nivel de energía a otro. Primero que nada, tenemos que considerar cómo un sistema de spins, en contraste con un spin individual, debe ser manejado. Para tal efecto, la magnetización estática de un sistema que contenga N electrones por unidad de volumen que estén libres para orientar sus spins con respecto al campo magnético debe ser calculada. Se hace hincapié aquí en que el magnetismo es un fenómeno inseparable de la Mecánica Cuántica, puesto que un sistema estrictamente clásico en equilibrio térmico es incapaz de exhibir momento magnético alguno, inclusive en la presencia de un campo magnético externo. El momento magnético de un átomo libre tiene tres orígenes: (1) el spin que corresponde al momento angular intrínseco de sus electrones, (2) el momento angular orbital de los electrones que giran en torno al núcleo atómico, y (3) el cambio en el momento angular orbital inducido por un campo magnético aplicado externamente. Los primeros dos efectos dán las contribuciones paramagnéticas a la magnetización, mientras que el tercero dá una contribución diamagnética. En el estado basal (1s) del átomo de hidrógeno el momento angular orbital es igual a cero, y el momento magnético observado es el que corresponde al momento angular intrínseco del electrón junto con un pequeño momento diamagnético inducido. Por su parte, en el estado 1s2 del helio tanto el momento angular orbital como el momento angular intrínseco son ambos ceros (los dos electrones con sus spins opuestos se cancelan mutuamente), y sólo hay un momento magnético inducido. Los átomos con capas exteriores completas (llenas) tienen cero momento magnético orbital y cero momento magnético de spin; estos momentos están asociados con elementos con capas exteriores incompletas.
Supondremos que en una muestra de material que pueda ser considerado como un sistema de spins la probabilidad de que un estado de energía se encuentre ocupado será proporcional al factor de Boltzmann, e-E/kT (esta suposición puede ser justificada utilizando para ello los argumentos de la Mecánica Cuántica Estadística). Ahora bien, de acuerdo a la distribución de Boltzmann, habrá más estados en un nivel bajo de energía (que para el caso del spin del electrón será -eħ/2mcB0 en presencia de un campo magnético) correspondiendo a los spins paralelos al eje-z que en un nivel más alto de energía (que para el caso del spin del electrón será +eħ/2mcB0 en presencia de un campo magnético) correspondiendo a los spins antiparalelos al eje-z.
PROBLEMA: Si se aplica un campo magnético a una muestra de material, determínese la fracción de partículas con momento angular intrínseco de 1/2 que de un total de partículas N serán paralelas al eje-z.
Designando como Na a las partículas que por su spin están situadas en el nivel más alto de energía, y como Nb a las partículas que por su spin están situadas en el nivel más bajo de energía, y designando como ΔE a la diferencia entre ambos niveles de energía, la relación de Boltzmann para el cociente entre ambas poblaciones de partículas será la siguiente (siendo k la constante de Boltzmann):
La diferencia entre los dos niveles de energía será:
Entonces tendremos la siguiente relación para la relación que hay entre ambas poblaciones de partículas:
o bien:
El número total N de partículas será entonces:
La diferencia ΔN que hay entre ambas poblaciones de partículas será:
Entonces la fracción ΔN/N de partículas que hay en el nivel superior de energía será:
Con esta fracción poblacional ΔN/N en nuestras manos, y considerando un total de N electrones con momento angular magnético μz para cada uno de ellos, podemos ver que la magnetización M del medio estará dada por la siguiente expresión:
Usando el resultado obtenido en el problema anterior se tiene entonces:
Supondremos que los electrones se encuentran en equilibrio térmico con su entorno a una temperatura absoluta (medida en grados Kelvin) T, y para mayor simplicidad supondremos que la energía térmica de cada spin, kT, es grande en comparación con la energía de interacción del spin con el campo magnético, o sea:
Esta suposición nos permite llevar a cabo una expansión en series de potencias de MacLaurin-Taylor tanto para el numerador como para el denominador de la expresión que tenemos para la magnetización del medio, lo cual nos resulta en:
Ahora bien, puesto que, en el sistema de unidades cgs-Gaussiano:
tenemos entonces para la magnetización del material la siguiente relación:
Experimentalmente, se encuentra que en muchos casos hay una relación lineal entre la magnetización M de una muestra de material y el campo magnético externo B0 que le es aplicado a la muestra, o sea que la variación en el campo magnético externo es proporcional a la magnetización inducida. Esto se formaliza con un cociente que se define como la susceptibilidad magnética de un medio por unidad de volumen:
En ambos sistemas de unidades la susceptibilidad magnética es adimensional. El tipo de comportamiento de la muestra de material puede ser definido por el valor de su susceptibilidad magnética. Cuando la susceptibilidad es pequeña y negativa, el material es un material diamagnético, cuando la susceptibilidad es pequeña y positiva, el material es un material paramagnético, cuando la susceptibilidad es grande y positiva el material es un material ferromagnético, y finalmente hay cierto tipo de material conocido como antiferromagnético para el cual la susceptibilidad es pequeña y positiva.
Haciendo uso de la conexión clásica que hay entre la susceptibilidad magnética y la permeabilidad magnética del medio (desafortunadamente esta última se suele representar con la letra griega μ, lo cual puede dar lugar a confusiones, confundiéndola fácilmente con el momento magnético), definiéndose la permeabilidad como una medida de la capacidad de un material para poder formar un campo magnético dentro de sí (o bien el grado de magnetización obtenida en respuesta a un campo magnético aplicado desde el exterior), tenemos entonces para la permeabilidad de nuestro material la siguiente fórmula:
Esta fórmula nos dá correctamente la permeabilidad magnética de materiales que exhiben un spin del tipo paramagnético, tales como soluciones en amonio de metales alcalinos y ciertos radicales orgánicos libres.
Volviendo al problema dinámico del spin del electrón inmerso dentro de un campo magnético estático uniforme externo B0 al cual se le aplica además un campo magnético oscilante B1 (suponiendo una oscilación de carácter sinusoidal) que sea perpendicular a B0, supóngase que el campo magnético B1 oscila con una frecuencia que es aproximadamente igual a la frecuencia de precesión del spin del electrón en el campo estático. Podemos, en principio, reemplazar al campo magnético oscilante por dos campos magnéticos en rotación, rotando en direcciones opuestas de tal manera que la suma vectorial de ambos campos será un vector que apunta en la dirección del campo oscilante. Se supone que los campos en rotación están ubicados en un plano que es perpendicular al campo estático B0:
Unicamente la componente del campo magnético que está rotando en la misma dirección que la dirección de rotación de la precesión del spin del electrón desempeñará un papel significativo en provocar transiciones de energía de un nivel a otro; la otra componente simplemente producirá una nutación pequeña y rápida del eje de spin de acuerdo a lo que nos dice la electrodinámica clásica. De este modo, el análisis que estamos llevando a cabo será simplificado suponiendo que la componente que sigue la misma dirección de rotación que la corresponde a la precesión es la única que existe; ignorándose la otra componente. Situando al campo magnético estático en la dirección positiva del eje-z y al campo oscilante rotando en el plano x-y, tendremos entonces la situación mostrada en la siguiente figura:
La interacción de los dos campos magnéticos, B0 y B1, con el spin del electrón, produce un operador Hamiltoniano de energía con la siguiente forma:
Obviamente, el hecho de simbolizar como B1 al campo rotatorio implica un campo de oscilación de amplitud 2B1. Introduciendo en la expresión para H los operadores matriciales del momento angular de spin tenemos entonces:
Este es un operador Hamiltoniano que depende de la variable tiempo, y por lo tanto la energía no se conserva. De cualquier manera, la ecuación de Schrödinger sigue reteniendo su forma original bajo estas circunstancias, de modo tal que la función de onda para este sistema debe seguir satisfaciendo la ecuación diferencial:
Resulta conveniente buscar las llamadas soluciones normales o estacionarias para esta ecuación, o sea soluciones para las cuales la probabilidad de encontrar al electrón en cualquiera de sus dos estados de energía se mantenga constante en el tiempo. Una solución normal de este tipo tendrá la forma:
Esta es una solución estacionaria en el sentido de que el tiempo aparece únicamente en factores de fase de módulo unidad (1). Si suponemos una solución de esta naturaleza, entonces al subsituír esta función de onda en la ecuación de onda de Schrödinger dependiente del tiempo se obtendrá la siguiente igualdad:
Esto representa una igualdad entre dos vectores columna; cada elemento de un vector columna debe ser igualado con el elemento que le corresponde del otro lado de la igualdad, resultando en el siguiente par de ecuaciones:
en donde las frecuencias angulares ω0 y ω1 están definidas de la siguiente manera:
El par de ecuaciones es un conjunto de ecuaciones homogéneas en dos incógnitas que tienen una solución no-trivial únicamente si se desvanece el determinante de los coeficientes:
Llevando a cabo las multiplicaciones indicada por el determinante se produce el siguiente polinomio característico:
Esto nos produce dos raíces para λ:
Con esto, cualquiera de las dos ecuaciones que forman parte del par de ecuaciones simultáneas de donde provino λ se pueden resolver para darnos:
Estos valores representan las funciones de onda para los estados estacionarios (steady-state) que están asociados con las dos raíces de λ.
El caso que nos interesa es aquél en el cual el campo magnético oscilante B1 aplicado externamente es de la misma frecuencia que la frecuencia normal de precesión del spin del electrón que le resulta al serle aplicado un campo magnético uniforme constante B0, algo semejante a la “sintonización” de un canal de radio AM/FM haciendo entrar a la frecuencia del receptor en resonancia con la frecuencia de la señal recibida (excepto que aquí lo que se varía es la frecuencia del transmisor manteniéndose fija la frecuencia del receptor). Entonces se tendrá:
y entonces de la ecuación que hemos obtenido arriba para λ se obtiene lo siguiente:
Entonces del resultado obtenido arriba para a2 se tiene:
De estos resultados, las dos soluciones posibles (normalizadas) para el problema de eigenvalores que se había postulado arriba resultan ser:
en donde el valor de a1 se ha seleccionado precisamente para que las dos funciones de onda estén normalizadas.
Usando lo anterior, investigaremos ahora lo que ocurre al llevarse a cabo la transición de un estado energético a otro (del estado con spin paralelo al estado con spin antiparalelo, o viceversa). Esto ya lo hemos visto con anterioridad al llevar a cabo el estudio del spin del electrón bajo el contexto de la Mecánica Matricial, en donde se le identificó como un vuelco del spin del electrón. Supóngase que en un tiempo inicial se ha medido el spin de un electrón, y que se ha determinado que está apuntando exactamente en la dirección positiva del eje-z. En este caso, la función de onda tiene la forma:
Escógase una combinación lineal de los dos estados estacionarios dados por la función de onda que estamos utilizando, de modo tal que la función resultante tenga esta forma justo cuando t.=.0. La combinación lineal que se necesita para tal cosa debe ser:
Expresada en forma explícita usando las dos soluciones determinadas por la función de onda de arriba, esto es igual a:
Llevando a cabo una inspección de esta función de onda, resulta obvio que para un tiempo t.=.0 la función de onda será tal que el spin estará apuntando en la dirección positiva del eje-z. Por otro lado, en un tiempo posterior, específicamente t.=.π/ω1, la función de onda será tal que la componente-z del momento angular intrínseco será -ħ/2. Esto significa que el spin del electrón se ha “volteado”, es decir, de estar apuntando en la dirección positiva del eje-z a pasado a estar apuntando en la dirección negativa del eje-z. Y un tiempo después, para t.=.2π/ω1, el momento angular del spin estará apuntando nuevamente en la dirección positiva del eje-z. Esto significa que el spin del electrón estará apuntando alternadamente en direcciones opuestas. Naturalmente, habrá tiempos en los cuales no se podrá afirmar con certeza si el spin está apuntando “hacia arriba” o si está apuntando “hacia abajo”, ya que habrá una probabilidad diferente de cero de que el spin esté apuntando en cualquiera de las dos direcciones.
El tratamiento que se ha dado arriba desde la perspectiva mecánico-cuántica ha sido considerando un campo de radiación electromagnética tratándolo no como un sistema dinámico sino como un campo de fuerza externa actuando sobre la partícula, sin considerar en lo absoluto los efectos mecánico-cuánticos asociados con el campo electromagnético en sí. Resulta evidente que este manejo no puede llevarnos hacia el concepto de los fotones. Este tipo de tratamiento clásico del campo electromagnético de radiación es válido si hay tantos fotones presentes en el campo que podemos considerar que estamos ante la presencia de los grandes números con los cuales se suele hacer la transición de la Mecánica Cuántica sub-microscópica a la mecánica clásica macroscópica. Un tratamiento así puede describir correctamente la emisión estimulada de radiación por un sistema atómico o la razón de absorción de energía por un sistema atómico, pero no nos puede dar la razón de radiación espontánea de un sistema atómico puesto que esto está estrechamente asociado con los efectos cuánticos del campo de radiación. Un tratamiento correcto en el cual el campo oscilante esté debidamente cuantizado (esto es lo que se ve en la Electrodinámica Cuántica) demuestra que durante un vuelco del spin se absorberá un fotón del campo aplicado o se radiará hacia el campo.
Los resultados obtenidos, válidos para un spin aislado, deben ser relacionados con el caso en el cual tenemos un sistema que consta de muchos electrones. Como vimos arriba, un sistema de electrones que entre en equilibrio térmico con su entorno al mismo tiempo que le está siendo aplicado un campo magnético uniforme de magnitud constante B0 tendrá una magnetización macroscópica M dada por la fórmula mostrada arriba. Podemos considerar que esto surge de un ensamble de N electrones con una cantidad de electrones:
que están inicialmente en la orientación que corresponde al nivel superior de energía, con sus spins antiparalelos al campo magnético B0, y con una cantidad de electrones:
inicialmente en la orientación que corresponde al nivel inferior de energía, con sus spins paralelos al campo magnético B0.
Un análisis similar al que hemos llevado a cabo arriba aplicado a un spin que está apuntando inicialmente en la dirección negativa del eje-z demuestra que dicho spin, originalmente apuntando en una dirección opuesta al spin que está orientado en la dirección positiva, permanecerá en tal situación cuando se lleva a cabo un “vuelco” de spin. La cancelación original de los momentos magnéticos de los spins que estén apuntando en direcciones contrarias será retenida bajo la acción del campo oscilante, y se dice que dos spins tales están apareados. Unicamente los spins excedentes en el estado energético más poblado (el estado inferior) darán una contribución al magnetismo neto del material. Este momento magnético neto que resulta de los spins “excedentes” apuntando en la dirección positiva del eje-z tiene el comportamiento dinámico del spin aislado que ha sido considerado arriba, y la magnetización macroscópica del material experimenta la cadencia arriba indicada de vuelcos.
Para concluír, vale la pena mencionar aquí que la idea del spin del electrón fue introducida por vez primera por George Uhlenbeck y Samuel Goudsmit en 1925 para explicar la doble estructura de las líneas espectrales y el efecto sobre las líneas que resulta de colocar la muestra emisora en un campo magnético fuerte (efecto Zeeman).