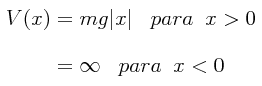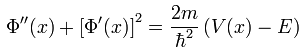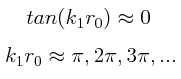¿Es aconsejable utilizar el procedimiento de aproximación WKB para la obtención de soluciones en el caso de problemas tales como el problema del oscilador armónico simple?
Ya se vió con anterioridad en otras entradas previas que el oscilador armónico simple, caracterizado por un potencial parabólico, tiene soluciones analíticas exactas cuando se recurre para ello a los polinomios de Hermite. La ventaja de dicho procedimiento es que es posible “pegar” las soluciones para la función de onda (dentro y fuera del pozo de potencial parabólico) de manera directa. En contraste, el procedimiento WKB presenta el problema de la indeterminación que ocurre cuando V.=.E a causa de la división por cero, problema que viene a complicar las cosas requiriendo como lo vimos en la entrada previa de una aproximación lineal cerca de cada punto de volteo x0 tras lo cual se tiene que resolver la ecuación diferencial:
en forma exacta para obtener una solución adicional (que viene siendo una tercera solución accesoria a las dos soluciones dadas por el método WKB para cada una de las dos regiones a ser conectadas) en forma exacta involucrando funciones de Bessel de orden ±1/3 cerca del punto de volteo, apareándose esta solución con las dos soluciones WKB seleccionando apropiadamente las constantes de integración. Claramente esto involucra un esfuerzo más laborioso y menos elegante que el que ya se vió para la resolución del problema del oscilador armónico simple mediante el uso de polinomios de Hermite. Esto sirve como recordatorio de que no porque se tenga cierto procedimiento de solución a la mano dicho procedimiento será necesariamente el mejor o el más conveniente, y a veces cuando se tiene una opción entre varios procedimientos de solución vale la pena sopesar los pros y los contras de cada uno de dichos procedimientos para cierto problema antes de embarcarse en una tarea que puede resultar más pesada de lo que debería ser.
Lo anterior no debe descorazonarnos sobre la utilidad que pueden tener algunas de las conclusiones que podemos obtener con la ayuda de la aproximación WKB. Considérese un pozo de potencial generalizado que unidimensionalmente divide al espacio en tres regiones, el cual está separado por dos puntos de volteo x1 y x2, siendo la región intermedia (la que está situada entre las regiones 1 y 3) una región equivalente a un pozo de potencial que admite soluciones oscilatorias. Supondremos que la función de onda se debe comporta en la región 2 como:
y se comporta en las regiones 1 y 3 como:
Aparentemente, el apareamiento de la función de onda ψ(x) entre dos regiones diferentes (una exponencial y la otra oscilatoria) es un asunto algo arbitrario que se puede llevar a cabo de distintas maneras seleccionando arbitrariamente las constantes de integración. Sin embargo, no es necesario que haya tanta arbitrariedad en el apareamiento. Se puede demostrar (mediante una técnica matemática propia de la Teoría de las Variables Complejas conocida como continuación analítica en un plano complejo z) que el apareamiento correcto yendo de la región 1 a la región 2:
Región 1 → Región 2
se puede lograr escogiendo las constantes de integración de modo tal que:
Del mismo modo, también se puede demostrar que el apareamiento correcto yendo de la región 3 a la región 2:
Región 1 → Región 2
se puede lograr escogiendo las constantes de integración de modo tal que:
La aparición de un ángulo de π/4 en las relaciones de conexión inter-regiones puede ser un poco desconcertante al principio. Desde el punto de vista estrictamente matemático, el par de soluciones en las dos regiones próximas cuando han sido apareadas correctamente debe relacionar ambas soluciones mediante un procedimiento propio de la Teoría de las Variables Complejas conocido como la continuación analítica, procedimiento que se lleva a cabo en un plano complejo. Esto nos permite cambiar el signo de:
sin tener que atravesar directamente el punto en el cual x.=.x0. Cuando se lleva a cabo la continuación analítica, el factor:
en la relación:
adquiere un ángulo de fase eiπ/4 del modo siguiente:
La comprensión plena de este procedimiento de continuación analítica tiene el inconveniente de que requiere de una familiarización con la Teoría de las Variables Complejas. Hablando no con rigorismo pleno sino heurísticamente, podemos visualizar una justificación al ángulo de π/4 de la manera siguiente: puesto que todo se reduce a “pegar” el extremo de una onda senoidal (o cosenoidal) que corresponde a la región oscilatoria con la punta recortada de una curva exponencial, suponiendo que en la región oscilatoria tenemos atrapada una media longitud de onda entonces lo que se está tratando de hacer es esencialmente lo siguiente:
Sin embargo, este intento está destinado al fracaso, puesto que al “alinear” los ejes horizontales para los cuales ambas funciones de onda tienen un valor igual a cero (haciénndolo en una forma parecida a como lo haría un niño de la escuela primaria con papel y tijeras recortando y alineando), eventualmente nos damos cuenta de que mientras que la función senoidal (o la función cosenoidal) puede tomar un valor igual a cero yéndose hacia valores negativos, la función exponencial ex no puede tomar valores negativos, sólo puede tomar valores positivos, de modo tal que al alinear ambas funciones verticalmente en forma tal que los ejes verticales coincidan para los valores en los que ambas funciones de onda ψ(x) tienen un valor igual a cero, se descubre algo como lo siguiente:
La única manera en la cual se puede “pegar” ambas funciones requiere sacar las tijeras y hacer un “recorte” de la función senoidal en el lindero en el cual será conectada con la función exponencial, y en el caso de una media longitud de onda un punto apropiado para ello es en el punto en el cual la onda senoidal ha excursionado una distancia π/4 más allá de su cresta (la curva exponencial también tendrá que tener algún recorte). De este modo, podemos ver que se vuelve posible juntar y aparear ambas regiones respetando, desde luego, el punto x.=.x0 en donde se hará la linearización:
El margen de maniobra que se tiene para poder “pegar” dos funciones de onda que corresponden a dos regiones distintas proviene del hecho de que el efecto de sumar (o restar) un potencial constante V0 a una función de onda en la ecuación de Schrödinger consiste simplemente en aumentar (o disminuír) la energía E en una cantidad semejante, desplazando la función de onda en un ángulo de fase φ con un factor e-iφ siendo φ.=.Vt/ħ. Sin embargo, no hay significado físico alguno relacionado con la fase de una función de onda, porque el valor calculado para una observable física no puede depender de una convención de fase.
Para cierta eigen-energía válida y fija, la unicidad de la función de onda en la región intermedia que puede sostener oscilaciones estacionarias implica que los argumentos coseno en las condiciones anteriores deben diferir a lo más en un múltiplo entero de π, o sea nπ. Tomando la diferencia en los argumentos cosenoidales, esto se traduce en lo siguiente:
Simplificando:
Observando que en las dos integrales los integrandos son iguales, e inspeccionando los límites de ambas integrales, se puede ver que ambas integrales se pueden agrupar dentro de una sola integral. Haciendo tal cosa y simplificando un poco más, esto nos lleva a la siguiente condición de consistencia:
Tomando en cuenta de que lo que está bajo el radical es en realidad el momentum p de la partícula, si hacemos un simple cambio de notación de la variable posición para simbolizarla como la coordenada generalizada de posición q, se vuelve aparente entonces que la condición de consistencia que hemos obtenido con la ayuda de la aproximación WKB es en realidad la vieja regla de cuantización Wilson-Sommerfeld.
Es importante enfatizar que no hay una sola condición de consistencia para todos los casos posibles e imaginables, hay varias clases de problemas para las cuales podemos obtener distintas condiciones de consistencia con la ayuda del método de aproximación WKB de modo tal que podamos aplicar la misma condición de consistencia a cierta clase de problemas. La condición de consistencia que acabamos de obtener aquí puede ser utilizada para obtener expresiones aproximadas para los niveles de energía de una partícula que está confinada dentro de un pozo de potencial, como podemos verlo en el siguiente ejercicio.
PROBLEMA: Obténgase el espectro de energía de una pelota perfectamente elástica que está rebotando verticalmente sobre una superficie dura en presencia de un campo gravitacional.
Este problema tiene una solución analítica exacta recurriendo a algo que se conoce como la función de Airy. Sin embargo, el problema se presta por su relativa sencillez a la aplicación de la condición de consistencia que acabamos de obtener mediante el uso del método de aproximación WKB, dándonos una oportunidad para poder comparar los resultados obtenidos mediante la aproximación WKB con los resultados exactos.
Clásicamente, si la pelota rebota elásticamente contra el suelo y no hay disipación de energía, regresando a la altura desde donde se le dejó caer, para nuevamente repetir indefinidamente un ciclo eterno de caídas y rebotes, la altura de la pelota en función del tiempo es simplemente una secuencia de parábolas:
La densidad de probabilidad (clásica) de encontrar a la pelota a cierta altura del suelo es máxima en el punto de volteo superior en donde la pelota al perder casi toda su velocidad invierte el sentido de su movimiento, y es mínima en el punto de volteo inferior en donde la pelota impacta elásticamente al suelo a toda velocidad invirtiendo nuevamente el sentido de su movimiento:
El potencial V(x), o mejor dicho la energía potencial de la partícula en presencia del campo gravitacional, como está estipulado el problema, se puede escribir de la siguiente manera (aunque resulta tentador utilizar a y para simbolizar a la coordenada vertical sobre la cual la pelota lleva a cabo su movimiento, por simplicidad retendremos el problema sobre el eje-x aprovechando el hecho de que el problema sigue siendo un problema unidimensional):
Designando como E a la energía de la pelota, podríamos ceder a la tentación de tratar de utilizar la condición de consistencia especificando como puntos de volteo de la pelota el punto en el cual la pelota está en contacto con la superficie dura invirtiendo en dicho punto (que llamaremos x1) la dirección de su movimiento y el punto en el cual la pelota alcanza su máxima altura invirtiendo también en dicho punto (que llamaremos x2) la dirección de su movimiento, lo cual se logra haciendo:
Sin embargo, la condición de consistencia fue obtenida bajo la suposición de que la función de onda bajo la aproximación WKB se “filtra” hacia la región x<x1, siendo que en el problema que estamos considerando aquí la función de onda se debe desvanecer por completo en los puntos de volteo x1 y x2 y debe ser igual a cero fuera de la región en la cual la pelota está rebotando. Una alternativa para salir de este dilema consiste en recurrir a una modificación del problema especificando una función potencial alterna V(x) como:
ignorando las soluciones pares de función de onda y considerando únicamente las soluciones impares (antisimétricas), lo cual garantiza que la función de onda se desvanecerá en x.=.0, y utilizando como puntos de volteo:
El tipo de potencial que se está utilizando aquí ya lo vimos en la resolución de un problema WKB previo, especificado en dicho problema como:
V(x) = α |x|
con la única diferencia de que aquí la constante α es igual al producto de la masa por la gravedad. La gráfica del pozo de potencial triangular que tenemos aquí, resaltándose la región en la cual se lleva a cabo el movimiento de la pelota entre los dos puntos de volteo, es la siguiente:
Para los estados de paridad impar, el espectro energético para el problema modificado debe ser igual que el espectro energético que corresponde al problema original. De este modo, la condición de consistencia aplicada al problema presente viene resultando en lo siguiente:
en donde el número cuántico n es impar por ser el que corresponde a las soluciones impares. La integral anterior es obviamente igual a:
o bien:
Sobre el lado derecho de la igualdad podemos hacer un poco de prestidigitación algebraica de la siguiente manera:
Entonces nos queda lo siguiente:
Podemos simplificar un poco la integración haciendo el siguiente despeje:
La integración es elemental y se puede llevar a cabo fácilmente con un cambio de variables:
De este modo, se tiene:
Entonces como resultado de la integración se tiene lo siguiente a ser evaluado entre límites:
Tomando los límites:
Despejando, obtenemos para las eigenenergías:
Por razones que pronto serán obvias, podemos reescribir esto último como:
siendo Fn una constante numérica que depende directamente del valor que tome el número cuántico n.
Como ya se había mencionado al principio de este problema, se sabe por otros recursos matemáticos que este problema de una pelota elástica rebotando sobre una superficie sólida tiene una solución analítica exacta sin necesidad de tener que recurrir a una aproximación como la aproximación WKB. La solución matemática se la debemos astrónomo británico George Biddell Airy, el cual obtuvo una solución para la ecuación de Airy:
que dicho sea de paso es la ecuación diferencial de segundo orden más sencilla con un punto de volteo (el punto en el cual el carácter de las soluciones cambia de oscilatorio a exponencial y viceversa). Las soluciones resultan ser los ceros de una función Ai(ξ) conocida como la función de Airy, o sea:
Ai(-ξn) = 0
con lo cual la solución analítica especificada con los ceros de la función de Airy viene quedando de la siguiente manera:
La función de Airy está definida de la siguiente manera:
Los ceros de la función Airy Ai(ξ) se pueden calcular con varias cifras significativas de precisión recurriendo a una de varias calculadoras disponibles en Internet para tal propósito. La siguiente gráfica nos dá una idea de la forma que toma la función de Airy así como una idea aproximada de la localización de los ceros de la función de Airy:
Resulta instructivo tabular los resultados obtenidos mediante la aproximación WKB y mediante el uso de los ceros de la función Airy en múltiplos de a (mg2ħ2/2)1/3:
La tabla comparativa nos muestra que la concordancia entre ambos métodos es excelente para valores pequeños del número cuántico n, siendo casi exacta para n.=.10. Este problema nos demuestra que aunque el método WKB sea tan sólo una aproximación, los resultados obtenidos con dicho método pueden superar incluso nuestras expectativas.
Al principio de la discusión de este problema, se mostró el comportamiento clásico de la pelota rebotando contra el suelo. El comportamiento cuántico se puede apreciar mejor trazando la función de onda (en color magenta) para el segundo estado excitado así como la densidad de probabilidad (el cuadrado de dicha función de onda, en color verde) sobreponiendo en la segunda gráfica la densidad de probabilidad predicha por el comportamiento clásico (en color rojo):
Resalta el hecho de que hay cierta probabilidad de encontrar a la partícula encima del punto de volteo, en una región clásicamente prohibida. De acuerdo al principio de correspondencia de Bohr, para estados energéticos muy excitados (para números cuánticos grandes), el comportamiento cuántico debe aproximarse al comportamiento clásico, y podemos ver a continuación cómo la semejanza entre el comportamiento cuántico (la línea de color verde en el segundo diagrama) y el comportamiento clásico (la línea de color rojo en el segundo diagrama) se vuelve más notoria para el 60avo estado excitado:
Resulta instructivo comparar el segundo diagrama con los diagramas en la entrada titulada “Oscilador armónico simple: solución ondulatoria” que muestran también cómo para números cuánticos grandes el comportamiento del oscilador armónico simple cuántico se aproxima al comportamiento del oscilador armónico simple clásico. Por otro lado, obsérvese cómo en la línea naranja horizontal en el primer diagrama (que marca el punto de volteo clásico) el comportamiento de la función de onda cambia de una naturaleza oscilatoria a una naturaleza que manifiesta una caída exponencial en la amplitud de la función de onda.
Hemos visto lo suficiente como para poder darle un segundo vistazo a la mecánica matemática que le permite a la aproximación WKB funcionar tan bien como lo hace (excepto en los puntos de volteo). Partiendo de la ecuación de Schrödinger independiente del tiempo para una función de onda Ψ(x):
que puede ser reescrita como:
postularemos que la función de onda Ψ(x) puede ser expresada como el exponencial de otra función Φ(x):
Esta es una conjetura utilizada ampliamente en los primeros intentos de resolución de muchos problemas físico-matemáticos, la cual tiene innegables ventajas. La primera ventaja es que la derivada de la función exponencial nos resulta en la misma función multiplicada por la derivada del argumento; no cualquier función matemática es capaz de hacer esto. Y la segunda ventaja es que un exponencial siempre puede ser expandido en series de Maclaurin-Taylor, lo cual permite simplificaciones posteriores o aproximaciones dentro de cierto rango de valores de la variable independiente. Al proponer una solución de este tipo, casi hemos logrado la obtención de las soluciones proporcionadas por el método WKB, en virtud de que ambas soluciones tienen en común el hecho de que ambas son soluciones que vienen de un exponencial. Cuando el argumento Φ(x) es real, entonces la solución es un exponencial creciente o decreciente dependiendo del signo. Y cuando el argumento Φ(x) es imaginario (o complejo) entonces la solución es senoidal o cosenoidal (o una mezcla de ambos). Pero las dos respuestas posibles, la exponencial pura y la senoidal-cosenoidal, vienen del hecho de haberse postulado una solución del tipo exponencial como lo hemos hecho arriba. Reemplazando Ψ(x) por eΦ(x) en la ecuación de Schrödinger, se tiene entonces:
en donde Φ'(x) = dΦ/dx y Φ''(x) = d2Φ/dx2. Supondremos ahora que la derivada Φ'(x) puede ser separada en dos partes, una parte real y una parte imaginaria, de la siguiente manera:
Al hacer esto, la amplitud de la función de onda es:
mientras que la fase de la función de onda viene siendo:
De este modo, la parte real para la ecuación de Schrödinger nos produce la siguiente ecuación:
mientras que la parte imaginaria para la ecuación de Schrödinger nos produce la siguiente ecuación:
Aquí es donde invocamos la aproximación semi-clásica expandiendo cada una de las funciones A(x) y B(x) como series de potencias en ħ. De las ecuaciones que tenemos arriba, se puede ver que las series de potencias deben empezar por lo menos con un orden de ħ-1 para que la parte real de la ecuación pueda ser satisfecha, lo cual especificaremos metiendo un factor 1/ħ en la expansión de las series de potencias de A(x) y B(x). Y para lograr un buen límite clásico, es necesario empezar las series de potencia con una potencia de ħ tan alta como sea posible, lo cual se logra con:
A un orden cero, las condiciones sobre A y B se pueden escribir de la manera siguiente:
Para la región en la cual la energía total E es mayor que la energía potencial (como ocurre en el movimiento clásico), o lo que es lo mismo, si la amplitud varía con lentitud suficiente en comparación con la fase, lo cual se cumple con A0(x) = 0), de lo anterior se deduce entonces que:
Repitiendo el mismo procedimiento sobre el siguiente orden de la expansión, se obtiene entonces como solución para la función de onda Ψ(x):
Por otro lado, para la región en la cual la energía total E es menor que la energía potencial (lo cual sólo puede ocurrir en el caso mecánico-cuántico), o lo que es lo mismo, si la fase varía con lentitud suficiente en comparación con la amplitud, lo cual se cumple con B0(x) = 0), se deduce entonces que:
Repitiendo el mismo procedimiento sobre el siguiente orden de la expansión, se obtiene entonces como solución para la función de onda Ψ(x):
Ambas soluciones para la función de onda son indeterminadas (o usando un término matemático un poco más elegante, se vuelven singulares) cerca de los puntos de volteo en donde la energía potencial es igual a la energía E, esto es V(x).=.E.
Para completar el procedimiento, las soluciones aproximadas deben ser encontradas en todas partes y sus coeficientes apareados para así especificar una buena solución global, dejando pendiente la solución cerca del punto de volteo que sabemos de antemano que no puede ser infinita.
Para un punto de volteo x1 y en la cercanía de la región E.=.V(x1), el término:
puede ser expandido en una serie de potencias Maclaurin-Taylor de la siguiente manera:
A un primer orden, se debe tener entonces:
Esta es precisamente el tipo de ecuación diferencial que es conocida como ecuación Airy, cuya solución puede ser expresada en términos de las funciones Airy Ai(p) y Bi(q):
Esta solución es utilizada para poder “conectar” las dos regiones bajo consideración (la región en la cual la energía E es mayor que el potencial V, y la región en la cual la energía E es menor que el potencial V). Cuando se tienen los dos coeficientes de un lado del punto de volteo, los otros dos coeficientes del otro lado del punto de volteo (correspondiendo a la otra región) pueden ser determinados recurriendo a la solución local que acabamos de obtener. Afortunadamente, las funciones Airy en los límites apropiados se volverán asintóticamente funciones senoidal, cosenoidal y exponencial. Un examen más detallado nos revela que los coeficientes C+ y C- que corresponden a las “fórmulas de conexión” están dados por:
Habiéndose señalado en la entrada previa que para la juntura de dos regiones distintas recurriendo al método de aproximación WKB se puede llevar a cabo una linearización en el punto de volteo en el cual las soluciones WKB se derrumban (al tenerse un denominador que produce una división entre cero), una linearización que eventualmente requiere echar mano de funciones de Bessel de orden fraccionario ±1/3, parecería que esa no es la única alternativa de solución, parecería que tenemos una segunda alternativa de solución que no requiere del uso de funciones de Bessel sino de las funciones Airy. Sin embargo, las soluciones dadas por las funciones de Airy realmente no serán diferentes a las soluciones dadas por las funciones de Bessel de orden fraccionario ±1/3, habido el hecho de que hay una relación directa entre ambas funciones de acuerdo con lo que se muestra a continuación:
En la entrada anterior vimos ya que las soluciones ofrecidas por el método de aproximación WKB nos ofrecen una alternativa para intentar darle una solución cuantitativa a un problema extremadamente importante en el campo de la física nuclear: el problema de la desintegración radioactiva, en el cual un elemento se descompone espontáneamente al fisionarse su núcleo, lo cual cambia el número atómico del elemento liberándose además partículas sub-atómicas y una energía de fisión que puede ser lo suficientemente grande como para que en cantidades apreciables del elemento en descomposición se pueda dar origen a una explosión atómica. La desintegración más importante, históricamente hablando, es aquella en la cual un núcleo inestable emite una partícula alfa, conocida como la desintegración alfa o como el decaimiento α:
Clásicamente, una partícula sólida (o un colectivo de partículas como la partícula α que pueda ser considerada como una unidad) atrapada dentro de una barrera de potencial cuya altura sea infinita (así tenga una anchura pequeña) no puede escapar hacia afuera de la barrera del mismo modo que una partícula sólida tampoco puede entrar desde fuera hacia adentro del núcleo atómico al ser rechazada por la barrera de potencial. Esto es ilustrado por el siguiente diagrama:
Sin embargo, desde la perspectiva de la Mecánica Ondulatoria, una partícula que deja de ser una partícula sólida para ser considerada como una onda de materia descrita por una función de onda Ψ(x) tendrá una probabilidad de escapar fuera de la barrera de pontencial en la manera que es ilustrada por el siguiente diagrama:
Para el análisis del problema del decaimiento radioactivo que ahora se dará con mayor detalle y sofisticación que en la entrada anterior, se se supondrá que la partícula α es una partícula con carga eléctrica Z.=.2e y con una masa M, encerrada dentro de un potencial nuclear rodeada por una barrera coulómbica, esto es, una barrera de potencial eléctrico que varía en razón inversa al cuadrado de la distancia como lo estipula la ley de Coulomb. La partícula α que se escapa hacia el exterior lleva a cabo un tunelaje (o tunelado) a través de la barrera. Una suposición adicional que será tomada para llevar a cabo el análisis es que la partícula α emerge en un estado-S, el equivalente de un estado basal, y por lo tanto sin contribución alguna a la barrera efectiva de potencial debida a efectos centrífugos (momento angular orbital). El aspecto de la función de energía potencial V(r) como una función de la distancia al centro del núcleo será como el que se ha mostrado en las figuras de arriba, en donde se puede apreciar que al potencial en el interior del núcleo atómico (el potencial nuclear) se le supone constante (V.=.-V0). Designaremos al radio del núcleo atómico como r0, y designaremos como rc al radio en el cual la energía cinética de la partícula será igual a cero fuera del núcleo. De este modo, tendremos tres regiones bajo consideración, cada una de las cuales tendrá su propia solución para la función de onda respectiva que tenga que ser apareada en el extremo (o los extremos) en donde se deben conectar las soluciones:
Para que pueda ocurrir el decaimiento a través de un tunelado de la partícula, resulta obvio que la partícula tiene que tener una energía positiva E. Postulado de esta manera, el problema se reduce a un problema radial unidimensional (un problema de simetría esférica), con la ecuación de eigenvalores de energía tomando la siguiente forma:
en donde por razones de simplicidad en el desarrollo posterior la función de onda ψ(r) ha sido reemplazada por la función alterna u(r).=.rψ(r), lo cual a su vez implica que en el centro del núclo u(0).=.0.
La solución en el interior del núcleo atómico que corresponde a la primera región es una solución exacta, la cual puede ser expresada de la siguiente manera:
en donde la constante k1 debe ser:
Para la segunda región, en la cual como podemos apreciarlo en las figuras obviamente habrá una caída de tipo exponencial, utilizaremos la siguiente solución WKB:
en donde:
Por último, para la tercera región, con la partícula fuera del núcleo atómico comportándose como una partícula libre, utilizaremos la siguiente solución WKB:
en donde:
En lo que toca a la segunda región, resulta conveniente reescribir la solución WKB de la siguiente manera:
o mejor aún:
En el fenómeno del decaimiento α, es de notarse que aunque la solución es de tipo oscilatorio en la tercera región esto no implica que se tengan ondas estacionarias en dicha región, ya que tal cosa sólo ocurre en los estados ligados. La solución WKB que se tiene aquí corresponde a una onda esférica que se expande radialmente hacia afuera del núcleo atómico. Esto implica que la solución tiene que tener el siguiente comportamiento asintótico
siendo β una constante de fase sin significado físico alguno. Se puede obtener tal solución en la región exterior del núcleo atómico haciendo uso de una de la siguiente ecuación de conexión que habíamos visto en una entrada previa:
En dicha relación de conexión, haciendo ξ.=.π/4, se obtiene la siguiente conexión:
Si en lugar de tomar ξ.=.π/4 se toma ξ.=.-π/4, el resultado será:
Cuando esto es multiplicado por i.=.√-1 y es sumado a lo anterior, el resultado será:
que resulta ser precisamente la forma que se requiere. Usando esta condición de “juntura” en el punto r.=.rc que se encuentra sobre la línea divisoria inter-regiones, se obtiene la siguiente relación de apareamiento:
o, lo que es lo mismo:
Obsérvese que se ha prescindido de las opciones de solución dadas arriba con exponentes negativos al no ser requeridas para esta situación.
La “conexión” apropiada de las soluciones en r.=.r0 en donde hay una discontinuidad de paso se puede obtener recurriendo a un añejo truco matemático que consiste en igualar derivadas logarítmicas. Haciendo uso del truco, esto dá:
siendo:
Existe otro requerimiento, el requerimiento de que la función de onda sea continua en el punto r.=.r0. Esto nos conduce entonces a lo siguiente:
o bien, despejando para A:
Empleando los valores anteriores para A y para B, encontramos que la función de onda que se ha filtrado fuera del núcleo atómico a través de la barrera de potencial viene siendo:
Bajo las condiciones usuales que se tienen en el interior del núcleo atómico, (k1/γ0)2 es relativamente pequeño en comparación con la unidad, o puesto de otra manera, la altura de la barrera coulómbica vista por la partícula α es mayor que la energía cinética dentro del núcleo. Consecuentemente, del resultado anterior para el cual se hizo uso del truco de las derivadas logarítmicas, se pueden tomar las siguientes aproximaciones:
Con esto, la función de onda externa en la tercera región se convierte en:
Resulta conveniente normalizar la solución a una probabilidad unidad (o unitaria) de encontrar a la partícula α en el interior del núcleo. Es importante notar que la función de onda exterior, que se extiende sobre todo el espacio y para grandes valores radiales y que tiene la siguiente forma asintótica:
no es una función de onda que pueda ser normalizada (al igual que la de cualquier partícula libre) en virtud de que ∫|ψ|2 dr diverge al ser tomada sobre todo el espacio. El núcleo atómico tendrá una probabilidad unidad de tener dentro del mismo a la partícula α cuando:
siendo c un factor de normalización a ser aplicado a las funciones de onda obtenidas para cada una de las tres regiones. Utilizando la solución para la función u(r) dada arriba para el interior del núcleo, vemos que:
de lo cual se obtiene:
Usando esto en la relación anterior para u(r) en la tercera región y restableciendo a ψ(r) en lugar de u(r) habiendo servido esto último su propósito intermedio, se tiene:
El decaimiento α de un núcleo está obviamente relacionado con el flujo de partículas hacia el exterior que atravesiesa una superficie esférica de radio r.=.R que es mayor que rc. Para determinar lo que ocurre en el caso del decaimiento α, podemos recurrir a la definición del flujo de densidad de probabilidad que vimos anteriormente al estudiar el significado de la probabilidad en la Mecánica Ondulatoria, específicamente la siguiente relación:
Usando en esto último la relación anterior para ψ(r), llegamos a lo siguiente:
El flujo F de partículas que atraviesan un cascarón esférico de radio r.=.R es entonces:
Si expresamos esto último en términos de la energía E, el radio r0 y el potencial V0, el flujo F de partículas viene siendo:
El flujo F de partículas hacia el exterior debe ser igual a la disminución de la probabilidad de que la partícula α se encuentre dentro del núcleo (cuando la probabilidad es igual a la unidad), una probabilidad que debe variar con el tiempo de la manera siguiente:
Integrando esto último, se puede ver que de aquí proviene la famosa ley del decaimiento exponencial para partículas radioactivas:
La vida media T1/2, del núcleo para una desintegración α está definida para cuando P.=.1/2, o sea:
Así pues, podemos ver que la determinación teórica del tiempo de vida media T1/2 de un elemento radioactivo requerirá evaluar el factor F de acuerdo a la expresión que se ha obtenido arriba. Evitaremos entrar en cálculos numéricos para no opacar un hecho importante: se ha desarrollado una metodología para poder conectar regiones diferentes, empleando primero la aproximación WKB para desarrollar expresiones en cada región de interés, y tras ello procediendo a conectar dichas regiones, lo cual equivale a tener que especificar parámetros específicos que permitan que una misma función de onda pueda ser graficada en forma suave y continua al ir pasando de una región a otra. Visto desde un punto de vista un poco más prosaico, se ha especificado la manera en la cual se pueden especificar las funciones matemáticas de una función de onda ψ(x) para que dicha función de onda pueda ser graficada automáticamente de un modo suave y continuo por algún programa computacional especializado al pasar través de varias regiones.
En el análisis que se acaba de efectuar aquí del problema de decaimiento radioactivo mediante el uso del método de aproximación WKB se ha empleado un nivel de sofisticación mayor al que el que fue utilizado en la entrada anterior para explorar el mismo problema, un nivel de sofisticación en cierta forma parecido al que se utiliza en publicaciones técnicas de la física contemporánea que detallan todo tipo de avances relacionados con la Mecánica Cuántica. Si el lector pudo seguir la línea de razonamiento que se acaba de utilizar arriba, puede dar por hecho que está ya mucho mejor preparado de lo que se imagina para poder leer y entender un buen número de las publicaciones contemporáneas que detallan los avances más recientes de la física cuántica.
Como en el caso del problema del decaimiento radioactivo, el método de aproximación WKB nos puede servir para obtener estimaciones sobre la probabilidad de que cierto evento ocurra. Tómese como muestra el caso en el cual se le aplica un campo eléctrico externo a un átomo (un experimento de este tipo puede dar lugar a un desdoblamiento de líneas espectrales en un efecto conocido como el efecto Stark). Se podría suponer como algo posible que la aplicación de un campo eléctrico externo ayude a que un electrón pueda escapar del átomo por medio del mecanismo de tunelaje, produciéndose la ionización del átomo. Podemos estimar la probabilidad de un evento de este tipo usando un modelo unidimensional algo crudo. Para ello, imaginemos una partícula atrapada en un pozo de potencial finito, aunque muy profundo. Suponiendo que la profundidad V0 del pozo de potencial sea mucho mayor que la cantidad ħ2/ma2, podemos estimar la energía de la partícula en el estado basal considerándola (aproximadamente) como la energía de la misma cuando está en un pozo de potencial de anchura 2a con paredes infinitamente altas, la cual de la expresión:
es simplemente, con n.=.1:
Supóngase ahora que se aplica un campo eléctrico intenso, lo cual equivale a introducir una perturbación H’ en el Hamiltoniano H del pozo de potencial finito que será igual a -ξx, de modo tal que si la intensidad del campo eléctrico externo es Eext entonces ξ.=.eEext siendo e la carga del electrón (hay que tener cuidado en no confundir la letra E utilizada para simbolizar un campo eléctrico con la letra E utilizada para simbolizar a la energía, esta es una consecuencia desafortunada e inevitable del agotamiento de una simbología con un número finito y muy reducido de caracteres). La aplicación del campo eléctrico externo introduce un cambio en la relación de energías. A continuación se muestra el pozo de potencial antes de la aplicación del campo eléctrico (figura superior) así como después de haberse aplicado el campo eléctrico:
Obviamente, como puede verse en el lado derecho de la figura inferior, hay ya cierta probabilidad de que la partícula pueda escaparse hacia la derecha por medio del mecanismo de tunelaje (el escape ocurre en el punto x0). Procederemos en una forma parecida a como lo hicimos al aplicar el método WKB al problema de la desintegración radioactiva en la entrada “El método de aproximación WKB II”, en donde se definió una cantidad γ. Haciendo lo mismo, escribiremos aquí lo siguiente:
De la segunda figura de arriba, se tiene que:
Puesto que para este problema se tiene que:
entonces:
Pero para la región a ser penetrada y que servirá como túnel a la partícula requiere que:
Por lo tanto:
Con la finalidad de simplificar, observando que:
y como:
se tiene entonces para γ el siguiente valor:
Teniendo γ, podemos estimar el tiempo promedio de vida τ para que la partícula (en este caso, un electrón) pueda escapar del átomo dejándolo ionizado. La única diferencia entre este problema y el caso del problema de la desintegración radioactiva es que el pozo de potencial en lugar de tener una anchura r1 tiene una anchura 2a, de modo que:
Para estimar la velocidad de la partícula, podemos equiparar a la energía cinética de la misma con su energía en su estado basal en el pozo de potencial:
De este modo, se tiene para el tiempo promedio de escape τ:
Si usamos algunos valores razonables en un sistema consistente de unidades (por ejemplo, unos 20 eV para V0 como la energía típica de enlace de un electrón situado en la capa electrónica más externa de un átomo típico, 10-10 metros para a como el radio atómico típico, y un campo eléctrico externo con una intensidad de 6×106 volts/metro que representa un campo eléctrico intenso obtenible en el laboratorio, además de los valores usuales para la masa y la carga del electrón), obtendremos en el sistema MKS-SI para γ un valor de:
que hace que el factor exponencial exp[2γ] = e102,150 se vuelva astronómicamente grande, lo cual a su vez se traduce en un tiempo de escape τ (dado en segundos) astronómicamente grande:
No es necesario obtener un número final, dada la magnitud extraordinaria del tiempo involucrado a causa del exponencial. Considerando que la edad del Universo es de apenas unos 1010 años, se concluye pese a lo crudo y primitivo del modelo que estamos utilizando que será prácticamente imposible ionizar un átomo mediante la aplicación de un campo eléctrico externo intenso si suponemos que tal cosa ocurra con la ayuda del simple efecto de tunelaje.