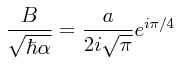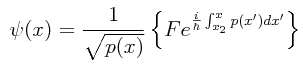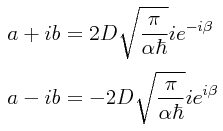Al estudiar las aplicaciones de la aproximación WKB para pozos de potencial con paredes que pueden ser infinitamente altas, se dió por hecho que tales paredes son verticales (desapareciendo por completo la función de onda ψ(x) volviéndose cero justo al tocar una pared vertical cuando ésta es infinitamente alta), de modo tal que las condiciones de frontera se vuelven triviales y las aproximaciones WKB se vuelven relativamente sencillas. Sin embargo, aún en los casos en los que las paredes que contienen a las partículas dentro de cierta región no son verticales, la aproximación WKB se puede seguir utilizando, tal fue el caso del decaimiento α de núcleos radioactivos en donde las paredes de la barrera de potencial no son infinitamente altas y una de ellas (la pared que representa la barrera del potencial Coulómbico) ni siquiera es vertical. Seguiremos explorando aquí lo que ocurre cuando hay puntos de volteo debidos a la forma del potencial V(x). A continuación veremos más de cerca lo que le ocurre a la función de onda ψ(x) en un punto de volteo en el cual la energía E de la partícula es igual a la energía potencial V, cuando la región situada a un lado del punto de volteo es una región clásica y la otra región es una región no-clásica, precisamente en donde la aproximación WKB pierde su poder. Para mayor simplicidad, manejaremos el caso del problema de un estado ligado, y para mayor simplicidad desplazaremos el sistema de coordenadas de forma tal que el punto de volteo que anteriormente estaba situado a un lado del origen del sistema de coordenadas quede ubicado justo en el origen, o sea en x.=.0, como se muestra en la siguiente figura (la línea recta de color café representa un potencial linearizado en la región de juntura en donde se pegan las dos soluciones WKB):
Como puede verse, en tal situación la aproximación WKB para las dos regiones dá dos soluciones, una para cada región. Para x menor que x.=.0 (suponiendo que V(x) permanece mayor que E para todos los valores posibles de x positivo, podemos o mejor dicho debemos excluír el exponente positivo en esta región porque éste explota conforme x.→.∞) en lo que consideraremos como la región # 1 (a la izquierda del punto de volteo), se tiene para la función de onda la siguiente aproximación WKB:
mientras que para x mayor que x.=.0 en lo que consideraremos como la región # 2 (a la derecha del punto de volteo):
La enorme dificultad en el punto de volteo es la misma que ya hemos visto antes, de que en la aproximación WKB la función de onda ψ(x) crece inconmensurablemente hacia el infinito conforme p(x), conforme podemos verlo en las dos expresiones anteriores. En la Naturaleza, la función de onda verdadera (no la que es aproximada por el método WKB) no posee tal comportamiento violento, lo que sucede simplemente es el la aproximación WKB fracasa en la proximidad de tal punto de volteo. Sin embargo, son precisamente las condiciones de frontera en los puntos de volteo las que determinan las energías permisibles de la partícula. El remedio usual consiste en “pegar” las soluciones WKB en la proximidad del punto de volteo con una “función de parche” ψp(x) que no explote en el punto de volteo y que nos permita “parchar” y pegar en el punto de volteo las dos soluciones WKB para cada región. En virtud de que solo necesitamos una función de parche en la vecindad de un punto de volteo, que será común a ambas regiones, podemos aproximar el potencial V(x) en dicho punto con una función linear como la siguiente:
La solución de la ecuación de Schrödinger en la cercanía de este punto de volteo es entonces:
en donde:
Si hacemos:
entonces las α pueden ser absorbidas dentro de la variable independiente, obteniéndose entonces la siguiente ecuación:
Esta es, desde luego, la ecuación diferencial de Airy que ya tratamos en la entrada anterior, y puesto que se trata de una ecuación diferencial de segundo orden hay dos soluciones linearmente independientes, las funciones de Airy Ai(z) y Bi(z) cuyas gráficas se reproducen a continuación:
La solución a la ecuación de Airy es una combinación linear de las dos funciones de Airy. La “función de parche” ψp(x) usada para “pegar” las dos regiones es por lo tanto:
en donde a y b son constantes numéricas apropiadas. Al ser ψp(x) la función de onda aproximada de parche en el origen en donde se lleva a cabo la juntura, nuestra tarea consiste en aparearla a las soluciones WKB que corresponden a cada una de las dos regiones de interés:
Se supone de inicio que las zonas de traslape están lo suficientemente cercanas al punto de volteo de modo tal que el potencial V linearizado es razonablemente correcto y con ello ψp(x) es una buena aproximación a la función de onda verdadera, pero al mismo tiempo las zonas de traslape están lo suficientemente alejadas del punto de volteo como para que la aproximación WKB sea suficientemente confiable. Siendo la aproximación linear:
válida en la zona intermedia del traslape, y considerando que:
podemos escribir para dicha zona lo siguiente:
En la región # 2 (a la derecha del punto de volteo cuando x es mayor que x.=.0) se tiene:
y por lo tanto la aproximación WKB puede ser escrita sobre dicha región de la siguiente manera:
Podemos usar las siguientes formas asintóticas de las funciones de Airy suponiendo valores de z positivos suficientemente grandes:
con las cuales podemos escribir la función linear de parchado en la zona de encuentro con la región # 2 de la manera siguiente:
Comparando esto con las constantes de la relación:
podemos ver que ello implica lo siguiente:
Podemos repetir el mismo procedimiento para la región # 1 (a la izquierda del punto de volteo cuando x es menor que x.=.0) en donde p(x) sigue dado por la ecuación:
pero en donde ahora se requiere intercambiar los límites de la integración al ser x negativo en la región que está siendo considerada:
De este modo, la función WKB resulta ser:
Por otro lado, recurriendo a la forma asintótica de la función Ai(z) suponiendo valores de z negativos suficientemente grandes:
se puede escribir lo siguiente:
De la fórmula de Euler sabemos que:
De este modo:
De nueva cuenta, estableciendo comparaciones podemos ver que:
y que:
de modo tal que, substituyendo lo que obtuvimos arriba para a:
se tiene finalmente:
Relaciones de este tipo son conocidas como fórmulas de conexión, porque nos permiten “pegar” las soluciones WKB que se obtienen a cada lado de un punto de volteo, y los coeficientes así obtenidos son conocidos como coeficientes de conexión. Expresando todo en términos de una sola constante de normalización D, y desplazando el punto de volteo del origen del sistema de coordenadas hacia un punto arbitrario que simbolizaremos como x2, la aproximación WKB que describe ambas regiones queda definida como dos funciones WKB, la primera para cuando x es menor que x2 (o sea, para valores negativos de x, al haber desplazado el origen del sistema de coordenadas para hacerlo coincidir con x2):
y la segunda para cuando x mayor que x2 (o sea, para valores positivos de x):
Supóngase que se tiene un pozo de potencial con una pared vertical en el lado izquierdo y del otro lado una pared inclinada en una forma como la que se muestra a continuación:
En este caso, ψ(0).=.0 (en la pared vertical del lado izquierdo) en virtud de que el potencial es infinitamente grande en dicho lugar y la función de onda no puede tener otro valor más que ese. En cambio, en x2 se tiene un punto de volteo en donde el potencial no se vuelve infinitamente grande. Puesto que suponemos que la partícula no va más allá de x2 al llegar al punto de volteo, se deduce que la partícula se encuentra en un movimiento oscilatorio y que su energía está cuantizada. Siendo así, la segunda de las últimas dos ecuaciones dadas arriba no es aplicable, y en este caso usamos únicamente la primera de ellas yendo desde x.=.0 hasta x.=.x2:
Para que esta expresión sea cierta desde el punto de vista matemático, se requiere que:
lo cual a su vez solo se cumple si:
o bien:
siendo n.=.1,2,3,... etc.
Aplicaremos el resultado que acabamos de obtener a un potencial parabólico que corresponde a lo que podríamos llamar un “medio oscilador armónico” definido de la siguiente manera:
Un potencial así tiene el siguiente aspecto (podemos imaginar este oscilador armónico simple como una masa conectada a un resorte que puede ser estirado pero no comprimido):
Claramente, este es precisamente el caso en el cual se tiene una pared sólida y rígida en el extremo izquierdo, y un punto de volteo en el extremo derecho, pudiéndose aplicar de inmediato la relación que se obtuvo arriba. Para esta situación se tiene lo siguiente:
siendo:
un punto de volteo. Llevando a cabo los pasos requeridos, se tiene entonces:
Este es un caso en el que la aproximación WKB nos entrega la solución exacta, ya que los niveles de energía son:
que resultan ser las soluciones impares para el oscilador armónico simple completo.
Se han considerado hasta este punto ejemplos en los cuales los puntos de volteo tienen todos ellos una pendiente que va “cuesta arriba”, esto es, en dichos puntos de volteo el potencial V(x) va aumentando conforme x va aumentando al movernos de izquierda a derecha, como en el siguiente caso en el cual en la coordenada x2 el punto de volteo que está situado en la pendiente de la curva del potencial va “cuesta arriba”:
Las relaciones generales WKB obtenidas arriba con la ayuda de los coeficientes de conexión nos proporcionan la aproximación para el caso en el cual el potencial V(x) en el cual está ubicado el punto de volteo en x2 tiene una pendiente que siempre va “cuesta arriba” dentro del rango de valores de interés. Sin embargo, podemos tener también el caso que en donde está situado el punto de volteo (que ubicaremos en la coordenada identificada como x1) el potencial V(x) tenga una pendiente que siempre va “cuesta abajo”, esto es, en dicho punto el potencial va disminuyendo conforme x va aumentando como en el siguiente caso en el cual en la coordenada x1 el punto de volteo que está situado en la pendiente de la curva del potencial va “cuesta abajo”:
En el caso de puntos de volteo situados en pendientes que van “cuesta abajo” como ocurre en la figura de arriba, para la obtención de los coeficientes de conexión se repite el procedimiento dado arriba que consiste en desplazar el origen del sistema de coordenadas hacia donde se encuentra el punto de volteo x1, como lo ilustra el siguiente gráfico animado (la región mostrada en color ciano es la que corresponde a la región “prohibida”, esto es, la región no-clásica, en donde el potencial V(x) es superior a la energía E de la partícula y por lo tanto la partícula clásicamente no puede penetrar en dicha región):
Efectuado el desplazamiento, se aplica la aproximación WKB a cada región con la finalidad eventual de “pegar” las soluciones WKB en la proximidad del punto de volteo con una “función de parche” ψp(x) que no explote en el punto de volteo y que nos permita “parchar” y pegar en el punto de volteo las dos soluciones WKB para cada región:
De este modo, desarrollando y finalmente desplazando nuevamente el punto de volteo x1 regresando al origen del sistema de coordenadas a su posición inicial, se obtiene la aproximación WKB que describe la zona ubicada en la región en donde x es menor que x1 y que está dada por (cómparese y obsérvese la simetría entre los dos casos):
mientras que la aproximación WKB que describe la zona ubicada en la región en donde x es mayor que x1 está dada por:
En este caso, al usar la relación:
hay que tomar en cuenta que V’(0) es ahora negativo y que:
con lo cual:
Las fórmulas de conexión que se obtienen resultan ser las mismas, produciendo una simetría en las soluciones obtenidas aquí con las que se obtuvieron arriba.
Un caso más general es aquél en el cual se tiene algo así como un pozo de potencial con dos puntos de volteo, uno a cada lado del pozo, ubicados en x1 y en x2:
Las regiones a la izquierda de x1 y a la derecha de x2 son regiones no-clásicas, mientras que la región interior comprendida entre los dos puntos de volteo x1 y x2 es una región clásica. La función de onda en la región interior comprendida entre ambos puntos de volteo puede ser escrita ya sea como:
cuando se aplica la solución obtenida arriba considerando una pendiente “cuesta arriba” en el segundo punto de volteo x2 del potencial V(x), y por el otro lado usando:
cuando se aplica la solución que se obtiene cuando se considera una pendiente “cuesta abajo” en el primer punto de volteo x1 del potencial V(x).
Puesto que los argumentos de las funciones senoidales deben ser iguales, en módulo π, o sea:
se deduce entonces que:
o lo que es lo mismo:
Esto es justo lo que obtuvimos previamente en una entrada anterior. Esta condición de cuantización es válida para pozos de potencial en los cuales ambos lados del pozo tienen paredes laterales que en vez de ser verticales una de ellas tiene una pendiente que va “cuesta abajo” y la otra tiene una pendiente que va “cuesta arriba”. Obsérvese que difiere de las condiciones de cuantización obtenidas con aproximaciones WKB para pozos de potencial con dos paredes verticales y con una pared vertical únicamente en el número que se le resta a n, ya sea 0, 1/2 ó 1/4. Puesto que la aproximación WKB dá sus mejores resultados en el rango semiclásico (valores grandes de n) la diferencia es más en apariencia que en substancia. De cualquier manera, el resultado es extraordinariamente potente porque nos permite calcular las energías aproximadas sin tener que resolver la ecuación de Schrödinger, con solo tener que evaluar una integral. Inclusive la misma función de onda ha terminado desapareciendo del panorama.
La metodología que se sigue en la aplicación del método de aproximación WKB a barreras de potencial es muy parecida a la que se utiliza en el análisis de lo que ocurre en lo que tiene que ver con pozos de potencial. Tómese como ejemplo la barrera de potencial V(x) que se muestra en la siguiente figura en la que se muestra el nivel de energía E de cierta partícula (o partículas) que se aproximan desde la derecha a la barrera de potencial:
Al igual que como ocurre en un pozo de potencial, se tienen aquí dos puntos de volteo en x1 y en x2. Hay tres regiones, y podemos escribir de inmediato las aproximaciones WKB para cada una de ellas. Estamos interesados en evaluar el coeficiente de transmisión T de las partículas que están llegando desde la izquierda de la barrera de potencial y que alcanzan a atravesar por tunelaje al otro lado de la barrera de potencial. Para la primera región (clásica) que está situada a la izquierda de x1, la aproximación WKB es la siguiente (emplearemos las mismas convenciones en la notación de las constantes A, B, C, D y F que se emplean para simbolizar partículas que se están moviendo hacia la izquierda y hacia la derecha en cada región que fueron usadas previamente en el análisis de tunelaje a través de barreras de potencial con paredes verticales):
Para la región (no-clásica) que está comprendida entre x1 y x2, la aproximación WKB es la siguiente:
Por último, para la región (clásica) que está situada a la derecha de x2, la aproximación WKB es la siguiente (no usaremos el término asociado con la constante E que se usaría para las partículas que se están moviendo de derecha a izquierda en esta región, en virtud de que para el cálculo del coeficiente de transmisión estamos interesados únicamente en la contribución de las partículas que están moviéndose de izquierda a derecha, esto es, partículas que lograron atravesar la barrera de potencial):
Como primer paso para poder establecer los coeficientes de conexión que conectan a la primera región con la segunda región, desplazaremos el origen del sistema de coordenadas hacia x1:
El siguiente gráfico animado nos muestra de manera más efectiva el desplazamiento que se está llevando a cabo del origen del sistema de coordenadas:
De este modo, para la región que está a la izquierda del (desplazado) origen del sistema de coordenadas, o sea para x menor que 0, la aproximación WKB viene quedando como (nótese el cambio en los límites de las integrales):
mientras que para la región que está a la derecha del (desplazado) origen del sistema de coordenadas, o sea para x mayor que 0, la aproximación WKB viene quedando como:
Tenemos pues una zona de traslape en la que se deben “pegar” las aproximaciones WKB para ambas regiones (la región que corresponde a x menor que 0, y la región que corresponde a x mayor que 0). Para la segunda región de traslape, usando la relación obtenida previamente:
se tiene entonces para la aproximación WKB en la segunda región lo siguiente:
mientras que la relación:
permanece sin cambios. Estableciendo las comparaciones y correspondencias apropiadas, obtenemos para los siguientes coeficientes de conexión lo siguiente:
Por otro lado, para la primera región de traslape, la aproximación WKB será:
y la función de parche ψp(x) usada para “pegar” las dos regiones será:
queda generalizada (con b.≠.0) a:
Recurriendo a la fórmula de Euler, esto lo podemos escribir de la siguiente manera:
Estableciendo las comparaciones y correspondencias apropiadas, obtenemos para los coeficientes de conexión lo siguiente:
Metiendo en esto último las expresiones obtenidas previamente para las constantes a y b, se tiene por lo tanto:
Hemos obtenido de este modo las fórmulas de conexión que nos relacionan a A, B, C y D en el punto x1.
En lo que concierne al punto de volteo situado en x2, éste está situado en una pendiente que va “cuesta abajo”. Siguiendo la misma metodología delineada previamente, podemos escribir la expresión de la aproximación WKB para la región (no-clásica) que está comprendida entre x1 y x2:
de la siguiente manera:
Hágase:
en una forma parecida a como se hizo para definir la cantidad γ utilizada en la solución del problema de tunelaje del decaimiento de partículas radioactivas estudiado en las entradas previas. Defínanse asimismo las siguientes cantidades:
Desplazaremos ahora el origen del sistema de coordenadas hacia x2. Este desplazamiento se puede visualizar con mayor claridad con el siguiente gráfico animado:
Tras haberse llevado a cabo el desplazamiento del origen del sistema de coordenadas, se tienen dos regiones; la región no-clásica para x menor que 0 queda situada a la izquierda y la región clásica para x mayor que 0 queda situada a la derecha. Para la región que está a la izquierda del (desplazado) origen del sistema de coordenadas, o sea para x menor que 0, la aproximación WKB viene quedando como:
mientras que para la región que está a la derecha del (desplazado) origen del sistema de coordenadas, o sea para x mayor que 0, la aproximación WKB viene quedando como:
La función de parche ψp(x) usada para “pegar” las dos regiones en la zona de traslape sigue siendo dada por la combinación linear de las funciones de Airy:
en donde, al igual que antes:
Para valores negativos de x, en la primera región:
Procediendo en forma semejante a como lo hicimos arriba, la aproximación WKB será:
mientras que para la función de parche ψp(x) usada para “pegar” las dos regiones se tiene:
Estableciendo las comparaciones y correspondencias apropiadas, obtenemos para los coeficientes de conexión lo siguiente:
Por otro lado, para valores positivos de x, en la segunda región:
Procediendo en forma semejante a como lo hicimos arriba, la aproximación WKB será:
y la función de parche ψp(x) usada para “pegar” las dos regiones será:
De nueva cuenta, recurriendo a la fórmula de Euler, esto lo podemos escribir de la siguiente manera:
Se tiene entonces que ia.+.b.=.0 tras establecer las comparaciones y correspondencias apropiadas, con lo cual obtenemos para los coeficientes de conexión lo siguiente:
Del mismo modo:
con lo cual:
Con esto, hemos obtenido todos los coeficientes de conexión que necesitamos, porque para obtener el coeficiente de transmisión T lo único que se requiere es encontrar la relación con la cual se pueda comparar la densidad de probabilidad de las partículas que están llegando desde la izquierda a la barrera de potencial, lo cual depende de la magnitud de A, con la densidad de probabilidad de las partículas que están saliendo de la barrera de potencial moviéndose también de izquierda a derecha, lo cual depende de la magnitud de F. Esto lo encontramos de la siguiente manera:
De este modo, la aproximación WKB para el coeficiente de transmisión T de partículas a través de la barrera de potencial será:
Obsérvese que para valores de ξ mucho mayores a la unidad, el denominador se aproxima a 1 con lo cual el coeficiente de transmisión T.=.exp[-2ξ] se convierte esencialmente en el mismo que se obtuvo para el problema de decaimiento radioactivo, o sea T.=.exp[-2γ].
Un ejemplo interesante de aplicación de la aproximación WKB que se puede citar es aquél en el cual consideramos potenciales esféricamente simétricos. Podemos aplicar el método WKB a la ecuación radial suponiendo para mayor simplicidad que l.=.0, en cuyo caso es razonable suponer que la aproximación WKB toma la forma:
en donde consideramos a r.=.0 como una pared infinitamente alta y tomamos a r0 como el punto de volteo. A modo de ejemplo, supondremos que el potencial radial V(r) es un potencial de tipo logarítmico que está dado por la siguiente relación:
siendo R una constante que nos ayuda a definir al potencial logarítmico. Un vistazo a la gráfica de este tipo de potencial nos revela que podemos esperar estados ligados con energía discreta
Aplicando la condición de cuantización dada por la aproximación WKB al potencial V(r), se tiene entonces:
La energía E de la partícula queda definida por lo anterior como:
Trabajaremos sobre la integral del siguiente modo:
En este tipo de integral, como en otras, resulta conveniente hacer una substitución de variable como la siguiente:
De este modo se tiene:
Por lo tanto:
Antes de tratar de efectuar la integración, tenemos que establecer la correspondencia entre los límites de integración que resultaron como consecuencia del cambio de variable. La correspondencia es la siguiente:
De este modo, se tiene:
La integral, como está dada, tiene una solución inmediata y directa mediante el uso de la función Gamma:
La función Gamma de 3/2 a su vez tiene un valor convencional que nos permite obtener lo siguiente:
Se comprueba con esto que los niveles de energía están discretizados, y estos tienen que ser:
Calculando la diferencia energética entre dos niveles de energía contiguos, podemos comprobar que esta diferencia es independiente de la masa m de la partícula o del valor de la constante R:
Habiendo visto la aplicación del método WKB al análisis de un problema en el que se tiene un potencial esféricamente simétrico, esta es una buena ocasión para intentar aplicarlo a otro problema de mayor interés, la estimación de las energías de enlace del electrón al átomo de hidrógeno. Un paso de esta índole requiere de mucha cautela, ya que la aplicación del método WKB a la ecuación radial presenta algunos problemas sutiles como los que tuvo que enfrentar Rudolph E. Langer en su papel clásico titulado “On the Connection Formulas and the Solutions of the Wave Equation” (Sobre las Fórmulas de Conexión y las Soluciones a la Ecuación de Onda) publicado en 1937 en el ejemplar 8 del volumen 51 de la revista Physical Review, algunos de los cuales fueron abordados más recientemente por Tatsuya Koike y Harris J. Silvestone en un trabajo titulado “Rereading Langer’s influential 1937 JWKB paper: the unnecesary Langer transformation; the two ħ’s” publicado en noviembre de 2009 en el Journal of Physics A: Mathematical and Theoretical. Para resolver la ecuación de Schrödinger con la aproximación WKB aplicada al caso del átomo de hidrógeno, Langer propuso la “transformación Langer”:
Al hacer esto, Langer encontró que la función radial para el hidrógeno en una aproximación WKB de primer orden actuaba como si el término conocido como “potencial centrífugo” fuese:
en lo que hoy es conocido como la corrección Langer, dando con ello cierta justificación a la substitución sugerida previamente en 1926 por Hendrik Anthony Kramers (precisamente uno de los que desarrollaron el método de aproximación Wentzel-Kramers-Brillouin) en su trabajo “Wellenmechanik und halbzahlige Quantisierung” (Mecánica ondulatoria y cuantización media-integral) publicado en el Zeitschrift für Physik que proporciona, a un primer orden, el comportamiento rl+1 correcto en el origen, el desplazamiento correcto de fase, y los niveles correctos de energía. No entraremos en tantos detalles. Para la resolución de este problema, usaremos la aproximación WKB:
Trabajando dentro del sistema de unidades MKS-SI, el momentum radial p(r) para el átomo de hidrógeno puede ser escrito de la siguiente manera:
Con la finalidad de no estar arrastando innecesariamente demasiada notación engorrosa, efectuaremos las siguientes substituciones:
De este modo, usando la aproximación WKB tal y como ha sido prescrita arriba, se tiene:
En el integrando tenemos una expresión cuadrática que sabemos de sobra que tiene que poseer dos raíces r1 y r2:
De este modo, se tiene lo siguiente para simplificar:
En este punto resuta útil recurrir a las tablas de integrales, dentro de las cuales podemos encontrar la siguiente forma convencional:
Por lo tanto:
Recurriendo a un conocido teorema del álgebra, se puede afirmar que:
Teniendo en cuenta:
Por lo tanto:
Este es el punto adecuado para restablecer las variables α y β a sus valores originales:
Simplificando:
Simplificando un poco más:
De este modo, obtenemos finalmente para los niveles de energía que resultan estar discretizados:
Usando valores numéricos para las constantes físicas que obran en en numerador, encontramos que:
Obsérvese que para n.».l así como n.».1/2, el resultado obtenido nos conduce a los niveles energéticos predichos por el model atómico planetario de Bohr.
Habiendo obtenido previamente en esta entrada la solución exacta con el método WKB para un potencial que corresponde a un “medio oscilador armónico”, vale la pena repasar la solución con el método WKB para el potencial que corresponde al verdadero oscilador armónico simple. En este caso, el momentum p(x) está dado por la expresión:
habiendo dos puntos de volteo x1 y x2, uno a cada lado de la parábola, los cuales son, desde luego:
La condición de cuantización obtenida con el método WKB para la región en la cual la partícula se encuentra oscilando entre un punto de volteo en x1 y el otro punto de volteo en x2 es:
De las tablas de integrales se obtiene la solución a lo que es una integral convencional:
Por lo tanto, usando esto como paso intermedio en el desarrollo de la solución WKB para el oscilador armónico simple, se tiene:
Como puede verse, el método WKB proporciona la solución exacta para los niveles de energía que corresponden al oscilador armónico simple.
Un problema algo más elaborado que también se puede analizar con la aproximación WKB es el problema del pozo de potencial doble como el siguiente:
Para una partícula que posea una energía E como la que se muestra en la figura, la región comprendida entre los puntos de volteo x1 y en x2 actúa como una barrera de potencial; una partícula que se encuentre en un pozo de potencial puede pasar al otro pozo por medio de tunelaje, y podemos estimar el coeficiente de transmisión de una región a otra tal y como lo hicimos arriba. Sin embargo, se escogemos los puntos de volteo x1 y x2 que se muestran en la siguiente figura:
lo que tenemos entonces es una situación en la que la partícula (o las partículas) está rebotando entre ambos puntos de volteo. Si unimos esta visión con la visión anterior, el panorama total resulta indudablemente más complicado, porque en cada pozo de potencial se pueden tener eigenestados discretos de energía en donde las partículas pueden permanecer semi-atrapadas, aunque puede haber un flujo de partículas por tunelaje del pozo de potencial izquierdo al pozo de potencial derecho y viceversa. Podemos obtener una mejor perspectiva sobre el método de solución requerido para el análisis de un problema de esta índole considerando un pozo de potencial doble simétrico construído a partir de pozos de potencial (parabólicos) que corresponden a los de un oscilador armónico simple:
Puesto que el potencial parabólico V(x) para un oscilador armónico simple sencillo centrado en el origen está dado por la expresión:
entonces la fórmula para el pozo de potencial situado a la izquierda del origen del sistema de coordenadas será (esta es esencialmente la ecuación de una parábola desplazada hacia la izquierda en a unidades):
mientras que la fórmula para el pozo de potencial situado a la derecha del origen del sistema de coordenadas será (esta es esencialmente la ecuación de una parábola desplazada hacia la derecha en a unidades):
En la figura mostrada arriba, se han destacado dos puntos de volteo x1 y x2 en el pozo de potencial que está situado a la derecha del origen del sistema de coordenadas, los cuales corresponden a los de una partícula de energía E que se encuentra en un estado ligado.
La solución general WKB para un pozo de potencial doble (no limitada al ejemplo que se acaba de dar en el cual se construye un pozo de potencial doble con dos pozos de potencial parabólicos) puede comenzar considerando dos puntos de volteo x1 y x2 como los que se muestran en la figura de arriba, los cuales subdividen en tres regiones al pozo de potencial situado al lado derecho del origen del sistema de coordenadas. Empleando los mismos procedimientos utilizados en los ejemplos anteriores, se encuentra que la aproximación WKB para la región situada entre el origen del sistema de coordenadas (x.=.0) y x1 es (entraremos en mayor detalle más abajo sobre la manera en la que se obtiene este resultado):
en donde se ha hecho la simplificación:
mientras que la aproximación WKB para la región situada entre x1 y x2 es:
entanto que la aproximación WKB para la región situada a la derecha de x2 es:
Para efectuar el “parchado” en x1, podemos escribir de la siguiente manera la aproximación WKB para la región situada entre el origen del sistema de coordenadas (x.=.0) y x1 usando como medida simplificadora la definición que se dió arriba de β:
A continuación, podemos desplazar el origen del sistema de coordenadas del pozo de potencial doble para hacerlo coincidir con x1:
con lo cual la aproximación WKB para valores de negativos de x (la región a la izquierda del origen del sistema de coordenadas puesto en x1) toma la siguiente forma:
mientras que la aproximación WKB para valores de positivos de x (la región a la derecha del origen del sistema de coordenadas puesto en x1) toma la siguiente forma:
Repitiendo los pasos dados en los ejemplos anteriores, se encuentra que los coeficientes de conexión para la zona de traslape situada en la región con valores negativos de x están especificados por:
mientras que los coeficientes de conexión para la zona de traslape situada en la región con valores positivos de x están especificados por:
De esto último se obtiene:
Combinando ambos resultados de las zonas de traslape se tiene entonces:
De esta manera es como se puede obtener entonces la aproximación WKB para la región situada entre el origen del sistema de coordenadas (x.=.0) y x1:
Ahora bien, al considerar la función de onda completa ψ(x) del pozo de potencial doble, si suponemos como medida simplificadora que la función de potencial V(x) para toda la región de interés es simétrica con respecto al origen del sistema de coordenadas (el que está puesto entre ambos pozos de potencial), entonces solo necesitamos considerar dos tipos de funciones de onda, las funciones de onda pares y las funciones de onda impares. Las funciones de onda impares necesariamente deben ser iguales a cero en el origen del sistema de coordenadas, o sea que ψ(0).=.0, mientras que para las funciones de onda pares si bien es cierto que no son iguales a cero al cruzar el punto x.=.0 la pendiente de las mismas debe ser igual a cero, o sea dψ(0)/dx.=.0. Trabajando sobre el caso de las funciones de onda impares, usando la condición para tales funciones de onda se tiene de la relación anterior que:
Si definimos una cantidad ξ de la siguiente manera:
entonces se tiene lo siguiente:
Por otro lado, para las funciones de onda pares, usando la condición:
se obtiene lo siguiente (omitiremos los detalles, los cuales son algo engorrosos):
Podemos combinar ambos resultados en uno solo:
Este es un resultado completamente general, y solo requiere que el pozo de potencial doble sea simétrico. Supóngase que estamos interesados en lo que ocurre cuando la barrera de potencial central situada entre ambos pozos de potencial es relativamente alta o relativamente ancha (o ambos). En tal caso, ξ toma un valor grande, y con mayor razón exp[ξ] toma un valor mucho más grande aún. Entonces la condición obtenida nos indica que β debe tener un valor muy cercano a un múltiplo medio integral de π. En base a esto, podemos escribir lo siguiente:
teniendo η un valor mucho menor que la unidad. Tomando la tangente de ambos lados de esta relación y desarrollando:
Puesto que estamos suponiendo que η tiene un valor mucho menor que la unidad, entonces:
Igualando esto con la condición obtenida arriba para el pozo de potencial doble:
De este modo:
En este punto, podemos percibir que cuando los dos pozos de potencial estén “intercomunicados” a causa de una barrera central de potencial que no sea infinitamente alta e impenetrable, entonces la eigenenergía En de una partícula en cualquiera de los dos pozos que de otro modo sería la misma que la que corresponde a una partícula de un oscilador armónico simple se desdoblará en dos niveles contiguos de energía que podemos simbolizar como En+ y En-. En efecto, si a la expresión que acabamos de obtener arriba la multiplicamos en ambos lados por la energía cuántica ħω, el primer término del lado derecho de la expresión es el mismo que el que corresponde a la cuantización de energía de un oscilador armónico simple, mientras que el segundo término del lado derecho de la expresión es el que se encarga de desdoblar la energía En en dos valores contiguos pero distintos. De este modo, a la pregunta: ¿qué tipo de comportamiento podemos esperar para una partícula que se encuentre atrapada en un pozo de potencial doble simétrico?, podemos responder que todo depende de la energía E de la partícula y del tipo que tenga la barrera central que separa ambos pozos. Si la energía de la partícula es suficientemente grande, mayor que la altura de la barrera central del potencial, entonces podrá estar “rebotando” libremente entre ambas paredes extremas del pozo de potencial doble. Si la energía de la partícula es muy baja, o lo que es lo mismo, si la barrera central es alta e impenetrable, lo cual en los resultados que se acaban de obtener arriba equivale a especificar la condición ξ.→.∞, en tal caso simplemente tendríamos dos osciladores armónicos desligados el uno del otro, y sus energías:
serían doblemente degeneradas, puesto que la partícula se puede encontrar tanto en el pozo de potencial izquierdo como en el pozo de potencial derecho. Sin embargo, cuando la barrera central del potencial es finita y relativamente estrecha, los dos pozos de potencial estarán “interconectados”, con lo cual la degeneración será removida. Los eigenestados de las funciones de onda pares ψn+(x) tendrán una energía ligeramente menor que aquellos de las funciones de onda impares ψn-(x). Por otro lado, una partícula que inicialmente se encuentre en el pozo de potencial izquierdo podrá escapar hacia el pozo de potencial derecho y regresar posteriormente al pozo de potencial izquierdo, oscilando entre ambas paredes extremas del doble pozo de potencial. Un problema de esta índole se puede manejar como algo equiparable a dos estados mezclados, de modo tal que la función de onda que describe a los estados mezclados será:
mientras que de lo anterior se obtiene que la densidad de probabilidad será:
El método de aproximación WKB, sumado al principio variacional y a las técnicas de perturbación, proporcionan alternativas de solución para problemas en los cuales no hay soluciones analíticas exactas a la ecuación de Schrödinger que se puedan expresar en forma cerrada mediante alguna fórmula. Para aquellas situaciones en las cuales estos métodos no son aplicables, queda como último recurso el recurrir a soluciones numéricas llevando cabo simulaciones con la ayuda de una computadora en vez de perder infructuosamente el tiempo buscando soluciones simbólicas que posiblemente no existan.