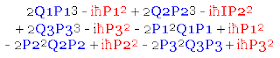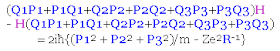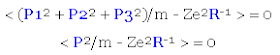Antes de atacar el problema del átomo de hidrógeno, Heisenberg emprendió la resolución matricial del problema del oscilador armónico simple, lo cual es afortunado porque el problema del átomo de hidrógeno resultó ser un problema más complicado que el problema del oscilador armónico simple. Históricamente hablando, fue Wolfgang Pauli el primero que obtuvo una solución matricial al problema del átomo de hidrógeno después de que recibiera una respuesta sarcástica de Heisenberg echándole en cara sus “nulas contribuciones” después de que Heisenberg hubiera recibido una carta de Pauli comparándolo con un “borrico” que no había producido nada de valor alguno (Pauli tomó esto como un reto, y tres semanas después le envió a Heisenberg una solución al problema del átomo de hidrógeno).
Siguiendo la filosofía de utilizar como punto de partida los resultados clásicos que involucran variables clásicas, substituyendo las variables por matrices, empezaremos por la misma ecuación clásica utilizada por Bohr para obtener su modelo atómico planetario del átomo de hidrógeno en la cual se estipula la energía total (simbolizada con la letra H que significa “Hamiltoniano”) como una energía que es igual a la suma de la energía cinética del electrón girando en torno al núcleo y la energía potencial del electrón con respecto al núcleo debida a la atracción eléctrica Coulómbica:
H = Ecinética + Epotencial
Siendo la energía cinética del electrón igual al cuadrado de su momentum entre el doble de su masa, y siendo la energía potencial igual a -Ze²/r, se tiene entonces (en unidades cgs-Gaussianas):
El momentum total se puede descomponer en las componentes del momentum a lo largo de tres ejes coordenados ortogonales (por ejemplo, las coordenadas Cartesianas rectangulares), lo cual nos permite escribir lo anterior de la siguiente manera:
Ahora tomaremos esta ecuación clásica, y la convertiremos en una ecuación matricial:
Obsérvese con detenimiento el último término. Puesto que no es permisible dividir algo entre una matriz en virtud de que tal operación no está definida matemáticamente, podemos hacer algo que se le acerca bastante, y ello consiste en utilizar la inversa de la matriz radial R, o sea R-1.
Los valores posibles de la energía representados por la matriz H serán los valores característicos eigen de dicha matriz, y sin ir más adelante estaríamos afirmando con la ecuación matricial anterior que los valores posibles de la energía del átomo de hidrógeno están discretizados, no pueden tomar cualquier valor entre los valores de energía que le son permisibles.
Para poder avanzar en la resolución del problema, llevaremos a cabo una descomposición de la distancia radial a lo largo de las tres coordenadas utilizadas para la especificación del problema usando la notación Q para simbolizar estas coordenadas de la posición con el objeto de estar más en conformidad con la notación de Born. Del mismo modo que en la geometría Euclideana clásica podemos descomponer un vector en tres componentes ortogonales y podemos obtener la longitud |r| de dicho vector sumando los cuadrados de cada una de las componentes:
r² = x² + y² + z²
supondremos que este tipo de descomposición será igualmente válida tratándose de matrices infinitas utilizadas para representar a las coordenadas de la posición:
R² = Q1² + Q2² + Q3²
Ahora bien, si tenemos un electrón orbitando en torno al núcleo atómico, este electrón necesariamente tendrá un momento angular que denotaremos matricialmente como L, y este momento angular lo podemos construír a partir de las matrices de Born para la posición Q y el momentum P. Para ello, tenemos que descomponer tanto a la matriz posición Q como a la matriz momentum P en sus componentes ortogonales Q1, Q2, y Q3 así como P1, P2, y P3 a lo largo de los tres ejes coordenados que están siendo utilizados con el objetivo de que se puedan aplicar las relaciones de conmutación de Born. A partir de estas matrices, podemos obtener las matrices L1, L2, y L3 que representan al momento angular del electrón.
En la solución de problemas de cualquier tipo, siempre resulta extremadamente útil tanto en la mecánica clásica como en la Mecánica Cuántica el poder identificar y utilizar cantidades que permanezcan constantes con el transcurso del tiempo, razón por la cual valoramos tanto principios tales como el de la conservación de energía, y el problema al que nos estamos abocando aquí no es ninguna excepción. Siendo el problema del átomo de hidrógeno un problema esencialmente orbital, no debe causar asombro que podamos dirigirnos de nueva cuenta a la mecánica clásica, específicamente a la mecánica celeste, recogiendo de dicha rama otra cantidad vectorial utilizada en el marco de la dinámica Newtoniana en donde en virtud de la fuerza de la gravedad también tenemos una fuerza atractiva que varía en forma análoga a la fuerza de atracción eléctrica de Coulomb para el átomo de hidrógeno (en razón inversa al cuadrado de la distancia). Se trata del vector de Laplace-Runge-Lenz (también conocido como el vector Runge-Lenz), una constante del movimiento del problema de los dos cuerpos en interacción gravitatoria mutua. Este vector fue utilizado por vez primera por Wilhelm Lenz en un papel publicado en 1924 sobre un tratamiento mecánico cuántico del átomo de hidrógeno perturbado. Antes de utilizarlo en su versión matricial para la resolución matricial del problema del átomo de hidrógeno, resulta conveniente hacer un repaso del origen clásico de este vector.
En la mecánica Newtoniana, para una fuerza central radial, la segunda ley de Newton puede ser expresada vectorialmente del modo siguiente utilizando la “notación del punto” puesto encima del vector momentum lineal p para denotar la derivada con respecto al tiempo (el vector radial r dividido entre la magnitud del vector, r/r, nos proporciona simplemente un vector unitario que apunta en la misma dirección de la fuerza que está ejerciendo la tracción):
Una cantidad que ciertamente permanece constante en la mecánica clásica es el momento angular L, para la cual tenemos el principio de la conservación del momento angular. Si tomamos el producto vectorial “cruz” de la expresión anterior con el vector momento angular L, podemos escribir entonces vectorialmente lo siguiente metiendo en el panorama una fuerza atractiva de carácter general f(r):
Esto puede ser convertido, también vectorialmente, en lo siguiente:
Esta última relación puede ser simplificada aún más observando lo siguiente:
Con esto, y puesto que el vector momento angular L es constante, la relación previa puede ser escrita de la siguiente manera:
Simplificando un poco:
Esta ecuación diferencial puede ser integrada de inmediato si conocemos la naturaleza de la fuerza atractiva (tratándose de la ley de la gravedad Newtoniana, la fuerza varía en razón inversa al cuadrado de la distancia, constituyéndose de este modo en el problema conocido clásicamente como el problema de Kepler). Este resultado puede ser escrito y simplificado aún más de la siguiente manera:
Hemos llegado así a una cantidad que permanece constante, una constante del movimiento, que hemos simbolizado como el vector A y la cual es igual a:
siendo este un vector de tres componentes en un espacio tridimensional Euclideano:
A = (A1, A2, A3)
Por la forma en la cual hemos definido al vector A, podemos ver que siendo el vector momento angular L perpendicular al vector p×L y siendo el vector radial r perpendicular al vector momento angular L = r×p, entonces el producto vectorial punto entre el vector A y el vector L será igual al escalar cero:
A · L = L · A = 0
Podemos tomar ahora al vector Runge-Lenz clásico, como se ha definido arriba, y hacer la transcripción del mismo hacia la Mecánica Matricial substituyendo las observables por matrices, tomando además en cuenta el hecho de que en vez de una fuerza de atracción gravitacional que varía en razón inversa al cuadrado de la distancia estaremos manejando una fuerza de atracción eléctrica que también varía en razón inversa al cuadrado de la distancia y cuyo potencial Ze²R-1 ya metimos arriba como parte del Hamiltoniano. Es de este modo como en la Mecánica Matricial las componentes de este vector de matrices A representadas mediante matrices son las siguientes (el lector alerta podrá reconocer aquí el reflejo de la operación del producto cruz de dos vectores como se acostumbra llevar a cabo en la física clásica):
Las componentes del vector de matrices Runge-Lenz tienen varias propiedades útiles para simplificar la resolución del problema. Una de tales propiedades que el lector puede comprobar por sí mismo mediante operaciones matriciales directas es la siguiente:
L1A1 + L2A2 + L3A3 = O
Esto no es más que el reflejo matricial de la ortogonalidad que ya se había señalado arriba para los vectores clásicos L y A.
Otra propiedad que el lector también puede comprobar por sí mismo es que la “longitud” del “vector” A (¡nótese que estamos hablando aquí de la “longitud” de un vector cuyas componentes individuales son matrices!) está dada por:
Se puede verificar que las componentes matriciales del vector-matriz Runge-Lenz A también satisfacen relaciones de conmutación de Born:
[L1, A2] = L1A2 - A2L1 = iħA3
[L2, A3] = L2A3 - A3L2 = iħA1
[L3, A1] = L3A1 - A1L3 = iħA2
[L2, A1] = L2A1 - A1L2 = - iħA3
[L3, A2] = L3A2 - A2L3 = - iħA1
[L1, A3] = L1A3 - A3L1 = - iħA2
[L2, A3] = L2A3 - A3L2 = iħA1
[L3, A1] = L3A1 - A1L3 = iħA2
[L2, A1] = L2A1 - A1L2 = - iħA3
[L3, A2] = L3A2 - A2L3 = - iħA1
[L1, A3] = L1A3 - A3L1 = - iħA2
mientras que las componentes matriciales del vector-matriz Runge-Lenz conmutan con las componentes matriciales del momento angular en base a la ortogonalidad arriba señalada:
L1A1 - A1L1 = O
L2A2 - A2L2 = O
L3A3 - A3L3 = O
L2A2 - A2L2 = O
L3A3 - A3L3 = O
Por otro lado:
El átomo de hidrógeno puede encontrarse en uno de muchos estados de energía posibles, empezando por el estado fundamental (basal) y cualquiera de los niveles excitados. Para simplificar las cosas consideraremos un sistema sencillo cuya energía está fija en un valor que designaremos como E. Esta es una cantidad a la cual para fines de cálculo se le asigna un número como a la masa del electrón y a la carga eléctrica del mismo. Puesto que esta es la única energía que el sistema podrá tener para nuestros propósitos, esta energía se puede representar matricialmente como EI siendo I una matriz identidad infinitamente grande. Normalmente utilizamos a la matriz Hamiltoniana H para representar todos los valores posibles de energía que puede tener un sistema, siendo en este caso el sistema un átomo de hidrógeno (una infinitud de valores posibles.) Pero siendo E el único eigen-valor de la matriz EI, esta matriz alterna representa una sola cantidad. Esta simplificación nos permitirá reemplazar a la matriz H con la matriz EI en nuestros desarrollos posteriores, en el entendido de que si los desarrollos son válidos para este valor de energía E serán igualmente válidos para todos los demás valores de energía posibles del átomo de hidrógeno. De cualquier manera, es importante no confundir al valor de la energía E con la matriz EI que representa a dicho valor.
Se asentará aquí como un hecho que la matriz radial R (cuyo valor representa la distancia que hay entre el núcleo del átomo y el electrón que orbita en torno al núcleo) conmuta con las matrices posición Q1, Q2 y Q3 y conmuta también con las componentes matrices del momento angular del electrón L1, L2 y L3, lo cual a su vez implica que también la matriz radial inversa R-1 conmuta con las matrices posición Q1, Q2 y Q3 y con las componentes matrices del momento angular del electrón L1, L2 y L3, siendo esto último fácil de demostrar, ya que si la matriz R conmuta con la matriz L2 (por ejemplo):
RL2 = L2R
entonces con pre-multiplicación y post-multiplicación matricial de la matriz inversa R-1 sobre ambos miembros de esta igualdad obtendremos lo siguiente:
PROBLEMA: Demostrar que la matriz R² conmuta con las matrices posición Q1, Q2 y Q3.
Usando el hecho de que las matrices posición conmutan todas entre sí:
Este mismo procedimiento se aplica fácilmente para demostrar que la matriz R² también conmuta con las matrices Q2 y Q3.
Se puede demostrar también, como lo hemos estado haciendo, que la matriz R² conmuta con las componentes matriciales del momento angular L1, L2 y L3, del mismo modo en que el cuadrado de la matriz del momentum P² (definido como P1² + P2² + P3²) conmuta con las componentes matriciales del momento angular L1, L2 y L3; y de hecho podemos demostrar que la matriz radial R debe conmutar con Q1, Q2 y Q3 así como con las matrices L1, L2 y L3, en virtud de que la matriz R puede ser obtenida como la raíz cuadrada de la matriz R² (definimos la raíz cuadrada de una matriz M como aquella matriz que multiplicada por sí misma producirá la matriz M). Tomando esto en cuenta, las componentes matriciales del momento angular L1, L2 y L3 deben conmutar con la matriz Hamiltoniana H que se ha definido arriba (la cual representa los valores posibles de la energía del átomo de hidrógeno) puesto que conmutan con R-1 y con P1² + P2² + P3², del mismo modo que la matriz de la energía H conmuta con A1, A2 y A3.
Al conmutar con la matriz de la energía H, las componentes matriciales del momento angular L1, L2 y L3 representan cantidades que también pueden ser medidas cuando el átomo de hidrógeno posee cierta cantidad de energía bien definida. Puesto que las componentes matriciales del momento angular L1, L2 y L3 no conmutan entre sí, las cantidades que representan no pueden ser medidas todas ellas juntas con precisión ilimitada ya que entra en acción el principio de incertidumbre. Sin embargo, hay diferentes valores posibles que las componentes matriciales del momento angular L1, L2 y L3 pueden tener cuando el átomo de hidrógeno está en un mismo estado de energía. Por lo tanto, la sola medición de la energía del átomo no nos determina de manera unívoca el estado del átomo. Estas otras cantidades que representan al momento angular orbital también deben ser medidas para fijar el estado del átomo. Supóngase que tenemos un solo átomo con una energía bien definida (en lugar de varios átomos con distintos valores posibles de energía). Este átomo puede ser descrito mediante la medición de estas cantidades cuando su energía posee un valor bien definido. Las cantidades representadas por las matrices L1, L2 y L3 (al igual que las cantidades representadas por las matrices A1, A2 y A3) pueden ser utilizadas para la descripción del átomo, mientras que la posición relativa y el momentum del átomo no pueden ser medidos cuando el átomo posee un valor bien definido de energía en virtud de que las matrices de la posición Q1, Q2 y Q3 así como las matrices del momentum P1, P2 y P3 no conmutan con la matriz de la energía H.
Definiremos ahora tres constantes matriciales K en función de las componentes del vector Runge-Lenz A para un átomo de hidrógeno que se encuentra en el estado fijo de energía que simplemente identificaremos como E:
En virtud de lo asentado previamente, tenemos que:
Por otro lado, también podemos obtener lo siguiente de lo que tenemos arriba:
Cada una de las constantes matriciales K1, K2 y K3 satisfacen las mismas relaciones de conmutación con las componentes del momento angular que L1, L2 y L3 que A1, A2 y A3 teniéndose lo siguiente:
Defínanse ahora las siguientes matrices en función de las componentes matriciales del momento angular y de las constantes matriciales K:
PROBLEMA: Demuéstrese la siguiente relación:
La solución se lleva a cabo por substitución matricial directa de las definiciones:
Del mismo modo, se pueden demostrar las siguientes relaciones:
PROBLEMA: Demuéstrese la siguiente relación:
De nueva cuenta, la solución se lleva a cabo por substitución matricial directa de las definiciones:
PROBLEMA: Demuéstrese que:
Por substitución matricial directa:
Del mismo modo:
Entonces, usando uno de los resultados anteriores:
Ahora bien, por otro lado tenemos:
Todo lo anterior nos conduce a lo siguiente:
Aquí sacaremos fuera las matrices K² e introduciremos la relación previa en la cual aparece en forma explícita el valor E de la energía del sistema:
Los momentos angulares L se cancelan mutuamente en el lado derecho dejándonos con la siguiente relación:
Esto lo podemos poner de la siguiente manera:
Esta es una ecuación puramente matricial. Puesto que cada matriz representa un valor físico, en el lado izquierdo de la ecuación los cuadrados de las matrices M1, M2, y M3 sumados representan un valor específico real que sólo puede ser positivo, requiriéndose por lo tanto que el lado derecho también sea un valor positivo al representar la matriz identidad I también un valor también positivo (el número 1). Pero si tenemos un signo negativo en el lado derecho, ¿de dónde puede salir la cantidad positiva que necesitamos en el lado derecho? Puesto que la masa no puede ser negativa, lo único que nos puede dar una inversión de signo es la energía E, y efectivamente los valores de la energía del átomo de hidrógeno son negativos en virtud de que se requiere suministrar energía al átomo para poder arrancarle el electrón. Esto nos confirma el signo negativo que se le ha dado a la energía del átomo de hidrógeno en el modelo atómico planetario de Bohr. Ahora bien, las relaciones de conmutación para las matrices K (usadas para definir las matrices M y N) las ligan directamente con el momento angular orbital L del electrón. Esto implica que las relaciones de conmutación para las matrices M deben ser las mismas que las relaciones de conmutación para las matrices J que representan el momento angular (tras dividir las matrices L entre ħ). E implica que los únicos valores que la cantidad matricial M1²+M2²+M3² puede representar deben ser j(.j+1) en donde j está restringido a tomar los valores:
j = 0, 1/2, 1, 3/2, 2, 5/2, 3, ... etc.
Con esto en mente, podemos proceder a convertir la ecuación matricial en una ecuación de valores y despejarla para obtener el valor de la energía E:
Si hacemos:
n = 2j + 1
entonces este número n sólo puede tomar los valores:
j = 1, 2, 3, 4, 5, 6, ...
y la energía del átomo de hidrógeno estará cuantizada de acuerdo con la siguiente fórmula para cada valor posible del número n:
Esta es la misma fórmula que la obtenida por Bohr con su modelo mecanístico del átomo de hidrógeno, y proporciona una confirmación contundente de solidez de la Mecánica Matricial.
Queda una duda por aclarar. ¿Cómo se extrae de la matriz H que representa la infinitud de valores de energía que puede tomar el átomo de hidrógeno un valor específico entre todos ellos que sea detectado en el laboratorio al llevarse a cabo una medición? La respuesta es que esto ocurre precisamente al llevarse a cabo el acto de medición. Empezando con la matriz H original, la cual tiene en sus entradas diagonales los valores posibles de energía, el acto de medición provoca un colapso que nos resulta en una matriz que posee un solo valor bien definido en lugar de una infinitud de ellos. Este valor de energía ε lo podemos representar matricialmente como εI, o sea una matriz identidad con el mismo valor apareciendo en cada entrada diagonal:
Hay otra forma un poco más elegante de representar este proceso de colapso que ocurre al llevarse a cabo el acto de medición. Considérese una matriz 4x4 con cuatro valores distintos, de la cual queremos extraer el valor puesto en el tercer renglón y la tercera columna. Para extraer dicho valor, post-multiplicamos la matriz con un vector columna v = [0,0,1,0] que entresacará todos los valores que corresponden a la tercera columna de la matriz. Y tras esto, pre-multiplicamos el resultado con la transpuesta del vector columna v (la transpuesta convierte al vector columna en un vector renglón), lo cual entresacará al valor que estaba en el tercer renglón produciéndonos la matriz más sencilla de todas, una matriz 1x1 (una matriz de un renglón y una columna) con el valor que queríamos obtener desde un principio, siendo este proceso paso a paso el siguiente:
Repasando lo que fue descrito en relación a esto en la entrada “El spin del electrón”, podemos ver que el vector v = [0,0,1,0] usado aquí es en realidad un vector de probabilidad al cual el acto de medición ha convertido en un vector de certeza, nulificando casi todos los componentes del vector de probabilidad original y dejando uno solo con un valor de 1. La longitud del vector sigue siendo igual a 1, lo que ha cambiado son los valores de sus componentes como consecuencia del acto de medición.
Como se había mencionado ya, no basta con medir el valor de la energía para tener plenamente especificado el estado del átomo. Es necesario medir las otras cantidades relacionadas con el momento angular orbital. Supóngase que el átomo está en cierto estado bien definido de energía En. Entonces n (que es igual a 2j+1) puede ser cualquier número entero positivo 1, 2, 3, 4, 5, ..., etc. Ahora bien, las relaciones de conmutación tanto para las matrices M1, M2 y M3 como para las matrices N1, N2 y N3 son las mismas que para las matrices L1, L2 y L3, las cuales son las mismas que para las matrices J1, J2 y J3 que representan al momento angular dividido entre ħ. Entonces los valores posibles que puede tomar tanto la cantidad representada por la matriz M3 (al igual que la matriz Lz) como por la cantidad representada por la matriz N3 son los siguientes situados entre -j y +j:
-j, - j + 1, - j + 2, ... , 0 , ... , j - 2, j - 1 , j
Hay un total de 2j+1 valores posibles tanto para la cantidad representada por la matriz M3 como para la cantidad representada por la matriz N3. Esto significa que la cantidad total posible de combinación de pares de valores (M3,N3) será igual a (2j+1)² o bien n². Para cada par posible de valores, habrá un estado del átomo al cual le corresponderá su propio par de valores, de modo tal que para el átomo habrá un total de n² estados posibles cuando esté en cierto valor de energía En. Ya hemos visto que puesto que los valores posibles del momento angular orbital son múltiplos enteros de la constante reducida de Planck ħ, los valores posibles de la cantidad representada por L² son l(l+1).ħ² para enteros no-negativos l. También habíamos visto arriba que:
En virtud de que K1²+K2²+K3² representa una cantidad positiva real, de la relación anterior se deduce:
l(l + 1).ħ² ≤ 4ħ² j( j + 1)
l(l + 1) ≤ 4 j( j + 1)
l(l + 1) ≤ 2 j(2 j + 2)
l ≤ 2 j
l(l + 1) ≤ 4 j( j + 1)
l(l + 1) ≤ 2 j(2 j + 2)
l ≤ 2 j
Por otro lado, siendo l = 2j+1, tendríamos entonces:
l(l + 1) = (2j + 1)(2j + 1 +1) = (2j + 1)(2j + 2)
y lo último que tenemos al lado derecho de las igualdades es ciertamente mayor que:
(2j)(2j+2)
Siendo 2j igual a n-1, los valores posibles que puede tomar l serán 0, 1, 2, 3, 4, ... , n-1., mientras que los valores posibles que puede tomar la cantidad representada por L3 (Lz) serán:
-l, - l + 1, - l + 2, ... , 0 , ... , l - 2, l - 1 , l
habiendo un total de 2l+1 valores posibles. Finalmente, la cantidad total posible de pares de valores 2l+1 representados por L² y por Lz estará dada por la suma:
(2·0 + 1) + (2·1 + 1) + (2·2 + 1) + ... + {2(n-1) + 1}
dando un total de n² estados posibles.
En el análisis que hemos llevado a cabo no hemos tomado en cuenta el spin del electrón, el cual puede tomar cualquiera de dos valores posibles. Tomándolo en cuenta, esto nos duplica la cantidad total de estados posibles en los cuales se puede encontrar el átomo de hidrógeno hasta 2n² para cada nivel de energía. Esto significa a la vez que en cada “capa” podrá haber 2, 8, 18, 32, etc. electrones, siendo ésta la configuración electrónica numérica de una capa cerrada propia de los gases nobles.
PROBLEMA: Mediante operaciones matriciales directas con las definiciones dadas arriba, se puede demostrar la siguiente relación matricial:
Encuéntrese una expresión para la esperanza matemática <R> de la matriz radial R para un estado en el cual cada una de las cantidades representadas por las matrices L1, L2 y L3 así como A1, A2 y A3 tienen el valor de cero.
El cuadrado de la magnitud del momento angular orbital L en función de sus componentes L1, L2 y L3 está dado por:
L² = L1² + L2² + L3²
Haciendo esta substitución arriba y tomando la esperanza matemática en ambos miembros de la igualdad matricial se tiene lo siguiente:
Para un estado en el que A1 = O, A2 = O y A3 = O, la expresión en el lado izquierdo de la igualdad se vuelve igual al número cero (al ser la esperanza matemática de la matriz cero O). Esto nos deja únicamente al lado derecho de la igualdad en el cual podemos aplicar el hecho de que la esperanza matemática de la suma de dos términos matriciales es igual a la suma de las esperanzas matemáticas de cada uno de los términos matriciales:
para poder así escribir lo siguiente:
Si los valores de las tres componentes del momento angular L1, L2 y L3 son iguales a cero, entonces las esperanzas matemáticas <L1²>, <L2²> y <L3²> también serán iguales a cero. Tomando en cuenta que la esperanza matemática de la matriz identidad I es igual a la unidad independientemente del tamaño que tenga esta matriz, esto nos deja entonces con:
Ignorando el factor numérico de 3/2, lo que tenemos en el lado derecho nos debe resultar familiar. Es precisamente la expresión del radio de la primera órbita del electrón para el átomo de hidrógeno en el modelo atómico planetario de Bohr. Si representamos esto último como a0, entonces la esperanza matemática para este radio atómico de acuerdo con la Mecánica Matricial de Heisenberg será igual a tres medios el radio de Bohr:
¿Cuál es la razón de la diferencia?
La explicación estriba en el hecho de que el valor del radio para la primera órbita en el modelo atómico planetario de Bohr es un valor numérico exacto, mientras que <R> es una esperanza matemática, un promedio que nos resulta de la media estadística de muchos valores posibles. Además es un hecho muy familiar para quienes han tomado un curso introductorio de Estadística que en un diagrama del tipo histograma, el valor máximo de la curva de distribución de probabilidades (valor que muchos toman como el valor más probable) es generalmente inferior al valor promedio que se encuentra a la derecha del valor tope. La Mecánica Ondulatoria que será estudiada posteriormente nos proporciona una manera de obtener tal distribución de probabilidades para la primera órbita del átomo de hidrógeno, cuya gráfica nos confirma esta aserción puesta aquí:
PROBLEMA: Si se define una matriz X en función de las matrices posición y momentum de la siguiente manera:
demuéstrese entonces que:
Explícitamente, los productos matriciales que tenemos que efectuar son los siguientes:
La resolución de este problema procede directamente a partir de las multiplicaciones matriciales que hay que llevar a cabo y que, recurriendo al hecho de que las matrices Q1, Q2, y Q3 conmutan entre sí del mismo modo como P1, P2, y P3, nos producen lo siguiente (los términos puestos en color rojo son términos que se van cancelando mutuamente en pares):
A continuación tenemos las simplificaciones que fueron utilizadas arriba para llevar a cabo la cancelación mutua en pares recurriendo al hecho de que las matrices Q1, Q2, y Q3 conmutan entre sí del mismo modo como lo hacen P1, P2, y P3:
Entonces el producto matricial múltiple con el que habíamos empezado se reduce a:
Aquí podemos llevar a cabo unas factorizaciones que nos permitirán una simplificación posterior:
Con esto podemos recurrir a la relación de Born:
[Q, P] = QP - PQ = iħI
PQ - QP = - iħI
PQ = QP - iħI
PQ - QP = - iħI
PQ = QP - iħI
con lo cual tenemos:
Entonces el producto matricial se puede seguir simplificando de la siguiente manera:
Aquí podemos llevar a cabo el siguiente agrupamiento:
Para continuar simplificando llegando al resultado deseado, tenemos por otro lado que:
Con estas igualdades la relación se convierte entonces en:
PROBLEMA: Dadas las siguientes relaciones como ciertas:
y usando como punto de partida el problema anterior así como la definición dada previamente para la matriz X, tomando asimismo en cuenta el hecho de que la matriz radial inversa R-1 conmuta con las matrices de posición Q1, Q2, y Q3, demuéstrese la siguiente relación:
Explícitamente, los productos matriciales que tenemos que efectuar son los siguientes:
Para abreviar, trabajaremos exclusivamente sobre los términos conteniendo Q1 y P1, haciendo extensivo lo que obtengamos sobre los términos conteniendo Q2 y P2 así como Q3 y P3 en base a la simetría del problema, lo cual viene siendo del producto matricial múltiple:
Usaremos ahora una de las relaciones dadas arriba en el encabezado del problema:
Reacomodando y usando el hecho de que Q1 conmuta con R-1:
Trabajando sobre la última expresión, vamos teniendo:
Puesto que para cualquier matriz R que sea invertible:
y puesto que R-1 conmuta con Q1, entonces la expresión que hemos estado reduciendo se reduce aún más a:
Haciendo extensible este resultado parcial anterior a las otras coordenadas (2 y 3) con un simple cambio de sub-índices, la expresión inicial del enunciado de este problema se va volviendo, sucesivamente:
PROBLEMA: Usando como punto de partida los problemas anteriores, demuéstrese que para el operador matricial Hamiltoniano de energía H dado arriba para el átomo de hidrógeno se cumple la siguiente relación:
Explícitamente, los productos matriciales que tenemos que efectuar son los siguientes:
Por reemplazo directo del operador Hamiltoniano H en la expresión que va al lado izquierdo de la igualdad, se tiene lo siguiente:
Usando los problemas resueltos con anterioridad, la simplificación de esto último que tenemos arriba es inmediata y obvia:
Viendo el enunciado de este problema, aquí se puede agregar que las matrices de la posición Q1, Q2, y Q3 así como las matrices del momentum P1, P2, y P3 no conmutan con la matriz del operador de energía Hamiltoniano H porque no pueden ser medidas con precisión ilimitada cuando la energía del sistema tiene un valor bien definido.
Ahora bien, habíamos visto al tratar “El principio de incertidumbre” que si las matrices A, B y C representan cantidades reales, y que si:
AB - BA = iC
entonces el principio de incertidumbre implicaba que la esperanza matemática <C> de la matriz C tenía que ser igual a cero para cualquier estado en el cual la cantidad representada por la matriz A o la matriz B tuviera un valor bien definido (un número). Si consideramos A = X y B = H en esta última relación de modo tal que se tenga:
XH - HX= iC
y si suponemos además que la matriz Hamiltoniana H representa un valor bien definido de energía que llamaremos E, entonces la esperanza matemática del lado derecho de la igualdad, para el problema que estamos manejando aquí, tendrá que ser igual a cero. En pocas palabras:
Puesto que la esperanza matemática de la suma de dos matrices es igual a la suma de las esperanzas matemáticas de cada una de dichas matrices:
tenemos entonces la siguiente relación (sacando además hacia afuera la masa y dividiendo ambos términos entre 2):
Este último resultado es sumamente interesante, si reconocemos lo que tenemos del lado izquierdo de la igualdad como la energía cinética de la partícula. Esencialmente, nos dice que la energía cinética de la partícula es igual a la mitad de la magnitud de la energía potencial. Puesto que al tomarse las esperanzas matemáticas lo que tenemos no son ya matrices sino números (promedios), en realidad lo que nos dice este resultado es que, en promedio, la energía cinética de la partícula es igual a la mitad de la magnitud de la energía potencial de la misma. Un resultado similar obtuvimos al llevar a cabo el análisis del átomo de hidrógeno con el modelo atómico planetario de Bohr, excepto que allí no estábamos hablando de promedios matemáticos sino de valores fijos únicos.
Si substituímos lo que hemos obtenido en la expresión matricial para el Hamiltoniano H tomando esperanzas matemáticas, e identificando a la esperanza matemática <H> del Hamiltoniano con un valor bien definido de energía E (un número), tenemos entonces lo siguiente:
Esta es la energía total para el átomo de hidrógeno. Compárese este resultado con el resultado intermedio utilizado por Bohr:
E = - Ze²/2r
Esto no nos manifiesta cuantización alguna para los niveles de energía del átomo de hidrógeno. La cuantización surge de modo casi inevitable cuando metemos dentro del análisis la ecuación matricial de Born, del mismo modo en el que surge también en el modelo atómico planetario de Bohr cuando se utiliza la condición de cuantización del momento angular L = nħ.