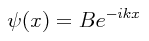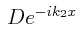Existen casos en los cuales esperamos que el comportamiento de las partículas como ondas de materia sea exactamente el mismo sin importar la naturaleza ondulatoria de las partículas. Un caso tal lo sería el de una partícula libre que “choca” elásticamente (sin transferencia de energía) en forma directa con una barrera de potencial infinitamente grande (o, más realísticamente, con una barrera de potencial cuya altura V0 es substancialmente mayor que la energía E de la partícula). En este caso, la onda de materia será reflejada en dirección opuesta al igual que como ocurriría con una partícula sólida que choca elásticamente con una pared. Sin embargo, si la barrera de potencial no es mucho muy grande en comparación con la energía de la partícula, y si además se trata de una barrera de potencial de anchura finita, debemos considerar la posibilidad de que por tratarse de una onda parte de la onda será reflejada y parte de la onda podrá atravesar la barrera de potencial. Estas dos situaciones se ilustran en las siguientes figuras:
Otro caso análogo es aquél conocido como el potencial escalón en el cual la barrera de potencial aunque no es infinitamente grande (en su altura vertical) posee una anchura (horizontal) que puede tomarse como infinita, en cuyo caso todo dependerá del hecho de que la energía de la onda de materia incidente sea menor que la altura de la barrera de potencial:
o mayor que la altura de la barrera de potencial:
En estas últimas dos situaciones, si se tratase de partículas sólidas entonces clásicamente la partícula con una energía E siempre será rebotada en dirección contraria cuando la barrera de potencial V0 sea mayor que la energía de la partícula, y siempre pasará íntegra por la barrera de potencial cuando la barrera de potencial sea menor que la energía de la partícula. Pero tratándose de ondas de materia, esto deja de ser cierto, sobre todo cuando recordamos que cuando un rayo de luz al pasar cerca de esquinas agudas manifiesta el fenómeno conocido como la difracción de la luz.
Antes de entrar a fondo en la resolución de problemas de transmisión y reflexión de partículas, consideraremos primero el siguiente caso sencillo de una partícula que pasa de una región de mayor potencial a una región de menor potencial:
Al hablar de una partícula, en realidad estamos hablando de una partícula típica que forma parte de un número sumamente grande de partículas que viajan junto a ella, de forma tal que los resultados obtenidos a continuación serán válidos no para una sola partícula aislada en lo particular sino para una cantidad enorme de partículas cuyo comportamiento promediado estadísticamente se acerca a lo que predice la Mecánica Cuántica.
Para guiarnos en lo que podemos esperar cuando una partícula pasa de una región de mayor potencial a una región de menor potencial podemos repasar lo que sucede cuando la luz, que viaja como una onda electromagnética, pasa de un medio de menor densidad a un medio de mayor densidad. La luz no sólo pierde velocidad, sino que su longitud de onda cambia. Esto es precisamente lo que dá lugar al fenómeno que conocemos como refracción cuando un rayo de luz pasa del aire al agua a cierto ángulo de la normal N:
El cambio en la longitud de onda así como el fenómeno de la refracción de la luz desde el aspecto ondulatorio se vuelven más claros cuando echando recurso del principio de construcción de Huygens-Fresnel dibujamos el frente de onda que pasa de un medio a otro:
Es importante notar que aunque el frente de onda pase perpendicularmente de un medio a otro (o de una región a otra con distintos potenciales) sin formar un ángulo con la vertical, el cambio en longitud de onda se dará de cualquier forma. Al viajar el frente de onda formando cierto ángulo con respecto a la vertical el efecto refractario manifiestará la naturaleza ondulatoria del frente de onda a través de los ángulos distintos formados por el “rayo de luz” en cada medio. Del mismo modo, podemos anticipar que la longitud de onda de una onda de materia cambiará al atravesar la partícula la interfaz que divide dos regiones distintas.
En el ejemplo en el que estamos trabajando, puesto que en la región # 1 la energía E de la partícula será igual a la suma de su energía cinética y de la energía potencial:
la velocidad de la partícula en la región # 1 estará dada entonces por:
Para esta velocidad, el momentum de la partícula viene siendo:
Por otro lado, para la onda de materia, tenemos la relación de De Broglie p.=.h/λ. Entonces la longitud de onda de la partícula en la región # 1 será:
Asimismo, la longitud de onda de la partícula en la región # 2 será:
Puesto que V1>V2, la longitud de onda λ2 en la región # 2 será menor que la longitud de onda λ1 en la región # 1, lo cual significa que tratándose de un fotón su energía aumentará al pasar de la región # 1 a la región # 2.
Podemos definir de la manera usual un índice de refracción de un medio relativo al otro mediante el cociente entre las dos longitudes de onda:
Una vez que hemos definido un índice de refracción, podemos echar mano de la conocida ley de Snell, que está basada en óptica ondulatoria clásica, para calcular la relación entre los ángulos de incidencia θ1 y refracción θ2:
Puesto que estamos considerando en todo esto un sistema compuesto no por una sola partícula sub-microscópica sino por muchas partículas, podemos considerarlo como un sistema a gran escala para el cual las leyes Newtonianas clásicas siguen siendo válidas. Cotejaremos ahora esta relación con la que se obtiene en base a la mecánica Newtoniana clásica, partiendo del supuesto de que la interfaz entre las regiones # 1 y # 2 es tal que ésta aplica una fuerza a las partículas conforme pasan de una región a otra, la cual actúa en una dirección perpendicular (normal) a la interfaz. Esto implica que conforme una partícula pasa de una región a otra, el componente del momentum lineal de la partícula que es paralelo a la superficie de la interfaz permanecerá invariable. Esta consistencia de la componente tangencial del momentum lineal de la partícula es lo que utilizamos para calcular la relación que hay entre θ1 y θ2 de acuerdo a la mecánica clásica. Expresamos el hecho de que las componentes tangenciales del momentum en ambas regiones se mantienen constantes con la siguiente relación:
p1 sen(θ1) = p2 sen(θ2)
A partir de esto, obtenemos nuevamente los resultados que ya obtuvimos arriba aplicando no la mecánica clásica sino los métodos de la óptica ondulatoria. Esto establece, para este problema en particular, la equivalencia que hay entre la óptica ondulatoria clásica y la mecánica clásica Newtoniana, con la novedad de que estamos extendiendo el resultado a ondas de materia.
La solución de problemas de transmisión y reflexión de partículas consiste esencialmente en la búsqueda de una función de onda ψ(x) tal que la función de onda sea una función continua al pasar de una región a otra, esto es que en la interfaz entre dos regiones distintas:
o sea:
ψ1(x) = ψ2(x)
Obviamente, no basta con que la función de onda sea una función continua al pasar de una región a otra. También es necesario que en el punto de encuentro, la función de onda de una región tenga la misma pendiente que la función de onda de la otra región, o sea:
Puesto en terminología un poco más formal, las soluciones a la ecuación de Schrödinger deben ser continuas y continuamente diferenciables.
Al empezar en el estudio de la ecuación de Schrödinger, habíamos visto que si consideramos una partícula libre viajera de modo tal que de antemano, a costa de dar por incierta la posición de la partícula demos por conocido con gran precisión el momentum de la partícula (principio de incertidumbre de Heisenberg), lo cual nos permite utilizar la relación de De Broglie para fijarle a la partícula una longitud de onda λ, entonces la función de onda que nos permite describir el movimiento unidimensional de tal partícula viajera cuando se desplaza a la derecha será la siguiente;
Habíamos visto también que una función de onda que describe a una partícula viajera cuando se desplaza hacia la izquierda está dada por la siguiente relación:
Sin pérdida alguna de generalidad, podemos tomar la ecuación de onda de Schrödinger independiente del tiempo y tomar lo siguiente como la función de onda de una partícula que se dirige hacia la derecha:
del mismo modo que podemos tomar lo siguiente como la función de onda de una partícula que se dirige hacia la izquierda:
Podemos, si así lo deseamos, calcular la constante de normalización para una partícula libre viajera. Sin embargo, en la resolución de problemas de transmisión y reflexión de partículas, esto rara vez es necesario en virtud de que las relaciones que estaremos buscando involucrarán fracciones matemáticas de estas constantes de normalización que a su vez nos darán la probabilidad de transmisión y reflexión de una partícula.
PROBLEMA: Encuéntrense los coeficientes de transmisión y reflexión de partículas para un potencial escalón especificado de la siguiente manera:
en una situación en la que la energía de las partículas que están incidiendo desde la izquierda sobre el potencial escalón es mayor que la energía del potencial escalón, o sea E>V0.
En este caso, también tenemos dos regiones que deben ser tomadas en consideración:
La colocación más apropiada de las coordenadas de la energía potencial V(x) en función de la coordenada horizontal de acuerdo al planteamiento del problema es la siguiente:
En este problema, el resultado clásico es sencillo. Para x<0 la velocidad de la partícula sólida es:
En x = 0 la partícula recibe una fuerza impulsiva que cambia su velocidad a:
para x>0. La partícula nunca es regresada hacia atrás por esta fuerza impulsiva siempre y cuando V0 sea menor que la energía de la E partícula. La situación cambia dramáticamente si en vez de una partícula sólida consideramos una onda de materia que incide sobre el potencial escalón desde la izquierda. En tal caso, de acuerdo con la relación de De Broglie, el momentum de la onda de materia en cada región en función de su longitud de onda λ tendrá un valor diferente dado por:
Esto significa que la longitud de onda λ de la onda de materia cambiará abruptamente de λ1 a λ2 de acuerdo con:
En este caso, si consideramos tanto a E como a V0 ambos positivos, la longitud de onda de la onda de materia aumentará al pasar la partícula de la región # 1 a la región # 2.
Sabemos de la mecánica ondulatoria clásica que cuando la longitud de onda cambia bruscamente en un tramo pequeño de longitud (comparado en distancia con la longitud de onda λ) parte de la onda es transmitida y parte de la onda es reflejada. Entonces, por sus propiedades ondulatorias, parte de la onda será transmitida y parte de la onda será reflejada, aunque en la interpretación estadística moderna dada a la función de onda esto significa que de una cantidad grande de partículas que inciden sobre el potencial escalón una parte de dichas partículas será transmitida y la otra parte será reflejada; y de acuerdo con el principio de conservación de partículas el total de partículas reflejadas sumado al total de partículas transmitidas será igual al total de partículas que inciden sobre el potencial escalón.
En la región # 1 en donde el potencial V(x) es igual a cero, la ecuación de Schrödinger estará dada por:
o bien:
La solución matemática general para este tipo de ecuación diferencial tiene la forma:
El primer término corresponde a una partícula moviéndose hacia la derecha que posee un valor preciso de momentum igual a p1.=.ħk1. Para poder describir una onda de materia a la cual se le pueda asignar alguna localización espacial, así sea con algo de incertidumbre Δx = σx, normalmente construiríamos un paquete de onda conteniendo cierto rango de valores del número de onda k. Sin embargo, en la región # 1 sólo nos es necesario localizar a la partícula en el rango -∞<x<0 para poder encontrar la probabilidad de transmisión o reflexión en x.=.0. Por lo tanto, el rango de valores de k puede ser muy estrecho, y podemos utilizar la función de onda:
para representar una partícula que incide desde la izquierda sobre el potencial escalón. Igualmente, la función:
es una onda moviéndose hacia la izquierda en la región #1 que interpretaremos como la onda reflejada.
Para la región # 2 en donde el potencial V(x) es igual a V0, la ecuación de Schrödinger estará dada por:
La solución matemática general para este tipo de ecuación diferencial tiene la forma:
La función:
describe una partícula-onda moviéndose hacia la derecha en la región # 2, mientras que la función:
describe una partícula-onda moviéndose hacia la izquierda también en la región # 2.
Puesto que, por hipótesis, todas las partículas están incidiendo sobre el potencial escalón desde la izquierda en la región # 1, no hay entonces fuentes de partículas en la región # 2 moviéndose hacia la izquierda, lo cual implica que debemos escoger D.=.0 para este problema. En pocas palabras:
Puesto que la función de onda y su pendiente deben ser continuas en el punto de unión de las regiones # 1 y # 2, tenemos entonces que las siguientes condiciones se deben cumplir al pie de la letra:
Usando las soluciones generales dadas arriba para ambas regiones, debemos tener entonces lo siguiente:
De este par de ecuaciones simultáneas, despejando para B en función de A, tenemos entonces:
Del mismo modo, despejando para C en función de A tenemos:
A estas alturas debe resultar más que obvio que las condiciones de frontera no pueden ser satisfechas sin que haya una onda reflejada en la región # 1; esto es, la solución B.=.0 no es posible.
Ahora bien, recordando que:
así como la fórmula de Euler:
eiθ = cos(θ) + i sen(θ)
se tiene:
|eiθ|2 = 1
podemos interpretar a |A|2 como la densidad de probabilidad de la partícula que incide desde la izquierda sobre el potencial escalón. De modo semejante, podemos interpretar a |B|2 como la densidad de probabilidad de la partícula reflejada y a |C|2 como la densidad de probabilidad de la partícula transmitida. Puesto que estamos utilizando funciones de onda no localizadas, no podemos normalizarlas, aunque esto no representa problema alguno porque lo que nos interesa obtener a fin de cuentas son las razones:
|B|2/|A|2 y |C|2/|A|2
las que nos definen la probabilidad relativa R de que una partícula sea reflejada y la probabilidad relativa T de que una partícula sea transmitida.
Un detalle muy importante en este tipo de problemas es que, para un potencial como el potencial escalón que no regresa a un valor de cero a la derecha de la barrera, el coeficiente de transmisión no es simplemente:
|C|2/|A|2
en donde A es la amplitud incidente y C es la amplitud transmitida, en virtud de que la onda transmitida viaja a una velocidad diferente. Pensando en términos de N partículas incidiendo desde la izquierda, la densidad numérica N|A|2 multiplicada por la velocidad v1 de las partículas nos dá la densidad de la corriente incidente de partículas N|A|2v1. De modo semejante, N|B|2v1 es la densidad de la corriente reflejada de partículas, y N|C|2v2 es la densidad de la corriente transmitida de partículas. Las velocidades respectivas en cada región está dadas por:
Si dividimos entre N, podemos igualmente tomar estas corrientes de probabilidad como corrientes de probabilidad para una sola partícula.
Si definimos el coeficiente de transmisión T como el cociente de la densidad de la corriente transmitida entre la densidad de la corriente incidente, tenemos entonces:
De las definiciones previas dadas para k1 y k2, tenemos que la primera fracción de esta expresión es igual a lo siguiente:
Por otro lado, la segunda fracción será igual a:
Entonces el “factor de corrección” para el coeficiente de transmisión quedará incorporado de la siguiente manera:
Poniendo el coeficiente de transmisión T en función de las energías E y V0, es así como llegamos a lo siguiente:
Con un ligero reacomodo, obtenemos de este modo nuestra relación final para el coeficiente de transmisión T en el potencial escalón para el caso en el cual E>V0:
Para E.».V0:, el coeficiente de transmisión T se reduce a:
En pocas palabras, tenemos una transmisión casi total de todas las partículas. Esto nos lo confirma visualmente la siguiente gráfica que nos muestra la forma en la cual varía el coeficiente de transmisión T conforme varía la energía E de la partícula (en múltiplos de V0) a la vez que se mantiene fijo el nivel del potencial V0:
De la gráfica resulta claro que cuando E<V0 no hay transmisión de partículas y todas las partículas son reflejadas hacia atrás (hacia la izquierda). Conforme E aumenta ligeramente por encima de V0, el coeficiente de transmisión de las partículas aumenta rápidamente acercándose a la unidad con casi todas las partículas pasando de la región # 1 a la región # 2.
Por otra parte, si definimos el coeficiente de reflexión R como el cociente de la densidad de la corriente reflejada entre la densidad de la corriente incidente, tenemos entonces:
Obsérvese que en este caso no es necesario utilizar un “factor de corrección” en virtud de que en la región # 1 tanto la partícula incidente como la partícula reflejada tienen la misma velocidad.
Poniendo el coeficiente de reflexión R en función de las energías E y V0, es así como llegamos a la expresión final para el coeficiente de reflexión para un potencial escalón:
Puesto que no tenemos una fuente de partículas en x.=.0, esperamos que:
T + R = 1
Esto es, cada partícula que llega a x.=.0 será transmitida o reflejada. La probabilidad de transmisión de una partícula sumada a la probabilidad de reflexión debe ser igual a la unidad. Este hecho lo podemos utilizar para verificar la integridad de los resultados que acabamos de obtener.
PROBLEMA: Demuéstrese que para el problema anterior en el que la energía de las partículas que están incidiendo desde la izquierda sobre una barrera de potencial escalón es mayor que la energía potencial de la barrera, o sea E>V0, la suma de los coeficientes de transmisión T y reflexión R es igual a la unidad.
La resolución de este problema es directa involucrando únicamente unos cuantos pasos de álgebra:
La resolución del problema que acaba de ser estudiado procede de manera similar para el caso en el que la energía E de la partícula es menor que la energía potencial V0 de la barrera.
PROBLEMA: Encuéntrense los coeficientes de transmisión y reflexión de partículas para un potencial escalón especificado de la siguiente manera:
en una situación en la que la energía de las partículas que están incidiendo desde la izquierda sobre el potencial escalón es menor que la energía del potencial escalón, o sea E<V0.
En este caso, tenemos las siguientes dos regiones que deben ser tomadas en consideración:
La colocación más apropiada de las coordenadas de la energía potencial V(x) en función de la coordenada horizontal de acuerdo al planteamiento del problema es la siguiente:
La ecuación de onda de Schrödinger así como la solución matemática de la misma para la región # 1 es la misma que la que ya vimos con anterioridad:
Sin embargo, para la región # 2, la ecuación de onda de Schrödinger nos arroja una solución matemática general de la misma que será diferente, la cual viene siendo (obsérvense en detalle los exponentes):
Debemos asignarle al coeficiente D un valor igual a cero, ya que de lo contrario la función de onda tomará un valor infinitamente grande conforme x→∞.
Nuevamente, recurrimos a las condiciones de frontera para poder “pegar” en la interfaz entre las regiones # 1 y # 2 las funciones de onda que corresponden a cada región:
De las condiciones de frontera obtenemos las siguientes dos ecuaciones:
Aquí es donde nos topamos con un problema serio, ya que no nos resulta fácil encontrar el coeficiente de transmisión T en virtud de que la energía E de la partícula para x>0 es negativa, lo cual correspondería a una velocidad imaginaria. Podemos sin embargo determinar el coeficiente de reflexión. Eliminando a C de las ecuaciones anteriores, obtenemos lo siguiente:
Tenemos entonces que:
Por lo tanto, el coeficiente de reflexión R debe ser:
Esto equivale a una reflexión total de las partículas cuando su energía no es suficiente para poder superar la altura V0 del potencial escalón. Este resultado es el mismo que el obtenido clásicamente. El coeficiente de transmisión debe ser entonces igual a cero:
T = 1 - R
T = 0
T = 0
Sin excepción, todos los problemas de transmisión y reflexión de partículas cuando un haz de partículas se topa con una barrera de potencial o con una caída de potencial requieren para su solución la igualación de las condiciones de frontera en la barrera desde la cual se pasa de una región de cierto potencial a otra región de potencial distinto, o sea la continuidad de la función de onda ψ(x) en el punto de transición de una región a otra, y la continuidad de las derivadas dψ/dx en la parte limítrofe en la cual la función de onda ψ(x) pasa de una región a otra.
PROBLEMA: Una partícula de masa grande resbalando sin fricción alguna sobre un piso a velocidad constante se aproxima a una orilla desde la cual cae hacia un nivel inferior en el cual el potencial está a un nivel V0 debajo del nivel original. Encuéntrese la probabilidad de que la partícula sea “reflejada” hacia atrás si la energía inicial E de la partícula es igual a la tercera parte de la profundidad del pozo de potencial.
Podemos imaginar con un exceso de imaginación algo como lo siguiente (no muy realista, pero sí fácilmente memorizable):
En este problema se tienen dos regiones distintas. Situando el origen x.=.0 del sistema de coordenadas en la orilla del escalón, la función de onda ψ(x) tanto en la región situada a la izquierda de la orilla del escalón como a la derecha de la orilla se pueden especificar en cada región de la siguiente manera:
en donde:
La primera condición de continuidad nos pide que en x.=.0 las funciones de onda de ambas regiones tengan el mismo valor:
Por otro lado, la segunda condición de continuidad nos pide que también en x.=.0 las pendientes dψ/dx de las funciones de onda de cada región tengan el mismo valor:
De ambas condiciones se obtiene, por lo tanto:
De este modo, el coeficiente de reflexión R viene siendo:
Entonces la probabilidad de que la megapartícula sea “reflejada hacia atrás” será:
Puede objetarse que la representación pictórica dada arriba usando una pelota de futbol soccer como “partícula” no es una representación realista por el simple hecho de que si la caída de la “megapartícula” hacia abajo ocurre bajo la acción de un potencial gravitacional, no es posible que esto ocurra con un cambio brusco (vertical) del potencial por el simple hecho de que el potencial gravitacional no actúa de esta manera. De hecho, el potencial gravitacional graficado en dos dimensiones tanto en el exterior como en el interior de un cuerpo que sirva como fuente de atracción gravitacional exhibe la siguiente forma de acuerdo a la ley de la gravitación universal de Newton (los puntos de inflexión en la curva bidimensional ocurren justo en la superficie del cuerpo que como fuente de atracción produce el potencial gravitacional):
Tomaremos la objeción como válida. Sin embargo, en lo que respecta al tamaño de la “megapartícula”, pudiera pensarse con cierta ingenuidad al principio que el resultado obtenido sólo puede ser válido para las partículas del mundo sub-microscópico para las cuales aplican los postulados de la Mecánica Cuántica, partículas tales como el electrón o el neutrón. Sin embargo, si repasamos el resultado obtenido arriba para el coeficiente de reflexión R, la masa no aparece en la fórmula. Esto significa que la fórmula es válida no sólo para partículas del tamaño del neutrón o del electrón.sino también para átomos, o inclusive para moléculas formadas por átomos de diversos elementos, o inclusive para macromoléculas. De hecho, y en principio, no hay limitación alguna. Esto puede parecer sorprendente considerando que en una situación así uno de cada nueve carros o aviones (considerados como megapartículas) cruzando una caída de potencial como la que se ha especificado arriba terminaría siendo “rebotado hacia atrás” por efectos puramente mecánico-cuánticos; y del mismo modo para poder “atravesar la barrera” con cierta seguridad probabilista se requerirían en promedio nueve intentos de los cuales uno fracasaría al ser reflejada hacia atrás la megapartícula. Sin embargo, antes de considerar la posibilidad de utilizar un efecto así para romper la barrera del “hiperespacio” (un término propio de la ciencia-ficción), cabe tener presente que no se conocen en la Naturaleza a escala macroscópica cambios tan bruscos de energía potencial que en sí sean discontinuidades matemáticas como las que hemos estado manejando en nuestros problemas de transmisión y reflexión de partículas, y si existen o pueden ser creados de alguna manera nadie ha encontrado hasta ahora la manera de lograrlo.