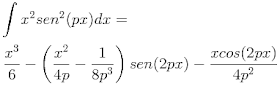Sea la función de onda φ(x) sin normalizar aún. Llámese a la función ya normalizada ψ(x). La normalización requiere la determinación de una constante de normalización A, la cual multiplicando a la función de onda φ(x) la convierte en una función ya normalizada ψ(x). Esto significa que:
ψ(x) = Aφ(x)
La condición de normalización sobre la onda normalizada requiere entonces lo siguiente:
Aunque la constante de normalización A fuese un número complejo o imaginario, al multiplicarla por su conjugado complejo A* se nos produce |A*A| = |A|², o sea un número real. Entonces:
Usando este resultado podemos proceder al cálculo de la expectativa de la variable posición cuando se nos dá una función que no ha sido normalizada:

La relación obtenida es válida no sólo para la esperanza matemática en la posición sino para cualquier tipo de operador que podamos definir dentro de la Mecánica Ondulatoria asociado con la cantidad física que está siendo representada por dicho operador siempre y cuando se trate de una función de onda φ(x) que aún no ha sido normalizada:
obténgase la constante de normalización A, así como las esperanzas matemáticas de la posición y del cuadrado de la posición. Hecho esto, obténgase la incertidumbre en la posición σx.
Podemos separar los exponenciales de la función de onda Ψ en un producto de exponenciales, un exponencial e-λ|x| que representa la parte real, y otro exponencial e-iωt que representa la parte imaginaria, y para mayor claridad usaremos para esta función de onda Ψ el color azul:
El conjugado complejo de esta función de onda, Ψ*, para el cual utilizaremos el color rojo además del asterisco para dar mayor claridad al asunto, es tras el cambio del signo del símbolo i:
La condición de normalización requiere lo siguiente:
Metiendo en esto tanto a la función de onda Ψ como a su conjugado complejo Ψ* tenemos tras la cancelación de los exponentes imaginarios:
Este tipo de integral requiere un manejo cuidadoso por el uso de las barras verticales para designar el valor absoluto.
e-2λ|x| significa que e-2λ|x| = e-2λx si x es positivo.
e-2λ|x| significa que e-2λ|x| = e2λx si x es negativo.
e-2λ|x| significa que e-2λ|x| = e2λx si x es negativo.
Para la evaluación de la integral tenemos entonces:
Con esto tenemos entonces:
La esperanza matemática de la posición se puede evaluar entonces a partir de la definición operacional de la misma:
Para llegar al resultado de cero en la cuarta línea no es necesario llevar a cabo integración alguna en la tercera línea si nos fijamos en la naturaleza del integrando, considerando lo que ocurre cuando sumamos una área positiva a una área negativa cuando las áreas son iguales. Definiendo una función par (“even”) como aquella para la cual f(-x) = f(x) y a una función impar (“odd”) como aquella para la cual f(-x) = -f(x), entonces:
g(x) = x__es una función impar
h(x) = e-2λ|x|__es una función par
h(x) = e-2λ|x|__es una función par
Y puesto que el producto de una función impar g(x) sobre una función par h(x) es igual a una función impar f(x), entonces el integrando es una función impar, y en virtud de que el integrando es una función impar, al evaluar la integral desde -∞ hasta cero obtendremos un resultado del signo opuesto al que obtenemos al evaluar la integral desde cero hasta +∞, y puesto que la integral evaluada desde -∞ hasta +∞ es igual a la suma de la integral evaluada desde -∞ hasta cero sumada a la integral evaluada desde cero hasta +∞, el “área negativa” cancela al “área positiva” dando como resultado cero.
La esperanza matemática del cuadrado de la posición se puede evaluar también a partir de la definición operacional de la misma:
Consultando tablas publicadas de integrales o Internet, encontramos la siguiente integral que más se acomoda a nuestros propósitos:
Usando esta integral y tomando los límites obtenemos lo siguiente para el cuadrado de la posición:
Teniendo la esperanza matemática del cuadrado de la posición, y la esperanza matemática de la posición que podemos elevar al cuadrado, podemos obtener sin problema alguno la incertidumbre en la posición recurriendo a la interpretación estadística de la misma como σx:
PROBLEMA: Para una partícula moviéndose unidimensionalmente dentro de una caja de longitud a, calcular las siguientes expectativas para el n-avo estado estacionario:
Verifíquese asimismo que el principio de incertidumbre se cumple para este problema. ¿Cuál es el estado que más se acerca al límite fijado por el principio de incertidumbre?
La función de onda para una partícula en una caja, suponiendo que el origen de las coordenadas está anclado en el extremo izquierdo de la caja como una barrera infinita de potencial, está dada por:
Empezaremos con la evaluación de la esperanza matemática para la posición de la partícula:
Consultando tablas publicadas de integrales o Internet, encontramos la siguiente integral que más se acomoda a nuestros propósitos (la integral mostrada fue tomada del Handbook of Mathematical Tables and Formulas de Richard Stevens Burington, la cual aparece como la integral # 281):
Llevando a cabo la integración:
Tomando los límites y simplificando:
El resultado obtenido nos dice que la partícula se la pasa tanto tiempo a la derecha de la mitad de la caja como a la izquierda.
La evaluación del cuadrado de la esperanza matemática para la posición de la partícula se lleva a cabo en una forma parecida:
Consultando tablas publicadas de integrales o Internet, encontramos la siguiente integral que más se acomoda a nuestros propósitos (la integral mostrada fue tomada del Handbook of Mathematical Tables and Formulas de Richard Stevens Burington, la cual aparece como la integral # 282):
Usando esta integral y tomando límites:
Simplificando obtenemos finalmente el siguiente resultado:
A continuación se llevará a cabo la evaluación de la esperanza matemática para el momentum de la partícula:
La razón por la cual la esperanza matemática del momentum, o mejor dicho, el momentum promedio, es igual a cero, es porque la partícula pasa tanto tiempo moviéndose hacia un lado de la caja (dirección positiva de la coordenada-x) como moviéndose en sentido contrario (dirección negativa de la coordenada-x), y por lo tanto su momentum, en promedio, es igual a cero.
Llevaremos a cabo ahora la evaluación de la esperanza matemática del cuadrado del momentum de la partícula:
Llevando a cabo la integración y tomando los límites obtenemos el resultado deseado:
Con lo que hemos obtenido podemos llevar a cabo la evaluación de las incertidumbres en la posición σx y en el momentum σp. Para la incertidumbre en la posición tenemos lo siguiente:
mientras que para la incertidumbre en el momentum tenemos lo siguiente:
El producto de las incertidumbres en la posición y en el momentum es entonces:
Para n = 1 el producto de las incertidumbres será igual a:
Obviamente, para n = 1 el producto de las incertidumbres en la posición y en el momentum es ligeramente mayor que ħ/2, cumpliéndose el principio de incertidumbre que nos dice que este producto no puede ser menor que ħ/2. Y para valores del número cuántico mayores que la unidad, el producto de las incertidumbres irá siendo aún mayor en tanto mayor vaya siendo el número cuántico, de modo tal que el principio de incertidumbre se cumple en todos los casos. Obviamente, para este problema el estado que más se acerca al límite fijado por el principio de incertidumbre es n = 1.
PROBLEMA: Dada la siguiente función de onda:
normalícese dicha función determinando el valor de la constante A. Hecho esto, obténgase con la ayuda de la ecuación de Schrödinger el valor que debe tener el potencia V(x) para que se pueda producir esta función de onda. Tras esto, obténganse las esperanzas matemáticas para la posición, el cuadrado de la posición, el momentum y el cuadrado del momentum. Usando los resultados, obténganse la incertidumbre en la posición y en el momentum, y determínese si se cumple el principio de incertidumbre para este problema.
Para la determinación de la constante A el punto de partida es la condición de normalización:
Para la función de onda proporcionada el lado izquierdo se evalúa a:
Tenemos entonces lo siguiente:
Podemos simplificar un poco las cosas cambiando los límites de integración para que esta se lleve a cabo de cero a +∞ en lugar de llevarse a cabo de -∞ hasta +∞, doblando el valor de la integral. Recurriremos también a las tablas de integración para evaluar la integral definida que nos resulta:
A continuación evaluaremos ∂²Ψ/∂x² y ∂Ψ/∂t para substituír dichos valores en la ecuación de Schrödinger, empezando con ∂Ψ/∂x:
Con esto procedemos a evaluar ∂²Ψ/∂x²:
Simplificando un poco:
Ahora evaluamos ∂Ψ/∂t:
Tanto ∂²Ψ/∂x² como ∂Ψ/∂t resultaron ser expresiones independientes del tiempo, lo cual nos permite recurrir a la ecuación de Schrödinger independiente del tiempo:
Substituyendo los resultados obtenidos tenemos entonces:
Simplificando un poco encontramos entonces que el potencial debe ser igual al resultado que se muestra al final:
Evaluamos a continuación la esperanza matemática de la posición:
No es necesario evaluar explícitamente la integral que aparece en la segunda línea, en virtud de que el integrando es una función impar, o sea f(-x) = -f(x), de modo que al evaluar la integral desde -∞ hasta cero obtendremos un resultado del signo opuesto al que obtenemos al evaluar la integral desde cero hasta +∞, y puesto que la integral evaluada desde -∞ hasta +∞ es igual a la suma de la integral evaluada desde -∞ hasta cero sumada a la integral evaluada desde cero hasta +∞, el “área negativa” cancela al “área positiva” dando como resultado cero.
La evaluación de la esperanza matemática del cuadrado de la posición procede de una forma similar:
Obsérvese que se han cambiado los límites de la integral para que se lleve a cabo desde cero hasta +∞, doblándose la magnitud del resultado. Esto lo podemos hacer porque el integrando es una función par, o sea f(-x) = f(x), de modo que al evaluar la integral desde -∞ hasta cero obtendremos el mismo resultado y con el mismo signo que el que obtenemos al evaluar la integral desde cero hasta +∞. La evaluación de la integral definida se simplifica enormemente si recurrimos a una tabla de integrales, en donde podemos encontrar lo siguiente:
Con esto podemos terminar de evaluar la integral deseada:
Para la evaluación de la esperanza matemática del momentum recurrimos a la definición del operador del momentum:
Podemos utilizar aquí ventajosamente varios de los resultados obtenidos previamente en este mismo problema:
De nueva cuenta, no es necesario evaluar explícitamente la integral que aparece en la segunda línea, en virtud de que el integrando es una función impar, o sea f(-x) = -f(x), de modo que al evaluar la integral desde -∞ hasta cero obtendremos un resultado del signo opuesto al que obtenemos al evaluar la integral desde cero hasta +∞, y puesto que la integral evaluada desde -∞ hasta +∞ es igual a la suma de la integral evaluada desde -∞ hasta cero sumada a la integral evaluada desde cero hasta +∞, el “área negativa” cancela al “área positiva” dando como resultado cero.
Para la evaluación de la esperanza matemática del cuadrado del momentum empezamos con el procedimiento usual:
Usando el resultado anterior que habíamos obtenido para ∂²Ψ/∂x² tenemos lo siguiente:
Las integrales definidas ya las habíamos evaluado previamente. Usando los resultados obtenidos con anterioridad esto último se convierte en:
Simplificando aún más y substituyendo el valor obtenido previamente para la constante de normalización tenemos finalmente el resultado que estábamos buscando:
La evaluación de la incertidumbre en la posición, σx, se puede llevar a cabo rápidamente usando los resultados obtenidos previamente para la esperanza matemática de la posición y la esperanza matemática del cuadrado de la posición:
Del mismo modo, la incertidumbre en el momentum estará dada por:
Multiplicando la incertidumbre en la posición por la incertidumbre en el momentum obtenemos el siguiente resultado:
En este caso, para el producto σxσp obtenemos precisamente el valor mínimo predicho por el principio de incertidumbre, o sea ħ/2, cumpliéndose plenamente la relación de igualdad. Esto se debe a que la función de onda Ψ es una función de onda Gaussiana.
Como lo hemos visto en la resolución de estos problemas, en la obtención de las esperanzas matemáticas para todas las cantidades físicas que nos puedan ser de interés toda la información que pueda obtenerse de un sistema sub-microscópico vendrá directamente de la función de onda utilizada para describir dicho sistema. Lo que no pueda obtenerse de la función de onda es algo que no se puede saber. En este contexto, la función de onda desempeña dentro de la Mecánica Cuántica un papel semejante al papel que desempeña el tensor métrico gμν en la Teoría General de la Relatividad al darnos toda la información que podamos obtener acerca de la curvatura del espacio-tiempo y las consecuencias de dicha curvatura en el movimiento de un cuerpo. Siendo la Mecánica Cuántica una ciencia inherentemente probabilista que en ocasiones parece sacada de un salón de juegos de azar, esto puede conducir a quienes piensan que todo puede y debe ser explicable en base a una ley universal de causa y efecto (lo que conocemos como una filosofía determinista) a suponer en la existencia de variables ocultas (hidden variables) que le darían a la Mecánica Cuántica una base clásicamente determinista en lugar de la base probabilista en la cual se mueve para describir el mundo sub-microscópico. Einstein era uno de aquellos que creían firmemente en la existencia de estas variables ocultas. Sin embargo, tales variables ocultas están fuera de las fundamentaciones matemáticas de la Mecánica Cuántica, y esto lo demostró formalmente John von Neumann. Hasta la fecha nadie ha propuesto una teoría convincente que nos pueda dar más información sobre un sistema físico que la información que nos proporciona la función de onda, y aunque científicos como David Bohm y John Bell han tratado de darle la vuelta al asunto, la verdad es que sus propuestas no dán más información sobre un sistema físico que la que podemos extraer con lo que ya sabemos y hemos visto. Si bien es cierto que de un universo probabilista, el universo que corresponde al mundo sub-microscópico de la Mecánica Cuántica, surge el universo determinista en el que todo es causa y efecto permitiendo el funcionamiento de la mecánica Newtoniana clásica (y también la mecánica relativista de Einstein) conforme las incertidumbres se van opacando al entrar en acción la ley de los grandes números, la flecha no parece funcionar en sentido contrario; no parece ser posible que de un universo matemático determinista pueda surgir un universo probabilista. Y aunque ello tal vez se antoje posible para quienes han estudiado superficialmente la teoría del caos en donde algo tan sencillo como el problema planetario de los tres cuerpos termina resultando en algo imposible de describir cuantitativamente a largo plazo (un determinismo que conduce a escenarios imposibles de anticipar matemáticamente), el resultado final no es precisamente lo que podríamos considerar como algo que se sujete a las leyes de la probabilidad y estadística que conocemos y con las que estamos familiarizados.