Al final de la entrada previa se obtuvieron las siguientes relaciones recursivas para el cálculo de los coeficientes Clebsch-Gordan cuyo uso ahora será sistematizado:
No hay que perder de vista el hecho de que estas relaciones lo que hacen esencialmente es “interconectar” coeficientes Clebsch-Gordan, tomando en cuenta que los productos bra-ket destacados en color azul son coeficientes Clebsch-Gordan, algo que puede ser resaltado aún más recurriendo a notación compacta y usando color magenta en lugar de color azul:
Es común encontrar estas relaciones recursivas expresadas en la literatura de una manera un poco diferente. La primera relación recursiva, la que se obtiene con la ayuda del operador de escalera J+, se puede escribir como:
en tanto que la segunda relación recursiva, la que se obtiene con la ayuda del operador de escalera J_, se puede escribir como:
La primera relación recursiva asociada con J+ nos dice que el coeficiente Clebsch-Gordan en el punto (m1,m2) especificado en el lado izquierdo de la ecuación está relacionado con los dos coeficientes en los puntos (m1-1,m2) y (m1,m2-1) especificados en el lado derecho de la ecuación:
mientras que la otra relación recursiva asociada con J_ nos dice que el coeficiente Clebsch-Gordan en el punto (m1,m2) especificado en el lado izquierdo de la ecuación está relacionado con los dos coeficientes en los puntos (m1+1,m2) y (m1,m2+1) especificados en el lado derecho de la ecuación:
En el uso de relaciones de recursividad para el cálculo de los coeficientes Clebsch-Gordan, resulta útil definir un plano conocido como el plano m1m2, en el cual identificamos mediante puntos discretos las combinaciones posibles de valores que los números cuánticos magnéticos m1 y m2 pueden ir tomando en un sistema que consta de dos partículas:
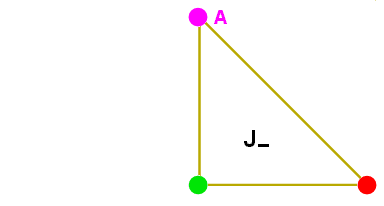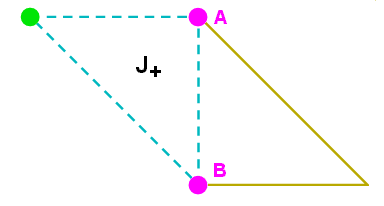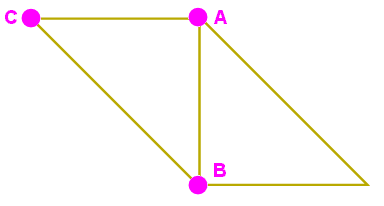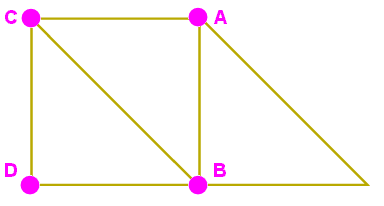
El hecho de que la magnitud máxima del número cuántico m1 no puede exceder el valor absoluto del número cuántico .j1 como tampoco el número cuántico m2 puede exceder el valor absoluto del número cuántico .j2, aunado al hecho de que la suma de m1 y m2 no puede exceder el valor del número cuántico m total impone ciertos límites en la región permisible dentro de la cual se pueden encontrar las combinaciones posibles que pueda haber para m1 y m2, destacada en la siguiente figura de color amarillo claro:
En la evaluación de los coeficientes Clebsch-Gordan el punto A en la figura puede tomarse como un punto de inicio para la aplicación de las relaciones de recursividad. Obviamente, no podemos movernos ni hacia arriba verticalmente ni hacia la derecha del punto A porque caeríamos fuera de la región permisible, podemos movernos sin embargo verticalmente hacia abajo o hacia la izquierda y hacia arriba del punto A siempre y cuando nos mantengamos dentro de la región permisible.
El siguiente gráfico animado nos muestra la manera en la cual empezando a partir de un punto A como el mostrado en la figura de arriba vamos obteniendo coeficientes Clebsch-Gordan en proximidad cercana usando ya sea la relación de recursividad J+ o la relación de recursividad J_ según sea la ubicación del coeficiente Clebsch-Gordan a ser evaluado:
Como lo muestra el gráfico animado, la relación J_ “conecta” al punto A únicamente con el punto inferior designado como B porque el sitio (m1+1,m2) que corresponde a un punto de color rojo queda fuera de la región permisible. Esto nos permite especificar al coeficiente en el punto B a partir del coeficiente en el punto A. Hecho esto, podemos recurrir a la relación J+ para “conectar” mediante un triángulo a los puntos A , B y C, lo cual nos permite especificar al coeficiente en el punto C a partir de los coeficientes en los puntos A y B. Hecho esto, podemos recurrir ahora a la relación J_ para “conectar” mediante un triángulo a los puntos B , C y D, lo cual nos permite especificar al coeficiente en el punto D a partir de los coeficientes en los puntos B y C. Procediendo de este modo, usando ambas relaciones J+ y J_, podemos determinar los coeficientes Clebsch-Gordan en todos los sitios ubicados dentro de la región permisible.
Usaremos las relaciones de recursividad para obtener los coeficientes Clebsch-Gordan de la sub-matriz general Clebsch-Gordan (2×2), que vimos en la entrada anterior. Haciendo:
podemos evaluar el primer elemento de la primera columna de la sub-matriz Clebsch-Gordan de la siguiente manera dejando fuera el término que cae fuera de la región permisible de combinaciones de valores (m1,m2):
Esto se puede simplificar un poco más removiendo los paréntesis dentro de los radicales:
Por lo tanto, haciendo uso de la normalidad del bra-ket en el lado derecho de la igualdad:
Despejando, se obtiene el primer coeficiente Clebsch-Gordan que va en la primera columna de la sub-matriz:
Procediendo de modo semejante, usando las condiciones:
se obtiene el segundo elemento que va en la primera columna de la sub-matriz Clebsch-Gordan:
Habiendo determinado los elementos que van en la primera columna, los elementos de la segunda columna se pueden determinar explotando las relaciones de ortogonalidad que nos dicen que:
y las relaciones de normalización que nos dicen que:
La solución simultánea de estas dos ecuaciones es única hasta cierto factor de fase arbitrario cuyo módulo es igual a la unidad, y el cual es seleccionado de modo tal que el primer elemento que va en la esquina superior derecha es real y positivo (visto desde un punto de vista más prosaico y computacional, la asignación de los signos a los demás elementos matriciales va al parejo con el requerimiento de que la sub-matriz Clebsch-Gordan sea unitaria, o sea igual al conjugado complejo de su transpuesta, lo cual no puede lograrse con una asignación errónea de signos). De este modo, los elementos que van en la segunda columna de la sub-matriz son:
Considérese ahora el importante problema de sumar el momento angular orbital (que designaremos como l) al momento angular de spin de una partícula cuyo spin es igual a 1/2. Para l.=.2, el número cuántico ml que corresponde al momento angular orbital puede tomar los valores ±2, ±1 y 0, y en una situación así el momento angular total .j puede tomar los valores (2)+(1/2).=.5/2 y (2)-(1/2).=.3/2, con el número cuántico magnético m total siendo m.=.mj.=.±5/2, ±3/2 y ±1/2 para .j.=.5/2; y mj.=.±3/2 y ±1/2 para .j.=.3/2. El plano m1m2 (que en este ejemplo podemos designar como plano mlms) tomará el siguiente aspecto en donde resaltan claramente dos renglones que corresponden a los valores permisibles del spin de +1/2 y -1/2:
Este tipo de problema es precisamente el que corresponde al acoplamiento spin-órbita o acoplamiento LS para un electrón que se encuentra ligado a un átomo hidrogenoide, es precisamente el tipo de acoplamiento que dá lugar a la estructura fina en los espectrogramas del hidrógeno atómico. También aquí el cálculo de los coeficientes Clebsch-Gordan se puede llevar a cabo mediante la aplicación de los operadores escalera sobre las funciones de onda. Y si bien para el caso general del acoplamiento de momentos angulares se obtienen expresiones largas y engorrosas, en este caso los principios pueden ser desarrollados de una manera sencilla. Considérese un electrón cuyo momento angular orbital m1 es igual a l y cuyo momento angular de spin m2 es igual a +1/2 (se sobreentiende una multiplicación por una constante física ħ que tomaremos como igual a la unidad). Puesto que:
se tiene entonces:
Usando las relaciones de recursividad obtenidas arriba para el caso de la sub-matriz general Clebsch-Gordan (2×2), los elementos que van en la primera columna de esta sub-matriz para el ejemplo del acoplamiento LS resultan ser:
Evaluando los otros dos elementos que corresponden a la segunda columna, la sub-matriz Clebsch-Gordan (2×2) para el caso del acoplamiento LS viene siendo:
A modo de ejemplo, las sub-matrices que corresponden a los casos l.=.1 y l.=.2 son:
Estas dos sub-matrices se pueden leer también como las tablas Clebsch-Gordan para los valores usados para especificar los acoplamientos 1×(1/2) cuando m.=.1/2 y 2×(1/2) cuando m.=.3/2.
Otra forma un poco distinta de comprender la resolución recursiva del problema del acoplamiento LS es recurriendo al plano m1m2 dado arriba. Como se ve en la figura, los sitios legales dentro de la región permisible están situados en dos renglones, el renglón superior que corresponde a ms.=.+1/2, y el renglón inferior que corresponde a ms.=.-1/2. Trabajando sobre el renglón superior que corresponde a ms.=.+1/2, y recurriendo a la relación de recursividad J_, entonces a la vez que vamos descartando los puntos superiores del triángulo (en color rojo) por estar fuera de la región permisible, podemos ir avanzando hacia la derecha evaluando uno a uno los coeficientes cada vez que ml aumenta en una unidad al ir considerando triángulos J_
nuevos, como lo destaca el siguiente gráfico animado que nos muestra cómo se van descartando en cada evaluación los términos que están fuera de la región permisible (puntos en color rojo):
En este gráfico animado, la evaluación recursiva se va llevando a cabo de izquierda a derecha conforme ml va aumentando en pasos unitarios manteniéndose constante el valor de ms. Al escoger trabajar en el renglón superior de puntos del plano m1m2, nuestro análisis será válido para el caso .j.=.l+(1/2). Puesto que ms no puede exceder +1/2, al usar la relación de recursividad J_ siempre nos mantendremos en el renglón superior de puntos al llevar a cabo la evaluación recursiva. Haciendo .j1.=.l y .j2.=.1/2, si tomamos la relación de recursividad puesta en el encabezado de este trabajo con el signo inferior (con lo cual escogemos a J_.) y si la modificamos un poco haciendo:
tendremos entonces para la primera evaluación llevada a cabo con el triángulo recursivo:
Usando m1.=.m-(1/2) como lo hicimos más arriba, se tiene entonces de acuerdo a la relación recursiva:
Despejando hacia la derecha se tiene entonces:
Simplificando:
Aplicando nuevamente la relación recursiva J_ sobre el ket que está a la derecha de esta igualdad y substituyendo aquí el resultado obtenido, vemos que:
Aplicando nuevamente la relación recursiva J_ sobre el ket que está a la derecha de esta igualdad y substituyendo el resultado obtenido en la relación de arriba (en esto consiste precisamente la recursividad), vemos que:
Obviamente, el procedimiento recursivo puede ser continuado hasta que m1.=.ml alcance su máximo valor que es l. Si hacemos esto y borramos los numeradores y denominadores de los radicales que por razones de claridad no se borraron en el resultado de arriba, llegamos entonces a la siguiente relación en la cual se darán a m, a m1, a m2 y a .j los valores que hacen destacar la naturaleza del problema como un problema propio del acoplamiento LS:
Trataremos ahora de darle un valor numérico específico al producto interno bra-ket que está en el lado derecho de esta igualdad. Considerando la configuración en la cual tanto ml como ms toman sus valores máximos (siendo en este caso l y 1/2 respectivamente), el valor total m (=.ml+ms) debe ser igual a l+(1/2), lo cual es posible únicamente para .j.=.l+(1/2) y no para .j.=.l-(1/2), de modo tal que el siguiente par de kets (uno en la representación m1m2 y el otro en la representación .jm) tienen que ser iguales:
con un factor de fase multiplicativo anexado a uno de los kets. Por convención, tomamos el factor de fase como un número real y positivo. De este modo, se tiene la siguiente relación de normalidad:
Con esto, y regresando a la relación obtenida recursivamente, se tiene entonces definido como nuestro primer coeficiente Clebsh-Gordan:
Así como se llevó a cabo la evaluación de los elementos del primer renglón (el renglón superior) de puntos, del mismo modo se puede llevar a cabo la evaluación de los elementos del segundo renglón (el renglón inferior de puntos) que corresponden a ms.=.-1/2. Hasta aquí, faltan por evaluar los otros tres coeficientes Clebsch-Gordan. Sin embargo, podemos hacer de otra manera lo que falta por hacer ahorrándonos una buena cantidad de trabajo teniendo en mente que la sub-matriz de coeficientes Clebsch-Gordan tiene que ser una matriz unitaria. Recordando que una matriz ortogonal de rotación del mismo tamaño también es una matriz unitaria, entonces haciendo la siguiente asignación:
y recurriendo a un truco matemático que consiste en hacer uso de la matriz ortogonal de rotación:
entonces, haciendo uso de la identidad trigonométrica:
podemos evaluar algebraicamente los otros tres coeficientes Clebsch-Gordan restantes que faltan en la matriz de arriba, todo evaluado a partir del primer elemento puesto en la esquina superior izquierda. Es precisamente el recurrir a este truco matemático para facilitar las cosas algo que muy seguramente condujo a los teóricos a enlazar el estudio de la adición de momentos angulares con las matrices ortogonales de rotación, lo cual terminó metiendo a la Teoría de Grupos en el asunto junto con el tema de las representaciones irreducibles. Con ligeros cambios notacionales, la sub-matriz Clebsch-Gordan (2×2) así obtenida para el caso del acoplamiento LS viene siendo esencialmente la misma cosa que lo obtuvimos arriba, y en realidad en ambos casos se requirió del uso de operadores escalera para poder “conectar” los puntos. Se debe enfatizar que, en la práctica, no se van obteniendo fórmulas cerradas (que pueden ser bastante largas y engorrosas) para después meterles valores específicos, sino que en cada paso recursivo se van asignando valores numéricos, de modo tal que la evaluación recursiva no es algebraica sino más bien numérica porque es lo que más se presta al uso de una computadora.
Habiendo visto el caso general de adición de dos momentos angulares para una misma partícula en donde uno de los momentos angulares es el momento angular orbital l y el otro es el momento angular del spin (1/2), resulta instructivo y provechoso retomar el mismo problema del acoplamiento LS para un valor específico de l llevando a cabo el análisis bajo la notación propia de la Mecánica Ondulatoria. Por razones de simplicidad, haremos ħ.=.1. Si el momento angular orbital l es igual a la unidad, entonces se tiene:
En base a lo que ya hemos visto, los números cuánticos magnéticos pueden tomar los siguientes valores:
Los números cuánticos que corresponden a los valores posibles que puede tomar el momento angular total .j.=.l+s tienen que estar dentro del rango:
Puesto que los números cuánticos para los momentos angulares siempre difieren en una unidad, habrá dos estados diferentes, siendo estos .j.=.1/2 (con s y l paralelos) y .j.=.3/2 (con s y l anti-paralelos) como lo muestra la siguiente figura:
Nos limitaremos aquí al caso .j.=.1/2. De acuerdo a la solución a la ecuación de Schrödinger, las funciones de onda del primer estado excitado del átomo de hidrógeno serán igual al producto de una parte radial y una parte angular, a lo cual incluiremos ahora la función de onda espinor que tiene que ver con el spin del electrón simbolizada como χ:
En virtud de que estamos interesados únicamente en la parte angular, ignoraremos la parte radial de la función de onda total que debe ser:
Para la función de onda del spin escribimos aquí χ1/2,ms en lugar de χ± (como lo habíamos hecho en las entradas “Operadores de rotación”) con la finalidad de unificar la notación. Puesto que queremos construír un estado con un momento angular total igual .j.=.1/2 con l.=.1, m sólo puede tomar dos valores que son +1/2 y -1/2. Para la función de onda de arriba, esto resulta en:
Como m solo puede tomar dos valores, los siguientes dos términos no existen:
y las sumatorias contienen (cada una de ellas) únicamente dos términos que son (se ha suprimido en el lado izquierdo el sub-índice l por ser superfluo para el análisis que se está llevando a cabo):
De las condiciones de normalización que ya se han estado viendo previamente, se obtienen las siguientes condiciones:
Mediante la aplicación de los mismos operadores escalera que se han estado utilizando en las entradas previas, se llega a las siguientes expresiones:
Aplicando J+ en ψ1/2,-1/2 y substituyendo ψ1/2,1/2 se obtiene:
Las funciones de onda son linealmente independientes, lo cual nos permite equiparar los coeficientes en ambos lados de la igualdad, obteniéndose de este modo:
Para mayor simplicidad, podemos reescribir las ecuaciones anteriores en la siguiente forma abreviada:
Repitiendo los pasos anteriores usando J_ en lugar de J+ sobre ψ1/2,1/2 e insertando ψ1/2,-1/2 se obtiene:
Esto junto con las condiciones de normalización permite obtener los valores numéricos de los coeficientes Clebsch-Gordan como:
Substituyendo estas constantes numéricas en las eigenfunciones de onda originales del momento angular total, estas eigenfunciones de onda se leen ahora como:
En caso de repetir desde el principio todo lo anterior para el caso .j.=.3/2, las eigenfunciones de onda que se obtendrán serán las siguientes:
Las funciones de onda completas para estos estados del átomo de hidrógeno (los cuales en notación espectroscópica vienen siendo los estados p1/2 y p3/2) se obtienen incluyendo como factor la parte radial que habíamos omitido. Estos estados son energéticamente degenerados en un potencial Coulómbico puro, pero se separan al haber un acoplamiento LS, y esta es la parte más interesante del fenómeno, ya que no es necesario aplicarle un campo magnético o un campo eléctrico a la muestra bajo análisis para que aparezcan las líneas que corresponden al acoplamiento LS. Aún sin la aplicación de un campo magnético o un campo eléctrico (lo cual dá origen a las líneas espectrales adicionales que aparecen debidas a los efectos Zeeman y Stark), las líneas características de la estructura fina del espectro atómico hacen su aparición por sí solas al introducir en la ecuación de Schrödinger el término del acoplamiento de potencial V(r)L·S que es precisamente el que se encarga de romper la simetría rompiendo con ello la degeneración de los estados y permitiendo observarlos. Repasando los resultados obtenidos arriba, puesto que el estado p1/2 es doblemente degenerado y el estado p3/2 es degenerado por partida cuadruple, entonces si el átomo es irradiado con luz formada por un espectro amplio de frecuencias se obtendrá un cociente de 2:1 para las intensidades de las líneas espectrales observadas en el laboratorio. Por regla general, la función de onda de un momento angular total .j en un potencial Coulómbico esfericamente simétrico puede ser construída acoplando las eigenfunciones del momento angular orbital Yl,m(θ,φ) y el momento angular de spin , produciéndose el acoplamiento χ1/2,ms:
Ya se ha visto previamente que, cuando se han definido valores para dos momentums angulares .j1 y .j2, la matriz general Clebsch-Gordan tiene el siguiente aspecto, sub-dividida en bloques matriciales para los distintos valores que vaya tomando el número cuántico m del momento angular total:
El primer bloque matricial (de color rojo, en el extremo superior izquierdo) contiene un solo coeficiente Clebsch-Gordan:
El segundo bloque matricial (de color magenta, el que está a la derecha y abajo del primer bloque matricial), cuando lo hay, es una matriz 2×2 cuyos cuatro coeficientes Clebsch-Gordan son los siguientes:
Y el tercer bloque matricial, cuando lo hay, (de color azul, el que está a la derecha y abajo del segundo bloque matricial), cuando lo hay, es una matriz 3×3 cuyos nueve coeficientes Clebsch-Gordan son los siguientes:
para distintos valores del número cuántico magnético total m, se tiene primero la situación en la cual:
Para este valor único, la unica posibilidad es:
Esta única posibilidad es la que se traduce en un solo coeficiente Clebsch-Gordan que es el único elemento dentro de una submatriz (1×1), la matriz destacada arriba de color rojo.
Para el siguiente valor de m, se tienen dos situaciones para los valores que puede tomar .j:
Bajo esta circunstancia, hay dos posibilidades distintas para los valores conjuntos que pueden tomar m1 y m2:
Esto es lo que resulta en una submatriz (2×2), la submatriz destacada arriba de color magenta.
Para el siguiente valor de m, se tienen tres situaciones para cada uno de los valores que puede tomar .j:
Bajo esta circunstancia, hay tres posibilidades distintas para los valores conjuntos que pueden tomar m1 y m2:
Esto es lo que resulta en una submatriz (3×3), la submatriz destacada arriba de color azul.
Para el siguiente valor de m, se tienen cuatro situaciones para cada uno de los valores que puede tomar .j:
Bajo esta circunstancia, hay cuatro posibilidades distintas para los valores conjuntos que pueden tomar m1 y m2:
Esto produce una submatriz (3×3).
Del mismo modo, se van produciendo submatrices (4×4), (5×5), (6×6), etc.
Como puede verse, en la gran matriz Clebsch-Gordan el valor de m es lo que distingue cada sub-matriz de la otra, mientras que dentro de cada submatriz el valor de m1 (o lo que es equivalente, el valor de m2, tomando en cuenta que en todo momento la suma de m1 y de m2 debe ser igual a m) es lo que identifica al renglón en el que va puesto cada elemento de la submatriz mientras que el valor de .j es lo que identifica a la columna en la que está situado el elemento submatricial.
Cada una de las submatrices Clebsch-Gordan resulta ser una matriz unitaria. Y si cada submatriz Clebsch-Gordan es una matriz unitaria, la matriz Clebsch-Gordan también lo debe ser.
PROBLEMA: Sabiendo que cada submatriz que forma parte de una matriz Clebsch-Gordan es unitaria, demuéstrese que la matriz general Clebsch-Gordan también lo será.
Sean las submatrices A, B, C, D, etc. los bloques submatriciales con los que se va formando una matriz Clebsch-Gordan que llamaremos CG. Si estas submatrices son unitarias, entonces el producto de cada una de estas submatrices por su transconjugada (no habiendo elementos complejos, la transconjugada se toma simplemente como la transpuesta) deberá ser igual a una matriz identidad cuyo tamaño será igual al tamaño de la submatriz que la produjo:
El producto de la matriz en bloques CG por su transconjugada CG† (esta última construída tomando la transconjugada de cada submatriz), siendo ambas matrices diagonales:
se lleva a cabo de manera trivial multiplicando las submatrices correspondientes, obteniéndose de este modo una matriz en bloques que tomados en conjunto producen una matriz identidad del mismo tamaño que la matriz CG:
Entonces la matriz Clebsch-Gordan debe ser también una matriz unitaria, y puesto que toda la matriz Clebsch-Gordan es unitaria, cada una de las submatrices que van puestas en la diagonal principal también lo deben ser. Esto impone el requerimiento de que las sub-matrices (1×1), tanto la que va puesta en el extremo superior izquierdo como la que va puesta en el extremo inferior derecho, contengan como único elemento a números de módulo 1. Esto último significa que no es absolutamente indispensable que esos números de módulo 1 sean reales, ya que pueden ser imaginarios o complejos, como en el caso del siguiente número a que es un número complejo:
Podemos verificar fácilmente que este es un número cuyo módulo es igual a la unidad:
Sin embargo, si permitimos que a sea un número complejo, esto traerá como consecuencia inmediata que la matriz Clebsch-Gordan contenga elementos (coeficientes Clebsch-Gordan) complejos o imaginarios, lo cual dificulta el análisis. Para evitar esta situación innecesaria, escogemos que a sea un número positivo y real, lo cual equivale a que a sólo pueda ser igual a +1. Este es el verdadero espírituo de la convención de fase Condon-Shortley, el simplificar un poco las cosas.
¿Qué podemos esperar que ocurra en la práctica al llevarse a cabo mediciones del momento angular en un experimento efectuado sobre un sistema combinado de dos partículas? Para responder a esta pregunta, considérese un experimento hipotético gedanken efectuado en un sistema formado con dos partículas cuyo momento angular de spin es igual a 1/2. Considérense dos observadores A y B, el primero de los cuales se encarga de llevar a cabo mediciones sobre los componentes de spin de una de las partículas (S1x, S1y y S1z) mientras que el otro observador B mide los componentes de spin de la otra partícula (S2x, S2y y S2z). Supóngase que el sistema se encuentra inicialmente en un estado en el que el momento angular total combinado S es igual a cero. Nos preguntamos ahora, ¿cuál es la probabilidad de que como resultado de una medición el observador A obtenga s1z.=.+ħ/2 suponiendo que el observador B no efectúa medición alguna? En una situación así, puesto que B no efectúa medición alguna, hay probabilidades iguales de obtener +ħ/2 y -ħ/2. ¿Y qué tal si la medición se lleva a cabo sobre s1x? La respuesta sigue siendo la misma, puesto que no hay una dirección espacial preferida sobre otra. Supóngase ahora que el observador B efectúa una medición sobre la partícula 2 obteniendo con una certeza absoluta el resultado s2z.=.+ħ/2. ¿Qué podemos concluír entonces acerca del resultado que pueda obtener el observador A si éste mide s1z? Puesto que el momento angular total combinado S del sistema es igual a cero, entonces:
y por lo tanto el observador A debe obtener como resultado s1z.=.-ħ/2. Ya que suponemos que el sistema combinado de partículas está en un estado tal que el momento angular total S es igual a cero, para la función de onda que describe a dicho sistema podemos reproducir el resultado obtenido en la entrada “Los coeficientes Clebsch-Gordan I”:
Al llevar a cabo el observador B su medición de s2z obteniendo +ħ/2, éste observador obviamente recoge la segunda parte de la función de onda mostrada arriba:
¿Y qué del caso en el cual el observador B nuevamente efectúa una medición sobre la partícula 2 obteniendo con una certeza absoluta el resultado s2z.=.+ħ/2 pero el observador A mide s1x.en lugar de medir s1z? Puesto que s1x y s1z son observables incompatibles, no es posible predecir el valor que será medido por el observador A, y en el mejor de los casos podrá obtener ya sea +ħ/2 o -ħ/2 con probabilidades iguales para ambos valores.
Al empezar el estudio de los coeficientes Clebsch-Gordan, se había tomado como punto de partida la suma de los momentos angulares de spin de dos partículas diferentes. Pese a su deceptiva sencillez, este problema no es tan trivial como parece. A principios del siglo XX y todavía hasta los años veinte, se creía que las partículas elementales sub-atómicas eran el protón, el neutrón y el electrón, con el fotón actuando como el quantum de energía electromagnética. Este feliz estado de cosas llegó a su fin con el descubrimiento de nuevas partículas que no eran ni protones ni neutrones ni electrones. Eventualmente, se llegó a sospechar que posiblemente algunas de las partículas consideradas como elementales no lo eran del todo, y que estas partículas estaban constituídas por otras partículas aún más elementales que ellas. Fue así como se llegó a postular la existencia de los quarks. El descubrimiento de estas partículas no fue motivado por algún experimento que demostrara en forma directa la existencia de las mismas, sino por consideraciones puramente teóricas basadas en los principios de la simetría. Esto ocurrió justo cuando la simetría se estaba estableciendo firmemente como el nuevo punto de partida de la Mecánica Cuántica.
De acuerdo a la teoría de los quarks, estas partículas poseen un tercio de la carga eléctrica elemental del protón (y consecuentemente, del electrón). Muchos físicos han llevado a cabo búsquedas intensas de quarks, tratando de producir quarks libres en aceleradores de partículas, tratando de encontrarlas en agua salina del mar, minerales, e inclusive rayos cósmicos. C.B.A. McCusher e I. Cairns creyeron haber encontrado en 1969 evidencias de quarks en rayos cósmicos altamente energéticos. Hay también serias dudas sobre el experimento encabezado por William N. Fairbank y sus colaboradores llevado a cabo en 1977, un experimento que es una versión moderna y refinada del experimento de la gota de aceite de Millikan, en el cual supuestamente había detectado cargas eléctricas fraccionales. La conclusión actual es que los quarks libres no existen en la Naturaleza.
En su postulación más rudimentaria, cada quark es portador de un momento angular de spin igual a 1/2. Dos quarks (o mejor dicho, un quark y un antiquark) se enlazan para formar juntos una partícula conocida como el mesón (entre cuyos ejemplos podemos citar el pión y el kaón). Suponiendo dos quarks que están en el estado basal, cada uno de ellos con un spin igual a 1/2, considerando las combinaciones posibles de spin se espera tener dos spins posibles para los mesones, 0 y 1:
Por otro lado, tres quarks se enlazan para formar juntos una partícula conocida como el barión (entre cuyos ejemplos podemos citar precisamente el protón y el neutrón). En base a un modelo tal, suponiendo tres quarks que están en el estado basal, cada uno de ellos con un spin igual a 1/2, considerando las combinaciones posibles de spin se espera tener tres spins posibles para los bariones, 1/2 y 3/2:
Naturalmente, un modelo de este tipo requiere ser refinado y formalizado, pero con lo que hemos visto aquí podemos imaginar un nuevo mundo de posibilidades a explorar.
PROBLEMA: Suponiendo que se tiene un sistema de dos partículas 1 y 2, que el momento angular de spin total para el sistema combinado de partículas es designado como S, y que la proyección del momento angular de spin sobre el eje-z de la primera partícula es designada como S1z, encuéntrese una expresión para la evaluación del siguiente conmutador:
Asimismo, generalícese el resultado obtenido.
En la resolución de este problema, usaremos la misma notación desarrollada en la entrada “Los coeficientes Clebsch-Gordan I” para el análisis de la suma de dos momentos angulares de spin. Usaremos también la siguiente identidad de conmutador:
Esta identidad se puede demostrar de una manera muy sencilla partiendo del lado derecho de la igualdad para llegar a la expresión en el lado izquierdo de la igualdad (respetando en todo momento la anticonmutatividad de los operadores A, B y C):
Usaremos también las siguientes relaciones de conmutación de Born tal y como aplican individualmente para la partícula 1:
Del mismo modo, recurriremos a las relaciones para observables compatibles de acuerdo a las cuales la evaluación del conmutador producirá un resultado igual a cero:
Con lo anterior, la resolución del problema procede de una manera directa:
Lo que aparece en la última línea se asemeja mucho a lo que se obtiene en un producto vectorial “cruz” clásico para un eje-z. Y de hecho, si repetimos el problema para S1x y S1y, los resultados obtenidos así lo confirman. Los resultados pueden resumirse y generalizarse en un “determinante vectorial” de la siguiente manera:
Usando el vector S1.=.(S1x,S1y,S1z), podemos condensar los resultados a una expresión del tipo propio del análisis vectorial clásico aunque se trate de algo que es esencialmente diferente por ser un resultado mecánico-cuántico sin paralelo alguno en la física clásica:
Vista desde un punto de vista más formal, la adición de dos momentums angulares J1 y J2 de cualquier tipo descansa sobre el hecho fundamental de que las relaciones de conmutación de Born para una misma partícula siguen siendo válidas cuando se trata de las observables incompatibles que no pueden ser medidas simultáneamente con un grado ilimitado de precisión (como siempre, el símbolo Levi-Civita εijk fija el signo de acuerdo al orden de permutación cíclica de los sub-índices):
al igual que las relaciones de conmutación de Born para las observables compatibles de una partícula con respecto a la otra que pueden ser medidas simultáneamente sin límite teórico alguno a la precisión de las mediciones:
Estas dos relaciones traen como consecuencia directa las relaciones generales de conmutación para los dos momentums angulares una vez ya acoplados:
Considerada la adición de dos momentos angulares desde la perspectiva de los operadores de rotación, por ejemplo la adición del momento angular de spin al momento angular orbital, la forma correcta de representar el acoplamiento (usando la notación que tomamos prestada de la Teoría de Grupos) es la siguiente:
En su forma más general, designando a los momentums angulares como .j1 y .j2, el acoplamiento queda escrito de la manera siguiente:
Desde el punto de vista de los operadores de rotación para ángulos infinitesimales δφ, ya hemos visto al tratar previamente el tema de los operadores de rotación que las relaciones correspondientes que funcionan muy bien son las siguientes:
Obsérvese cómo para el caso que nos ocupa es necesario especificar en ambas expresiones el mismo eje de rotación n y el mismo ángulo de rotación infinitesimal δφ. Ya hemos visto que haciendo una composición de estos operadores podemos obtener los operadores de rotación para ángulos finitos, los cuales resultan ser operadores exponenciales:
De este modo, el acoplamiento general de dos momentums angulares visto desde la perspectiva de ángulos de rotación finitos queda expresado como:
La adición de los dos momentums angulares que se lleva a cabo resultando en un momento angular total J puede representarse simbólicamente de la siguiente manera:
en donde el 1 es el operador identidad que corresponde al espacio del momento angular de la primera partícula, y el 1 es el operador identidad que corresponde al espacio del momento angular de la segunda partícula. Para minimizar confusiones en la interpretación de la simbología, a veces se escribe lo anterior de la siguiente manera:
Esto se escribe de la siguiente manera (mucho más conocida) para representar la adición de momentums angulares:
aunque en realidad no se trate de una simple suma aritmética.
Si hemos de sintetizar y generalizar de alguna manera lo que hemos visto en esta serie de entradas, podemos decir que hay dos opciones distintas de kets de base para llevar a cabo la suma de momentos angulares, estando basada la primera opción (la representación {m1,m2}) en los eigenkets simultáneos de los operadores J12, J22, J1z y J2z, simbolizados frecuentemente como:
Obviamente los cuatro operadores mecánico-cuánticos para esta primera opción conmutan todos ellos entre sí, dando lugar a las siguientes eigen-ecuaciones:
La segunda opción (la representación {.j,m}) está basada en los eigenkets simultáneos de los operadores J2, J12, J22 y Jz, simbolizados frecuentemente como:
También en este caso los cuatro operadores mecánico-cuánticos de esta segunda opción conmutan todos ellos entre sí, dando lugar a las siguientes eigen-ecuaciones:
Para llevar a cabo la transformación de una base de eigenkets a la otra (de una representación a la otra), recurrimos a la relación de completitud o cerradura que nos permite definir el siguiente operador identidad:
Injertando este operador identidad y reagrupando bras y kets, obtenemos entonces el siguiente resultado:
en el cual los coeficientes de una matriz que conecta ambas bases de eigenkets, la matriz Clebsch-Gordan, aparecen de modo natural. Una propiedad importante de estos coeficientes es que son iguales a cero a menos de que:
Esto se puede demostrar fácilmente de la siguiente manera:
Tomando los tres productos internos bra-ket, aplicando las eigen-ecuaciones dadas arriba y simplificando, se obtiene entonces el resultado a ser demostrado:
Otra propiedad importante es que los coeficientes también serán iguales a cero cuando estén fuera del rango de eigen-valores:
lo cual es obvio cuando se tiene en mente el modelo de la suma vectorial de los momentos angulares J1 y J2 conocido como la regla del triángulo.
Los coeficientes Clebsch-Gordan de la matriz de transformación entre las dos bases de eigenkets forman una matriz unitaria por la forma en la cual fueron especificados con la ayuda del operador identidad usado arriba. Los elementos de esta matriz de transformación, aunque se pueden especificar como reales, complejos o imaginarios, se toman como reales por la convención Condon-Shortley. Una consecuencia directa de esta convención es que los coeficientes usados para ir de la representación la representación {m1,m2}a la representación {.j,m} son los mismos que los coeficientes usados en la transformación inversa para ir de la representación la representación {.j,m} a la representación {m1,m2}. Puesto que una matriz unitaria es también ortogonal, se tiene la siguiente condición de ortogonalidad en una de las representaciones:
mientras que la condición de ortogonalidad en la otra representación viene siendo:
En esta última relación, para el caso especial en el cual:
se obtiene entonces la condición de normalización para la representación {.j,m}:
Para la evaluación de los coeficientes Clebsch-Gordan se recurre a los operadores escalera J+ y J_ aplicados en forma repetitiva (recursiva) que permita ir evaluando coeficientes nuevos a partir de los que van siendo evaluados. Esta táctica es válida para cualquier caso general.
El uso que se le dé a los coeficientes Clebsch-Gordan depende de la situación en particular que esté siendo analizada. A manera de ejemplo, si un átomo de hidrógeno se encuentra en el estado ψn,l,m, entonces como lo hemos visto arriba el momento angular neto del electrón (orbital más spin) podrá ser l+(1/2) ó l-(1/2). Si a esto le agregamos el spin del protón que se encuentra en el núcleo atómico, el número cuántico del momento angular total del átomo podrá ser l+1, l ó l-1, y l puede ser realizado de dos maneras distintas, dependiendo de que el electrón solo se encuentre en la configuración l+(1/2) ó en la configuración l-(1/2). Hay pues varios efectos que se antoja posible observar en el laboratorio, y la importancia relativa entre ellos dependerá de las intensidades relativas que se observen en las líneas espectrales. La disponibilidad de las tablas Clebsch-Gordan permite resolver de manera rápida y expedita problemas tales como: (a) Si una partícula de spin 1 y otra partícula de spin 2 se encuentran en reposo (en el estado fundamental) en una configuración tal que el spin total es igual a 3 y la componente-z de la configuración es igual a 1 (o sea que el eigenvalor de Sz es igual a ħ), ¿cuáles serán los valores que se medirán para la componente-z del momento angular de la partícula de spin 2, y cuál será la probabilidad de obtener cada uno de dichos valores?, o (b) Un electrón con su spin apuntando “hacia abajo” se encuentra en el estado ψ5,1,0 del átomo de hidrógeno. Si se pudiera medir el cuadrado del momento angular total de electrón (no incluyendo al spin del protón), ¿qué valores se podrán obtener, y cuál será la probabilidad de obtener cada uno de dichos valores? Todo este tipo de problemas se pueden resolver brevemente con los principios elementales que se han establecido y consultando tablas de coeficientes Clebsch-Gordan apropiadas a cada caso.
Antes de dejar el tema, se ha de mencionar un símbolo alterno para la representación de los coeficientes Clebsch-Gordan, el símbolo 3-j de Wigner, el cual está relacionado de la siguiente manera con los símbolos que hemos estado usando aquí:
Los coeficientes Clebsch-Gordan volverán a aparecer nuevamente cuando tomemos el tema de los operadores tensoriales. Y las propiedades de los coeficientes Clebsch-Gordan conducen directamente a un teorema importante de la Mecánica Cuántica: el teorema Wigner-Eckart.