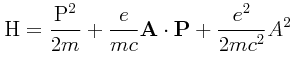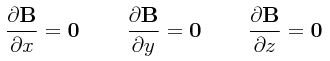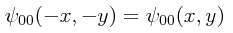Interacción con un campo electro-magnético II

La relación que se obtuvo en la entrada anterior para el Hamiltoniano H es válida dentro de la mecánica clásica. Pero en la Mecánica Cuántica, el Hamiltoniano H pasa a ser un operador al igual que p y A, y por ésta razón usaremos P en lugar de p en la relación cuántica para H, precisamente para resaltar su naturaleza como operador:

Si hubiésemos partido de esta relación para H tomándola como un postulado, quedaría la duda sobre si el operador H es un operador Hermitiano, habido el hecho de que la relación por sí sola no nos dice si los operadores P y A son conmutativos o no, lo cual introduce una ambigüedad. Una ambigüedad de esta naturaleza puede ser eliminada fácilmente haciendo la siguiente modificación:

Si de algo podemos estar absolutamente seguros es que esto último sí es una relación Hermitiana. Sin embargo, no es necesario llegar a estos extremos, porque como parte del procedimiento que aquí nos ocupa se puede demostrar formalmente que los operadores P y A sí son conmutativos (véase más abajo), y podemos retener la fórmula original sin necesidad de tener que hacerla Hermitiana para los operadores P y A.

El Hamiltoniano H obtenido se puede substituír en la ecuación de Schrödinger dependiente del tiempo:

Puesto que trataremos a los campos eléctrico y magnético como entidades aplicadas externamente, los operadores A y Φ en el Hamiltoniano H serán simplemente funciones ordinarias de la posición y el tiempo.

Tomemos pues el Hamiltoniano H obtenido, considerado como un operador mecánico cuántico, y hagamos las siguientes substituciones que suponen una interacción únicamente con un campo magnético en ausencia de un potencial eléctrico y que suponen que la carga q es la que corresponde a la carga negativa de un electrón:

con lo cual se tiene para trabajar:

En función del potencial vectorial A, la intensidad del campo magnético está dada por:

Puesto que estamos considerando un campo magnético B exclusivamente, en ausencia total de un potencial electroestático Φ, la condición de Lorentz:

se reduce a:

Por otra parte, previamente en ésta obra se ha demostrado ya la validez de la siguiente relación:

que en un sistema de coordenadas rectantulares Cartesianas se puede extender en tres dimensiones a lo siguiente:

o bien:

Esto último, junto con la reducción de Lorentz dada arriba en ausencia de un potencial electroestático, nos lleva a la siguiente relación de conmutatividad:

De este modo, expandiendo el Hamiltoniano H, y haciendo uso de ésta relación de conmutatividad, se obtiene lo siguiente:

Antes de continuar, se dará solución a un problema que nos será de utilidad posterior.

PROBLEMA: Tomando la relación B.=.∇×A como válida, y representando un vector radial cualquiera como r, demuéstrese que para un campo magnético uniforme (constante) la siguiente es una relación válida:

Tomaremos la relación a demostrar como una relación válida, y le aplicaremos en ambos lados el operador ∇ en operación de producto cruz (o como dirían los matemáticos, el rotacional en virtud de que una operación así proporciona la manera de saber si un campo vectorial cualquiera exhibe una rotación):

Lo que tenemos del lado derecho es lo que se conoce como un producto vectorial triple que involucra como vector simbólico al operador ∇, lo cual nos obliga a ejercer precaución al momento de aplicar alguna fórmula vectorial para simplificarlo. En vez de sufrir, recurriremos al libro Análisis Vectorial del Profesor Hwei P. Hsu y tomaremos de dicho libro una de las identidades vectoriales que aparecen al final del mismo (el libro proporciona una demostración de la validez de todas las fórmulas e identidades vectoriales que aparecen en el mismo):

Haciendo f.=.B y g.=.r, se tiene entonces:

Por las leyes de Maxwell, ∇·B.=.0, de modo tal que lo que se muestra en color rojo se desvanece. Además, se tiene lo siguiente para el vector radial r:

Entonces (obsérvese el uso del vector cero 0):

Para continuar simplificando trabajando sobre los últimos dos términos de la anterior relación, obtendremos antes dos resultado intermedios. Por un lado:

mientras que por otro lado:

y puesto que, para un campo vectorial magnético B uniforme y constante que no manifiesta ninguna variación en cualesquiera de los tres ejes coordenados (obsérvese nuevamente el uso del vector cero 0):

se tiene entonces que:

De este modo, usando los dos resultados intermedios anteriores:

Así pues, revirtiendo todos los pasos anteriores y partiendo de la relación B.=.∇×A que se supone válida, se obtiene como válida la relación que se quería demostrar:

De este modo, el segundo término del Hamiltoniano H que estamos desarrollando puede ser escrito de la siguiente manera:

En el producto escalar triple el punto y la cruz de pueden intercambiar sin alterar el valor del mismo, lo cual se resume en la siguiente identidad:

De este modo, se tiene:

Aquí podemos reconocer de inmediato a r×P como L, el momento angular que en mecánica cuántica hemos elevado a la categoría de operador:

En lo que toca al tercer término del Hamiltoniano H que estamos desarrollando, podemos hacer uso de la identidad vectorial de Lagrange y así escribir:

Para simplificar las cosas, se acostumbra seleccionar un campo magnético uniforme que apunte en la dirección del eje-z y cuya magnitud sea B. Siendo así, se tiene entonces que:

y se tiene lo siguiente:

con lo cual el Hamiltoniano H se reduce a la expresión que se muestra a continuación:

Puesto que:

el Hamiltoniano H que acabamos de obtener se puede descomponer del modo siguiente:

Es una buena ocasión para rememorar el hecho que el operador del momento angular L_z conmuta con el operator P_z.

PROBLEMA: Demuéstrese que el operador del momento angular L_z conmuta con el operator P_z.

En coordenadas rectangulares Cartesianas, las relaciones para el operador del momento angular L_z y para el operador del momentum P_z están dadas respectivamente por las siguientes expresiones:

La manera de verificar la conmutatividad o no-conmutatividad de cualquier par de operadores en Mecánica Cuántica es recurrir al conmutador, aplicando el conmutador sobre una función de onda “monigote” ψ y desarrollar lo más que se pueda para ver hacia dónde nos conduce el procedimiento:

De éste modo, no queda duda alguna de que el operador del momento angular L_z conmuta con el operador del momentum P_z:

Del mismo modo, se puede demostrar fácilmente que el operador del momento angular L_z conmuta con otros operadores del momentum linear (y obviamente con los cuadrados de las coordenadas de la posición):

Siendo así, se concluye que el operador L_z conmuta con el operador Hamiltoniano H, y por lo tanto ambos operadores conmutan con el operador P_z. En virtud de que los tres operadores H, P_z y L_z conmutan el uno con el otro, debe ser posible escoger funciones de onda que sean simultáneamente eigenfunciones de los tres operadores (téngase presente que aquí el momentum P ya no es simplemente el momentum cinético mv y que la componente-z del momento angular L_z ahora contiene una parte que corresponde al término A del momentum generalizado). Regresando al operador Hamiltoniano H, sabemos ya por la ecuación de onda independiente del tiempo de Schrödinger que tal Hamiltoniano tiene que generar una serie de valores propios eigen al actuar sobre una función de onda ψ general para el sistema:

¿Pero cuáles serán éstos eigenvalores? ¿Cómo podemos determinar la forma de la relación que sea capaz de generar los eigenvalores de energía? Acabamos de ver arriba que el Hamiltoniano puede ser descompuesto en tres partes: una parte representa la energía asociada con el movimiento en las direcciones x y y , y la otra parte representa la energía asociada con el movimiento en la dirección-z (o sea el término que involucra a L_z). La primera parte, puesta entre un par de corchetes grandes, es la parte que ha sido designada mediante el operador H_a:

Ésto nos debe resultar familar.

PROBLEMA: Demuéstrese que el Hamiltoniano H_a dado arriba tiene la misma forma que la que corresponde a la suma de dos osciladores lineares (armónicos simples).

Puesto que estamos considerando al campo magnético B constante y uniforme, hágase:

a sabiendas de que k será una constante porque en su evaluación aparecen puras constantes físicas como la carga eléctrica e de la partícula, la masa m de la partícula y la velocidad de la luz c. Usando ésto en la expresión para el Hamiltoniano y reacomodando términos se obtiene la conclusión buscada:

Esto es simplemente el Hamiltoniano de un oscilador armónico simple en dos dimensiones, y tiene una energía que es la suma de las energías de dos osciladores armónicos lineares.

PROBLEMA: Obténganse la función de onda para un sistema compuesto por dos osciladores armónicos, demostrando asimismo con el resultado obtenido que las funciones de onda para el oscilador armónico simple bidimensional son pares para números cuánticos pares y son impares para números cuánticos impares.

La función general de onda para un oscilador armonico simple unidimensional es (no confundir aquí la notación H usada para representar los polinomios de Hermite con la H usada arriba para representar el operador Hamiltoniano):

En base a ésta relación, las primeras dos funciones de onda tanto para el estado basal (n.=.0) como para el primer estado excitado (n.=.1) del oscilador armónico simple unidimensional son:

La función general de onda para un oscilador armónico bidimensional es igual al producto de las funciones de onda de dos osciladores armónicos simples, uno para cada coordenada en un sistema de coordenadas rectangulares Cartesianas:

La función de onda del oscilador armónico bidimensional será, por lo tanto:

El estado basal (fundamental) del oscilador armónico bidimensional es definido como aquél estado para el cual los dos números cuánticos q y r son ambos iguales a cero, y tal estado será:

Es fácil ver que con un cambio en los signos de ambas coordenadas la función de onda para el estado basal del oscilador armónico bidimensional permanece inalterada. Se concluye entonces que para el estado basal la función de onda es una función de onda par:

Y en lo que corresponde al primer estado excitado, el cual es un estado degenerado, es fácil ver que la función de onda para el primer estado excitado del oscilador armónico bidimensional cambia de signo si ambas coordenadas cambian de signo:

Se concluye entonces que para el primer estado excitado (el cual tiene una degeneración de dos tantos) del oscilador armónico bidimensional la función de onda cambia de signo cuando ambas coordenadas cambian de signo, y exhibe por lo tanto el comportamiento de una función de onda impar.

Inspeccionando el comportamiento general para otros estados superiores, se concluye que la función de onda del oscilador armónico bidimensional cuyo número cuántico definimos como:

n = q + r

es par para números cuánticos pares:

n = 0, 2, 4, 6, 8, ...

y es impar para números cuánticos impares.

n = 1, 3, 5, 7, 9, ...

PROBLEMA: Obténganse los eigenvalores de energía para un sistema compuesto por dos osciladores armónicos.

Ya sabemos qué aspecto tiene el Hamiltoniano para cada oscilador. Aquí el punto relevante son los eigenvalores de energía producidos cuando un oscilador armónico es resuelto con la ecuación de onda independiente del tiempo de Schrödinger. Así tenemos las siguientes dos eigenecuaciones independientes para cada oscilador considerado por separado:

Para un sistema que consta de dos osciladores armónicos, el Hamiltoniano H del sistema será igual a la suma de los Hamiltonianos de cada uno de los dos osciladores armónicos simples, de modo tal que tomados ambos como parte de un solo sistema la ecuación de onda independiente del tiempo de Schrödinger para el sistema tomará la siguiente forma:

El sistema como tal debe estar caracterizado no por los dos números cuánticos independientes q y r sino por un solo número cuántico n formado por la suma de los números cuánticos q y r. De éste modo, la eigenecuación para el sistema de dos osciladores armónicos se puede escribir de la siguiente manera:

Obsérvese que los niveles de energía del sistema son degenerados en virtud del origen de la ecuación para los eigenvalores. Solo para n.=.0 que a su vez implica que q.=.r.=.0 no hay degeneración alguna. Para cualquier otro valor de n, necesariamente hay degeneración. Para n.=.4, por ejemplo, este número cuántico puede ser producido por cualquiera de las combinaciones:

..q..	..r..
4	0
3	1
2	2
1	3
0	4

Tenemos pues los eigenvalores que corresponden a lo que podríamos considerar como el “número cuántico principal” n (que corresponde al oscilador armónico bidimensional) producidos bajo la acción del operador H_a.

Puesto que la relación que conecta a la constante k con la frecuencia angular ω en un oscilador armónico simple es la siguiente:

entonces usando el valor de k que se definió arriba en la solución del antepenúltimo problema la frecuencia angular ω a la que nos estamos refiriendo tiene que ser:

La parte del Hamiltoniano H que corresponde al operador P²_z (o sea H_b) no representa problema alguno:

Ahora enfocaremos nuestra atención la parte del Hamiltoniano que hemos simbolizado como H_c y que nos debe regresar mediante la ecuación independiente del tiempo de Schrödinger aquella energía asociada por la acción del campo magnético con el movimiento en la dirección de la coordenada-z, o sea el término que involucra a L_z, y antes de continuar es importante hacer una pausa para reflexionar sobre la presencia del operador del momento angular L_z en el operador Hamiltoniano H que acabamos de obtener arriba. Estamos familiarizados ya con éste tipo de operador en el tratamiento que se le dió a la solución del problema del átomo de hidrógeno mediante la ecuación de Schrödinger independiente del tiempo con la ayuda del sistema de coordenadas esféricas, en donde el electrón está sujeto a la atracción de un potencial central V(r), lo cual llevó a la solución del problema teniéndose que incluír las funciones de onda angulares conocidas como armónicas esféricas. Pero lo que estamos analizando aquí es el movimiento de una partícula libre que no se encuentra sujeta a ninguna fuerza de atracción central que la pueda mantener en algún tipo de órbita cerrada, sino que simplemente se mueve en presencia de campos eléctrico E y/o magnético B. ¿Qué hace aquí el operador del momento angular? No se requeriría en lo absoluto la presencia de dicho operador si se tratara de una partícula completamente libre desplazándose siempre en línea recta en una sola dirección. Pero el solo hecho de aplicar un campo eléctrico E o un campo magnético B a la partícula implica necesariamente que mientras dure la interacción la partícula no podrá mantener su desplazamiento en una sola dirección, será desviada entrando en una trayectoria curva. Y al tomar una trayectoria curva, inevitablemente hace su aparición un momento angular asociado con la partícula, y el momento angular tanto en la mecánica clásica como en la mecánica cuántica es una cantidad que se conserva rigurosamente, y hasta la fecha no se ha encontrado ningún experimento en donde se viole el principio de la conservación del momento angular. De hecho, mucho de lo “cuántico” en la Mecánica Cuántica proviene del requerimiento universal del principio de la conservación de la cantidad de movimiento angular. Más aún, si una partícula con carga eléctrica penetra en una región ya sea pequeña o grande en donde haya un campo magnético B constante y uniforme, es posible que la partícula quede atrapada por breve tiempo dentro de dicho campo al tomar una órbita circular cerrada, sin que ello implique la existencia de un potencial central V(r) que mantenga a la partícula en una trayectoria cerrada. Este es precisamente el principio con el cual fué concebido el ciclotrón por el físico Ernest O. Lawrence. Precisamente por ésta razón en el estudio de la interacción de una partícula con un campo electromagnético vuelve a aflorar el símbolo ω que está asociado con la frecuencia de ciclotrón. No nos meteremos aquí en la posibilidad de mantener una partícula en forma permanente en una órbita circular cerrada con el solo hecho de encaminarla hacia un campo magnético en una región situada entre los polos de un imán, por el simple hecho de que al entrar la partícula en una órbita circular cerrada la partícula se estará acelerando (se trata de una aceleración centrípeta) hacia el punto central de su órbita, y la física clásica predice que toda partícula que sea sometida a una aceleración (o una desaceleración, en cuyo caso estamos hablando de lo que se conoce en la literatura como un bremsstrahlung) radiará energía en forma continua, y ésta radiación vendrá a expensas de una disminución continua del radio de la órbita hasta que el movimiento curvilíneo ha desaparecido por completo. No solo se trata de una radiación electromagnética cuya existencia se ha comprobado una y otra vez a nivel macroscópico con instrumentos de laboratorio, se trata del mismo fenómeno que derrumbó la confianza de los teóricos en el modelo atómico planetario de Bohr para el átomo de hidrógeno. De cualquier modo, así sea para el estudio y análisis de interacciones de corta duración con un campo electromagnético intenso, tenemos que retener el concepto del operador del momento angular L_z tal y como aparece en el Hamiltoniano que tenemos arriba.

La parte del Hamiltoniano H que corresponde al operador L_z (o sea H_c), rememorando la eigenecuación correspondiente al operador L_z que nos produce los eigenvalores de energía que irán aparejados con el número cuántico magnético m_l , vendrá siendo para el caso presente:

Tenemos ya tres eigenecuaciones que suministran los eigenvalores de energía que corresponden a cada una de las tres porciones en que hemos subdividido el Hamiltoniano H (H_a, H_b y H_c), la primera siendo aquella que corresponde a un oscilador armónico bidimensional, la segunda siendo la que corresponde al operador del momento angular L_z, y la tercera siendo la que corresponde al operador del momentum P_z, con el último par de eigenvalores simbolizados como m_l y p_z respectivamente en concordancia con la notación que se ha estado usando previamente dentro de ésta obra. Las tres funciones de onda que corresponden a los tres operadores H_a, L_z y P_z son independientes (las eigenecuaciones que producen se resuelven por separado) aunque la función de onda general para el sistema en sí sabemos que debe ser igual el producto de esas tres funciones de onda (al igual que como ocurre con la solución cuántica del problema del átomo de hidrógeno en donde mediante el empleo de coordenadas esféricas se llega a tres funciones de onda distintas mediante el método de separación de variables).

La función de onda general ψ que es simultáneamente una eigenfunción de los tres operadores mutuamente conmutativos H_a, L_z y P_z se puede escribir de la siguiente manera:

De este modo tenemos el siguiente sistema de eigenecuaciones en donde los tres sub-índices puestos al pie de la función de onda del sistema son también los números cuánticos que aparecen en las ecuaciones de eigenvalores para cada operador:

Con nuestra notación aumentada, reafirmamos el hecho de que la función de onda basal (fundamental) n.=.0 para el oscilador armónico bidimensional es una función par bajo un cambio de signo en las coordenadas x y y:

El primer estado excitado, con n.=.1, es una función impar bajo un cambio de signo en ambos x y y. De este modo, se reafirma bajo nueva notación que une a los tres números cuánticos que funciones de onda pares están asociadas con números cuánticos n pares, y funciones de onda impares están asociadas con números cuánticos n impares. Pero por otro lado, al igual que como lo hicimos para el oscilador armónico bidimensional, se puede argumentar también que la función de onda para el operador L_z del momento angular del oscilador armónico bidimensional es par cuando ambas coordenadas cambian de signo, y es impar cuando solo una de las coordenadas cambian de signo, lo cual no es difícil de ver al usar como referencia lo que ocurre con el mismo operador L_z:

Esto implica que, puesto que tanto para el oscilador armónico bidimensional como para lo que le corresponde al operador L_z, en cada caso el número cuántico asignado a cada función de onda de éstos dos términos es par cuando la función de onda es par bajo un cambio de signo en ambas coordenadas, y es impar cuando la función de onda es impar bajo un cambio de signo en ambas coordenadas, siendo por lo tanto n y m_l ambos pares o impares, y puesto que la energía total de un electrón en un campo magnético uniforme no puede ser negativa tomando en cuenta que el Hamiltoniano H es el cuadrado de un operador Hermitiano:

entonces con un nuevo número cuántico r se puede afirmar que:

y como lo anterior siempre será positivo (mayor o igual que cero) ello nos permite deducir que:

De éste modo, de lo que se ha hablado arriba se puede deducir que la ecuación de energía-eigenvalores para el Hamiltoniano total H se puede escribir del siguiente modo:

Cabe agregar aquí que para poder llegar a ésta misma función de onda se podrían haber utilizado operadores escalera, aunque a estas alturas tal cosa no será ya necesaria. Con el nuevo número cuántico r propuesto arriba que agrupa los efectos del oscilador armónico bidimensional aunado a la contribución a la energía que resulta de la acción del operador del momento angular L_z, la  ecuación de energía-total eigenvalores se puede escribir de la siguiente manera:

La cantidad p_z representa el momentum de la partícula en la dirección-z. La energía total de la partícula (que supondremos se trata de un electrón) está compuesta de la energía cinética asociada con movimiento a lo largo del eje-z y la energía asociada con movimiento en el plano xy dada como:

Obsérvese de la ecuación de energía-total eigenvalores que el movimiento en las direcciones x y y tiene lo que se conoce como efecto de fluctuación del punto cero conectado con el movimiento (para un valor de r.=.0 la energía del sistema no es igual a cero) como en el caso del oscilador arrmónico simple, y por ende al hacer r.=.0 la energía más baja de un electrón inmerso dentro de un campo magnético uniforme no es igual a cero sino a ħω. Este resultado puede parecer algo sorprendente, tomando en cuenta el hecho de que el electrón no está confinado por el campo magnético a una región pequeña del espacio y por el contrario puede existir en cualquier lugar en un volumen relativamente grande; parecería que el principio de incertidumbre no nos conduciría aquí a una incertidumbre en el momentum y la contribución resultante a la energía cinética de la partícula.

El Hamiltoniano:

no es el único posible para el problema del movimiento de una partícula inmersa en un campo magnético uniforme; existe un número infinito de potenciales vectoriales A que pueden ser utilizados para representar un campo magnético uniforme a lo largo de la dirección-z.

PROBLEMA: Para el par de ecuaciones:

demostrar que si se hace la transformación:

entonces, para que la relación para el campo eléctrico E permanezca inalterada en forma, se vuelve necesario hacer también la siguiente substitución:

Si el potencial vectorial A es reemplazado por A'.=.A.+.∇f siendo f.=.f.(x,y,z) una función escalar, entonces la ecuación para el campo eléctrico toma el siguiente aspecto:

Resulta obvio que para que la ecuación para E no cambie en forma, se requiere hacer también la siguiente substitución:

con la cual:

El par inseparable de transformaciones:

es conocido ampliamente como transformación gauge (se pronuncia como “geish”) que se puede tomar en su sentido literal como una “recalibración” de variables que respeta la esencia de lo que está siendo “recalibrado”, y en la transformación gauge que tenemos aquí para que la cosa funcione bien no se puede hacer la una sin la otra. La propiedad fundamental de una transformación de gauge es que no modifica ninguna propiedad observable física, las propiedades físicas permanecen invariantes bajo la invariancia ofrecida por las transformaciones gauge.

PROBLEMA: Demostrar que si B.=.∇×A, entonces el potencial vectorialA no está determinado en forma única por B.

Sea f.=.f.(x,y,z) una función escalar arbitraria, y fórmese un campo vectorial A' de la siguiente manera:

Entonces, usando el operador nabla ∇ para aplicar el producto cruz a ambos miembros de lo anterior, vemos que:

En el estudio del Análisis Vectorial se demuestra que el rotacional del gradiente de una función escalar (que es lo que viene siendo físicamente el segundo término de lo anterior) es igual a cero, de modo tal que se tiene entonces:

Por lo tanto, B no solo puede ser expresado como B.=.∇×A sino también como B.=.∇×A' siendo A y A' diferentes, lo cual indica que A no está determinado unívocamente por B puesto que f es una función completamente arbitraria que puede tener cualquier valor diferente de cero.

PROBLEMA: Demuéstrese que si se ha de requerir que el potencial vectorial A represente el mismo campo magnético B que A', siendo:

entonces una condición para lograr que se cumpla tal requerimiento está dada por:

siendo ∇² el operador Laplaciano:

Partiremos del requerimiento que se está pidiendo que se cumpla:

Resulta obvio que a menos de que se cumpla la condición indicada, el potencial vectorial A no podrá representar el mismo campo magnético B que A'.

A continuación desarrollaremos un ejemplo de un potencial vectorial alterno aceptable:

PROBLEMA: Compruébese que bajo la siguiente función escalar f.=.f.(x,y,z):

el campo magnético B representado por:

es el mismo que el campo magnético representado por A.

Aplicando el operador Laplaciano a la función escalar proporcionada, se obtiene lo siguiente:

Se concluye que el campo magnético A' obtenido agregando el gradiente de la función escalar proporcionada representará el mismo campo magnético que el campo magnético A.

PROBLEMA: Demostrar que los siguientes dos gauges:

producen el mismo campo magnético B.

Para el primer “gauge” se tiene:

Y para el segundo “gauge” se tiene:

Se comprueba entonces que ambos “gauges” producen exactamente el mismo campo magnético constante y uniforme de magnitud B apuntando en dirección positiva del eje-z.

Usando el potencial vectorial A' obtenido en los problemas de arriba mediante la relación escalar:

tenemos ahora dos “gauges” distintos. Expresados A y A' en notación de componentes Cartesianos, se tiene lo siguiente primero para el potencial vectorial A:

Y en lo que toca al potencial vectorial A', se tiene lo siguiente:

que produce el siguiente A':

Exhibidos en sus componentes Cartesianos, los “gauges” A y A' parecen realmente distintos. Y sin embargo, ya se demostró arriba que ambos “gauges” producen el mismo campo magnético B, con lo cual las ecuaciones de Maxwell permanecerán intactas tras el cambio de un gauge a otro.

De cualquier modo, y ésto es lo que realmente importa, si usamos el segundo potencial vectorial A' entonces lo que sí cambia realmente es el Hamiltoniano H del sistema.

PROBLEMA: Obtener el Hamiltoniano H del sistema que está siendo estudiado, reemplazando el gauge A por el gauge A'.

La operación pedida arroja el siguiente resultado:

Con el potencial vectorial A', la ecuación energía-eigenvalores toma el siguiente aspecto:

Es posible que a éstas alturas el lector se esté preguntando a sí mismo: y a fin de cuentas, ¿qué es lo que se ha ganado aquí con el cambio de gauge? La respuesta radica en la facilidad lograda para darle una interpretación a las consecuencias físicas de lo que está sucediendo y a la simplificación en los manejos matemáticos que se están llevando a cabo. Con fines comparativos, vale la pena poner juntos uno a un lado del otro los Hamiltonianos H producidos tanto con A como con A':

Estos son los dos Hamiltonianos resultantes de dos “gauges” diferentes usados para describir el mismo sistema físico. Sin embargo, notamos que en el segundo “gauge” ya no hay referencia alguna al operador del momento angular L_z; ahora todo lo que aparece son referencias a los momentums lineales P_x, P_y y P_z en el segundo Hamiltoniano. Y resulta que es mucho más fácil lidiar con expresiones en las que aparecen operadores del momentum linear que expresiones en las que aparece el momento angular. Tómese por ejemplo el operador del momentum P_x sobre la coordenada-x:

Resulta fácil comprobar que la siguiente función de onda es lo que se requiere para poder establecer la eigenecuación de valores relacionados con éste operador:

He aquí la verificación del hecho afirmado:

Póngase atención cuidadosa en la eigenecuación que aparece en la última línea y la distinción notacional que se hace entre el operador del momentum P_x (en letra mayúscula) y el eigenvalor del momentum p_x (en letra minúscula y en itálicas), un número real que puede tomar cualquier valor del momentum lineal a lo largo de la coordenada-x que se pueda medir en un laboratorio (y el cual obviamente no está discretizado). Compárese ahora lo anterior con el operador del momento angular L_z expresado en coordenadas Cartesianas:

Este operador del momento angular ya no es tan fácil de manejar como el operador del momentum linear. Recuérdese cómo al recurrir a dicho operador del momento angular en la solución del problema del átomo de hidrógeno, se tuvo que recurrir a un cambio de coordenadas Cartesianas a coordenadas esféricas, y las funciones de onda (angulares) requeridas tuvieron que ser expresadas en armónicas esféricas complicando el asunto. Ningún físico quiere ni siquera pensar en la idea de tener que resolver un problema cuya solución se presta con mayor facilidad al uso de coordenadas esféricas (o coordenadas polares) que al uso de coordenadas rectangulares Cartesianas. Aquí ni siquiera haremos el intento por tratar de definir alguna función de onda que podamos usar como tal en el análisis mecánico-cuántico de una partícula libre que atraviesa un campo electromagnético.

Enfocándonos en el primer Hamiltoniano que hemos obtenido arriba usando el “gauge” A, la variable z viendo siendo lo que los estudiosos de la mecánica clásica formal identifican como una coordenada cíclica (obsérvese que no aparece en el Hamiltoniano en cuestión) mientras que P_x es a la vez una constante del movimiento en dicho Hamiltoniano (obsérvese que P_x tampoco aparece en la expresión del primer Hamiltoniano). Pero con la transformación que se ha llevado a cabo para obtener el segundo Hamiltoniano, x ahora se ha convertido en una coordenadas cíclica. Aceptamos como un hecho fundamental que los operadores P_x y P_z conmutan, y por lo tanto en el segundo Hamiltoniano los operadores H, P_x y P_z conmutan. Esto sugiere de inmediato que las funciones de onda ahora pueden ser escogidas cada una de ellas para ser eigenfunciones simultáneas de éstos operadores; y se propone aquí que tal función de onda general tendrá la siguiente forma que corresponde al producto de tres funciones de onda, la primera viene siendo la que corresponde al operador del momentum P_x, la segunda viene siendo la que corresponde al operador del momentum P_z, y la tercera una función de onda G(.y) que (afortunadamente) como se verá más abajo no tendremos necesidad alguna de especificar:

Si aplicamos el operador del momentum P_x a ésta función general de onda ψ del segundo Hamiltoniano, se obtiene lo siguiente:

Y si se vuelve a aplicar el mismo operador sobre lo anterior, el resultado será:

Metiendo ésto en la ecuación para el Hamiltoniano con el gauge A', no cuesta mucho trabajo comprobar de primera mano que la función G(y) satisface:

en donde habiendo hecho:

se puede ver que se tiene un Hamiltoniano:

que nos produce la siguiente eigenecuación en donde no aparece ninguna mención a las coordenadas x y z (excepto con p_x que es un eigenvalor y no un operador) simplificando considerablemente la cosa:

y justificándose así a G(y) como una auténtica función de onda en el pleno sentido de la palabra (¡y sin necesidad de tener que indagar la naturaleza de la misma!).

Entre las simplificaciones que se pueden llevando a cabo sobre la ecuación de energía-eigenvalores que se acaba de obtener, se encuentra que resulta útil hacer la siguiente substitución:

No cuesta mucho trabajo comprobar lo que se puede lograr con la substitución:

De este modo, podemos hacer la siguiente simplificación:

Bien, hemos llegado a ésto. ¿Y ahora qué sigue? Sin duda alguna, los Hamiltonianos obtenidos con cada “gauge”, tanto con A como con A', son distintos. Pero si de algo debemos estar completamente seguros es que ambos Hamiltonianos describen la misma situación física. No debemos esforzarnos mucho para poder reconocer que lo que tenemos arriba es esencialmente la expresión para un oscilador armónico simple unidimensional de frecuencia (angular circular):

La energía asociada con éste movimiento se puede escribir de inmediato, usando los resultados obtenidos previamente:

Las energías permisibles:

son conocidas como niveles Landau dentro de lo que se conoce como la cuantización de Landau, un efecto predicho teóricamente por vez primera por el físico soviético Lev Davidovich Landau, se trata de la cuantización de las órbitas de ciclotrón de partículas cargadas que se desplazan en campos magnéticos, en donde como consecuencia de dicha cuantización las partículas cargadas sólo pueden ocupar órbitas con valores discretos de energía. Los niveles de Landau son degenerados, con un número de electrones por nivel directamente proporcional a la fuerza del campo magnético aplicado.

En términos de la frecuencia (circular) ω introducida en la discusión del mismo problema usando el otro “gauge” (véase más arriba en ésta entrada):

tenemos que la relación entre ω y ω₁ es:

con lo cual:

se convierte en:

lo cual (como ya se debería de haber anticipado) es idéntico al resultado obtenido previamente con el primer Hamiltoniano:

Resulta evidente que la eigenenergía E es independiente del momentum en la dirección de la coordenada-x, o sea p_x. Este momentum es, sin embargo, una constante del movimiento que puede tomar cualquier valor dentro del rango continuo:

En virtud de ésto, hay una degeneración infinita asociada con cada estado de energía, y no podemos hablar ya de estados completamente discretizados. De la ecuación anterior:

puede verse que para cada valor de energía hay un número infinito de posibilidades para los dos números cuánticos n y m_l. Lo único que se requiere es que:

sea constante, y n puede tomar cualquier valor integral en el rango n.≥.0, mientras m_l puede tomar cualquier valor dentro del rango:

El Hamiltoniano para cualquiera de los dos gauges que tenemos arriba (el Hamiltoniano con gauge A y el Hamiltoniano con gauge A') puede ser modificado de inmediato para incluír un término de interacción del momento magnético del spin de la partícula con el campo externo. De éste modo, si el término:

es añadido, la energía resultante para la partícula (que supondremos sigue siendo un electrón) será:

en donde el signo (±) se refiere a las dos orientaciones posibles del spin del electrón en relación con la dirección del campo magnético aplicado.

Los cambios de gauge, cuando son bien llevados a cabo, no deben causar preocupación al lector en lo que toca a la posibilidad de que se pueda trastocar la descripción del sistema físico con el que estamos trabajando. Se puede demostrar formalmente mediante una substitución directa que si la transformación del potencial vectorial:

se lleva a cabo, la forma original de la ecuación energía-eigenvalores se obtiene si también se lleva a cabo la siguiente substitución:

PROBLEMA: Verifíquese, mediante substitución directa, que si se hace el siguiente cambio de gauge tanto en el potencial vectorial A como en el potencial escalar (eléctrico) Φ:

en donde la función f es una función escalar de la posición y del tiempo, entonces el Hamiltoniano conservará su forma original si se cambia también la función de onda substituyéndola con la siguiente función de onda:

Nuestro punto de partida será el Hamiltoniano H para una partícula cargada moviéndose dentro de un campo magnético. Para simplificar un poco las cosas, tomaremos por lo pronto un potencial eléctrico Φ igual a cero haciéndolo a un lado, ya tendremos oportunidad de volver a meterlo poco después:

El operador general del momentum P (válido para tres dimensiones) expresado en coordenadas Cartesianas se puede escribir del siguiente modo:

Con ésto, el Hamiltoniano toma el siguiente aspecto en el sistema de unidades CGS-Gaussianas:

Al efectuar la transformación de “gauge” reemplazando el potencial vectorial A por el potencial vectorial A', se tiene lo siguiente:

El cambio de gauge implica desde luego:

con lo cual se tiene, en el sistema de unidades CGS-Gaussianas:

En el desarrollo que se estará llevando a cabo, el factor 1/c impone un peso adicional a una notación que ya de por sí es algo engorrosa y prolija. Es válido simplificar el desarrollo haciendo c.=.1 con la intención de restablecer después dicho factor en los resultados finales (de cualquier modo, aún borrando permanentemente el factor 1/c el desarrollo es válido dentro del sistema de unidades MKS-SI):

Empezaremos por aplicar éste Hamiltoniano H a la función de onda ψ' tras lo cual el Hamiltoniano debe (según se espera) mantener su forma original sin cambio alguno al llevar a cabo las transformaciones de gauge:

con lo cual, tomando en cuenta que al haber hecho la simplificación c.=.1 la función de onda ψ' será:

y se tiene entonces:

Esto nos lleva al siguiente desarrollo intermedio (el factor 1/2m será ignorado aunque debe tenerse en cuenta durante el desarrollo que sigue allí presente aunque no se le vea; obsérvese también cómo se eliminan los dos términos comunes pero con signos opuestos enmarcados en líneas de color rojo):

Hemos obtenido el efecto de aplicar el operador Hamiltoniano a la función de onda ψ'. Pero en lo que estamos realmente interesados es en aplicar el operador dos veces, lo cual se logra volviendo a aplicar el operador en una segunda ocasión al resultado que se acaba de obtener arriba (seguiremos ignorando el factor 1/2m):

De este modo, y reestableciendo el factor 1/2m que se había omitido por cuestiones de simplicidad, el desarrollo que se ha llevado a cabo nos ha llevado del punto de partida que aparece en el lado izquierdo a lo que aparece en el lado derecho de la siguiente igualdad:

Meteremos ahora el potencial eléctrico Φ' que por cuestiones de simplicidad habíamos estado omitiendo arriba:

Recurrimos ahora a la transformación gauge para el potencial Φ' (recuérdese que la función f se ha definido como una función de la posición y del tiempo):

con lo cual se tiene en el lado derecho de la expresión previa:

Pero de lo que se ha visto con anterioridad, ya se sabe que:

Entonces se puede llevar a cabo la siguiente simplificación:

con lo cual queda demostrado que (reestableciendo el factor 1/c):

se convierte, con la función de onda usada como “monigote”, y una vez llevadas a cabo las transformaciones gauge, en lo siguiente:

En pocas palabras, todo permanece igual, en forma. El par de transformaciones gauge dejaron intacta la forma original del Hamiltoniano. Puesto que la transformación propuesta arriba para la función de onda es justo lo que se requiere para que el Hamiltoniano permanezca intacto en forma cuando se le aplica el par de transformaciones gauge con el que hemos trabajado éste problema, es común ver en textos y literatura científica que al hablar de transformaciones gauge se incluye tal transformación de la función de onda refiriéndose así a lo que vendría siendo un trío inseparable de ecuaciones para llevar a cabo transformaciones gauge dentro de la Mecánica Cuántica:

Hemos cubierto aquí lo que se espera que ocurra cuando un electrón de valencia ligado a un átomo interactúa con un campo electro-magnético. En la siguiente entrada veremos lo que se puede esperar que ocurra cuando es todo el átomo el que se considera que actúa con el campo electromagnético que le es aplicado, y para variar consideraremos un campo electromagnético clásico como el que Maxwell postuló para describir a la luz como una onda continua con campos eléctrico y magnético, en donde el campo magnético oscila completamente en fase con el campo eléctrico.