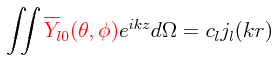Es muy importante tener en cuenta que el análisis que será llevado a cabo aquí, al igual que como sucedió con el análisis del esparcimiento de ondas electromagnéticas que vimos previamente, es un análisis independiente del tiempo, la variable tiempo no aparecerá aquí en ninguna parte. Esto no nos debe causar preocupación alguna, después de todo, en el análisis clásico llevado a cabo por Rutherford tampoco aparece la variable tiempo en ninguna parte, como tampoco aparece el tiempo como variable en el análisis de la difracción de las ondas de materia que ocurre en el experimento de la doble rendija, ya que los patrones de difracción e interferencia que aparecen como consecuencia de la naturaleza ondulatoria de la materia no son algo que manifiesten algún tipo de “movimiento”, se trata de patrones estáticos, fijos. Podemos, si así lo deseamos, meter a la variable tiempo dentro del panorama, en cuyo caso tenemos que utilizar la ecuación de Schrödinger dependiente del tiempo en lugar de la ecuación de Schrödinger independiente del tiempo. Sin embargo, antes de complicar el asunto, queremos estar seguros de que en un análisis que sea independiente del factor tiempo podemos obtener resultados que en cierto modo se asemejen a los resultados clásicos obtenidos por Rutherford, ya después tendremos ocasión para obtener algo más sofisticado.
Otra cosa que dejaremos en claro es que en esta entrada y en las entradas que le siguen estaremos limitando nuestras discusiones a esparcimientos elásticos en los cuales la energía de la partícula incidente es igual a la energía de la partícula esparcida, no habiendo captura alguna de partículas ni pérdida de energía en las partículas desviadas. En pocas palabras, el número total de partículas se mantiene constante: las partículas esparcidas son igual en número a las partículas incidentes. Cuando no ocurre tal cosa, entonces en lugar de estar hablando acerca de secciones transversales de esparcimiento estaríamos hablando de una sección eficaz de captura, lo cual nos pone firmemente en el terreno de la física nuclear y en un tópico que en tiempos remotos estaba limitado a las aspiraciones y sueños de los alquimistas: la transmutación de elementos.
De acuerdo a lo que hemos visto hasta este punto, cuando un haz con un flujo de partículas igual a N partículas por centímetro cuadrado por segundo incide sobre un centro de esparcimiento, se puede esperar que haya partículas moviéndose y alejándose del centro de esparcimiento en todas las direcciones posibles. Designemos como dN al flujo de partículas esparcidas hacia un elemento de ángulo sólido dΩ en relación a una dirección especificada por los ángulos θ y φ. Esperamos que dN sea proporcional al flujo incidente de partículas N y al tamaño del ángulo sólido dΩ:
dN = σ(θ,φ)NdΩ
De esta relación, el flujo radial (hacia afuera) de partículas hacia un elemento diferencial de ángulo sólido dΩ es NσdΩ en donde N es el flujo incidente. Aquí la constante de proporcionalidad, que generalmente será una función de los ángulos θ y φ, es simbolizada como σ(θ,φ). Una inspección de la relación dada arriba revela que σ(θ,φ) tiene las dimensiones de área. Puesto que se supone que la distribución de partículas esparcidas sobre un plano que es perpendicular a la dirección de movimiento del haz incidente es uniforme, resulta obvio que una interpretación consistente requiere que σ(θ,φ) sea el área de la sección transversal del haz incidente a través de la cual pasan todas las partículas que son esparcidas hacia un elemento infinitesimal de ángulo sólido dΩ delimitado por los ángulos θ y φ. Por esta misma razón la constante de proporcionalidad σ es conocida como la sección transversal diferencial de esparcimiento del haz. La expresión dada arriba tiene que ser integrada sobre todos los elementos infinitesimales de ángulo sólido dΩ para proporcionar el flujo total de partículas esparcidas por el centro dispersor, lo cual sirve para definir la sección transversal total de esparcimiento σT:
En algunos casos (sobre todo en la fenomenología que concierne a la física nuclear), se vuelve necesario trabajar con situaciones en las cuales el blanco, además de provocar el esparcimiento del haz incidente, absorbe partículas del haz incidente. Para esto, se puede definir en forma análoga una sección transversal de absorción total. El concepto de sección transversal puede ser generalizado aún más para incluír fenómenos que involucran producción de partículas y fotones, transmutación de los núcleos usados como blanco, etc.
Para definir un elemento de ángulo sólido dΩ, podemos usar la siguiente figura en la cual suponemos que un haz de partículas incide de abajo hacia arriba sobre un centro de esparcimiento (de color rojo) que está ubicado en el origen O de un sistema de coordenadas esféricas:
Desde el punto de vista clásico, suponemos que antes de aproximarse al centro de esparcimiento una cantidad de dN partículas atraviesa cada segundo una superficie anular 2πbdb (destacada en color amarillo) en donde b es el parámetro de impacto (la distancia perpendicular que hay entre el sentido de movimiento de una partícula cualquiera y la línea imaginaria eje-z que pasa por el centro del núcleo dispersor situado en O y que es paralela al sentido de movimiento de la partícula), y que después del esparcimiento dichas partículas atraviesan en igual cantidad (por unidad de tiempo) un elemento diferencial de ángulo sólido dΩθ (o sea la superficie anular infinitesimal que le dá una vuelta completa a la esfera, destacada en color verde); de modo tal que todas las partículas que están entrando por la superficie de color amarillo emergen en igual número por la superficie de color verde. De la figura es obvio que obtenemos dΩθ tomando el elemento infinitesimal de ángulo sólido dΩ delimitado entre φ y φ+dφ e integrando dicho elemento entre φ.=.0 y φ.=.2π para obtener dΩθ. Al llevar a cabo el análisis del esparcimiento de partículas desde el punto de vista de la Mecánica Ondulatoria, mantendremos vigente el mismo sistema de coordenadas esféricas y la misma definición convencional que le hemos dado al elemento infinitesimal de ángulo sólido.
En la discusión previa, se ha supuesto que el blanco está anclado e inmóvil en un centro de esparcimiento fijo, y que los ángulos polar (θ) y azimutal (φ), usados para caracterizar el esparcimiento están dados en relación con el sistema de coordenadas esféricas cuyo origen O coincide con el centro del núcleo dispersor. Sin embargo, en la práctica, los centros de esparcimiento rara vez se encuentran fijos, ya que rebotan bajo el efecto de las mismas fuerzas que dan lugar al esparcimiento; el centro de esparcimiento rebotante absorbe alguna energía (y momentum) de la partícula incidente, con el monto exacto dependiendo del ángulo de esparcimiento y las masas relativas de las partículas incidentes y dispersoras. En una situación más realista, hay dos sistemas de coordenadas en relación a los cuales se puede describir el esparcimiento, los cuales son de importancia significativa. Uno de ellos, conocido como el sistema de laboratorio, está fijo en el espacio, con las partículas blanco en reposo (antes del rebote). Este es el sistema con respecto al cual se hace referencia a todos los ángulos que son medidos en el laboratorio cuando se lleva a cabo un experimento. Sin embargo, al llevar a cabo las mediciones del esparcimiento en términos del potencial entre las partículas del haz y las partículas blanco, el sistema de centro-de-masas resulta más conveniente. Como el nombre implica, en este sistema el centro de masa de la partícula incidente y la partícula blanco es estacionario. En el sistema de centro de masas, se puede describir al esparcimiento como teniendo lugar en un centro de esparcimiento fijo (el centro de masa), con las dos partículas (la partícula incidente y la partícula blanco) permaneciendo colineares con este centro y ambas partículas moviéndose ya sea acercándose o alejándose del centro con momentums iguales. La colinearidad surge en virtud de la conservación del momentum, y el ángulo azimutal φ debe ser el mismo en ambos sistemas. Sin embargo, los ángulos θ que miden el cambio en dirección entre los momentums inicial (antes del esparcimiento) y final (después del esparcimiento) difieren en los dos sistemas. Un argumento geométrico directo (clásico) demuestra que la relación entre los dos ángulos está dado por:
en donde m1 es la masa de la partícula incidente y m2 es la masa del blanco. Resulta claro que cuando m2.».m1, la conversión de los ángulos medidos en el sistema del laboratorio a los ángulos del centro de masa que son físicamente más significativos produce cambios pequeños en el ángulo. Esta ecuación está basada en la imagen dada por la trayectoria clásica de partículas. Sin embargo, la relación entre los dos sistemas de referencia está determinada únicamente por los principios fundamentales de la conservación de la energía y la conservación del momentum, y puesto que estos principios son igualmente válidos tanto en la Mecánica Cuántica como en la teoría clásica, la relación se puede aplicar por igual a problemas de esparcimiento clásico y cuántico.
Como ya lo hemos visto en las entradas previas, un haz de partículas monoenergéticas (todas ellas con la misma energía) puede ser descrito bajo contexto mecánico-cuántico considerándolo como si fuese una onda plana. Tal onda plana se extiende infinitamente en el espacio, mientras que el haz que se utiliza en los hechos en cualquier experimento de esparcimiento necesariamente está limitado en extensión en la dirección transversal (la dirección de su movimiento) y por lo tanto, del principio de incertidumbre de Heisenberg, no puede estar compuesto de partículas libres cuyos momentums y energía son conocidos con precisión. Sin embargo, esto no destruye la utilidad de la descripción de un haz monoenergético con una onda plana, porque para haces con secciones transversales macroscópicas la incertidumbre en el momentum es insignificante.
En la descripción mecánico-cuántica del esparcimiento de partículas, la función de onda total que describe la “trayectoria” de una partícula puede ser separada en dos partes: una parte que representa a la partícula incidente, y otra parte que representa a la partícula esparcida. Como una primera simplificación, podemos seguir tomando a la parte incidente como una onda plana cuyo comportamiento ondulatorio puede ser simbolizado mediante la expresión eikz, (o con mayor generalidad suponiendo un número de onda k tridimensional y un vector posición tridimensional r, tomando el producto punto de ambos, o sea k·r). Bajo este concepto, el esparcimiento de las partículas incidentes consiste en una onda plana que incide en forma continua sobre un núcleo dispersor, y una onda esférica que representa a las partículas que se alejan en todas direcciones (las ondas esféricas requieren de un factor 1/r para que la amplitud de las ondas vaya disminuyendo al aumentar la distancia, ya que de lo contrario se tendría una fuente de creación infinita de energía):
Sin embargo, esta idealización supone que todas las partículas incidentes son esparcidas, lo cual no es necesariamente cierto. De hecho, como ocurrió en el experimento de Rutherford, puede haber muchas partículas que prácticamente emergen en la misma dirección en la que entraron, las cuales representan una onda plana, y si hemos de ser realistas en lo que al experimento de Rutherford concierne, la onda plana saliente no es muy diferente de la onda plana incidente. Esto nos lleva a considerar el flujo de salida no como un simple flujo de ondas esféricas sino como la suma de dos flujos:
Podemos representar esta situación de una manera dinámica con el siguiente archivo gráfico animado:
La generación de ondas esféricas a partir de ondas planas incidentes es reminiscente del principio de Huyghens, usualmente esquematizado de la siguiente manera:
Sin embargo, esta ilustración dinámica, aún vista tridimensionalmente, representa la generación de mitades de casquetes esféricos (encaminados en la ilustración tanto hacia la derecha como hacia arriba y hacia abajo). En cambio, en lo que corresponde al esparcimiento de ondas electromagnéticas (o bien, ondas de materia, como es el caso que aquí nos ocupa), estamos hablando de ondas esféricas completas, lo cual incluye la parte de las ondas esféricas que se dirigen encaminadas en sentido opuesto (de derecha a izquierda) a la dirección en la cual se mueven las ondas planas que están incidiendo (de izquierda a derecha) sobre el obstáculo o el centro dispersor, lo cual puede (y de hecho dá) lugar a interferencias de ambas ondas en ambos lados del centro de dispersión, lo cual dá lugar a su vez a un efecto conocido como el esparcimiento sombra (shadow scattering en la literatura técnica inglesa) que veremos en mayor detalle después.
Si hacemos a un lado la posibilidad de que pueda haber una captura de partículas incidentes como ocurre en fenómenos propios de la física nuclear en los cuales hay transmutación de elementos y en donde el número de partículas incidentes no es igual al número de partículas esparcidas o bien las partículas esparcidas son diferentes físicamente a las partículas incidentes, y nos enfocamos por lo pronto en los fenómenos de esparcimiento en los cuales hay un esparcimiento puro sin captura de partículas, entonces una cosa debe ser absolutamente cierta: el número de partículas incidentes debe ser igual al número de partículas esparcidas. Esto lo podemos expresar con mayor rigor dentro de la Mecánica Cuántica reafirmando el hecho de la conservación de la probabilidad. Si suponemos que la densidad de probabilidad ρ una función de onda ψ está definida de acuerdo al criterio de Born:
entonces es un asunto directo derivar de la ecuación de onda de Schrödinger dependiente del tiempo la ecuación de continuidad:
en donde el vector tridimensional j representa el flujo de probabilidad. De esto se tiene que:
Si llevamos a cabo una integración del flujo de probabilidad sobre una superficie esférica suficientemente grande para obtener el flujo neto, sabemos que como resultado de dicha integración llevada a cabo sobre el producto vectorial punto de j con elementos infinitesimales de superficie dS se debe obtener:
Estas dos últimas relaciones nos dicen simplemente que dentro de la superficie esférica imaginaria no hay una “fuente” o un “drenaje” de partículas (no se están creando ni se están destruyendo partículas, todo lo que entra es igual a todo lo que sale). El flujo saliente (que consta de dos partes o dos funciones de onda) debe ser igual al flujo incidente.
El que la onda de partículas posterior al esparcimiento sea un compuesto de un frente de ondas planas y un frente de ondas esféricas con efectos anticipables de interferencia nos complica algo las cosas, porque la onda total resultante del esparcimiento consta no de un componente sino de dos. Si representamos a la parte que representa a las partículas esparcidas como ξ, entonces apelando al principio de superposición lineal que permite la suma directa de dos funciones de onda la función de onda total se puede escribir de la siguiente manera:
De este modo, la onda de probabilidad que llega al detector de partículas consiste en una superposición linear de la onda esférica ξ que representa a las partículas esparcidas y la onda planar incidente eikz (tomando la dirección de propagación en el sentido del eje-z) que es transmitida y que representa a las partículas que no experimentan esparcimiento alguno.
Resulta conveniente ubicar al origen del sistema de coordenadas en el centro del causante del esparcimiento de las partículas cuando se toma el centro de esparcimiento como fijo. Para centros de esparcimiento que no permanecen fijos en una misma posición, el centro de masa es entonces el origen apropiado. Lejos del centro de esparcimiento, la onda esparcida debe representar un flujo de partículas que se están moviendo radialmente hacia afuera. La función de onda esparcida ξ debe tener entonces una forma asintótica como la que se muestra a continuación:
en donde f.(θ,φ) es una función que especifica la dependencia angular de la onda esparcida. Puede verse que, de este modo, ξ representa una onda saliente. Si colocamos un detector de partículas para observar las partículas esparcidas, del modelo anterior se puede esperar que el resultado final sea un patrón complejo de interferencia que generalmente exhibirá un comportamiento oscilatorio al llevar a cabo una observación polar (a un ángulo θ con respecto a la dirección del haz incidente) a distancias suficientemente grandes del centro en donde ocurre la “colisión”:
En este punto, esta última ilustración nos puede llevar a formularnos una pregunta importante: si en el análisis cuántico (no clásico) del esparcimiento de partículas los experimentos de esparcimiento deben manifestar patrones de interferencia en las pantallas detectoras, ¿por qué razón Rutherford y sus colaboradores no detectaron jamás tal cosa en sus experimentos (lo cual posiblemente les habría causado asombro)? La primera respuesta a esto es que bajo las condiciones particulares en las que se llevaron a cabo los experimentos (un detector óptico de alcance visual muy limitado, una fuente de pocas partículas relativamente hablando, etc.), la naturaleza ondulatoria de la materia no era algo que pudiese ser detectado por Rutherford y sus colaboradores aún si en lugar de la medición llevada a cabo a lo largo de un “anillo circular” (girando el visor en torno a un plano alrededor de la lámina de oro) se hubiera usado una pantalla esférica cubriendo casi en su totalidad el centro del esparcimiento. La segunda respuesta es que para que la naturaleza ondulatoria de la materia como ondas de probabilidad pudiera salir a flote, se hubiera requerido de un haz incidente formado por una cantidad relativamente grande de partículas, además de que se hubiera requerido de una pantalla esf erica con “registro de memoria” (una película fotográfica) para que el efecto visual acumulativo de las partículas esparcidas pudiera ir dando origen a los patrones de interferencia y difracción ocasionados por las ondas de materia esparcidas. En el experimento clásico de la doble rendija llevado a cabo con un haz luminoso, podemos ver directamente los patrones de interferencia en la pantalla plana receptora porque la cantidad de “cuantos” de luz que lleva el haz de luz incidente es lo suficientemente grande para que se pueda ver la formación de los patrones de interferencia, mientras que en un experimento de esparcimiento de partículas tales como electrones o partículas sub-atómicas la cantidad de partículas no es lo suficientemente grande (al menos no lo era en el experimento llevado a cabo por los colaboradores de Rutherford) como para que tal cosa se manifieste excepto a un muy largo plazo, y ello suponiendo que cada partícula esparcida vaya dejando un registro permanente en la pantalla detectora en lugar de un registro temporal.
No cuesta mucho trabajo verificar por substitución directa de la función de onda ξ en la ecuación de onda de Schrödinger independiente del tiempo que, asintóticamente (para valores suficientemente grandes de r), la expresión:
obedece en efecto la ecuación de Schrödinger para una partícula libre. Aunque tentativamente se podría suponer que la distribución angular:
representa siempre un número real, hay varios casos (entre los cuales se encuentra un teorema que veremos posteriormente en otra entrada, el teorema óptico) en los cuales para poder obtener una interpretación correcta y consistente dentro de la Mecánica Cuántica se le debe suponer a la distribución angular no como un número real sino como un número complejo.
Recordando lo que vimos previamente bajo el contexto de la Mecánica Ondulatoria en relación con la interpretación probabilista de un flujo de partículas, en este caso el flujo de partículas esparcidas S que en realidad es un flujo de probabilidad puede ser obtenido directamente de la relación que ya obtuvimos previamente en la serie de entradas que tratan acerca de la “Interpretación probabilista de ψ” (el conjugado complejo de la función de onda ξ se representará poniéndole una barrita horizontal encima, o sea que tomaremos a ξ como ξ*):
en donde hemos usado el color azul convencional para denotar una función y el color rojo para denotar el conjugado complejo de dicha función. Podemos ver que, asintóticamente para radios grandes:
Por otro lado, el operador diferencial vectorial ∇ (nabla) puede ser expresado en cualquier sistema de coordenadas que nos resulte más ventajoso para el problema en particular que estemos manejando. En un problema que involucra ondas esféricas, resulta más conveniente recurrir a un sistema de coordenadas esféricas (r,θ,φ) que a un sistema de coordenadas rectangulares Cartesianas (x,y,z). En un sistema de coordenadas esféricas, el operador diferencial ∇ está dado por la siguiente relación:
en donde r0, θ0 y φ0, son vectores unitarios ortogonales de base en las direcciones de r, θ, y φ crecientes.
Haciendo uso de la regla de Leibniz (regla del producto) tratándose del operador diferencial simbólico ∇, tenemos entonces que:
Del mismo modo:
Llevaremos a cabo una parte del desarrollo (la otra parte es similar y no requiere de nuevas explicaciones). Aplicando el operador diferencial ∇ (expresado en coordenadas esféricas) a la función de onda ξ, se tiene:
Tomando en cuenta la naturaleza de la diferenciación parcial, lo anterior se puede expresar como:
Premultiplicando ambos lados de esto último por ξ y reemplazando en el lado izquierdo lo que éste representa, se tiene (los pares de factores en color magenta en cada término se cancelan mutuamente):
habiéndose utilizado en la simplificación anterior el desarrollo intermedio:
Procediendo del mismo modo, podemos obtener una relación parecida aunque ligeramente diferente para (∇ξ)ξ. En la simplificación posterior de la relación que estamos tratando de obtener para el flujo de probabilidad S y tomando en cuenta que suponemos a la relación de distribución angular como un número complejo, supondremos que dicha relación siempre se puede expresar como la suma de una parte real que denominaremos Re{.f.(θ,φ)} y una parte imaginaria que denominaremos como Im{.f.(θ,φ)}. Siendo así, se tiene entonces:
De esto es obvio que:
Desarrollando todo lo anterior y simplificando, se obtiene lo siguiente:
en donde se recalca de nuevo que r0, θ0 y φ0 son respectivamente vectores unitarios de base en las direcciones de r, θ, y φ crecientes, y en donde, desde luego:
Como puede verse en la fórmula obtenida arriba, el flujo S es un vector tridimensional (esta es la razón por la cual se le está simbolizando con letra negrita), ya que está dado en función de los vectores unitarios de base r0, θ0 y φ0, lo cual nos permite representar sus componentes de la siguiente manera en un sistema de coordenadas esféricas:
Para valores grandes de la distancia radial en donde la relación asintótica dada anteriormente es válida, las componentes angulares dejan de ser importantes y únicamente la componente radial Sr se vuelve relevante, esto es:
quedando entonces como componente útil únicamente el primer término de S en la fórmula de arriba, al que le agregamos el sub-índice r para indicar que se trata del término puramente radial:
siendo v la velocidad clásica de la partícula. Se agregará aquí que, numéricamente, esto último es igual a la densidad de probabilidad multiplicada por la velocidad, para un flujo unitario de partículas incidentes implícito en la expresión:
Todas las partículas esparcidas pueden ser consideradas como moviéndose hacia afuera. La función f.(θ,φ) puede ser relacionada con la sección transversal diferencial σ(θ,φ) para el centro de esparcimiento comparando la relación obtenida arriba para Sr con la relación:
dN = σ(θ,φ)NdΩ
De esta expresión, el flujo radial hacia afuera penetrando en un elemento de ángulo sólido dΩ es NσdΩ en donde N es el flujo incidente de partículas. Esto puede ser convertido en el flujo radial hacia afuera por unidad de área a una distancia radial r del centro de esparcimiento, recurriendo a la definición esencial de lo que es un elemento diferencial de ángulo sólido:
El flujo radial hacia afuera por unidad de área en los ángulos θ y φ, Sesp, es por lo tanto:
El flujo incidente N se obtiene aplicando la ecuación:
a eikz, la parte que representa el flujo incidente. Esto nos produce el siguiente resultado:
Por lo tanto:
y entonces:
Obsérvese que al calcular los flujos de densidad de probabilidad, tomamos por separado las dos partes del lado derecho de la expresión:
ignorando los efectos de interferencia entre eikz y ξ que inevitablemente habrían aparecido si esta ecuación para ψ se hubiera utilizado para el cálculo del flujo S. Podemos justificar esto como un procedimiento correcto mediante las siguientes consideraciones. El haz incidente de partículas es representado por el término eikz que corresponde a un haz de extensión infinita en una dirección transversal a la dirección de la propagación (como ocurre con la representación gráfica de una onda senoidal, infinta en extensión en ambos sentidos tanto a la izquierda como a la derecha). Esto es físicamente imposible, y de hecho en un laboratorio uno trabaja con haces que están confinados a una región espacial firmemente acotada y definida. Los términos de interferencia entre eikz y ξ representan una situación en la que tanto los haces incidentes y esparcidos están presentes en un detector de partículas. El haz esparcido está ausente, sin embargo, en un lugar (lejos del núcleo en donde se lleva a cabo el esparcimiento) en donde el haz esparcido es usualmente detectado. Los términos de interferencia se aplican únicamente a las regiones en donde las ondas incidentes y esparcidas se traslapan, y el efecto más importante de un traslape así es la pérdida, por esparcimiento, de partículas que venían en el haz original. Si se lleva a cabo una medición en una región en donde estén presentes tanto partículas incidentes como partículas esparcidas, se vuelve necesario utilizar algún dispositivo para selección del momentum que admita únicamente partículas esparcidas, y de nueva cuenta los efectos de interferencia desaparecerían.
Como se indicó arriba, los términos no radiales (o sea, los términos que involucran las componentes angulares θ y φ) en la expresión:
han sido ignorados, puesto que disminuyen a mayor rapidez con una distancia radial r cada vez mayor que como lo hace el término radial. Sin embargo, tienen una interpretación física importante. Como se verá posteriormente, una onda plana incidente contiene componentes que corresponden a un momento angular diferente de cero en torno al centro de esparcimiento. Clásicamente, estos corresponden a los parámetros de impacto de las partículas que forman las partes del haz incidente que no están dirigidas directamente hacia el núcleo dispersor. La dependencia radial de 1/r3 del flujo ondulatorio esparcido no-radial es esencial para la preservación del momento angular. Puesto que S puede ser interpretado como la densidad de las partículas multiplicada por la velocidad de las mismas, rS puede ser interpretado como como la densidad del momento angular. De la expresión dada arriba para S, esta densidad del momento angular tiene una dependencia radial 1/r2, tal y como ocurre con la componente para el flujo radial de partículas, resultando en una conservación del momento angular de las partículas conforme se mueven hacia afuera después de que se ha llevado a cabo el esparcimiento de las mismas.
Para el cálculo relacionado únicamente con el flujo de partículas que están siendo esparcidas (alejándose radialmente hacia afuera como consecuencia del esparcimiento), podemos utilizar cualquier superficie que incluya al centro de esparcimiento. En efecto, considerando las siguientes tres figuras:
sabemos que la superficie de contorno azul mostrada en la figura inferior no nos servirá para tales cálculos en virtud de que carece de una fuente interior de partículas que estén siendo radiadas hacia afuera, el flujo neto a través de dicha superficie (de acuerdo al teorema de la divergencia de Gauss) es cero. Por otro lado, comparando las dos figuras superiores, resulta evidente que será mucho más fácil utilizar para los cálculos una superficie esférica (como la que se muestra en la figura superior izquierda) que una superficie elaboradamente distorsionada (como la que se muestra en la figura superior derecha).
Antes de continuar adelante, es importante aclarar que en lo que resta de esta entrada, aunque una partícula libre pueda ser caracterizada por un número cuántico de spin ms, en lo que resta de esta entrada no se tomará en cuenta el efecto del spin intrínseco en el análisis que llevaremos a cabo del esparcimiento de partículas.
Cuando el potencial V que produce un esparcimiento de partículas es esféricamente simétrico, podemos emplear un método conocido como el método de las ondas parciales, así llamado porque emplea una descomposición de la función de onda ψ en ondas esféricas. Antes de considerar el método de las ondas parciales para el tratamiento de problemas de esparcimiento, consideraremos primero la representación como una onda esférica de una partícula libre. En la ausencia de un campo electromagnético, el operador Hamiltioniano de una partícula libre es:
Como se discutió previamente al tratar el tema del momento angular bajo la perspectiva de la Mecánica Ondulatoria, este operador Hamiltioniano H conmuta con el operador del momento angular L, y consecuentemente también con el operador L2. Los tres operadores H, Lz y L2 forman un conjunto de tres operadores mecánico-cuánticos todos los cuales conmutan entre sí, lo cual nos permite seleccionar funciones de onda que sean simultáneamente eigenfunciones de estos tres operadores. Tales funciones de onda se pueden escribir de la siguiente manera expresándose la función de onda total como el producto de una función de onda radial y una parte angular:
La energía de una partícula libre es, desde luego:
siendo Ylm(θ,φ) la misma armónica esférica de la que hemos estado hablando en entradas previas. Hemos visto ya que la parte radial es una función de onda que satisface la ecuación diferencial:
siendo el operador del momentum Pr:
Para el caso en el cual l.=.0, la solución a la ecuación diferencial viene siendo:
La forma cosenoidal de la solución tiene que ser excluida tratándose de una partícula libre, porque es singular en el origen en donde el valor de r.=.0 produce una división entre cero. Ya hemos visto en las dos entradas previas este mismo tipo de soluciones. Son las funciones esféricas de Bessel y de Neumann para un orden cero:
Así pues, haremos a un lado la función esférica de Neumann a causa de la singularidad en el origen, y nos limitaremos a utilizar la función esférica de Bessel de orden cero. La función radial j0 satisface una relación de normalización especificada como:
La función radial también puede ser normalizada de la siguiente manera en los términos de un flujo de partículas:
en donde hemos recurrido a las funciones esféricas de Hankel:
Obsérvese que de esta manera la ecuación para j0(kr) expresada por medio de las funciones esféricas de Hankel representa una onda estacionaria que consiste en la suma de una parte entrante y una parte saliente.
PROBLEMA: Demuéstrese que:
Tomando como punto de partida la definición de la función esférica de Hankel h0(1):
insertamos aquí las soluciones de las funciones de Bessel y Neumann de orden cero obteniendo el resultado deseado:
Puesto que la función esférica de Hankel h0(2) es el conjugado complejo de la función esférica de Hankel h0(1), se deduce de inmediato que:
Procediendo de la misma manera como lo hicimos en este problema, podemos obtener las formas exponenciales de las funciones de Hankel de orden uno y de orden dos:
PROBLEMA: Demuéstrese que:
Tomando las funciones esféricas de Hankel:
y sumando ambas igualdades miembro a miembro, obtenemos entonces:
Substituyendo en el lado derecho las formas exponenciales obtenidas en el problema anterior, obtenemos el resultado pedido:
Nos fijaremos ahora como objetivo el obtener el flujo total W para la parte saliente de partículas (considerado como llevándose a cabo a través de una superficie esférica cuyo centro es el núcleo de esparcimiento) para el caso específico en el cual l.=.0. Para ello, calcularemos primero el flujo por unidad de área S de la manera usual para una función de onda ψ:
Para el caso que nos ocupa, con l.=.0 en el cual el flujo es esféricamente simétrico, con un flujo puramente radial (hacia afuera, emanando de la superficie de una esfera imaginaria) sin dependencia angular alguna en los ángulos θ y φ (es decir, isotrópico), el vector tridimensional S expresado en coordenadas esféricas se reduce a su componente radial Sr, lo cual nos permite llevar a cabo el reemplazo:
De este modo, la expresión a ser evaluada se reduce a:
La función de onda en cuestión debe ser igual (por el método matemático de separación de variables) al producto de una parte radial y una parte angular (la cual es en cierto modo trivial para el caso l.=.0). Habíamos dicho arriba que la parte saliente de la función de onda está dada por:
mientras que la parte angular para el caso l.=.0 está dada por la armónica esférica Y00, o bien puesto de otro modo:
Entonces, por substitución directa:
Por un lado, sabemos que siendo Y00 simplemente igual a la constante numérica 1/√4π (no habiendo dependencia angular alguna), razón por la cual:
Además, puesto que la función esférica de Hankel h0(2) es el conjugado complejo de la función esférica de Hankel h0(1), juntando esto con lo anterior se tiene por lo tanto:
Es necesario desarrollar la expresión que tenemos dentro de los paréntesis cuadrados, para lo cual recurriemos a las definiciones de las funciones esféricas de Hankel (los términos mostrados en color magenta se eliminan en pares):
En este punto, y para poder continuar simplificando lo que tenemos entre paréntesis, recurrimos a las expresiones trigonométricas de las funciones de Bessel y Neumann de orden cero, con lo cual:
Por lo tanto, el flujo radial (hacia afuera) de partículas por unidad de área superficial está dado por:
Por lo tanto, el flujo total W de partículas para la parte saliente (considerado como llevándose a cabo a través de una superficie esférica de radio r cuyo centro es el núcleo de esparcimiento) es:
Este resultado que hemos obtenido es válido cuando el momento angular de las partículas que forman parte del haz incidente es igual a cero, o sea para la onda esférica parcial para la cual l.=.0 ó la onda parcial-0. El siguiente paso consiste en usar lo anterior como punto de partida para obtener resultados que sean válidos para cualquier valor de l, o sea para la onda parcial-1 (onda parcial para l.=.1), la onda parcial-2 (onda parcial para l.=.2), etc., siendo igualmente válido el referirnos a cada una de estas ondas parciales como la l-onda parcial; cada valor de l representa la l-onda parcial.
Para el caso general, o sea para todos los valores de l y no únicamente para l.=.0, podemos recurrir a los operadores clase T (tal vez encuentre el lector conveniente en este punto darle un repaso a las entradas tituladas “Los operadores clase T” y “La partícula libre”) para generar otras soluciones además de las soluciones dadas arriba. El operador del momentum P.=.-iħ∇ conmuta con el Hamiltoniano, y el operador:
P+ = Px + iPy
es un operador de clase T+. Como ya se vió previamente en las entradas citadas, el operador P+ operando sobre una eigenfunción de L2 con m.=.l da lugar a una nueva eigenfunción de ambos operadores con los sub-índices de ambos operadores elevados en una unidad. Puesto que P+ conmuta con H, la función que resulta también es una eigenfunción de H. De este modo, la función:
es también una solución a las eigenecuaciones de H, Lz y L2. Puesto que ψk00 es una función únicamente de r, esto puede ser escrito de la siguiente manera:
Omitiendo los factores de normalización, esto es:
De este modo, la función general radial que estábamos buscando puede ser escrita como (el signo ha sido seleccionado para estar en conformidad con la definición usual que se le dá a la función esférica de Bessel):
Todas las funciones singulares de Bessel y de Hankel pueden ser generadas de la misma manera substituyendo la expresión singular que aparece en el lado derecho de la relación anterior, la cual puede ser tomada como la definición matemática formal de dichas funciones. Por la manera en la cual estas funciones son generadas, resulta obvio que dichas funciones satisfacen la ecuación radial dada arriba:
que puede ser simplificada para dar:
Las funciones esféricas de Bessel (al igual que las funciones esféricas de Neumann) son las mismas que ya se han definido en las entradas previas, siendo dichas funciones para los primeros tres valores de l:
Conforme el orden de las funciones esféricas de Bessel aumenta, los valores de x en los cuales la función difiere apreciablemente de cero también aumentan. Para valores radiales pequeños, la función de Bessel puede ser evaluada con la aproximación asintótica:
Una expresión conveniente para una función de onda ψklm que corresponde a valores definitivos y mutuamente compatibles del operador Hamiltoniano de energía H y los operadores del momento angular L2 y Lz (a través de los tres números cuánticos k, l y m respectivamente) es la siguiente que está basada en las funciones esféricas de Bessel:
Esto es normalizado de modo tal que el flujo radial total W hacia afuera (o hacia adentro, según sea el caso) de partículas sea:
El flujo total W de la parte saliente, para cuyo cálculo utilizamos la superficie de una esfera de gran tamaño (lo cual equivale a tomar la aproximación r.→.∞), está dado por la relación anterior, en donde:
En esta expresión se está adoptando la siguiente simbolización:
mediante la cual con un signo (+) usado como super-índice para la función de onda se está representando la parte saliente (hacia afuera, emanando del origen) de un flujo de partículas, siendo esto la parte radial una función de Hankel del tipo que usualmente se define con un super-índice (1). En contraste, adoptamos la simbolización:
mediante la cual con un signo (-) usado como super-índice para la función de onda se está representando la parte entrante (hacia adentro, dirigida hacia el origen) de un flujo de partículas, siendo esto la parte radial una función de Hankel del tipo que usualmente se define con un super-índice (2). En efecto, ψ+ representa una fuente de partículas:
mientras que ψ- representa un sumidero de partículas:
La integración de la expresión:
se debe llevar a cabo sobre todos los elementos infinitesimales de ángulos sólidos a un radio fijo. El flujo Sr es evaluado en forma más conveniente en la región asintótica para valores grandes de r. Por lo que vimos previamente en las entradas relativas al esparcimiento de las ondas de luz y los aspectos matemáticos de las ondas esféricas, sabemos ya que las expresiones asintóticas para las funciones esféricas de Bessel y Neumann cuando se les considera unidimensionalmente para el eje-x de las abcisas en un sistema de coordenadas Cartesianas son:
Estas mismas expresiones, cuando la distancia que está siendo considerada es una distancia radial r, se pueden reescribir con un sencillo cambio notacional:
De acuerdo con estas relaciones asintóticas, para valores grandes de l (suficientemente mayores que l), se tiene que el flujo radial (saliente, hacia afuera) W de partículas es independiente del número cuántico l y está dado por la relación que obtuvimos anteriormente arriba:
Hemos visto en las entradas previas que una onda plana puede ser representada mediante una expansión infinita en términos de una suma de ondas esféricas, funciones precisamente de la forma:
que constituyen un conjunto completo de funciones. Resulta conveniente simplificar un poco las cosas tomando la onda plana como una onda que se propaga en la dirección del eje-z; con lo cual la función de onda es independiente del ángulo φ (esto supone una simetría esférica), y la expansión de una onda plana eikz en función de ondas esféricas consistiendo únicamente de términos con m.=.0:
El problema fundamental en la evaluación de una onda plana eikz en función de una suma infinita de ondas esféricas se reduce a la evaluación de los coeficientes cl de la expansión para eikz. Esto se puede lograr si la expansión para eikz se multiplica en ambos lados por Yl’0 y se lleva a cabo la integración sobre todos los elementos infinitesimales de ángulo sólido para un radio fijo r:
El símbolo Σ de la sumatoria es intercambiable con el símbolo ∫ de la integral, y siendo cl una constante y cl y jl.(kr) independiente de los ángulos θ y φ estos se pueden sacar fuera de la integral, teniendo entonces:
El propósito de lo anterior es aprovechar el hecho de que las armónicas esféricas Ylm, al ser definidas en función de polinomios de Legendre que son ortogonales, también son ortogonales, siendo la relación de ortogonalidad:
Haciendo l’.=.l y m.=.0 en esta relación de ortogonalidad, se puede ver que (recuérdese que las armónicas esféricas Ylm, convencionalmente, están normalizadas):
Enunciado con mayor claridad y poniendo los límites de la integración sobre un ángulo sólido Ω que abarque todo el espacio dentro de una esfera, así como expresando el elemento infinitesimal de ángulo sólido dΩ en coordenadas esféricas -o sea sen(θ)dθdφ-, lo anterior es lo mismo que:
Ahora bien, en virtud de la ortogonalidad de las armónicas esféricas, la sumatoria en la que estamos trabajando se reduce a un solo término de la sumatoria quedando los demás términos eliminados. Para poder apreciar esto mejor, considérese l’.=.2, l variable y m’.=.m.=.0. Entonces en la siguiente expansión todos los términos destacados en color magenta se nulifican quedando como único término aquél para el cual l’.=.l.=.2:
Nuestra expresión viene quedando entonces del siguiente modo (eliminándose el símbolo Σ):
Ahora bien, como se vió en las entradas concernientes a los operadores escalera del momento angular, podemos obtener Ylm de Yll mediante la aplicación repetida del operador escalera de descenso L- del momento angular mediante la siguiente relación:
Puesto que en nuestro análisis de problemas de esparcimiento estamos suponiendo una simetría azimutal para la cual necesariamente m.=.0, la relación anterior se reduce a:
Tomando el conjugado complejo de esto último, podemos escribir lo anterior de la siguiente manera:
Antes de continuar adelante, vale la pena hacer hincapié en el hecho de que el super-índice l en el operador escalera es un exponente que indica que dicho operador se aplica l veces sobre el operando que tiene a su derecha, trátese de un operador escalera de ascenso:
o de un operador escalera de descenso:
Por otro lado, y recordando la condición que debe cumplir un operador mecánico-cuántico Q para que sea Hermitiano (usamos aquí el símbolo dr para representar un elemento infinitesimal de volumen):
entonces, por la forma en la que están definidos los operadores escalera de ascenso y descenso del momento angular L, ambos son operadores Hermitianos y de hecho:
Con esto en mente, la expresión en la que estamos trabajando y que puede ser escrita de la siguiente manera (el símbolo integral sencillo sigue representando aquí una doble integración llevada a cabo sobre un elemento de ángulo sólido):
se puede volver a escribir de la siguiente forma aplicando la esencia misma de la definición de Hermiticidad (nótese que en lugar de un operador escalera de descenso aplicado l veces tenemos un operador escalera de ascenso aplicado l veces sobre el operando que se encuentra a su derecha):
Obsérvese que lo que hemos hecho aquí es aplicar repetidamente (l veces) la definición del concepto de Hermiticidad, que equivale a establecer las siguientes correspondencias (bajo un símbolo de integración):
Por otro lado, vimos también que Yll está dado por:
de lo cual, al tomar el conjugado complejo de Yll se tiene (obsérvese el cambio en el signo del exponencial eilφ):
Podemos substituir esto en la expresión en la que hemos estado trabajando. Por otro lado, y para continuar con la evaluación simbólica de todo lo que tenemos bajo el signo integral, podemos reemplazar el operador escalera de ascenso L+ por lo siguiente que ya hemos obtenido y hemos estado utilizando desde que empezamos a trabajar con los operadores escalera del momento angular:
Esto implica que al aplicar l veces el operador escalera L+ se generará (ħ)l que cancelará y eliminará el mismo (ħ)l que tenemos en el denominador de la fracción multiplicativa que aparece fuera de la expresión integral en la que estamos trabajando. Por otro lado, al aplicar l veces el operador escalera L+ se generará también eilφ que cancelará y eliminará el exponencial e-ilφ que tenemos dentro del símbolo integral; y al no haber funciones de φ dentro del símbolo integral podemos proceder adelante con la integración que corresponde a φ sobre toda su extensión:
reduciendo la doble integral a una integral sencilla llevada a cabo sobre el operando de θ, eliminando a la variable φ del panorama. Esto a su vez implica que en la aplicación repetida l veces del operador escalera L+ la diferenciación parcial con respecto a φ se desprecia. Por ejemplo:
De este modo, el operador escalera aplicado l veces sobre el operando a su derecha tendrá el siguiente efecto:
Aún con la simplificación indicada al haber eliminado del panorama la diferenciación parcial con respecto a φ, una aplicación posterior repetida de este operador escalera L+ eventualmente genera primero dos términos, después cuatro términos, después ocho términos, y así sucesivamente, saliendo aparentemente fuera de control. Sin embargo, si en cada caso se va llevando a cabo la integración con respecto a θ, se encuentra que al ir tomando límites todos los términos se van eliminando excepto el término que involucra a sen2l(θ) que a su vez multiplica el término sen(θ) que vino de la inclusión del elemento diferencial dΩ en coordenadas esféricas (la corroboración de esto es tedioso y prolongado, razón por la cual se omitirán los detalles matemáticos), y lo que viene quedando después de la aplicación repetida l veces del operador L+ sobre el operando es la siguiente relación ridículamente sencilla:
De este modo, simplificando la expresión (que es ahora una integral sencilla al haber integrado a la variable φ a 2π) y usando las siguientes simplificaciones:
con un poco de álgebra adicional llegamos a lo siguiente:
Para quienes tienen entrenamiento formal previo en matemáticas les será obvio al inspeccionar la relación obtenida que es evidente que en el lado derecho tenemos una forma para generar una función esférica de Bessel. Resulta conveniente evaluar esto último en el límite asintótico r.→.0. En particular, puesto que:
la integral que aparece en el lado derecho de la expresión toma la forma:
Esta integral puede ser evaluada como una función Beta. De las tablas de integrales, se tiene que:
Haciendo n.=.2l+1, la integral toma la forma:
Obsérvese que estamos usando una notación matemática sobre la cual no debe de haber confusión alguna. Antes de continuar adelante, daremos un repaso a un concepto usado frecuentemente pero sobre el cual hay muchas confusiones en virtud de que casi nunca se le cubre con el detalle con el cual debería ser explicado, el concepto de los factoriales dobles, los cuales se definen de la siguiente manera:
Compárense cuidadosamente estas dos definiciones con la definición usual dada al factorial ordinario que se simboliza como n! Los factoriales dobles están relacionados a los factoriales ordinarios mediante las siguientes expresiones:
Ambas relaciones son fáciles de verificar. Por ejemplo, para n.=.5:
PROBLEMA: Demuéstrese que:
Para la primera relación, se tiene:
Podemos usar este resultado que acabamos de obtener para demostrar la segunda relación:
Habiendo obtenido una solución para la integral que teníamos arriba en el lado derecho de la expresión, podemos ir al lado izquierdo de la expresión yendo también al límite r.→.0, para lo cual recurrimos a la definición convencional de la aproximación asintótica de la función esférica de Bessel dada arriba:
reemplazando el argumento por kr:
y reescribiendo esto último usando en el denominador la definición del factorial doble:
Teniendo las expresiones asintóticas para r.→.0 tanto en el lado izquierdo como en el lado derecho de la expresión en la que hemos estado trabajando, estamos por fin en condiciones de poder obtener la constante cl que estabamos buscando desde un principio:
Estos son los coeficientes cl que estabamos buscando desde un principio para la evaluación de los coeficientes cl de la expansión de una onda plana eikz en función de ondas esféricas. Por lo tanto, la expansión de una onda plana eikz en función de una suma infinita de ondas esféricas está dada por la siguiente expresión:
Hemos visto también con anterioridad queYl0 puede ser expresada como un polinomio de Legendre:
Por lo tanto, substituyendo esto último en la expresión anterior, llegamos finalmente al siguiente resultado importante:
Hemos obtenido esta relación usando exclusivamente las herramientas y los conceptos de la Mecánica Cuántica. Sin embargo, obsérvese que es exactamente el mismo resultado que obtuvimos previamente en la entrada titulada “Esparcimiento de las ondas de luz” haciendo uso de las herramientas de la electrodinámica clásica. En efecto, hemos “absorbido” al electromagnetismo clásico dentro de la Mecánica Cuántica. Y aunque la relación fue obtenida con la ayuda de aproximaciones asintóticas, la relación en sí es una relación exacta y válida para todos los valores de l. Podemos tomar esto como una evidencia adicional, además de las muchas otras que ya tenemos, sobre la consistencia interna y el alcance de los conceptos de la Mecánica Cuántica. Ahora bien, puesto que la función esférica de Bessel para cada onda-l se puede expresar en base a las funciones de Hankel:
podemos extraer de inmediato otra conclusión importante: cada una de las ondas parciales esféricas en la expansión obtenida consiste de una parte entrante (un sumidero) y una parte saliente (una fuente).
Ahora bien, de las siguientes dos ecuaciones:
podemos obtener el flujo de probabilidad Wl para la l-onda parcial, para lo cual tenemos que distinguir cuidadosamente la parte angular de la segunda relación (lo cual haremos con color magenta) separándola de la parte radial:
De este modo (usando la coloración usual azul y roja para distinguir una función de onda de su conjugado complejo), se tiene:
Sabemos por lo que hemos visto previamente en otras entradas que la magnitud del flujo de densidad de probabilidad para una onda plana es:
El cociente (o la razón) de estos dos flujos de probabilidad es entonces:
Llamamos a σl la sección transversal para la l-onda parcial. Físicamente, es el área efectiva en torno al origen del sistema de coordenadas que es atravesada por una partícula que se encuentre en el estado-l del momento angular. Podemos obtener la misma expresión de una manera que pudiéramos considerar en cierto modo “clásica”. Para esto, considérese una partícula con un momentum p.=.ħk que clásicamente pase a una distancia √l(l+1)/k si el cuadrado de su momento angular es l(l+1)ħ2. Si suponemos que el área de un anillo anular con un radio interno igual a:
y con radio externo igual a:
es el “blanco de tiro” σl para aproximarse al origen del centro de esparcimiento cuando la partícula se encuentra en un estado de momento angular k, entonces:
Los últimos dos pasos en la obtención de esta expresión para σl los podemos ilustrar con la siguiente figura que nos muestra la sección transversal en su forma “clásica” para el haz de partículas que se encaminan hacia un centro de esparcimiento con un parámetro de impacto tal que el cuadrado de su momento angular es l(l+1)ħ2:
Hasta este punto hemos considerado únicamente funciones de onda para una partícula libre. Supóngase ahora que hay un dispersor esféricamente simétrico ubicado en el origen. Los operadores del momento angular conmutan con el operador Hamiltoniano H, y por lo tanto la l-onda parcial entrante es reflejada hacia afuera como el mismo tipo de onda, esto es, no hay esparcimiento de partículas fuera de sus estados de momento angular. Considérese la onda esférica entrante:
Al no haber un dispersor ubicado en el origen, esta función de onda se colapsa sobre el origen convirtiéndose en la onda esférica saliente:
Cuando se coloca un dispersor esféricamente simétrico en el origen, y suponiendo que en el centro no hay absorción alguna de partículas incidentes, el único efecto que puede tener el dispersor es el de producir un desplazamiento de fase en la onda saliente. Con el dispersor presente, la onda saliente se vuelve entonces:
El desplazamiento de fase δl está relacionado con la interacción con el núcleo dispersor, como veremos después en mayor detalle.
Haciendo uso de las funciones de Hankel, y suponiendo que no hay un dispersor de partículas ubicado en el origen, la expansión dada arriba de la onda plana se puede escribir del siguiente modo:
Cuando hay un dispersor de partículas puesto en el origen, las ondas salientes son desplazadas en fase, y la función de onda es entonces:
De este modo, el efecto del dispersor consiste en producir una onda esparcida saliente:
además de la onda incidente original. Obsérvese que el flujo total saliente de la l-onda parcial es el mismo con o sin un dispersor puesto en el origen, pero ahora la onda saliente ha sido dividida en dos partes: la onda esparcida y la parte saliente de la onda plana incidente.
De la ecuación que hemos obtenido para ξ, el flujo de probabilidad saliente para la l-onda esparcida es igual al flujo entrante de la l-onda parcial multiplicado por el factor:
Por lo tanto, la sección transversal de esparcimiento σl(e) hacia la l-onda parcial, de la ecuación:
viene siendo:
con lo cual la sección transversal total de esparcimiento es:
Este es esencialmente otro resultado que ya obtuvimos en la entrada titulada “Esparcimiento de las ondas de luz”. La sección transversal de esparcimiento máxima ocurre cuando el desplazamiento de fase del esparcimiento es ±π/2, ±3π/2, ..., y es cuatro veces más grande que la entrada de la sección transversal de entrada. Esto dá lugar a una aparente paradoja, ya que hasta cuatro tantos más de partículas pueden ser esparcidas en la l-onda parcial como partículas que llegan al esparcidor con este momento angular. Este comportamiento paradójico está relacionado al esparcimiento sombra y la manera en que se define la onda esparcida.