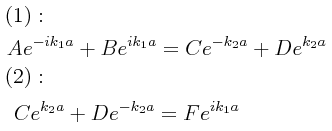La solución del caso idealizado desde el aspecto ondulatorio mediante la ecuación de Schrödinger procede de la misma manera que todos los demás casos de transmisión y reflexión de partículas: subdivimos la región de estudio en regiones dentro de las cuales el potencial se mantiene constante, y tras esto “pegamos” las soluciones de cada región apelando al requerimiento obligatorio de que en cada interfaz en donde hay un cambio de potencial la función de onda debe ser continua al pasar de una región a otra, al igual que la primera derivada de la función de onda también debe ser continua en el punto de encuentro en la interfaz de dos regiones.
PROBLEMA: Encuéntrense los coeficientes de transmisión y reflexión de una barrera finita de potencial rectangular especificada de la siguiente manera:
para una situación en la que la energía de las partículas que están incidiendo desde la izquierda sobre la barrera de potencial es menor que la energía potencial de la barrera, o sea E<V0. Asimismo, investíguese el comportamiento del coeficiente de transmisión tanto para la situación en la cual se varía la anchura de la barrera como para la situación en la cual varía E-V0 .
En este caso, tenemos las siguientes tres regiones que deben ser tomadas en consideración:
La colocación más apropiada de las coordenadas de la energía potencial V(x) en función de la coordenada horizontal de acuerdo al planteamiento del problema es la siguiente:
La ecuación de Schrödinger independiente del tiempo para las regiones |x| > a (región 1 y región 3) en donde la energía potencial es igual a cero a está dada por:
Y en lo que cabe a la región intermedia (la región 2), en donde la energía de la partícula es menor que la energía potencial V0 de la barrera, la ecuación de Schrödinger independiente del tiempo para esta región |x| < a es igual a:
Entonces, hablando desde el punto de vista estrictamente matemático, las soluciones a la ecuación de Schrödinger fuera de la barrera (regiones 1 y 3) son del tipo:
mientras que las soluciones a la ecuación de Schrödinger dentro de la barrera (región 2) son del tipo:
La solución matemática más general a la ecuación que corresponde a la región 1 es:
La solución matemática más general a la ecuación de onda que corresponde a la región 2 es:
Por último, la solución matemática más general a la ecuación de onda que corresponde a la región 3 es:
De este modo, en su forma más general, los flujos posibles de partículas para las regiones bajo consideración serán los siguientes:
De acuerdo con lo que hemos visto anteriormente al introducir por vez primera a la ecuación de Schrödinger, la función de onda de una partícula viajera libre que se está desplazando hacia la derecha está dada por una relación como la siguiente:
mientras que la función de onda de una partícula viajera libre que se está desplazando hacia la izquierda está dada por una relación como la siguiente:
Puesto que todas las partículas están incidiendo desde la izquierda sobre la barrera de potencial y no hay fuentes de partículas en la región x>+, como tampoco hay fronteras que produzcan ondas de materia reflejadas moviéndose hacia la izquierda para x>+a, debemos darle a la amplitud G un valor de cero, con lo cual la función de onda para la región # 3 es simplemente:
Las condiciones de frontera (boundary conditions) en la interfaz que hay entre la región 1 y la región 2 así como la interfaz que hay entre la región 2 y la región 3 nos dictan que la función de onda debe ser continua al pasar de una región a otra, del mismo modo que la primera derivada de la función de onda también debe ser continua en el punto de encuentro en la interfaz de dos regiones. Estos requerimientos, enunciados matemáticamente, son los siguientes:
Por lo tanto, somos llevados en forma directa al siguiente conjunto de ecuaciones:
Podemos combinar las ecuaciones (1) y (3) para eliminar el coeficiente D:
Despejando para B:
En forma semejante, podemos volver a combinar las ecuaciones (1) y (3) para eliminar el coeficiente C:
Despejando para nuevamente para B:
Por otro lado, podemos combinar las ecuaciones (2) y (4) para obtener una expresión para el coeficiente C en función del coeficiente F:
Despejando para C:
Del mismo modo, podemos combinar nuevamente las ecuaciones (2) y (4) para obtener una expresión para el coeficiente D en función del coeficiente F:
Despejando para D:
Usando la ecuación (7) en la ecuación (5) tenemos entonces:
Del mismo modo, usando la ecuación (8) en la ecuación (6):
Igualando las ecuaciones (9) y (10) tenemos lo siguiente:
Simplificando un poco:
Hágase:
Entonces:
Regresando las variables temporales p y q a sus valores originales:
A continuación, podemos tomar la magnitud absoluta de ambos miembros de la igualdad anterior, tomando en cuenta de que para cada lado respectivamente se aplican las relaciones:
Entonces:
Usando la relación hiperbólica:
cosh²(x) - senh²(x) = 1
se tiene entonces:
Pero el coeficiente de transmisión T está definido como el cociente |F|²/|A|² del flujo total de partículas transmitidas (que atraviesan la barrera de potencial moviéndose hacia la derecha) al flujo total de partículas incidentes. Substituyendo las relaciones para k1 y k2 vemos que:
con lo que finalmente tenemos:
La penetración de una barrera de potencial cuando la energía potencial V0 es mayor que la energía E de la partícula es algo que no puede suceder en el ámbito de la física clásica, en donde la partícula incidente siempre rebota elásticamente sin atravesarla. Estamos aquí frente a un fenómero puramente cuántico.
En la siguiente figura tenemos una ilustración de cómo las soluciones matemáticas a las tres regiones de interés, una vez “pegadas”, proporcionan la solución ondulatoria al problema de la penetración de una barrera por una onda de materia:
En el exterior de la barrera, tenemos funciones de onda de tipo senoidal, mientras que en el interior de la barrera tenemos un decaimiento exponencial que generará una onda de menor amplitud que la onda que incidió desde el lado izquierdo de la barrera.
Podemos obtener una mejor perspectiva de lo que está sucediendo al tomar aproximaciones si preparamos unas gráficas del coeficiente de transmisión T con E<V0 conforme variamos la anchura de la barrera de potencial mientras mantenemos fijo el potencial V0, y conforme variamos el potencial V0 mientras mantenemos fija la anchura de la barrera.
En un esfuerzo por obtener algunos resultados realistas, utilizaremos energías de reposo mc² estandarizadas. En particular, para la masa m de la partícula utilizaremos la energía de reposo aproximada de una partícula α, o sea mc² = 3758 MeV. Esto nos permite utilizar el valor ħc.=.197.3 MeV-F (unidad de longitud en fermis) directamente en las fórmulas para T. Supondremos que la energía de la partícula es E = 5 MeV.
Examinemos primero el caso en el cual mantenemos fijo a un valor constante al potencial V0 = 15 MeV con E<V0. Para una anchura de la barrera igual a cero en el cual a = 0 (no hay barrera de potencial alguna) tendremos una transmisión perfecta de todas las partículas. Conforme la anchura de la barrera de potencial va en aumento (en este caso, cuando se acerca a 1 fermi) el coeficiente de transmisión cae hasta haber una reflexión casi total de partículas para todos los fines prácticos:
Por otro lado, para una barrera de potencial con una anchura fija tomando el valor a = 0.5 fermi, conforme la altura V0 de la barrera de potencial es reducida el coeficiente de transmisión T se acerca a la unidad indicando una transmisión casi total.
Este tipo de problema de penetración a través de una barrera de potencial en donde clásicamente no puede haber transmisión alguna de partículas sólidas es de importancia fundamental para la explicación de fenómenos tales como el fenómeno del decaimiento radioactivo, la base fundamental de la física nuclear, del cual el caso más conocido y el primero en ser estudiado a fondo es el decaimiento de partículas alfa en el cual una partícula alfa (compuesta por dos protones y dos neutrones) es expulsada espontáneamente del núcleo atómico:
La teoría de la penetración de una barrera de potencial por partículas actuando como ondas de materia fue utilizada por George Gamow en 1928 para explicar la enorme variación en la vida media de decaimiento α. En general, entre menor sea la energía de la fuente radioactiva de partículas α, tanto mayor será la vida media de las partículas. Las energías de partículas α obtenidas de fuentes radioactivas naturales tienen un rango de variación entre 4 MeV y 7 MeV, mientras que las vidas medias tienen un rango de variación entre 10-6 segundo y 1010 años. Gamow supuso que el núcleo atómico puede ser considerado como un pozo de potencial como el siguiente conteniendo una partícula α, descrito en su exterior por un potencial Coulómbico clásico:
Para un radio interior menor que el radio R del núcleo, la partícula α es atraída y retenida por la fuerza nuclear, mientras que fuera del núcleo la fuerza nuclear es considerada insignificante y el potencial está dado por la ley de Coulomb V(r) = KZze²/r, en donde Ze es la carga eléctrica nuclear y ze es la carga eléctrica de la partícula α. Dentro del núcleo, se considera que la partícula α rebota (oscila) de un lado a otro siendo reflejada por la barrera de potencial en su pared r = R. Tomando el radio del núcleo como R = 10 fermis = 10-14 metro, para una partícula puntual α de carga ze a una distancia de 10 fermis del núcleo de carga Ze la energía de Coulomb KZze²/r es de aproximadamente 28 MeV para un número atómico Z = 100, claramente fuera del rango de energías de entre 4 MeV y 7 MeV de las partículas α que son expulsadas fuera del núcleo. Clásicamente, la partícula α jamás podría escapar puesto que su energía total es menor que la energía potencial de la barrera. Sin embargo, si la partícula α es considerada como una onda de materia, entonces hay una pequeña probabilidad de que la partícula α se podrá fugar a través de la barrera de potencial sin ser reflejada en la pared de la barrera. Aún sin conocer prácticamente nada acerca de lo que ocurre en el interior del núcleo atómico, podemos estimar la velocidad de la partícula α en el interior del núcleo recurriendo al principio de incertidumbre, y tomando la relación de Louis de Broglie para usar la aproximación mv ≈ ħ/R, obtenemos una velocidad interior aproximada de v ≈ 107 metros/seg. Suponiendo que la partícula α rebota en el interior de la barrera con esta velocidad, entonces golpeará la barrera con una frecuencia:
v/2R ≈ (107 metros/seg)/[2(10-14 metro)] ≈ 1022 veces/segundo
Si la barrera de potencial fuese rectangular como lo muestran las figuras de arriba, la probabilidad de penetración en cada intento sería proporcional a e-2ka siendo a la anchura de la barrera que corresponde a la energía E de la partícula α. La probabilidad por segundo de escapar sería entonces:
La vida media será entonces:
Aún suponiendo que en el exterior el potencial es Coulómbico, los cálculos en realidad son más elaborados en virtud de que, fuera de la barrera de potencial, el exponente ka debe ser reemplazado por:
Este tipo de evaluaciones, al carecer de una solución exacta, requiere forzosamente de algún tipo de aproximación, como la aproximación WKB. Sin entrar en mayores detalles, podemos ver aquí cómo una pequeña variación en la energía E de la partícula conducirá a una gran variación en la vida media τ de la partícula, porque la energía E al igual que la distancia exterior rext que estará prefijada por la intersección de la energía de la partícula con la curva exterior del potencial Coulómbico aparecen en el exponente de la vida media τ de la partícula. A modo de ejemplo, para una energía igual a 4 MeV se tiene que rext es igual a unos 70 fermis mientras que para una energía E igual a 6 MeV se tiene que rext es igual a unos 47 fermis. La vida media para E = 4 MeV está en el orden de 1010 años, o sea unos 1017 segundos. Para E = 4 MeV el factor e2[ka] debe ser alrededor de 1039 = e90 de acuerdo a la fórmula para la edad media τ dada arriba. Esto nos permite hacer un estimativo tosco de la vida media de la partícula para E = 6 MeV haciendo la cruda aproximación de que el exponente [2ka] es proporcional a la anchura exterior de la barrera dada por:
Δr = rext - R
Entonces:
Con e55 ≈ 1024 obtenemos entonces para una vida media de E = 6 MeV:
τ ≈ 10-22 · 1024 segundos ≈ 22 segundos
Aunque esta es una aproximación sumamente tosca, nos dá una explicación sobre la enorme dependencia de la vida media de la partícula en función de la energía total de la misma. Un cambio pequeño en la energía E o en el radio nuclear conduce a un cambio grande en un exponencial que a su vez se traduce en grandes cambios en la vida media. Cálculos mecánico-cuánticos más detallados muestran una dependencia exponencial de la vida media τ en la energía E que están en acuerdo excelente con los resultados experimentales, comprobando que el decaimiento α es un caso de penetración de una barrera de potencial.
Otra confirmación experimental de la penetración de una barrera de potencial es el caso del efecto Ramsauer-Townsend, consecuencia del fenómeno que ocurre cuando el tamaño 2a de la barrera es aproximadamente igual a la mitad de la longitud de onda de la partícula dentro de la barrera. La onda reflejada en x = +a ha recorrido una longitud de onda completa justo cuando regresa a x = -a. Puesto que hay una diferencia de fase de 180°, las dos ondas dentro de la barrera (la que viaja a la derecha y la que viaja a la izquierda) tienden a cancelarse (la cancelación en realidad no es completa porque las amplitudes de ambas ondas no son iguales). Esto significa que, para cierto tamaño de la barrera, habrá cierta energía de la partícula para la cual la reflexión es prácticamente igual a cero, y por lo tanto la transmisión de la partícula a través de la barrera será casi completa. Aunque los átomos no aparecen en realidad como barreras de potencial rectangulares a los electrones que inciden en ellos, los átomos de los gases nobles o inertes tienen fronteras bien definidas por su estructura electrónica de capa cerrada. La siguiente gráfica obtenida experimentalmente nos muestra las áreas transversales de dispersión en función de la energía (medida en electrón-volts) para electrones incidentes en los gases neón, kriptón, xenón y radón, mostrando claramente en el lado izquierdo que a una energía que corresponde a 1 eV el área de sección transversal se desploma correspondiendo a una transmisión casi perfecta de partículas (electrones):
La penetración de una barrera no es una propiedad exclusiva de las ondas de materia. También se dá en el caso de las ondas electromagnéticas. Un experimento relativamente fácil de llevar a cabo con dos prismas y un rayo láser es el siguiente:
En el arreglo mostrado arriba, un haz luminoso que entra por la izquierda en el primer prisma incide eventualmente sobre una superficie en la cual hay una interfaz de vidrio-aire. Si removemos el segundo prisma situado en el lado derecho, observaremos que a un ángulo mayor que el ángulo conocido clásicamente como el ángulo crítico el rayo luminoso es reflejado totalmente en el interior del primer prisma, y sale reflejado hacia abajo. No se observará rayo luminoso alguno en una pantalla que esté situada a la derecha. En virtud de la naturaleza ondulatoria de la luz, el campo eléctrico ε no es idénticamente igual a cero al pasar al aire, pero decrece exponencialmente a unas cuantas longitudes de onda de la superficie de salida del prisma. Pero conforme vamos acercando el segundo prisma, formando lo que es en esencia una barrera de potencial, además del rayo reflejado hacia abajo habrá un rayo de luz que se transmitirá directamente a través de la barrera y que saldrá del lado derecho del sistema formado por los dos prismas sin tocarse, un rayo de luz cuya intensidad aumentará volviendose notoria al estar separados los prismas por el grosor de una hoja delgada de papel, hasta que, cuando las dos caras opuestas de los prismas se tocan, no habrá reflexión alguna en el interior del sistema al pasar la luz a través de lo que viene siendo en esencia un “cubo de vidrio”, eliminándose en efecto la superficie reflectora interna.
La explicación mecánico-cuántica de la penetración a través de una barrera de potencial en donde clásicamente no puede haber transmisión alguna de partículas sólidas abre la puerta a la posibilidad de que una partícula que esté atrapada dentro de un pozo de potencial pueda tener una cierta probabilidad de escapar del pozo no escalando hasta la altura máxima de la barrera mediante algún suministro de energía para después caer hacia una región de menor potencial, sino atravesando la barrera en forma espontánea, lo cual dependerá fundamentalmente de la anchura de la barrera a ser atravesada, y esto es algo que sirve para explicar muchas reacciones químicas y nucleares que no sería posible explicar de otra manera: